弹簧力值计算公式

弹簧刚度系数计算公式
弹簧刚度系数是弹簧的力学性质之一，它是指单位长度或单位位移所需要的力的大小。

弹簧刚度系数的计算公式为：
k = F/x
其中，k为弹簧刚度系数，单位为N/m或N/mm；F为弹簧所受的力，单位为N；x为弹簧的变形量，单位为m或mm。

在计算弹簧刚度系数时，需要注意以下几点：
1. 弹簧的变形量应该是弹簧长度的变化量，而不是弹簧的直径
或横截面积的变化量。

2. 弹簧刚度系数的值与弹簧的形状、材料、尺寸等因素有关，
因此在实际应用中需要根据具体情况进行计算。

3. 在弹簧所受力的范围内，弹簧的变形量与所受力成正比，因
此弹簧刚度系数应该是一个常数，但在弹簧所受力超过一定范围后，弹簧的变形量将不再与所受力成正比，此时弹簧刚度系数将发生变化。

综上所述，弹簧刚度系数是一个重要的弹簧力学参数，计算公式为k = F/x，可以根据实际情况进行计算，并需要注意弹簧的形状、材料、尺寸等因素。

- 1 -。

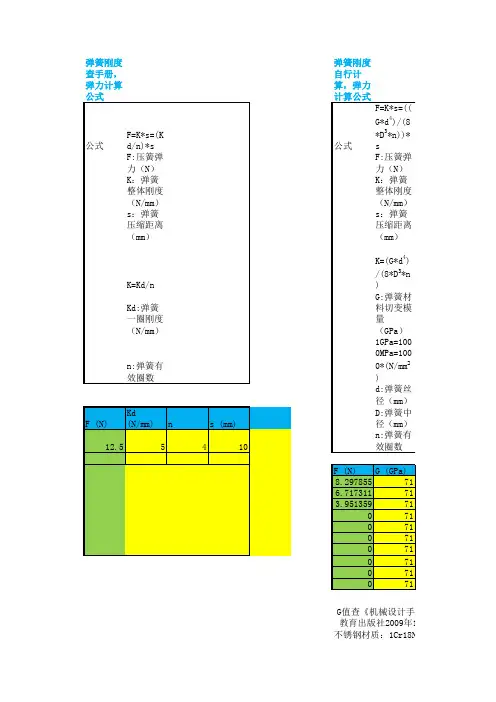
弹簧刚度查手册，弹力计算公式弹簧刚度自行计算，弹力计算公式
公式F=K*s=(Kd/n)*s公式F=K*s=((G*d4)/(8*D3*n))*s F:压簧弹力（N）F:压簧弹力（N）
K：弹簧整体刚度（N/mm）K：弹簧整体刚度（N/mm）
s：弹簧压缩距离（mm）s：弹簧压缩距离（mm）
K=Kd/n K=(G*d4)/(8*D3*n)
Kd:弹簧一圈刚度（N/mm）G:弹簧材料切变模量（GPa）
n:弹簧有效圈数1GPa=1000MP2)
d:弹簧丝径（
D:弹簧中径（mm）
n:弹簧有效圈数
G值查《机械设计手册（
教育出版社2009年1月第2版）P313，表1
不锈钢材质：1Cr18Ni9
自行计算，弹力计算公式
((G*d4)/(8*D3*n))*s
弹力（N）
K：弹簧整体刚度（N/mm）
s：弹簧压缩距离（mm）
4)/(8*D3*n)
材料切变模量（GPa）
000MPa=1000*(N/mm2)
丝径（mm）
D:弹簧中径（mm）
n:弹簧有效圈数
手册（第2版）吴宗泽 高志 主编》（高等版社2009年1月第2版）P313，表14-2 弹簧常用材料18Ni9Ti。

胡克弹性定律指出，在弹性极限范围内，弹簧的弹性力f 与弹簧的长度x 成正比，即f =-kx，k 是一个物体的质量弹性系数，该系数由材料的性质决定，负号表示弹簧产生的弹性力与其延伸(或压缩)方向相反弹簧常数: 以k 表示，当弹簧被压缩时，载荷(kgf/mm)增加1mm 的距离，弹簧常数公式(单位: kgf/mm) : k = (g d4)/(8dm3 nc) g = 钢丝的刚度模量: 钢琴丝g = 8000; 不锈钢丝g = 7300; 磷青铜丝g = 4500;黄铜丝g = 3500d = 线径= 0d = 外径= id = 内径= md = 中径= do-dn = 转速总数弹簧常数的计算例子: 线径= 2.0 mm，外径= 22 mm，总匝数= 5。

5圈，钢丝材料= 钢琴钢丝k = (gxd4)/(8xdm3xnc) = (8000x24)/(8x203x3.5) = 0.571 kg f/mmpull，张力弹簧的k 值与压力弹簧的k 值相同。

张力弹簧的初始张力: 初始张力等于拉开彼此接近的弹簧所需的力，并发生在弹簧轧制成型之后。

在制作张力弹簧时，由于钢丝材质、线径、弹簧指数、静电现象、油脂、热处理、电镀等的不同，使得各张力弹簧的初始张力不均匀。

因此，在安装各种规格的张力弹簧时，应该预张力到平行弯道之间一定距离的力称为初张力。

初始张力= p-(kxf1) = 最大载荷-(弹簧常数x 拉伸长度)扭转弹簧常数: 以k 表示，当弹簧扭转时，载荷(kgf/m)增加1个扭转角。

弹簧常数(单位: kgf/mm) : k = (exd #)/(1167 xdmxpnxr) e = 钢丝的刚度模量: 钢琴线e = 21000，不锈钢线e = 19400，磷青铜线e =11200,黄铜丝e = 11200d = 线径= 0d = 外径= id = 内径= md = 中径= do-dn = 载荷作用下转臂的总长度= 3.1416。

弹簧力值计算公式是用来计算弹簧的弹力或拉力的公式。

弹簧力值与弹簧的压缩或伸展量成正比，具体公式如下：
F = kx
其中，F代表弹簧力值，k是弹簧的刚度系数，x是弹簧的压缩或伸展量。

这个公式可以用于计算任何类型的弹簧，包括螺旋弹簧、板簧、扭簧等等。

弹簧力值与弹簧的材质、尺寸、形状等因素有关，而弹簧的压缩或伸展量则与弹簧受力后的伸长或压缩量有关。

在实际应用中，需要根据具体的弹簧类型和工况条件来确定弹簧的刚度系数k和压缩或伸展量x。

例如，对于螺旋弹簧，可以通过查阅相关手册或计算公式来得到刚度系数k的值，然后根据实际受力情况计算出压缩或伸展量x的值，最终得到弹簧力值F。

需要注意的是，弹簧力值计算公式只适用于线性弹力关系，即弹簧的弹力与压缩或伸展量成正比。

如果需要计算非线性弹力关系，则需要采用其他更复杂的公式或算法。

弹簧的劲度系数k的公式
弹簧的劲度系数k代表了弹簧所具有的弹性特性，也被称为弹簧的弹性
系数或刚度系数。

劲度系数k的公式是弹簧的弹力F和弹簧的形变量x之间
的比例关系，可以用以下公式表示：
k = F / x
其中，k表示劲度系数，单位为N/m；F表示弹力，单位为牛顿（N）；
x表示形变量，单位为米（m）。

弹簧的劲度系数k决定了弹簧恢复形变的能力，即在受力后弹簧的回弹
情况。

劲度系数越大，弹簧的回弹能力越强，也就是弹簧越硬，需要施加更
大的力才能使弹簧发生形变。

反之，劲度系数越小，弹簧的回弹能力越弱，
弹簧相对较软，只需要较小的力即可产生形变。

劲度系数k的值取决于弹簧的材料、长度、直径以及弹簧的结构等因素。

常见的劲度系数k的单位是牛顿/米（N/m），但在某些情况下，也可能使用
其他单位，如牛顿/厘米（N/cm）或牛顿/毫米（N/mm），具体取决于所使
用的单位系统。

了解弹簧的劲度系数k的公式和意义对于设计和应用弹簧的工程师和物
理学家来说是至关重要的。

通过适当选择劲度系数k，可以实现对弹簧的控
制和调节，使其在各种应用中发挥最佳的功能。

弹力系数k的计算公式弹力系数k的计算公式是描述弹簧或弹性体的弹性特性的重要参数。

在物理学和工程学中，弹簧常常用于各种机械系统中，而弹力系数k则是描述弹簧的硬度和弹性的重要指标。

弹力系数k的计算公式可以根据不同类型的弹簧或弹性体来进行推导和计算。

下面将分别介绍弹簧和弹性体的弹力系数k的计算公式。

对于弹簧而言，弹力系数k可以通过胡克定律来计算。

胡克定律指出，当弹簧受到外力作用时，其形变与受力成正比。

根据胡克定律，弹力系数k可以通过以下公式来计算：k = F / x其中，k表示弹力系数，单位是牛顿/米（N/m）；F表示施加在弹簧上的力，单位是牛顿（N）；x表示弹簧的形变量，单位是米（m）。

通过测量施加在弹簧上的力和弹簧的形变量，就可以计算出弹力系数k的数值。

对于弹性体而言，弹力系数k的计算公式则取决于弹性体的形状和材料特性。

一般来说，弹性体的弹力系数k可以通过杨氏模量来计算。

杨氏模量是描述材料刚度和弹性的重要参数，可以通过以下公式来计算：E =F / (A * Δl / l)其中，E表示杨氏模量，单位是帕斯卡（Pa）；F表示施加在弹性体上的力，单位是牛顿（N）；A表示弹性体受力部位的横截面积，单位是平方米（m²）；Δl表示弹性体的形变量，单位是米（m）；l表示弹性体的初始长度，单位是米（m）。

通过测量施加在弹性体上的力、弹性体受力部位的横截面积以及形变量，就可以计算出弹力系数k的数值。

除了以上介绍的计算公式外，还有一些特殊情况下的弹力系数k的计算公式。

例如，在液体中的弹性体或者非线性弹簧等情况下，需要根据具体情况来推导和计算相应的弹力系数k的公式。

总之，弹力系数k的计算公式是描述弹簧或弹性体的重要参数，可以通过胡克定律或者杨氏模量来进行计算。

根据具体情况，还可以推导出其他特殊情况下的计算公式。

通过测量施加在弹簧或弹性体上的力和形变量，就可以得到相应的弹力系数k的数值。

弹簧伸长量计算公式是x=F/k，k是弹性系数，有时要减去原长算力。

弹簧测力计的原理是：在弹性限度范围内，弹簧的伸长与受到的拉力成正比，由F=kx可知，弹簧的变化量：x=F/k。

弹簧伸长量：拉伸后弹簧长度-弹簧原来长度，弹簧原来长度就是在竖直方向上不挂重物时的长度或是水平方向上自由伸长的长度。

弹簧伸长量与拉力关系公式是FL=Gh，在克服重力做功相同的情况下，F与L成反比例关系。

弹簧的伸长随拉力的增大而增大，且二者的商始终不变，故得出结论：在弹性限度内，弹簧的伸长与所受的拉力成正比。

计算弹簧的伸长与拉力的比值可知：1cm2N=0.5cm/N，故每1N的间距应为0.5cm．弹簧伸长 2.5cm所挂物体的质量：m=Gg=2.5cm÷0.5cm/N10N/kg=0.5kg。

弹簧的曲度系数
弹簧系数k的计算公式为：k=（g×d^4）/（8×nc×dm^3）n/mm，其中g=线材的刚性模数，单位n/mm^2（即切变模量），d=线径（mm），d0=外径（mm）dm=中径=d0-d（mm），n=总圈数，nc=有效圈数=n-2。

劲度系数，即倔强系数（弹性系数）。

它描述单位形变量时所产生弹力的大小。

k值大，说明形变单位长度需要的力大，或者说弹簧“韧”。

劲度系数又称刚度系数或者倔强系数。

劲度系数在数值上等于弹簧伸长（或缩短）单位长度时的弹力。

在弹性限度内，弹簧的弹力可由f=kx,x为弹簧的伸长的长度；k为劲度系数，表示弹簧的一种属性，它的数值与弹簧的材料，弹簧丝的粗细，弹簧圈的直径，单位长度的匝数及弹簧的原长有关。

在其他条件一定时弹簧越长，单位长度的匝数越多，k值越小。

弹簧力值计算公式弹簧力值是指弹簧所施加的力的大小，可以通过弹簧公式来计算。

弹簧力值计算公式包括胡克定律和胡克定律的应用。

1.胡克定律胡克定律的数学表达式为：F = kx其中F是弹簧所施加的力（弹簧力值）k是弹簧的劲度系数x是弹簧的形变。

2.劲度系数劲度系数是表示弹簧刚度的物理量，它衡量了弹簧单位形变所产生的力的大小。

劲度系数可以通过实验获得，也可以通过弹簧的材料和几何形状来计算。

根据胡克定律，可以得到计算弹簧力值的公式：F = kx其中F是弹簧力值，也是弹簧所施加的力的大小k是弹簧的劲度系数x是弹簧的形变。

4.弹簧力值计算实例为了更好地理解弹簧力值的计算，下面给出一个弹簧力值计算的实例：假设弹簧的劲度系数k=100N/m，弹簧形变x=0.1m，要计算该弹簧所施加的力。

根据弹簧力值计算公式：F = kx代入已知数值：F=100N/m×0.1mF=10N所以，该弹簧所施加的力为10N。

通过上述实例，我们可以看到，弹簧力值的大小取决于弹簧的劲度系数和形变的大小。

当劲度系数较大或者形变较大时，弹簧力值也较大。

5.弹簧力值的应用弹簧力值的计算公式在很多物理和工程问题中都有应用。

例如，可以用弹簧力值来计算弹簧系统的振动频率、弹簧比例的起伏等。

总结：弹簧力值的计算公式是 F = kx，其中 F 表示弹簧力值，k 表示弹簧的劲度系数，x 表示弹簧的形变。

弹簧力值的大小取决于劲度系数和形变的大小。

弹簧力值的计算公式在物理和工程问题中有多种应用。

弹簧弹力计算公式标准化管理部编码-[99968T-6889628-J68568-1689N]弹力计算公式压力弹簧初拉力计算F0=〖｛π×d 3｝÷(8×D)〗×79mpaF0=｛×(5×5×5)÷(8×33)｝×79=117 kgf1.压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；2.弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；3.弹簧常数公式（单位：kgf/mm）；K=(G×d4)/(8×D3×Nc)G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300 ，60Si2MnA钢丝G=7900，磷青铜线G=4500 ，黄铜线G=3500d=线径(钢丝直径)D=中径N=总圈数Nc=有效圈数F=运动行程(550mm)弹簧常数计算范例：线径=5.0mm , 中径=20mm , 有效圈数=圈 ,钢丝材质=不锈钢丝K=(G×d4)/(8×D3×Nc)=(7900×54)/(8×203×=mm×(F=100)=812 kgf拉力弹簧拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧弹簧常数：以 k 表示,当弹簧被扭转时，每增加1°扭转角的负荷 (kgf/mm)弹簧常数公式（单位：kgf/mm）：K=(E×d4)/(1167×D×p×N×R)E=线材之钢性模数：琴钢丝E=21000 ，不锈钢丝E=19400 ，磷青铜线E=11200 ，黄铜线E=11200d=线径(钢丝直径)D=中径N=总圈数R=负荷作用的力臂p=。

弹簧劲度系数计算公式弹簧是一种常见的机械元件，广泛应用于各种机械设备中。

弹簧的主要作用是储存和释放能量，使机械设备具有弹性和缓冲作用。

弹簧的弹性特性与其劲度系数密切相关。

本文将介绍弹簧劲度系数的计算公式及其应用。

弹簧劲度系数是指单位长度弹簧所需的力量，使其产生单位长度的形变。

弹簧劲度系数的计算公式为：k = F / Δl其中，k表示弹簧劲度系数，单位为牛顿/米（N/m）；F表示弹簧所受的力，单位为牛顿（N）；Δl表示弹簧的形变量，单位为米（m）。

弹簧劲度系数的计算公式可以用于计算各种类型的弹簧，包括拉伸弹簧、压缩弹簧和扭转弹簧等。

在实际应用中，弹簧的劲度系数是一个重要的参数，它决定了弹簧的弹性特性和使用寿命。

弹簧劲度系数的计算方法有多种，其中最常用的方法是静态拉伸法。

该方法需要将弹簧固定在一端，另一端施加一定的拉力，然后测量弹簧的形变量和所受的力，即可计算出弹簧的劲度系数。

在实际应用中，弹簧的劲度系数还可以通过试验和模拟计算等方法进行确定。

试验方法需要使用专门的测试设备，对弹簧进行拉伸、压缩和扭转等测试，以获得弹簧的劲度系数和其他性能参数。

模拟计算方法则需要使用计算机模拟软件，对弹簧的结构和材料进行建模和分析，以获得弹簧的劲度系数和其他性能参数。

弹簧劲度系数的应用非常广泛，涉及到各种机械设备和工业生产过程。

例如，汽车悬挂系统中的弹簧需要具有一定的劲度系数，以保证车辆的稳定性和舒适性；机械加工过程中的弹簧需要具有一定的劲度系数，以保证加工精度和效率；医疗设备中的弹簧需要具有一定的劲度系数，以保证设备的安全性和可靠性等。

弹簧劲度系数是弹簧的重要性能参数之一，其计算公式和应用方法对于弹簧的设计、制造和应用具有重要的意义。

在实际应用中，需要根据具体的需求和条件选择合适的计算方法和测试方法，以获得准确的劲度系数和其他性能参数。

恒力弹簧计算公式恒力弹簧具有恒定的弹性力，无论弹簧的形变大小，弹簧回复力都保持不变。

恒力弹簧的计算公式可以通过弹簧的材料特性和几何参数来确定，具体公式如下：1.弹簧的劲度系数（弹性系数）k弹簧的劲度系数（弹性系数）k是衡量弹簧刚性的一个关键参数，它定义为单位长度变化引起的弹性力的比例系数。

劲度系数的单位为牛顿/米（N/m），表示在1米长度的弹簧上施加的力会引起弹簧的延伸或压缩。

通常情况下，恒力弹簧的劲度系数可以通过以下公式计算：k=(Gd^4)/(8N(D-d)^3)其中，k是弹簧的劲度系数（弹性系数），G是弹簧材料的切变模量，d是弹簧线径，D是弹簧外径，N是弹簧的有效圈数。

2.弹簧的材料切变模量G弹簧的材料切变模量G是衡量材料抵抗切变应力的能力。

材料切变模量通常可以通过断裂弹性模量E和泊松比v来计算：G=E/(2(1+v))其中，E是断裂弹性模量，v是泊松比。

3.弹簧的劲度弹簧的劲度是指弹簧在单位长度的变形下所存储的弹性能量。

当弹簧被施加外力时，根据胡克定律，弹簧会产生变形，储存弹性势能。

弹簧的劲度可以通过以下公式计算：U = (1/2)kx^2其中，U是弹簧的劲度，k是弹簧的劲度系数（弹性系数），x是弹簧的变形长度。

4.弹簧的变形长度弹簧的变形长度是指施加外力后，弹簧相对于其原始未受外力状态的变化长度。

弹簧的变形长度可以通过以下公式计算：x=(F/k)-L其中，x是弹簧的变形长度，F是施加在弹簧上的外力，k是弹簧的劲度系数（弹性系数），L是弹簧的原始长度。

这些是恒力弹簧计算的主要公式，根据公式可以确定弹簧的劲度系数、材料切变模量、劲度和变形长度，并进一步计算弹簧在各种应力情况下的性能。

在实际工程中，根据具体要求和参数，通过这些公式可根据设计需求来计算弹簧的性能参数。

压力弹簧力度计算器及计算公式
k=(Gd^4)/(8nD^3)
其中，k为弹簧力度（N/m），G为剪切模量（Pa），d为线径（m），n为有效圈数（个），D为直径（m）。

在实际应用中，可以使用压力弹簧力度的计算器来方便快速地计算压
力弹簧的力度。

以下是一个步骤简单的压力弹簧力度计算器的设计示例：
1.接收输入数据
-输入弹簧的剪切模量G、线径d、有效圈数n和直径D的数值。

-验证输入数据的有效性，例如检查是否为非负数、是否满足一定的
范围条件等。

2.进行计算
-根据上述公式，利用输入的数值计算弹簧力度k的值。

-注意在计算过程中要进行单位换算，确保输入和输出的单位一致。

3.显示结果
-将计算得到的弹簧力度k的值以合适的格式显示给用户。

-可以选择显示在计算器界面上，或者输出到外部设备。

4.提供重置功能
-可以为计算器添加一个重置按钮，使用户可以清空上一次计算的数据，重新输入新的数据进行计算。

这样设计的压力弹簧力度计算器可以方便快速地进行压力弹簧力度的计算，提高计算的准确性和效率。

需要注意的是，压力弹簧力度的计算公式只适用于满足一定条件的弹簧，例如线材直径与弹簧直径之比要在一定范围内。

对于复杂的形状或材质特殊的压力弹簧，可能需要借助专业软件或进行试验测定力度。

总结起来，压力弹簧力度是一个重要的物理量，能够帮助我们了解弹簧的变形特性和力学行为。

通过使用压力弹簧力度计算器和计算公式，我们可以便捷地计算压力弹簧的力度，为实际应用提供参考和指导。

弹簧力的计算1.压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负2.弹簧常数：以K表示，当弹簧被压缩时，每增加1mm距离的负荷3.弹簧常数公式(单位：k=(G*d^4)/(8*MD^3*Nc)G=线材的钢性模数：琴钢丝G=8000；不锈钢丝G=7300；磷青铜线G=4500；黄铜d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2线径计扭力弹簧：1.弹簧常数：以K表示，当弹簧被告扭转时，每增加1°扭转角的负荷拉力弹簧的K值与压力弹簧的计算公式相同：被张力=P-(K×F1)=最大负荷-(弹簧常数×拉伸长度)拉力弹簧的被告张力：被张力等于适足拉开互相紧贴的弹簧所需的力，被张力在弹簧卷制成形成发生在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距的力称为初张力。

2.弹簧常数公式，(单位：kgf/mm)k=(E×d^4)/(1167×Dm×P×N×R)3.E=线材之钢性模数：琴钢丝:E=2100；不锈钢丝E=19400；磷青铜线E=11200；铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-d成发生。

拉力弹簧得每个拉力弹簧初始拉力间距的力称为初张力。

R=负荷作用的P=3.1416力臂N=总圈数Nc=有效圈数=N-2。