三角函数和反三角函数
- 格式：doc
- 大小：1.00 MB
- 文档页数：23
下载文档原格式
合集下载
三角函数与反三角函数转换
三角函数与反三角函数转换
三角函数与反三角函数是数学中的重要概念。
三角函数包括正弦、余弦、正切等，用于描述角度与三角形之间的关系。
反三角函数则是
三角函数的反函数，用于求解角度值。
下面我们来介绍三角函数和反
三角函数的相互转换。
首先是三角函数的转换。
假设有一个角度θ，那么它的三角函数可以通过正弦函数(sin)、余弦函数(cos)和正切函数(tan)来表示。
例如，θ的正弦值就是sin(θ)，余弦值就是cos(θ)，正切值就是
tan(θ)。
而反过来，如果我们已知一个三角函数的数值，想要求解对应的
角度θ，就需要用到反三角函数。
反三角函数包括反正弦函数(asin)、反余弦函数(acos)和反正切函数(atan)。
例如，如果已知一个角度的
正弦值为x，那么它的角度就可以表示为θ=asin(x)。
需要注意的是，反三角函数的结果通常是一个弧度值，而不是角度。
如果需要将弧度转换为角度，可以使用度数制与弧度制的转换公式。
在实际问题中，三角函数和反三角函数常用于解决各种几何问题、物理问题和工程问题。
它们在计算机图形学、信号处理和导航等领域
也有广泛的应用。
总之，三角函数和反三角函数之间的转换关系是数学中重要的基
本知识点，对于理解和应用三角函数有着重要的作用。
希望上述介绍
能对您有所帮助。
三角函数值与反三角函数值
三角函数值与反三角函数值三角函数是数学中常见的函数之一，它与三角形的边长和角度之间存在着密切的关系。
而反三角函数则是对三角函数的逆运算，用来求解角度。
在数学和物理等领域中，三角函数和反三角函数都有着广泛的应用。
三角函数包括正弦函数（sin）、余弦函数（cos）、正切函数（tan）等。
这些函数的值与角度之间有着明确的对应关系。
例如，对于一个角度为θ的三角形，其正弦值sin(θ)定义为对边与斜边的比值，余弦值cos(θ)定义为邻边与斜边的比值，正切值tan(θ)定义为对边与邻边的比值。
正弦函数的值域在[-1, 1]之间，在数学和物理中经常用于描述波动和振动现象。
例如，当我们观察到一种周期性的波动或振动时，可以利用正弦函数来描述其变化规律。
正弦函数的图像呈现出周期性的波形，振幅决定了波动的强度，周期决定了波动的频率。
余弦函数与正弦函数类似，也是一种周期性函数，其图像与正弦函数的图像相似，只是相位不同。
余弦函数的值域同样在[-1, 1]之间，它可以用来描述角度的变化规律。
在几何学和物理学中，经常会用到余弦函数来计算两个向量之间的夹角，或者描述物体在运动过程中的轨迹。
正切函数是另一种重要的三角函数，其定义为正弦值与余弦值的比值。
正切函数的图像呈现出周期性的波动，但与正弦函数和余弦函数不同的是，正切函数在某些点上会出现无穷大的值。
这意味着在一些特殊的角度下，正切函数的值变得非常大，甚至无法表示。
因此，在实际应用中，我们需要注意正切函数的定义域，并避免出现无意义的结果。
与三角函数相对应的是反三角函数，它是对三角函数的逆运算。
反三角函数用来求解角度，将已知的三角函数值转化为对应的角度值。
常见的反三角函数包括反正弦函数（arcsin）、反余弦函数（arccos）、反正切函数（arctan）等。
这些函数的定义域和值域与对应的三角函数相反，例如反正弦函数的定义域为[-1, 1]，值域为[-π/2, π/2]。
反三角函数在几何学、物理学和工程学等领域中有着广泛的应用。
三角函数的反函数与反三角函数计算
三角函数的反函数与反三角函数计算在数学中，三角函数是非常重要的一类函数，包括正弦函数、余弦函数、正切函数等。
而三角函数的反函数与反三角函数计算则是在解决各种三角函数相关问题时不可或缺的工具。
本文将详细介绍三角函数的反函数和反三角函数的概念，以及如何进行计算。
一、三角函数的反函数三角函数的反函数是指，通过将三角函数的值作为输入，计算出与之对应的角度。
以正弦函数为例，正常情况下我们通过给定一个角度，计算出其对应的正弦值。
而反函数则是给定一个正弦值，计算出其对应的角度。
以正弦函数sin(x)为例，其反函数记为arcsin(x)或者sin^(-1)(x)。
表示为sin^(-1)(x)=y，其中x为正弦函数的值，y表示对应的角度。
当x∈[-1,1]时，arcsin(x)存在唯一的解。
二、反三角函数的计算反三角函数包括反正弦函数（arcsin），反余弦函数（arccos），反正切函数（arctan）等。
它们的定义和使用方法如下：1. 反正弦函数（arcsin）：反正弦函数arcsin(x)的定义域为[-1,1]，值域为[-π/2,π/2]。
我们可以通过输入正弦函数的值，来计算对应的角度。
例如，如果要计算sin^(-1)(0.5)，即要求正弦函数为0.5时，对应的角度。
我们可以使用计算器或查表得到结果，arcsin(0.5)≈π/6，即30°。
2. 反余弦函数（arccos）：反余弦函数arccos(x)的定义域为[-1,1]，值域为[0,π]。
与反正弦函数类似，我们可以通过输入余弦函数的值，计算对应的角度。
例如，要计算cos^(-1)(0.5)，即要求余弦函数为0.5时，对应的角度。
可以得到arccos(0.5)≈π/3，即60°。
3. 反正切函数（arctan）：反正切函数arctan(x)的定义域为实数集，值域为[-π/2,π/2]。
我们可以通过输入正切函数的值，计算对应的角度。
例如，要计算tan^(-1)(1)，即要求正切函数为1时，对应的角度。
三角函数及反三角函数
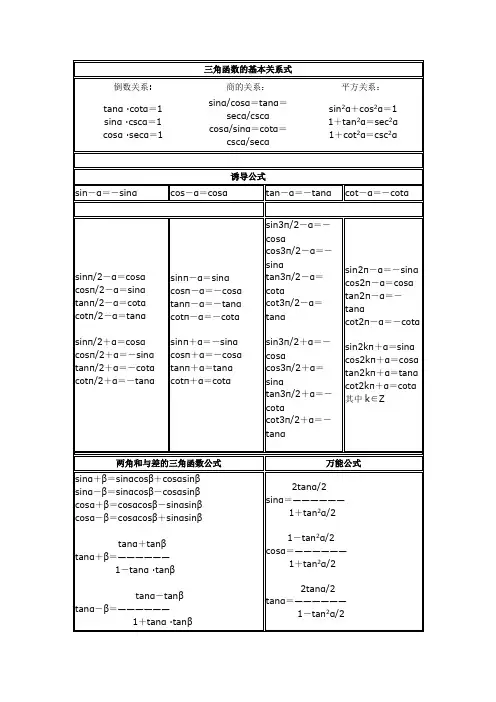
半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α＝2sinαcosαcos2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α2tanαtan2α＝—————1－tan2αsin3α＝3sinα－4sin3αcos3α＝4cos3α－3cosα3tanα－tan3αtan3α＝——————1－3tan2α三角函数的和差化积公式三角函数的积化和差公式α＋βα－βsinα＋sinβ＝2sin—－－·cos—－—2 2α＋βα－βsinα－sinβ＝2cos—－－·sin—－—2 2α＋βα－βcosα＋cosβ＝2cos—－－·cos—－—2 2α＋βα－βcosα－cosβ＝－2sin—－－·sin—－—2 2 si nα·cosβ=1/2sinα+β+sinα-βcosα·sinβ=1/2sinα+β-sinα-βcosα·cosβ=1/2cosα+β+cosα-βsinα·sinβ=-1/2cosα+β-cosα-β化asinα ±bcosα为一个角的一个三角函数的形式辅助角的三角函数的公式函数变换反三角函数三角函数的反函数;是多值函数..它们是反正弦Arcsin x;反余弦Arccos x;反正切Arctan x;反余切Arccot x等;各自表示其正弦、余弦、正切、余切、正割、余割为x的角..为限制反三角函数为单值函数;将反正弦函数的值y限在y=-π/2≤y≤π/2;将y为反正弦函数的主值;记为y=arcsin x；相应地;反余弦函数y=arccos x的主值限在0≤y≤π；反正切函数y=arctan x 的主值限在-π/2<y<π/2；反余切函数y=arccot x的主值限在0<y<π..反三角函数实际上并不能叫做函数;因为它并不满足一个自变量对应一个函数值的要求;其图像与其原函数关于函数y=x对称..其概念首先由欧拉提出;并且首先使用了arc+函数名的形式表示反三角函数;而不是f-1x.反三角函数主要是三个：y=arcsinx;定义域-1;1;值域-π/2;π/2;图象用红色线条；y=arccosx;定义域-1;1;值域0;π;图象用兰色线条；y=arctanx;定义域-∞;+∞;值域-π/2;π/2;图象用绿色线条；sinarcsinx=x;定义域-1;1;值域-π/2;π/2证明方法如下：设arcsinx=y;则siny=x ;将这两个式子代如上式即可得为限制反三角函数为单值函数;将反正弦函数的值y限在y=-π/2≤y≤π/2;将y为反正弦函数的主值;记为y=arcsin x；相应地;反余弦函数y=arccos x的主值限在0≤y≤π；反正切函数y=arctan x的主值限在-π/2<y<π/2；反余切函数y=arccot x的主值限在0<y<π..反三角函数实际上并不能叫做函数;因为它并不满足一个自变量对应一个函数值的要求;其图像与其原函数关于函数y=x对称..其概念首先由欧拉提出;并且首先使用了arc+函数名的形式表示反三角函数;而不是f-1x.1正弦函数y=sin x在-π/2;π/2上的反函数;叫做反正弦函数..arcsin x表示一个正弦值为x的角;该角的范围在-π/2;π/2区间内..2余弦函数y=cos x在0;π上的反函数;叫做反余弦函数..arccos x表示一个余弦值为x 的角;该角的范围在0;π区间内..3正切函数y=tan x在-π/2;π/2上的反函数;叫做反正切函数..arctan x表示一个正切值为x的角;该角的范围在-π/2;π/2区间内..反三角函数主要是三个：y＝arcsinx;定义域-1;1 ;值域-π/2;π/2图象用红色线条；y=arccosx;定义域-1;1 ; 值域0;π;图象用蓝色线条；y=arctanx;定义域-∞;+∞;值域-π/2;π/2;图象用绿色线条；sinarcsin x=x;定义域-1;1;值域-1;1 arcsin-x=-arcsinx证明方法如下：设arcsinx=y;则siny=x ;将这两个式子代入上式即可得其他几个用类似方法可得cosarccos x=x; arccos-x=π-arccos xtanarctan x=x; arctan-x=-arctanx反三角函数其他公式arcsin-x=-arcsinxarccos-x=π－arccosxarctan-x=-arctanxarccot-x=π－arccotxarcsinx+arccosx=π/2=arctanx+arccotxsinarcsinx=x=cosarccosx=tanarctanx=cotarccotx当x∈—π/2;π/2时;有arcsinsinx=x当x∈0;π;arccoscosx=xx∈—π/2;π/2;arctantanx=xx∈0;π;arccotcotx=xx〉0;arctanx=π/2-arctan1/x;arccotx类似若arctanx+arctany∈—π/2;π/2;则arctanx+arctany=arctanx+y/1-xy。
三角函数与反三角函数公式与图像
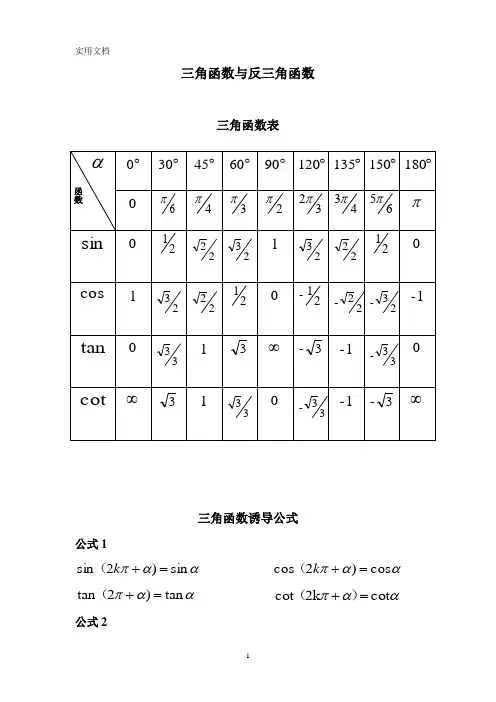
三角函数与反三角函数三角函数表三角函数诱导公式公式1ααπsin )2sin =+k （ ααπcos )2cos =+k （ααπtan )2tan =+（ ααπcot 2k cot =+）（公式2ααπ-sin sin =+）（ ααπ-cos cos =+）（ααπtan tan =+）（ ααπcot cot =+）（公式3ααsin -)-sin(= ααcos -cos =）（αα-tan -tan =）（ αα-cot -cot =）（ 公式4ααπsin -sin =）（ ααπ-cos -cos =）（ααπtan )(tan -=- ααπ-cot -cot =）（公式5ααπ-sin -2sin =）（ ααπcos -2cos =）（ααπtan )2(tan -=- ααπ-cot 2(cot =-）公式6ααπcos 2sin =+）（ ααπ-sin 2cos =+）（ ααπcot )2(tan -=+ααπ-tan 2cot =+）（ ααπcos -2sin =）（ααπsin -2cos =）（ ααπcot )2(tan =-ααπtan -2cot =）（推算公式ααπ-cos 23sin =+）（ ααπsin 23cos =+）（ααπcot )23(tan -=+ ααπ-tan 23cot =+）（ααπcos )23sin -=-（ ααπ-sin -23cos =）（ααπcot )23(tan =- ααπtan )23cot =-（三角函数公式一 基本关系式1cos sin 22=+α 1cot tan =⋅αααααcos sin tan = αααsin cos cot = 二 两角和差公式ααβαβαsin cos cos sin sin ⋅+⋅=+）（βαβαβαsin cos -cos sin -sin ⋅⋅=）（βαβαβαsin sin -cos cos cos ⋅⋅=+）（βαβαβαsin sin cos cos -cos ⋅+⋅=）（βαβαβαtan tan 1tan tan )tan(⋅-+=+ βαβαβαtan tan 1tan -tan )-tan(⋅+=三 二倍角的正弦，余弦和正切公式αααcos sin 22sin ⋅=ααααα2222sin 2-11-cos 2sin -cos cos2===ααα2tan 1tan 22tan -=四 半角正弦，余弦和正切公式）（ααcos -1212sin 2= ）（ααcos 1212cos 2+=αααcos 1cos 12tan 2+-=αααααsin cos 1cos 1sin 2tan -=+=五 三倍角正弦，余弦和正切公式ααα3sin 4-sin 33sin =αααcos 3-cos 43cos 3=ααα233tan 31tan tan 3tan --=六 万能公式2tan 12tan 2sin 2ααα+=2tan12tan-1cos 22ααα+=2tan12tan 2tan 2ααα-=七 辅助角公式)sin(cos sin 22ϕααα++=+b a b a )cos(22ϕα-+=b a其中：bab a b b a a =+=+=ϕϕϕtan cos sin 2222八 三角函数和差化积公式）（）（2-cos 2sin 2sin sin βαβαβα⋅+=+）（）（2-sin 2cos 2sin -sin βαβαβα⋅+=）（）（2-cos 2cos 2cos cos βαβαβα⋅+=+）（）（2-sin 2sin 2-cos -cos βαβαβα⋅+=九 三角函数积化和差公式[]）（）（βαβαβα-sin sin 21cos sin ++=⋅ []）（）（βαβαβα-sin -sin 21sin cos +=⋅ []）（）（βαβαβα-cos cos 21cos cos ++=⋅ []）（）（βαβαβα-cos -cos 21-sin sin +=⋅反三角函数公式下α可取αα-arcsin -arcsin =）（ απαarccos --arccos =）（ααarctan )(arctan -=- απαarccot )-arccot -=（2arccot arctan arccos arcsin παααα=+=+αα=）（arcsin sin αα=）（arccos cosαα=)(arctan tan αα=）（arccot cotαα=）（sin arcsin ），（22-ππα∈αα=）（cos arccos ），（πα0∈αα=)(tan arctan ），（22-ππα∈αα=）（cot arccot ），（πα0∈αα1arctan arctan = 0>ααα1arccotarccot =0>α)1(arctan arctan arctan αββαβα-+=+ 其中)2,2(arctan arctan ππβα-∈+三角函数图像一 正弦函数x x f sin )(=定义域：R x ∈ 值域：]1,1[)(-∈x f二 余弦函数x x f cos )(=定义域：R x ∈ 值域：]1,1[)(-∈x f三 正切函数x x f tan )(=定义域：Z k k x R x ∈+≠∈,2ππ且 值域：R x f ∈)(四 余切函数x x f cot )(=定义域：Z k k x R x ∈≠∈,π且 值域：R x f ∈)(反三角函数图像一 反正弦函数x x f arcsin )(=定义域：]1,1[-∈x 值域：]2,2[)(ππ-∈x f二 反余弦函数x x f arccos )(=定义域：]1,1[-∈x 值域：],0[)(π∈x f11 三 反正弦函数 x x f arctan )(=定义域：R x ∈ 值域：)2,2()(ππ-∈x f四 反余切函数 x x f arccot )(=定义域：R x ∈ 值域：),0()(π∈x f。
三角函数与反三角函数
三角函数与反三角函数三角函数是数学中一个重要的概念，它们在解决几何问题、物理问题以及工程问题等方面起着不可替代的作用。
与之相对应的，反三角函数是解三角函数方程时经常使用的工具。
本文将介绍三角函数和反三角函数的定义、性质以及它们在实际问题中的应用。
一、三角函数的定义与性质三角函数是利用一个角的弧度或角度值，计算该角对应三角比值的函数。
常见的三角函数包括正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)等。
1. 正弦函数正弦函数sin(x)的定义是：在单位圆上，角x所对应点的纵坐标值。
正弦函数的性质有：- 周期性：sin(x)的周期是2π，即sin(x + 2π) = sin(x)。
- 奇偶性：正弦函数是奇函数，即sin(-x) = -sin(x)。
2. 余弦函数余弦函数cos(x)的定义是：在单位圆上，角x所对应点的横坐标值。
余弦函数的性质有：- 周期性：cos(x)的周期是2π，即cos(x + 2π) = cos(x)。
- 偶性：余弦函数是偶函数，即cos(-x) = cos(x)。
3. 正切函数正切函数tan(x)的定义是：在单位圆上，角x所对应点的纵坐标值与横坐标值的比值。
正切函数的性质有：- 周期性：tan(x)的周期是π，即tan(x + π) = tan(x)。
- 奇偶性：正切函数是奇函数，即tan(-x) = -tan(x)。
除了这三个常见的三角函数，还有诸如余割函数csc(x)、正割函数sec(x)和余切函数cot(x)等函数，它们的性质可以通过正弦函数和余弦函数的倒数关系得到。
二、反三角函数的定义与性质反三角函数是三角函数的反函数。
在实际问题中，我们经常需要求解三角函数方程，即已知三角函数的值，求解相应角的值。
此时就需要用到反三角函数。
常见的反三角函数包括反正弦函数arcsin(x)、反余弦函数arccos(x)、反正切函数arctan(x)等。
1. 反正弦函数反正弦函数arcsin(x)的定义是：满足sin(y) = x的角y，其中y的取值范围是[-π/2, π/2]。
三角函数与反三角函数总结 简洁版
二、反三ቤተ መጻሕፍቲ ባይዱ函数:
函数 反正弦 反余弦 反正切 反余切 反正割 反余割
表示（与三角函数一一对应) 若 x sin y ，则 y arc sin x 若 x cos y ，则 y arc cos x 若 x tan y ，则 y arc tanx 若 x cot y ，则 y arc cotx 若 x sec y ，则 y arcsec x 若 x cscy ，则 y arccscx
tan( ) tan tan 1 tan tan
tan( ) tan tan 1 tan tan
5、二倍角公式：
sin 2 2sin cos cos 2 cos 2 sin 2 2cos 2 1 1 2sin 2
tan 2 2 tan 1 tan 2
6、降幂公式：
三角函数与反三角函数
一、三角函数：
1、定义：
名称
正弦
定
sin
义
对边 斜边
y r
余弦
cos
邻边 斜边
x r
正切
tan
对边 邻边
y x
余切
cot
邻边 对边
x y
正割
sec
斜边 邻边
r x
余割
csc
斜边 对边
r y
2、正六边形法则：
图形结构：
上弦、中切、下割； 左正、右余、中间 1
图形关系：
tan cot 1 (1)倒数关系： SinCsc 1
2
sin
1 cos 2
2
2
cos
1
cos 2
2
7、辅助角公式：
a sin x b cos x a2 b2 sin(x )
三角函数、反三角函数
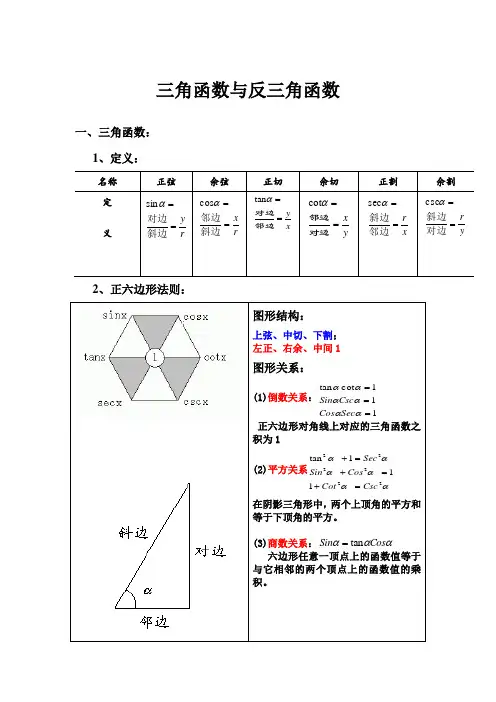
定义直角三角形三角函数定义在直角三角形中，当平面上的三点A、B、C的连线，AB、AC、BC，构成一个直角三角形，其中∠ACB为直角。
对∠BAC而言，对边（opposite）a=BC、斜边（hypotenuse）c=AB、邻边（adjacent）b=AC，则存在以下关系：基本函数英文缩写表达式语言描述正弦函数sine sin a/c ∠A的对边比斜边余弦函数cosine cos b/c ∠A的邻边比斜边正切函数tangent tan a/b ∠A的对边比邻边余切函数cotangent cot b/a ∠A的邻边比对边正割函数secant sec c/b ∠A的斜边比邻边余割函数cosecant csc c/a ∠A的斜边比对边注：正切函数、余切函数曾被写作tg、ctg，现已不用这种写法。
secx=1/cosx、cscx=1/sinx变化规律正弦值随着角度的增大（或减小）而增大（或减小），余弦值随着角度的增大（或减小）而减小（或增大）；正切值随着角度的增大（或减小）而增大（或减小），余切值随着角度的增大（或减小）而减小（或增大）；正割值随着角度的增大（或减小）而增大（或减小），余割值随着角度的增大（或减小）而减小（或增大）。
特殊角在三角函数中，有一些特殊角，例如30°、45°、60°，这些角的三角函数值为简单单项式，计算中可以直接求出具体的值。
这些函数的值参见下表格：角度0°15°30°45°60°90°120°135°150°180°270°弧度sin值cos值tan 值不存在不存在cot 值不存在不存在几何性质函数图象函数对称轴对称中心图象无（kπ/2+π/2,0）正切三角函数图像无最小正周期如果一个函数f （x ）的所有周期中存在一个最小的正数，那么这个最小的正数就叫做f （x ）的最小正周期（minimal positive period ）.例如，正弦函数的最小正周期是2π.对于正弦函数y=sinx, 自变量x 只要并且至少增加到x+2π时，函数值才能重复取得正弦函数和余弦函数的最小正周期是2π。
三角函数和反三角函数的转换公式
三角函数和反三角函数的转换公式三角函数和反三角函数是数学中常见的函数，它们在许多领域中都有广泛的应用，如物理学、工程学、计算机科学等。
在研究三角函数和反三角函数的过程中，我们常常需要用到它们之间的转换公式。
本文将详细介绍三角函数和反三角函数的转换公式。
一、正弦函数和反正弦函数的转换公式：正弦函数的定义域为实数集，值域为[-1, 1]，记作sin(x)。
反正弦函数的定义域为[-1, 1]，值域为实数集，记作arcsin(x)。
它们之间的转换公式如下：1. sin(arcsin(x)) = x，其中x属于[-1, 1]。
这个公式表明，在[-1,1]范围内，对任意的x，正弦函数和反正弦函数可以互相抵消，得到原来的值。
2. arcsin(sin(x)) = x + 2kπ，其中k为整数。
这个公式表明，对于任意的实数x，在[-π/2,π/2]范围内，正弦函数和反正弦函数也可以互相抵消，得到原来的值。
而在其他范围内，由于正弦函数的周期性，需要加上2kπ，其中k为整数。
二、余弦函数和反余弦函数的转换公式：余弦函数的定义域为实数集，值域为[-1, 1]，记作cos(x)。
反余弦函数的定义域为[-1, 1]，值域为实数集，记作arccos(x)。
它们之间的转换公式如下：1. cos(arccos(x)) = x，其中x属于[-1, 1]。
这个公式表明，在[-1,1]范围内，对任意的x，余弦函数和反余弦函数可以互相抵消，得到原来的值。
2. arccos(cos(x)) = x + 2kπ，其中k为整数。
这个公式表明，对于任意的实数x，在[0,π]范围内，余弦函数和反余弦函数也可以互相抵消，得到原来的值。
而在其他范围内，由于余弦函数的周期性，需要加上2kπ，其中k为整数。
三、正切函数和反正切函数的转换公式：正切函数的定义域为实数集，值域为全体实数，记作tan(x)。
反正切函数的定义域为全体实数，值域为[-π/2, π/2]，记作arctan(x)。
反三角函数与三角函数
反三角函数与三角函数
三角函数和反三角函数是高中数学中非常常用的两个概念，并且被用于几何图形、微积分
和物理学中。
三角函数是描述夹角大小与两边周长之间正反比关系的数学函数。
常用的三角函数有
sinx,cosx,tanx,cotx等函数，它们都是在直角坐标系上定义的函数。
它们的定义域都是（–π,π），可以用来描述夹角大小与两边周长之间的正反比关系。
反三角函数是取一个三角函数的反函数，主要包括sin-1x,cos-1x,tan-1x,cot-1x等函数。
它们的定义域在（-π/2, π/2），可以求解给出的夹角和其边的比例。
三角函数与反三角函数之所以如此重要，是因为它们是多种数学概念及其物理现象的基础。
如牛顿第二定律，依靠经典的三角函数可以求得电磁学 troubling 的力学意义，揭示了
问题的本质。
因此，三角函数与反三角函数被称为数学与物理学中“钥匙”。
综上所述，三角函数与反三角函数都是高中数学重要的科目，也是物理学中应用广泛的重
要概念。
它们可以用来描述夹角大小与两边周长之间的正反比关系，也可以用于物理学应
用中非常重要的概念。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 三角、反三角函数一、考纲要求1.理解任意角的概念、弧度的意义，能正确进行弧度和角度的互换。
2.掌握任意角的正弦、余弦、正切的定义，了解余切、正割、余割的定义，掌握同角三角函数的基本关系式，掌握正弦、余弦的诱导公式，理解周期函数与最小正周期的意义。
3.掌握两角和与两角差的正弦、余弦、正切公式，掌握二倍角的正弦、余弦、正切公式。
4.能正确运用三角公式，进行简单三角函数式的化简，求值和恒等式的证明。
5.了解正弦函数、余弦函数，正切函数的图像和性质，会用“五点法”画正弦函数，余弦函数和函数y=Asin(wx+ϕ)的简图，理解A 、w 、ϕ的物理意义。
6.会由已知三角函数值求角，并会用符号arcsinx 、arccosx 、arctgx 表示。
7.掌握正弦定理、余弦定理，并能初步运用它们解斜三角形，能利用计算器解决三角形的计算问题。
8.理解反三角函数的概念，能由反三角函数的图像得出反三角函数的性质，能运用反三角函数的定义、性质解决一些简单问题。
9.能够熟练地写出最简单的三角方程的解集。
二、知识结构1.角的概念的推广： (1)定义：一条射线OA 由原来的位置OA ，绕着它的端点O 按一定方向旋转到另一位置OB ，就形成了角α。
其中射线OA 叫角α的始边，射线OB 叫角α的终边，O 叫角α的顶点。
(2)正角、零角、负角：由始边的旋转方向而定。
(3)象限角：由角的终边所在位置确定。
第一象限角：2k π＜α＜2k π+2π,k ∈Z 第二象限角：2k π+2π＜α＜2k π+π,k ∈Z 第三象限角：2k π+π＜α＜2k π+23π,k ∈Z第四象限角：2k π+23π＜α＜2k π+2π,k ∈Z(4)终边相同的角：一般地，所有与α角终边相同的角，连同α角在内(而且只有这样的角)，可以表示为k ·360°+α，k ∈Z 。
(5)特殊角的集合：终边在坐标轴上的角的集合｛α｜α＝2πk ，k ∈Z ｝ 终边在一、三象限角平分线上角的集合｛α｜α＝k π+4π，k ∈Z ｝ 终边在二、四象限角平分线上角的集合｛α｜α＝k π-4π，k ∈Z ｝终边在四个象限角平分线上角的集合｛α｜α＝k π-4π，k ∈Z ｝2.弧度制：(1)定义：用“弧度”做单位来度量角的制度，叫做弧度制。
(2)角度与弧度的互化： 1°＝180π弧度，1弧度＝(π180)° (3)两个公式：(R 为圆弧半径，α为圆心角弧度数)。
扇形面积公式：S=21lR=21｜α｜R 23.周期函数：(1)定义：对于函数y=f(x)，如果存在一个非零常数T ，使得x 取定义域内的任意值时，都有f(x+T)=f(x)，那么函数y=f(x)叫做周期函数，其中非零常数T 叫做这个函数的一个周期，如果T 中存在一个最小的正数，则这个最小正数叫做这个函数的最小正周期。
(2)几个常见结论：①如果T 是函数y=f(x)的一个周期，那么kT(k ∈Z ，且k ≠0)也是y=f(x)的周期。
(1)②如果T 是函数y=f(x)的一个周期，那么ωT也是y=f(wx)(w ≠0)的周期。
③一个周期函数不一定有最小正周期，如常函数y=f(x)=c 。
4.三角函数定义： (1)定义：设α是一个任意大小的角，P(x ，y)是角α终边上任意一点，它与原点的距离｜PO ｜=r,那么角α的正弦、余弦、正切、余切、正割、余弦分别是sin α=ry,cos α=r x ,tg α=y r ,ctg α=y x ,Sec α=r x ,csc α=ry(如图(1))。
(2)六个三角函数值在每个象限的符号：(如图(2))(3)同角三角函数的基本关系式：倒数关系：sin α·csc α=1,cos α·sec α=1,tg α·ctg α=1 商数关系：tg α=ααcos sin ,ctg α=ααsin cos 平方关系：sin 2α+cos 2α=1,1+tg 2α=sec 2α,1+ctg 2α=csc 2α(4)诱导公式：α2k π+α-απ-απ+α2π-α 2π-α 2π+α 正弦 sin α -sin α sin α -sin α -sin α cos α cos α 余弦 cos α cos α -cos α -cos α cos α sin α -sin α 正切 tg α -tg α -tg α tg α -tg α ctg α -ctg α 余切 ctg α -ctg α -ctg α ctg α -ctg αtg α-tg α上述公式可以总结为：奇变偶不变，符号看象限。
5.已知三角函数值求角 6.三角函数的图象和性质： (1)三角函数线：如图(3)，sin α=MP,cos α=OM,tg α=AT,ctg α=BS函数y=Asin(wx+ϕ)的图像可以通过下列两种方式得到： ϕ＞0，图像左移ϕ(1)y=sinx y=sin(x+ϕ) ϕ＜0，图像右移｜ϕ｜ w ＞1，横坐标缩短为原来的w1倍 y=sin(wx+ϕ)0＜w ＜1，横坐标伸长为原来的w1倍 A ＞1，纵坐标伸长为原来的A 倍y=Asin(wx+ϕ) 0＜A ＜1，纵坐标缩短为原来的A 倍 w ＞1,横坐标缩短为原来的w1倍 (2)y=sinx 0＜w ＜1,横坐标伸长为原来的w1倍 ϕ＞0，图像左移wϕ y=sin(wx)ϕ＜0,图像右移wϕA ＞1，纵坐标伸长为原来A 倍y=sin(wx+ϕ) y=Asin(wx+ϕ) 0＜A ＜1，纵坐标缩短为原来A 倍8.两角和与差的三角函数： (1)常用公式：两角和与差的公式：sin(α±β)＝sin αcos β±cos αsin β， cos(α±β)=cos αcos β sin αsin β， tg(α±β)=βαβαtg tg tg tg 1±倍角公式：sin2α=2sin αcos α，cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α， tg2α=αα212tg tg -.半角公式：sin2α=±2cos 1α-, cos 2α=±2cos 1α+, tg 2α=±ααcos 1cos 1+-=ααcos 1sin +=ααsin cos 1-.积化和差公式：sin αcos β=21〔sin(α+β)+sin(α-β)〕, cos αsin β=21〔sin(α+β)-sin(α-β)〕cos αcos β=21〔cos(α+β)+cos(α-β)〕,sin αsin β=-21〔cos(α+β)-cos(α-β)〕和差化积公式： sin α+sin β=2sin2βα+cos2βα-,sin α-sin β=2cos 2βα+sin 2βα-cos α+cos β=2cos 2βα+cos 2βα- ,cos α-cos β=-2sin 2βα+sin 2βα-万能公式：sin α=21222ααtgtg+，cos α=212122ααtgtg +-,tg α=21222ααtgtg -(2)各公式间的内在联系：(3)应注意的几个问题：①凡使公式中某个式子没有意义的角，都不适合公式。
②灵活理解各公式间的和差倍半的关系。
③在半角公式中，根号前的符号由半角所在像限来决定。
④常具的变形公式有：cos α=ααsin 22sin ,sin 2α=22cos 1α-,cos 2α=22cos 1α+,tg α+tgβ＝tg(α+β)(1-tg αtg β).⑤asin α+bcos α=22b a +sin(α+ϕ).(其中ϕ所在位置由a ，b 的符号确定，ϕ的值由tg ϕ=ab确定)。
9.解斜三角形：在解三角形时，常用定理及公式如下表： 名称 公式 变形内角和定理A+B+C=π2A +2B ＝2π-2C，2A+2B ＝2π-C 余弦定理a 2=b 2+c 2-2bccosAb 2=a 2+c 2-2accosB c 2=a 2+b 2-2abcosCcosA=bc a c b 2222-+cosB=ac b c a 2222-+cosC abc b a 2222-+正弦定理A a sin =B b sin =Ccsin =2R R 为ΔABC 的外接圆半径a=2RsinA,b=2RsinB,c=2RsinC sinA=R a 2,sinB=R a 2,sinC=Rc 2 射影定理acosB+bcosA=c acosC+cosA=b bcosC+ccosB=a面积公式①S Δ=21ah a =21bh b =21ch c 111sinA=ab S ∆2 S ∆2③S Δ=Rabc4 ④SΔ=c)-b)(P -a)(P -P(P (P=21 (a+b+c)) ⑤S Δ=21(a+b+c)r (r 为ΔABC 内切圆半径)sinC=abS ∆2 10.反三角函数： 名称 反正弦函数 反余弦函数反正切函数反余切函数 定义y=sinx(x ∈〔-2π,2π〕的反函数，叫做反正弦函数，记作x=arsiny y=cosx(x ∈〔0,π〕)的反函数，叫做反余弦函数，记作x=arccosyy=tgx(x ∈(-2π, 2π)的反函数，叫做反正切函数，记作x=arctgyy=ctgx(x ∈(0,π))的反函数，叫做反余切函数，记作x=arcctgy 理解arcsinx 表示属于［-2π,2π］ 且正弦值等于x 的角 arccosx 表示属于［0，π］，且余弦值等于x 的角arctgx 表示属于(-2π,2π)，且正切值等于x 的角arcctgx 表示属于(0，π)且余切值等于x 的角 图像性质 定义域 ［-1，1］ ［-1，1］ (-∞，+∞) (-∞，+∞) 值域［-2π，2π］ ［0，π］(-2π，2π) (0，π) 单调性 在〔-1，1〕上是增函数在［-1，1］上是减函数 在(-∞，+∞)上是增数在(-∞，+∞)上是减函数奇偶性arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctg(-x)=-arctgx arcctg(-x)=π-arcctgx 周期性都不是同期函数恒等式 sin(arcsinx)=x(x ∈［-1，1］)arcsin(sinx)=x(x ∈［-2π,2π］) cos(arccosx)=x(x ∈［-1,1］) arccos(cosx)=x(x ∈［0,π］) tg(arctgx)=x(x ∈R)arctg(tgx)=x （x ∈(-2π,2π)） ctg(arcctg x)=x(x ∈R) arcctg(ctgx)=x (x ∈(0,π))互余恒等式arcsinx+arccosx=2π(x ∈［-1,1］) arctgx+arcctgx=2π(X ∈R)11.三角方程：(1) 最简单三角方程的解集：方程方程的解集sinx=a ｜a ｜＞1Φ｜a ｜=1｛x ｜x=2k π+arcsina,k ∈z ｝cosx=a ｜a ｜＞1 Φ｜a ｜=1 ｛x ｜x=2k π+arccosa,k ∈z ｝｜a ｜＜1 ｛x ｜x=2k π±arccosa,k ∈z tgx=a ｛x ｜x=k π+arctga,k ∈z ｝ ctgx=a ｛x ｜x=k π+arcctga,k ∈z ｝(2)简单三角方程：转化为最简单三角方程。