昆明理工大学--2008年《理论力学》工程力学班试题A答案

昆明理工大学工程力学习题册答案一、选择题1. 在平面力系中，力对点的矩的常用单位是（A）A. N·mB. N/mC. N·sD. N·m^2答案：A2. 平面汇交力系的平衡方程是（C）A. Fx=0, Fy=0, M=0B. Fx=0, Fy=0C. Fx=0, Fy=0, M=0（其中M为力矩）D. Fx=0, Fy=0, M≠0答案：C3. 在空间力系中，力的投影与原力的关系是（B）A. 投影等于原力B. 投影小于等于原力C. 投影大于原力D. 投影与原力无关答案：B二、填空题1. 力对物体的作用效果包括______和______。

答案：使物体发生形变，使物体产生运动2. 平面力系中的合力可以用______和______来确定。

答案：力的大小，力的方向3. 在平面力系中，力矩的计算公式为______。

答案：M=F×d（其中F为力，d为力臂）三、计算题1. 已知：力F=10N，作用点距离A点4cm，求力F 对A点的力矩。

解：力矩的计算公式为M=F×d，其中d为力臂，即作用点到力作用点的距离。

本题中，d=4cm=0.04m。

所以，M=10N×0.04m=0.4N·m。

答案：0.4N·m2. 平面汇交力系中，已知F1=20N，F2=30N，F3=40N，求该力系的合力。

解：首先，将F1和F2合成，得到合力F12。

F12的大小为F12=√(F1^2+F2^2+2F1F2cosθ)，其中θ为F1和F2之间的夹角。

假设F1和F2之间的夹角为60°，则F12=√(20^2+30^2+2×20×30×cos60°)=√(400+900+ 1200×0.5)=√(2000)=44.72N。

然后，将F12与F3合成，得到合力F123。

F123的大小为F123=√(F12^2+F3^2+2F12F3cosθ)，其中θ为F12和F3之间的夹角。

理论力学A 卷参考答案一、选择题1-6 DABADC二、填空题(1) 绝对速度 相对速度 牵连速度(2) 平动 转动 (3) 1442222=+b y b x ，2bk ，2bk 2 (4) l M2，l M(5) 2p ml ω=，（→）； 2(65/24)o L m l ω=，逆时针方向(6) mL ω/2，mL 2ω/3，mL 2ω2/6三、计算题1、解：（1）设圆柱O 有向下滚动趋势，取圆柱O0=∑A M ----0sin max 1T =-⋅-⋅M R F R θP0=∑y F ----0cos N =-θP F又N max F M δ= ……………………2分设圆柱O 有向上滚动趋势，取圆柱O0=∑A M ----0sin max 2T =+⋅-⋅M R F R θP0=∑y F ----0cos N =-θP F ……………………2分又N max F M δ=……………………2分系统平衡时： ……………………2分)cos (sin 1T θR θP F δ-=（2）设圆柱O 有向下滚动趋势.0=∑C M 0m a x =-⋅M R F s0=∑y F 0c o s N =-θP F 又θδcos P R F s = 所以θδcos P R F s = (2)只滚不滑时，应有 θP f F f F s s s cos N =≤ R f s δ≥同理，圆柱O 有向上滚动趋势时得 R f s δ≥只滚不滑时，Rf s δ≥ (2)2、解：速度分析：1. 杆AB 作平面运动，基点为B.……………………….1分2.动点 ：滑块 A ，动系 ：OC 杆……………………….2分 沿v B 方向投影：……………………….1分……………………….1分 沿vr 方向投影：……………………….1分加速度分析：n t ABAB B A a a a a ++=……………………….2分 沿v C 方向投影：……………………….2分……………………….1分……………………….1分3、 解：突然解除约束瞬时，杆OA 将绕O 轴转动，不再是静力学问题。

第七章点的合成运动一、是非题7.1.1动点的相对运动为直线运动，牵连运动为直线平动时，动点的绝对运动必为直线运动。

（x ）7.1.2无论牵连运动为何种运动，点的速度合成定理V a V e V r都成立。

（V）7.1.3某瞬时动点的绝对速度为零，则动点的相对速度和牵连速度也一定为零。

（X ）7.1.4当牵连运动为平动时，牵连加速度等于牵连速度关于时间的一阶导数。

（V ）7.1.5动坐标系上任一点的速度和加速度就是动点的牵连速度和牵连加速度。

（X ）7.1.6不论牵连运动为何种运动，关系式都成立。

（X ）7.1.7只要动点的相对运动轨迹是曲线，就一定存在相对切向加速度。

（X ）7.1.8在点的合成运动中，判断下述说法是否正确：（1 ）若v r为常量，则必有a r=0。

（x）（2 ）若e为常量，则必有a e=0. （X）（3）若v r// 3e则必有a c 0。

（V）7.1.9在点的合成运动中，动点的绝对加速度总是等于牵连加速度与相对加速度的矢量和。

（X ）7.1.10当牵连运动为定轴转动时一定有科氏加速度。

（X ）二、填空题7.2.1牵连点是某瞬时动系上与动点重合的那一点。

_______7.2.2在V e与V r共线情况下，动点绝对速度的大小为V a V。

+ V「，在V：Vr| 情况下，动点绝对速度的大小为V a v'Ve V，在一般情况下，若已知V e、V r ,应按V_ V e V r ________________ 计算V a的大小。

三、选择题:7.3.1动点的牵连速度是指某瞬时牵连点的速度，它相对的坐标系是（A ）。

A、定参考系B、动参考系C、任意参考系7.3.2 在图示机构中，已知s a bsin t，且t （其中a、b、3均为常数），杆长为L，若取小球A为动点，动系固结于物块B，定系固结于地面，则小球的牵连速度V e的大小为（B ）。

AA、LB、b cos tC、b cos t L cos tD、b cos t L四、计算题741杆OA 长L ,由推杆BC 通过套筒B 推动而在图面内绕点 0转动，如图所示。

《理论力学A 》考试试题A 课程号：63125203 考试方式： 闭卷 使用专业、年级： 任课教师：考试时间：一、是非题（对画√，错画×）（共5题，每题2分，共10分）1.受平面任意力系作用的刚体，力系的合力为零，刚体就一定平衡。

( )2.定轴转动刚体上各点的角速度相同。

( )3.力系的主矢和主矩都与简化中心的位置有关。

（ ）4.一个刚体若动量为零，该刚体就一定处于静止状态。

（ ）5.定轴转动刚体对其转轴的动量矩等于刚体对其转轴的转动惯量与刚体 角加速度的乘积。

（ ） 二、选择题（共10题，每题3分，共30分）1.图示，已知1F 、2F 、α，则1F 和2F 在x 轴上的投影为 。

（a ）αcos 11F F x =，02=x F ； （b ）αcos 11F F x -=，02=x F ；（c ）αcos 11F F x =，22F F x =； （d ）αcos 11F F x -=，22F F x -= 2.图示杆件的作用力F 对杆端O 点的力矩()=F M O 。

（a ）Fa ； （b ）Fa -； （c ）Fl ； （d ）Fl -3.正立方体如图示，棱长为a ，在A 点作用一力F ，该力对y 轴之矩 为 。

（a ）()Fa F M y = ；（b ）()0=F M y ；（c ）()Fa F M y -= 4.静滑动摩擦因数s f 等于摩擦角f ϕ的 。

（a ）正弦； （b ）正切； （c ）余弦；（d ）余切。

5.如图所示汇交力系的力多边形表示 。

（a ）力系的合力等于零； （b ）力系的合力是R ； （c ）力系的主矩不为零。

6. 图示均质细直杆，质量为m ，长为l ，绕O 轴转动的角速度为ω，则杆的 动量大小为 。

（a ）ωml 21； （b ）ωml ； （c ）07.均质滑轮半径为R ，对O 轴的转动惯量为J ，绳子的一端绕在滑轮上， 另一端挂有质量为m 的物体A 。

α 昆 明 理 工 大 学 理 论 力 学 测 验 试 卷 理论力学B(1) 日期： 年 月 日专业： 学号： 姓名：一、 是非题 （每题2分。

正确用√，错误用×，填入括号内。

）1、在平面任意力系中，若其力多边形自行闭合，则力系平衡。

（ × ）2、若将某力沿两不相互垂直的轴分解，则其分力的大小一定不等于该力在这两个轴上的投影的大小。

（ ∨ ）3、不平衡的任意力偶系总可以合成为一个合力偶，合力偶矩等于各分力偶矩的代数和。

（ × ）4、若平面力系对一点的主矩为零，则此力系不可能合成为一个力偶。

（ ∨ ）5、若点的法向加速为零，则该点轨迹的曲率必为零。

（ × ）6、定轴转动刚体上点的速度可以用矢积表示为r v，其中 是刚体的角速度矢量，r是从定轴上任一点引出的矢径。

（ ∨ ）二、 选择题 （每题3分。

请将答案的序号填入划线内。

）1、平面任意力系向作用平面内任意一点简化，其主矢与简化中心 ② ，主矩与简化中心 ① 。

①有关 ； ② 无关。

2、若斜面倾角为α，物体与斜面间的摩擦系数为f ，欲使物体能静止在斜面上，则必须满足的条件是 ③ 。

① tg f ≤α； ② tg f > α ； ③ tg α≤ f. ； ④ tg α> f 。

3、作用在一个刚体上的两个力F A 、F B ，满足F A ＝－F B 的条件，则该二力可能是 ② 。

① 作用力和反作用力或一对平衡的力 ； ② 一对平衡的力或一个力偶； ③ 一对平衡的力或一个力和一个力偶 ； ④ 作用力和反作用力或一个力偶。

4、汇交于O 点的平面汇交力系，其平衡方程式可表示为二力矩形式。

即0)(i AF m， 0)(i B F m ，但必须 ② 。

① A 、B 两点中有一点与O 点重合 ； ② 点O 不在A 、B 两点的连线上； ③点O 应在A 、B 两点的连线上。

5、半径为r 的车轮沿固定弧面作纯滚动，若某瞬时轮子的角速度为ω，角加速度为α，则轮心O 的切向加速度和法向加速度的大小分别 为 ④ 。

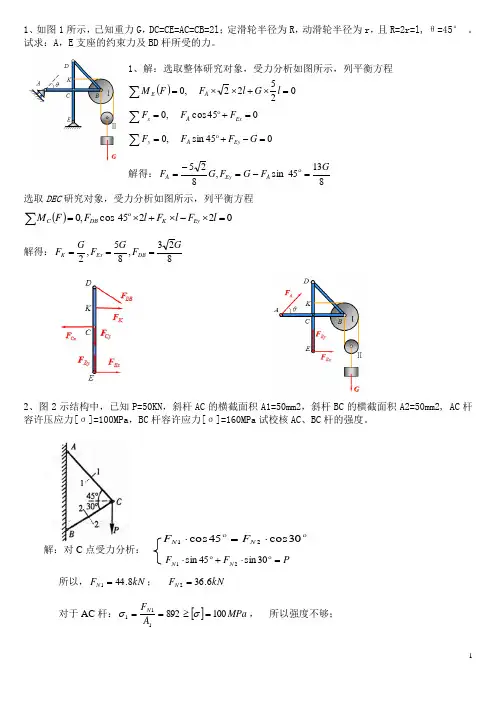
1、如图1所示，已知重力G ，DC=CE=AC=CB=2l ；定滑轮半径为R ，动滑轮半径为r ，且R=2r=l, θ=45° 。

试求：A ，E 支座的约束力及BD 杆所受的力。

1、解：选取整体研究对象，受力分析如图所示，列平衡方程()045sin ,0045 cos ,002522,0=-+==+==⨯+⨯⨯=∑∑∑G F F FF F F lG l F F M Ey A yEx A xA E解得：81345 sin ,825GF G F G F A Ey A =-=-=选取DEC 研究对象，受力分析如图所示，列平衡方程()02245 cos ,0=⨯-⨯+⨯=∑l F l F l FF M Ey K DBC解得：823,85,2GF G F G F DB Ex K ===2、图2示结构中，已知P=50KN ，斜杆AC 的横截面积A1=50mm2，斜杆BC 的横截面积A2=50mm2, AC 杆容许压应力[σ]=100MPa ，BC 杆容许应力[σ]=160MPa 试校核AC 、BC 杆的强度。

解：对C 点受力分析：所以，kN F N 8.441=； kN F N 6.362= 对于AC 杆：[]MPa A F N 100892111=≥==σσ， 所以强度不够； 30cos 45cos 21⋅=⋅N N F F P F F N N =⋅+⋅30sin 45sin 21对于BC 杆：[]MPa A F N 160732222=≥==σσ， 所以强度不够。

3、图3传动轴上有三个齿轮，齿轮2为主动轮，齿轮1和齿轮3消耗的功率分别为KW 756.0和KW 98.2。

若轴的转速为min /5.183r ，材料为45钢，[]MPa 40=τ。

根据强度确定轴的直径。

3、解:(1) 计算力偶距 m N nP m .3.39954911== m N nP m .155954933== m N m m m .3.194312=+=(2) 根据强度条件计算直径从扭矩图上可以看出，齿轮2与3 间的扭矩绝对值最大。

昆明理工大学2007～2008学年第一学期《理论力学》期末考试试卷（A 卷）答案1. 是非判断题(每题2分，共20分。

)1、×';2、×;3、√;4、×;5、×;6、×;7、√;8、√;9、√;10、√二、选择题（每题3分，共12分）ACD;AAA;C;C;三、填空题 （本题共13分）1. （本题6分）图(a )的 ω = 0 ，α =R a /； 图(b ) 的ω =R a /cos θ，α =R a /sin θ； 图(c ) 的ω =R a /，α = 0 。

2. （本题4分） L 2m ω(1分); ωω222224652322131mL L m L m mL =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+(1分);画出方向(共2分)3. （本题2分） PL/24. （本题2分）5四、计算题1. （本题10分）如图4.1所示横梁，F 1= F 2= F 3=F 用虚位移原理求解系统B 和D 处反力。

解：(1)把B 点约束力视作为主动力。

设给系统虚位移如图（图2分）。

系统虚功方程为：021=---δϕδδδM y F y F y F F E B B(2分) ==>567111MF F B +=(1分)(2)把D 点约束力视作为主动力。

设给系统虚位移如图（图2分）。

系统虚功方程为：032=++G F D D y F y F y F δδδ(2分) ==>F F B 2827=(1分)2. （本题15分）3. 弯成直角的曲杆OAB 以角速度ω= 常数绕O 点作逆时针转动。

在曲杆的AB 段装有滑筒C ，滑筒与在滑道内运动的铅直杆DC 铰接于C ，O 点与DC 位于同一铅垂线上。

设曲杆的OA段长为r ，求当φ=30°时DC 杆的速度和加速度。

（解）：如图，在点O 建立参考基和曲杆连体基1e e 和。

对于曲杆OAB ，CD 杆上的C 点为动点。

昆明理工大学2008～2009学年第一学期《理论力学》期末考试试卷（B 卷）一、是非判断题(每题2分，共20分。

正确用√，错误用×，填入括号中)1. 静力学公理中，二力平衡公理和加减平衡力系公理适用于一般物体。

（ ）2. 只要平面力偶的力偶矩保持不变，可将力偶的力和力臂作相应的改变，而不影响其对刚体的效应。

（ ） 3. 只要是空间力系就可以列出6 个独立的平衡方程。

（ ） 4. 运动学只研究物体运动的几何性质，而不涉及引起运动的物理原因。

（ ） 5. 无论牵连运动为何种运动，点的速度合成定理r e a v v v +=都成立。

（ ）6. 平面运动刚体的动能可由其质量及质心速度完全确定。

（ ）7. 内力既不能改变质点系的动量和动量矩，也不能改变质点系的动能。

（ ）8. 任意质点系平衡的充要条件是：作用于质点系的主动力在系统的任何虚位移上所做的虚功之和等于零。

（ ） 9. 动力学普遍方程是指：在理想约束条件下，质点系的主动力和惯性力在体系的约束所允许的任意的虚位移上所作的虚功之和等于零。

（ ） 10. 定轴转动刚体的同一转动半径线上各点的速度速度矢量相互平行，加速度矢量也相互平行。

（ ）二、选择题（每题3分，共12分）1. 图示三铰拱架中，若将作用于构件AC 上的力偶M 搬移到构件BC 上，则A 、B 、C 各处的约束力 。

A. 都不变；B. 只有C 处的不改变；C. 都改变；D. 只有C 处的改变。

图2.12. 一正方形以等角速ω绕O 轴转动，小球M 以匀速u 沿板内半径为R 的圆槽运动，则M 的绝对加速度为 。

A. u 2R 2ωω-B. /R u R 22+ωC. R u u 2R 22/+-ωωD. 2u/R)R(+ω图2.23. 直角刚杆AO = 2m ，BO = 3m ，已知某瞬时A 点的速度 A v = 6m/s ；而B 点的加速度与BO 成α= 60°角。

一、填空题1.理论力学中的三个组成部分为____静力学______、____运动学______和____动力学______。

2.力是物体之间相互的___机械_______作用，力的作用效果应是使物体的__运动状态________发生改变，也可使物体的___形状_______发生变化。

3.作用力和反作用力是两物体间的相互作用，他们同时存在，同时消失，且大小___.相等_______、方向___相反_______，其作用线沿___同一直线_______，分别作用于这两个物体上。

4.平面力系分为_ 平面汇交_________力系、___平面平行_______力系和__平面一般________力系。

5.在力的投影中，若力平行于X轴，则Fx=___ F _______若力平行于Y轴，则Fy=____ F ______;若力垂直于X轴，则Fx=___0 _______；若力垂直于Y轴，则Fy=____ 0 ______。

6.力偶三要素是；力偶矩的大小、___力的大小_______和____力偶的转向______。

7.作用在物体上各力的作用线都在___同一平面_______，并呈____任意分布______的力系，称为平面一般力系。

8.平面一般力系的两个基本问题是_平面一般力系的简化__及其_ 平衡条件的应用_________。

9.材料力学的研究模型为____杆____、____块_____、______板_____和______壳____。

10.杆件变形的基本形式有___轴向拉伸与压缩________、__扭转变形______、__剪切变形_______和_____弯曲变形______。

二判断题1.力使物体运动状态发生变化的效应称力的外效应。

（Ⅴ）2.二力等值、反向、共线，是刚体平衡的充分必要条件。

（Ⅴ）3.二力平衡公理、加减平衡力系公理、力的可传性原理只适用于刚体。

（Ⅴ）4.根据力的可传性原理，力可在刚体上任意移动而不改变该力对刚体的作用效果。