流动阻力系数

关于阻力计算的公式一、圆形直管内的流动阻力：1）计算水平圆管内阻力的一般公式—范宁（Fanning ）公式：22u d l f p ρ⋅⋅λ=∆①其中λ为摩擦系数，量纲为一；l 为管长；d 为管径；ρ为流体密度；u 为流速。

本式表明流体流动阻力Δp f 与流动管道长度呈正比；与管道直径呈反比，与流体动能ρu 2/2呈正比。

层流时摩擦系数有准确计算公式，是将式①和式②联立计算，完全靠理论推导方法得出。

公式如下：ρη=λu d 64由此式可见，圆形直管内流体层流流动时，摩擦系数与流体黏度呈正比，与管径、流速、流体密度呈反比。

湍流流动摩擦系数是根据实验得到的公式，最为常用是莫狄（Moody ）摩擦系数图。

2）层流时直圆管内的阻力计算公式—哈根-泊谡叶（Han gen-Poiseuille ）公式：2f lu 32p η=∆②由该式可见，层流时支管阻力Δp f 与管长l 、速度u 、黏度η的一次方成正比，与管径d 的平方呈反比。

二、局部阻力流体在管内流动时，还要受到管件、阀门等局部阻碍而增加的流动阻力，称为局部阻力。

它还包括由于流通截面的扩大或缩小而产生的阻力。

局部阻力可按式③计算：2u d l p 2e f ρλ=∆③或2u p 2f ρζ=∆④其中l e 为当量长度，即将局部阻力折合成相当长度的直管来计算；ζ成为局部阻力系数。

l e 和ζ都是由实验来确定的。

三、总阻力若将流体在管路中流动阻力归结为直管阻力和局部阻力之和，对于流体流动等直径管路，如果将局部阻力以当量长度表示，则阻力计算式为：g2u )d l l (g R h 2u )d l l (R p 2e f 2e f ∑+λ=∑=∑ρ∑+λ=∑ρ=∆或式中l —管路中直径为d 的直管长度，m;Σl e —管路上全部管件与阀门等的当量长度之和，m;u —流体流经管路的速度，m/s如果还有部分局部阻力必须用阻力系数表示，则阻力计算式为：g2u )d l l (g R h 2u )d l l (R p 2e f 2e f ζ∑+∑+λ=∑=∑ρζ∑+∑+λ=∑ρ=∆或式中Σζ—管路上部分管件和阀门等的阻力系数之和。

流体阻力系数一个物体在流体（液体或气体）中和流体有相对运动时，物体会受到流体的阻力。

阻力的方向和物体相对于流体的速度方向相反，其大小和相对速度的大小有关。

在相对速率v 较小时，阻力f的大小与v 成正比：f = kv式中比例系数k 决定于物体的大小和形状以及流体的性质.在相对速率较大以致于在物体的后方出现流体漩涡时,阻力的大小将与v平方成正比。

对于物体在空气中运动的情形,阻力f = CρAv v/2式中，ρ是空气的密度,A 是物体的有效横截面积，C 为阻力系数。

物体在流体中下落时，受到的阻力随速率增大而增大，当阻力和重力平衡时，物体将以匀速下落。

物体在流体中下落的最大速率称为终极速率，又称为收尾速率。

对在空气中下落的物体，它的终极速率为：如图关键字：2.2.4 流体流动阻力的计算流动阻力的大小与流体本身的物理性质、流动状况及壁面的形状等因素有关。

化工管路系统主要由两部分组成，一部分是直管，另一部分是管件、阀门等。

相应流体流动阻力也分为两种：直管阻力：流体流经一定直径的直管时由于内摩擦而产生的阻力；局部阻力：流体流经管件、阀门等局部地方由于流速大小及方向的改变而引起的阻力。

1. 流体在直管中的流动阻力如图1-24所示，流体在水平等径直管中作定态流动。

在1-1′和2-2′截面间列柏努利方程，因是直径相同的水平管，若管道为倾斜管，则由此可见，无论是水平安装，还是倾斜安装，流体的流动阻力均表现为静压能的减少，仅当水平安装时，流动阻力恰好等于两截面的静压能之差。

把能量损失表示为动能的某一倍数。

令则（2-19）式（2-19）为流体在直管内流动阻力的通式，称为范宁（Fanning）公式。

式中为无因次系数，称为摩擦系数或摩擦因数，与流体流动的Re及管壁状况有关。

根据柏努利方程的其它形式，也可写出相应的范宁公式表示式：压头损失（2-20）压力损失 (2-21)值得注意的是，压力损失是流体流动能量损失的一种表示形式，与两截面间的压力差意义不同，只有当管路为水平时，二者才相等。

流体管路流动阻力系数的测定1 绪论流体基本理论为物理设计工程提供了基本的设计和分析方法，而流体管路流动阻力系数是求解流体传动系统、蒸汽系统、水喷射柴油发动机系统等的基本模型，已广泛地用于工程设计和实验测试的方法中。

应用阻力系数来分析流体流动在管路系统中的分布特性及流动状态，对工程设计中的管路系统有重要的导向作用，其精确的测试对工程实际应用至关重要。

2 流体管路流动阻力系数的测定主要从两个方面考虑，即实验测定管路内部阻力系数和实验测定管路外部阻力系数。

实验参数主要包括管路外表面断面积、流体性能参数、流体流量和管路弯曲参数等，其中流体性能参数对实验结果影响最大。

（1）内部阻力系数测试管路内部阻力基本理论分析公式是：f = 0.0775(N/D)(ρ/μ)0.5。

其中f是管道内部阻力系数，N为流体质量流量，D为管径，ρ为流体密度，μ为流体粘度。

另外，直管情况下，管路内部阻力系数计算公式f = 0.0225(N/D2)(ρ/μ)0.5，弯曲情况下，管路内部阻力系数计算公式f = 0.075(N/D2)(ρ/μ)0.5。

管路内部阻力系数测试一般采用内部试验管路，通过在里头装压力表，测量管路端部压力差，得到阻力系数f。

流体流动在管路系统中的外部阻力系数的近似计算公式是：f = k/D，其中f是管道外部阻力系数，k是摩擦係数，D为管径。

外部阻力系数测试一般采用蒙特卡洛试验，一般原理是通过在不同管路中改变流体流量，来获得不同的阻力表达式，从而求取摩擦係数。

3 结论流体管路流动阻力系数是求解流体传动系统、蒸汽系统、水喷射柴油发动机系统等的基本模型，精确的测试对工程实际应用至关重要。

管路内部阻力系数的测试主要通过在管路内安装压力表，测量压降求出；外部阻力系数测试一般采用蒙特卡洛法，通过获得不同的阻力表达式求取摩擦係数。

流动阻力系数计算公式好的，以下是为您生成的文章：在咱们的日常生活和各种工程应用中，流动阻力系数可是个相当重要的概念。

您要是想搞明白流体在管道或者通道里怎么流动，怎么消耗能量，那这个流动阻力系数的计算公式就必须得弄清楚。

我先给您讲讲流动阻力系数到底是个啥。

简单来说，它就是用来衡量流体在流动过程中遇到阻力大小的一个参数。

就好比您在路上跑步，遇到风大的时候您跑起来就更费劲，这风的阻力就大；而流动阻力系数就是用来定量描述这种阻力大小的。

比如说，在管道里流动的液体，它受到管道内壁的摩擦阻力，还有因为管道形状变化、拐弯等产生的局部阻力。

这时候，咱们就得靠流动阻力系数的计算公式来算出这些阻力到底有多大。

我给您举个小例子吧。

有一次我去朋友的工厂参观，他们正在调试一条新的输液管道。

本来想着一切都应该顺顺利利的，结果发现液体的输送速度怎么都达不到预期。

大家就开始琢磨到底是哪儿出了问题。

后来一检查，发现是最初计算流动阻力系数的时候出了差错。

那咱们就来说说常见的流动阻力系数计算公式。

对于层流，也就是那种流体流动很平稳、有规律的情况，流动阻力系数可以用一个相对简单的公式来计算。

但要是到了湍流，也就是流体流动比较混乱、没什么规律的时候，这计算公式可就复杂多了。

再比如说，在一个有很多弯头和变径的管道系统中，计算流动阻力系数就得把每个部分的阻力都考虑进去，这可真是个细致又麻烦的活儿。

而且，影响流动阻力系数的因素那可多了去了。

流体的性质，像黏度、密度；管道的材料和粗糙度；还有流动的速度等等，都会让这个系数发生变化。

在实际应用中，要准确地计算流动阻力系数，可不能马虎。

得把各种因素都考虑周全，还得选择合适的计算公式。

要不然，就像我朋友工厂那次一样，会出大问题的。

总之，流动阻力系数计算公式虽然有时候让人头疼，但只要咱们认真对待，搞清楚其中的原理和规律，还是能把它拿下的，让它为咱们的工作和生活服务。

不知道我这么讲，您对流动阻力系数计算公式有没有更清楚一些呢？。

水流阻力系数的确定方法
水流阻力系数的确定方法有多种，以下列举三种常用的方法：
1.理论公式法：根据流体力学原理，当流体在直管中流动时，阻力系数可以表示
为ξ=fi⋅dL，其中fi为摩擦系数，L为直管的长度，d为直管的内径。

当流体的流动状态为层流时，摩擦系数可以从流体力学推导而得：fi=Re64。

而当流体的流动状态为湍流时，摩擦系数无法采用理论分析方法完全推导而得，一般需要实验的方法。

2.实验测定法：通过实验测量得到水流的阻力系数。

在实验中，可以设置一系列
不同管径和流速的直管，记录每个管径和流速下的压力降和流速，然后根据公式Δp=ξ⋅ρ⋅2u2计算阻力系数。

3.经验数据法：根据实际应用中的经验数据确定水流阻力系数。

在实际应用中，
可以通过对已有的管道系统进行测量和计算，得到水流阻力系数的经验值。

这些经验值可以作为新管道系统设计时的参考。

需要注意的是，水流阻力系数的确定方法应根据具体情况选择。

在工程应用中，一般采用实验测定法和经验数据法来确定水流阻力系数。

同时，对于特殊的水流条件或需要精确计算的情况，可以采用理论公式法进行计算。

常用水的阻力系数对照表阻力系数是工程师和科学家们在设计和计算液体流动性能时使用的一个重要参数。

在液体流动中，液体会受到管壁强度的阻力，而这个阻力大小会受到许多因素的影响，如：液体的黏度、管道的尺寸和形状、液体的流速等等。

对于液体在管道中的运动，阻力系数是必须要考虑的一个因素。

以下是常用水的阻力系数及其对照表：1. 直管的阻力系数在直管中，水的流动受到管道的粗糙程度和管径大小的影响。

粗糙程度越小，管径越大，水的运动速度越大，阻力系数就越小。

以下是不同直管内径和壁粗的阻力系数对照表：直管内径 (mm) | 壁粗 (mm) | 阻力系数---|---|---50 | 0.05 | 0.00975 | 0.05 | 0.008100 | 0.05 | 0.007125 | 0.05 | 0.006150 | 0.05 | 0.0052. 弯头的阻力系数弯头在管道中起到了转向和调节流量的作用，但同时也会产生一定的阻力。

弯头的阻力系数受到弯头的曲率半径和弯角大小的影响。

以下是不同弯头曲率半径和弯角的阻力系数对照表：弯头曲率半径 (mm) | 弯角 (°) | 阻力系数---|---|---250 | 90 | 0.9500 | 90 | 0.41000 | 90 | 0.2250 | 45 | 0.3500 | 45 | 0.151000 | 45 | 0.083. 泵的阻力系数泵在液体输送中的作用不可忽略，但泵也会产生一定的阻力。

泵的阻力系数受到泵的流量和扬程大小的影响。

以下是不同泵流量和扬程的阻力系数对照表：泵流量 (m³/h) | 泵扬程 (m) | 阻力系数---|---|---1 | 10 | 0.12 | 20 | 0.23 | 30 | 0.34 | 40 | 0.45 | 50 | 0.5总结以上是常用水的阻力系数对照表，通过对这些数据的了解，可以更好地设计和计算液体输送管道的性能，提高工程效率和减少能源消耗。

流体流动阻力实验报告一、实验目的。

本实验旨在通过测量不同流速下流体通过不同形状截面管道时的流动阻力，探究流体流动阻力与流速、管道形状的关系，从而加深对流体力学的理解。

二、实验原理。

1. 流体流动阻力。

当流体通过管道流动时，由于管壁的摩擦力和管道内部的涡流等原因，会产生一定的阻力，称为流体流动阻力。

2. 流体流动阻力系数。

流体流动阻力系数与流速、管道形状等因素有关，通常用Reynolds数来表征，即Re=ρVD/μ，其中ρ为流体密度，V为流速，D为管道直径，μ为流体粘度。

不同形状的管道在不同流速下，其流动阻力系数也会有所不同。

三、实验装置。

1. 实验装置包括流速测量装置、管道系统、压力传感器、数据采集系统等。

2. 流速测量装置采用激光多普勒测速仪，能够准确测量流体通过管道的流速。

3. 管道系统包括不同形状截面的管道，用于测量不同形状管道的流动阻力。

四、实验步骤。

1. 将不同形状截面的管道依次连接到流速测量装置上，并通过数据采集系统记录流体通过管道的流速。

2. 调节流速测量装置，分别测量不同流速下流体通过不同形状管道的流速和压力。

3. 根据测得的数据，计算流体流动阻力系数，并绘制流速与流动阻力的关系曲线。

五、实验结果与分析。

1. 通过实验测得不同形状管道在不同流速下的流动阻力系数，发现在相同流速下，不同形状管道的流动阻力系数存在明显差异。

2. 经过分析发现，流体流动阻力系数与管道形状、流速等因素密切相关，其中流速对流动阻力系数的影响较大。

3. 实验结果与理论分析基本吻合，验证了流体流动阻力与流速、管道形状的关系。

六、实验结论。

1. 流体流动阻力与流速、管道形状密切相关，流速越大、管道形状越复杂，流动阻力越大。

2. 实验结果可为工程实践提供参考，对流体在管道内的流动阻力有一定的指导意义。

七、实验总结。

本实验通过测量不同形状管道在不同流速下的流动阻力系数，探究了流体流动阻力与流速、管道形状的关系，加深了对流体力学的理解。

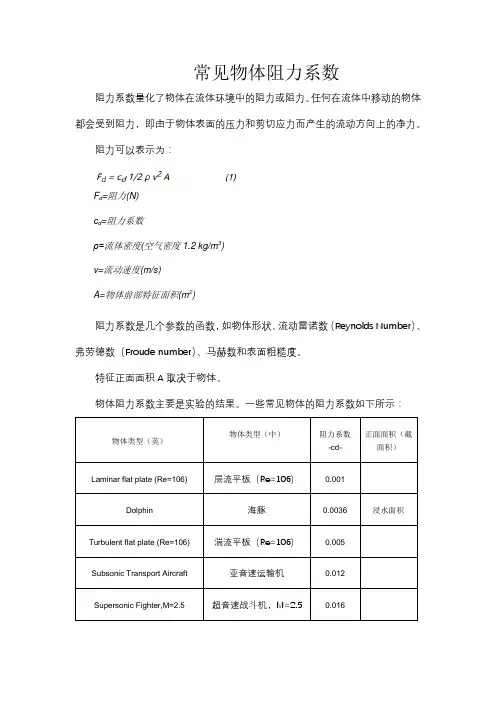
常见物体阻力系数
阻力系数量化了物体在流体环境中的阻力或阻力。

任何在流体中移动的物体都会受到阻力，即由于物体表面的压力和剪切应力而产生的流动方向上的净力。

阻力可以表示为：
F d=阻力(N)
c d=阻力系数
ρ=流体密度(空气密度1.2 kg/m3)
v=流动速度(m/s)
A=物体前部特征面积(m2)
阻力系数是几个参数的函数，如物体形状、流动雷诺数（Reynolds Number）、弗劳德数（Froude number）、马赫数和表面粗糙度。

特征正面面积A取决于物体。

物体阻力系数主要是实验的结果。

一些常见物体的阻力系数如下所示：。

化工原理阻力系数化工原理中的阻力系数是指液体在管道中流动时所受到的阻力与流体速度之间的关系。

阻力系数的大小与管道的几何形状、管道壁面粗糙度、液体的性质以及流体流动的状态等因素有关。

在流体力学中，我们通常用雷诺数（Re）来描述流体的流动状态，即Re＝（ρVD）/µ，其中ρ表示流体的密度，V表示流速，D表示管道的直径，µ表示流体的动力粘度。

当雷诺数小于2100时，流体为层流状态；当雷诺数大于4000时，流体为紊流状态；当雷诺数在2100和4000之间时，流体为过渡状态。

对于不同状态的流体流动，阻力系数的计算方法也有所不同。

以下分别介绍在层流、过渡和紊流状态下的阻力系数计算方法。

在层流状态下，阻力系数可以通过泊肃叶公式进行计算，即f = 16/Re，在这个公式中，f表示摩擦阻力系数，Re表示雷诺数。

在过渡状态下，阻力系数的计算比较复杂，通常需要通过实验获得。

一种常用的实验方法是在不同流速下测量液体在管道中的压降，然后根据实验数据进行曲线拟合，得到阻力系数的表达式。

在紊流状态下，液体在管道中流动时会产生较大的涡流和湍流，此时阻力系数的计算比较困难。

通常可以借助于Colebrook-White公式来近似计算，即1/√f =-2log10（ε/D/3.7 + 2.51/Re√f），其中ε表示管道壁面的粗糙度。

通过迭代计算，可以得到近似的阻力系数。

需要注意的是，在实际工程中，通常使用标准的管道阻力系数图表或计算软件来获得阻力系数的值。

这些图表或软件通常根据大量的实验数据进行推导，可以方便地根据管道的直径、流速和液体性质等参数获得阻力系数的值。

总结起来，化工原理中的阻力系数是液体在管道中流动时所受到的阻力与流体速度之间的关系。

阻力系数的计算方法取决于流体的流动状态，包括层流、过渡和紊流状态。

在实际工程中，通常使用标准的管道阻力系数图表或计算软件来获得阻力系数的值。

管路流体流动计算公式管路流体流动是工程领域中一个非常重要的问题，它涉及到许多工程设计和运行中的关键参数，如流速、压力损失、管道尺寸等。

为了准确地预测管路流体流动的性能，工程师们需要借助一些流体力学的基本原理和计算公式来进行分析和计算。

本文将介绍一些常用的管路流体流动计算公式，希望能够为工程师们提供一些参考和帮助。

1. 流体流速计算公式。

在管路流体流动中，流速是一个非常重要的参数，它直接影响到流体的输送能力和压力损失。

根据连续方程和动量方程，可以得到流速计算公式如下：\[V = \frac{Q}{A}\]其中，V表示流速，Q表示流量，A表示管道的横截面积。

这个公式非常简单，但是在实际工程中非常有用，可以用来计算流速和流量之间的关系。

2. 压力损失计算公式。

在管路中，由于摩擦阻力和局部阻力的存在，流体会产生一定的压力损失。

为了准确地预测压力损失，可以使用达西-魏布努斯公式来进行计算：\[ΔP = f \cdot \frac{L}{D} \cdot \frac{ρV^2}{2}\]其中，ΔP表示压力损失，f表示摩擦阻力系数，L表示管道长度，D表示管道直径，ρ表示流体密度，V表示流速。

这个公式可以很好地描述管道中的摩擦阻力和局部阻力对压力损失的影响，是工程设计中常用的计算公式之一。

3. 阻力系数计算公式。

在管路流体流动中，阻力系数是一个非常重要的参数，它描述了管道内摩擦阻力的大小。

根据实验数据和理论分析，可以得到一些常用的阻力系数计算公式，如克氏公式、普朗特公式等。

这些公式可以用来计算不同流态下的阻力系数，为工程设计和运行提供了重要的参考数据。

4. 流体动力学计算公式。

在管路流体流动中，流体动力学是一个非常重要的问题，它描述了流体在管道中的运动规律和流态特性。

根据纳维-斯托克斯方程和雷诺数理论，可以得到一些常用的流体动力学计算公式，如雷诺数计算公式、流态特性计算公式等。

这些公式可以用来描述不同流态下流体的运动规律和特性，为工程设计和运行提供了重要的参考数据。

流体流动阻力系数的测定实验报告
本实验通过测量不同直径、长度和流速的圆柱模型在流体中的流
动阻力，来确定流体流动阻力系数的大小。

本实验的目的是为了加深
对于流体静力学基础理论的理解，并且对于实际应用有重要的意义。

实验装置是由流体实验台、差压计、流量计、水泵、水槽等组成。

首先，我们将不同形状、尺寸的模型放置在水槽中，然后将水泵打开，将流速保持在一定值，并通过差压计和流量计测量实验数据。

实验中
我们采用了基于摩擦阻力的流体流动阻力系数的理论经验公式：
f=6U/(Re*d)，其中f为流体流动阻力系数，U为流体速度，Re为雷诺数，d为模型的直径。

根据实验数据和理论公式，我们可以得出不同直径、长度和速度
下的流体流动阻力系数，并对数据进行分析和比较。

通过对实验数据
的分析，我们发现流体流动阻力系数与雷诺数、模型直径有关系。

当
直径增大时，流体流动阻力系数也会随之增大；当雷诺数增大时，流
体流动阻力系数也会增大。

这是由于雷诺数大小反映了流体的流动状态，当流动状态更加复杂时，摩擦阻力也会增大。

综合实验数据和理论公式，我们可以得出结论，流体流动阻力系
数与模型的直径、长度和流速、流体的粘度和密度有关系。

在实际生
产和工程应用时，可以根据流体流动阻力系数以及其他相关因素，来
设计和选择合适的流体系统，提高生产效率和降低成本。

总之，本实验通过对流体流动阻力系数的研究，深化了我们对于
流体静力学基础理论的理解，同时也为实际应用提供了重要的基础。

通过实验的过程，我们也学会了如何进行实验数据的收集和分析，提
高了我们的实验技巧和科研素养。

流体流动阻力计算公式好嘞，以下是为您生成的关于“流体流动阻力计算公式”的文章：咱先来说说啥是流体流动阻力。

就好比你在河里游泳，水会对你有阻力，让你游得没那么轻松；又或者家里的水管里水流淌的时候，也会遇到阻碍。

这就是流体流动阻力。

那怎么计算这个阻力呢？这就得提到一些公式啦。

常见的流体流动阻力计算公式有达西-韦斯巴赫公式（Darcy-Weisbach Equation），这公式看起来有点复杂，但是别怕，咱们慢慢说。

它是这样的：$h_f = \frac{f L v^2}{2gD}$ 。

这里面的$h_f$ 表示沿程水头损失，$f$ 叫摩擦系数，$L$ 是管道长度，$v$ 是平均流速，$g$ 是重力加速度，$D$ 是管道直径。

比如说，有一根长长的水管，水在里面哗哗地流。

咱们知道了水管的长度、直径，水的流速，还有通过一些实验或者经验确定了摩擦系数，就能用这个公式算出水流在这根水管里受到的阻力有多大啦。

我记得有一次，在学校的实验室里，我们做了一个关于流体流动阻力的实验。

那时候，大家都兴奋又紧张，围着实验设备，眼睛一眨不眨地盯着。

老师在旁边耐心地指导我们，告诉我们怎么测量水管的各种参数，怎么准确地记录数据。

我们小组负责的是测量水流的速度。

拿着那个小小的流速计，心里还挺忐忑，就怕测错了影响整个实验结果。

小心翼翼地把流速计放到水管里，眼睛紧紧盯着读数，然后赶紧记下来。

等所有的数据都测完，开始用公式计算的时候，那心情，就跟等待考试成绩似的。

算出来结果一看，和预期的差不多，大家都欢呼起来。

那种通过自己的努力，运用知识得到答案的感觉，真的太棒了！再来说说局部阻力的计算。

局部阻力可不像沿程阻力那么“听话”，它的情况更复杂一些。

比如说管道突然变粗或者变细了，水流拐弯了，或者有阀门、三通这些东西，都会产生局部阻力。

计算局部阻力常用的方法有阻力系数法和当量长度法。

阻力系数法就是通过乘以一个阻力系数来计算局部阻力损失，而当量长度法是把产生局部阻力的部分等效成一段长度的直管，然后用沿程阻力的公式来计算。

直管摩擦阻力系数
直管摩擦阻力系数，又称为直管流动阻力系数，是指水流、气流等流体在直管内流动时所产生的摩擦阻力，是衡量流体绝对流速受到摩擦阻力影响的量。

用η表示，η = f (ρm, νm, d)，其中ρm为流体的流动密度，νm为流量度，d为管道直径，f为一函数，它受管道参数的影响，η的数值是由给定的ρm, νm和管道参数而定的。

直管摩擦阻力系数是生物过程中发生变化中最重要的参数之一，它可以用来估算河流的流速、水位及管道的阻力等参数。

在水工学设计中，它也是使用较多的参数。

根据国内外实验和理论分析研究，可以得出以下结论：
1、直管摩擦阻力系数随着流速的增加而增大，且随着流量的增加而减小。

因此，在相同的流量下，流速越快，摩擦阻力越大；
2、直管摩擦阻力系数随着管径的增大而减小。

当管径超过一定尺寸时，该系数可以被认为是恒定的；
3、随着流体运动物性的改变，直管摩擦阻力系数也会发生变化，流体的温度越高，则抗摩擦能力越强，因此，摩擦系数也随着温度的升高而减小；
4、温度的增加可以减小粘度，从而使摩擦系数变小，在温度较高的情况下，摩擦系数会增大；
5、气泡的存在会减小摩擦系数，在有气泡存在的情况下，摩擦系数会减小；
6、随着流体粘度的增加，摩擦系数也会随之变大；
7、摩擦系数受桨板和沿管壁附着物的影响，如果有污染物或固体悬浮物附着在沿管壁上，摩擦系数会增大。

以上就是关于直管摩擦阻力系数的一些简介，其实它是一个相对复杂，受诸多因素影响的学科。

它不仅与流体流量有关，也与流体密
度、流体粘度、管径等有关，同时还受到温度、气泡、污染物和沿管
壁悬浮附着物影响等等，因此，要准确得出真实的直管摩擦阻力系数，实验加以分析就显得尤为重要。

聚酯纤维的阻力系数
1、聚酯纤维阻力系数
聚酯纤维是一种非常轻质的纤维材料，经常用于工业和运动用品，特别是在航空航天等高性能领域。

由于聚酯纤维的低重量、良好的性能和低成本，它已成为建筑、航空和汽车等制造工艺中非常受欢迎的材料之一。

聚酯纤维的流体动力学性能和力学性能是基于其能够提供可预
测的力学性能而被广泛采用的最重要的原因之一。

因此，流动阻力系数（FRC）是流体动力学性能中最重要的测量参数之一，它可以用来
确定流体与聚酯纤维材料的相互作用是否具有稳定性。

聚酯纤维的流动阻力系数可以通过实验室或野外测试来确定，并可以用来估计与现场应用相关的性能。

一般认为，聚酯纤维的流动阻力系数范围大约为0.1至3.5 N/m2，具体取决于纤维的直径、构成
成分和流体参数。

聚酯纤维的流动阻力系数受到多种因素的影响，如流体的参数（比如流速、密度和粘度）、纤维的构成成分和结构（如纤维直径）等。

其中，纤维直径对流动阻力系数的影响是最显著的，纤维直径越大，流动阻力系数越大。

此外，聚酯纤维的流动阻力系数的稳定性也受到流体参数的影响，特别是当流体粘度发生变化时，流动阻力系数的变化会受到很大的影响。

因此，在进行定性和定量分析时，流体粘度的变化必须要考虑在内。

总之，聚酯纤维的流动阻力系数大约在0.1至3.5 N/m2之间，它受到纤维直径和流体参数的影响。

水流阻力公式在我们的日常生活中，水的流动是一个常见的现象。

无论是潺潺流淌的小溪，还是汹涌澎湃的江河，水都在不断地流动着。

但你有没有想过，水流在流动的过程中会遇到阻力，而这个阻力是可以通过一个公式来计算的呢？这就是水流阻力公式。

咱们先来说说水流阻力是咋回事儿。

就好比你在操场上跑步，风会阻碍你的速度，让你跑得更费劲；水在流动的时候，也会遇到各种各样的阻碍，这就是水流阻力。

那水流阻力公式到底是啥呢？它一般可以表示为：$R = \frac{\rho v^2 C_d A}{2}$ 。

这里面的每个字母都有它特定的含义，$\rho$ 表示流体的密度，$v$ 表示流速，$C_d$ 是阻力系数，$A$ 是物体在垂直于流动方向上的投影面积。

为了让大家更好地理解这个公式，我给大家讲一个我自己的亲身经历。

有一次我去公园散步，看到公园里有一个小小的人工瀑布。

瀑布的水倾泻而下，在下面形成了一个小水潭。

我就站在旁边观察，发现水流从高处落下的时候，速度很快，但是到了水潭里，速度就明显慢下来了。

我当时就在想，这水流的速度变化，不就是因为受到了阻力嘛！如果把这个瀑布想象成一个大的水流通道，从上面流下来的水就像是高速行驶的汽车，而水潭就像是一个突然出现的障碍物，让水流不得不减速。

这就好比公式中的流速 $v$ 发生了变化，从而导致水流阻力也跟着改变。

再比如说，咱们家里的水龙头。

当你把水龙头拧开一点点，水就会慢慢地流出来；要是你把水龙头拧大，水就会“哗哗”地冲出来。

这水流速度的不同，产生的阻力也是不一样的。

水流速度快的时候，阻力相对就大；水流速度慢的时候，阻力也就小一些。

而且，水流阻力还和管道的粗细有关系。

你想想，如果管道很细，水在里面流动的空间就小，就会受到更多的阻碍；要是管道很粗，水就能够更顺畅地流过去，阻力自然就小了。

这就好像公式中的投影面积 $A$ ，面积越大，阻力可能就越大。

还有哦，不同的液体，它们的密度 $\rho$ 不一样，产生的水流阻力也不同。