一年级上 数学思维训练 奥数 第12讲 简单的排列与组合

小学数学中的简单排列和组合问题解析在小学数学的学习中，排列和组合是一种重要的数学运算，它们涉及到数学中的多种概念和方法。

本文将对小学数学中的简单排列和组合问题进行解析，并介绍相关的概念、方法和应用。

一、排列问题排列是指从若干不同的元素中选取若干个元素进行排列的操作。

排列的顺序很重要，因此不同的排列方式会得到不同的结果。

在小学数学中，常见的排列问题包括：选取若干个元素进行排队、选取若干个元素进行站队等。

1. 排队问题排队问题是指将若干个人或物按照一定的顺序进行排队的操作。

假设有5个人（A、B、C、D、E），要求将他们按照一定的顺序排成一队，求出共有多少种不同的排队方式。

根据排列的性质，我们知道第一个人有5种选择，第二个人有4种选择，以此类推，第五个人有1种选择。

因此，总的排队方式为5 × 4 × 3 × 2 × 1 = 120种。

2. 站队问题站队问题是指将若干个人或物按照一定的顺序进行站队的操作。

假设有5个人（A、B、C、D、E），要求将他们按照一定的顺序站成一列，求出共有多少种不同的站队方式。

与排队问题类似，第一个人有5种选择，第二个人有4种选择，以此类推，第五个人有1种选择。

因此，总的站队方式为5 × 4 × 3 × 2 ×1 = 120种。

二、组合问题组合是指从若干不同的元素中选取若干个元素进行组合的操作。

组合的顺序不重要，因此相同的元素组合方式只计算一次。

在小学数学中，常见的组合问题包括：从若干个物品中选取若干个进行搭配、从若干个元素中选取若干个进行组队等。

1. 搭配问题搭配问题是指从若干个物品中选取若干个进行搭配的操作。

假设有3个颜色的帽子（红、黄、蓝）、2种颜色的衣服（白、黑）和2种颜色的鞋子（棕、灰），要求从这些物品中选取一个帽子、一件衣服和一双鞋子进行搭配，求出共有多少种不同的搭配方式。

根据组合的性质，我们知道从3个帽子中选取一个的方式有3种选择，从2种衣服中选取一件的方式有2种选择，从2种鞋子中选取一双的方式有2种选择。

小学数学排列组合思维训练的案例与经验分享数学排列组合是小学阶段的重要知识点之一，但对于一些学生来说，这部分内容可能会相对较难理解和应用。

因此，本文旨在分享一些小学数学排列组合思维训练的案例和经验，帮助学生更好地掌握和应用这一知识点。

一、概念解释和基础练习在开始介绍实际案例之前，首先需要对排列组合的基本概念进行解释和掌握。

排列是指从一组不同元素中选取若干个元素按照一定的顺序排列，而组合则是从一组不同元素中选取若干个元素，顺序不重要。

理解这两个概念是掌握排列组合的基础，可以通过一些基础练习来加强对概念的理解。

例如，给出3个数字：1、2、3，可以让学生列出所有可能的排列和组合。

通过这种练习，学生可以逐渐熟悉排列和组合的概念，并通过实际操作来加深对其理解。

二、生活实例中的排列组合训练为了让学生更好地理解和应用排列组合知识，在教学中可以引入一些生活实例，通过实际案例进行排列组合思维的训练。

下面举几个例子：1. 电子密码锁的密码设置电子密码锁通常由4个数字键组成，要求设计一个4位数密码。

通过这个案例，可以引导学生思考如何从0至9这10个数字中选择4个来设置密码。

通过计算，学生可以得出10个数字中选择4个的排列数，帮助他们理解和应用排列组合的知识。

2. 出游的服装搭配假设一个学生要进行一次2天的郊游，他希望准备足够的衣服搭配。

现在学生手中有5件上衣和3条裤子可供选择。

通过这个案例，可以让学生思考如何进行衣服的搭配，即从5件上衣和3条裤子中选择两个进行搭配，让学生计算有多少种不同的搭配方式。

三、进一步拓展思维和应用除了以上的基础案例外，还可以通过一些更复杂的排列组合思维训练案例，进一步拓展学生的思维和应用能力。

1. 牛顿和苹果树牛顿坐在苹果树下，苹果树上有7个苹果。

牛顿想要选择3个苹果带回家，问他有多少种不同的选择方式？通过这个案例，可以让学生计算从7个苹果中选择3个的组合数，并进一步计算不同的选择方式的总数。

如何解决简单的组合与排列问题组合与排列问题是数学中的一个重要分支，也是我们日常生活中经常遇到的一类问题。

它们涉及到将一组元素按照一定规则进行排列组合，从而得到不同的结果。

在解决这类问题时，我们可以运用一些基本的方法和技巧，以便更加高效地求解。

首先，我们来了解一下组合与排列的概念。

组合是指从一组元素中选取若干个元素，不考虑元素的顺序，而排列则是考虑元素的顺序。

例如，有3个元素A、B、C，从中选取2个元素进行排列，可能的结果有AB、AC、BA、BC、CA、CB；而进行组合时，可能的结果有AB、AC、BC。

可以看出，排列的结果要比组合多，因为排列考虑了元素的顺序。

在解决组合与排列问题时，我们可以运用一些基本的原则和方法。

首先，要明确问题的具体要求，确定需要进行排列还是组合。

其次，要明确元素的个数和选取的个数，这有助于我们确定问题的规模。

接下来，可以运用一些常用的公式和技巧进行求解。

在求解组合问题时，我们可以使用组合公式。

组合公式表示从n个元素中选取r个元素的组合数，可以用C(n, r)来表示。

组合公式的计算公式为C(n, r) = n! / (r! * (n-r)!)，其中n!表示n的阶乘。

例如，如果有5个元素，需要选取3个元素进行组合，可以计算C(5, 3) = 5! / (3! * (5-3)!) = 10。

这意味着从5个元素中选取3个元素进行组合，共有10种可能的结果。

而在求解排列问题时，我们可以使用排列公式。

排列公式表示从n个元素中选取r个元素进行排列，可以用P(n, r)来表示。

排列公式的计算公式为P(n, r) = n! /(n-r)!。

例如，如果有5个元素，需要选取3个元素进行排列，可以计算P(5, 3) = 5! / (5-3)! = 60。

这意味着从5个元素中选取3个元素进行排列，共有60种可能的结果。

除了使用公式进行计算外，我们还可以运用一些技巧来解决组合与排列问题。

例如，可以使用递归的方法进行求解。

数学思维训练——排列问题、组合问题一、排列问题例1、乐乐周末准备先去动物园玩，再去博物馆，请问他一共有多少种路线可以走？【分析】1、审题，提取题目重点信息。

乐乐先去动物园，再去博物馆，一共有多少种路线可以走。

2、解题方法。

方法一：连线法（连线要全面、有序地进行，做到不重复、不遗漏）方法二：计算法乐乐去动物园有4种路线，从动物园到博物馆有3种路线，则乐乐从家到博物馆一共有4×3=12(种)3、写出答案。

（学会用乘法做题速度更快）答：一共有12种路线可以走。

举一反三小练笔：1、小天有3件上衣、3条裤子和2双鞋，每天小天要穿一件上衣、一条裤子和一双鞋，请问小天一共有多少种穿法？3×3×2=18（种）答：小天一共有18种穿法。

2、学校举办运动会，准备了许多小彩旗和旗杆，彩旗的颜色有红、黄、蓝三种，旗杆有木制的和塑料的两种，男生、女生在拿彩旗加油的时候，一共有多少种可能？3×2×2=12(种）答：一共有12种可能。

3、下面是学校午餐的菜单，一共有多少种搭配方法？(每种搭配方法只能有一种主食、一种菜品和一种汤）2×4×2=16（种）答：一共有16种搭配方法。

二、组合问题例2、用1、3、5、7这四个数字不重复组合，可以组成几个比200大的数？【分析】1、认真审题。

（先读题，在列出组成数字的条件）用4个不同的数字组合，可以列出几个比200大的数。

2、用题目中的数字列出所有符合条件的情况。

比200 大的数，分两种情况讨论。

(1)组成的数为三位数三位数比200 大的话，百位是3、5、7 三种情况，数字不能重复，则十位有三个数字可用，即有3种情况，同理个位有2种情况。

则一共有3×3×2=18(个)(2)组成的数为四位数。

组成的四位数无论什么情况都比200 大，所以只需要列出所有组成的四位数的情况即可。

千位有4种情况，百位在千位用了一个数字后有3种情况，同理十位有2种情况，个位有1种情况。

96第十二讲 分 类ʌ知识概述ɔ小朋友们,在日常生活中,你是不是注意到,超市商品的摆放都是按照不同的类型摆放的,商场里的商品也是有条理地把同一类的东西放在一起,人们购物时就能很方便地挑选自己想要购买的商品㊂这实际上就是分类㊂这一讲我们就一起来动手实践,初步学会在不同的事物中寻找共同的特征,将同一类型的物品归成一类㊂例题精学例1 将下面同类的东西圈起来㊂ʌ思路点拨ɔ 这幅图上有鸡㊁梨㊁苹果㊁香蕉㊂图中的梨㊁苹果㊁香蕉都属于水果,是同一类物品,因此把三种水果圈在一起,而鸡是动物,和水果不是同一类物品,因此不能圈在一起㊂同步精练1.将下面同类的东西圈起来㊂(1)(2)97(3)(4)2.下面图中有飞机㊁轮船㊁鸭子㊁小汽车㊁马㊁蝴蝶㊁金鱼㊁火箭,把这些东西分成两类,应该怎样分呢?3.下面的六件物品,要把它们分成两类,应该怎样分比较合理98例2 你能将每一行中不同类的物品圈出来吗?①②③ʌ思路点拨ɔ 仔细观察每一行,第1行的5件物品中,有4件都是水果㊂青菜不是水果,所以应该圈出的物品是青菜㊂第2行的5件物品中,有4件都是食品㊂小汽车不是食品,所以应该圈出来的是小汽车㊂第3行的5件物品中,有4件都是学习用品㊂皮球不是学习用品,所以应该圈出的物品是皮球㊂同步精练1.你能将每一行中不同的物品圈出来吗?①②③992.把下面会飞的动物涂上颜色㊂3.下面第一行画了一个文具盒㊁一个抽屉㊁一只箱子,第二㊁三行画了帽子㊁小刀㊁小飞机㊁尺子㊁小汽车㊁上衣㊁铅笔㊁裤子㊁坦克㊁钢笔㊁围巾㊁小手枪,要把这些东西放入第一行的文具盒㊁抽屉㊁箱子里,怎样放比较合理?100例3 下面的物品,可以怎样分类?ʌ思路点拨ɔ 仔细观察上面的物品,可以看出有些是有生命的,能自己行走;有些是没有生命的,自己不能行走㊂这样就可以把上面的物品按照是否有生命,能不能自己行走来分类,一类是有生命的动物,一类是没有生命的交通工具㊂也可以按照行走的位置来分类,一类是天上飞的,一类是地上跑的,一类是水上行的㊂同步精练1.将下面的图形分一分,把同类的序号写在一个圈里㊂2.把下面的茶杯分一分,把同类的序号写在一个圆圈里,你能用不同的方法分吗101(1)(2)3.把每一组图中的东西分类,你有几种不同的分法?例4下面每组有4张卡片,每一张卡片上都排列着4个数㊂你能找出每组中排列规律与其他三张不一样的那张卡片吗(1)2345 78910 6543 5678(2)8642129631086416141210ʌ思路点拨ɔ第一组的4张卡片,第1,2,4张上的数都是逐渐增加1,第3张卡片上的数是逐渐减少1㊂所以,第3张卡片上的数的排列规律与其他三张不一样㊂第二组的4张卡片中,第1,3,4张卡片上的数都是逐渐减少2,第2张卡片上的数是逐渐减少3,与其他三张不一样㊂同步精练1.下面每组数中,哪一个数与其他三个不一样,把它圈出来㊂(1)2469(2)7162312(3)152516352.下面每组数中,哪一行的规律和其他三行不一样?把它圈出来㊂(1)468100246357914710(2)7777543299992222102103 (3)87 6 55 4 3 26 7 8 99 8 7 6(4)7 5 315 7 9 111 3 5 73 5 7 93.把下面6幅图分一分,你有几种不同的分法?(1)ʻʻʻʻʻʻ (2)һһһһһһ(3)ӘӘӘӘӘӘ(4)ʀʀʀʀʀʀ (5)әәәәәә (6)练习卷一㊁圈一圈㊂把不同类的圈起来㊂1.2.3.4.5.6.7.104105 二㊁分一分㊂1.下面6件物品,要把他们分为两类,应该如何分类比较合理?2.找出与其他三种不同的东西,并把它圈出来㊂(1)(2)3.把下面图中的东西分类,你有几种不同的分法?106三㊁连一连㊂把小动物与他们要吃的东西连起来㊂四㊁填一填㊂按要求分类㊂(只需要写上序号)1071.按长袖㊁短袖分㊂长袖短袖2.按有没有领带分㊂有领带没有领带3.按颜色分㊂黑色的白色的五㊁想一想㊂1.下面六个图形,有几种不同的分法?(开动脑筋,你一定会想出不同的方法!)2.下图中每一行的规律是什么?哪一行与其他三行不同?3.下面每组数中,哪一行的规律与其他三行不一样?把它圈出来㊂(1)2222 3333 7654 7777(2)1357 2468 7543 46810(3)2345 5678 9876 3456(4)2346 4568 5432 1235108。

小学数学排列与组合问题数学是一门让人们思考和逻辑能力得到提升的学科。

在小学阶段，数学教育旨在培养学生的基础数学知识和问题解决能力。

其中，排列与组合是数学中一个重要的概念，它涉及到数的排列和组合方法的计算。

在本文中，我们将探讨小学数学中的排列与组合问题，并通过一些例子来帮助读者更好地理解和应用这一概念。

一、排列问题排列是指从给定的元素中按照一定的规则选择若干个元素进行排列的问题。

在小学数学中，我们通常会碰到两种常见的排列问题：全排列和部分排列。

1. 全排列全排列是指从给定的元素中选择所有元素进行排列的问题。

假设我们有3个元素A、B、C，那么它们的全排列有6种，分别是ABC、ACB、BAC、BCA、CAB、CBA。

2. 部分排列部分排列是指从给定的元素中选择一部分元素进行排列的问题。

假设我们有3个元素A、B、C，我们要求从中选择2个元素进行排列，那么它们的部分排列有6种，分别是AB、AC、BA、BC、CA、CB。

在排列问题中，我们可以使用数学公式来计算全排列和部分排列的数量。

全排列的计算公式为n!（n的阶乘），其中n表示元素的个数。

部分排列的计算公式为n! / (n - m)!，其中n表示元素的个数，m表示选择的元素个数。

二、组合问题组合是指从给定的元素中选择若干个元素进行组合的问题。

在小学数学中，我们通常会碰到两种常见的组合问题：无重复组合和有重复组合。

1. 无重复组合无重复组合是指从给定的元素中选择若干个不重复的元素进行组合的问题。

假设我们有3个元素A、B、C，我们要求从中选择2个元素进行组合，那么它们的无重复组合有3种，分别是AB、AC、BC。

2. 有重复组合有重复组合是指从给定的元素中选择若干个元素进行组合的问题，允许选择的元素重复。

假设我们有3个元素A、B、C，我们要求从中选择2个元素进行组合，那么它们的有重复组合有6种，分别是AA、AB、AC、BB、BC、CC。

在组合问题中，我们可以使用数学公式来计算无重复组合和有重复组合的数量。

小学一年级数学综合专项测题认识简单的数学排列和组合数学排列和组合是小学一年级数学中的重要内容。

通过学习排列和组合，孩子们可以了解到事物的排列方式和组合方式，提高他们的观察力、逻辑思维和问题解决能力。

本文将介绍一些简单的数学排列和组合题目，帮助小学一年级的孩子们更好地理解和掌握这一知识点。

1. 排列问题排列是指将一组事物按照一定的顺序进行排列。

对于小学一年级的孩子们，可以从以下几个方面进行训练：(1) 颜色排列问题：老师给小明和小红各准备了3个小球，颜色分别是红、黄、蓝。

请列出所有可能的颜色排列顺序。

解答：共有6种可能的排列顺序：红黄蓝、红蓝黄、黄红蓝、黄蓝红、蓝红黄、蓝黄红。

(2) 数字排列问题：给定数字1、2、3，请列出所有可能的三位数排列。

解答：共有6种可能的排列：123、132、213、231、312、321。

2. 组合问题组合是指从一组事物中选取若干个进行组合。

对于小学一年级的孩子们，可以从以下几个方面进行训练：(1) 果汁组合问题：小明家里有三种口味的果汁，分别是橙汁、苹果汁和西瓜汁。

小明想要选择两种口味的果汁，一共有多少种组合方式？解答：共有三种组合方式：橙汁+苹果汁、橙汁+西瓜汁、苹果汁+西瓜汁。

(2) 水果组合问题：小红爸爸给小红准备了四种水果，分别是苹果、香蕉、橙子和草莓。

小红想要选择三种水果组成一个水果盘，一共有多少种组合方式？解答：共有四种组合方式：苹果+香蕉+橙子、苹果+香蕉+草莓、苹果+橙子+草莓、香蕉+橙子+草莓。

通过解答以上数学排列和组合题目，可以帮助小学一年级的孩子们对这一知识点有更深入的理解。

在实际生活中，排列和组合的应用也是非常广泛的。

比如，在做饭时选择不同的食材组合，可以制作出各种美味的菜肴；在穿衣时选择不同的服装组合，可以展现出不同的个性和风格。

总结起来，数学排列和组合是小学一年级数学中的重要内容。

通过学习排列和组合，并通过解答一些简单的题目，可以帮助孩子们提高观察力、逻辑思维和问题解决能力。

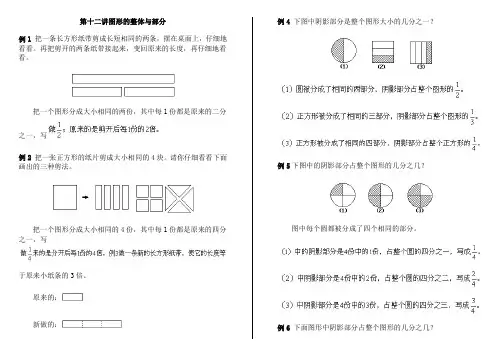
第十二讲图形的整体与部分例1 把一条长方形纸带剪成长短相同的两条，摆在桌面上，仔细地看看。

再把剪开的两条纸带接起来，变回原来的长度，再仔细地看看。

把一个图形分成大小相同的两份，其中每1份都是原来的二分之一，写例2 把一张正方形的纸片剪成大小相同的4块。

请你仔细看看下面画出的三种剪法。

把一个图形分成大小相同的4份，其中每1份都是原来的四分之一，写于原来小纸条的3倍。

原来的：新做的：例4 下图中阴影部分是整个图形大小的几分之一？例5下图中的阴影部分占整个图形的几分之几？图中每个圆都被分成了四个相同的部分。

例6 下面图形中阴影部分占整个图形的几分之几？（1）中的大等边三角形被分成了四个相同的小三角形，带阴影的小三（2）中的垂线将大三角形分成了相同的两部分，带阴影的小三角形占（3）中的大等边三角形先被分成了相同的四部分，阴影小三角形又是习题十二1．下图中哪个图形是整个长方形的二分之一？2．下图中阴影部分的长度是全长的几分之一？3．下图中的三个长方形纸带，哪一个是带阴影图形长度的4倍？4．下图中阴影部分占整个图形的几分之几？5．下图中阴影部分占整个图形的几分之几？6．下图中阴影部分占整个图形的几分之几？7．下图中阴影部分占整个图形的几分之几？习题十二解答3．（2）是阴影部分长度的4倍。

第十三讲折叠描痕法如何将一个图形分成相同的几部分呢？这里介绍一种简单易行的方法——折叠描痕法。

例1 把正方形分成相同的四部分。

第一步：对角折第二步：再对角折第三步：展开，描痕。

例2 把大等边三角形分成相同的四部分，使每部分的形状都与原图形一样。

第一步：左右对角折，然后展开，描痕成虚线，虚线与底边交点就是底边中点。

第二步：将上角折下，使角顶与底边中点重合。

第三步：折左角、折右角，如图示。

第四步：展开，描痕。

例3 用折叠描痕法等分一个长方形纸条。

（1）对折1次，展开描痕，数一数，纸条被等分成几份？（2）对折2次，展开描痕，数一数，纸条被等分成几份？（3）对折3次，展开描痕，数一数，纸条被等分成几份？（4）对折4次，展开描痕，数一数，纸条被等分成几份？（5）对折5次，展开描痕，数一数，纸条被等分成几份？解：习题十三用折叠描痕法等分图形：1．把一张正方形的纸分成四等份，你能想出三种折叠方法来吗？2．把一张长方形的纸分成八等份，你能想出多少种不同的折叠方法来？3．把一张圆形的纸分成二等份、四等份、八等份和十六等份。

数字排列与组合的思维训练数字排列与组合是一种常见的数学概念，在许多领域都有广泛的应用。

通过掌握数字排列与组合的基础知识，并进行相关的思维训练，可以提高我们的逻辑思维能力和问题解决能力。

本文将介绍数字排列与组合的基本概念，探讨其在实际生活中的应用，并提供一些思维训练的例题。

1. 数字排列与组合的基本概念数字排列与组合是指从给定的一组数字中选择若干个数字进行排列或组合的方式。

排列是指从一组数字中按照一定顺序选择若干个数字进行排列，组合则是指从一组数字中无序地选择若干个数字进行组合。

排列的计算公式为：P(n, m) = n! / (n-m)!其中，n表示总的数字个数，m表示选择的数字个数，"!"表示阶乘。

阶乘是指从1到该数的所有正整数相乘，例如5! = 5 × 4 × 3 × 2 × 1 = 120。

组合的计算公式为：C(n, m) = n! / (m! × (n-m)!)2. 数字排列与组合的应用数字排列与组合在实际生活中有着广泛的应用。

以下是几个常见的应用场景：2.1. 抽奖活动在抽奖活动中，我们常常需要从一堆数字中选择若干个数字组成中奖号码。

这就涉及到了数字的组合问题。

根据组合的计算公式，我们可以轻松地计算出有多少种中奖的可能性。

2.2. 密码破解密码破解也是数字排列与组合常见的应用之一。

在某些情况下，我们需要尝试不同的数字组合来解开密码，通过排列和组合的方式进行试验，可以提高密码破解的效率。

2.3. 地址编码在地址编码中，我们常常需要将字母和数字进行排列和组合，生成独一无二的地址编码。

通过掌握数字排列与组合的知识，我们能够更加高效地生成地址编码，提高工作效率。

3. 思维训练例题下面是一些数字排列与组合的思维训练例题，帮助读者更好地理解和掌握相关概念。

3.1. 从数字1、2、3、4中选择3个数字进行排列，问共有多少种排列方式？解答：根据排列的计算公式，P(4, 3) = 4! / (4-3)! = 4! / 1! = 4 × 3 × 2 = 24。