编译原理-实验报告4-逆波兰

Java实现《编译原理》中间代码⽣成-逆波兰式⽣成与计算-程序解析Java 实现《编译原理》中间代码⽣成 -逆波兰式⽣成与计算 - 程序解析编译原理学习笔记（⼀）逆波兰式是什么？逆波兰式（Reverse Polish notation，RPN，或逆波兰记法），也叫后缀表达式（将运算符写在操作数之后）⼀般的表达式⼜称中缀表达式，这种表达式的⼆元运算符放在两个运算量之间。

⽽逆波兰表达式⼜称后缀表达式，这种表达式把运算符放在运算量后⾯。

⽐如如 a+b 的逆波兰式表⽰为 ab+注意：逆波兰式是⼀个⽆括号表达式；逆波兰式的运算符出现的顺序就是原表达式的运算顺序。

（⼆）逆波兰式编译原理有什么关系？逆波兰式，三元式，四元式等是编译原理 - 中间代码⽣成阶段的常见的中间代码形式。

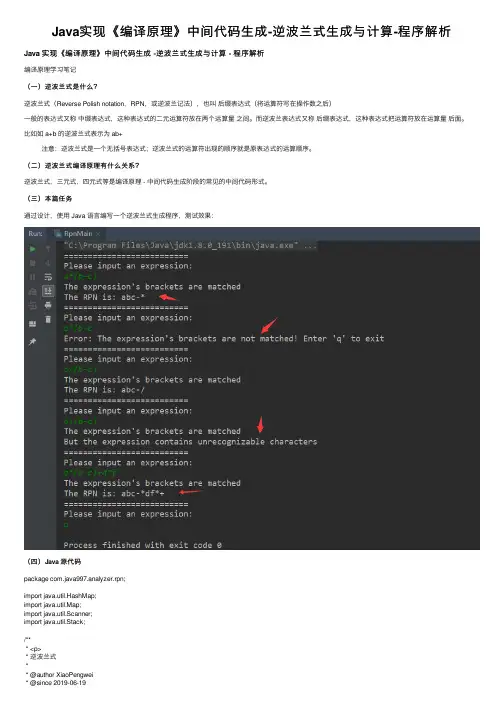
（三）本篇任务通过设计，使⽤ Java 语⾔编写⼀个逆波兰式⽣成程序，测试效果：（四）Java 源代码package com.java997.analyzer.rpn;import java.util.HashMap;import java.util.Map;import java.util.Scanner;import java.util.Stack;/*** <p>* 逆波兰式** @author XiaoPengwei* @since 2019-06-19*/public class RpnMain {/*** 检查算术表达术括号是否匹配, 语法是否正确** @param s 算术表达术* @return boolean*/public boolean isMatch(String s) {//括号符号栈Stack<Character> charStack = new Stack<>();//将表达式的字符串转换成数组char[] charArray = s.toCharArray();//遍历数组for (char aChar : charArray) {if (aChar == '(') {charStack.push(aChar);} else if (aChar == ')') {//如果是 ) , 且栈为空则返回 falseif (charStack.isEmpty()) {return false;} else {//如果是 ) , 且栈不为空则返回 false//peek() 是返回栈顶的值, 不做其他操作if (charStack.peek() == '(') {//把栈顶的值删除charStack.pop();}}}}//⾛到这⾥, 栈为空则表达式正确return charStack.empty();}/*** 判断是否为操作符 + - * /** @param charAt* @return boolean*/public boolean isOperator(char charAt) {return charAt == '+' || charAt == '-' || charAt == '*' || charAt == '/'; }/*** 根据正确的表达式, 获取逆波兰式** @param input* @return ng.String*/public StringBuilder getRpn(String input) {//结果StringBuilder sb = new StringBuilder();sb.append("The RPN is: ");//运算符栈Stack<Character> opStack = new Stack();//运算符优先级Map<Character, Integer> opMap = new HashMap(5);opMap.put('(', 0);opMap.put('+', 1);opMap.put('-', 1);opMap.put('*', 2);opMap.put('/', 2);//处理字符串for (int i = 0; i < input.length(); i++) {//如果是'('直接压栈if (input.charAt(i) == '(') {opStack.push('(');} else if (new RpnMain().isOperator(input.charAt(i))) {//如果是运算符char curOp = input.charAt(i);//如果运算符栈是空，就直接压栈if (opStack.isEmpty()) {opStack.push(curOp);} else if (opMap.get(curOp) > opMap.get(opStack.peek())) {//运算符栈不为空，且当当前运算符的优先级⽐站内第⼀个运算符的优先级⾼的时候，压栈 opStack.push(curOp);} else {//栈不为空，且运算符的优先级⼩于等于栈顶元素for (int j = 0; j <= opStack.size(); j++) {//弹出栈内第⼀个元素char ch = opStack.pop();sb.append(ch);if (opStack.isEmpty()) {opStack.push(curOp);break;} else if (opMap.get(curOp) > opMap.get(opStack.peek())) {opStack.push(curOp);break;}}}} else if (input.charAt(i) == ')') {//如果是')'就把站内'('上的元素都弹出栈for (int j = 0; j < opStack.size(); j++) {char c = opStack.pop();if (c == '(') {break;} else {sb.append(c);}}} else if ('A'<=input.charAt(i)&&input.charAt(i)<='Z'){//如果是字母就直接添加sb.append(input.charAt(i));}else if ('a'<=input.charAt(i)&&input.charAt(i)<='z'){//如果是字母就直接添加sb.append(input.charAt(i));}else if (Character.isDigit(input.charAt(i))){//如果是数字sb.append(input.charAt(i));}else {return new StringBuilder("But the expression contains unrecognizable characters");}}//把栈内剩余的运算符都弹出站for (int i = 0; i <= opStack.size(); i++) {sb.append(opStack.pop());}return sb;}public static void main(String[] args) {RpnMain rpnMain = new RpnMain();Scanner sc = new Scanner(System.in);while (true) {System.out.println("==========================\nPlease input an expression:");String input = sc.nextLine();if ("q".equals(input)) {sc.close();return;} else {if (rpnMain.isMatch(input)) {System.out.println("The expression's brackets are matched");// 获取逆波兰式System.out.println(rpnMain.getRpn(input));} else {System.out.println("Error: The expression's brackets are not matched! Enter 'q' to exit");}}}}}测试：。

逆波兰表达式逆波兰表达式表达式⼀般由操作数(Operand)、运算符(Operator)组成，例如算术表达式中，通常把运算符放在两个操作数的中间，这称为中缀表达式(Infix Expression)，如A+B。

波兰数学家Jan Lukasiewicz提出了另⼀种数学表⽰法，它有两种表⽰形式：把运算符写在操作数之前，称为波兰表达式(Polish Expression)或前缀表达式(Prefix Expression)，如+AB；把运算符写在操作数之后，称为逆波兰表达式(Reverse Polish Expression)或后缀表达式(Suffix Expression)，如AB+；其中，逆波兰表达式在编译技术中有着普遍的应⽤。

算法：⼀、将中缀表达式转换成后缀表达式算法：1、从左⾄右扫描⼀中缀表达式。

2、若读取的是操作数，则判断该操作数的类型，并将该操作数存⼊操作数堆栈3、若读取的是运算符(1) 该运算符为左括号"("，则直接存⼊运算符堆栈。

(2) 该运算符为右括号")"，则输出运算符堆栈中的运算符到操作数堆栈，直到遇到左括号为⽌。

(3) 该运算符为⾮括号运算符：(a) 若运算符堆栈栈顶的运算符为括号，则直接存⼊运算符堆栈。

(b) 若⽐运算符堆栈栈顶的运算符优先级⾼或相等，则直接存⼊运算符堆栈。

(c) 若⽐运算符堆栈栈顶的运算符优先级低，则输出栈顶运算符到操作数堆栈，并将当前运算符压⼊运算符堆栈。

4、当表达式读取完成后运算符堆栈中尚有运算符时，则依序取出运算符到操作数堆栈，直到运算符堆栈为空。

⼆、逆波兰表达式求值算法：1、循环扫描语法单元的项⽬。

2、如果扫描的项⽬是操作数，则将其压⼊操作数堆栈，并扫描下⼀个项⽬。

3、如果扫描的项⽬是⼀个⼆元运算符，则对栈的顶上两个操作数执⾏该运算。

4、如果扫描的项⽬是⼀个⼀元运算符，则对栈的最顶上操作数执⾏该运算。

5、将运算结果重新压⼊堆栈。

中国计量学院《编译原理设计》课程论文题目：中缀表达式的逆波兰表示学生姓名：学号：学生专业：班级：二级学院：一、摘要编译原理是计算机科学与技术专业最重要的一门专业基础课程，内容庞大，涉及面广，知识点多。

由于该课程教、学难度都非常大，往往费了大量时间而达不到预期教学效果俗语说：学习的最好方法是实践。

本课程设计正是基于此，力求为学生提供一个理论联系实际的机会，通过布置一定难度的课题，要求学生独立完成。

我们这次课程设计的主要任务是编程实现对输入合法的中缀表达式进行词法分析、语法分析，构造相应的逆波兰式，计算后缀表达式的值输出结果。

逆波兰式也叫后缀表达式，即将运算符写在操作数之后。

通过实践，建立系统设计的整体思想，锻炼编写程序、调试程序的能力，学习文档编写规范，培养独立学习、吸取他人经验、探索前言知识的习惯，树立团队协作精神。

同时，课程设计可以充分弥补课堂教学及普通实验中知识深度与广度有限的缺陷，更好地帮助学生从全局角度把握课程体系。

关键字：逆波兰式；语法分析；中缀表达式二、实验综述在通常的表达式中，二元运算符总是置于与之相关的两个运算对象之间，所以，这种表示法也称为中缀表示。

对中缀表达式的计值，并非按运算符出现的自然顺序来执行其中的各个运算，而是根据算符间的优先关系来确定运算的次序，此外，还应顾及括号规则。

因此，要从中缀表达式直接产生目标代码一般比较麻烦。

相对的，逆波兰式在计算机看来却是比较简单易懂的结构。

因为计算机普遍采用的内存结构是栈式结构，它执行先进后出的顺序。

三、实验意义对于实现逆波兰式算法，难度并不大，但为什么要将看似简单的中缀表达式转换为逆波兰式，原因就在于这个简单是相对人类的思维结构来说的，对计算机而言中缀表达式是非常复杂的结构。

相对的，逆波兰式在计算机看来却是比较简单易懂的结构。

因为计算机普遍采用的内存结构是栈式结构，它执行四、系统分析词法分析基本原理：词法分析程序完成的是编译第一阶段的工作。

编译原理上机报告名称：逆波兰式的产生及计算学院：信息与控制工程学院专业：计算机科学与技术班级：计算机1401班姓名：叶达成2016年11月4日一、上机目的通过设计、编制、调试一个典型的语法分析程序，实现对词法分析程序所提供的单词序列进行语法检查和结构分析，进一步掌握常用的语法分析方法。

1、选择最有代表性的语法分析方法，如LL(1) 语法分析程序、算符优先分析程序和LR分析分析程序，并至少完成两个题目。

2、选择对各种常见程序语言都用的语法结构，如赋值语句（尤指表达式）作为分析对象，并且与所选语法分析方法要比较贴切。

⑴实验前的准备按实验的目的和要求，编写语法分析程序，同时考虑相应的数据结构。

⑵调试调试例子应包括符合语法规则的算术表达式，以及分析程序能够判别的若干错例。

⑶输出对于所输入的算术表达式，不论对错，都应有明确的信息告诉外界。

⑷扩充有余力的同学，可适当扩大分析对象。

譬如：①算术表达式中变量名可以是一般标识符，还可含一般常数、数组元素、函数调用等等。

②除算术表达式外，还可扩充分析布尔、字符、位等不同类型的各种表达式。

③加强语法检查，尽量多和确切地指出各种错误。

二、基本原理和上机步骤基本原理：将运算对象写在前面，而把运算符号写在后面。

用这种表示法表示的表达式也称做后缀式。

逆波兰式的特点在于运算对象顺序不变，运算符号位置反映运算顺序。

采用逆波兰式可以很好的表示简单算术表达式，其优点在于易于计算机处理表达式。

上机步骤：(1)构造一个栈，存放运算对象。

(2)读入一个用逆波兰式表示的简单算术表达式。

(3)自左至右扫描该简单算术表达式并判断该字符，如果该字符是运算对象，则将该字符入栈。

若是运算符，如果此运算符是二目运算符，则将对栈顶部的两个运算对象进行该运算，将运算结果入栈，并且将执行该运算的两个运算对象从栈顶弹出。

如果该字符是一目运算符，则对栈顶部的元素实施该运算，将该栈顶部的元素弹出，将运算结果入栈。

(4)重复上述操作直至扫描完整个简单算术表达式的逆波兰式，确定所有字符都得到正确处理，我们便可以求出该简单算术表达式的值。

竭诚为您提供优质文档/双击可除编译原理中间代码生成实验报告篇一：编译原理-分析中间代码生成程序实验报告课程名称编译原理实验学期至学年第学期学生所在系部年级专业班级学生姓名学号任课教师实验成绩计算机学院制开课实验室：年月日篇二：编译原理实验中间代码生成实验四中间代码生成一．实验目的：掌握中间代码的四种形式（逆波兰式、语法树、三元式、四元式）。

二．实验内容：1、逆波兰式定义:将运算对象写在前面，而把运算符号写在后面。

用这种表示法表示的表达式也称做后缀式。

2、抽象（语法）树：运算对象作为叶子结点，运算符作为内部结点。

3、三元式：形式序号：（op,arg1,arg2）4、四元式：形式（op,arg1,arg2,result）三、以逆波兰式为例的实验设计思想及算法(1)首先构造一个运算符栈，此运算符在栈内遵循越往栈顶优先级越高的原则。

(2)读入一个用中缀表示的简单算术表达式，为方便起见,设该简单算术表达式的右端多加上了优先级最低的特殊符号“#”。

(3)从左至右扫描该算术表达式，从第一个字符开始判断，如果该字符是数字，则分析到该数字串的结束并将该数字串直接输出。

(4)如果不是数字，该字符则是运算符，此时需比较优先关系。

做法如下：将该字符与运算符栈顶的运算符的优先关系相比较。

如果，该字符优先关系高于此运算符栈顶的运算符，则将该运算符入栈。

倘若不是的话，则将此运算符栈顶的运算符从栈中弹出，将该字符入栈。

(5)重复上述操作(1)-(2)直至扫描完整个简单算术表达式，确定所有字符都得到正确处理，我们便可以将中缀式表示的简单算术表达式转化为逆波兰表示的简单算术表达式。

四、程序代码：//这是一个由中缀式生成后缀式的程序#include#include#include#include#definemaxbuffer64voidmain(){chardisplay_out(charout_ch[maxbuffer],charch[32]);//intcaculate_array(charout_ch[32]);staticinti=0;staticintj=0;charch[maxbuffer],s[maxbuffer],out[maxbuffer];cout cin>>ch;for(i=0;i {out[i]=ch[i];}cout while(out[j]!=#)cout j++;}cout display_out(s,out);//caculate_array;}chardisplay_out(charout_ch[32],charch[]) {inttop=-1;inti=0,data[maxbuffer],n;intj=0;charsta[20];while(ch[i]!=#){if(isalnum(ch[i])){while(isalnum(ch[i])){out_ch[j]=ch[i];j++;i++;}out_ch[j]=;j++;else{switch(ch[i]){case+:case-:if(sta[top]==(||top==-1) {top++;sta[top]=ch[i];i++;}else{//j--;out_ch[j]=sta[top];j++;top--;//i++;}break;//break;case*:case/:if(sta[top]==*/) {out_ch[j]=sta[top];j++;//i++;top--;}else{top++;sta[top]=ch[i];i++;}break;//break;case(:top++;sta[top]=ch[i];i++;break;case):if(sta[top]==() {top--;i++;}if(top==-1){//cout }else{//while(sta[top]!=?(?){ out_ch[j]=sta[top];top--;j++;//}break;}break;/*case?#?:out_ch[j]=?#?; j++;break;*/default:cout ch[i]=#;j=0;break;}}}while(top!=-1){out_ch[j]=sta[top];j++;top--;}out_ch[j]=#;n=0;co(:编译原理中间代码生成实验报告)utwhile(out_ch[n]!=#){cout n++;}cout j=0;returnout_ch[maxbuffer];}五、实验结果：要求：自己给出3个测试用例，观察结果。

实验4.1 目标代码生成-逆波兰式一、实验目的结合课堂上理论知识，将算术表达式首先转化为逆波兰式(后缀表达式)，然后再转化为目标代码(即假想栈式汇编代码)，以此来了解编译器工作的原理。

二、实验环境1.常用微机一台。

2.c++编译环境（常见如vc6.0）。

三、实验要求将逆波兰直接转化为目标代码并输出。

不考虑生成的目标代码质量，并且忽略机器的特性的细节。

变量寄存器使用R0-R7，对于MOV指令，左边为源操作数，右边为目的操作数。

对于其他运算指令，目的操作数和源操作数进行运算，结果保存在存储源操作数的寄存器中，如ADD 3 4，汇编代码为MOV 3 R0 ADD 4 R0。

四、实验过程1.实验算法1.1逆波兰式生成算法首先设一个运算符栈，当从左到右扫描一个表达式时，若扫描到运算分量，将其保存在数组中。

若扫描到运算符，若运算符栈为空，则该运算符入栈，若栈不为空，则比较运算符的优先级，若当前运算符优先级小于等于栈顶运算符优先级，则将栈顶运算符保存到数组中，并且出栈，继续比较当前运算符和栈顶符号的优先级。

若当前运算符优先级大于栈顶优先级，则当前运算符入栈。

只要碰到’(‘，就进栈，当表达式已扫描完，将栈中的运算依次存入数组中，并出栈。

最后打印出数组的值，’(‘和’)’不存入数组中，所以不输出。

1.2目标代码生成算法首先设一个运算分量栈，开始扫描生成的逆波兰式。

若扫描的是运算分量，则将运算分量入栈。

若扫描到运算符，则按给定的运算符是几目运算(本程序并没有考虑一目运算符，所有的运算符都是二目)，将运算分量栈中栈顶元素保存在一个字符数组变量中，并出栈，然后将字符串变量和栈顶元素生成该运算符的目标代码。

最后把运算结果的寄存器入栈，直到扫描完逆波兰式。

2.程序主要函数说明(1)string Apoland(string expre):将表达式转化为逆波兰式输出。

(2)int top(string ch):本程序中所使用的寄存器为通用寄存器R0-R7，用单字符@，#，<，>，[，]，{，}来代替8个寄存器入栈，函数返回的是寄存器的号，如R0，@代替其进栈，栈顶为@时，则返回0。

编译原理课程实验报告班级学号姓名实验名称逆波兰式的产生一、实验目的：将非后缀式用来表示的算术表达式转换为用逆波兰式来表示的算术表达式，并计算用逆波兰式来表示的算术表达式的值。

二、实验要求：输出的格式如下：(1)逆波兰式的生成及计算程序，编制人：姓名，学号，班级(2)输入一以#结束的中缀表达式(包括+—*/（）数字#)：在此位置输入符号串如(28+68)*2#(3)逆波兰式为：28&68+2*(4)逆波兰式28&68+2*计算结果为192备注：(1)在生成的逆波兰式中如果两个数相连则用&分隔，如28和68，中间用&分隔；(2)在此位置输入符号串为用户自行输入的符号串。

注意：1.表达式中允许使用运算符（+-*/）、分割符（括号）、数字，结束符#；2.如果遇到错误的表达式，应输出错误提示信息（该信息越详细越好）；三、实验过程：（一）准备：1.阅读课本有关章节，2.考虑好设计方案；3.设计出模块结构、测试数据，初步编制好程序。

（1）定义部分：定义常量、变量、数据结构。

（2）初始化：设立算符优先分析表、初始化变量空间（包括堆栈、结构体、数组、临时变量等）；（3）控制部分：从键盘输入一个表达式符号串；（4）利用算符优先分析算法进行表达式处理：根据算符优先分析表对表达式符号串进行堆栈（或其他）操作，输出分析结果，如果遇到错误则显示错误信息。

（5）对生成的逆波兰式进行计算。

（二）上课上机：将源代码拷贝到机上调试，发现错误，再修改完善。

第二次上机调试通过。

四、实验结果（1）写出程序流程图（2）给出运行结果。

中国计量学院《编译原理设计》课程论文题目：中缀表达式的逆波兰表示学生姓名：学号：学生专业：班级：二级学院：一、摘要编译原理是计算机科学与技术专业最重要的一门专业基础课程，内容庞大，涉及面广，知识点多。

由于该课程教、学难度都非常大，往往费了大量时间而达不到预期教学效果俗语说：学习的最好方法是实践。

本课程设计正是基于此，力求为学生提供一个理论联系实际的机会，通过布置一定难度的课题，要求学生独立完成。

我们这次课程设计的主要任务是编程实现对输入合法的中缀表达式进行词法分析、语法分析，构造相应的逆波兰式，计算后缀表达式的值输出结果。

逆波兰式也叫后缀表达式，即将运算符写在操作数之后。

通过实践，建立系统设计的整体思想，锻炼编写程序、调试程序的能力，学习文档编写规范，培养独立学习、吸取他人经验、探索前言知识的习惯，树立团队协作精神。

同时，课程设计可以充分弥补课堂教学及普通实验中知识深度与广度有限的缺陷，更好地帮助学生从全局角度把握课程体系。

关键字：逆波兰式；语法分析；中缀表达式二、实验综述在通常的表达式中，二元运算符总是置于与之相关的两个运算对象之间，所以，这种表示法也称为中缀表示。

对中缀表达式的计值，并非按运算符出现的自然顺序来执行其中的各个运算，而是根据算符间的优先关系来确定运算的次序，此外，还应顾及括号规则。

因此，要从中缀表达式直接产生目标代码一般比较麻烦。

相对的，逆波兰式在计算机看来却是比较简单易懂的结构。

因为计算机普遍采用的内存结构是栈式结构，它执行先进后出的顺序。

三、实验意义对于实现逆波兰式算法，难度并不大，但为什么要将看似简单的中缀表达式转换为逆波兰式，原因就在于这个简单是相对人类的思维结构来说的，对计算机而言中缀表达式是非常复杂的结构。

相对的，逆波兰式在计算机看来却是比较简单易懂的结构。

因为计算机普遍采用的内存结构是栈式结构，它执行四、系统分析词法分析基本原理：词法分析程序完成的是编译第一阶段的工作。

i=0; zf=0; j=0; h=0; while(wfh[i]!='$') { ch1=wfh[i]; ch2=wfh[i+1]; if(ch1>='0' && ch1<='9') { if((ch2>='0'&& ch2<='9') || ch2=='.' || zf=1; else zf=0; } if(ch1=='.') { if(ch2>='0'&& ch2<='9'&& j<=1 ) zf=1;
ch2=='e'||ch2=='$' )
zf=1; elsh
zf=0; } if(ch1=='e'){ if(ch2>='0' && ch2<='9' && h<=1||ch2=='+'||ch2=='-')
zf=1; else zf=0; } if(ch1=='+' || ch1=='-'){
if(i==0) break; if(ch2>='0' && ch2<='9'||ch2=='$') zf=1; else zf=0; } if (zf==0) break; else i++; } if(zf==0) printf("Input number are error!\n"); else printf("Input number are right!\n"); }

逆波兰式生成程序一、实验的性质、目的和任务1、培养学生初步掌握编译原理实验的技能。

2、验证所学理论、巩固所学知识并加深理解。

3、对学生进行实验研究的基本训练。

二、实验内容掌握语法分析的基本思想，并用高级语言编写逆波兰式生成程序三、实验要求利用逆波兰式生成算法编写程序，将从键盘上输入的算术表达式（中缀表达式）转化成逆波兰式。

四、常用运算符的优先关系如上表所示的优先关系矩阵表示了+，-，*，/，↑，（，）等七种运算符之间的相互优先关系。

“＞、＜、＝”三种符号分别代表“大于”、“小于”、“相等”三种优先关系。

左边的“＝”与右边的“（”之间没有优先关系存在，所以表中为空白。

逆波兰表达式生成算法的关键在于比较当前运算符与栈顶运算符的优先关系，若当前运算符的优先级高于栈顶运算符，则当前运算符入栈，若当前运算符的优先级低于栈顶运算符，则栈顶运算符退栈。

五、程序流程图六、程序源代码#include <iostream> #include <stack>#include <string>using namespace std;int prior(char op){if(op=='+'||op=='-')return 1;if(op=='*'||op=='/')return 2;return 0;}string middletolast(string middle) {stack<char> op;string ans;for(int i=0;i<middle.size();i++) {char c=middle[i];if(c>='0'&&c<='9'){ans.append(1,c);}else{if(c=='(')op.push('(');else{if(c==')'){while(op.top()!='('){ans.append(1,op.top());op.pop();}op.pop();}else{if(op.empty()){op.push(c);}else{if(prior(c)>prior(op.top()))op.push(c);else{while(!op.empty()&&prior(c)<=prior(op.top())){ans.append(1,op.top());op.pop();}op.push(c);}}}}}}while(!op.empty()){ans.append(1,op.top());op.pop();}return ans;}int main(){string mdata,res;cout<<"请输入常规表达式：\n"<<endl;cin>>mdata;res=middletolast(mdata);for(int i=0;i<res.size();i++){if(i==0)cout<<res[i];elsecout<<' '<<res[i];}cout<<endl;return 0;}七、实验结果。

实验一约瑟夫环问题基本要求需要基于线性表的基本操作来实现约瑟夫问题需要利用数组来实现线性表输入输出格式输入格式：n，m输出格式1：在字符界面上输出这n个数的输出序列输出格式2：将这n个数的输出序列写入到文件中实验原理设编号为1-n的n(n>0)个人按顺时针方向围成一圈．首先第1个人从1开始顺时针报数．报m的人(m 为正整数)．令其出列。

然后再从他的下一个人开始，重新从1顺时针报数，报m的人，再令其出列。

如此下去，直到圈中所有人出列为止。

求出列编号序列。

利用数组对每个人排序。

利用while函数找到数到m的人，当第L个人出圈之后，报数，并在用后面的人依次填充。

实验程序#include<iostream>using namespace std;int main(){int A[100],n,m;cout<<"输入总人数和喊到的数字:\n";cin>>n>>m;int i,j,k=n;for(i=0;i<n;i++)A[i]=i+1; //让数组的值从1开始while(k>0){for(j=1;j<m;j++)i=(i+1)%k; //寻找第一个喊到m的人cout<<A[i]<<" ";for(j=i+1;j<k;j++) //从i+1开始继续向后喊数A[j-1]=A[j];k--; //剩余人数}cout<<"\n"<<A[i];cout<<endl;return 0;}。

(编译原理)逆波兰式算法的源代码一.实验目的1．深入理解算符优先分析法2．掌握FirstVt和LastVt集合的求法有算符优先关系表的求法3．掌握利用算符优先分析法完成中缀表达式到逆波兰式的转化二.实验内容及要求将非后缀式用来表示的算术表达式转换为用逆波兰式来表示的算术表达式，并计算用逆波兰式来表示的算术表达式的值。

程序输入/输出示例：输出的格式如下：(1)(2)输入一以#结束的中缀表达式(包括+—*/（）数字#)(3)(4)逆波兰式备注：(1)在生成的逆波兰式中如果两个数相连则用&分隔，如28和68，中间用&分隔；串。

注意：1.表达式中允许使用运算符（+-*/）、分割符（括号）、数字，结束符#；2.如果遇到错误的表达式，应输出错误提示信息（该信息越详细越好）；3.对学有余力的同学，测试用的表达式事先放在文本文件中，一行存放一个表达式，同时以分号分割。

同时将预期的输出结果写在另一个文本文件中，以便和输出进行对照；三.实验过程1、逆波兰式定义将运算对象写在前面，而把运算符号写在后面。

用这种表示法表示的表达式也称做后缀式。

逆波兰式的特点在于运算对象顺序不变，运算符号位置反映运算顺序。

采用逆波兰式可以很好的表示简单算术表达式，其优点在于易于计算机处理表达式。

2、产生逆波兰式的前提中缀算术表达式3、逆波兰式生成的实验设计思想及算法(1)首先构造一个运算符栈，此运算符在栈内遵循越往栈顶优先级越高的原则。

(2)读入一个用中缀表示的简单算术表达式，为方便起见,设该简单算术表达式的右端多加上了优先级最低的特殊符号“#”。

(3)从左至右扫描该算术表达式，从第一个字符开始判断，如果该字符是数字，则分析到该数字串的结束并将该数字串直接输出。

(4)如果不是数字，该字符则是运算符，此时需比较优先关系。

做法如下：将该字符与运算符栈顶的运算符的优先关系相比较。

如果，该字符优先关系高于此运算符栈顶的运算符，则将该运算符入栈。

内蒙古工业大学信息工程学院实验报告课程名称：编译原理实验名称：语法制导把表达式翻译成逆波兰式实验类型：验证性□ 综合性□ 设计性□实验室名称：电力大楼九楼东机房班级：计13-1学号：201320201045姓名：徐铭贝组别：同组人：成绩：实验日期：2016-6一)实验目的进一步掌握语法制导翻译的概念，理解中间语言，设计出错处理程序方法，掌握把表达式翻译成中间语言的算法。

(二)实验内容1．从左到右扫描中缀表达式，经语法分析找出中缀表达式出现的错误并给出错误的具体位置和类型。

一个运算符栈存放暂时不能出现的运算符，逆波兰区存放逆波兰表达式。

2．测试所编程序，给出正确和错误的结果。

(三)实验要求1．学生课前要认真阅读实验指导，理解实验内容与相关理论知识的关系，并完成预习报告2．用C语言或其它高级语言编写程序3．写出实验报告实验二语法制导把表达式翻译成逆波兰式一、实验名称语法制导把表达式翻译成逆波兰式二、实验目的通过上机实习加深对语法指导翻译原理的理解，进一步掌握语法制导翻译的概念，掌握运算符优先权的算法，将语法分析所识别的表达式变换成中间代码的翻译方法。

三、表达式生成逆波兰式的算法1、初始化△送到运算符栈。

2、扫描左括号“（”，把△送到运算符栈。

3、扫描到变量，把它送到逆波兰区。

4、扫描到运算符（1）栈内运算符比较a.栈内运算符>=栈外运算符，把栈内运算符送到逆波兰区。

b.栈内运算符<栈外运算符，把栈外运算符入栈。

( 2 ) 栈内是△把运算符入栈。

5、扫描右括号“)”。

( 1 )栈内是运算符，把栈内运算符送到逆波兰区。

( 2 )栈内是△则△退栈，读入下一个字符。

6、扫描到#（结束符）( 1 )栈内是运算符，把栈内运算符送到逆波兰区。

( 2 )栈内是△结束，否则继续分析。

四、程序清单#include<stdio.h>int jg[30];int fh[30];char fuhao[30][30]; //char fuhao1[30];int fuhao2[30];int number4=0;int number5=0;int bds[30];int number3=0; //表达式char fh1[6]={'(','+','-','*','/','^'}; //关系表int number1=0; //结果int number2=0; //符号int main(){int gx,gx1; //比较关系char aa; //字符int a,b,c=0,sum=0; //平常使用的while(1){c=0;while(1){scanf("%c",&aa);bds[number3]=aa;number3++;if(aa=='#'){for(a=number2-1;a>=0;a--){jg[number1]=fh[a];number1++;}break;}if(aa<='z'&&aa>='a'){jg[number1]=aa;number1++;// printf("aaa\n");}if(aa=='('){fh[number2]=aa;number2++;// printf("bbb\n");}if(aa=='+'||aa=='-'||aa=='*'||aa=='/'||aa=='^') // (<+=-<*=/<^<) {while(1){gx=0;gx1=0;for(a=0;a<6;a++){if(aa==fh1[a])gx=a;if(number2==0){break;}if(fh[number2-1]==fh1[a])gx1=a;}if(number2==0){fh[number2]=aa;number2++;break;}if(gx==1||gx==2){gx=1;}if(gx1==1||gx1==2){gx1=1;}if(gx==4||gx==3){gx=2;}if(gx1==4||gx1==3){gx1=2;}if(gx1>=gx){if(number2==0){// printf("ge2ge2ge2\n");fh[number2]=aa;number2++;break;}// printf("gege\n");jg[number1]=fh[number2-1];// printf("%c\n",fh[number2-1]);fh[number2-1]='\0';number1++;number2--;continue;}else{// printf("ge1ge1\n");fh[number2]=aa;number2++;break;}}}if(aa==')'){// printf(")))\n");for(a=number2-1;a>=0;a--){if(fh[a]=='('){fh[a]='\0';number2--;break;}else {jg[number1]=fh[a];number1++;fh[a]='\0';number2--;}}}}for(a=0;a<number1;a++){printf("%c",jg[a]);}printf("\n");for(a=0;a<number3-1;a++){if(bds[a]<='z'&&bds[a]>='a')if(bds[a+1]<='z'&&bds[a+1]>='a') {fuhao[number4][number5]=bds[a];number5++;}else{fuhao[number4][number5]=bds[a];fuhao2[number4]=number5+1;number5=0;fuhao1[number4]='a'+number4;number4++;}}printf("从前到后依次为:\n");for(a=0;a<number4;a++){printf("%c:::%s\n",fuhao1[a],fuhao[a]);}for(a=0;a<number4;a++){printf("%c",fuhao1[a]);sum=sum+fuhao2[a];for(;(jg[sum]<='z'&&jg[sum]>='a')!=1;sum++) { if(sum>=number1){break;}printf("%c",jg[sum]);}}printf("\n");for(a=0;a<30;a++){jg[a]='\0';fh[a]='\0';for(b=0;b<30;b++){fuhao[a][b]='\0';}}number1=0;number2=0;number3=0;number4=0;number5=0;sum=0;}return 0;}五、算法思想有三个数组分别存放的是符号、变量、优先级、之后输入字符，进行判断是什么东西，之后再对他们进行进出符号，变量直接进，判断优先级（老师上课所讲的逆波兰式如何生成），最后显示出其逆波兰式。

第四章语义分析和中间代码生成4.1 完成下列选择题：(1) 四元式之间的联系是通过实现的。

a. 指示器b. 临时变量c. 符号表d. 程序变量(2) 间接三元式表示法的优点为。

a. 采用间接码表，便于优化处理b. 节省存储空间，不便于表的修改c. 便于优化处理，节省存储空间d. 节省存储空间，不便于优化处理(3) 表达式(┐A∨B)∧(C∨D)的逆波兰表示为。

a. ┐AB∨∧CD∨b. A┐B∨CD∨∧c. AB∨┐CD∨∧d. A┐B∨∧CD∨(4) 有一语法制导翻译如下所示：S→bAb {print″1″}A→(B {print″2″}A→a {print″3″}B→Aa) {print″4″}若输入序列为b(((aa)a)a)b，且采用自下而上的分析方法，则输出序列为。

a. 32224441 b. 34242421c. 12424243d. 34442212【解答】(1) b (2) a (3) b (4) b4.2 何谓“语法制导翻译”？试给出用语法制导翻译生成中间代码的要点，并用一简例予以说明。

【解答】语法制导翻译(SDTS)直观上说就是为每个产生式配上一个翻译子程序(称语义动作或语义子程序)，并且在语法分析的同时执行这些子程序。

也即在语法分析过程中，当一个产生式获得匹配(对于自上而下分析)或用于归约(对于自下而上分析)时，此产生式相应的语义子程序进入工作，完成既定的翻译任务。

用语法制导翻译(SDTS)生成中间代码的要点如下：(1) 按语法成分的实际处理顺序生成，即按语义要求生成中间代码。

(2) 注意地址返填问题。

(3) 不要遗漏必要的处理，如无条件跳转等。

例如下面的程序段：if (i>0) a=i+e-b*d; else a=0;在生成中间代码时，条件“i>0”为假的转移地址无法确定，而要等到处理“else”时方可确定，这时就存在一个地址返填问题。

此外，按语义要求，当处理完(i>0)后的语句(即“i>0”为真时执行的语句)时，则应转出当前的if语句，也即此时应加入一条无条件跳转指令，并且这个转移地址也需要待处理完else之后的语句后方可获得，就是说同样存在着地址返填问题。

5.1目的和要求1、掌握表达式由中缀式转变成后缀式的过程。

2、学会用栈这种数据结构实现的方法。

5.2实验环境Windows XP + VC++6.05.3实验准备写出一个中缀式，分析可能得到的后缀式s=（a+b）*c 后缀式sab+c*=s<a 后缀式sa<a=b&c=d 后缀式ab=cd=&a>b|c=d 后缀式ab>cd=|5.4实验内容及步骤1、输入已给的文本格式的扫描程序biaoda.cpp文件，然后编译运行，检查修改错误。

2、编译成功后，提示输入表达式，用回车键查看输出的结果。

3、比较自己分析的结果和屏幕上的输出结果。

给出代码没有‘=’，‘<’,‘>’,‘&’,‘|’运算结果错误5.5实验小结1、得到的经验。

中缀表达式转换为后缀表达式2、遇到的主要问题。

运算符优先级不清楚，自行查找。

3、改进方案。

在原代码中加入有关‘=’，‘<’,‘>’,‘&’,‘|’的运算。

else if(str[i]=='&'|| str[i]=='|') {while((S.top!=S.base)&&(*(S.top-1)!='(')) {Pop(S,ch);exp[j]=ch;j++;}Push(S,str[i]);} else if(str[i]=='=') {while((*(S.top-1)=='=')){Pop(S,ch);exp[j]=ch;}Push(S,str[i]);} /* end of else if */else if(str[i]=='+'||str[i]=='-') {while((S.top!=S.base)&&(*(S.top-1)!='(')){Pop(S,ch);exp[j]=ch;j++;}Push(S,str[i]);} /* end of else if */else if(str[i]=='<'||str[i]=='>') {while((S.top!=S.base)&&(*(S.top-1)!='(')){Pop(S,ch);exp[j]=ch;j++;}Push(S,str[i]);} /* end of else if */else if (str[i]=='*'||str[i]=='/'){while((*(S.top-1)=='*')||(*(S.top-1)=='/')) {Pop(S,ch);exp[j]=ch;j++;}Push(S,str[i]);} /* end of else if */i++;} /* end of while */exp[j]='#';cout<<"\n\n输入的表达式";i=1;while(str[i+1]!='#'){cout<<str[i];} /* end of while */ cout<<"逆波兰表达式为：\n"; i=0;while(exp[i]!='#'){cout<<exp[i];i++;}}。

逆波兰式的产生及计算一、目的与要求1、目的通过上机实习，加深对语法制导翻译原理的理解，掌握将语法分析所识别的语法范畴变换为某种中间代码的语义翻译方法。

2、要求（1）选用目前世界上普遍采用的语义分析方法──语法制导翻译技术。

（2）语义分析对象重点考虑经过语法分析后已是正确的语法范畴，实习重点是语义子程序。

（3）中间代码选用比较常见的形式，例如四元式。

二、背景知识属性文法：A=(G，V，F)，其中：G：一个CFG, 属性文法的基础。

V：有穷的属性集：每个属性与一个文法符号相关联，这些属性代表与文法符号相关的语义信息，如：类型、地址、值、代码、符号表内容等等。

属性与变量一样，可以进行计算和传递，属性加工的过程即是语义处理的过程。

属性加工与语法分析同时进行。

属性的表示：标始符（或数），写在相应文法的下边，点记法：E.Val,E.Place,E.Type…。

F：关于属性的属性断言或一组属性的计算规则(称为语义规则)。

断言或语义规则与一个产生式相联，只引用该产生式左端或右端的终结符或非终结符相联的属性。

属性有两类：综合属性：归约型属性，用于“自下而上”传递信息。

继承属性：推导型属性，用于“自上而下”传递信息。

综合属性的例子：非终结符E、T及F都有一个综合属性val,符号digit有一个综合属性，它的值由词法分析器提供。

与产生式L→E对应的语义规则仅仅是打印由E产生的算术表达式的值的一个过程，我们可认为这条规则定义了L的一个虚属性。

某些非终结符加上标是为了区分一个产生式中同一非终结符多次出现。

设表达式为3＊5+4，则语义动作打印数值19。

3*5+4的带注释的分析树继承属性的例子：继承属性的自上而下定值（Real id1，id2，id3）：Real id1，id2，id3的分析树L－属性文法：一个属性文法称为L－属性文法，如果对于每个产生式A→X1X2…Xn，满足：1、Xj（1≤j≤n）的继承属性仅依赖于下述属性值中的一种：A的继承属性或产生式右部位于Xj左边的符号X1，X2，…，Xj-1的属性。

课程实习报告题目：逆波兰表达式班级：智能1201班姓名：易全政学号：201208070123完成日期：2014.3.27一、需求分析1、本程序要求输入一个包含四则运算且操作数为正数的逆波兰表达式，并利用堆栈求出结果值2、输入的的后缀表达式由键盘输入到字符界面，并要求相邻的操作数之间用空格隔开，最后以‘#’字符作为结束标识符3、如果该后缀表达式正确，那么在字符界面上输出其结果，计算结果小数点后面保留两位有效数字，如果不正确，请在字符界面上输出表达式错误提示4、测试数据输入2 3 * 1 -#输出5二、概要设计1、抽象数据类型为实现上述程序的功能，应该以字符串存入输入的字符以及操作数为实现操作数的保存以及运算，应该利用堆栈来完成2、算法的基本思想通过键盘一些字符与操作数，利用一个字符串来保存，并同时定义一个栈与字符串指针，每次栈里面保存当前输入的操作数，而当遇到运算符时将栈顶与栈的上个元素进行相应的运算，并将栈顶元素弹出同时保存进入新的栈顶中，在最后进行判断从而实现对输入正确的逆波兰表达式输出其运算结果。

3、程序的流程程序的流程由三个模块组成：（1）输入模块：输入字符串，并将地址赋给字符串指针（2）运算模块：输入字符的判断，操作数的入栈以及相应的运算（3）输出模块：对于符合条件的逆波兰表达式输出运算结果三、详细设计1、物理数据类型题目要求输入一行运算表达式，为一个字符串，并定义字符串指针保存其地址；定义一个顺序栈，用double型数组来保存栈内元素；用typedef定义一个新的结构体类型；含有很多的int与double型的变量；23、算法的时空分析根据程序的实现情况可知，算法运行时间主要集中在do while循环上，所以对于该字符串，若含有n个字符，则必有产生的时间代价为：Θ（n）；4、输入输出的格式输入请输入要计算的表达式：//提示等待输入输出等待输出输出的式子的构成为：输入的表达式= 运算结果或者输入的表达式--- error四、测试结果第一组测试：单字符减加乘除：输入2 3 4 + - 5 * 3 /#输出2 3 4 + - 5 * 3 /# =-8.33第二组测试：连续字符的加减乘除输入12 34 + 234 – 2 * 3 /#输出12 34 + 234 – 2 * 3 /# =-125.33第三组测试：输入错误情况测试输入1 2 3 -#输出1 2 3 -#———Input error!第四组测试：计算错误情况测试输入3 0 /#输出3 0 /#———Input error!五、实验心得本次实验通过在栈的基础上要进行对逆波兰表达式的计算，最初只是进行了单个字符的计算，并且很容易的就编出来了并且验证争取，但是在处理连续字符，例如12 2 *# 上却多次尝试但是都没有效果，就是在用cin输入字符串时，遇到空格键会自动终止，但是运算结果不正确，因为在同学的提示下利用getline来输入字符串就可以避免这种情况，因为我在原有程序的基础上做出了改进，并实现了最后的编程。