相关分析与回归分析及曲线估计

统计学中的相关分析与回归分析的关系统计学是一门研究如何收集、整理、描述和解释数据的学科。

在统计学中，相关分析和回归分析是两个重要的方法，用于了解和探究变量之间的关系。

尽管相关分析和回归分析在某些方面有相似之处，但它们在目的、数据类型和结果解释方面存在一些差异。

相关分析是一种用于衡量和描述两个或多个变量之间关联关系的方法。

相关分析可以帮助我们确定变量之间的线性相关程度，即一个变量的变化伴随着另一个变量的变化。

通过计算相关系数，我们可以了解这种关系的强度和方向。

常用的相关系数包括皮尔逊相关系数和斯皮尔曼等级相关系数。

与此不同，回归分析旨在建立一个数学模型，以描述和预测因变量与自变量之间的关系。

回归分析可以通过拟合曲线或平面来表示变量之间的关系，并用方程式来描述这种关系。

回归分析使用的模型可以是线性回归、多项式回归、对数回归等。

通过回归分析，我们可以根据自变量的值来估计因变量的值，并评估自变量对因变量的影响程度。

虽然相关分析和回归分析在某些情况下可互相转化，但它们具有不同的目标和应用范围。

相关分析主要用于探索变量之间的关系，确定它们之间的关联强度和方向，但不提供因果关系。

而回归分析则旨在建立一个模型，通过这个模型可以对未知的因变量进行预测，并且可以评估自变量对因变量的影响。

此外，相关分析和回归分析适用于不同类型的数据。

相关分析通常用于分析连续变量之间的关系，而回归分析可以应用于连续变量、二分类变量和多分类变量之间的关系。

在实际应用中，相关分析和回归分析常常结合使用。

首先，我们可以通过相关分析来初步检验变量之间是否存在关系。

如果相关分析结果显示两个变量之间存在显著相关性，我们可以进一步使用回归分析来建立一个模型，以更好地理解和预测这种关系。

在总结中，统计学中的相关分析和回归分析是两个相互关联的方法。

相关分析用于探究变量之间的关系和相关性，而回归分析则用于建立一个数学模型，描述和预测因变量与自变量之间的关系。

简述数学中的回归分析与相关性检验回归分析和相关性检验是数学中常用的两种统计方法，用于研究变量之间的关系和进行预测分析。

本文将简要介绍回归分析和相关性检验的基本概念和应用。

一、回归分析回归分析是一种用于研究自变量和因变量之间关系的统计方法。

它通过建立一个数学模型，来描述自变量对因变量的影响程度和趋势。

回归分析常用于预测和解释变量之间的关系，同时还可以用于控制其他因素对因变量的影响。

在回归分析中，自变量通常是独立变量，而因变量是被解释或预测的变量。

回归分析的基本原理是找到最佳拟合的直线或曲线，使得因变量的观测值与预测值之间的误差最小。

常见的回归分析方法包括线性回归、多元回归、非线性回归等。

线性回归是最常见的回归分析方法之一，它假设自变量和因变量之间存在线性关系。

线性回归模型可以表示为：Y = β0 + β1X + ε，其中Y表示因变量，X表示自变量，β0和β1表示回归系数，ε表示误差项。

通过最小二乘法可以估计出回归系数的值，进而进行预测和推断。

多元回归是一种包含多个自变量的回归分析方法。

它可以用于研究多个自变量对因变量的影响，并控制其他因素的影响。

多元回归模型可以表示为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε，其中X1、X2、...、Xn表示多个自变量。

非线性回归是一种用于研究非线性关系的回归分析方法。

它通过拟合非线性函数来描述自变量和因变量之间的关系。

非线性回归模型的形式可以根据具体问题进行选择，例如指数模型、对数模型、幂函数模型等。

回归分析广泛应用于各个领域，例如经济学、社会学、医学等。

它可以帮助研究人员理解变量之间的关系，预测未来趋势，以及进行决策和政策制定。

二、相关性检验相关性检验是一种用于判断两个变量之间关系强度和方向的统计方法。

它可以帮助研究人员确定变量之间是否存在相关性，以及相关性的程度。

常用的相关性检验方法包括皮尔逊相关系数、斯皮尔曼相关系数等。

皮尔逊相关系数用于度量两个连续变量之间的线性相关性，取值范围在-1到1之间。

相关分析和回归分析客观事物之间的关系分为函数关系和统计关系，函数关系也就是我们通常所说的一一对应的关系，而统计关系是指两事物之间的一种非一一对应的关系，即当一个变量x取一定值时，另一变量y无法依确定的函数取唯一确定的值。

事物之间的统计关系是普遍存在，且有的关系强，有的关系弱。

相关分析和回归分析都是以不同方式测度事物之间统计关系的有效工具。

实际应用中。

这两种分析方法经常互相结合渗透。

一、相关分析相关分析通过图形和数值两种方式，能够有效的揭示事物之间统计关系的强弱程度。

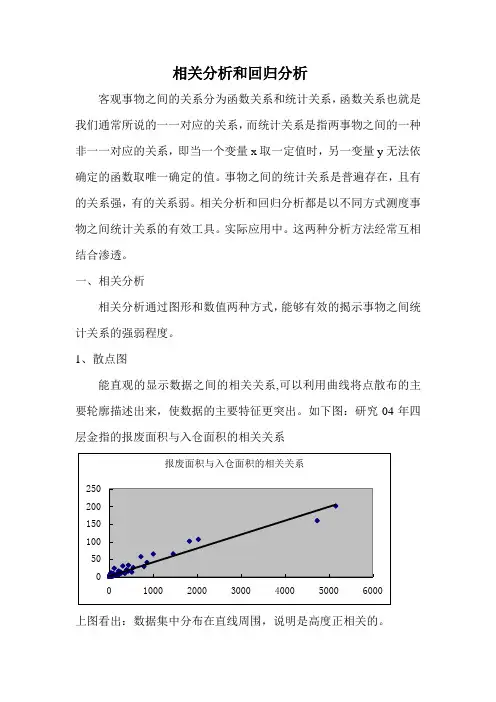
1、散点图能直观的显示数据之间的相关关系,可以利用曲线将点散布的主要轮廓描述出来，使数据的主要特征更突出。

如下图：研究04年四层金指的报废面积与入仓面积的相关关系上图看出：数据集中分布在直线周围，说明是高度正相关的。

2、相关系数散点图能直观的展现变量之间的统计关系，但并不精确。

相关系数以数值的方式精确的反映了两个变量间线形相关的强弱程度。

➢ R=yyxx xy L L L ，其中xx L =∑=--ni ix x12)(，∑=----=ni i i xy y y x x L 1))((，∑=--=ni i yy y y L 12)(.➢ 相关系数R 的取值在-1~+1之间。

➢ R>0表示两变量之间存在正的线性相关关系；R<0表示两变量之间存在负的线性相关关系。

➢ R=1表示两变量存在完全正相关；R=-1表示两变量存在完全负相关；R=0表示两变量不存在线性相关关系。

➢ |R|>0.8表示两变量之间具有较强的线性关系；|R|<0.3表示两变量之间的线性相关关系较弱。

上例中，R=0.974,说明报废面积与入仓面积之间是强正相关的。

二、一元线性回归在实际应用中，我们常常需要考虑某一现象与影响它的最主要因素的关系，回归分析不仅可以揭示变量x 对变量y 的影响大小，还可以由回归方程进行预测和控制。

一元线性回归是最简单的回归模型。

第三章相关分析与回归模型的建立与分析相关分析和回归分析是统计分析方法中最重要内容之一，是多元统计分析方法的基础。

相关分析和回归分析主要用于研究和分析变量之间的相关关系，在变量之间寻求合适的函数关系式，特别是线性表达式。

◆本章主要内容：1、对变量之间的相关关系进行分析（Correlate）。

其中包括简单相关分析（Bivariate）和偏相关分析（Partial）。

2、建立因变量和自变量之间回归模型（Regression），其中包括线性回归分析（Linear）和曲线估计（Curve Estimation）。

◆数据条件：参与分析的变量数据是数值型变量或有序变量。

§3.1 相关分析在SPSS中，可以通过Analyze菜单进行相关分析（Correlate），Correlate菜单如图3.1所示。

图3.1 Correlate 相关分析菜单§3.1.1 简单相关分析两个变量之间的相关关系称简单相关关系。

有两种方法可以反映简单相关关系。

一是通过散点图直观地显示变量之间关系，二是通过相关系数准确地反映两变量的关系程度。

§3.1.1.1 散点图SPSS软件的绘图命令集中在Graphs菜单。

下面通过例题来介绍具体操作方法。

例1：数据库SY-8中的变量X表示山东省人均国内生产总值，Y表示山东省城镇居民的消费额（资料来源：山东省2003年统计年鉴），现画出散点图来观察两个变量的关联程度。

具体操作步骤如下：首先打开数据SY-8，然后单击Graphs Scatter,打开Scatter plot散点图对话框，如图3.2所示。

然后选择需要的散点图，图中的四个选项依次是：Simple 简单散点图Matrix 矩阵散点图Overlay 重叠散点图3-D 三维散点图图3.2 散点图对话框如果只考虑两个变量，可选择简单的散点图Simple，然后点击Define，打开Simple Scatterplot对话框,如图3.3所示。

回归分析与相关分析的联系：研究在专业上有一定联系的两个变量之间是否存在直线关系以及如何求得直线回归方程等问题，需进行直线相关和回归分析。

从研究的目的来说，若仅仅为了了解两变量之间呈直线关系的密切程度和方向，宜选用线性相关分析；若仅仅为了建立由自变量推算因变量的直线回归方程，宜选用直线回归分析。

从资料所具备的条件来说，作相关分析时要求两变量都是随机变量（如：人的身长与体重、血硒与发硒）；作回归分析时要求因变量是随机变量，自变量可以是随机的，也可以是一般变量(即可以事先指定变量的取值，如：用药的剂量)。

在统计学教科书中习惯把相关与回归分开论述，其实在应用时，当两变量都是随机变量时，常需同时给出这两种方法分析的结果；另外，若用计算器实现统计分析，可用对相关系数的检验取代对回归系数的检验,这样到了化繁为简的目的。

回归分析和相关分析都是研究变量间关系的统计学课题，它们的差别主要是：1、在回归分析中，y被称为因变量，处在被解释的特殊地位，而在相关分析中，x与y处于平等的地位，即研究x与y的密切程度和研究y与x的密切程度是一致的；2、相关分析中，x与y都是随机变量，而在回归分析中，y是随机变量，x可以是随机变量，也可以是非随机的，通常在回归模型中，总是假定x是非随机的；3、相关分析的研究主要是两个变量之间的密切程度，而回归分析不仅可以揭示x对y的影响大小，还可以由回归方程进行数量上的预测和控制。

1．为什么要对相关系数进行显著性检验？在对实际现象进行分析时，往往是利用样本数据计算相关系数（）作为总体相关系数（）的估计值，但由于样本相关系数具有一定的随机性，它能否说明总体的相关程度往往同样本容量有一定关系。

当样本容量很小时，计算出的不一定能反映总体的真实相关关系，而且，当总体不相关时，利用样本数据计算出的也不一定等于零，有时还可能较大，这就会产生虚假相关现象。

为判断样本相关系数对总体相关程度的代表性，需要对相关系数进行显著性检验。

回归分析与相关性的模型与估计回归分析与相关性是统计学中常用的方法，用于探究变量之间的关系及其中一个变量对另一个变量的预测能力。

回归分析可以通过建立模型并进行估计，揭示变量之间的线性或非线性关系，并可用于预测和解释。

本文将介绍回归分析的基本原理、常见的回归模型以及相关性的度量方法。

一、回归分析的基本原理回归分析是一种通过建立变量之间的数学模型来研究它们之间关系的统计方法。

回归分析假设变量之间存在一种数量上的关系，其中一个变量被称为因变量，其余变量是自变量。

回归分析的目标是根据自变量的取值来预测因变量的取值。

在回归分析中，最常用的模型是线性回归模型。

线性回归模型假设因变量与自变量之间存在线性关系，通过拟合一条直线或平面来描述这种关系。

模型的表示形式为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε，其中Y是因变量，X1至Xn是自变量，β0至βn是回归系数，ε是误差项。

二、常见的回归模型除了线性回归模型外，还有其他常见的回归模型用于描述不同类型的关系。

其中一些模型包括：1. 多项式回归模型：用于描述因变量与自变量之间的非线性关系。

多项式回归模型拟合数据时，可根据需要选择二次、三次或更高次的多项式。

2. 对数回归模型：用于描述自变量与因变量之间的指数增长关系。

对数回归模型可以将数据的指数关系转化为线性关系，并使用线性回归方法进行拟合。

3. 幂函数回归模型：用于描述因变量与自变量之间的幂函数关系。

幂函数回归模型可以拟合数据中的非线性关系，并能适应各种曲线形状。

这些回归模型的选择应基于问题的特点和数据的性质，以及对变量之间关系的理论认识。

三、相关性的度量方法相关性是衡量两个变量之间线性关系强度的一种指标。

常见的相关性度量方法包括相关系数和残差分析。

1. 相关系数：常见的相关系数有皮尔逊相关系数和斯皮尔曼相关系数。

皮尔逊相关系数用于测量两个连续变量之间的线性关系，取值范围为-1到1，值越接近于1或-1表示关系越强；而斯皮尔曼相关系数适用于测量非线性关系或序列数据。

回归分析与相关分析联系、区别简单线性回归分析是对两个具有线性关系的变量,研究其相关性,配合线性回归方程,并根据自变量的变动来推算和预测因变量平均发展趋势的方法;回归分析Regression analysis通过一个变量或一些变量的变化解释另一变量的变化;主要内容和步骤：首先依据经济学理论并且通过对问题的分析判断,将变量分为自变量和因变量,一般情况下,自变量表示原因,因变量表示结果；其次,设法找出合适的数学方程式即回归模型描述变量间的关系；接着要估计模型的参数,得出样本回归方程；由于涉及到的变量具有不确定性,接着还要对回归模型进行统计检验,计量经济学检验、预测检验；当所有检验通过后,就可以应用回归模型了;回归的种类回归按照自变量的个数划分为一元回归和多元回归;只有一个自变量的回归叫一元回归,有两个或两个以上自变量的回归叫多元回归;按照回归曲线的形态划分,有线性直线回归和非线性曲线回归;相关分析与回归分析的关系一相关分析与回归分析的联系相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续;相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度;只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义;如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前,就进行回归分析,很容易造成“虚假回归”;与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的;二相关分析与回归分析的区别1．相关分析中涉及的变量不存在自变量和因变量的划分问题,变量之间的关系是对等的；而在回归分析中,则必须根据研究对象的性质和研究分析的目的,对变量进行自变量和因变量的划分;因此,在回归分析中,变量之间的关系是不对等的;2．在相关分析中所有的变量都必须是随机变量；而在回归分析中,自变量是确定的,因变量才是随机的,即将自变量的给定值代入回归方程后,所得到的因变量的估计值不是唯一确定的,而会表现出一定的随机波动性;3．相关分析主要是通过一个指标即相关系数来反映变量之间相关程度的大小,由于变量之间是对等的,因此相关系数是唯一确定的;而在回归分析中,对于互为因果的两个变量如人的身高与体重,商品的价格与需求量,则有可能存在多个回归方程;需要指出的是,变量之间是否存在“真实相关”,是由变量之间的内在联系所决定的;相关分析和回归分析只是定量分析的手段,通过相关分析和回归分析,虽然可以从数量上反映变量之间的联系形式及其密切程度,但是无法准确判断变量之间内在联系的存在与否,也无法判断变量之间的因果关系;因此,在具体应用过程中,一定要注意把定性分析和定量分析结合起来,在定性分析的基础上展开定量分析;。

研究生《生物统计学》课程第六讲相关分析与回归分析主要内容：一、线性相关分析1、两变量相关分析2、多变量相关分析二、回归分析1、一元线性回归分析2、多元线性回归分析3、曲线回归分析一、线性相关分析：用于研究变量之间密切程度的统计方法使用SPSS中Correlate模块相关系数是以数值的方式精确地反映两个变量之间线性关系的强弱程度，利用相关系数进行变量间线性关系的分析，即相关分析。

包括两个步骤：①计算样本的相关系数r；②对两样本来自的总体是否存在显著的线性关系进行推断。

Pearson简单相关系数：计算连续变量或等间距测度的变量之间的相关系数（系统默认）；Kendall τ相关系数：等级相关系数，只能在两变量均属于有序分类时使用；Spearman等级相关系数：度量定序型变量间的线性相关关系，非参数相关分析。

（一）两变量相关分析1、案例分析：有人研究黏虫孵化历期平均温度（x, ℃）与历期天数（y, d）之间的关系，求出平均温度与历期天数的线性相关系数x，平均温度（℃）y, 历期天数（d）（1） 建立数据文件，在Variable Vew 中定义变量“平均温度”、“历期天数”，小数位数均为1，输入数据；（2） 相关分析：[Analyze]=>[Correlate]=>[Bivariate]（两变量相关分析），打开[BivariateCorrelation]主对话，将“平均温度”、“历期天数”引进[Variables]（变量）框； （3） 在[Correlation Coefficients]复选框中选择“Pearson ”（系统默认），选中[Flagsignificant correlations]，将对显著的相关系数加“*”标志（若为1个星号*，表示P<，差异显著；若为2个星号**，表示P<，差异极显著）；（4） 单击[Options]进入“选项”对话框，选择[Means and standard deviations]计算各变量的平均值与标准差，[Continue]返回； （5） 单击[OK]，运行相关分析。