数学建模买房问题
- 格式:doc
- 大小:79.96 KB
- 文档页数:10

题目:最佳购房方案组号:姓名:学校:摘要:本文是关于购房优化设计问题,即在以下给出的三种购房方式中,确定最佳的购房方案:(1)首付15万元,其余可办银行按揭。
(2)现房价不稳,同时目前股市看涨,推迟买房,先把购房的15万元去买股票,等股票赚了钱再去买房子。
(3)现在某银行又一种理财产品,除有2.1%保息之外,还有分红。
若运气好,又10%以上的利率。
根据题意,建立了三个数学模型。
模型一:利用银行按揭的相关知识建立银行按揭的数学模型计算出月供金额和供房期限模型二:根据股票相关的知识,以及股市行情走势和收集的相关数据,利用Markowitz模型及二次规划建立一套数学方法,来解决如何通过多元化的组合降低组合资产中的风险问题,并用证券价格的评估模型的固定增长模型计算出预期股利的现在价。
模型三:根据某银行的实际情况,及收集到的相关数据,建立银行理财分红模型。
由于模型二的方法风险较大但有较高的收益作为补偿,而模型一还款期限太长并且没有收益,模型三收益太少且延迟了买房时间,所以满足题目要求的最终方案是模型二。
最后,对设计规范的合理性进行了充分和必要的论证。
关键词:按揭Markowitz模型股利银行利率预期股利的现在价分红风险系数问题分析小李夫妻俩都有一份固定的工作,每个月都有6400元的工资收入,现今租用别人的房子,房租为1000/月,但需要买一套属于自己的住房,面积120平米,价格3600/平米。
现有三种方案可以使小李买到属于自己的住房:方案一、首付15万元,其余可办银行按揭。
对于此方案,小李只要支付首付款,则可立即入住,就不需要再交房租,不过现在又存在一个问题,到底是使用等额本息还款法(即:等额法)还是等额本金还款法(即:递减还款法),鉴于这两种方法还款,由于等额本息还款法(即:等额法)的优点在于借款人可以准确掌握每月的还款额,有计划地安排家庭的收支。
比较方便、易记。
缺点是利息支出总额相对较高,适合收入稳定,预期收入变化不大,购买住房用于自住的客户;而等额本金还款法(即:递减还款法)的优点在于利息支出相对较少,缺点是每月还款额逐步递减,前期还款压力较大。
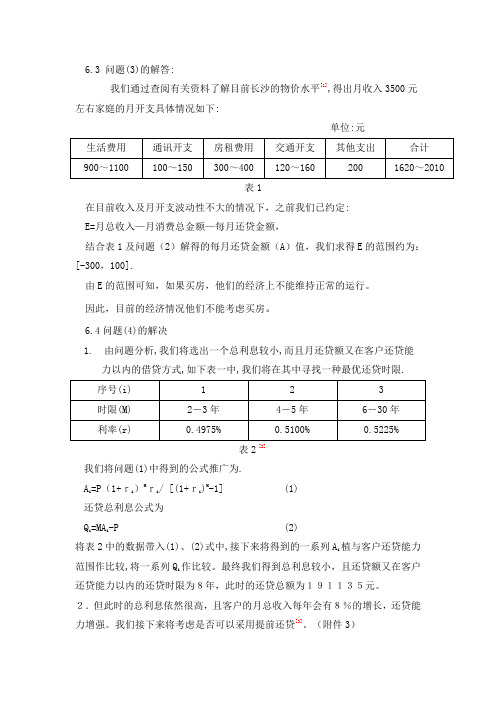
6.3 问题(3)的解答:我们通过查阅有关资料了解目前长沙的物价水平[1],得出月收入3500元左右家庭的月开支具体情况如下:单位:元表1在目前收入及月开支波动性不大的情况下,之前我们已约定:E=月总收入—月消费总金额—每月还贷金额,结合表1及问题(2)解得的每月还贷金额(A)值,我们求得E的范围约为:[-300,100].由E的范围可知,如果买房,他们的经济上不能维持正常的运行。
因此,目前的经济情况他们不能考虑买房。
6.4问题(4)的解决1.由问题分析,我们将选出一个总利息较小,而且月还贷额又在客户还贷能力以内的借贷方式,如下表一中,我们将在其中寻找一种最优还贷时限.表2 [2]我们将问题(1)中得到的公式推广为.A i =P(1+ri)Mri/ [(1+ri)M-1] (1)还贷总利息公式为Q i =MAi-P (2)将表2中的数据带入(1)、(2)式中,接下来将得到的一系列Ai植与客户还贷能力范围作比较,将一系列Qi作比较。
最终我们得到总利息较小,且还贷额又在客户还贷能力以内的还贷时限为8年,此时的还贷总额为191135元。
2.但此时的总利息依然很高,且客户的月总收入每年会有8%的增长,还贷能力增强。
我们接下来将考虑是否可以采用提前还贷[3]。
(附件3)(1)除开提前还贷总额,剩余的等额还贷总额的计算公式:X=A·T1+A·T2+A·T3+……………+A·TR(3)(2)随着收入的增长,除去日常支出和正常还贷外,可用提前还贷总额:Y=[G(1+8%)-J-A]T2+[G(1+8%)2-J-A]T3+……+[G(1+8%)R-1-J-A]TR-1(4)(其中T1、T2、、T3……TR-1=12个月份.R=M-Y/A)如果实施提前还贷,则还贷总额可表示为:Z=X+Y=AT1+ATR+G(1+8%)T2[1-(1+8%)R-1]/[1-(1+8%)]-A(T2+T3+……TR-1)(5)由于TR并不一定为12个月,我将其估计如表3:表3(3)将表2中的数据分别代入(5)中,即得Z1、Z2Z3Z4估计值。

购房贷款的数学建模.doc一、问题提出现在人们购房的方式大多通过贷款实现。
贷款的还款方式主要有等额本金和等额本息两种。
那么如何理性地选择合适的还款方式,以确保不会因为贷款而增加过多的经济负担。
因此,通过数学建模来分析和探讨贷款的还款方式选择问题,有助于人们更好地管理自己的财务和购房计划。
二、问题分析(一)贷款基础知识1. 总贷款金额P:指的是购房人申请银行贷款的款项总额,包括贷款本金和利息。
2. 贷款期限n:指的是购房人约定的贷款还款期限,通常为5年、10年、15年、20年、25年、30年。
3. 年利率i:指的是购房人所承担的贷款利率,通常为基准利率上浮5%至30%不等。
(二)等额本金和等额本息还款方式1. 等额本金还款方式:等额本金还款方式是指每个月还款数额相同,但是每个月所支付的利息和本金比例不同。
这是因为每个月的还款中,本金所占比例是相同的,而利息所占比例随着未还本金的减少而减少。
三、模型建立假设购房人贷款时间为n个月,贷款总额为P元,月利率为i,则等额本金还款方式有如下计算公式:每月还款单价a= P/n + i*P*(1-(t-1)/n)第t个月,购房人所要偿还的贷款金额为Mt= a*(n-t+1)其中,t∈[1, n]四、实例分析某购房人决定申请银行30年的贷款,贷款金额为100万元,年利率为6.55%,现在需要选择合适的还款方式,从而更好地管理自己的经济财务。
首先我们可以根据等额本金还款方式的计算公式计算每月还款额a=100/360+6.55%/12*(1-(1-1/360)^360)=3,693.19元月份本月归还额每月本金归还额每月还款额还款总额1 3716.25 2500.00 3693.19 3693.19…………此时,我们可以将表格转化为折线图来直观感受等额本金还款方式与等额本息还款方式的还贷情况。
从图可见,等额本金的还款总额为1,109,536.16元,平均每个月还款3,081.49元。

住房的合理定价问题摘要房价的合理性已成为当今社会的热门话题。
本文依照题中所给出的数据,对3个问题分别建立模型并求解。
针对问题1,首先利用Excel建立图表,绘制出历年房价走势图。
然后,对原始数据进行拟合,得出指数型及多项式型拟合方程,并在原图上绘制出趋势线。
同时,求出确定性系数R2,依据R2是否接近于1判断拟合程度好坏,即检验拟合方程的有效性。
计算得出的指数型及二阶多项式型拟合方程:x,(i) =678.8le0.1281i、x2(i) =12.59i2 50.274i 716.38,由此预测出2010 年房价分别为4080元/平米、3888元/平米。
为了增加预测的可靠性,再结合二次指数平滑法对2010年房价进行预测。
通过比较实际值与预测值的平均偏差值ME的大小,选择出合适的o预测出2010年的房价为3800元/平米。
最后,建立三元线性回归模型,将上述三种方法对历年房价的预测值分别作为自变量x1、x2、X3的原始数据,以实际房价P(i)作为因变量,用Matlab软件拟合出多元线性方程:P f1(i) =—0.0202 —0.1389 刘⑴ 1.1319 X2(i) 0.0084 X3(i)。
代入相关数据,求出历年的最终房价预测值为3866元/平米。
针对问题2,通过Excel绘制出历年平均房价与人均GDP的关系走势图,且自动生成对原始数据进行拟合后的指数型和自变量为2阶、3阶、4阶的多项式型拟合方程及各自的确定性系数R2o R2的值分别为:0.8673; 0.9929 ; 0.9982; 0.9986。
由此判断,因2阶多项式型拟合方程的R2不仅十分接近于1,且相对于3阶、4阶的多项式方程更为简便,故选择:A 2P(i) =(_7E _06) [G(i)] 0.3236 G(i) -177.06 为平均房价与人均GDP 的关系方程。
最后,在联系当下实际状况的基础上对建立的模型进行研究,分析出平均房价与人均GDP的关系。

西安邮电学院第九届大学生数学建模竞赛参赛作品参赛队编号: 016赛题类型代码: A题2 房价问题摘 要随着我国房地产市场的不断升温,居民买房难愈来愈严重。
定一个合适的房价既照顾到居民的需求也满足方差开发商的盈利需要是十分必要的,要达到这些目的都要用到数学模型来进行量化。
在本文中,我们经研究解决了城市房价模型,找出了影响房价的主要因素,建立预测下一阶段的房产均价的一个模型,同时也对政策对调控房价所起的作用作了详细的分析说明。
在解决房价模型问题时,我们用了多元线性回规模型和蛛网模型同时对相关变量进行分析和处理,最终找出了影响房价的主要因素为生产成本和供需关系。
并对房价的形成、演化机理和房地产投机进行了深入细致的分析。
模型一,我们通过比较西安房价近11年来的变化及城镇居民收入变化情况,找到买房难的根结。
模型二,在房价预测方面,我们选用多元线性回归,蛛网模型同时对相关变量进行分析和处理,最终找出影响房价的主要因素为生产成本和供需关系,求出房价预测的计算表达式。
模型三,我们取定一个时间段内某几个房价新政,结合新政出台时间前后某地房价的变化情况分析了房价新政对房价的调控作用。
我们选取房价新政的标准是根据政策内容对相关经济指标有直接作用效果。
最终我们发现,新政出台后,虽然房价依然是居高不下,但房价上涨速率得到了一定的控制,变化渐缓。
关键字:楼市 预测 蛛网模型 线性回归一、问题重述住房问题关系国计民生,既是经济问题,更是影响社会稳定的重要民生问题。
2008年受国际金融危机的影响,部分购房需求受到抑制,2009年在国家税收、土地等调控政策作用下,一度受到抑制的需求得到释放,适度宽松的货币政策使信贷规模加大,为房地产开发和商品房购买提供了比较充裕的资金,房地产市场供求大增,带动了整体回升。
但有的城市房价过高,上涨过快,加大了居民通过市场解决住房问题的难度,另一方面,部分投机者也通过各种融资渠道买入房屋囤积,期望获得高额利润,也是导致房价居高不下的原因之一。
数学建模提出问题:某人购房,需要贷款,等额本息还款法,等额本金还款法,某人贷款40万,还款期为10年,贷款利率为6%。
1、月供金额2、总的支付利息比较两种贷款法,给出你的方案。
一、分析问题解决此问题需要建立数学模型,找出偿还贷款的金额最少时的最优解,这是一个优化问题,这就是说在不同的约束条件下,只要建模合理,答案可以是多种。
建立优化问题的模型最主要的是用数学符号和式子表述决策变量、构造目标函数和确定约束条件。
对于等额本息还款方式和等额本金还款方式,分别建立了与之对应的模型,然后根据题中所给的数据,分别求解出两种方式的还款额,并得到最优解,最后根据自己的实际情况合理选择还款方式。
二、模型假设1、假设贷款人在还款期间有能力支付银行要求的还款费用。
2、还款期间还款人没有任何意外事件。
3、贷款利率在还清前一直为6%。
三、参数说明设贷款总额为A,银行年利率为a,月利率为β,总期数为m(个月),月还款额为X,总支付利息为Y,还款总额为B。
四、模型的建立与求解1、等额本息还款模型的建立与求解。
等额本息还款,也称定期付息,即借款人每月按相等的金额偿还贷款本息,其中每月贷款利息按月初剩余贷款本金计算并逐月结清。
把按揭贷款的本金总额与利息总额相加,然后平均分摊到还款期限的每个月中。
作为还款人,每个月还给银行固定金额,但每月还款额中的本金比重逐月递增、利息比重逐月递减。
假设这批贷款是一次性到帐的,为使模型便于运算,也假设这批贷款是某一年的第一天就到帐的,利息也是从那一天开始产生。
等额本息还款公式的推导如下,个个月所欠银行的贷款为:第一个月:A(1+β)-X第二个月:[A(1+β)-X](1+β)-X=A(1+β)^2 -X[1+(1+β)]第三个月:{[A(1+β)-X](1+β)-X}(1+β)-X= {[A(1+β)-X](1+β)-X}(1+β)-X由此可得第n月后的所欠银行数额为:A(1+β)^n-X[1+(1+β)+(1+β)^2+…+(1+β)^(n-1)] =A(1+β)^n-X[(1+β)^n-1]/β由于还款总期数为m,也即第m月刚好还完银行所有贷款,因此有:A(1+β)^m-X[(1+β)^m-1]/β = 0 由此求得:X = Aβ(1+β)^m/[(1+β)^m-1]带入数值得:X=4417总支付利息为:总利息=月还款额×贷款月数-本金,带入数值得:Y=4417×120-400000=130040还款总额为:B=400000+130040=530040元讨论:如果按等额本息还款法,还款人的月供金额为4417元人民币,这种还款方法所要求金额较大,对于一般收入者来说可无力承受,按一般城市的消费来说,还款人的月收入应在6000元以上就可承受等额本息还款法。
A题:购房贷款问题蒋萍(08(3)班 08211337)【摘要】随着人们生活水平的不断提高,越来越多的人正在购置房产用于居住或进行置业投资。
但是购房投资是一项金额较大的投资,要人们一次性支付比较困难。
但随着市场经济的发展,向银行贷款购房成了我们买房的主要方式。
我们知道,如果向银行贷款就需要直接面对提供担保、偿还借贷的问题,现实生活中人们选择贷款的期数、月还款额时,却往往因为缺乏这方面的知识,而带来一定的盲目性,给自己带来或多或少的经济损失。
所以在这个市场经济时代,面对不同的决策方案,正确的决策意味着经济资源的最优配置。
本文就购房贷款问题,展开一系列的讨论。
针对购房问题进行全面分析,利用递推数列将实际问题数学化,建立了一个数学模型。
利用计算机程序算出结果,不仅求出了各种还款方式的还款金额和利息,而且还指出了等额还款是最优的还款方式。
【关键词】递推数列贷款额利息贷款期限还款额1.问题重述小王夫妇计划贷款20万元购买一套房子,他们打算用20年的时间还清贷款。
目前,银行的利率是0.6%/月。
他们采用等额还款的方式(即每月的还款额相同)偿还贷款。
1. 在上述条件下,小王夫妇每月的还款额是多少?共计付了多少利息?2. 在贷款满5年后,他们认为他们有经济能力还完余下的款额,打算提前还贷,那么他们在第6年初,应一次付给银行多少钱,才能将余下全部的贷款还清?3. 如果在第6年初,银行的贷款利`率由0.6%/月调到0.8%/月,他们仍然采用等额还款的方式,在余下的15年内将贷款还清,那么在第6年后,每月的还款额应是多少?4. 小王夫妇认为,随着他们工作经历的增长,家庭收入也会随着增长,因此,打算采用逐步增加还款额的还款方式来偿还贷款,具体的办法是:如果第1年的每月还款额是1000元的话,那么第2年的每月还款额就是1500元,第3年的每月还款额是2000元,第4年的每月还款额是2500元,以此类推。
在此情况下,如果贷款利率还是0.6%/月,那么,第1年的每月还款额是多少?以后各年的每月还款额又是多少?共计付了多少利息?5. 在4提出的还款方式下,在贷款满5年后,打算在第6年初一次还清全部余款,那么,一次的还款额是多少?如果第6年初,银行的贷款利率由0.6%/月调到0.8%/月,从第6年起,以后各年的每月还款额是多少?6. 综合上述问题,为小王夫妇(实际上是打算贷款购房的人)写一份报告,帮助他们分析各种方法的利弊,和偿还贷款的计划。
借贷买房问题(数学建模)曾有一家报纸刊登一则广告称:对于大多数工薪阶层的人士来说,想买房,简直是天方夜谭。
现在有这样一栋住宅楼,每套只需自备款七万元,其余由公司贷款,可分期付款,每月只需付八百元,十年还清,那么,这对您还有什么问题呢?现在的问题是:这房子究竟值多少钱,即如果一次付款要付多少钱?如果没有能力一次付款,实际上,相当于借了多少钱?为什么要每月付八百元?试根据广告所提供的信息和银行的贷款利率,对上述问题进行研究,供购房者参考。
1.假设房子的总价为M元,买者需借A0元,月利率为R,借期为n个月,每月付X元,到第n个月欠款An元,则第n+1个月(含利息)欠款。
An=(1+R)An-x, n=0,1,2,.....于是可得n n-1 n-2An=A0(1+R) –x[(1+R) +(1+R) +....+(1+R)+1]n=A0(1+R) -X[(1+R) -1/R], n=0,1,2,.....即得AN,A0,X ,R,N之间的关系。
2.就广告而言,已知N=10年=120个月,X=800元,A0=(M-70000)元,则要求10年还清,即A120=0,从而得120 1200=A0(1+R) -800/R[(1+R) -1],于是120 120A0=800[(1+R) -1]/R(1+R)不妨设月利率R=0.01,则由上式可算出A0=55760元,于是房子的总价为M=70000+55760=125760元,由此可知,一次性付款额不应大于M,否则,就应该自己去贷款,不要借公司的钱了。
3.某高校青年教师张某为买房向公司借贷A0=60000元,月利率R=0.01,若要每月还一次钱,需25年=300月还清,张老师希望知道平均每月还多少钱?根据前面的讨论,要25年=300个月还清,即要300 300A300=A0(1+R) -X(1+R) -1/R=0可以解得X=632元,即平均每月还632元,25年可还清。
大学生数学建模_房价预测
一、问题的提出房地产问题一直是人们的热议话题,尤其是近几年更是成为人们关注的问题。
不错,房地产作为一个行业,不仅关系国家经济命脉,它还是影响民生问题的主要因素,所以搞好房产建设不仅是国家与房产商的任务,我们也应了解其中的一些运作原理来帮助我们更好的适应社会环境。
为此,对房产业的了解就显得颇为紧急,而房价问题一直是人们关注的首要问题,下面我们将用数学模型来解决房产中的以下实际问题,仔细分析影响房价的因素以及它们之间的关系。
问题一:通过分析找出影响房价的主要原因并且通过建立一个城市房价的数学模型对其进行细致的分析。
问题二:分析影响房价主要因素随时间的变化关系,并且预测其下一阶段的变化和走势。
问题三:选择某一地区(以西安为例),通过分析____年至____年房价变化与影响因素之间的关系,预测下一阶段该地区房价的走势。
问题四:通过分析结果,给出房产商和购房者的一些合理建议。
二、模型假设和符号说明假设假设
一、房地产产品具有一定的生产周期假设
二、房价的计算只考虑人均可支配收入和生产成本假设
三、理想房价是仅基于成本得到的房价,不考虑供求假设
四、成本的花费包括地价(地面地价)、建筑费用和各种税收假设
五、不考虑其他影响如(地理位置,环境等)符号说明:_1代表人均可支配收入,_2代表建造成本,y为房产均价,其中a和
三、模型建立与求解我们主要用到的是数学模型是用最小二乘法对影响房价的各个因素进行拟合,从而解除出性方程组,其中用到的主要数学软件是matla。
呼伦贝尔学院Hulunbeier University数学建模竞赛论文论文题目:租房还是买房姓名1:学号:专业:姓名2:学号:专业:姓名3:学号:专业:2011 年 5 月8 日承诺书我们仔细阅读了呼伦贝尔学院数学建模的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B中选择一项填写):租房还是买房所属学院(请填写完整的全名):参赛队员(打印并签名) :1.2.3.日期: 2011 年 5 月 9 日评阅编号(由组委会评阅前进行编号):编号专用页评阅编号(由组委会评阅前进行编号):赛区初评记录(可供评阅时使用):复评结果:租房还是买房一、摘要我国房地产自20世纪末走出低谷以来,其迅猛发展的势头备受世人瞩目,不仅作为国民经济的支柱产业而对国家宏观经济运行产生巨大影响,而且更与广大百姓的自身利益息息相关。
住房问题关系国计民生,既是经济问题,更是影响社会稳定的重要民生问题。
从住房制度改革以来短短几年时间,中国大地上几乎所有城市房产如雨后春笋般拔地而起。
随着我国房地产市场不断升温,由于我国的法制不健全,尤其是金融以及改革领域里出现了各种失误导致房价过高,上涨过快。
随着外来人口向大城市集中,租金也大幅度增加。
5月31日,央行公布的第一季度货币政策执行报告显示:北京居民房贷月供收入比(借款人住房贷款的月房产支出与收入之比)为42%,仅次于上海的45%而排名第二。
6月1日《新京报》报道,在北京、上海等10个大城市中,62%的借款人在买房置业时没有考虑过租房,其中北京高达90%.置业用途中自住、空置、出租的比例为84∶10∶6.这一调查结果至少说明三个问题:目前北京市居民房贷月供比例偏高,也就是目前的房价相对收入来说偏高;在北京租房的价格也很高,因此居民90%不考虑租房;置业后空置比例高于出租比例,说明房价增值快,而持有房屋的成本低,因此很多业主对房租收入不太关心。
买房还是租房,这是个困扰很多人的问题。
从租售比的角度看,北京、上海等大城市的房价过高,存在泡沫,因此目前应该租房。
但是,从投资的角度看,很多人认为房产从长期看是升值的,是投资,而房租却是消费,因此应该买房。
买房的主要收入是房租和房产升值,主要成本是按揭的债务成本和投入的本金的机会成本,外加房屋持有成本。
租房的主要收入是省下来的买房首付款加上每月房租低于按揭款部分的投资收益,主要成本就是房租。
把每年的收益/支出按通货膨胀率进行折现,就可以算出买房和租房的回报净现值。
当这两个净现值相等时,买房与租房没有区别。
论文以租房还是买房作为主要对象,通过买房和租房的回报净现值的分析,利用线性规划中的单变量求解找到了买房和租房的回报净现值相等的情况,绘制了一条曲线。
对房产升值与租售比进行作图比较,研究房价与租金的关系,并展开讨论、分析和建立数学模型,利用数学软件进行求解。
并在结果分析中做出了具体而又详实的分析。
使它们之间的关系更为明晰。
根据市场房屋价格的变化情况,综合考虑家庭收入、租金收入、储蓄及贷款利率、房屋折旧率、房屋空置率等因素,建立数学模型,为家庭进行住房投资做出决策。
关键词:租金房产升值净现值租售比线性规划房屋空置率二、问题重述1.1问题背景住房问题关系国计民生,既是经济问题,更是影响社会稳定的重要民生问题。
随着现在经济的快速发展,买房还是租房,这是个困扰很多人的问题。
从租售比的角度看,北京、上海等大城市的房价过高,存在泡沫,因此目前应该租房。
但是,从投资的角度看,很多人认为房产从长期看是升值的,是投资,而房租却是消费,因此应该买房。
那么到底应该买房还是租房呢?根据市场房屋价格的变化情况,综合考虑家庭收入、租金收入、储蓄及贷款利率、房屋折旧率、房屋空置率等因素,通过买房和租房的回报净现值的分析,利用线性规划中的单变量求解找到了买房和租房的回报净现值相等的情况,绘制了一条曲线。
建立数学模型,利用Matlap数学软件得出最优解,为家庭进行住房投资做出决策。
1.2问题假设通过市场分析找出影响房价的主要原因,并建立一个城市房价的数学模型,对房价的形成和房地产投机进行深入细致的分析。
对房产升值与租售比进行作图比较,研究房价与租金的关系。
三.符号说明P:房价(元/平方米)p1:理想房价(元/平方米)A :地价(元/平方米)B :建安造价(元/平方米)σ1 :税率(%)p:房租q:银行按揭x:还亲戚借款y:差额k:房租增长幅度7%四、模型假设假设一、房地产产品具有一定的生产周期假设二、银行贷款利率二十年维持不变。
假设三、房租价格以每年7%的幅度增长。
假设四、供需平衡指:供应量=需求量假设五、北京的房产升值速度应该不低于8%左右假设六、需求量受到本周期的实际房价的影响。
五、问题分析问题①分析:本问是要求我们通过分析相关数据,找出影响房价的主要原因,然后根据这些因素建立一个城市房价的数学模型。
同时,根据得出的结论深入细致的分析房价形成、演化机理和房地产投机。
针对本问,我们利用了网络等相关资源,查找各主导因素间的变化关系,确立变量,从而建立模型。
首先,我们可以确定的是房地产业红火发展的关键是社会经济的各项指标综合决定的,社会经济指标的发展是地产业持续发展的推动力。
由此,我们分析相关数据的目的是要得出几条对房地产业影响较大的社会经济指标,从而为继续研究奠定好基石。
我们知道,要去逐一分析每一种经济因素是不可能办到的,只能抓住主要因素去着重分析。
所以我们经互联网搜索及查阅相关资料,大致得出以下几条对房价的影响产生主导作用的因素:建安成本,市场供求变化,土地成本、各种税费以及当地居民人均收入等。
然而,针对本问,虽然我们从相关资料中获取了大量数据,但从实际出发来看这些数据只能作为理论支撑的基础,模型并不是只针对某一个城市,而是具有普遍用途,这样才能完美的达到本题的目的所在通过分析我们知道以下几个关系,成本决定理想价格;理想价格和房价决定需求量;理想价格和地产商的预测价格决定了供应量;需求量和供应量又共同决定了房价。
那么首先我们来求理想房价p1,根据理想房价的求法得出其表达式P1=(1+σ1)*(A+B)……………①令1+σ1=a (1+σ1)*B=b,a和b 均不为正常数,则可得:P1=b+a*A…………………………②从公式①和②中可以看出,地价与理想房价之间为线性正相关关系,同时地价与理想房价之间影响的程度因建安成本、税率和容积率的不同而不同,再者我们可以笼统地说理想房价就是成本费用的具体体现,根据假设,成本不变,所以理想房价也不变。
问题②分析:首先,我们找到了北京市 2009 年有关房价、房屋租金的一些数据,根据题目,我们将用 matlab 软件对相关数据进行拟合,对房价与房屋租金建立相关关系,结合其所得结果与现实情况加以分析。
买房的主要收入是房租和房产升值,主要成本是按揭的债务成本和投入的本金的机会成本,外加房屋持有成本。
租房的主要收入是省下来的买房首付款加上每月房租低于按揭款部分的投资收益,主要成本就是房租。
把每年的收益/支出按通货膨胀率进行折现,就可以算出买房和租房的回报净现值。
当这两个净现值相等时,买房与租房没有区别通过这个模型,我发现买房与租房的关系与两个参数相关:租售比和房产升值速度。
当房产升值速度很快时,即使是租售比很高,如达到1:30左右,买房也比租房值。
而如果房产升值的速度很低,甚至是负值时,只有租售比很低,买房才划算。
六、模型建立问题①模型建立:北京这套房子的基本情况:1、房价:每平米12000;楼层:20层;面积:45平米;契税:16200;房屋维修基金:10800;装修及家具电器款:43000;合计:61万。
2、首付款金额:20万;来源:亲戚借款;约定年利率:6%(银行同期贷款利率为5.94%);利息滚动方式:年复利;还款方式:第1年—第十年不支付任何本息,第11年-第20年每月支付2000,第21年年初一次性支付520648。
3、银行贷款金额:41万;年利率:同期银行贷款利率的七折,即5.94%*0.7=4.158%;利息滚动方式:月复利;贷款年限:30年;还款方式:每月等额还款1994元。
4、房子现时租赁价格:每年24000元(水电物业等杂费由承租方另外支付)。
问题②模型建立:我建立了一个模型来计算为期20年的买房和租房的回报净现值。
表一:七、模型求解问题①模型求解:第一年:房租24000,银行按揭1994*12=23928,还亲戚借款0,差额24000-23928=72 第二年:房租24000*1.07=25680,银行按揭23928,还亲戚借款0,差额1752第三年:房租27477.6,银行按揭23928,还亲戚借款0,差额3549.6第四年:房租29401.03,银行按揭23928,还亲戚借款0,差额5473.03第五年:房租31459.10,银行按揭23928,还亲戚借款0,差额7531.10第六年:房租33661.24,银行按揭23928,还亲戚借款0,差额9733.24。
第十一年:房租47211.57,银行按揭23928,还亲戚借款24000,差额-716.43第十二年:房租50516.38,银行按揭23928,还亲戚借款24000,差额2588.38第十三年:房租54052.53,银行按揭23928,还亲戚借款24000,差额6124.53。
第二十年:房租86796.55,银行按揭23928,还亲戚款24000,差额38868.55二十年房租合计:983891.81,银行按揭还款合计478560,还亲戚借款支出240000,净赚983891.81-478560-240000= 265331.81问题②模型求解:通过这个模型,我发现买房与租房的关系与两个参数相关:租售比和房产升值速度。
我利用线性规划中的单变量求解找到了买房和租房的回报净现值相等的情况,绘制了一条曲线。
图一:八、结果分析问题①结果分析:第21年年初,卖掉房子收入100万,一次性还清银行剩余贷款195586,并按约定一次性支付给亲戚520648,净赚1000000-195586-520648=283766。
加上前面二十年用房租抵按揭净赚的265331.81,净赚283766+265331.81=549097.81。
如果说2030年一套二手单身公寓只能卖100万,那么这549097.81就完全足够买一部跑车了。