初中几何八大经典模型(一)

初中数学八大经典模型数学是人类探索宇宙奥秘的手段，在它的领域里有着深厚的文化底蕴，从古至今都有强大的科学后果，也激发了前所未有的实际活动。

初中数学是一门极其有趣的学科，它拥有独特的传统知识，拥有丰富的讲解内容。

尽管初中数学涉及的内容很多，但其八大模型却是最基本也是最重要的。

下面，就来认识下其中的八大经典模型。

第一经典模型是“极坐标函数”，该模型在数学的宇宙中扮演着重要的角色，它可以描述和表示曲线在多维空间中的分布规律。

它的坐标系定义和应用都是极其有趣的，在很多实际的例子中，它的应用非常广泛。

第二经典模型是“极限”，它是一种数学概念，表示某个变量在某一时刻改变量趋近于某一值。

它可以用来分析函数在不同情况下的变化趋势，也可以用来推导结论。

第三经典模型是“微积分”，它是数学科学的核心模型，可以解决函数变化等问题，是推动数学发展的重要力量。

微积分主要是研究函数在某一点处或某一范围内的变化情况，如果掌握了这个模型，就可以合理的解释和推导函数的弯曲程度，即变化的极限。

第四经典模型是“偏微分方程”，它具有比较强的数学思维，可以用来研究某些动态系统的变化，描述的是一类线性不变的方程组，它的求解非常复杂，要求掌握一定的知识，但是它的应用在科学界非常广泛，如运动算法，流体力学等都有它的身影。

第五经典模型是“图论”，它是一种数学模型，可以用来描述某种新的连接结构，它可以用来描述复杂的网络关系，根据顶点和边的不同来描述不同的复杂系统，它是一种抽象的数学模型，可以用来描述复杂的网络结构，也可以用来解决一系列问题。

第六经典模型是“几何变换”，它是数学上研究几何图形变换的模型，主要是探讨几何图形随着某种变换函数而发生变化的情况，其内容很好理解，学习相关概念和知识，也能够运用它来解决一系列几何问题，其实它也是几何学的基础。

第七经典模型“统计学”，它是研究数据分析方法的一种模型，它可以用来描述一组数据的特征，推断出它的规律和趋势，用来找出未知问题的答案，统计学是一种发现客观规律的重要工具，如果掌握了它，就可以更加有效的分析和挖掘隐藏在数据背后的价值。

八年级下册数学几何模型大全数学几何模型是一个非常重要的数学学科，是把空间中的图形或者实体同数学联系起来的学科。

几何模型不仅在数学中有很重要的作用，在生活中也有着广泛的应用。

下面我们将介绍一些比较常见的八年级下册数学几何模型。

（一）圆的平面几何模型1.圆的圆心角：圆的圆心角是指围绕圆心的一个角度。

圆心角对应的线段叫做弧，一个圆被分割成的每一个扇形的圆心角度数相等，比如60度、90度、120度等等。

可以将圆分成若干个扇形，每个扇形的圆心角都是一样的。

2.圆的直径、半径和周长：圆的周长是所有弧长的总和，也就是一个圆的周长等于两倍的半径乘以圆周率（π），即2πr。

圆的直径等于圆的半径的两倍，即2r。

（二）平面几何模型1.三角形的内心、外心、重心：一个三角形的三个高线所交的点叫做重心，三角形内切圆圆心叫做内心，三角形外接圆圆心叫做外心。

内心到三角形每一边的距离相等，外心到三角形每一边的距离也相等。

2.菱形的特性：菱形是四个相等的角和四条相等的边组成的图形，相邻的两边是平行的，对角线平分。

用平行四边形的性质可以证明，对角线的交点是菱形的重心、内心和外心。

（三）立体几何模型1.正方体、长方体、平行六面体的特性：正方体、长方体、平行六面体是立方体的三个特殊形式。

正方体各个面的面积和体积是相等的，长方体的体积是它的三条边的积，平行六面体的底面积和高的乘积等于它的体积。

2.圆柱、圆锥和球体的特性：圆柱的体积等于底面积和高的积，圆锥的体积等于底面积和高的积再除以三，球体的体积等于半径的立方乘以圆周率再乘以四分之三。

（四）平面坐标系的几何模型1.坐标系下的图形方程：在平面直角坐标系中，一条函数图像的方程是由一组有序数对 (x, y) 所组成的集合。

在二维空间中，x 坐标代表水平方向上的位置，y 坐标代表垂直方向上的位置。

2.平面上两点的距离公式：平面直角坐标系中，点 A 的坐标是$(x_1,y_1)$，点 B 的坐标是 $(x_2,y_2)$。

以下是初二上册数学中常见的几何模型：
1. 三角形模型：用于研究三角形中的各种关系和定理，例如三角形的全等、相似和角平分线等。

2. 平行四边形模型：用于研究平行四边形的性质和判定，例如对角线相等、对角线互相平分等。

3. 矩形模型：用于研究矩形的性质和判定，例如四个角都是直角、对角线相等且互相平分等。

4. 菱形模型：用于研究菱形的性质和判定，例如四边相等、对角线互相垂直且平分等。

5. 勾股定理模型：用于研究勾股定理的证明和应用，例如直角三角形的三边关系等。

6. 圆模型：用于研究圆的性质和判定，例如圆周角定理、切线的判定和性质等。

7. 扇形模型：用于研究扇形的性质和面积计算，例如扇形的弧长和面积公式等。

8. 角平分线模型：用于研究角平分线的性质和判定，例如角的平分线与对边的关系等。

9. 中位线模型：用于研究中位线的性质和判定，例如中位线的长度等于它所截两边的平均值等。

10. 直角三角形模型：用于研究直角三角形的性质和判定，例如勾股定理的逆定理、直角三角形斜边的中线等于斜边的一半等。

以上是初二上册数学中常见的几何模型，掌握这些模型对于解决几何问题非常重要。

七年级数学几何模型大全七年级的小伙伴们，今天咱们来唠唠七年级数学里那些超有趣的几何模型。

一、角平分线模型1. 双角平分线模型- 想象一下，有一个角，然后从这个角的顶点引出两条角平分线。

比如说∠AOB，OC平分∠AOB，OD平分∠AOC。

这里面就有很多好玩的关系哦。

- 如果设∠AOB = 2α，那么∠AOC=α，∠AOD = α/2。

这里面的关键就是根据角平分线的定义，把角之间的关系找出来。

就像分蛋糕一样，角平分线就是把角这个“大蛋糕”分成相等的“小蛋糕”。

- 而且还有个重要的结论呢，如果两个角平分线所夹的角是β，那么β = 1/2∠AOB或者β = 1/2 (∠AOB - ∠COD)，这就看具体的图形情况啦。

2. 邻补角角平分线模型- 当有两个邻补角的时候，它们的角平分线可是很特别的。

比如说∠AOC和∠BOC是邻补角，OE平分∠AOC，OF平分∠BOC。

- 因为∠AOC+∠BOC = 180°，又因为OE和OF是角平分线，所以∠EOC+∠FOC=1/2(∠AOC + ∠BOC)=90°。

这就像两个小伙伴，把相邻的两块“角蛋糕”各自分一半，然后这两半加起来正好是个直角呢。

二、平行线模型1. “Z”字形模型（内错角模型）- 当有两条平行线被第三条直线所截的时候，就会出现像“Z”字一样的图形。

比如说直线a∥b，直线c与a、b相交。

- 这里面的内错角是相等的哦。

就好像在两条平行的铁轨（a和b）上，有一根枕木（c）横过来，形成的内错角就像在铁轨两边对称的位置，它们的大小是一样的。

- 如果∠1和∠2是内错角，那么∠1 = ∠2。

这个结论在证明角相等或者计算角的度数的时候可太有用啦。

2. “F”字形模型（同位角模型）- 还是两条平行线被第三条直线所截，不过这个时候是同位角的关系。

就像“F”字的形状。

- 同位角也是相等的呢。

比如说∠3和∠4是同位角，只要a∥b，那么∠3 = ∠4。

可以想象成在平行的道路（a和b）上，同样位置的标记（∠3和∠4），它们的角度肯定是一样的呀。

初中数学八大几何模型归纳
初中数学中的八大几何模型包括:
1. 三角形相关模型：三角形的各种性质、三角形的面积计算、三角形的周长计算等;
2. 四边形相关模型：四边形的各种性质、四边形的面积计算、四边形的周长计算等;
3. 圆相关模型：圆的各种性质、圆的面积计算、圆的周长计算、圆的弧长计算等;
4. 相似三角形相关模型：相似三角形的定义、相似三角形的判定、相似三角形的面积计算等;
5. 直角三角形相关模型：直角三角形的定义、直角三角形的判定、直角三角形的面积计算等;
6. 二次函数相关模型：二次函数的定义、二次函数的图像、二次函数的值域、二次函数的对称轴等;
7. 轴对称相关模型：轴对称的定义、轴对称的图像、轴对称的性质、轴对称的图形设计等;
8. 平移相关模型：平移的定义、平移的性质、平移的图像等。

这些几何模型是初中数学中非常重要的知识点，学生在学习过程中需要熟练掌握。

此外，这些模型也是中考数学考试中经常出现的知识点，学生需要在平时的学习中多加练习，熟练掌握各种计算方法和技巧。

一、常见的八大类几何模型在解决几何题目时，我们经常会遇到一些常见的几何模型。

这些模型包括但不限于：直角三角形、等腰三角形、等边三角形、直接相似三角形、等腰梯形、菱形、正方形和矩形。

1. 直角三角形直角三角形是一个内角为90度的三角形。

在求解直角三角形题目时，可以运用勾股定理、正弦定理、余弦定理等方法。

2. 等腰三角形等腰三角形是指两边相等的三角形。

在解决等腰三角形问题时，可以利用等角定理、等边角定理等。

3. 等边三角形等边三角形是指三边相等的三角形。

解决等边三角形问题时，可以利用等边三角形的性质，如高、中线等。

4. 直接相似三角形直接相似三角形是指对应角相等的两个三角形。

在对直接相似三角形进行解题时，可以利用相似三角形的性质，如边比例定理等。

5. 等腰梯形等腰梯形是指有两对对边相等的梯形。

解决等腰梯形问题时，可以运用梯形的性质以及各边的关系。

6. 菱形菱形是指四条边都相等的四边形。

在解决菱形问题时，可以利用菱形的性质，如对角线垂直平分、对角相等等。

7. 正方形正方形是指四条边相等且四个角均为直角的四边形。

解决正方形问题时，可以利用正方形的性质，如对角线相等、对角线垂直等。

8. 矩形矩形是指四边均为直角的四边形。

在解决矩形问题时，可以利用矩形的性质，如对角线相等、邻边互相垂直等。

二、60种解题技巧在解决几何题目时，我们还可以运用一些解题技巧来更快更准确地得出答案。

下面列举了60种解题技巧，以供参考。

1. 勾股定理2. 余弦定理3. 正弦定理4. 度角关系5. 弧度制下的两点间弧长相关关系6. 三角恒等变形7. 各角平分线8. 高度定理9. 中线定理10. 角平分线定理11. 等角定理12. 外角定理13. 内角定理14. 中位线定理15. 等腰三角形的性质16. 等边三角形的性质17. 相似三角形的三边对应比例关系18. 相似三角形的高度关系19. 相似三角形的边对应比例关系20. 相似三角形的面积关系21. 三角形高到底关系22. 三角形高乘底除以2的面积公式23. 三角形内切圆24. 三角形外接圆25. 正方形的性质26. 矩形的对角线关系27. 矩形的邻边互相垂直关系28. 长方形的面积公式29. 长方形的周长公式30. 菱形的性质31. 菱形对角线垂直平分32. 平行四边形的性质33. 平行四边形的对角线相等关系34. 平行四边形的对角互补35. 梯形的中位线关系36. 梯形的对角线垂直关系37. 梯形的高关系38. 圆的性质39. 圆周角的关系40. 圆心角的关系41. 切线关系42. 切线长定理43. 余弦定理的推广44. 余角关系45. 同位角关系46. 交叉线定理47. 锐角三角函数的关系48. 平行线夹角关系49. 余切函数的关系50. 同义形的面积公式51. 直角三角形斜边上的高52. 各角平分线角度关系53. 三角形中位线长度关系54. 三角形中位线平行长的关系55. 等角三角形三角函数的关系56. 三角形半周长乘外切圆内切圆面积关系57. 圆相关不等式58. 反证法59. 斜率性质60. 坐标系下平移关系解决几何问题时，首先要熟练掌握常见的八大类几何模型，然后灵活运用各种解题技巧，以便更加高效地解决问题。

初中经典几何模型专题01 截长补短模型证明问题【专题说明】截长补短法在初中几何教学中有着十分重要的作用,它主要是用来证线段的和差问题,而且这种方法一直贯穿着整个几何教学的始终.那么什么是截长补短法呢?所谓截长补短其实包含两层意思,即截长和补短.截长就是在较长的线段上截取一段等于要证的两段较短的线段中的一段,证剩下的那一段等于另外一段较短的线段.当条件或结论中出现a+b=c时，用截长补短．【知识总结】1、补短法：通过添加辅助线“构造”一条线段使其为求证中的两条线段之和，在证所构造的线段和求证中那一条线段相等；2、截长法：通过添加辅助线先在求证中长线段上截取与线段中的某一段相等的线段，在证明截剩部分与线段中的另一段相等。

3、截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，使之与特定线段相等，再利用三角形全等有关性质加以说明，这种做法一般遇到证明三条线段之间关系时常用。

如图1，若证明线段AB,CD,EF之间存在EF=AB+CD,可以考虑截长补短法截长法：如图2，在EF上截取EG=AB,在证明GF=CD即可；补短法：如图3，延长AB至H点，使BH=CD,再证明AH=EF即可.【类型】一、截长“截长”是指在较长的线段上截取另外两条较短的线段，截取的作法不同，涉及四种方法。

【类型】二、补短“补短”指的是选取两条较短线段中的一条进行延长，使得较短的两条线段共线并寻求解题突破，根据辅助线作法的不同也涉及四种不同的方法。

【基础训练】1、如图，AC平分∠BAD，CE⊥AB于点E，∠B+∠D=180°，求证：AE=AD+BE.2、如图，已知在△ABC中，∠C=2∠B,∠1=∠2，求证：AB=AC+CD3、如图，在五边形ABCDE中，AB=AE,BC+DE=CD,∠B+∠E=180°，求证：AD平分∠CDE.4、已知四边形ABCD中，∠ABC+∠ADC=180°，AB=BC如图2，点P,Q分别在线段AD,DC上，满足PQ=AP+CQ,∠ADC求证：∠PBQ=90°-125、如图，在△ABC中，∠B=60°，△ABC的角平分线AD、CE相交于点O，求证：AE+CE=AC.6、如图所示，AB∥CD,BE,CE分别是∠ABC,∠BCD的平分线，点E在AD上，求证：BC=AB+CD.7、四边形ABCD中，BD＞AB,AD=DC,DE⊥BC,BD平分∠ABC （1）证明：∠BAD+∠BCD=180°（2）DE=3,BE=6,求四边形ABCD的面积.8、已知：在△ABC中，AB=CD-BD,求证：∠B=2∠C.9、如图，△ABC中，BD⊥AC于点D，CE⊥AB于点E，且BD,CE交于点F，点G是线段CD上一点，连接AF，GF，若AF=GF,BD=CD.（1）求∠CAF的度数（2）判断线段FG与BC的位置关系，并说明理由.【巩固提升】1．如图，在△ABC中，∠A＝60°，BD，CE分别平分∠ABC和∠ACB，BD，CE交于点O，试判断BE，CD，BC的数量关系，并加以证明．2．如图，AD//BC，DC⊥AD，AE平分∠BAD，E是DC的中点．问：AD，BC，AB之间有何关系？并说明理由．3．如图，已知DE＝AE，点E在BC上，AE⊥DE，AB⊥BC，DC⊥BC，请问线段AB，CD和线段BC有何大小关系？并说明理由．4．如图，AB∥CD，B E，CE分别是∠ABC和∠BCD的平分线，点E在AD上．求证：BC＝AB＋CD.5．如图，在R t△ABC中，∠C＝90°，BC＝AC，∠B＝∠CAB＝45°，AD平分∠BAC交BC于D，求证：AB＝AC＋CD.6．如图，在△ABC中，∠ABC＝60°，AD，CE分别平分∠BAC，∠ACB，AD，CE交于O.(1)求∠AOC的度数；(2)求证：AC＝AE＋CD.专题01 截长补短模型证明问题【专题说明】截长补短法在初中几何教学中有着十分重要的作用,它主要是用来证线段的和差问题,而且这种方法一直贯穿着整个几何教学的始终.那么什么是截长补短法呢?所谓截长补短其实包含两层意思,即截长和补短.截长就是在较长的线段上截取一段等于要证的两段较短的线段中的一段,证剩下的那一段等于另外一段较短的线段.当条件或结论中出现a+b=c时，用截长补短．【知识总结】1、补短法：通过添加辅助线“构造”一条线段使其为求证中的两条线段之和，在证所构造的线段和求证中那一条线段相等；2、截长法：通过添加辅助线先在求证中长线段上截取与线段中的某一段相等的线段，在证明截剩部分与线段中的另一段相等。

八年级下册数学几何模型大全数学几何模型是指根据数学几何理论，通过抽象和抽象为物体所形成的模型。

这些模型能够帮助我们更好地理解和应用数学几何的知识，提高解题能力。

下面是八年级下册数学几何模型的相关参考内容。

1. 平面几何模型：(1) 正方形模型：通过正方形的特点和性质，帮助学生理解正方形的定义、边长和周长的关系，以及正方形与其他几何图形的联系。

(2) 矩形模型：通过矩形的特点和性质，帮助学生理解矩形的定义、边长和周长的关系，以及矩形与其他几何图形的联系。

(3) 直角三角形模型：通过直角三角形的特点和性质，帮助学生理解勾股定理和三角形的角度关系，以及直角三角形与其他几何图形的联系。

2. 空间几何模型：(1) 平行四边形模型：通过平行四边形的特点和性质，帮助学生理解平行四边形的定义、对角线关系以及面积计算方法。

(2) 立方体模型：通过立方体的特点和性质，帮助学生理解立方体的定义、体积计算方法，以及立方体与其他几何图形的联系。

(3) 圆锥模型：通过圆锥的特点和性质，帮助学生理解圆锥的定义、体积计算方法，以及圆锥与其他几何图形的联系。

3. 旋转体几何模型：(1) 圆柱体模型：通过圆柱体的特点和性质，帮助学生理解圆柱体的定义、体积计算方法，以及圆柱体与其他几何图形的联系。

(2) 圆锥模型：通过圆锥的特点和性质，帮助学生理解圆锥的定义、体积计算方法，以及圆锥与其他几何图形的联系。

(3) 球模型：通过球的特点和性质，帮助学生理解球的定义、体积计算方法，以及球与其他几何图形的联系。

4. 相似几何模型：(1) 相似三角形模型：通过相似三角形的特点和性质，帮助学生理解相似三角形的定义、比例关系和性质，以及相似三角形与其他几何图形的联系。

(2) 相似多边形模型：通过相似多边形的特点和性质，帮助学生理解相似多边形的定义、比例关系和性质，以及相似多边形与其他几何图形的联系。

(3) 相似几何体模型：通过相似几何体的特点和性质，帮助学生理解相似几何体的定义、比例关系和性质，以及相似几何体与其他几何图形的联系。

初中数学几何模型归纳1. 直线模型：直线是最基本的几何图形，可以用直线方程y = kx + b 来表示。

其中，k 是斜率，b 是截距。

2. 点模型：点是几何图形中的基本元素，可以用坐标(x, y) 来表示。

3. 线段模型：线段是由两个端点确定的有限长度的直线部分。

线段可以用起点和终点的坐标来表示。

4. 射线模型：射线是由一个端点和一个方向确定的无限延伸的直线部分。

射线可以用起点和方向向量来表示。

5. 角模型：角是由两条射线的公共端点和这两条射线之间的夹角组成的。

角可以用顶点、始边和终边来表示。

6. 三角形模型：三角形是由三条边和三个内角组成的多边形。

三角形可以用三边的长度和三个内角的大小来表示。

7. 四边形模型：四边形是由四条边和四个内角组成的多边形。

四边形可以用四边的长度和四个内角的大小来表示。

8. 圆模型：圆是由一个圆心和一个半径确定的平面上的所有点到圆心的距离都等于半径的图形。

圆可以用圆心和半径来表示。

9. 椭圆模型：椭圆是由两个焦点和一个长轴、短轴确定的平面上的所有点到两个焦点的距离之和等于常数的图形。

椭圆可以用两个焦点和长轴、短轴的长度来表示。

10. 双曲线模型：双曲线是由两个焦点和一个实轴、虚轴确定的平面上的所有点到两个焦点的距离之差等于常数的图形。

双曲线可以用两个焦点和实轴、虚轴的长度来表示。

11. 正多边形模型：正多边形是由相等的边和相等的内角组成的多边形。

正多边形可以用边数和内角度数来表示。

12. 梯形模型：梯形是由一对平行边和一对非平行边组成的四边形。

梯形可以用两对边的长度和夹角来表示。

13. 矩形模型：矩形是由四个直角和两对相等的边组成的四边形。

矩形可以用两对边的长度和夹角来表示。

14. 正方形模型：正方形是特殊的矩形，它的四个边都相等且四个角都是直角。

正方形可以用边长来表示。

15. 三角形面积模型：三角形的面积可以通过底边长度和高来计算，公式为S = (底边长度×高) / 2。

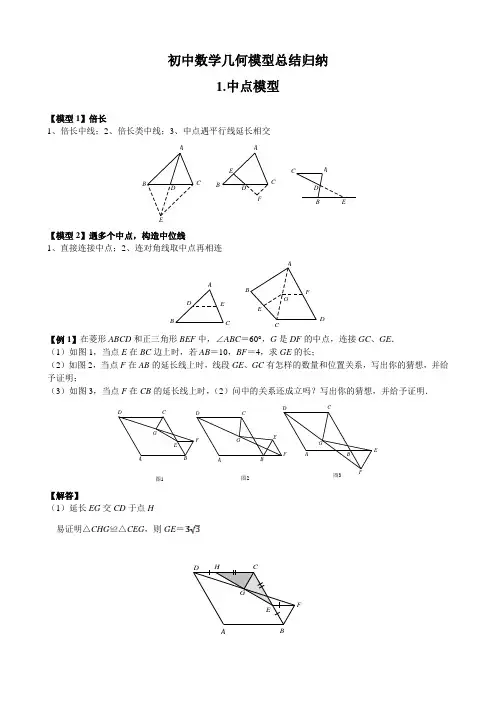
初中数学几何模型总结归纳1.中点模型【模型1】倍长1、倍长中线；2、倍长类中线；3、中点遇平行线延长相交ABCD E ABC DEFEDCBA【模型2】遇多个中点，构造中位线1、直接连接中点；2、连对角线取中点再相连GABCDEFABCD E【例1】在菱形ABCD 和正三角形BEF 中，∠ABC ＝60°，G 是DF 的中点，连接GC 、GE ． （1）如图1，当点E 在BC 边上时，若AB ＝10，BF ＝4，求GE 的长；（2）如图2，当点F 在AB 的延长线上时，线段GE 、GC 有怎样的数量和位置关系，写出你的猜想，并给予证明；（3）如图3，当点F 在CB 的延长线上时，（2）问中的关系还成立吗？写出你的猜想，并给予证明．图3图2图1ACDEFGDEFGCDEGABBFCBA【解答】（1）延长EG 交CD 于点H 易证明△CHG ≌△CEG ，则GE ＝HBEGCFAD（2）延长CG 交AB 于点I ，易证明△BCE ≌△FIE ，则△CEI 是等边三角形，GE ＝3GC 错误!未找到引用源。

，且GE ⊥GCF（3）EJ【例2】如图，在菱形ABCD 中，点E 、F 分别是BC 、CD 上一点，连接DE 、EF ，且AE ＝AF ，∠DAE ＝∠BAF .（1）求证：CE ＝CF ； （2）若∠ABC ＝120°，点G 是线段AF 的中点，连接DG 、EG ，求证：DG ⊥EG .GFE DC BAE H GF EDCBA【解答】（1）证明△ABE ≌△ADF 即可；（2）延长DG 与AB 相交于点H ，连接HE ，证明△HBE ≌△EFD 即可【例3】如图，在凹四边形ABCD 中，AB ＝CD ，E 、F 分别为BC 、AD 的中点，BA 交EF 延长线于G 点，CD 交EF 于H 点，求证：∠BGE ＝∠CHE . 【解答】取BD 中点可证，如图所示：JA BCDE F GH2.角平分线模型【模型1】构造轴对称【模型2】角平分线遇平行构等腰三角形【例4】如图，平行四边形ABCD 中，AE 平分∠BAD 交BC 边于E ，EF ⊥AE 交边CD 于F 点，交AD 边于H ，延长BA 到G 点，使AG ＝CF ，连接GF .若BC ＝7，DF ＝3，EH ＝3AE ，则GF 的长为_______.HGFEDCBA【解答】延长FE 、AB 交于点I ，易得CE ＝CF ，BA ＝BE ，设CE ＝x ，则BA ＝CD ＝3＋x ，BE ＝7－x ， 3＋x ＝7－x ，x ＝2，AB ＝BE ＝5，AE ＝，作AJ ⊥BC ，连接AC ，求得GF ＝AC ＝3JIAB CDEFGH3.手拉手模型【条件】OA ＝OB ，OC ＝OD ，∠AOB ＝∠COD【结论】△OAC ≌△OBD ，∠AEB ＝∠AOB ＝∠COD （即都是旋转角）；OE 平分∠AEDDC EBAOOABEC D 导角核心图形：八字形CBAO【例5】（2014重庆市A 卷）如图，正方形ABCD 的边长为6，点O 是对角线AC 、BD 的交点，点E 在CD 上，且2DE CE ，连接BE ．过点C 作CF ⊥BE ，垂足是F ，连接OF ，则OF 的长为________．FABCOEDDE CBA【例6】如图，△ABC 中，∠BAC ＝90°，AB ＝AC ，AD ⊥BC 于点D ，点E 在AC 边上，连接BE ，AG ⊥BE于F ，交BC 于点G ，求∠DFG ． GFE DCBAABC【答案】45°【例7】（2014重庆B 卷）如图，在边长为ABCD 中，E 是AB 边上一点，G 是AD 延长线一点，BE ＝DG ，连接EG ，CF ⊥EG 交EG 于点H ，交AD 于点F ，连接CE 、BH ．若BH ＝8，则FG＝_____________．HGDE CBAFABE G【答案】4.邻边相等对角互补模型【模型1】【条件】如图，四边形ABCD 中，AB ＝AD ，∠BAD ＋∠BCD ＝∠ABC ＋∠ADC ＝180° 【结论】AC 平分∠BCDEB【模型2】【条件】如图，四边形ABCD 中，AB ＝AD ，∠BAD ＝∠BCD ＝90° 【结论】① ∠ACB ＝∠ACD ＝45°； ② BC ＋CDABCECB【例8】如图，矩形ABCD 中，AB ＝6，AD ＝5，G 为CD 中点，DE ＝DG ，FG ⊥BE 于F ，则DF 为_____.F ABCEDGG DE【例9】如图，正方形ABCD 的边长为3，延长CB 至点M ，使BM ＝1，连接AM ，过点B 作BN ⊥AM ，垂足为N ，O 是对角线AC 、BD 的交点，连结ON ，则ON 的长为__________. OMN DCBA【例10】如图，正方形ABCD 的面积为64，△BCE 是等边三角形，F 是CE 的中点，AE 、BF 交于点G ，则DG 的长为___________. GFEABCDEC【答案】45.半角模型【模型1】【条件】如图，四边形ABCD 中，AB ＝AD ，∠BAD ＋∠BCD ＝∠ABC ＋∠ADC ＝180°，∠EAF ＝12∠BAD ， 点E 在直线BC 上，点F 在直线CD 上 【结论】BE 、DF 、EF 满足截长补短关系FEDCBA【模型2】【条件】如图，在正方形ABCD 中，已知E 、F 分别是边BC 、CD 上的点，且满足∠EAF ＝45°，AE 、AF 分别与对角线BD 交于点M 、N ． 【结论】①BE ＋DF ＝EF ； ② ABE ADF AEF S S S ∆∆∆+=；③AH ＝AB ；④2ECF C AB ∆=；⑤BM 2＋DN 2＝MN 2；⑥△ANM ∽△DNF ∽△BEM ∽△AEF ∽△BNA ∽△DAM （由AO ：AH ＝AO ：AB ＝1：可得到△ANM 和△AEF 相似比为1）⑦AMN MNFE S S ∆=四边形；⑧△AOM ∽△ADF ；△AON ∽△ABE ；⑨△AEN 为等腰直角三角形，∠AEN ＝45°，△AFM 为等腰直角三角形，∠AFM ＝45°；⑩A 、M 、F 、D 四点共圆，A 、B 、E 、N 四点共圆，M 、N 、F 、C 、E 五点共圆．H NM FEDCBA【模型2变形】【条件】在正方形ABCD 中，已知E 、F 分别是CB 、DC 延长线上的点，且满足∠EAF ＝45° 【结论】BE ＋EF ＝DFFEDCB A【模型2变形】【条件】在正方形ABCD 中，已知E 、F 分别是BC 、CD 延长线上的点，且满足∠EAF ＝45° 【结论】DF ＋EF ＝BEAB C DEF【例11】如图，△ABC 和△DEF 是两个全等的等腰直角三角形，∠BAC ＝∠EDF ＝90°，△DEF 的顶点E与△ABC 的斜边BC 的中点重合，将△DEF 绕点E 旋转，旋转过程中，线段DE 与线段AB 相交于点P ，射线EF 与线段AB 相交于点G ，与射线CA 相交于点Q .若AQ ＝12，BP ＝3，则PG ＝__________.Q PGD FECBA【解答】连接AE ，题目中有一线三等角模型和半角模型设AC ＝x ，由△BPC ∽△CEQ 得BP CE ＝BE CQ ， 3/（22x ）＝22x /（x ＋12），解得x ＝12 设PG ＝y ，由AG 2＋BP 2＝PG 2得32＋(12－3－x )2＝x 2，解得x ＝5【例12】如图，在菱形ABCD 中，AB ＝BD ，点E 、F 在AB 、AD 上，且AE ＝DF ．连接BF 与DE 交于点G ，连接CG 与BD 交于点H ，若CG ＝1，则S 四边形BCDQ ＝__________．HGFED CB A【解答】346.一线三等角模型【条件】∠EDF ＝∠B ＝∠C ，且DE ＝DF 【结论】△BDE ≌△CFDFEDCBA【例13】如图，正方形ABCD 中，点E 、F 、G 分别为AB 、BC 、CD 边上的点，EB ＝3，GC ＝4，连接EF 、FG 、GE 恰好构成一个等边三角形，则正方形的边为__________.GA B CDEF【解答】如图，构造一线三等角模型，△EFH ≌△FGI 则BC ＝BF ＋CF ＝HF －BH ＋FI －CI ＝GI －BH ＋HE －CI ＝733IH F ED C B A G7.弦图模型【条件】正方形内或外互相垂直的四条线段 【结论】新构成了同心的正方形LK JIHGFECDB AHG FEDCBA【例14】如图，点E 为正方形ABCD 边AB 上一点，点F 在DE 的延长线上，AF ＝AB ，AC 与FD 交于点G ，∠F AB 的平分线交FG 于点H ，过点D 作HA 的垂线交HA 的延长线于点I .若AH ＝3AI ，FH ＝22，则DG ＝__________．I H AGFEDCB【解答】1742【例15】如图，△ABC 中，∠BAC ＝90°，AB ＝AC ，AD ⊥BC 于点D ，点E 是AC 中点，连接BE ，作AG ⊥BE 于F ，交BC 于点G ，连接EG ，求证：AG ＋EG ＝BE ．FE CGDBABC【解答】过点C 作CH ⊥AC 交AG 的延长线于点H ，易证8.最短路径模型【两点之间线段最短】 1、将军饮马Q2、费马点【垂线段最短】【两边之差小于第三边】【例16】如图，矩形ABCD 是一个长为1000米，宽为600米的货场，A 、D 是入口，现拟在货场内建一个收费站P ，在铁路线BC 段上建一个发货站台H ，设铺设公路AP 、DP 以及PH 之长度和为l ，求l 的最小值．【解答】3500600 ，点线为最短．【例17】如图，E 、F 是正方形ABCD 的边AD 上的两个动点，满足AE ＝DF，连接CF 交BD 于G ，连接BE 交AG 于H ，若正方形的边长为2，则线段DH 长度的最小值为______________________．【解答】如图，取AB 中点P ，连接PH 、PD ，易证PH ≥PD -PH 即DH ≥15-．【例18】如图所示，在矩形ABCD 中，AB ＝4，AD ＝24，E 是线段AB 的中点，F 是线段BC 上的动点，△BEF 沿直线EF 翻折到△EF B '，连接B D '，B D '最短为________________．【解答】4【例19】如图1，□ABCD 中，AE ⊥BC 于E ，AE ＝AD ，EG ⊥AB 于G ，延长GE 、DC 交于点F ，连接AF ．（1）若BE ＝2EC ，AB ＝13，求AD 的长；（2）求证：EG ＝BG ＋FC ；（3）如图2，若AF ＝25，EF ＝2，点M 是线段AG 上一动点，连接ME ，将△GME 沿ME 翻折到△ME G '，连接G D '，试求当G D '取得最小值时GM 的长．图1 图2 备用图【解答】（1）3（2）如图所示（3）当DG ′最小时D 、E 、G '三点共线解得43173-=+'=MN N G GMEH【练习1】如图，以正方形的边AB为斜边在正方形内作直角三角形ABE，∠AEB＝90°，AC、BD交于O．已知AE、BE的长分别为3、5，求三角形OBE的面积．【解答】25【练习2】问题1：如图1，在等腰梯形ABCD 中，AD∥BC，AB＝BC＝CD，点M，N分别在AD，CD上，∠MBN21∠ABC，试探究线段MN，AM，CN有怎样的数量关系？请直接写出你的猜想；问题2：如图2，在四边形ABCD中，AB＝BC，∠ABC＋∠ADC＝180°，点M，N分别在DA，CD延长线，若∠MBN＝12∠ABC仍然成立，请你进一步探究线段MN，AM，CN又有怎么样的关量关系？写出你的猜想，并给予证明。