总复习知识点

初中英语总复习(全册)知识点归纳一、词汇知识点1. 名词：表示人、事物、地点等的名称。

如：teacher, book, Beijing。

2. 动词：表示行为、状态、感觉等。

如：run, sleep, like。

3. 形容词：修饰名词或代词，描述人或事物的特征。

如：beautiful, tall, kind。

4. 副词：修饰动词、形容词、其他副词等，表示时间、地点、程度等。

如：quickly, slowly, very。

5. 代词：替代名词的词语。

如：he, she, it, they。

6. 介词：表示位置、关系、方式等。

如：in, on, at。

7. 连词：连接两个词、短语、句子等。

如：and, but, or。

8. 数词：表示数量的词语。

如：one, two, first。

二、语法知识点1. 时态：英语中常用的时态有一般现在时、一般过去时、一般将来时等。

2. 句型：英语中常见的句型有陈述句、疑问句、祈使句等。

3. 从句：包括定语从句、名词性从句和状语从句等。

4. 否定形式：在英语中通过在句子中加入否定词来表示否定的意思。

5. 疑问形式：在英语中通过改变句子语序或加入疑问词来构成疑问句。

6. 介词短语：一种由介词和它的宾语构成的结构，用来修饰名词或动词。

三、阅读技巧1. 抓主题：阅读时要注意抓住文章的主题，从中找出关键信息。

2. 理解词义：通过上下文，猜测不认识的单词的意思。

3. 推理推断：通过已知信息进行推理，得出未知信息。

4. 划重点：将文章中所述的重要信息标记出来，有助于记忆和理解。

5. 阅读速度：提高阅读速度的技巧有先读标题、段落开头和结尾。

以上是初中英语总复的知识点归纳，希望对你的复有所帮助！。

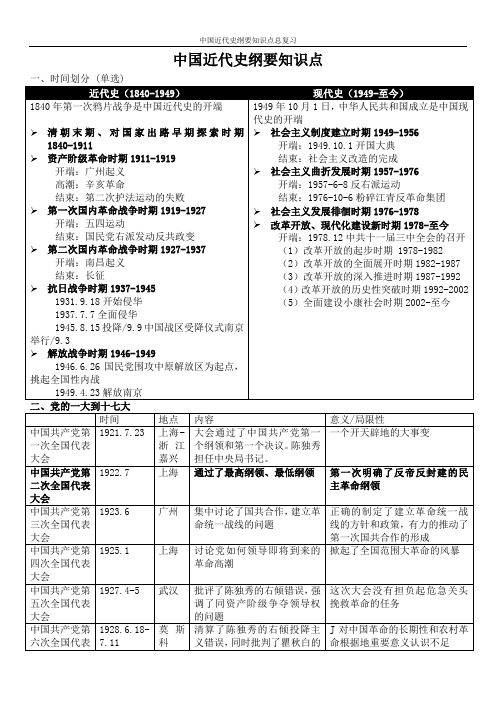
中国近代史纲要知识点※最低纲领：消除内乱，打倒军阀，建设国内和平；推翻国际帝国主义的压迫，达到中华民族完全独立；统一中国为真正的民主共和国※历史时期的总任务：团结全国各族人民，自力更生，艰苦风斗，逐步实现工业、农业、国防和科学技术现代化，把我国建设为高度文明、高民主的社会主义国家※“我国正处于社会主义的初级阶段”的两层含义：我国社会已经是社会主义社会；我国的社会主义社会还处在初级阶段持艰苦风斗的作风※《共同纲领》内容包括：新中国的国体和政体的规定；新中国的基本民族政策；新中国的外交工作原则1、中国近代史上第一个不平等的条约——《中英南京条约》2、中国近代史上第一个被侵略的战争——第一次鸦片战争3、中国近代史上第一次反侵略的斗争——三元里斗争4、中国近代史上睁眼看世界的第一人——林则徐5、中国近代史上第一个带有资本主义色彩的改革方案——《资政新编》6、中国近代史上第一个对洋务运动的指导思想作出比较完整表述的——冯桂芬7、中国近代史上创办的第一个翻译学堂——京师同文馆8、中国近代史上第一个资产阶级革命组织——兴中会9、中国近代史上第一个资产阶级革命政党——同盟会10、中国近代史上第一套资产阶级共和国建国方案——三民主义学说11、中国近代史上第一部资产阶级共和国性质的宪法法典——《中华民国临时约法》12、新文化运动的第一篇白话文小说——《狂人日记》鲁迅13、中国近代史上第一次彻底的反帝反封建的革命运动——五四运动14、中国历史上第一个地方共产党组织——上海共产主义小组15、中国近代史上第一次提出反帝反封建的革命纲领的会议——中共二大16、中国近代史上第一次工人运动的高潮——香港海员大罢工（为起点）17、中国近代史上打响了武装反抗国民党反动派的第一枪——南昌起义18、毛泽东第一次明确的提出工农武装割据思想的文章——《中国的红色政权为什么能够存在？》、《井冈山的斗争》19、中国近代史上第一个农村革命根据地——井冈山革命根据地20、抗战中，国民党的第一次大捷——台儿庄战役21、抗战中第一次重大胜利——平型关战役22、中国政府第一次提出“四个现代化”目标的会议——三届人大一次会议23、中国共产党历史上第一个土地法——1928年12月井冈山土地法24、中华苏维埃第一次全国代表大会——在江西瑞金县叶坪村召开25、中国历史上第一个真正代表人民利益的政府——中华苏维埃政府（1931年）26、苏联第一个照会中国政府，决定同中华人民共和国建立外交关系——1949.10.227、中国人民政府颁布新中国第一部法律——《中华人民共和国婚姻法》1950.528、中国爆炸了第一颗原子弹——1964.1029、中国爆炸了第一颗氢弹——1967.730、中国第一颗人造地球卫星发射成功——1970.4六、重大理论1、两对主要矛盾和两大历史任务的内容及关系：答：(1)两对主要矛盾及其关系➢两对矛盾：帝国主义与中华民族的矛盾、封建主义与人民大众的矛盾是两对主要矛盾，而帝国主义与中华民族的矛盾，是各种矛盾中最主要的矛盾。

小学语文基础知识点大全第一部分：基础知识要点一、汉语拼音：1.掌握23个声母：b p m f d t n l g k h j q x zc s zh ch sh r y w2.掌握24个韵母：1) 单韵母：a o e i u ü2) 复韵母8个：ai ei ui ao ou iu ie üe3) 鼻韵母分为前鼻音和后鼻音。

前鼻音为：an en in un ün后鼻音为：ang eng ing ong3.特殊韵母：er 它不能和声母相拼，只单独作为字音。

4.整体认读音节16个：zi ci si zhi chi shi ri yi yu wu ye yue yin yun yuan ying5.标调：a o e i u ü，标调时按顺序，iu并列标在后，i上标调去掉点；ü与j q x y相拼时去两点，如ju qu xu yu 。

6.字母表：A B C D E F G H I J K L M N O P Q R S T U V W X Y Za b c d e f g h i j k l m n o p q r s t u v w x y z7.隔音符号：以a o e 开头的音节紧跟在其它音节后面时，音节的界限容易发生混淆，因此音节间要用隔音符号（'）隔开。

如海鸥hǎi 'ōu二、查字典的方法：1.音序查字法。

如：鼎dǐng先在“拼音音节索引”中找出音序（D），再查找音节（dǐng）及所对应的页码。

2.部首查字法。

如查“挥”字，先在“部首目录”中找到（扌），再找到部首所对应的“检字表”页码，在“检字表”相应部首下及剩余笔画数（6画）下找到要查的字及正文页码。

3.数笔画查字法。

在阅读中遇到不知读音，又很难确定部首的字，就只能用数笔画的方法来查了。

首先，在“难检字索引”中的相应笔画数下找到该字，再打开所对应的正文页码就可查到这个字。

如查“乙”，在“难检字索引”中查（1）画。

高考总复习历史必背的知识点大全高考总复习历史必背的知识点一、中国古代史1、历代赋税制特征、演变原因及作用2、水利建设及作用3、历代休养生息政策对国家兴盛、民众生活的关系4、城市发展的趋势、特点;15---16世纪中西方城市发展的差异5、清康乾盛世的原因、本质及与西方发展的差异6、统一多民族国家的建立与巩固，民族间的相互取长补短二、中国近代现代史1、近代国人对待西方文化态度的逐渐变化，西方文化对近代中国社会发展的影响。

2、近代前期(1919年前)中国追赶世界现代化潮流的两次机遇、成就及经验教训。

(指第二次鸦片战争后的“中外和好”时期，辛亥革命后的民主共和时期)。

3、19世纪中日现代化道路二阶段、背景、措施、结果比较。

4、几次思想解放运动对社会发展、社会变革的影响。

5、在19世纪末20世纪初的社会巨变中，中国政治、经济、思想文化运动或措施的背景、内容、意义。

6、对20世纪30年代国民政府经济、外交建设的客观分析、评价。

(经济建设为抗战奠定了物质基础。

)7、中共探索社会主义建设道路的经验、教训。

8、新中国外交的不断成熟，(国家利益是根本出发点，现在是独立自主、灵活务实的和平外交。

9、亚洲(尤其是新加坡、南朝鲜)经济发展及其对中国的启示。

10、城市经济改革与产业结构调整。

11、对传统文化的扬弃、继承创新;对世界文化的理解、宽容、尊重、合理吸收。

12、用眼光审视中共领导新民主主义革命和社会主义建设的历程。

三、世界近代现代史1、科技革命对人类历史发展的全方位影响(促进生产力、经济发展，生产关系调整，阶级、阶层、上层建筑的变化，产业结构的调整，经济重心转移，国家地位变化，国际关系格局调整，世界体系构建，东方从属西方;促进城市化，生活方式变化，思想观念变化;同时，也带来人口膨胀，治安混乱，道德沦丧，资源破坏，环境污染，贫富差别，城乡差别，南北差距扩大等问题)2、19世纪世界经济重心转移及其原因3、新兴民族独立国家的现代化历程((在独立前，必须先反殖反帝，取得民族独立，解决现代化的政治前提，独立后，现代化建设有成就，土耳其较典型，但各国各地很不均衡，都有许多制约因素，如国内的专制统治，经济基础差，国民素质低，经济政策、结构不合理等，国际有不平等的经济政治秩序等。

总复习必修一化学知识点总结高考总复习必修一化学知识点总结(1)根本概念1.区分元素、同位素、原子、分子、离子、原子团、取代基的概念。

正确书写常见元素的名称、符号、离子符号，包括IA、IVA、VA、VIA、VIIA族、稀有气体元素、1～20号元素及Zn、Fe、Cu、Hg、Ag、Pt、Au等。

2.物理变化中分子不变，化学变化中原子不变，分子要改变。

常见的物理变化：蒸馏、分馏、焰色反响、胶体的性质(丁达尔现象、电泳、胶体的凝聚、渗析、布朗运动)、吸附、蛋白质的盐析、蒸发、别离、萃取分液、溶解除杂(酒精溶解碘)等。

常见的化学变化：化合、分解、电解质溶液导电、蛋白质变性、干馏、电解、金属的腐蚀、风化、硫化、钝化、裂化、裂解、显色反响、同素异形体互相转化、碱去油污、明矾净水、结晶水合物失水、浓硫酸脱水等。

(注：浓硫酸使胆矾失水是化学变化，枯燥气体为物理变化)3.理解原子量(相对原子量)、分子量(相对分子量)、摩尔质量、质量数的涵义及关系。

4.纯洁物有固定熔沸点，冰水混和、H2与D2混和、水与重水混和、结晶水合物为纯洁物。

混合物没有固定熔沸点，如玻璃、石油、铝热剂、溶液、悬浊液、乳浊液、胶体、高分子化合物、漂白粉、漂粉精、天然油脂、碱石灰、王水、同素异形体组成的物质(O2与O3)、同分异构体组成的物质C5H12等。

5.掌握化学反响分类的特征及常见反响：a.从物质的组成形式：化合反响、分解反响、置换反响、复分解反响。

b.从有无电子转移：氧化复原反响或非氧化复原反响c.从反响的微粒：离子反响或分子反响d.从反响进展程度和方向：可逆反响或不可逆反响e.从反响的热效应：吸热反响或放热反响6.同素异形体一定是单质，同素异形体之间的物理性质不同、化学性质根本一样。

红磷和白磷、O2和O3、金刚石和石墨及C60等为同素异形体，H2和D2不是同素异形体，H2O和D2O也不是同素异形体。

同素异形体互相转化为化学变化，但不属于氧化复原反响。

湘教版小学科学六年级(上册)知识点总复习1、植物的根总向下、向水生长，茎与叶总朝着阳光生长，植物都有向光性、向水性、向地性。

2、阳光、水分、温度、土壤是影响植物生长的基本因素，但不同的植物对这些因素的需求和适应能力是不一样的。

如:大树适应阳光充足，灌木适于荫，苔藓适于潮湿阴暗，香蕉适于温暖多雨，针叶松适于寒冷，仙人掌适于干旱等。

3、植物的生存是有地域性的，有些植物只适宜生活在南方，有些植物只适宜生活在北方。

植物的这些习性是在长期适应当地的环境中形成的，它们的生活习性也决定了它们一般只能在具备这些环境因素的地方生存。

南方阳光雨水充足，但不一定适合任何植物生长。

4、爬山虎沿墙而上，为的是获取更多的阳光。

沙漠中的仙人掌，叶子是针状的，为的是减少水分蒸发。

5、产于北方的水果有:苹果、葡萄、梨子、哈密瓜等。

产于南方的水果有:柑橘、荔枝、橙子、香蕉、芒果、菠萝、火龙果、榴莲等。

6、动物的生存也受到环境的影响，如北极熊有肥厚脂肪和密集体毛御寒、骆驼有自由关闭的鼻孔，储存脂肪的驼峰和粗大开叉的脚趾等来适应沙漠环境。

动物还通过冬眠、迁徙、换毛等方法来适应环境变化。

7、食物链总是从植物开始，到凶猛的肉食动物结束。

如:水稻→稻螟虫→青蛙→蛇8、池塘中除了生活着植物和动物，还生活着微生物。

它们能把死亡的动、植物尸体分解。

如果没有微生物，动、植物的尸体都将堆积起来。

9、自然界中得所有生物都无法避免成为食物链的成员，生物之间通过食物关系来达到相互依存相互制约的作用。

一种生物的生存受到影响时，也会影响许多与之相关的生物种类。

严重时会造成某种物种灭绝。

10、环境污染、盲目的物种引进、大量捕杀动物和砍伐森林在历史上都造成过部分地区的生态灾难。

11、什么叫食物链?请举例写出自然界中的食物链。

答:食物关系就像链条一样把各种生物紧紧联系在一起，我们把它叫做食物链。

如:浮游生物→孑孓水虿→鱼;水藻→虾→小鱼→大鱼→人;蚊子→蜘蛛→螳螂→黄雀→蛇;青草→野兔→狐狸→狼。

小学六年级总复习知识点数的认识一、整数和小数1、自然数、0、整数（1）数物体的时候 , 用来表示物体个数的 0,1,2,3 叫做自然数 .（2）一个物体也没实用 0 表示 . 0 也是自然数 .（3） 0 和自然数都是整数 .注：但不可以说整数只包含0 和自然数2、十进制计数法（ 1）一 ( 个 ) 、十、百、千、万都叫做计数单位.此中“一”是计数的基本单位.（2）10 个一是十 ,10 个十是百 10 个一百亿是一千亿每相邻两个计数单位之间的进率都是十 . 这类计数方法叫做十进制计数法 .3、整数的读法和写法读数时, 从高位起, 一级一级地往下读, 属于亿级和万级的要读出级名 . 3 读作 : 六亿八千四百五十二万八千五百六十三。

读数时 , 每级末端的“ 0”都不读 , 其余数位有一个 0 或连续几个 0 都只读一个 0. 00 读作：八十亿零四十万六千。

写数时 , 从高位起 , 一级一级地往下写, 哪一位上一个单位也没有, 就在哪个数位上写0。

4. 四舍五入法求一个数的近似数, 要看尾数的最高位上的数是几, 如果比于 5, 5 小 , 就把尾数都舍去; 假如尾数最高位上的数是就把尾数舍去后, 要向它的前一位进 1.5 或大5. 整数大小的比较比较两个多位数的大小, 第一看它们位数的多少, 位数许多的数较大;假如两个数的位数同样,那么第一看最高位, 最高位上的数较大的 , 这个数就大 ;假如最高位同样, 则左侧第二位上的数较大的, 这个数就大6.小数把整数“ 1”均匀分红 10 份 ,100 份这样的一份或几份分别是十分之几 , 百分之几能够用小数表示 .小数点右侧第一位是十分位, 计数单位是十分之一; 第二位是百分位 , 计数单位是百分之一小数部分的最大计数单位是十分之一, 没有最小的计数单位。

小数部分有几个数位, 就叫做几位小数.7.小数的读法和写法读小数时 , 小数的整数部分按整数的读法来读, 小数点读作“点” , 小数部分依据次序读出每一个数位上的数字.写小数时 , 整数部分依据整数的写法来写, 小数点写在个位右下角 , 小数部分按序写出每一个数位上的数字.8.小数的性质小数的末端添上 0 或许去掉0, 小数的大小不变.运用小数的性质, 能够在小数末端添上0. 如： =也能够把小数化简 .=9.小数点数位挪动惹起小数大小的变化小数点向右 ( 左 ) 挪动一位、两位、三位本来的数就扩大 ( 减小 )10 倍、 100 倍、 1000 倍假如要把一个数扩大或减小10 倍、 100 倍只需要挪动小数点 , 数位不够时用0 补足。

高考理综物理总复习重要知识点归纳总结高中物理复题纲第一章：力一、力F：物体对物体的作用。

力的三要素包括大小、方向和作用点。

物体间力的作用是相互的，即作用力与反作用力，但它们不在同一物体上，不是平衡力。

作用力与反作用力是同性质的力，有同时性。

二、力的分类：1、按性质分：重力G、弹力N、摩擦力f2、按效果分：压力、支持力、动力、阻力、向心力、回复力。

3、按研究对象分：外力、内力。

重力G由于受地球吸引而产生，竖直向下。

重心的位置与物体的质量分布与形状有关。

质量均匀、形状规则的物体重心在几何中心上，不一定在物体上。

弹力由于接触形变而产生，与形变方向相反或垂直接触面。

摩擦力阻碍相对运动的力，方向与相对运动方向相反。

滑动摩擦力与材料有关，与重力、压力无关。

相同条件下，滚动摩擦小于滑动摩擦。

静摩擦力可以用二力平衡来计算。

力的合成与分解遵循平行四边形定则。

以分力F1、F2为邻边作平行四边形，合力F的大小和方向可用这两个邻边之间的对角线表示。

平动平衡是指共点力使物体保持匀速直线运动状态或静止状态。

解题方法是先受力分析，然后根据题意建立坐标系，将不在坐标系上的力分解。

如受力在三个以内，可用力的合成。

利用平衡力来解题。

第二章：直线运动一、运动：1、参考系可以任意选取，但尽量方便解题。

2、质点是研究物体比周围空间小得多时，任何物体都可以作为质点。

只有质量，没有形状与大小。

3、位移s是矢量，方向起点指向终点。

表示位置的改变。

路程是标量，质点初位置与末位置的轨迹的长度，表示质点实际运动的长度。

4、时刻是某一瞬间，用时间轴上的一个点表示。

如4s，第4秒。

时间是起始时刻与终止时刻的间隔，在时间轴上用线段表示。

如4秒内，第4秒内。

ma速度v是一个矢量，表示运动的快慢，可以用公式v=s/t计算，其中s为位移，t为时间。

常用的速度单位是米每秒，也可以用千米每小时表示。

在s-t图中，速度的大小可以用正切tgθ计算。

平均速度是变速运动中位移与对应时间之比，而瞬时速度是质点某一瞬间的速度，大小为速率，标量。

初中地理总复习(全册)知识点归纳①、赤道为0°，赤道以北为北纬（0°—90°N），赤道以南为南纬（0°—90°S）。

赤道将地球平分南、北两个半球。

纬度数从赤道向北、向南逐渐增大。

纬度最大值90°。

②、人们规定：0°—30°为低纬度；30°—60°为中纬度；60°—90°为高纬度。

四、经线和经度1、经线：在地球仪上，连结南、北两极并垂直于纬线的弧线。

经线有三个特点：⑴、指示南北方向；⑵、长度都相等；⑶、自成半圆。

2、经度：⑴、经度的起点是0°经线，也称“本初子午线”。

0°经线以东为东经（0°—180°E）；以西为西经（0°—180°W），所以东西经最大度数为180°。

经度数从0°经线向东、向西逐渐增大。

⑵、180°经线：180°E和180°W重合的经线。

⑶、任何一个经线圈，都把地球分成相等的两个半球。

国际上规定20°W和160°E两条经线组成的经线圈，作为划分东西两个半球的分界线。

如：15°W位于东半球；165°E位于西半球。

五、经纬网1、利用经纬网确定地面上任何一点的位置。

2、读经纬网图，能回答有关问题（举例说明）⑴、A 点的经纬度：30°W 40°NB 点的经纬度：10°W 10°N⑵、从东西半球看：A 点位于西半球 B点位于东半球；从南北半球看：A 点位于北半球 B点位于北半球。

⑶、从低、中、高纬度来看：A 点在中纬度地区B 点在低纬度地区。

⑷、从地球五带来看：A 点在北温带 B 点在热带。

（A 地区有四季变化，B 地区有阳光直射。

）⑸、A 点位于B 点的西北方向。

六、世界的海陆分布1、海洋与陆地：海洋占71%，陆地占29%。

整式的加减、乘除及因式分解整式加减一、知识点回顾1、单项式：由数与字母的乘积组成的代数式称为单项式。

补充：单独一个数或一个字母也是单项式，如a ，5……单项式系数和次数：系数：次数：2、多项式：几个单项式的和叫做多项式。

在多项式中每个单项式叫做多项式的项，其中不含字母的项叫常数项。

多项式里次数最高项的次数，就是这个多项式的次数。

例如，多项式3x-2最高的项就是一次项3x ，这个多项式的次数是1，它是一次二项式4、整式的概念：单项式与多项式统称整式二、整式的加减1、同类项：所含字母相同，相同字母的指数也分别相同的项叫做同类项，所有的常数项都是同类项。

合并同类项：把多项式中同类项合并在一起，叫做合并同类项。

合并同类项时，把同类 项的系数相加，字母和字母的指数保持不变。

2、去括号的法则：如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号 ；如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号 ．3、整式加减的运算法则（1）如果有括号，那么先去括号。

（2）如果有同类项，再合并同类项。

整式乘除及因式分解一、幂的运算：1、同底数幂的乘法法则：（都是正整数）同底数幂相乘，底数不变，指数相加。

注n m n m a a a +=∙n m ,意底数可以是多项式或单项式。

2、幂的乘方法则：（都是正整数）幂的乘方，底数不变，指数相乘。

如： mn n m a a =)(n m ,10253)3(=-幂的乘方法则可以逆用：即 如：m n n m mn a a a )()(==23326)4()4(4==3、积的乘方法则：（是正整数）。

积的乘方，等于各因数乘方的积。

n n n b a ab =)(n 4、同底数幂的除法法则：（都是正整数，且同底数幂相除，底数不n m n m a a a -=÷n m a ,,0≠)n m 变，指数相减。

5、零指数； ，即任何不等于零的数的零次方等于1。

10=a 二、单项式、多项式的乘法运算：6、单项式与单项式相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。

初中数学总复习知识点整理(最全)知识点分类
1. 整数
1.1 整数的概念
1.2 整数的进位与退位
1.3 整数的加减法
1.4 整数的乘法
1.5 整数的除法
2.分数
2.1 几个基本概念
2.2 分数的基本性质2.3 分数的加减法
2.4 分数的乘法
2.5 分数的除法
3. 小数
3.1 小数的概念
3.2 小数与分数的转化3.3 小数的加减法
3.4 小数的乘法
3.5 小数的除法
4.代数
4.1 代数式的概念和性质4.2 代数式的加减法
4.3 代数式的乘法
4.4 公式和方程
4.5 解一元一次方程
5. 轴对称与余弦定理5.1 轴对称的基本概念5.2 轴对称的性质
5.3 用轴对称解题
5.4 余弦定理的概念和性质
5.5 用余弦定理解题
6.勾股定理与三角函数
6.1 勾股定理的概念和性质
6.2 在平面直角坐标系中应用勾股定理6.3 用勾股定理解决实际问题
6.4 三角函数的定义和性质
6.5 用三角函数解决实际问题
知识点重点
- 整数的进位与退位
- 分数的加减法
- 代数式的乘法
- 解一元一次方程
- 用轴对称解题
- 用余弦定理解题
- 用勾股定理解决实际问题- 用三角函数解决实际问题知识点易错点
- 乘方与加减混淆
- 分数的错位相乘
- 代数式乘法计算错误
- 方程解错
- 三角函数概念混淆
- 勾股定理和余弦定理运用错误
- 计算精度不足
以上是初中数学的总复习知识点整理，祝您考试顺利！。

英语知识点总复习（集合6篇）英语知识点总复习第1篇【语法】特殊疑问句基本规律一般问句语序﹙疑问词﹙组﹚不作主语﹚一般问句语序﹙疑问词﹙组﹚不作主语﹚特殊问句=疑问词﹙组﹚﹢谓语……﹙疑问词﹙组﹚作主语﹚常用句型1)询问职业、身份What is your father? He is a2)询问姓名、关系Who is that boy? He is my brother3)询问相貌特征 4)询问目的What is she like?=What does she look like? What did they come here for?She is To attend a5)询问原因 6)询问天气Why did they come here? How is the weather today?Because they have a meeting to = What is the weather like today?7)询问颜色 8)询问尺寸What dolor is her skirt? What size does he wear?It’s He wars9)询问钟点 10)询问星期What time is it? What day is it today?It’s It’s11)询问几号 12)询问年龄What is the date today? How old is he?It’s May He is13)询问多久 14)询问长度How long have you been here? How long is the bridge?For five It’s 50015)询问距离 16)询问频度How far is it from here to the zoo? How often do you come back? It’s 6 Once a17)询问多快 18)询问数量How soon will she arrive? How many jackets do you have?In an How much coffee do you want?19)询问价格 20)询问高度How much is it? How tall is she?How much does it cost? How high is the tower?二.难点讲评’s your favorite subject?你最喜欢的学科是什么?释：1)favorite是形容词“最喜欢的”，作定语或表语。

小升初数学总复习总归纳(必备知识点大全)小升初数学总复必备知识点总归纳.常用单位换算1、长度单位换算：1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米2、面积单位换算：1平方千米=100公顷1公顷=平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米3、体(容)积单位换算：1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升4、重量单位换算：1吨=1000千克1千克=1000克1千克=1公斤5、人民币单位换算：1元=10角1角=10分1元=100分6、时间单位换算：1世纪=100年1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天,闰年2月29天平年全年365天,闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒经常利用数量干系等式1、份数：每份数×份数＝总数总数÷每份数＝份数总数÷份数＝每份数2、倍数：1倍数×倍数＝几倍数几倍数÷1倍数＝倍数几倍数÷倍数＝1倍数3、路程：速度×时间＝路程路程÷速度＝时间路程÷时间＝速度4、价量：单价×数量＝总价总价÷单价＝数量总价÷数量＝单价5、工作量：工作效率×工作时间＝工作总量工作总量÷工作效率＝工作时间工作总量÷工作时间＝工作效率6、数据运算：加数＋加数＝和和－一个加数＝另一个加数被减数－减数＝差被减数－差＝减数差＋减数＝被减数因数×因数＝积积÷一个因数＝另一个因数被除数÷除数＝商被除数÷商＝除数商×除数＝被除数经常利用图形计较公式1、正方形（C：周长S：面积a：边长）周长＝边长×4 C=4a面积=边长×边长S=a×a2、正方体（V:体积a:棱长）表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3、长方形（C：周长S：面积a：边长）周长=(长+宽)×2 C=2(a+b)面积=长×宽S=ab4、长方体（V:体积s:面积a:长b:宽h:高）表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh) 体积=长×宽×高V=abh5、三角形（s：面积a：底h：高）面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形（s：面积a：底h：高）面积=底×高s=ah7、梯形（s：面积a：上底b：下底h：高）面积=(上底+下底)×高÷2 s=(a+b)×h÷28、圆形（S：面积C：周长лd=直径r=半径）1周长=直径×л=2×л×半径C=лd=2лr面积=半径×半径×л9、圆柱体（v:体积h:高s：底面积r:底面半径c:底面周长）侧面积=底面周长×高=ch(2лr或лd)表面积=侧面积+底面积×2体积=底面积×高体积＝侧面积÷2×半径10、圆锥体（v:体积h:高s：底面积r:底面半径）体积=底面积×高÷3奥数常用公式.1、平均数总数÷总份数＝平均数2、和差问题：(和＋差)÷2＝大数(和－差)÷2＝小数3、和倍问题：和÷(倍数－1)＝小数小数×倍数＝大数(大概和－小数＝大数)4、差倍问题：差÷(倍数－1)＝小数小数×倍数＝大数(或小数＋差＝大数)5、相遇问题相遇路程＝速度和×相遇时间相遇时间＝相遇路程÷速度和速度和＝相遇路程÷相遇时间6、追及问题追及距离＝速度差×追及时间追及时间＝追及距离÷速度差速度差＝追及距离÷追及时间7、流水问题顺流速度＝静水速度＋水流速度逆流速度＝静水速度－水流速度8、浓度问题溶质的重量＋溶剂的重量＝溶液的重量溶质的重量÷溶液的重量×100%＝浓度溶液的重量×浓度＝溶质的重量溶质的重量÷浓度＝溶液的重量9、利润与折扣问题利润＝售出价－成本利润率＝利润÷成本×100%＝(售出价÷成本－1)×100% 涨跌金额＝本金×涨跌百分比利息＝本金×利率×时间税后利息＝本金×利率×时间×(1－20%)10、盈亏问题(盈＋亏)÷两次分配量之差＝参加分配的份数(大盈－XXX)÷两次分配量之差＝参加分配的份数(大亏－小亏)÷两次分配量之差＝参加分配的份数应出格留意奥数中的植树问题1、非封闭线路上的植树问题,主要可分为以下三种情形:⑴如果在非关闭线路的两头都要植树,那末:全长＝株距×(株数－1)株距＝全长÷(株数－1)⑵如果在非封闭线路的一端要植树,另一端不要植树,那么: 株数＝段数＝全长÷株距全长＝株距×株数2株距＝全长÷株数⑶如果在非关闭线路的两头都不要植树,那末株数＝段数－1＝全长÷株距－1全长＝株距×(株数＋1)株距＝全长÷(株数＋1)2、封闭线路上的植树问题株数＝段数＝全长÷株距全长＝株距×株数株距＝全长÷株数奥数中的常用数据及规律1、圆周率常取数据3.14×1＝3.143.14×2＝6.283.14×3＝9.423.14×4＝12.563.14×5＝15.73.15×6＝18.843.14×7＝21.983.14×8＝25.123.14×9＝28.262、常用特殊数的乘积25×3＝7525×4＝×8＝×3＝375125×4＝×8＝×16＝ 37×3=1113、常用平方数11²=121 12²=144 13²=169 14²=196 15²=22516²=256 17²=289 18²=324 19²=361 10²=10020²=400 30²=900 40²=1600 50²=2500 60²=3600770²=4900 80²=6400 15²=225 25²=625 35²=122545²=2025 55²=3025 65²=4225 75²=5625 85²=72254、关于经常利用分数与小数的互化5、常用立方数1³=1 2³=8 3³=27 4³=64 5³=1256³=216 7³=343 8³=512 9³=729XXX数学应掌握的基本概念、数理规律及应用第一章数和数的运算一、概念（一）整数1整数的意义：自然数和都是整数.2自然数：我们在数物体的时候,用来透露表现物体个数的1,2,3……叫做自然数.一个物体也没有,用透露表现.0也是自然数.3计数单元：一（个）、十、百、千、万、十万、百万、千万、亿……都是计数单元.每相邻两个计数单元之间的进率都是10.这样的计数法叫做十进制计数法.4数位：计数单位按照一定的顺序排列起来,它们所占的位置叫做数位.5数的整除：整数a除以整数b(b≠）,除得的商是整数而没有余数,我们就说a能被3b整除,大概说b能整除a .如果数a能被数b（b≠）整除,a就叫做b的倍数,b就叫做a的约数（或a的因数）.倍数和约数是相互依存的.因为35能被7整除,所以35是7的倍数,7是35的约数.一个数的约数的个数是有限的,其中最小的约数是1,最大的约数是它本身.例如：10的约数有1、2、5、10,其中最小的约数是1,最大的约数是10.一个数的倍数的个数是无限的,其中最小的倍数是它本身.3的倍数有：3、6、9、12……其中最小的倍数是3 ,没有最大的倍数.个位上是、2、4、6、8的数,都能被2整除,例如：202、480、304,都能被2整除..个位上是或5的数,都能被5整除,例如：5、30、405都能被5整除..一个数的各位上的数的和能被3整除,这个数就能被3整除,例如：12、108、204都能被3整除.一个数各位数上的和能被9整除,这个数就能被9整除.能被3整除的数不一定能被9整除,但是能被9整除的数一定能被3整除.一个数的末两位数能被4（或25）整除,这个数就能被4（或25）整除.例如：16、404、1256都能被4整除,50、325、500、1675都能被25整除.一个数的末三位数能被8（或125）整除,这个数就能被8（或125）整除.例如：1168、4600、5000、都能被8整除,1125、、5000都能被125整除.能被2整除的数叫做偶数.不能被2整除的数叫做奇数.也是偶数.自然数按能否被2整除的特征可分为奇数和偶数.一个数,如果只有1和它本身两个约数,这样的数叫做质数（或素数）,100以内的质数有：2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97.一个数,如果除了1和它本身还有别的约数,这样的数叫做合数,例如4、6、8、9、12都是合数.1不是质数也不是合数,自然数除了1外,不是质数就是合数.如果把自然数按其约数的个数的不同分类,可分为质数、合数和1.每个合数都可以写成几个质数相乘的形式.其中每个质数都是这个合数的因数,叫做这个合数的质因数,例如15=3×5,3和5叫做15的质因数.把一个合数用质因数相乘的形式表示出来,叫做分解质因数.例如把28分解质因数几个数公有的约数,叫做这几个数的公约数.其中最大的一个,叫做这几个数的最大公约数,例如12的约数有1、2、3、4、6、12；18的约数有1、2、3、6、9、18.其中,1、2、3、6是12和1 8的公约数,6是它们的最大公约数.公约数只有1的两个数,叫做互质数,成互质关系的两个数,有下列几种情况：1和任何自然数互质.相邻的两个自然数互质.两个不同的质数互质.当合数不是质数的倍数时,这个合数和这个质数互质.两个合数的公约数只有1时,这两个合数互质,如果几个数中任意两个都互质,就说这几个数两两互质.如果较小数是较大数的约数,那么较小数就是这两个数的最大公约数.如果两个数是互质数,它们的最大公约数就是1.几个数私有的倍数,叫做这几个数的公倍数,个中最小的一个,叫做这几个数的最小公倍数,如2的倍数有2、4、6、8、10、12、14、16、18……3的倍数有3、6、9、12、15、18……其中6、12、18……是2、3的公倍数,6是它们的最小公倍数..如果较大数是较小数的倍数,那么较大数就是这两个数的最小公倍数.如果两个数是互质数,那末这两个数的积就是它们的最小公倍数.几个数的公约数的个数是有限的,而几个数的公倍数的个数是无限的.（二）小数41小数的意义：把整数1均匀分红10份、100份、1000份……得到的十分之几、百分之几、千分之几……可以用小数透露表现.一位小数透露表现十分之几,两位小数透露表现百分之几,三位小数透露表现千分之几……一个小数由整数部分、小数部分和小数点部分组成.数中的圆点叫做小数点,小数点左边的数叫做整数部分,小数点左边的数叫做整数部分,小数点右边的数叫做小数部分.在小数里,每相邻两个计数单位之间的进率都是10.小数部分的最高分数单位“十分之一”和整数部分的最低单位“一”之间的进率也是10.2小数的分类纯小数：整数部分是零的小数,叫做纯小数.例如：0.25、0.368都是纯小数.带小数：整数部分不是零的小数,叫做带小数.例如：3.25、5.26都是带小数.有限小数：小数部分的数位是有限的小数,叫做有限小数.例如：41.7、25.3、0.23都是有限小数.无限小数：小数部分的数位是无限的小数,叫做无限小数.例如：4.33……3.……无限不循环小数：一个数的小数部分,数字排列无规律且位数无限,这样的小数叫做无限不循环小数.例如：∏循环小数：一个数的小数部分,有一个数字或者几个数字依次不断重复出现,这个数叫做循环小数.例如：3.555……0.0333……12.……一个轮回小数的小数部分,顺次不竭反复出现的数字叫做这个轮回小数的轮回节.例如：3.99……的轮回节是“9”, 0.5454……的轮回节是“54”.纯循环小数：循环节从小数部分第一位开始的,叫做纯循环小数.例如：3.111……0.5656……混循环小数：循环节不是从小数部分第一位开始的,叫做混循环小数. 3.1222……0.……写轮回小数的时候,为了简便,小数的轮回部分只需写出一个轮回节,并在这个轮回节的首、末位数字上各点一个圆点.如果轮回节只有一个数字,就只在它的上面点一个点.例如：3.777……XXX写作0.……XXX写作.（三）分数1分数的意义：把单元“1”均匀分红多少份,透露表现这样的一份大概几份的数叫做分数.在分数里,中间的横线叫做分数线；分数线下面的数,叫做分母,表示把单位“1”平均分成多少份；分数线下面的数叫做分子,表示有这样的多少份.把单位“1”平均分成若干份,表示其中的一份的数,叫做分数单位.2分数的分类真分数：分子比分母小的分数叫做真分数.真分数小于1.假分数：分子比分母大或者分子和分母相等的分数,叫做假分数.假分数大于或等于1.带分数：假分数可以写成整数与真分数合成的数,通常叫做带分数.3约分和通分把一个分数化成同它相等但是分子、分母都比较小的分数,叫做约分.分子分母是互质数的分数,叫做最简分数.把异分母分数分别化成和原来分数相等的同分母分数,叫做通分.（四）百分数1透露表现一个数是另一个数的百分之几的数叫做百分数,也叫做百分率或百分比.百分数平日用"%"来透露表现.百分号是透露表现百分数的符号.二、方法（一）数的读法和写法1.整数的读法：从高位到低位,一级一级地读.读亿级、万级时,先依照个级的读法去读,再在背面加一个“亿”或“万”字.每一级开端的都不读出来,其它数位连续有几个都只读一个零.2.整数的写法：从高位到低位,一级一级地写,哪一个数位上一个单元也没有,就在那个5数位上写0.3.小数的读法：读小数的时候,整数部分按照整数的读法读,小数点读作“点”,小数部分从左向右顺次读出每一位数位上的数字.4.小数的写法：写小数的时候,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字.5.分数的读法：读分数时,先读分母再读“分之”然后读分子,分子和分母按照整数的读法来读.6.分数的写法：先写分数线,再写分母,最后写分子,依照整数的写法来写.7.百分数的读法：读百分数时,先读百分之,再读百分号前面的数,读数时依照整数的读法来读.8.百分数的写法：百分数通常不写成分数形式,而在原来的分子后面加上百分号“%”来表示.（二）数的改写一个较大的多位数,为了读写方便,常常把它改写成用“万”或“亿”作单位的数.有时还可以根据需要,省略这个数某一位后面的数,写成近似数.1.准确数：在实际生活中,为了计数的简便,可以把一个较大的数改写成以万或亿为单位的数.改写后的数是原数的准确数.例如把改写成以万做单位的数是万；改写成以亿做单位的数12.543亿.2.近似数：按照实际需求,我们还可以把一个较大的数,省略某一位背面的尾数,用一个近似数来透露表现.例如：省略亿背面的尾数是13亿.3.四舍五入法：要省略的尾数的最高位上的数是4或者比4小,就把尾数去掉；如果尾数的最高位上的数是5或者比5大,就把尾数舍去,并向它的前一位进 1.例如：省略万后面的尾数约是35万.省略亿后面的尾数约是47亿.4.大小比较1.比较整数大小：比较整数的大小,位数多的那个数就大,如果位数相同,就看最高位,最高位上的数大,那个数就大；最高位上的数相同,就看下一位,哪一位上的数大那个数就大.2.比力小数的大小：先看它们的整数部分,,整数部分大的那个数就大；整数部分不异的,十分位上的数大的那个数就大；十分位上的数也不异的,百分位上的数大的那个数就大……3.比较分数的大小:分母相同的分数,分子大的分数比较大；分子相同的数,分母小的分数大.分数的分母和分子都不相同的,先通分,再比较两个数的大小.（三）数的互化1.小数化成分数：原来有几位小数,就在1的背面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分.2.分数化成小数：用分母去除分子.能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位小数.3.一个最简分数,如果分母中除了2和5之外,不含有其他的质因数,这个分数就能化成有限小数；如果分母中含有2和5之外的质因数,这个分数就不能化成有限小数.4.小数化成百分数：只要把小数点向右挪动两位,同时在背面添上百分号.5.百分数化成小数：把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位.6.分数化成百分数：通常先把分数化成小数（除不尽时,通常保留三位小数),再把小数化成百分数.7.百分数化成小数：先把百分数改写成分数,能约分的要约成最简分数.（四）数的整除1.把一个合数分解质因数,平日用短除法.先用能整除这个合数的质数去除,一直除到商是质数为止,再把除数和商写成连乘的形式.2.求几个数的最大公约数的方法是：先用这几个数的公约数连续去除,一直除到所得的商只有公约数1为止,然后把所有的除数连乘求积,这个积就是这几个数的的最大公约数.3.求几个数的最小公倍数的方法是：先用这几个数（或其中的部分数）的公约数去除,一直除到互质（或两两互质）为止,然后把所有的除数和商连乘求积,这个积就是这几个数的6最小公倍数.4.成为互质关系的两个数：1和任何自然数互质；相邻的两个自然数互质；当合数不是质数的倍数时,这个合数和这个质数互质；两个合数的公约数只有1时,这两个合数互质.（五）约分和通分约分的方法：用分子和分母的公约数（1除外）去除分子、分母；平日要除到得出最简分数为止.通分的方法：先求出原来的几个分数分母的最小公倍数,然后把各分数化成用这个最小公倍数作分母的分数.三、性质和规律（一）商不变的规律商不变的规律：在除法里,被除数和除数同时扩展大概同时减少不异的倍,商不变.（二）小数的性质小数的性质：在小数的开端添上零大概去掉零小数的大小不变.（三）小数点位置的挪动引起小数大小的变革1.小数点向右移动一位,原来的数就扩大10倍；小数点向右移动两位,原来的数就扩大100倍；小数点向右移动三位,原来的数就扩大1000倍……2.小数点向左移动一位,原来的数就缩小10倍；小数点向左移动两位,原来的数就缩小100倍；小数点向左移动三位,原来的数就缩小1000倍……3.小数点向左移或者向右移位数不够时,要用“0"补足位.（四）分数的基本性质分数的基本性质：分数的分子和分母都乘以大概除以不异的数（零除外）,分数的大小不变.（五）分数与除法的关系1.被除数÷除数=被除数/除数2.因为零不能作除数,所以分数的分母不能为零.3.被除数相当于分子,除数相当于分母.四、运算的意义（一）整数四则运算1整数加法：把两个数合并成一个数的运算叫做加法.在加法里,相加的数叫做加数,加得的数叫做和.加数是部分数,和是总数.加数+加数=和一个加数=和－另一个加数2整数减法：已知两个加数的和与其中的一个加数,求另一个加数的运算叫做减法.在减法里,已知的和叫做被减数,已知的加数叫做减数,未知的加数叫做差.被减数是总数,减数和差划分是部分数.加法和减法互为逆运算.3整数乘法：求几个不异加数的和的简便运算叫做乘法.在乘法里,相同的加数和相同加数的个数都叫做因数.相同加数的和叫做积.在乘法里,0和任何数相乘都得0. 1和任何数相乘都的任何数.一个因数×一个因数=积一个因数=积÷另一个因数4整数除法：已知两个因数的积与其中一个因数,求另一个因数的运算叫做除法.在除法里,已知的积叫做被除数,已知的一个因数叫做除数,所求的因数叫做商.乘法和除法互为逆运算.在除法里,0不能做除数.因为和任何数相乘都得0,所以任何一个数除以0,均得不到7一个确定的商.被除数÷除数=商除数=被除数÷商被除数=商×除数（二）小数四则运算1.小数加法：小数加法的意义与整数加法的意义相同.是把两个数合并成一个数的运算.2.小数减法：小数减法的意义与整数减法的意义不异.已知两个加数的和与个中的一个加数,求另一个加数的运算.3.小数乘法：小数乘整数的意义和整数乘法的意义相同,就是求几个相同加数和的简便运算；一个数乘纯小数的意义是求这个数的十分之几、百分之几、千分之几……是多少.4.小数除法：小数除法的意义与整数除法的意义相同,就是已知两个因数的积与其中一个因数,求另一个因数的运算.5.乘方:求几个不异因数的积的运算叫做乘方.例如3×3 =32（三）分数四则运算1.分数加法：分数加法的意义与整数加法的意义相同.是把两个数合并成一个数的运算.2.分数减法：分数减法的意义与整数减法的意义不异.已知两个加数的和与个中的一个加数,求另一个加数的运算.3.分数乘法：分数乘法的意义与整数乘法的意义相同,就是求几个相同加数和的简便运算.4.乘积是1的两个数叫做互为倒数.5.分数除法：分数除法的意义与整数除法的意义相同.就是已知两个因数的积与其中一个因数,求另一个因数的运算.（四）运算定律1.加法交换律：两个数相加,交换加数的位置,它们的和不变,即a+b=b+a .2.加法结合律：三个数相加,先把前两个数相加,再加上第三个数；或者先把后两个数相加,再和第一个数相加它们的和不变,即（a+b)+c=a+(b+c) .3.乘法交换律：两个数相乘,交换因数的位置它们的积不变,即a×b=b×a.4.乘法结合律：三个数相乘,先把前两个数相乘,再乘以第三个数；或者先把后两个数相乘,再和第一个数相乘,它们的积不变,即(a×b)×c=a×(b×c) .5.乘法分配律：两个数的和与一个数相乘,可以把两个加数分别与这个数相乘再把两个积相加,即(a+b)×c=a×c+b×c .6.减法的性质：从一个数里连续减去几个数,可以从这个数里减去所有减数的和,差不变,即a-b-c=a-(b+c) .（五）运算法则1.整数加法计算法则：相同数位对齐,从低位加起,哪一位上的数相加满十,就向前一位进一.2.整数减法计算法则：相同数位对齐,从低位加起,哪一位上的数不够减,就从它的前一位退一作十,和本位上的数合并在一起,再减.83.整数乘法计算法则：先用一个因数每一位上的数分别去乘另一个因数各个数位上的数,用因数哪一位上的数去乘,乘得的数的末尾就对齐哪一位,然后把各次乘得的数加起来.4.整数除法计较法则：先从被除数的高位除起,除数是几位数,就看被除数的前几位；如果不够除,就多看一位,除到被除数的哪一位,商就写在哪一位的上面.如果哪一位上不够商1,要补“”占位.每次除得的余数要小于除数.5.小数乘法法则：先依照整数乘法的计较法则算出积,再看因数中共有几位小数,就从积的右侧起数出几位,点上小数点；如果位数不够,就用“”补足.6.除数是整数的小数除法计算法则：先按照整数除法的法则去除,商的小数点要和被除数的小数点对齐；如果除到被除数的末尾仍有余数,就在余数后面添“”,再继续除.7.除数是小数的除法计较法则：先移动除数的小数点,使它变成整数,除数的小数点也向右移动几位（位数不够的补“”）,然后按照除数是整数的除法法则进行计算.8.同分母分数加减法计算方法:同分母分数相加减,只把分子相加减,分母不变.9.异分母分数加减法计较方法:先通分,然后依照同分母分数加减法的的法则进行计较.10.带分数加减法的计算方法:整数部分和分数部分划分相加减,再把所得的数归并起来.11.分数乘法的计算法则:分数乘整数,用分数的分子和整数相乘的积作分子,分母不变；分数乘分数,用分子相乘的积作分子,分母相乘的积作分母.12.分数除法的计较法则:甲数除以乙数（除外）,即是甲数乘乙数的倒数.（六）运算顺序1.小数四则运算的运算顺序和整数四则运算顺序不异.2.分数四则运算的运算顺序和整数四则运算顺序相同.3.没有括号的混合运算:同级运算从左往右依次运算；两级运算先算乘、除法,后算加减法.4.有括号的混合运算:先算小括号内里的,再算中括号内里的,最后算括号外面的.5.第一级运算：加法和减法叫做第一级运算.6.第二级运算：乘法和除法叫做第二级运算.五、具体应用（一）整数和小数的应用1简单应用题（1）简朴应用题：只含有一种基本数量干系,或用一步运算解答的应用题,平日叫做简朴应用题.（2）解题步调：a审题相识题意：相识应用题的内容,晓得应用题的前提和问题.读题时,不丢字不添字边读边考虑,弄明白题中每句话的意义.也可以复述前提和问题,帮助相识题意.b选择算法和列式计算：这是解答应用题的中心工作.从题目中告诉什么,要求什么着手,逐步根据所给的条件和问题,联系四则运算的含义,分析数量关系,确定算法,进行解答并标明正确的单位名称.9。

总复习第一部分数与代数一、分数乘法1.分数乘分数，用分数的分子与整数相乘的积作积的（），（）不变。

2.分数乘分数，用分子相乘的积作积的（），分母相乘的积作积的（）。

二、分数除法1.乘积是1的两个数互为（）。

2.求一个数的倒数，只需要将它的分子、分母交换位置即可。

1的倒数是（），（）没有倒数。

3.分数除法的意义与（）除法的意义相同，都是已知两个因数的（）与其中一个因数，求（）的运算。

4.分数除法的计算方法：甲数除以乙数（0除外），等于甲数（）乙数的（）。

三、比和按比例分配1．两个数相除又叫两个数的（）。

2.“：”是比号，读作：比。

比号前面的数叫做比的（），比号后面的数叫做比的（）。

3.比的（）除以比的（）所得的商，叫做（）。

比值通常用（）表示，也可以用小数或整数表示。

比的前项相当于除法中的（），分数中（）；比号相当于除法中的（），分数中的（）；比的后项相当于除法中的（），分数中的（）。

4.比的前项和后项同时乘或除以相同是数（0除外），比值（），这叫做比的基本性质。

5.一个比的前项和后项只有公因数（），这样的比叫做最简整数比。

将一个比化成最简整数比的过程叫做（）。

6.把一个数量按照一定的比来进行分配，这种分配方法通常叫做（）。

用分数法求解比例分配问题时，先求出各部分数占（）的几分之几，最后再分别乘（），就可求出各部分应该分配到的量。

四、分数混合运算1.分数混合运算的运算顺序；在有括号的的算式里，要先算（）里面的，再算（）里面的，最后算中括号外面的；在没有括号的算式里，如果含有两级运算，先算（）运算，再算（）运算，如果只含有同一级运算，就按照（）的顺序依次计算。

2.分数混合运算的简算，（）的运算规律和运算性质对于分数同样适用，应用运算规律或运算性质可以使计算（）。

五、负数1.像+3、+15、+20，……这样的数都是（）。

像—6、—10，—155，……这样的数都是（）。

0既不是（），也不是（）。

2.正、负数的读写方法：写正数时，加上“+”或者省略“+”两种形式都可以，但是读正数时，写出“+”的，一定要读出（）号；省略“+”的，（）号就不需要读出来。

小学数学总复习知识点整理(最全) XXX数学复资料第一章数和数的运算一概念（一）整数1 .整数的意义自然数和都是整数。

2 .自然数我们在数物体的时候，用来表示物体个数的1，2，3……叫做自然数。

一个物体也没有，用表示。

也是自然数。

3.计数单位：一（个）、十、百、千、万、十万、百万、千万、亿……都是计数单位。

每相邻两个计数单位之间的进率都是10。

这样的计数法叫做十进制计数法。

4.数位计数单位按照一定的顺序排列起来，它们所占的位置叫做数位。

5.数的整除整数a除以整数b(b≠），除得的商是整数而没有余数，我们就说a能被b整除，或者说b能整除a。

如果数a能被数b（b≠）整除，a就叫做b的倍数，b就叫做a的约数（或a的因数）。

倍数和约数是相互依存的。

因为35能被7整除，所以35是7的倍数，7是35的约数。

一个数的约数的个数是有限的，其中最小的约数是1，最大的约数是它本身。

例如：10的约数有1、2、5、10，其中最小的约数是1，最大的约数是10。

一个数的倍数的个数是无限的，其中最小的倍数是它本身。

3的倍数有：3、6、9、12……其中最小的倍数是3，没有最大的倍数。

个位上是、2、4、6、8的数，都能被2整除，例如：202、480、304，都能被2整除。

个位上是或5的数，都能被5整除，例如：5、30、405都能被5整除。

一个数的列位上的数的和能被3整除，这个数就能被3整除，例如：12、108、204都能被3整除。

一个数列位数上的和能被9整除，这个数就能被9整除。

能被3整除的数不一定能被9整除，但是能被9整除的数一定能被3整除。

一个数的末两位数能被4（或25）整除，这个数就能被4（或25）整除。

例如：16、404、1256都能被4整除，50、325、500、1675都能被25整除。

一个数的末三位数能被8（或125）整除，这个数就能被8（或125）整除。

例如：1168、4600、5000、都能被8整除，1125、、5000都能被125整除。

初三化学总复习重要知识点总结归纳1. 化学变化：生成了其它物质的变。

2. 物理变化：没有生成其它物质的变化。

3. 物理性质：不需要发生化学变化就表现出来的性质，如:颜色、状态、密度、气味、熔点、沸点、硬度、水溶性等。

4. 化学性质：物质在化学变化中表现出来的性质，如:可燃性、助燃性、氧化性、还原性、酸碱性、稳定性等。

5. 常用仪器及使用方法(1)用于加热的仪器--试管、烧杯、蒸发皿、燃烧匙。

(2)测容器--量筒(视线与量筒内液体凹液面的最低点保持水平)。

(3)称量器--托盘天平(左物右码)。

(4)加热器皿--酒精灯。

(5)分离物质及加液的仪器--漏斗、长颈漏斗、分液漏斗。

6. 化学实验基本操作第二单元：空气1. 组成：N2 78%、O2 21%、稀有气体0.94%、CO20.03%,其它气体与杂质0.03%。

2. 空气中氧气的测定原理：压强差(1) 可燃物要求：足量且产物是固体，红磷。

(2) 装置要求：气密性良好操作要求：冷却到室温后打开弹簧夹。

(3) 现象：放热，有大量白烟产生，打开弹簧夹后，广口瓶内液面上升约1/5体积。

(4) 结论：O2约占空气体积的1/5。

.(5) 探究：①液面上升小于1/5原因：装置漏气，红磷量不足，未冷却完全。

②能否用铁、镁代替红磷?不能，原因：铁不能在空气中燃烧，镁会与N2、CO2反应。

③能否用碳、硫代替红磷?不能，原因：产物是气体，不能产生压强差。

3. 氧气的性质和制备(1)氧气的化学性质：支持燃烧，供给呼吸。

铁在氧气中燃烧烧集气瓶中放少量水或细砂的目的：防止溅落的高温熔化物炸裂瓶底。

硫在氧气中燃烧集气瓶中放入少量水的目的：吸收SO2，防止其污染空气。

(2)氧气的制备:工业制氧气——分离液态空气法(原理:液氮和液氧的沸点不同物理变化) 实验室制氧气原理a.气体制取与收集装置的选择发生装置：固固加热型、固液不加热型 (根据反应物的状态和反应条件) 收集装置：根据气体的密度、溶解性。

小学数学总复习知识大纲概览北师大版小学数学知识点总复习可以涵盖多个方面，包括数与代数、空间与图形、统计与概率等。

以下是对这些知识点的详细总结：一、数与代数1. 数的认识●整数：包括正整数、0和负整数。

正整数如1, 2, 3,...；0是最小的自然数，也是偶数；负整数如-1, -2, -3,...。

●小数：把整数“1”平均分成10份、100份、1000份...取其中的1份或几份得到的数。

小数由整数部分、小数点和小数部分组成。

●分数：把单位“1”平均分成若干份，表示这样一份或几份的数。

真分数小于1，假分数大于或等于1。

●百分数：表示一个数是另一个数的百分之几的数。

2. 数的运算●四则运算：包括加、减、乘、除四种基本运算。

运算顺序为先乘除后加减，有括号时先算括号内的。

●运算定律：o加法交换律：a+b=b+ao加法结合律：(a+b)+c=a+(b+c)o乘法交换律：a×b=b×ao乘法结合律：(a×b)×c=a×(b×c)o乘法分配律：(a+b)×c=a×c+b×c●小数的四则运算：与整数运算类似，但需注意小数点对齐。

●分数的四则运算：包括分数的加、减、乘、除以及分数的化简和通分。

3. 数的整除与约数倍数●整除：整数a除以整数b（b≠0），除得的商是整数且没有余数，则称a能被b整除。

●约数与倍数：若a能被b整除，则a是b的倍数，b是a的约数。

●质数与合数：质数只有1和它本身两个约数；合数除了1和它本身外还有其他约数。

●分解质因数：将一个合数用质因数相乘的形式表示出来。

二、空间与图形1. 平面图形●点、线、面：点是最基本的图形元素；线由无数个点组成；面由无数条线组成。

●角：有锐角、直角、钝角、平角、周角等。

●三角形：按角分有锐角三角形、直角三角形、钝角三角形；按边分有等腰三角形、等边三角形、任意三角形。

三角形内角和为180°。