最新(文章)算术平方根的双重非负性

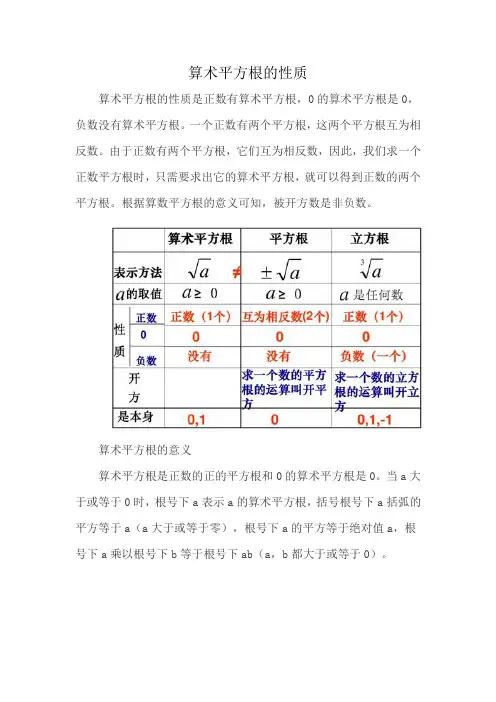
算术平方根的性质
算术平方根的性质是正数有算术平方根，0的算术平方根是0，负数没有算术平方根。

一个正数有两个平方根，这两个平方根互为相反数。

由于正数有两个平方根，它们互为相反数，因此，我们求一个正数平方根时，只需要求出它的算术平方根，就可以得到正数的两个平方根。

根据算数平方根的意义可知，被开方数是非负数。

算术平方根的意义
算术平方根是正数的正的平方根和0的算术平方根是0。

当a大于或等于0时，根号下a表示a的算术平方根，括号根号下a括弧的平方等于a（a大于或等于零），根号下a的平方等于绝对值a，根号下a乘以根号下b等于根号下ab（a，b都大于或等于0）。

算术平方根的双重非负性
算术平方根√a(a≥0)具有双重非负性，一是被开方数具有非负性，即a≥0；二是算平方根本身具有非负性，即√a≥0。

算术平方根的双重非负性还有两个特征，一是兼容性，二是隐含性。

算术平方根的性质
双重非负性
如果x=√a
那么：1.a≥0（若小于0，则为虚数）
2.x≥0
与平方根的关系
正数的平方根有两个，它们为相反数，其中非负的平方根，就是这个数的算术平方根。

负数没有算术平方根。

算术平方根的产生
根号（即算术平方根）的产生源于正方形的对角线长度“根号二”，这个“根号二”的发现一度引起了毕达哥拉斯学派的恐慌。

因为按当时的权威解释（也就是毕达哥拉斯学派的学说），万物皆数（也就是说世界上所有的事物都可以用有理数来表示）。

对于这个无理数“根号二”，最终人们选取了用根号来表示。

算术平方根的双重非负性算术平方根的定义：一般地，如果一个正数x的平方等于a，即ax=2，那么这个正数x就叫做a 的算术平方根，记为“a”，读作“根号a”．特别地，我们规定0的算术平方根是0，即00=.算术平方根定义中的两层含义：a中的a是一个非负数，即0a≥，a的算术平方根a也是一个非负数，≥．这就是算术平方根的双重非负性．例题：已知x，y为有理数，且x－1＋3(y－2)2＝0，求x－y的值．解析：算术平方根和完全平方式都具有非负性，即≥，a2≥0，由几个非负数相加和为0，可得每一个非负数都为0，由此可求出x 和y的值，进而求得答案．()20,20y≥-≥，且x－1＋3(y－2)2＝0∴x-1=0，y-2=0.∴x=1,y=2∴x－y＝1－2＝－1.方法总结：算术平方根、绝对值和完全平方式都具有非负性，即≥，|a|≥0，a2≥0，当几个非负数的和为0时，各数均为0.巩固练习：1.若|x－2|+3-y=0,则xy=______.2.已知()0232212=++++-zyx，求x+y+z的值.3. △ABC 的三边长分别为a ，b ，c ，且a ，b 满足04412=+-+-b b a ，求c 的取值范围．参考答案：1. xy =62. 解：因为21-x ≥0，()22+y ≥0，23+z ≥0，且()0232212=++++-z y x ， 所以21-x =0，()22+y =0，23+z =0， 解得21=x ，2-=y ，23-=z ， 所以x +y +z = 3-．3. 解：由04412=+-+-b b a ，可得0)2(12=-+-b a ，因为 1-a ≥0，2)2(-b ≥0， 所以1-a =0，2)2(-b =0，所以a = 1，b = 2，由三角形三边关系定理有：b- a < c < b +a ，即1 < c < 3．。

利用算术平方根的非负性进行计算算术平方根的非负性是指一个非负实数的算术平方根也是非负的。

在数学中，利用算术平方根的非负性可以进行各种计算，包括求解方程、简化公式、推导关系等。

本文将对如何利用算术平方根的非负性进行计算进行详细的阐述。

首先，让我们来了解一下算术平方根的定义。

给定一个非负实数x，我们称一个非负实数y满足y²=x为x的算术平方根。

符号上，我们用√x表示x的算术平方根。

根据定义，我们有√x≥0，即算术平方根是非负数。

基于算术平方根的非负性，我们可以进行几种常见的计算。

首先，我们可以利用算术平方根的非负性求解方程。

考虑一个方程x²=a，其中a是已知的非负实数。

根据算术平方根的非负性，我们知道方程的解必然是非负实数。

因此，我们可以得出x=√a。

例如，对于方程x²=4，根据算术平方根的非负性，我们得出x=±√4=±2，即x可以是2或者-2、取非负解，我们得到x=2其次，我们可以利用算术平方根的非负性简化公式。

例如，我们考虑计算下列表达式：√(a²+b²)根据算术平方根的非负性，我们知道√(a²+b²)≥0。

因此，无需进行进一步计算，可以直接得出结果为非负实数0。

此外，我们也可以利用算术平方根的非负性推导关系。

例如，考虑两个非负实数a和b，满足a>b。

我们可以利用算术平方根的非负性证明以下关系：√a>√b首先，我们可以用反证法来证明上述关系。

假设√a≤√b，根据算术平方根的非负性，我们可以得到a≤b。

然而，这与假设a>b矛盾，因此原假设不成立。

所以我们可以得到√a>√b。

这个结论表明，对于两个非负实数，如果一个大于另一个，则它们的算术平方根之间的大小关系也是相同的。

综上所述，利用算术平方根的非负性进行计算可以大大简化问题。

我们可以利用算术平方根的非负性求解方程、简化公式以及推导关系。

二次根式的双重非负性在解题中的运用式子a表示非负数a的算术平方根，它是一个非负数，而a是被开方数，它也是一个非负数，这就是二次根式的双重非负性。

它在初、高中数学中占有重要的位置，所以在解题中一定要注意这两个隐含条件。

现列举出这一性质在中考解题中的运用归类如下，以供大家参考，不对之处敬请指正。

类型一：确定自变量的取值范围例：若下列式子有意义，试确定x的取值范围。

评析：纵览《数学课程标准》（2011年版）（以下简称《标准》）及现行初中教材，可以归纳出在初中阶段对字母的取值有要求的只有三种情况：①分式中的分母不能为零。

②二次根式中被开方数要大于等于零。

③零指数幂的底数不能为零。

抓住这三点就能准确地求出自变量的取值范围，通过这样训练，就能使其条件从隐含形态转变为显形形态而成为一种数学思想，从而促成学生模型思想的生成。

类型二：求代数式的值评析：解决此类题用到了“几个非负数的和为零，那么每一个加数一定为零”和“如果被开方数互为相反数，要使得两个被开方数同时有意义，那么这两个被开方数一定同时为零”这种模型思想。

而依据《标准》，初中阶段涉及的非负数有绝对值、偶次方和二次根式。

这也正符合《标准》增加的提高学生的运算能力的要求。

有了这些理念，学生就能明白算理，做到运算正确、有据、合理、简洁，学生的数学思想就能自然生成。

类型三：化简对于利用二次根式的双重非负性在化简中又包含以下几种情形：1.默认条件。

例： 18a3b2c=3ab2ac。

这类题目如果没有注明条件，在解题中就认为所有的字母都是非负数。

2.给定条件。

评析：由于思维定势的影响，学生见惯了被开方数是没有带负号正数的情况，而对于被开方数是-a这种形式的正数不习惯，这就需要教师注重发挥学生想象力，不断积累经验。

解决这类问题关键一定要抓住二次根式的双重非负性质，就能找到突破口，从而化难为易。

这体现了《标准》中“读懂学生的基础，读懂学生的思路，读懂学生的错误，读懂学生的情感”的要求。

二次根式两个非负性的运用四川倪先德)0a≥的式子叫做二次根式．正确理解并灵活运用二次根式的这一定义，是解一些与二次根式相关的问题的关键．)0a≥是一个非负数．这个非负数可用数表示，也可用代数式表示，如5)3a≥等．这里实质包含两个非负性：a非负和a 非负．)0a≥表示非负数到本单元为止，已学习三个非负数：绝对值、平方数、算术平方根，它们有独特性质：若几个非负数的和为零，则它们分别为零，它还有一些性质，以后还要继续研究，非负数及它的性质，是重要的解题方法之一，务必要熟练掌握，才能灵活应用．例1．若1+-ba与42++ba互为相反数，则=+2004)(ba_____．解：∵1+-ba与42++ba互为相反数，∴10a b-+=．又∵10a b-+≥0，∴⎩⎨⎧=++=+-421baba，解之得：⎩⎨⎧-=-=12ba．∴200420042004()(21)3a b+=--=．二、若有a存在，则0a≥由于只有非负数才有平方根和算术平方根，负数没有平方根和算术平方根．所以0a≥是a 存在的必要前提．例2．要使代数式32-x有意义，则x的取值范围是（）A．2≠x B．2x≥C．2>x D．2x≤解：要使代数式32-x有意义，就要求：20x-≥，所以，2x≥；选B．三、若有2a-存在，则0a=0=由于2a-存在，则20a-≥．即20a≤，而2a是非负数，所以0a=．例3．2004x-值．解：∵2)2005(--x存在，∴20050x-=即2005x=0=，2004200520041x-=-=．四、若a与a-同时存在，则0a=0==例4．若200420052005+-+-=xxy，求x y-的值．解：因为2005-x和x-2005同时存在，所以20052004x y==，．所以200520041x y -=-=．。

(文章)算术平方根的双重非负性........................................算术平方根的双重非负性一般地，如果一个正数x 的平方根等于 a ，即x 2=a ，那么这个正数x 叫做a 的算术平方根。

0的算术平方根是0。

其中算术平方根有一个非常重要的性质，就是它的双重非负性，即①被开方数0≥a ；②0≥a 。

这一性质在解题中有着极其广泛应用，以下举例说明。

一、利用非负性①被开方数0≥a例1 x 为何值时，下列各式有意义。

⑴x -； ⑵x x +-1； ⑶14+x ； ⑷12+x ； ⑸112--x解：⑴当0≥-x ，即0≤x ，x -有意义；⑵当01≥-x 且0≥x ，即10≤≤x 时，x x +-1有意义；⑶当01>+x ，即1->x 时，14+x 有意义 ；⑷当012≥+x ，即x 取任意实数时，12+x 有意义；⑸当012>--x ，即(),012>+-x 012<+x 时，112--x 有意义，但无论x 取任何数，12+x 都不会是负数，故原式无意义。

评注：对于⑶、⑸这样的式子，除了应用被开方数0≥a 的性质外，还要注意分母不能为0。

例2 若x 、y 满足42112=+-+-y x x ，则xy 的值为 。

解：由被开方数0≥a 得，021,012≥-≥-x x21,21≤≥x x 所以21=x 把21=x 代入等式得4=y 故2421=⨯=xy ，应填2。

评注：这里应用了被开方数0≥a ，而x x 2112--与是相反数，互为相反数的只有0，所以012=-x 。

可以解出x 、y 值。

例3 比较x -5与()36-x 的大小。

解：由被开方数0≥a 得5,05≤≥-x x因此，06<-x ，()063<-x 所以x -5>()36-x 评注：本题看起来无从下手，其实隐含着被开方数0≥a 这一条件，应用这一条件可以求出x 的取值范围，然后依据x 的取值范围计算比较大小。