八年级上学期月考试卷

一、选择题（本大题共12小题，共36.0分）1.如果AD是△ABC的中线，那么下列结论：CB; ②AB=AC; ③S△ABD=S△ACD.其中一定成立的有() ①BD=12A. 3个B. 2个C. 1个D. 0个2.若一个正n边形的每个内角为144∘，则这个正n边形的所有对角线的条数是()A. 7B. 10C. 35D. 703.已知a，b，c是△ABC的三条边长，化简|a+b−c|−|c−a−b|的结果为()A. 2a+2b−2cB. 2a+2bC. 2cD. 04.将一张三角形纸片剪开分成两个三角形，这两个三角形不可能()A. 都是直角三角形B. 都是钝角三角形C. 都是锐角三角形D. 是一个直角三角形和一个钝角三角形5.把一个多边形纸片沿一条直线截下一个三角形后，变成一个十八边形，则原多边形纸片的边数不可能是()A. 16B. 17C. 18D. 196.在△ABC中，，则此三角形是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形7.画△ABC中AB边上的高，下列画法中正确的是()A. B.C. D.8.如果三角形的两边长分别为3和5，则周长L的取值范围是()．A. 6<L<15B. 6<L<16C. 11<L<13D. 10<L<169.如图，在△ABC中，∠BAC=90°，BD平分∠ABC，CD//AB交BD于点D，已知∠ACB=34°，则∠D的度数为()A. 30°B. 28°C. 26°D. 34°10.满足下列条件的△ABC中，不是直角三角形的是()A. ∠A=2∠B=3∠CB. ∠B+∠A=∠CC. 两个内角互余D. ∠A：∠B：∠C=2：3：511.如图，三角形纸片ABC中，∠A=65°，∠B=75°，将∠C沿DE对折，使点C落在△ABC外的点C′处，若∠1=20°，则∠2的度数为()A. 80°B. 90°C. 100°D. 110°12.如图，有一条等宽纸带，按图折叠时(图中标注的角度为40°)，那么图中∠ABC的度数等于()A. 70°B. 60°C. 50°D. 40°二、填空题（本大题共5小题，共15.0分）13.如图，△ABC中，∠A=55°，将△ABC沿DE翻折后，点A落在BC边上的点A′处．如果∠A′EC=70°，那么∠A′DB的度数为______．14.如图，在△ABC中，已知点D、E、F分别是BC、AD、CE的中点，且S△ABC=4，则S△BEF=．15.如图，小林从P点向西直走8米后，向左转，转动的角度为α，再走8米，如此重复，小林共走了72米回到点P，则α为______．16.已知AH为△ABC的高，若∠B=40°，∠ACH=65°，则∠BAC的度数为______°.17.如图，木工师傅做完门框后，为了防止变形，常常像图中所示那样钉上两条斜拉的木条(图中的AB、CD)，这样做的数学道理是__________________________。

八年级上册第一次月考试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪种细胞器在所有细胞中都存在？A. 线粒体B. 叶绿体C. 溶酶体D. 内质网2. 地球上生命起源的假说中，哪一种被广泛接受？A. 自然发生说B. 宇宙生命论C. 化学进化说D. 热泉生命起源说3. 下列哪个过程是光合作用的一部分？A. 光反应B. 呼吸作用C. 脱水缩合D. 有丝分裂4. 下列哪个是原核生物？A. 细菌B. 真菌C. 藻类D. 动物5. 下列哪种物质是DNA复制时所需的？A. RNA聚合酶B. DNA聚合酶C. 氨基酸D. 核糖核苷酸二、判断题（每题1分，共5分）1. 细胞壁对细胞具有支持和保护作用。

（）2. 基因是遗传信息的携带者。

（）3. 有丝分裂过程中，染色体数量在后期加倍。

（）4. 蛋白质是生物体主要的能源物质。

（）5. 光合作用只能在光照条件下进行。

（）三、填空题（每题1分，共5分）1. 细胞中的能量转换器有_________和_________。

2. 基因位于_________上，它决定了生物的_________。

3. 有丝分裂间期主要进行_________的复制和有关蛋白质的合成。

4. 光合作用的实质是_________制造有机物，释放_________。

5. 呼吸作用的主要场所在_________。

四、简答题（每题2分，共10分）1. 简述细胞膜的功能。

2. 什么是遗传？什么是变异？3. 有丝分裂的意义是什么？4. 光合作用和呼吸作用的区别和联系是什么？5. 原核细胞和真核细胞有什么异同？五、应用题（每题2分，共10分）1. 如果一个细胞在分裂过程中染色体数量加倍，但细胞质未分裂，这是什么过程？它有什么意义？2. 某种植物在遮光条件下生长，其叶片颜色会变浅，为什么？3. 如果一个生物体的基因发生了突变，可能会导致什么后果？4. 为什么说线粒体是细胞的“动力车间”？5. 光合作用中，光反应和暗反应是如何协同工作的？六、分析题（每题5分，共10分）1. 分析细胞结构和功能的关系。

2024-2025学年八年级生物上学期第一次月考卷（考试时间：60分钟试卷满分：50分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．测试范围：人教版八上第五单元第一、二章。

5.难度系数：0.76．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共15个小题，每小题1分，共15分。

每小题只有一个选项符合题目要求。

1．我国美丽富饶的南海诸岛有许多是珊瑚礁形成的。

珊瑚礁由珊瑚虫的分泌物堆积而成。

珊瑚虫属于腔肠动物，其显著特征是（）A．体内有消化腔，有口无肛门B．身体呈背腹扁平，左右对称C．体表有外骨骼包围，足分节D2．下列词语中提到的动物不属于节肢动物的是（）A．金蝉脱壳B．庄周梦蝶C．乌贼喷墨D．虾兵蟹将3．下列关于几种无脊椎动物的叙述错误的是（）A．软体动物用足运动，大多具有贝壳B．环节动物身体分节，比线形动物运动更灵活C．比较节肢动物和环节动物，前者的结构更复杂D．腔肠动物身体辐射对称，可从各方向捕获猎物、进行防御，因而比扁形动物更高等4．用吸管吸取少许墨汁，将墨汁慢慢地滴在鱼口的前方，可看到的现象是（）A．墨汁从口吸入后，从鳃盖流出B．墨汁从口吸入后，进入鱼的身体，最后可能从鱼的肛门排出C．墨汁从口吸入后，又从口里吐出D．墨汁没有进入鱼的口里5．鲫鱼游泳的动力主要来自（）A．尾部和躯干部的摆动B．尾鳍的摆动C．胸鳍和尾鳍的摆动D．所有鱼鳍的协调运动6．“天高任鸟飞”，各种姿态的鸟在蓝天中翱翔，形成一幅美丽的画卷，关于鸟类适于飞行的结构特征，叙述错误的是（）A．身体呈流线型，减少飞行中空气的阻力B．气囊可以扩大气体交换的面积C．骨骼轻、薄，有的骨中空，可以减轻体重D．胸肌特别发达，为飞行提供足够的动力7．鳖，俗名“甲鱼”，营养价值高，乃宴席上品。

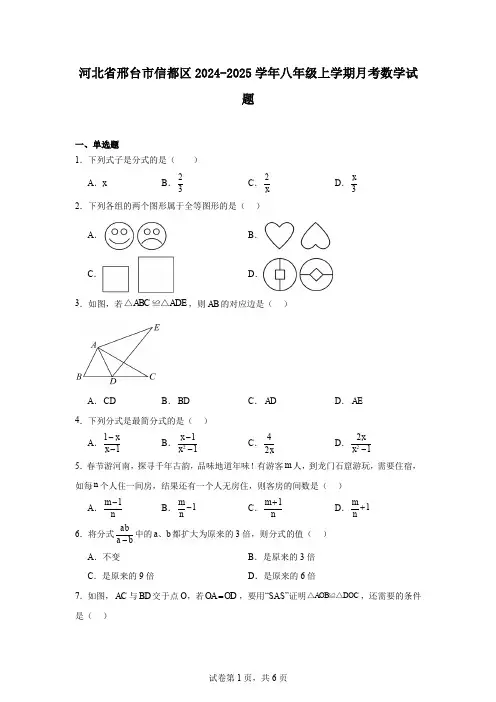
河北省邢台市信都区2024-2025学年八年级上学期月考数学试题一、单选题1．下列式子是分式的是（ ）A ．xB ．23C ．2xD ．3x 2．下列各组的两个图形属于全等图形的是（ ）A ．B ．C ．D ．3．如图，若ABC ADE △≌△，则AB 的对应边是（ ）A ．CDB ．BDC ．AD D ．AE4．下列分式是最简分式的是（ ）A ．11x x --B ．211x x --C ．42xD ．221x x - 5．春节游河南，探寻千年古韵，品味地道年味！有游客m 人，到龙门石窟游玩，需要住宿，如每n 个人住一间房，结果还有一个人无房住，则客房的间数是（ ）A ．1m n -B ．1m n -C ．1m n +D ．1m n+ 6．将分式ab a b-中的a b 、都扩大为原来的3倍，则分式的值（ ） A ．不变B ．是原来的3倍C ．是原来的9倍D ．是原来的6倍7．如图，AC 与BD 交于点O ，若OA OD =，要用“SAS”证明AOB DOC △≌△，还需要的条件是（ ）A ． OB OC =B ． AB DC = C ．AD ∠=∠ D ．B C ∠=∠8．已知1313a a =□，能使等式恒成立的运算符号是（ ） A ．＋B ．－C ．·D ．÷ 9．若分式52x--的值为负数，则x 的取值范围是（ ） A ．x ＜2 B ．x ＞2 C ．x ＞5 D ．x ＜﹣210．下列各命题的逆命题成立的是（ ）A ．对顶角相等B ．如果两个数相等，那么它们的绝对值相等C ．两直线平行，同位角相等D ．如果两个角都是45︒，那么这两个角相等11．若将分式2223x x y -与分式2()x x y -通分后，分式2()x x y -的分母变为2（x ﹣y ）（x+y ），则分式2223x x y -的分子应变为（ ） A ．6x 2（x ﹣y ）2 B ．2（x ﹣y ） C ．6x 2 D ．6x 2（x+y ） 12．工人师傅常用角尺平分一个任意角，具体做法如下：如图，已知AOB ∠是一个任意角，在边OA 、OB 上分别取OM ON =，移动角尺，使角尺两边相同的刻度分别与点M 、N 重合，就可以知道射线OC 是AOB ∠的角平分线．依据的数学基本事实是（ ）A ．两边及其夹角分别相等的两个三角形全等，B ．两角及其夹边分别相等的两个三角形全等．C ．两角分别相等且其中一组等角的对边相等的两个三角形全等．D ．三边分别相等的两个三角形全等．13．化简分式23311x x x-+--过程中开始出现错误的步骤是（ ） 23333(1)11(1)(1)(1)(1)x x x x x x x x x --++=---+-+-…………① 331(1)(1)x x x x --+=+-………② 22(2)(1)x x x --=+-…………③ 21x =--…………④ A ．① B ．② C ．③ D ．④14．如图，课本上给出了小明一个画图的过程，这个画图过程说明的事实是（ ）A ．两个三角形的两条边和夹角对应相等，这两个三角形全等B ．两个三角形的两个角和其中一角的对边对应相等，这两个三角形全等C ．两个三角形的两条边和其中一边对角对应相等，这两个三角形不一定全等D ．两个三角形的两个角和夹边对应相等，这两个三角形不一定全等二、填空题15．把2336a b ab-约分后，分母是22b ，分子是 16．关于x 的分式方程5222m x x+=--． （1）若方程的根为1x =，则m =；（2）若方程有增根，则m =三、解答题17．如图所示，在边长为1的正方形网格图中，点A B C D 、、、均在正方形网格格点上．（1）图中与线段AD 的长相等的线段是；（2）B D ∠+∠=︒．18．已知：如图，直线a b 、被直线c 所截，1∠与2∠互补，求证：a b P ．19．如图，ADE BCF V V ≌，8cm AD =，6cm CD =，30A ∠=︒，80E ∠=︒．(1)求BD 的长．(2)求BCF ∠的度数．20．如图，小明家住在河岸边的B 处，河对岸的A 处有一棵树，他想要测得这棵树与自己家之间的距离AB ．设计了下面的方案：在与B 点同侧的河岸边选择一点C ，测得75ABC ∠=o ，35ACB ∠=o ，然后在M 处立了标杆，使75MBC ∠=o ，35MCB ∠=o ，此时测得MB 的长就是A ，B两点间的距离．小明设计的方案是否正确？请说明理由．21．已知分式2x a+-（a，b为常数）满足表格中的信息：(1)则b的值是______；(2)求出c的值______．22．根据如图所示的程序，求输出D的化简结果．23．直角三角形ABC中，90ACB∠=︒，直线l过点C．(1)当AC BC =时，如图1，分别过点A 和B 作AD ⊥直线l 于点D ，BE ⊥直线l 于点E ．求证：ACD CBE V V≌； (2)当8cm AC =，6cm BC =时，过B 作BP l ⊥于P 点，延长BP 到F 点，使PF BP =．点M 是AC 上一点，点N 是CF 上一点，分别过点M 、N 作MD ⊥直线l 于点D ，NE ⊥直线l 于点E ．点M 从A 点出发，以每秒1cm 的速度沿A C →路径运动，终点为C ．点N 从F 点出发，以每秒3cm 的速度沿F C B C F →→→→路径运动，终点为F ．点M 、N 同时开始运动，各自达到相应的终点时停止运动．设运动时间为t 秒，请求出所有使MDC △与CEN V全等的t 的值．24．甲，乙两个工程队分别接到36千米的道路施工任务．以下是两个工程队的施工规划．(1)问甲工程队完成施工任务需要多少天？(2)若要尽快完成施工任务，乙工程队应采取哪种方案？说明你的理由．。

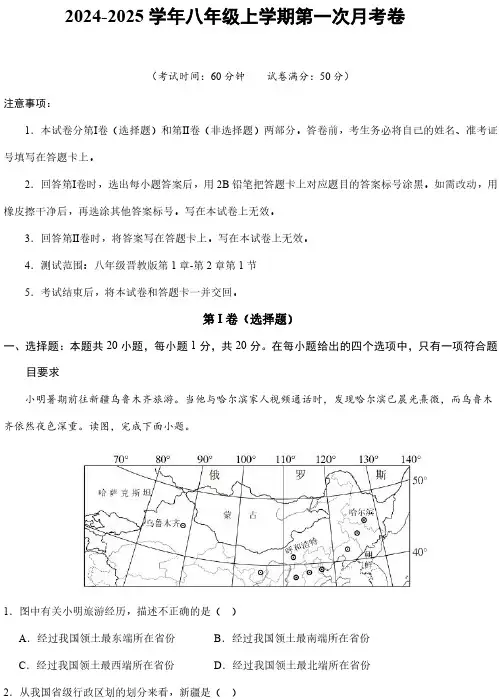
2024-2025学年八年级上学期第一次月考卷（考试时间：60分钟试卷满分：50分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．测试范围：八年级晋教版第1章-第2章第1节5．考试结束后，将本试卷和答题卡一并交回。

第I卷（选择题）一、选择题：本题共20小题，每小题1分，共20分。

在每小题给出的四个选项中，只有一项符合题目要求小明暑期前往新疆乌鲁木齐旅游。

当他与哈尔滨家人视频通话时，发现哈尔滨已晨光熹微，而乌鲁木齐依然夜色深重。

读图，完成下面小题。

1．图中有关小明旅游经历，描述不正确的是（）A．经过我国领土最东端所在省份B．经过我国领土最南端所在省份C．经过我国领土最西端所在省份D．经过我国领土最北端所在省份2．从我国省级行政区划的划分来看，新疆是（）A．直辖市B．特别行政区C．自治区D．民族乡3．正方形代表亚欧大陆，虚线代表北回归线和北极圈，图中阴影能正确反映中国位置的是（）A．B．C．D．4．我国幅员辽阔，东西相距5500千米，跨经度60多度，这就造成了（）A．B．C．D．读“我国管辖的海域空间结构示意图”和“南海诸岛图”，完成下面小题。

5．我国主张的领海宽度、陆地和海洋国土面积之和分别约为（）A．12海里1260万平方千米B．200海里960万平方千米C．24海里1260万平方千米D．350海里960万平方千米6．关于南沙群岛及其周边海域的叙述，错误的是（）A ．位于北温带B ．拥有丰富的海洋资源C ．主权历代以来都属于中国D ．联系太平洋与印度洋的重要海上通道下图示意我国人口分布，读图完成下面小题。

7．我国人口分布总体特征是（）A ．东多西少B ．北多南少C ．内陆多，沿海少D ．第一阶梯人口多8．关于图中人口分界线的描述，准确的是（）A ．A 为黑龙江省漠河市B ．B 为云南省昆明市C ．A 所在省份行政中心为哈尔滨D ．B 所在省份简称是粤9．下列属于影响人口分布的社会经济条件是（）①交通便利②经济发达③地势平坦④医疗水平高A ．①②③B ．①②④C ．①③④D ．②③④“大国点名，没你不行”。

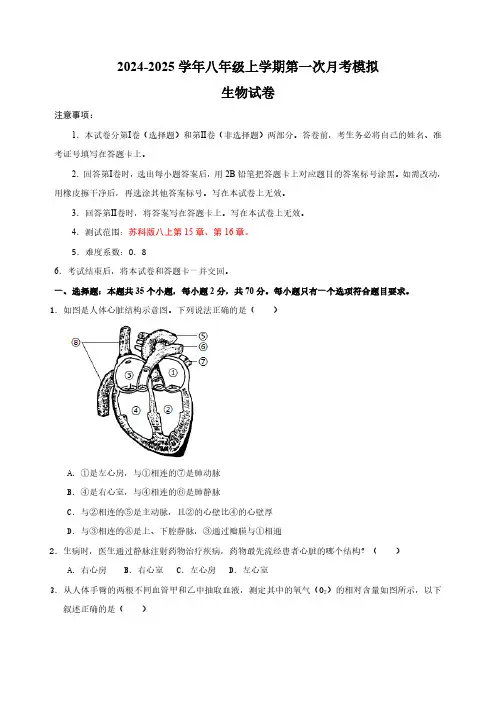
2024-2025学年八年级上学期第一次月考模拟生物试卷注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．测试范围：苏科版八上第15章、第16章。

5．难度系数：0．86．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共35个小题，每小题2分，共70分。

每小题只有一个选项符合题目要求。

1．如图是人体心脏结构示意图。

下列说法正确的是（ ）A．①是左心房，与①相连的⑦是肺动脉B．④是右心室，与④相连的⑥是肺静脉C．与②相连的⑤是主动脉，且②的心壁比④的心壁厚D．与③相连的⑧是上、下腔静脉，③通过瓣膜与①相通2．生病时，医生通过静脉注射药物治疗疾病，药物最先流经患者心脏的哪个结构？（ ）A．右心房B．右心室C．左心房D．左心室3．从人体手臂的两根不同血管甲和乙中抽取血液，测定其中的氧气（O2）的相对含量如图所示，以下叙述正确的是（ ）A．甲是动脉血B．乙呈鲜红色C．甲是从静脉中抽取的D．乙是从动脉中抽取的4．张华的父亲因感到身体不适到医院就诊，经医生检查，心率为90次/分，血压为16/10．7kPa，血常规化验结果如下。

根据测量和化验的结果，推断该人测定值不正常的项目及可能患有的疾病分别是（）A．血压、高血压B．白细胞总数、急性炎症C．红细胞计数、贫血D．血红蛋白、贫血5．新鲜的血液加入抗凝剂静置一段时间后，出现了分层现象，如（如图）。

下列关于该实验的叙述，正确的是（）A．分布在①层的物质只有水B．聚集在②层的细胞能运输氨基酸C．聚集在③层的细胞是血小板D．该实验说明血液包括血浆和血细胞6．血液是反映人体健康状况的“晴雨表”。

江西省吉安市2024-2025学年八年级上学期第一次月考数学试卷一、单选题1．若下列各组数值代表三根木棒的长度，则不能用它们摆成三角形的是（ ） A ．3cm,4cm,5cm B ．8cm,8cm,14cm C ．6cm,7cm,11cmD ．1cm,2cm,4cm2．如图，过BAF ∠的边AF 上一点E 作CD AB ∥．若,40BE AF BED ⊥∠=︒，则A ∠的度数是（ ）A ．45︒B ．50︒C ．80︒D ．60︒3．如图，在四边形ABCD 中，A D α∠+∠=，ABC ∠的平分线与BCD ∠的平分线相交于点P ，则P ∠的度数是（ ）A ．12αB ．902πα︒−C ．1902α︒+D ．180α︒−4．如图，ABC V 中，8AB =，10AC =，点D 是BC 边上的中点，连接AD ，若ACD 的周长为20，则ABD △的周长是（ ）A ．16B ．18C ．20D ．225．如图，已知MB=ND ，∠MBA=∠NDC ，下列条件中不能判定△ABM ≌△CDN 的是（ ）A ．M N ∠=∠B ．A NCD ∠=∠C ．AM CN =D ．AM//CN6．如图，CAB DAB ∠=∠，那么添加下列一个条件后，仍无法判定ABC ABD △≌△的是（ ）A ．ABC ABD ∠=∠B ．BC BD = C ．C D∠=∠D ．AC AD =二、填空题7．如图，从数学的角度看房屋顶部支撑架，它运用了三角形的 性．8．两个完全相同的正五边形都有一边在直线l 上，且有一个公共顶点O ，其摆放方式如图所示，则∠AOB 等于 度9．已知等腰三角形的两条边长分别是2和4，则它的周长是 ．10．正五边形ABCDE 与等边三角形EMN 如图放置，C ，M ，D ，N 在同一直线上，则MED∠度数为 ．11．如图，在四边形ABCD 中，∠A ＝90°，AD ＝3，BC ＝5，对角线BD 平分∠ABC ，则BCD 的面积为 ．三、解答题12．如图，点D 是ABC V 的边BC 上任意一点，求证：2AB BC AC AD ++>．13．若一个多边形的内角和与它的外角和相等，求这个多边形边数．14．如图，在直角△ABC 中，∠C ＝90°，∠CAB 的平分线AD 交BC 于D ，若DE 垂直平分AB ，求∠B 的度数．15．为了进一步探究三角形中线的作用，数学兴趣小组合作交流时，小丽在组内做了如下尝试：如图，在ABC V 中，AD 是BC 边上的中线，延长AD 到点E ，使DE AD =，连接BE ．【探究发现】（1）图中AC 与BE 的数量关系是 ，位置关系是 ．【初步应用】（2）若5AB =，3AC =，求AD 的取值范围．16．如图所示，已知AC BD ∥，AE 、BE 分别平分CAB ∠和DBA ∠，点E 在CD 上，求证：AB AC BD =+．17．如图，在ABC V 中，D 为AB 上一点，E 为AC 中点，连接DE 并延长至点F ，使得EF ED =，连接CF ．(1)求证：CF AB ∥(2)若50ABC ∠=︒，连接BE ，BE 平分ABC ∠，AC 平分BCF ∠，求A ∠的度数． 18．如图，B 处在A 处的南偏西40︒方向，C 处在A 处的南偏东10︒方向，C 处在B 处的北偏东85︒方向，求ABC ∠和ACB ∠的度数．19．如图，在ABC V 中，=60B ∠︒，AD 平分BAC ∠，CE 平分BCA ∠，AD CE 、交于点F ，CD CG =，连接FG ．(1)求证：FD FG =；(2)线段FG 与FE 之间有怎样的数量关系，请说明理由；(3)若60B ∠≠︒，其他条件不变，则（2）中的结论是否仍然成立？请直接写出判断结果，不必说明理由．20．如图AB AC =,AD AE =,BAC DAE ∠=∠,125∠=︒,230∠=︒.求3∠的度数.21．认真阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题． (1)探究1：如图1，在ABC 中，O 是ABC ∠与ACB ∠的平分线BO 和CO 的交点，猜想BOC ∠与A ∠之间存在怎样的数量关系？并说明你的猜想．(2)探究2：如图2中，O 是ABC ∠与外角ACD ∠的平分线BO 和CO 的交点，试分析BOC ∠与A ∠有怎样的关系？请说明理由．(3)探究3：如图3中，O 是外角DBC ∠与外角ECB ∠的平分线BO 和CO 的交点，则BOC ∠与A ∠有怎样的关系？请说明理由．22．如图，AB BC =，90ABC ∠=︒，点P 在射线AB 上，且90CEP ∠=︒，点F 在EP 上且EF EC =，连接AF ，取AF 的中点G ，连接EG 并延长至H ，使GH GE =，连接AH ．(1)如图1，当点P 在线段AB 上时． ①用等式表示AH 与CE 的数量关系；②连接BH，BE，直接写出BH，BE的数量关系和位置关系；(2)如图2，当点P在线段AB的延长线上时，依题意补全图形2，猜想②中的结论是否还成立，并证明．。

八年级上学期语文月考试卷一、积累运用（30分）1．下面选项中，加点字注音和书写完全正确的一项是（）（2分）A．畎．亩(quǎn)万仞．(rèn)荷．担(hè)拂．士(fú)B．穷匮．(．kuì) 箕．畚(qī) 魁．父(kuí) 孀．妻(shuāng)C．始龀．(chèn) 介胄．(zhòu) 棘．门(jí) 曩．者(nǎng)D．提携．(xié) 折戟．(jǐ) 殷．勤(yīn) 燕．脂(yàn)2．下列句子中加点的成语使用不正确的一项是( )(2分)A．透过十五倍的放大镜，才能看到针孔中的两只大熊猫，微雕艺术令人叹为观止．．．．。

B．好的书需要多读，重要的书必须常常反复阅读，每读一次都会让你觉得开卷有益．．．．。

C．在辛苦劳顿、险象迭生．．．．的探险路上，她像男人一样坚强。

D．一时间，保健品市场出现了参差不齐．．．．的局面。

3．下面句子没有语病的一项是（）（2分）A．杨绛先生学贯中西，著述丰硕，成就非凡，享誉海内外。

B．是否坚持一个中国的原则，是维护两岸关系和平发展的关键。

C．随着智能手机的普及，使得我们周围出现了大量的“低头族”。

D．为了提高同学们的语文素养，我市学校很多都在开展“读经典作品，建书香校园”的活动。

4．依次填入下列横线处的句子，语序恰当，语意连贯的一组是( )(2分)“浅阅读”对我们增长学问、开阔眼界无疑起到促进作用。

________，________，________，________，________，它使知识向精、深、专的方向挺进。

“深阅读”对传统文化的传承和国民素质的提升更加重要。

①而“深阅读”就是深度阅读，它讲究反复咀嚼、品味、思考②但是，浅阅读本身存在无法克服的缺点和不足③那么对于国家和民族将是灾难性的④如果仅限于浅阅读，过分热衷于浅阅读⑤表现为走马观花、浅尝辄止、泛泛而读A．①②④⑤③B．②①④③⑤C、⑤④③①②D．②⑤④③①5．下面关于文学常识和文化常识的表述不正确的一项是（）（2分）A．《愚公移山》反映了我国古代劳动人民改造自然的伟大气魄和惊人毅力，也说明了要克服困难，就必须下定决心，坚持奋斗。

江西省2024-2025学年八年级上学期第一次月考数学试题一、单选题1. 在ABC 中，已知3AC =，4BC =，则AB 的取值范围是（ ）A. 68AB <<B. 17AB <<C. 214AB <<D. 114AB <<【答案】B【解析】【分析】根据三角形三边关系求解．【详解】解： 在ABC 中，3AC =，4BC =， ∴BC AC AB BC AC −<<+，∴4343AB −<<+，即17AB <<．故选B ．【点睛】本题考查三角形三边关系的应用，解题的关键是掌握三角形两边之和大于第三边，两边之差小于第三边．2. 如图，△ABC ≌△ABD ，若∠ABC ＝30°，∠ADB ＝100°，则∠BAC 的度数是（ ）．A. 30°B. 100°C. 50°D. 80°【答案】C【解析】 【分析】根据全等三角形的性质得到∠C 的度数，然后利用三角形内角和定理计算即可.【详解】解：∵△ABC ≌△ABD ，∴∠C ＝∠ADB ＝100°，∴∠BAC ＝180°－100°－30°＝50°，故选C.【点睛】本题考查了全等三角形的性质和三角形内角和定理，熟知全等三角形的对应边相等，对应角相等是解题关键.3. 如图，在ABC 中，AB AC =，AE AF =，AD BC ⊥，垂足为D ．则全等三角形有（ ）A. 2组B. 3组C. 4组D. 5组【答案】C【解析】 【分析】本题主要考查了全等三角形的性质和判定，先根据HL 证明Rt ADE ≌Rt ADF ，可得DE DF =，进而得出Rt ABD △≌Rt ACD △，可得BD CD =，即可得出BE CF =，再根据SSS 证明ABE ≌ACF △，ACE △≌ABF △，可得答案．【详解】∵AE AF =，AD AD =，∴Rt ADE ≌Rt ADF ，∴DE DF =．∵AB AC =，AD AD =，∴Rt ADB △≌Rt ADC ，∴BD CD =，∴B D D E C D D F −=−，即BE CF =．∵AB AC =，AE AF =，∴ABE ≌ACF △．∵B D D F C D D E +=+，即BF CE =．∵AB AC =，AE AF =，∴ABF △≌ACE △．全等三角形有4组．故选：C ．4. 如图，在ABC 中，,ABC ACB ∠∠的平分线交于点O ，连接AO ，过点O 作,,OD BC OE AB ABC ⊥⊥△的面积是16，周长是8，则OD 的长是（ ）A. 1B. 2C. 3D. 4【答案】D【解析】 【分析】本题主要考查了角平分线的性质，先过点O 作OF AC ⊥于点F ，然后根据角平分线的性质，证明OE OF OD ==，然后根据ABC 的面积AOB =△的面积BOC +△的面积AOC +△的面积，求出答案即可．【详解】如图所示：过点O 作OF AC ⊥于点F ，OB ，OC 分别是ABC ∠和ACB ∠角平分线，OD BC ⊥，OE AB ⊥，OF AC ⊥，OE OD OF ∴==，16ABC AOB BOC AOC S S S S =++= ， ∴11116222AB OE BC OD AC OF ⋅+⋅+⋅=， 11116222AB OD BC OD AC OD ⋅+⋅+⋅=， 1()162OD AB BC AC ++=， 8++= AB BC AC ，4OD ∴=，故选：D ．5. 如图，ABC ∆中，AB BC =，点D 在AC 上，BD BC ⊥．设BDC α∠=，ABD β∠=，则（ ）的A. 3180αβ+°B. 2180αβ+°C. 390αβ−=°D. 290αβ−=°【答案】D【解析】 【分析】根据三角形外角等于不相邻两个内角的和，直角三角形两锐互余解答【详解】解：AB BC = ，A C ∴∠=∠，A αβ−∠= ，90C α+∠=°，290αβ∴=°+，290αβ∴−=°，故选：D ．【点睛】本题考查了三角形外角，直角三角形，熟练掌握三角形外角性质，直角三角形两锐角性质，是解决此类问题的关键6. 下列条件，不能判定两个直角三角形全等的是（ ）A. 两个锐角对应相等B. 一个锐角和斜边对应相等C. 两条直角边对应相等D. 一条直角边和斜边对应相等【答案】A【解析】【分析】本题主要考查全等的判定方法，熟练掌握判定方法是解题的关键．根据判定方法依次进行判断即可．【详解】解：A 、两个锐角对应相等，不能判定两个直角三角形全等，故A 符合题意；B 、一个锐角和斜边对应相等，利用AAS 可以判定两个直角三角形全等，故B 不符合题意；C 、两条直角边对应相等，利用SAS 可以判定两个直角三角形全等，故C 不符合题意；D 、一条直角边和斜边对应相等，利用HL 可以判定两个直角三角形全等，故D 不符合题意；故选：A ．7. 如图，在ACD 和BCE 中，,,,,AC BC AD BE CD CE ACE m BCD n ===∠=∠= ，AD 与BE 相交于点P ，则BPA ∠的度数为（ ）A. n m −B. 2n m −C. 12n m −D. 1()2n m − 【答案】D【解析】 【分析】由条件可证明△ACD ≌△BCE ，根据全等三角形的性质得到∠ACB 的度数，利用三角形内角和可求得∠APB=∠ACB ，即可解答．【详解】在△ACD 和△BCE 中AC BC AD BE CD CE＝＝＝∴△ACD ≌△BCE （SSS ），∴∠ACD=∠BCE ，∠A=∠B ，∴∠BCA+∠ACE=∠ACE+∠ECD ，∴∠ACB=∠ECD=12（∠BCD-∠ACE ）=12×（n-m ） ∵∠B+∠ACB=∠A+∠BPA ，∴BPA ∠=∠ACB=1()2n m −. 故选D ．【点睛】此题考查全等三角形的判定和性质，掌握全等三角形的判定方法（即SSS 、SAS 、ASA 、AAS 和HL ）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键．8. 如图，EB 交AC 于M ，交FC 于D ，AB 交FC 于N ，90E F ∠=∠=°，B C ∠=∠，AE AF =，给出下列结论：①12∠=∠；②BE CF =；③ACN ABM ≌；④CD DN =．其中正确的结论有（ ）A. 4个B. 3个C. 2个D. 1个【答案】B【解析】 【分析】根据90E F ∠=∠=°，B C ∠=∠，AE AF =，可得ABE ACF ≌，三角形全等的性质BE CF =；BAE CAF ∠=∠可得①12∠=∠；由ASA 可得ACN ABM ≌，④CD DN =不成立．【详解】解：∵90E F ∠=∠=°，B C ∠=∠，AE AF =，∴ABE ACF ≌，∴BE CF =；BAE CAF ∠=∠，故②符合题意；∵BAE BAC CAF BAC ∠−∠=∠−∠，∴12∠=∠；故①符合题意；∵ABE ACF ≌∴B C ∠=∠，AB AC =，又∵BAC CAB ∠=∠∴ACN ABM ≌，故③符合题意；∴AM AN =，∴MC BN =，∵,B C MDC BDN ∠=∠∠=∠， ∴MDC NDB ≌，∴CD DB =，∴CD DN =不能证明成立，故④不符合题意．故选：B ．【点睛】本题考查三角形全等的判定方法和三角形全等的性质，难度适中．9. 已知AOB ∠，下面是“作一个角等于已知角，即作A O B AOB ′′′=∠∠”的尺规作图痕迹．该尺规作图的依据是（ ）A. SASB. SSSC. AASD. ASA【答案】B【解析】 【分析】本题主要考查了尺规作图作一个角等于已知角、全等三角形判定等知识点，掌握尺规作图作一个角等于已知角的作法成为解题的关键．根据“作一个角等于已知角，即作A O B AOB ′′′=∠∠”的尺规作图痕迹，结合全等三角形的判定定理即可解答．【详解】解：由题意可知，“作一个角等于已知角，即作A O B AOB ′′′=∠∠”的尺规作图的依据是SSS ．故选：B ．10. 如图，在四边形ABCD 中，对角线AC 平分BAD ∠，AB AC >，下列结论正确的是（ ）A. AB AD CB CD −>−B. AB AD CB CD −=−C. AB AD CB CD −<−D. AB AD −与CB CD −的大小关系不确定【答案】A【解析】 【分析】先通过在AB 上截取AE =AD ，得到一对全等三角形，利用全等三角形的性质得到对应边相等，再利用三角形的三边关系和等量代换即可得到A 选项正确．【详解】解：如图，在AB 上取AE AD =，对角线AC 平分BAD ∠，BAC DAC ∴∠=∠，在ACD ∆和ACE ∆中，的AD AE BAC DAC AC AC = ∠=∠ =， ()ACD ACE SAS ∴∆≅∆，CD CE ∴=，BE CB CE >− ，AB AD CB CD ∴−>−．故选：A ．【点睛】本题考查了全等三角形的判定与性质、角平分线的定义和三角形的三边关系，要求学生能根据已知条件做出辅助线构造全等三角形，并能根据全等三角形的性质得到不同线段之间的关系，利用三角形三边关系判断大小，解决本题的关键是牢记概念和公式，正确作辅助线构造全等三角形等．二、填空题11. 若正多边形的一个外角为60°，则这个正多边形的边数是______．【答案】六##6【解析】【分析】本题考查了多边形的外角和，熟练掌握任意多边形的外角和都是360度是解答本题的关键．根据任意多边形的外角和都是360度求解即可．【详解】解：360606°÷°=．故答案为：六．12. 四条长度分别为2cm ，5cm ，8cm ，9cm 的线段，任选三条组成一个三角形，可以组成的三角形的个数是___________个.【答案】2【解析】【分析】从4条线段里任取3条线段组合，可有4种情况，看哪种情况不符合三角形三边关系，舍去即可．【详解】解：四条木棒的所有组合：2，5，8和2，5，9和5，8，9和2，8，9；∵2+5=7<8，∴2，5，8不能组成三角形；∵2+5=7<9，∴2，5，9不能组成三角形；∵5+8=13>9，∴5，8，9能组成三角形；∵2+8=10>9，∴2，8，9能组成三角形．∴ 5，8，9和2，8，9能组成三角形．只有2个三角形．故答案是：2．【点睛】此题主要考查了三角形三边关系，三角形的三边关系：任意两边之和＞第三边，任意两边之差＜第三边；注意情况的多解和取舍．13. 如图，在ABC 中，AD BC ⊥，AE 平分BAC ∠，若140∠=°，230∠=°，则B ∠=______．【答案】40°##40度【解析】【分析】本题考查了三角形的角平分线，高线的定义；由AE 平分BAC ∠，可得角相等，由140∠=°，230∠=°，可求得EAD ∠的度数，在直角三角形ABD 在利用两锐角互余可求得答案．【详解】解：AE 平分BAC ∠12EAD ∴∠=∠+∠，12403010EAD ∴∠=∠−∠=°−°=°，Rt ABD 中，9090401040BBAD ∠=°−∠=°−°−°=°． 故答案为：40°．14. 如图，BE 平分∠ABC ，CE 平分外角∠ACD ，若∠A ＝52°，则∠E 的度数为_____．【答案】26°【解析】【分析】根据三角形的外角等于和它不相邻的两个内角的和即可得答案．【详解】∵BE 平分∠ABC ，CE 平分外角∠ACD ，∴∠EBC ＝12∠ABC ，∠ECD ＝12∠ACD ， ∴∠E ＝∠ECD ﹣∠EBC ＝12（∠ACD ﹣∠ABC ） ∵∠ACD-∠ABC=∠A ，∴∠E ＝12∠A ＝12×52°＝26° 故答案为26°【点睛】本题考查三角形外角性质，三角形的一个外角，等于和它不相邻的两个内角的和；熟练掌握外角性质是解题关键.15. 如图1，123456∠+∠+∠+∠+∠+∠为m 度，如图2，123456∠+∠+∠+∠+∠+∠为n 度，则m n −=__________．【答案】0【解析】【分析】将图1原六边形分成两个三角形和一个四边形可得到m 的值，将图2原六边形分成四个三角形可得到n 的值，从而得到答案．【详解】解：如图1，将原六边形分成两个三角形和一个四边形，，1234562180360720m ∴°=∠+∠+∠+∠+∠+∠=×°+°=°，如图2，将原六边形分成四个三角形，，∴°=∠+∠+∠+∠+∠+∠=×°=°，1234564180720n∴==，m n720∴−=，m n故答案为：0．【点睛】本题考查了多边形的内角和，此类问题通常连接多边形的顶点，将多边形分割成四边形和三角形，通过计算四边形和三角形的内角和，求得多边形的内角和．16. 如图，∠E＝∠F＝90°，∠B＝∠C，AE＝AF．给出下列结论：①∠1＝∠2；②BE＝CF；③ ACN≌ ABM；④CD＝DN．其中符合题意结论的序号是_____．【答案】①②③【解析】【分析】此题考查的是全等三角形的判定和性质的应用，只要先找出图中的全等三角形就可判断题中结论是否正确．【详解】∵∠E=∠F=90°，∠B=∠C，AE=AF，∴△ABE≌△ACF（AAS），∴AC=AB，BE=CF，即结论②正确；∵AC=AB，∠B=∠C，∠CAN=∠BAM，∴△ACN≌△ABM（ASA），即结论③正确；∵∠BAE=∠CAF，∵∠1=∠BAE-∠BAC，∠2=∠CAF-∠BAC，∴∠1=∠2，即结论①正确；∴△AEM ≌△AFN （ASA ），∴AM =AN ，∴CM =BN ，∵∠CDM =∠BDN ，∠C =∠B ，∴△CDM ≌△BDN ，∴CD =BD ，无法判断CD =DN ，故④错误，∴题中正确的结论应该是①②③．故答案为：①②③．【点睛】此题考查了三角形全等的判定和性质；对图中的全等三角形作出正确判断是正确解答本题的关键．三、解答题17. 如图，已知点D ，E 分别AB ，AC 上，B C ∠=∠，DC BE =，求证：ABE ACD △△≌．【答案】见解析【解析】【分析】本题考查了全等三角形的判定，根据已知条件选择恰当的判定方法是解题的关键．【详解】解：在ABE 和ACD 中，B C A A BE DC ∠=∠ ∠=∠ =， ∴()AAS ABE ACD ≌．18. 如图，请你仅用无刻度直尺作图．在（1）在图①中，画出三角形AB 边上的中线CD ；（2）在图②中，找一格点D ，使得ABC CDA △△≌．【答案】（1）见解析 （2）见解析【解析】【分析】（1）如图，连接CD 即可；（2）按如图所示，找到点D ，连接AD CD ，即可．【小问1详解】【小问2详解】如图，CDA 即为所求；【点睛】本题考查了作图，三角形中线的性质、全等三角形的判定方法，掌握中线的性质及全等三角形判定的方法是关键．19. （1）在ABC 中，ABC ∠的角平分线和ACB ∠的角平分线交于点P ，如图1，试猜想P ∠与A ∠的关系，直接写出结论___________：（不必写过程）（2）在ABC 中，一个外角ACE ∠的角平分线和一个内角ABC ∠的角平分线交于点P ，如图2，试猜想P ∠与A ∠的关系，直接写出结论____________；（不必写过程） （3）在ABC 中，两个外角EBC ∠的角平分线和FCB ∠的角平分线交于点P ，如图3，试猜想P ∠与A ∠的关系，直接写出结论_________，并予以证明．【答案】（1）1902P A∠=°+∠；（2）12P A∠=∠；（3）1902P A∠=°−∠【解析】【分析】（1）根据三角形的内角和定理表示出∠ABC+∠ACB，再根据角平分线的定义求出∠PBC+∠PCB，然后根据三角形的内角和定理列式整理即可；（2）根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACE=∠A+∠ABC，∠PCE=∠P+∠PBC，再根据角平分线的定义可得∠PBC=12∠ABC，∠PCE=12∠ACE，然后整理即可得证；（3）根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠PBC+∠PCB，然后利用三角形的内角和定理列式整理即可得解．【详解】解：（1）1902P A ∠=°+∠；理由：在△ABC中，∠ABC+∠ACB=180°-∠A，∵点P为角平分线的交点，∴1=2PBC ABC∠∠，1=2PCB ACB∠∠，∴∠PBC+∠PCB=12（∠ABC+∠ACB）=12（180°-∠A）=90°-12∠A，在△PBC中，∠P=180°-（90°-12∠A）=90°+12∠A；故答案为：1902P A ∠=°+∠；（2）12P A ∠=∠．理由：由三角形的外角性质得，∠ACE=∠A+∠ABC，∠PCE=∠P+∠PBC，∵外角∠ACE的角平分线和内角∠ABC的角平分线交于点P，∴∠PBC=12∠ABC，∠PCE=12∠ACE，∴12（∠A+∠ABC）=∠P+12∠ABC，∴∠P=12∠A；（3）1902P A ∠=°−∠； 证明： 外角EBC ∠的角平分线和FCB ∠的角平分线交于点P ，11()()22PBC PCB A ACB A ABC ∴∠+∠=∠+∠+∠+∠ 111()90222A A ABC ACB A =∠+∠+∠+∠=∠+° 在PBC ∆中，11180909022P A A ∠=°−∠+°=°−∠． 故答案为：1902P A ∠=°−∠； 【点睛】本题考查的是三角形内角和定理，角平分线的定义和三角形外角的性质，熟记性质与概念是解题的关键，要注意整体思想的利用．20. 如图，在ABC 中，AE 为边BC 上的高，点D 为边BC 上的一点，连接AD ．（1）当AD 为边BC 上的中线时，若6AE =，ABC 的面积为30，求CD 的长；（2）当AD 为BAC ∠的角平分线时，若6636C B ∠=°∠=°，，求DAE ∠的度数．【答案】（1）5 （2）15°【解析】【分析】本题考查了用三角形中线求三角形面积、三角形外角性质、直角三角形性质．（1）利用三角形中线定义及三角形面积求出CD 长；（2）利用三角形内角和先求BAC ∠，再用外角性质和直角三角形性质求出DAE ∠．【小问1详解】∵AD 为边BC 上的中线， ∴1152ADC ABC S S == ， ∵AE 为边BC 上的高， ∴1152DC AE ××=， ∴5CD =．【小问2详解】∵6636C B ∠=°∠=°，∴18078BAC B C =°−−=°∠∠∠，∵AD 为BAC ∠的角平分线，∴39BAD DAC ∠=∠=°，∴393675ADC BAD B ∠=∠+∠=°+°=°，∵AE BC ⊥，∴90AED ∠=°，∴9015DAE ADC ∠=°−∠=°21. 如图，点A ，D ，B ，E 在同一直线上，AC ＝DF ，AD ＝BE ，BC ＝EF ．求证：AC ∥DF ．【答案】详见解析【解析】【分析】根据等式的性质得出AB ＝DE ，利用SSS 证明△ABC 与△DEF 全等，进而解答即可．【详解】证明：∵AD ＝BE ，∴AD +DB ＝BE +DB ，∴AB ＝DE ，在△ABC 与△DEF 中，AB DE AC DF BC EF = = =，∴△ABC ≌△DEF （SSS ），∴∠A ＝∠FDE ，∴AC ∥DF ．【点睛】此题主要考查了平行线的性质和判定，全等三角形的判定和性质，做题的关键是找出证三角形全等的条件．22. 如图，在ACB △中，90ACB ∠=°，CD AB ⊥于D ．（1）求证：ACD B ∠=∠；（2）若AF 平分CAB ∠分别交CD 、BC 于E 、F ，求证：CEF CFE ∠=∠．【答案】（1）见解析 （2）见解析【解析】【分析】本题考查了直角三角形的性质，三角形角平分线的定义，对顶角的性质，余角的性质，难度适中． （1）由于ACD ∠与B ∠都是BCD ∠的余角，根据同角的余角相等即可得证；（2）根据直角三角形两锐角互余得出9090CFA CAF AED DAE ∠=°−∠∠=°−∠，，再根据角平分线的定义得出CAF DAE ∠=∠，然后由对顶角相等的性质，等量代换即可证明CEF CFE ∠=∠．【小问1详解】证明：90ACB ∠=° ，CD AB ⊥于D ，90ACD BCD ∴∠+∠=°，90B BCD ∠+∠=°，ACD B ∴∠=∠；【小问2详解】证明：在Rt AFC △中，90CFA CAF ∠=°−∠，同理Rt AED △中，90AED DAE ∠=°−∠．又AF 平分CAB ∠，CAF DAE ∴∠=∠，AED CFE ∴∠=∠，又CEF AED ∠=∠ ，CEF CFE ∴∠=∠．23. 如图，AC ，BD 相交于点O ，OB OD =，A C ∠=∠，求证：△≌△AOB COD ．在【答案】见解答【解析】【分析】本题主要考查全等三角形的判定，熟练掌握判定方法是解题的关键．根据全等三角形的判定方法证明即可．【详解】证明：AOB 和COD △中，A C AOB COD OB OD∠=∠ ∠=∠ = ， (AAS)AOB COD ∴≌△△．24. 材料阅读：如图①所示的图形，像我们常见的学习用品—— 圆规．我们不妨把这样图形叫做 “规形图 ”．解决问题：（1）观察“规形图 ”，试探究BDC 与A B C ∠∠∠，，之间的数量关系，并说明理由；（2）请你直接利用以上结论，解决以下两个问题：Ⅰ．如图② ，把一块三角尺 DEF 放置在ABC 上，使三角尺的两条直角边DE DF ，恰好经过点B C ，，若40A ∠=°，则ABD ACD +=∠∠ ° ． Ⅱ．如图③ ，BD 平分ABP CD ∠，平分ACP ∠，若40130A BPC ∠=°∠=°，，求BDC ∠的度数．【答案】（1） BDC A B C ∠=∠+∠+∠，理由见解析（2）Ⅰ．50；Ⅱ． 85°【解析】【分析】本题考查的是三角形内角和定理，三角形外角性质以及角平分线的定义得运用．根据题意连接AD 并延长至点 F ，利用三角形外角性质即可得出答案．Ⅰ．由（1）可知BDC A B C ∠=∠+∠+∠，因为40A ∠=°，90D ∠=︒，所以904050ABD ACD ∠+∠=°−°=°；Ⅱ．由（1）的已知条件，由于BD 平分ABP CD ∠，平分ACP ∠，即可得出在1452ABD ACD ABP ACP ∠+∠=∠+∠=°（），因此4540=85BDC ∠=°+°°． 【小问1详解】 解：如图连接AD 并延长至点 F ， 根据外角的性质，可得 BDF BAD B ∠=∠+∠， CDF C CAD ∠=∠+∠， 又∵BDC BDF CDF BAC BAD CAD ∠=∠+∠∠=∠+∠，， ∴BDC BAC B C ∠=∠+∠+∠；【小问2详解】解：Ⅰ． 由（1）可得，BDC ABD ACD A ∠=∠+∠+∠； 又∵4090A D ∠=°∠=°，， ∴9040=50ABD ACD ∠+∠=°−°°， 故答案为：50； Ⅱ．由（1），可得BPC ABP ACP BDC BAC ABD ACD ∠=∠+∠+∠∠=∠+∠+∠，， ∴1304090ABP ACP BPC BAC ∠+∠=∠−∠=°−°=°， 又∵BD 平分ABP CD ∠，平分ACP ∠， ∴1452ABD ACD ABP ACP ∠+∠=∠+∠=°（）， ∴4540=85BDC ∠=°+°°．。

2023-2024学年八年级上学期12月份质量监测数学（本试卷共6页，25题，全卷满分：120分，考试用时：120分钟）1．答题前，先将自己的姓名、准考证号写在试题卷和答题卡上，并将准考证条形码粘贴在答题卡上的指定位置．2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上相应题目的答案标号涂黑．写在试题卷、草稿纸和答题卡上的非答题区域均无效．3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非答题区域均无效．4．考试结束后，将答题卡上交．一、选择题（在下列各题的四个选项中，只有一项是符合题意的．请在答题卡中填涂符合题意的选项．本大题共10个小题，每小题3分，共30分）1.体育是一个锻炼身体，增强体质，培养道德和意志品质的教育过程，是培养全面发展的人的一个重要方面，下列体育图标是轴对称图形的是（）A. B. C. D.2.如图，空调安装在墙上时，一般都会采用如图所示的方法固定，这种方法应用的几何原理是（）A.三角形两边之差小于第三边B.三角形两边之和大于第三边C.垂线段最短D.三角形的稳定性3.用下列长度的三条线段能组成三角形的是（）A.2cm，3cm，5cmB.8cm，12cm，2cmC.5cm，10cm，4cmD.3cm，3cm，5cm4.2023年9月9日，上海微电子研发的28nm浸没式光刻机的成功问世，标志着我国在光刻机领域迈出了坚实的一步．已知28nm为0.000000028米，数据0.000000028用科学记数法表示为（）A.102.810-⨯ B.82.810-⨯ C.62.810-⨯ D.92.810-⨯5.下列运算正确的是（）A.()1432a a = B.236a a a ⋅= C.()32626a a -=- D.842a a a ÷=6.一个多边形的内角和是外角和的2倍，则这个多边形的边数为（）A.4B.5C.6D.77.下列等式成立的是（）A.22(1)1x x -=- B.22(1)1x x x +=++C.2(1)(1)1x x x +-+=- D.2(1)(1)1x x x -+--=--8.下列说法：①三角形的外角等于两个内角之和；②三角形的重心是三条垂直平分线的交点；③有一个角等于60︒的等腰三角形是等边三角形；④分式的分子与分母乘（或除以）同一个整式，分式的值不变，其中正确的个数有（）A.0个 B.1个 C.2个 D.3个9.如图，在ABC 中，AB AC =，点D ，P 分别是图中所作直线和射线与AB ，CD 的交点．根据图中尺规作图的痕迹推断，以下结论错误的是（）A.PBC ACD ∠=∠B.ABP CBP ∠=∠C.A ACD ∠=∠D.AD CD=10.如图，在ABC 中，90BAC ︒∠=，AD 是高，BE 是中线，CF 是角平分线，CF 交AD 于点G ，交BE 于点H ，给出以下结论：①BE BCE S S =△A △；②AFG AGF ∠=∠；③2FAG ACF ∠=∠；④BH CH =；⑤::AC AF BC BF =．其中结论正确的有（）A.2个B.3个C.4个D.5个二、填空题（本大题共6个小题，每小题3分，共18分）11.因式分解：316y y -=______．12.在平面直角坐标系中，点P (3，﹣2)关于y 轴对称的点的坐标是____．13.若分式211x x --的值为0，则x 的值为______．14.如图，PA OA ⊥，PB OB ⊥，PA PB =，26POB ∠=︒，则APO ∠=________°．15.如图，等边ABC 中，D 为AB 的中点，过点D 作DFAC ⊥于点F ，过点F 作FE BC ⊥于点E ，若4AF =，则线段BE 的长为________．16.如图，在平面直角坐标系中，点()7,0A ，()0,12B ，点C 在AB 的垂直平分线上，且90ACB ∠=︒，则点C 的坐标为________．三、解答题（本大题共9个小题，第17、18、19题每小题6分，第20、21题每小题8分，第22、23题每小逪9分，第24、25题每小题10分，共72分，解答应写出必要的文字说明，证明过程或演算步骤）17.计算：()2202301|3|120243-⎛⎫-+-+- ⎪⎝⎭．18.先化简，再求代数式221122x x x x ⎡⎤-⎛⎫-÷⎢⎥ ⎪++⎝⎭⎢⎥⎣⎦的值，其中2x =．19.如图，在ABC 中，DE 是线段AB 的垂直平分线．（1）若35B ∠=︒．求ADC ∠的度数：（2）若AD CD =．求证：AC AB ⊥．20.如图，在正方形网格中，点A 、B 、C 、M 、N 都在格点上．（1）作△ABC 关于直线MN 对称的图形△A'B'C'；（2）若网格中最小正方形的边长为1，则△ABC 的面积为；（3）点P 在直线MN 上，当△PAC 周长最小时，P 点在什么位置，在图中标出P 点．21.如图，在四边形ABCD 中，AB CD ，连接BD ，点E 在BD 上，连接CE ，若12∠=∠，AB ED =．（1）求证：BD CD =．（2）若13555A BCE ∠=︒∠=︒，，求DBC ∠的度数．22.【阅读理解】若x 满足(32)(12)100x x --=．求()()223212x x -+-的值．解：设32x a -=，12x b -=．则()()3212100x x a b --=⋅=，()()321220a b x x +=-+-=．()()()22222232122202100200x x a b a b ab -+-=+=+-=-⨯=．我们把这种方法叫做换元法．利用换元法达到简化方程的目的．体现了转化的数学思想．【解决问题】（1）若x 满足()()1025x x --=．则()()22102x x -+-=________；（2）若x 满足()()222025202266x x -+-=．求()()20252022x x --的值；（3）如图，在长方形ABCD 中，25cm AB =，点E ，F 是边BC ，CD 上的点，13cm EC =，且cm BE DF x ==．分别以FC ，CB 为边在长方形ABCD 外侧作正方形CFGH 和CBMN ，若长方形CBQF 的面积为2300cm ，求图中阴影部分的面积之和．23.ABC 中，AB AC =，点D 是边AB 上一点，BCD A ∠=∠．（1）如图1，试说明CD CB =的理由；（2）如图2，过点B 作BE AC ⊥，垂足为点E ，BE 与CD 相交于点F ．①试说明2BCD CBE ∠=∠的理由；②如果BDF V 是等腰三角形，求A ∠的度数．24.如图，在平面直角坐标系中，A 点在第二象限、坐标为(,)m m -．（1）若关于x 的多项式24x x m ++是完全平方式，直接写出点A 的坐标：________；（2）如图1，ABO 为等腰直角三角形．分别以AB 和OB 为边作等边ABC 和等边OBD ，连接OC ，AD ；①若4=AD ，求OC 的长；②求COB ∠的度数．（3）如图2，过点A 作AM y ⊥轴于点M ，点E 为x 轴正半轴上一点，K 为ME 延长线上一点，以MK 为直角边作等腰直角三角形MKJ ，90MKJ ∠=︒，过点A 作AN x ⊥轴交MJ 于点N ，连接EN ．试猜想线段AN ，OE 和NE 的数量关系，并证明你的猜想．25.定义：若分式A 与分式B 的差等于它们的积．即A B AB -=，则称分式B 是分式A 的“可存异分式”．如11x +与12x +．因为()()1111212x x x x -=++++，11112(1)(2)x x x x ⨯=++++．所以12x +是11x +的“可存异分式”．（1）填空：分式12x +________分式13x +的“可存异分式”（填“是”或“不是”；）（2）分式4x x -的“可存异分式”是________；（3）已知分式2333x x ++是分式A 的“可存异分式”．①求分式A 的表达式；②若整数x 使得分式A 的值是正整数，直接写出分式A 的值；（4）若关于x 的分式22n mx m n +++是关于x 的分式21m mx n-+的“可存异分式”，求2619534n n ++的值．。