【分析】初二(下)数学压轴题——线段差的最大值

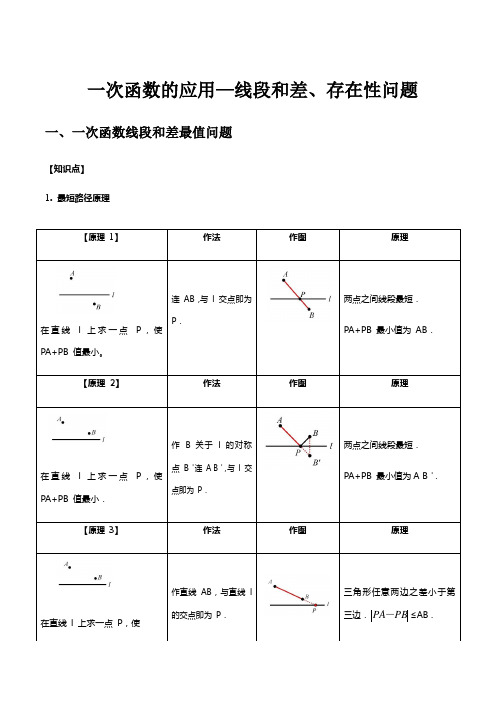
一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P，使PA+PB 值最小。

连AB，与l 交点即为P．两点之间线段最短．PA+PB 最小值为AB．【原理2】作法作图原理在直线l 上求一点P，使PA+PB 值最小．作 B 关于l 的对称点B＇连A B＇，与l 交点即为P．两点之间线段最短．PA+PB 最小值为A B＇．【原理3】作法作图原理在直线l 上求一点P，使作直线AB，与直线l的交点即为P．三角形任意两边之差小于第三边．≤AB .PBPA－（1）求线段和最小时动点坐标或直线解析式； （2）求三角形周长最小值；（3）求线段差最大时点的坐标或直线解析式。

3. 口诀：“和小异，差大同”（一）一次函数线段和最小值问题【例题讲解】★★☆例题1．在平面直角坐标系xOy 中，y 轴上有一点P ，它到点(4,3)A ，(3,1)B 的距离之和最小，则点P 的坐标是( ) A ．(0,0)B ．4(0,)7C ．5(0,)7D ．4(0,)5【答案】C的值最大 .【原理 4】作法作图原理在直线 l 上求一点 P ，使的值最大 .作 B 关于 l 的对称点 B ＇作直线 A B ＇，与 l 交点即为 P ．三角形任意两边之差小于第三边．≤A B ＇ .PB PA －PB PA －PB PA －【解析】解：作A 关于y 轴的对称点C ，连接BC 交y 轴于P ，则此时AP PB +最小，即此时点P 到点A 和点B 的距离之和最小，(4,3)A ，(4,3)C ∴-，设直线CB 的解析式是y kx b =+，把C 、B 的坐标代入得：3413k bk b =-+⎧⎨-=+⎩，解得：47k =-，57b =，4577y x ∴=-+，把0x =代入得：57y =， 即P 的坐标是5(0,)7，故选：C ．【备注】本题考查了轴对称-最短路线问题，一次函数的解析式，坐标与图形性质等知识点，关键是能画出P 的位置，题目比较典型，是一道比较好的题目．★★☆练习1．如图，在平面直角坐标系中，已知点(2,3)A ，点(2,1)B -，在x 轴上存在点P 到A ，B 两点的距离之和最小，则P 点的坐标是 ．【答案】(1,0)-【解析】解：作A 关于x 轴的对称点C ，连接BC 交x 轴于P ，则此时AP BP +最小，A 点的坐标为(2,3)，B 点的坐标为(2,1)-，(2,3)C ∴-，设直线BC 的解析式是：y kx b =+，把B 、C 的坐标代入得：2123k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩．即直线BC 的解析式是1y x =--，当0y =时，10x --=，解得：1x =-，P ∴点的坐标是(1,0)-．故答案为：(1,0)-．【备注】本题考查了一次函数图象上点的坐标特征，用待定系数法求一次函数的解析式，轴对称-最短路线问题的应用，关键是能找出P 点，题目具有一定的代表性，难度适中．★★☆练习2．如图，直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，以线段AB 为边在第一象限内作正方形ABCD ．若点P 为x 轴上的一个动点，求当PC PD +的长最小时点P 的坐标．【答案】详见解析【解析】解：直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，则点A 、B 的坐标分别为：(0,3)，(4,0)，如图所示，过点C 作CH x ⊥轴交于点H ，90ABO BAO ∠+∠=︒，90ABO CBH ∠+∠=︒，CBH BAO ∴∠=∠，又90AOB CHB ∠=∠=︒，AB BC =，()AOB BHC AAS ∴∆≅∆，4CH OB ∴==，3HB OA ==，故点(7,4)C ，同理可得点(3,7)D ，确定点C 关于x 轴的对称点(7,4)C '-，连接C D '交x 轴于点P ，则此时PC PD +的长最小，将点C '、D 的坐标代入一次函数表达式并解得： 直线CD 的表达式为：116144y x =-+， 当0y =时，6111x =，故点61P，0)．(11【备注】本题考查的是一次函数上坐标点的特征，涉及到点的对称性、正方形性质等，本题的难点在于：通过证明三角形全等，确定点C、D的坐标．★★☆例题2．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，3OB=，D为边OB的中点，若E为x轴上的一个动点，当CDE∆的周长最小时，求点E OA=，4的坐标()A．(3,0)-B．(1,0)C．(0,0)D．(3,0)【答案】B【解析】解：如图，作点D关于x轴的对称点D'，连接CD'与x轴交于点E，连接DE．若在边OA上任取点E'与点E不重合，连接CE'、DE'、D E''由DE CE D E CE CD D E CE DE CE'+'=''+'>'='+=+，可知CDE∆的周长最小．OB=，D为边OB的中点，42∴=，OD∴，(0,2)D在矩形OACB 中，3OA =，4OB =，D 为OB 的中点，3BC ∴=，2D O DO '==，6D B '=，//OE BC ，Rt ∴△D OE Rt '∽△D BC '，∴OE D OBC D B '=' 即236OE = 1OE =，∴点E 的坐标为(1,0)故选：B ．【备注】此题主要考查轴对称--最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是三角形两边之和大于第三边．★★☆练习1．如图，在平面直角坐标系中，点A 、B 的坐标分别为(1,4)和(3,0)，点C 是y 轴上的一个动点，连接AC 、BC ，当ABC ∆的周长最小值时，ABC ∆的面积为 ．【答案】3【解析】解：如图，作点A 关于y 轴的对称点A '，连接A B '交y 轴于点C '，此时ABC ∆'的周长最小，设直线A B ' 的解析式为y kx b =+，(1,4)A '-，(3,0)B ，∴430k b k b -+=⎧⎨+=⎩，1k ∴=-，3b =，∴直线A B ' 的解析式为3y x =-+，当0x =时，3y =，(0,3)C ∴'，ABC AA BAA C S SS∆'''∴=-11242122=⨯⨯-⨯⨯ 413=-=．所以ABC ∆'的面积为3．故答案为：3．【备注】本题考查了轴对称、最短路线问题、坐标与图形性质、三角形的面积，解决本题的关键是掌握轴对称的性质．★★☆练习2．如图，在平面直角坐标系中，直线122y x =+与x 轴、y 轴分别交于A 、B 两点，以AB 为边 在第二象限内作正方形ABCD ．（1）求点A 、B 的坐标，并求边AB 的长；（2）求点C 和点D 的坐标；（3）在x 轴上找一点M ，使MDB ∆的周长最小，请求出M 点的坐标，并直接写出MDB ∆的周长最小值．【答案】详见解析【解析】解： （1）对于直线122y x =+， 令0x =，得到2y =；令0y =，得到4x =-，(4,0)A ∴-，(0,2)B ，即4OA =，2OB =， 则224225AB =+=；（2）过D 作DE x ⊥轴，过C 作CF y ⊥轴，四边形ABCD 为正方形，AB BC AD ∴==，90ABC BAD BFC DEA AOB ∠=∠=∠=∠=∠=︒，90FBC ABO ∠+∠=︒，90ABO BAO ∠+∠=︒，90DAE BAO ∠+∠=︒，FBC OAB EDA ∴∠=∠=∠，()DEA AOB BFC AAS ∴∆≅∆≅∆，2AE OB CF ∴===，4DE OA FB ===，即426OE OA AE =+=+=，246OF OB BF =+=+=，则(6,4)D -，(2,6)C -；（3）如图所示，连接BD ，找出B 关于y 轴的对称点B '，连接DB '，交x 轴于点M ，此时BM MD DM MB DB +=+'='最小，即BDM ∆周长最小，(0,2)B ，(0,2)B ∴'-，设直线DB '解析式为y kx b =+，把(6,4)D -，(0,2)B '-代入得：642k b b -+=⎧⎨=-⎩，解得：1k =-，2b =-，∴直线DB '解析式为2y x =--，令0y =，得到2x =-，则M 坐标为(2,0)-， 此时MDB ∆的周长为21062+．【备注】本题属于一次函数综合题，涉及的知识有：待定系数法求一次函数解析式，坐标与图形性质，勾 股定理，全等三角形的判定与性质，正方形的性质，对称性质，以及一次函数与坐标轴的交点，熟练掌握 性质及定理是解本题的关键（二）一次函数线段差最大值问题【例题讲解】★★☆例题1．已知，如图点(1,1)A ，(2,3)B -，点P 为x 轴上一点，当||PA PB -最大时，点P的坐标为( )A ．1(,0)2B ．5(,0)4C ．1(,0)2-D ．(1,0)【答案】A【解析】解：作A 关于x 轴对称点C ，连接BC 并延长交x 轴于点P ， (1,1)A ，C ∴的坐标为(1,1)-，连接BC ，设直线BC 的解析式为：y kx b =+，∴123k b k b +=-⎧⎨+=-⎩， 解得：21k b =-⎧⎨=⎩， ∴直线BC 的解析式为：21y x =-+， 当0y =时，12x =， ∴点P 的坐标为：1(2，0)，当B ，C ，P 不共线时，根据三角形三边的关系可得：||||PA PB PC PB BC -=-<，∴此时||||PA PB PC PB BC -=-=取得最大值．故选：A ．【备注】此题考查了轴对称、待定系数法求一次函数的解析式以及点与一次函数的关系．此题难度较大，解题的关键是找到P 点，注意数形结合思想与方程思想的应用．★★☆练习1．平面直角坐标系中，已知(4,3)A 、(2,1)B ，x 轴上有一点P ，要使PA PB -最大，则P 点坐 标为【答案】(1,0)【解析】解：(4,3)A 、(2,1)B ，x 轴上有一点P ，||PA PB AB ∴-，∴当A ，B ，P 三点共线时，PA PB -最大值等于AB 长，此时，设直线AB 的解析式为y kx b =+，把(4,3)A 、(2,1)B 代入，可得3412k b k b =+⎧⎨=+⎩， 解得11k b =⎧⎨=-⎩， ∴直线AB 的解析式为1y x =-，令0y =，则1x =，P ∴点坐标为(1,0)，故答案为：(1,0)． 【备注】本题主要考查了坐标与图形性质，利用待定系数法求得直线AB 的解析式是解决问题的关键． ★★☆练习2．如图，在平面直角坐标系中，点A 的坐标为(0,4)，点B 的坐标为(6,0)，点P 在一次函数1322y x =+的图象上运动，则PB PA -的最大值为( )A ．2B ．233C ．4D ．143【答案】C【解析】解：如图，作点A 关于直线1322y x =+的对称点K ，连接AK 交直线于H ，连接PK ．AK PH ⊥，(0,4)A ，∴直线AK 的解析式为24y x =-+，由132224y x y x ⎧=+⎪⎨⎪=-+⎩，解得12x y =⎧⎨=⎩， (1H ∴，20，AH KH =，(2,0)K ∴．PB PA PB PK KB ∴-=-，∴当点P 在BK 的延长线上时，P B P K BK '-'=的值最大，最大值为624-=，故选：C ．【备注】本题考查一次函数图象上的点的特征、轴对称等知识，解题的关键是学会利用对称解决最值问题 属于中考常考题型．【题型知识点总结】一次函数最短路径问题注意事项：1. 根据“和小异，差大同”判断是否需要作对称；2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。

中考数学方法、技巧9-二次函数中的最值问题题型分析
题型一【铅垂高系列】
中考高频考点，常常考在压轴题部分，最常见以考查面积的最值为考点，做法常常作铅锤高，利用坐标法构造面积的二次函数，求得面积最值.
题型二【线段和差最值篇】
中考高频考点，常常考查将军饮马，和的最小值（利用两边之和大于第三边求解），或者线段差的最大值（利用三角形两边之差小于第三边来求解）；还有期间涉及到的隐圆问题，也和最值有关。

题型三【构造二次函数模型求最值】
设坐标，构造二次函数，也叫做设坐标法。

题型四【加权线段最值】
利用阿氏圆或者胡不归模型（以上内容公众号中都有的哦），将加权线段进行转化，进而求得最值。

题型五【几何构造最值篇】
几何构造常考于特殊的边和角度时，利用构造特殊图形进行求解。

专题13 几何中的最值与定值问题【类型综述】线段和差的最值问题，常见的有两类：第一类问题是“两点之间，线段最短”．两条动线段的和的最小值问题，常见的是典型的“牛喝水”问题，关键是指出一条对称轴“河流”第二类问题是“两点之间，线段最短”结合“垂线段最短”．【方法揭秘】两条动线段的和的最小值问题，常见的是典型的“牛喝水”问题，关键是指出一条对称轴“河流”（如图1）．三条动线段的和的最小值问题，常见的是典型的“台球两次碰壁”或“光的两次反射”问题，关键是指出两条对称轴“反射镜面”（如图2）．两条线段差的最大值问题，一般根据三角形的两边之差小于第三边，当三点共线时，两条线段差的最大值就是第三边的长．如图3，P A与PB的差的最大值就是AB，此时点P在AB的延长线上，即P′．解决线段和差的最值问题，有时候求函数的最值更方便，本讲不涉及函数最值问题．图1 图2 图3如图4，正方形ABCD的边长为4，AE平分∠BAC交BC于E．点P在AE上，点Q在AB上，那么△BPQ 周长的最小值是多少呢？如果把这个问题看作“牛喝水”问题，AE是河流，但是点Q不确定啊．第一步，应用“两点之间，线段最短”．如图5，设点B关于“河流AE”的对称点为F，那么此刻PF＋PQ 的最小值是线段FQ．第二步，应用“垂线段最短”．如图6，在点Q运动过程中，FQ的最小值是垂线段FH．这样，因为点B和河流是确定的，所以点F是确定的，于是垂线段FH也是确定的．图4 图5 图6【典例分析】例1 如图1，二次函数y ＝a (x 2－2mx －3m 2)（其中a 、m 是常数，且a ＞0，m ＞0）的图像与x 轴分别交于A 、B （点A 位于点B 的左侧），与y 轴交于点C (0,－3)，点D 在二次函数的图像上，CD //AB ，联结AD ．过点A 作射线AE 交二次函数的图像于点E ，AB 平分∠DAE ． （1）用含m 的式子表示a ； （2）求证：AD AE为定值；（3）设该二次函数的图像的顶点为F ．探索：在x 轴的负半轴上是否存在点G ，联结GF ，以线段GF 、AD 、AE 的长度为三边长的三角形是直角三角形？如果存在，只要找出一个满足要求的点G 即可，并用含m 的代数式表示该点的横坐标；如果不存在，请说明理由．图1例2如图1，已知抛物线的方程C 1：1(2)()y x x m m=-+- (m ＞0)与x 轴交于点B 、C ，与y 轴交于点E ，且点B 在点C 的左侧．（1）若抛物线C 1过点M (2, 2)，求实数m 的值； （2）在（1）的条件下，求△BCE 的面积；（3）在（1）的条件下，在抛物线的对称轴上找一点H ，使得BH ＋EH 最小，求出点H 的坐标； （4）在第四象限内，抛物线C 1上是否存在点F ，使得以点B 、C 、F 为顶点的三角形与△BCE 相似？若存在，求m 的值；若不存在，请说明理由．图1例3 如图1，抛物线y ＝ax 2＋bx ＋c 经过A (－1,0)、B (3, 0)、C (0 ,3)三点，直线l 是抛物线的对称轴． （1）求抛物线的函数关系式；（2）设点P 是直线l 上的一个动点，当△P AC 的周长最小时，求点P 的坐标；图1例4如图1，已知A 、B 是线段MN 上的两点，4=MN ，1=MA ，1>MB ．以A 为中心顺时针旋转点M ，以B 为中心逆时针旋转点N ，使M 、N 两点重合成一点C ，构成△ABC ，设x AB =． （1）求x 的取值范围；（2）若△ABC 为直角三角形，求x 的值； （3）探究：△ABC 的最大面积？图1例5如图1，在平面直角坐标系中，抛物线y ＝ax 2－2ax －3a （a ＜0）与x 轴交于A 、B 两点（点A 在点B 的左侧），经过点A 的直线l ：y ＝kx ＋b 与y 轴负半轴交于点C ，与抛物线的另一个交点为D ，且CD ＝4AC ． （1）直接写出点A 的坐标，并求直线l 的函数表达式（其中k 、b 用含a 的式子表示）； （2）点E 是直线l 上方的抛物线上的动点，若△ACE 的面积的最大值为 54 ，求a 的值；（3）设P 是抛物线的对称轴上的一点，点Q 在抛物线上，以点A 、D 、P 、Q 为顶点的四边形能否成为矩形？若能，求出点P 的坐标；若不能，请说明理由．图1 备用图【变式训练】一、单选题1．如图，AB为⊙O的直径，C为⊙O上一点，其中AB=4，∠AOC=120°，P为⊙O上的动点，连AP，取AP中点Q，连CQ，则线段CQ的最大值为（）A．3B．1+C．1+3D．1+2．如图，已知，以为圆心，长为半径作，是上一个动点，直线交轴于点，则面积的最大值是（）A．B．C．D．3．如图，矩形ABCD 中，AB＝4，AD＝3，P 是边CD 上一点，将△ADP沿直线AP对折，得到△APQ．当射线BQ交线段CD于点F时，DF的最大值是（）A．3B．2C．47--D．454．如图，由两个长为，宽为的全等矩形叠合而得到四边形，则四边形面积的最大值是（）A．15B．16C．19D．205．如图，在△ABC中，AB＝AC＝5，BC＝6，AD⊥BC于D，点E，F分别在AD，AB是，则BE＋EF的最小值是A．4B．4.8C．5D．5.46．如图，在菱形ABCD中，AB=6，∠A=135°，点P是菱形内部一点，且满足，则PC+PD 的最小值为（）A．B．C．6 D．7．在Rt△ABC中，∠ACB=90°，AC=4，BC=8，D，E是AB和BC上的动点，连接CD，DE则CD+DE的最小值为（）A．8B．C．D．二、解答题8．问题发现：（）如图①，中，，，，点是边上任意一点，则的最小值为__________．（）如图②，矩形中，，，点、点分别在、上，求的最小值．（）如图③，矩形中，，，点是边上一点，且，点是边上的任意一点，把沿翻折，点的对应点为点，连接、，四边形的面积是否存在最小值，若存在，求这个最小值及此时的长度；若不存在，请说明理由．9．问题提出：如图1，在Rt△AB C中，∠ACB=90°，CB=4，CA=6，⊙C半径为2，P为圆上一动点，连结AP、BP，求AP+BP的最小值．（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB上取点D，使CD=1，则有，又∵∠PCD=∠BCP，∴△PCD∽△BCP．∴，∴PD=BP，∴AP+BP=AP+PD．请你完成余下的思考，并直接写出答案：AP+BP的最小值为．（2）自主探索：在“问题提出”的条件不变的情况下，AP+BP的最小值为．（3）拓展延伸：已知扇形COD中，∠COD=90°，OC=6，OA=3，OB=5，点P是上一点，求2PA+PB的最小值．10．已知二次函数y=x2+2bx+c（b、c为常数）．（Ⅰ）当b=1，c=﹣3时，求二次函数在﹣2≤x≤2上的最小值；（Ⅱ）当c=3时，求二次函数在0≤x≤4上的最小值；（Ⅲ）当c=4b2时，若在自变量x的值满足2b≤x≤2b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式．11．已知四边形ABCD，AD∥BC，AB⊥BC，AD=1，AB=2，BC=3．（1）如图1，若P 为AB 边上一点以PD ，PC 为边作平行四边形PCQD ，请问对角线PQ 的长是否存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．（2）若P 为AB 边上任意一点，延长PD 到E ，使DE=PD ，再以PE ，PC 为边作平行四边形PCQE ，请问对角线PQ 的长是否也存在最小值？如果存在，请直接写出最小值，如果不存在，请说明理由．（3）如图2，若P 为直线DC 上任意一点，延长PA 到E ，使AE=AP ，以PE 、PB 为边作平行四边形PBQE ，请问对角线PQ 的长是否存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．12．（本题满分12分）（1）【问题】如图1，点A 为线段BC 外一动点，且BC a =， 6AB =．当点A 位于__________时线段AC 的长取得最大值，且最大值为__________（用含a 、b 的式子表示）．（2）【应用】点A 为线段B 除外一动点，且3BC =， 1AB =．如图2所示，分别以AB 、AC 为边， 作等边三角形ABD 和等边三角形ACE ，连接CD 、BE ． ①请找出图中与BE 相等的线段，并说明理由． ②直接写出线段BE 长的最大值．（3）【拓展】如图3，在平面直角坐标系中，点A 的坐标为()2,0，点B 的坐标为()5,0，点P 为线段AB 外一动点，且2PA =， PM PB =， 90BPM ∠=︒．请直接写出线段AM 长的最大值及此时点P 的坐标．13．如图，已知中，，边上的高，四边形为内接矩形．当矩形是正方形时，求正方形的边长．设，矩形的面积为，求关于的函数关系式，当为何值时有最大值，并求出最大值．14．如图，抛物线与坐标轴相交于、、三点，是线段上一动点（端点除外），过作，交于点，连接．直接写出、、的坐标；求抛物线的对称轴和顶点坐标；求面积的最大值，并判断当的面积取最大值时，以、为邻边的平行四边形是否为菱形．15．如图，抛物线过O、A、B三点，A（4,0）B（1，-3），P为抛物线上一点，过点P的直线y=x+m与对称轴交于点Q.（1）直线PQ与x轴所夹锐角的度数，并求出抛物线的解析式.（2）当点P在x轴下方的抛物线上时，过点C(2,2)的直线AC与直线PQ交于点D，求： PD+DQ的最大值；②PD.DQ的最大值.16．问题提出（1）如图1，点A 为线段BC 外一动点，且BC=a ，AB=b ，填空：当点A 位于 时，线段AC 的长取得最大值，且最大值为 （用含a ，b 的式子表示）． 问题探究（2）点A 为线段BC 外一动点，且BC=6，AB=3，如图2所示，分别以AB ，AC 为边，作等边三角形ABD 和等边三角形ACE ，连接CD ，BE ，找出图中与BE 相等的线段，请说明理由，并直接写出线段BE 长的最大值． 问题解决：（3）①如图3，在平面直角坐标系中，点A 的坐标为（2，0），点B 的坐标为（5，0），点P 为线段AB 外一动点，且PA=2，PM=PB ，∠BPM=90°，求线段AM 长的最大值及此时点P 的坐标．②如图4，在四边形ABCD 中，AB=AD ，∠BAD=60°，BC=42，若对角线BD ⊥CD 于点D ，请直接写出对角线AC 的最大值．17．如图14，AB 是O 的直径，,2AC BC AB ==，连接AC ．（1）求证：045CAB ∠=； （2）若直线l 为O 的切线，C 是切点，在直线l 上取一点D ，使,BD AB BD =所在的直线与AC 所在的直线相交于点E ，连接AD ．①试探究AE 与AD 之间的数量关系，并证明你的结论； ②EBCD是否为定值？若是，请求出这个定值；若不是，请说明理由． 18.如图，动点M 在以O 为圆心，AB 为直径的半圆弧上运动（点M 不与点A B 、及AB 的中点F 重合），连接OM .过点M 作ME AB ⊥于点E ，以BE 为边在半圆同侧作正方形BCDE ，过M 点作O 的切线交射线DC 于点N ，连接BM 、BN .（1）探究：如左图，当M 动点在AF 上运动时； ①判断OEM MDN ∆∆是否成立？请说明理由；②设ME NCk MN+=，k 是否为定值？若是，求出该定值，若不是，请说明理由；③设MBN α∠=，α是否为定值？若是，求出该定值，若不是，请说明理由； （2）拓展：如右图，当动点M 在FB 上运动时；分别判断（1）中的三个结论是否保持不变？如有变化，请直接写出正确的结论.（均不必说明理由） 19.已知抛物线32-+=bx x y （b 是常数）经过点)0,1(-A . （1）求该抛物线的解析式和顶点坐标；（2）P(m ，t)为抛物线上的一个动点，P 关于原点的对称点为'P . ①当点'P 落在该抛物线上时，求m 的值；②当点'P 落在第二象限内，2'A P 取得最小值时，求m 的值.20.如图，在平面直角坐标系中，抛物线12++=bx ax y 交y 轴于点A ，交x 轴正半轴于点)0,4(B ，与过A 点的直线相交于另一点)25,3(D ，过点D 作x DC ⊥轴，垂足为C .11（1）求抛物线的表达式；（2）点P 在线段OC 上（不与点O 、C 重合），过P 作x PN ⊥轴，交直线AD 于M ，交抛物线于点N ，连接CM ，求PCM ∆面积的最大值；（3）若P 是x 轴正半轴上的一动点，设OP 的长为，是否存在，使以点N D C M 、、、为顶点的四边形是平行四边形？若存在，求出的值；若不存在，请说明理由.。

专题10二次函数与线段最值定值及数量关系问题图形运动的过程中，求两条线段之间的函数关系，是中考数学的热点问题．产生两条线段间的函数关系，常见的情况有两种，一是勾股定理，二是比例关系．还有一种不常见的，就是线段全长等于部分线段之和．由比例线段产生的函数关系问题，在两种类型的题目中比较常用．一是由平行线产生的对于线段成比例，二是相似三角形的对应边成比例．一般步骤是先说理产生比例关系，再代入数值或表示数的字母，最后整理、变形，根据要求写出定义域．关键是寻找比例关系，难点是有的整理、变形比较繁琐，容易出错．【例1】（2021•沈阳）如图，平面直角坐标系中，O是坐标原点，抛物线y＝﹣x2+bx+c与x轴交于A、B两点（点A在点B的左侧），点B坐标是（3，0）．抛物线与y轴交于点C（0，3），点P是抛物线的顶点，连接PC．（1）求抛物线的函数表达式并直接写出顶点P的坐标．（2）直线BC与抛物线对称轴交于点D，点Q为直线BC上一动点．①当△QAB的面积等于△PCD面积的2倍时，求点Q的坐标；②在①的条件下，当点Q在x轴上方时，过点Q作直线l垂直于AQ，直线y＝x﹣交直线l于点F，点G在直线y＝x﹣上，且AG＝AQ时，请直接写出GF的长．【例2】（2021•滨州）如下列图形所示，在平面直角坐标系中，一个三角板的直角顶点与原点O重合，在其绕原点O旋转的过程中，两直角边所在直线分别与抛物线y＝x2相交于点A、B（点A在点B的左侧）．（1）如图1，若点A、B的横坐标分别为﹣3、，求线段AB中点P的坐标；（2）如图2，若点B的横坐标为4，求线段AB中点P的坐标；（3）如图3，若线段AB中点P的坐标为（x，y），求y关于x的函数解析式；（4）若线段AB中点P的纵坐标为6，求线段AB的长．【例3】（2021•盘锦）如图，抛物线y＝﹣x2+2x+6与x轴交于A，B两点（点A在点B的左侧），与y 轴交于点C，直线y＝x﹣2与y轴交于点D，与x轴交于点E，与直线BC交于点F．（1）点F的坐标为；（2）如图1，点P为第一象限抛物线上的一点，PF的延长线交OB于点Q，PM⊥BC于点M，QN⊥BC于点N，若＝，求点P的坐标；（3）如图2，点S为第一象限抛物线上的一点，且点S在射线DE上方，动点G从点E出发，沿射线DE方向以每秒4个单位长度的速度运动，当SE＝SG，且tan∠SEG＝时，求点G的运动时间t．【例4】（2021•巴中）已知抛物线y＝ax2+bx+c与x轴交于A（﹣2，0）、B（6，0）两点，与y轴交于点C （0，﹣3）．（1）求抛物线的表达式；（2）点P在直线BC下方的抛物线上，连接AP交BC于点M，当最大时，求点P的坐标及的最大值；（3）在（2）的条件下，过点P作x轴的垂线l，在l上是否存在点D，使△BCD是直角三角形，若存在，请直接写出点D的坐标；若不存在，请说明理由．【例5】（2020•孝感）在平面直角坐标系中，已知抛物线y＝ax2+4ax+4a﹣6（a＞0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为点D．（1）当a＝6时，直接写出点A，B，C，D的坐标：A，B，C，D；（2）如图1，直线DC交x轴于点E，若tan∠AED=43，求a的值和CE的长；（3）如图2，在（2）的条件下，若点N为OC的中点，动点P在第三象限的抛物线上，过点P作x 轴的垂线，垂足为Q，交AN于点F；过点F作FH⊥DE，垂足为H．设点P的横坐标为t，记f＝FP+FH．①用含t的代数式表示f；②设﹣5＜t≤m（m＜0），求f的最大值．【例6】（2020•恩施州）如图1，抛物线y=−14x2+bx+c经过点C（6，0），顶点为B，对称轴x＝2与x轴相交于点A，D为线段BC的中点．（1）求抛物线的解析式；（2）P为线段BC上任意一点，M为x轴上一动点，连接MP，以点M为中心，将△MPC逆时针旋转90°，记点P的对应点为E，点C的对应点为F．当直线EF与抛物线y=−14x2+bx+c只有一个交点时，求点M的坐标．（3）△MPC在（2）的旋转变换下，若PC=2（如图2）．①求证：EA＝ED．②当点E在（1）所求的抛物线上时，求线段CM的长．【题组一】1．（2021•青山区模拟）已知抛物线y＝ax2﹣4ax﹣12a与x轴相交于A，B两点，与y轴交于C点，且OC ＝OA．设抛物线的顶点为M，对称轴交x轴于点N．（1）求抛物线的解析式；（2）如图1，点E（m，n）为抛物线上的一点，且0＜m＜6，连接AE，交对称轴于点P．点F为线段BC上一动点，连接EF，当PA＝2PE时，求EF+BF的最小值．（3）如图2，过点M作MQ⊥CM，交x轴于点Q，将线段CQ向上平移t个单位长度，使得线段CQ 与抛物线有两个交点，求t的取值范围．2．（2021•赣州模拟）已知抛物线C1：y＝x2﹣4x+3m和C2：y＝mx2﹣4mx+3m，其中m≠0且m≠1．（1）抛物线C1的对称轴是，抛物线C2的对称轴是；（2）这两条抛物线相交于点E，F（点E在点F的左侧），求E、F两点的坐标（用含m的代数式表示）并直接写出直线EF与x轴的位置关系；（3）设抛物线C1的顶点为M，C2的顶点为N；①当m为何值时，点M与点N关于直线EF对称？②是否存在实数m，使得MN＝2EF？若存在，直接写出实数m的值，若不存在，请说明理由．3．（2021•桓台县二模）在平面直角坐标系中，抛物线y＝x2+bx+c交x轴于A，B两点，点A，B的坐标分别为（﹣1，0），（3，0），点M为顶点．（1）求抛物线的解析式；（2）过点M作y轴的垂线，垂足为C，过点B作y轴的平行线，交CM于点D，点H为OC上的任一点，将线段HB绕点H逆时针旋转90°到HP．求∠PCD的度数；（3）在（2）的条件下，将点H改为y轴上的一动点，连接OP，BP，求OP+BP的最小值．4．（2021•成都模拟）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）求抛物线的解析式．（2）点D为第一象限内抛物线上的一动点，作DE⊥x轴于点E，交BC于点F，过点F作BC的垂线与抛物线的对称轴和y轴分别交于点G，H，设点D的横坐标为m．①求DF+HF的最大值；②连接EG，若∠GEH＝45°，求m的值．【题组二】5．（2021•攸县模拟）材料：对抛物线，定义：点叫做该抛物线的焦点，直线叫做该抛物线的准线，且该抛物线上任意一点到焦点的距离与它到准线的距离相等．运用上述材料解决如下问题：如图所示，已知抛物线C：y＝ax2﹣4ax的图象与x轴交于O、A两点，且过点．（1）求抛物线C的解析式和点A的坐标；（2）若将抛物线C的图象先向左平移2个单位，再向上平移1个单位得到抛物线C'的图象．①求抛物线C'的焦点坐标和准线方程．②设M为抛物线C'位于第一象限内图象上的任意一点，MN⊥x轴于点N，求MN+MA的最小值，并求出取得这个最小值时点M的坐标．6．（2021•南沙区一模）已知，抛物线y＝mx2+x﹣4m与x轴交于点A（﹣4，0）和点B，与y轴交于点C．点D（n，0）为x轴上一动点，且有﹣4＜n＜0，过点D作直线l⊥x轴，且与直线AC交于点M，与抛物线交于点N，过点N作NP⊥AC于点P．点E在第三象限内，且有OE＝OD．（1）求m的值和直线AC的解析式．（2）若点D在运动过程中，AD+CD取得最小值时，求此时n的值．（3）若△ADM的周长与△MNP的周长的比为5：6时，求AE+CE的最小值．7．（2021•宝安区模拟）（1）已知二次函数经过点A（﹣3，0）、B（1，0）、C（0，3），请求该抛物线解析式；（2）点M为抛物线上第二象限内一动点，BM交y轴于点N，当BM将四边形ABCM的面积分为1：2两部分时，求点M的坐标；（3）点P为对称轴上D点下方一动点，点Q为直线y＝x第一象限上的动点，且DP＝OQ，求BP+BQ 的最小值并求此时点P的坐标．8．（2021•茶陵县模拟）如图，在平面直角坐标系中，抛物线y＝ax2+bx+3（a≠0）与x轴交于点A（﹣1，0）、B（3，0），与y轴交于点C，点P是直线BC上方抛物线上的动点．（1）求抛物线的解析式；（2）如图①，连接BC与OP，交于点D，求当的值最大时点P的坐标；（3）如图②，过点P作PD∥AC交x轴于点D，交BC于点E，求BE的最大值及点P的坐标．【题组三】9．（2021•东莞市校级一模）如图，抛物线y＝ax2+bx+3与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于C点，抛物线的对称轴l与x轴交于M点．（1）求抛物线的函数解析式；（2）设点P是直线l上的一个动点，当PA+PC的值最小时，求PA+PC长；（3）已知点N（0，﹣1），在y轴上是否存在点Q，使以M、N、Q为顶点的三角形与△BCM相似？若存在，请求出点Q的坐标；若不存在，请说明理由．10．（2021•怀化模拟）如图，已知抛物线y＝ax2+bx+3的对称轴是直线x＝1，与x轴交于点A、B，与y 轴交于点C，其中点A的坐标是（﹣1，0）．（1）直接写出点B的坐标并求出抛物线的解析式；（2）点P是抛物线上的一个动点．①当∠PCB＝∠OCB时，求点P的坐标；②当点P在B、C两点之间运动时，连接AP，交BC于点Q，设t＝，求当t值最大时点P的坐标．11．（2021•罗湖区三模）如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）直接写出抛物线的解析式：；（2）点D为第一象限内抛物线上的一动点，作DE⊥x轴于点E，交BC于点F，过点F作BC的垂线与抛物线的对称轴和y轴交于点G、H，设点D的横坐标为m．①求DF+HF的最大值；②连接EG，若∠GEH＝45°时，求m的值．12．（2021•南海区二模）如图1，抛物线y＝x2+bx+c与x轴交于A、B两点，点A、B分别位于原点左、右两侧，且AO＝2BO＝4，过A点的直线y＝kx+c交y轴于点C．（1）求k、b、c的值；（2）在抛物线的对称轴上是否存在一点P，使△ACP为直角三角形？若存在，直接写出所有满足条件的点的坐标；若不存在，请说明理由；（3）如图2，点M为线段AC上一点，连接OM，求AM+OM的最小值．【题组四】13．（2020•西宁二模）如图，在平面直角坐标系中，已知抛物线y＝ax2+bx+c与x轴交于A（5，0），B（﹣1，0）两点，与y轴交于点C（0，52）．（1）求抛物线的解析式；（2）若点M是抛物线的顶点，连接AM，CM，求△AMC的面积；（3）若点P是抛物线上的一个动点，过点P作PE垂直y轴于点E，交直线AC于点D，过点D作x 轴的垂线，垂足为点F，连接EF，当线段EF的长度最短时，求出点P的坐标．14．（2020•涡阳县一模）如图，抛物线y＝ax2+bx+c（a≠0）与直线y＝x+1相交于A（﹣1，0），B（4，m）两点，且抛物线经过点C（5，0）．（1）求抛物线的解析式．（2）点P是直线上方的抛物线上的一个动点，求△ABP的面积最大时的P点坐标．（3）若点P是抛物线上的一个动点（不与点A点B重合），过点P作直线PD⊥x轴于点D，交直线AB 于点E．当PE＝2ED时，求P点坐标；（4）设抛物线与y轴交于点F，在抛物线的第一象限内，是否存在一点M，使得AM被FC平分？若存在，请求出点M的坐标；若不存在，说明理由．15．（2020•哈尔滨模拟）如图，抛物线y＝ax2+bx+5经过坐标轴上A、B和C三点，连接AC，tan C=355OA＝3OB．（1）求抛物线的解析式；（2）点Q在第四象限的抛物线上且横坐标为t，连接BQ交y轴于点E，连接CQ、CB，△BCQ的面积为S，求S与t的函数解析式；（3）已知点D是抛物线的顶点，连接CQ，DH所在直线是抛物线的对称轴，连接QH，若∠BQC＝45°，HR∥x轴交抛物线于点R，HQ＝HR，求点R的坐标．16．（2020•皇姑区校级一模）如图，在平面直角坐标系中，抛物线y=−12x2+bx+c与x轴交于点A，B，其中点B的坐标为（4，0），与y轴交于点C（0，2）．（1）求抛物线y=−122+bx+c和直线BC的函数表达式；（2）点P是直线BC上方的抛物线上一个动点，当点P到直线BC的距离最大时，求点P的坐标；（3）连接点O与（2）中求出的点P，交直线BC于点D，点N是直线BC上的一个动点，连接ON，作DF⊥ON于点F，点F在线段ON上，当OD=5DF时，请直接写出点N的坐标．【题组五】17．（2020•岳阳二模）如图，已知抛物线y＝x2+bx+c与x轴相交于A（﹣1，0），B（m，0）两点，与y 轴相交于点C（0，﹣3），抛物线的顶点为D．（1）求抛物线的解析式；（2）若点E在x轴上，且∠ECB＝∠CBD，求点E的坐标．（3）若P是直线BC下方抛物线上任意一点，过点P作PH⊥x轴于点H，与BC交于点M．①求线段PM长度的最大值．②在①的条件下，若F为y轴上一动点，求PH+HF的最小值．18．（2020•白云区模拟）如图，抛物线y＝x2+bx+c交x轴于点A，B两点，OA＝1，与y轴交于点C，连接AC，tan∠OAC＝3，抛物线的对称轴与x轴交于点D．（1）求点A，C的坐标；（2）若点P在抛物线上，且满足∠PAB＝2∠ACO，求直线PA在与y轴交点的坐标；（3）点Q在抛物线上，且在x轴下方，直线AQ，BQ分别交抛物线的对称轴于点M、N．求证：DM+DN 为定值，并求出这个定值．19．（2020•福安市校级模拟）已知，抛物线y＝ax2，其中a＞0．（1）如图1，若点A、B是此抛物线上两点，且分属于y轴两侧，连接AB与y轴相交于点C，且∠AOB ＝90°．求证：CO=1；（2）如图2，若点A是此抛物线上一点，过点A的直线恰好与此抛物线仅有一个交点，且与y轴交于点B，与x轴相交于点C．求证：AC＝BC．20．（2020•德城区一模）已知，在以O为原点的直角坐标系中，抛物线的顶点为A（﹣1，﹣4），且经过点B（﹣2，﹣3），与x轴分别交于C、D两点．（1）求直线OB以及该抛物线相应的函数表达式；（2）如图1，点M是抛物线上的一个动点，且在直线OB的下方，过点M作x轴的平行线与直线OB 交于点N，求MN的最大值；（3）如图2，过点A的直线交x轴于点E，且AE∥y轴，点P是抛物线上A、D之间的一个动点，直线PC、PD与AE分别交于F、G两点．当点P运动时，EF+EG是否为定值？若是，试求出该定值；若不是，请说明理由．【题组六】21．（2020•青山区模拟）如图，在平面直角坐标系xOy中，一次函数y=54x+m（m为常数）的图象与x轴交于点A（﹣3，0），与y轴交于点C，以直线x＝1为对称轴的抛物线y＝ax2+bx+c（a、b、c为常数，且a≠0）经过A、C两点，并与x轴的正半轴交于点B（1）求m的值及抛物线的函数表达式；（2）是否存在抛物线上一动点Q，使得△ACQ是以AC为直角边的直角三角形？若存在，求出点Q的横坐标；若存在，请说明理由；（3）若P是抛物线对称轴上一动点，且使△ACP周长最小，过点P任意作一条与y轴不平行的直线交抛物线于M1（x1，y1），M2（x2，y2）两点，试问1δ212是否为定值，如果是，请求出结果，如果不是请说明理由．（参考公式：在平面直角坐标系中，若A（x1，y1），B（x2，y2），则A，B两点间的距离为AB=(1−2)2+(1−2)2）22．（2020•新都区模拟）已知：在平面直角坐标系中，抛物线y＝ax2﹣2ax+4（a＜0）交x轴于点A、B，与y轴交于点C，AB＝6．（1）如图1，求抛物线的解析式；（2）如图2，点R为第一象限的抛物线上一点，分别连接RB、RC，设△RBC的面积为s，点R的横坐标为t，求s与t的函数关系式；（3）在（2）的条件下，如图3，点D在x轴的负半轴上，点F在y轴的正半轴上，点E为OB上一点，点P为第一象限内一点，连接PD、EF，PD交OC于点G，DG＝EF，PD⊥EF，连接PE，∠PEF＝2∠PDE，连接PB、PC，过点R作RT⊥OB于点T，交PC于点S，若点P在BT的垂直平分线上，OB ﹣TS=23，求点R的坐标．23．（2020•自贡）在平面直角坐标系中，抛物线y＝ax2+bx+3与x轴交于点A（﹣3，0）、B（1，0），交y 轴于点N，点M为抛物线的顶点，对称轴与x轴交于点C．（1）求抛物线的解析式；（2）如图1，连接AM，点E是线段AM上方抛物线上一动点，EF⊥AM于点F，过点E作EH⊥x轴于点H，交AM于点D．点P是y轴上一动点，当EF取最大值时：①求PD+PC的最小值；②如图2，Q点为y轴上一动点，请直接写出DQ+14OQ的最小值．24．（2020•凉山州）如图，二次函数y＝ax2+bx+c的图象过O（0，0）、A（1，0）、B（32，32）三点．（1）求二次函数的解析式；（2）若线段OB的垂直平分线与y轴交于点C，与二次函数的图象在x轴上方的部分相交于点D，求直线CD的解析式；（3）在直线CD下方的二次函数的图象上有一动点P，过点P作PQ⊥x轴，交直线CD于Q，当线段PQ的长最大时，求点P的坐标．。

2021年八下期中考试金牌压轴题训练（三）（时间：60分钟总分：100）班级姓名得分一、单选题1．将图1中周长为32的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形，并将它们按图2的方式放入周长为48的长方形中，则没有覆盖的阴影部分的周长为（）A．16B．24C．30D．40【答案】D【分析】设1号正方形的边长为x，2号正方形的边长为y，则3号正方形的边长为x+y，4号正方形的边长为2x+y，5号长方形的长为3x+y，宽为y-x，根据图1中长方形的周长为32，求得x+y=4，根据图2中长方形的周长为48，求得AB=24-3x-4y，根据平移得：没有覆盖的阴影部分的周长为四边形ABCD的周长=2（AB+AD），计算即可得到答案．【详解】设1号正方形的边长为x，2号正方形的边长为y，则3号正方形的边长为x+y，4号正方形的边长为2x+y，5号长方形的长为3x+y，宽为y-x，由图1中长方形的周长为32，可得，y+2（x+y）+（2x+y）=16，解得：x+y=4，如图，∵图2中长方形的周长为48，∵AB+2（x+y）+2x+y+y-x=24，∵AB=24-3x-4y，根据平移得：没有覆盖的阴影部分的周长为四边形ABCD的周长，∵2（AB+AD）=2(24-3x-4y+x+y+2x+y+y-x)=2（24-x-y）=48-2（x+y）=48-8=40，故选：D．．【点睛】此题考查整式加减的应用，平移的性质，利用平移的性质将不规则图形变化为规则图形进而求解，解题的关键是设出未知数，列代数式表示各线段进而解决问题．2．如图，已知∠MON=30°，点123......A A A 、、在射线ON 上，点123......B B B 、、在射线OM 上，111OA A B =，12B A OM ⊥，222OA A B =，23B A OM ⊥，以此类推，若11OA =，则66A B 的长为（ ）A ．6B ．152C ．32D ．72964【答案】C【分析】 根据等腰三角形的性质以及平行线的性质，=30MON ∠︒，111OA A B =，得到1=30∠︒，由12B A OM ⊥，得到1OA 的长度，进而得到22122A B B A =，根据已知得出33124A B B A =，44128A B B A =，551216A B B A =，进而得出答案．【详解】∵=30MON ∠︒，111OA A B =，12B A OM ⊥∵1=30∠︒，∵===60︒∠3∠4∠12，∵11OA =，∵111A B =，∵21121A B A A ==，∵22OA =，∵222OA A B =，∵22122A B B A =∵23B A OM ⊥，∵122334////B A B A B A∵1===30︒∠∠6∠7，==90︒∠5∠8∵3323324A B B A OA ===，∵331244A B B A ==，441288A B B A ==，55121616A B B A ==，以此类推：66123232A B B A ==．故选：C ．【点睛】此题主要考查了等边三角形的性质以及等腰三角形的性质，根据已知得出33124A B B A =，44128A B B A =，551216A B B A =，进而发现规律是解题关键．3．若不等式组213x x a->⎧⎨≤⎩的整数解共有三个，则a 的取值范围是（ ） A ．56a ≤<B ．56a <≤C ．56a <<D ．56a ≤≤【答案】A首先确定不等式组的解集，利用含a 的式子表示，根据整数解的个数就可以确定有哪些整数解，根据解的情况可以得到关于a 的不等式，从而求出a 的范围．【详解】解不等式2x -1＞3，得：x ＞2，∵不等式组整数解共有三个，∵不等式组的整数解为3、4、5，则56a ≤<，故选A ．【点睛】本题考查了一元一次不等式组的整数解，正确解出不等式组的解集，确定a 的范围，是解答本题的关键．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．二、填空题4．如图，在正方形ABCD 中，3AB =，P 为平面内任意一点，1CP =，连接PD ，将线段PD 绕着点D 顺时针旋转90︒，得到线段DQ ，连接CQ ，则3DQ CQ +的最小值为_________．【分析】根据正方形的性质证明()△△QDA PDCSAS ≅，得出点Q 在以点A 为圆心，1为半径的圆上运动，根据题意判断计算即可；由题意可知DQ DP =，90QDP ∠=︒，∵四边形ABCD 是正方形，∵DA DC =，90ADC ∠=︒，∵ADC ADP QDP ADP ∠-∠=∠-∠，即QDA PDC ∠=∠，∵()△△QDA PDCSAS ≅， ∵1QA PC ==，∵点Q 在以点A 为圆心，1为半径的圆上运动，如图所示，在AD 上取一点E ，使13AE =，则13AE AQ AQ AD ==， ∵△QAE△DAQ ， ∵13QE QD =，13DQ CQ CQ QE +=+＞CE ， 当Q 位于Q '的位置时，13DQ CQ +取得最小值CE ，13CE ===∵1333DQ CQ DQ CQ ⎛⎫+=+⎪⎝⎭【点睛】本题主要考查了四边形综合，准确利用相似三角形和全等三角形性质求解是解题的关键． 5．如图，在等边ABC 中，6AC =，点O 在AC 上，且2AO =，点P 是AB 上一动点，连结OP ，将线段OP 绕点O 逆时针旋转60°得到线段OD ．要使点D 恰好落在BC 上，则AP 的长是___．【答案】4【分析】根据题意得OP =OD ，∵POD =60°，又∵ABC 是等边三角形，所以∵A =∵B =∵C =60°，∵AOP +∵APO =120°，∵AOP +∵COD =120°，所以∵APO =∵COD 从而∵APO ∵∵COD ，则AP =CO ；又AO =2，AC =6，则AP =4．【详解】解：根据题意得，OP =OD ，∵POD =60°，∵∵ABC 是等边三角形，∵∵A =∵B =∵C =60°，又∵∵AOP +∵APO =120°，∵AOP +∵COD =120°，∵∵APO =∵COD ，∵在∵APO 和∵COD 中，==A C APO COD OP OD ∠∠⎧⎪∠∠⎨⎪=⎩，∵∵APO ∵∵COD （AAS ），∵AP =CO ，又∵AO =2，AC =6，即CO =4，∵AP =4；故答案为：4．【点睛】本题考查了等边三角形的性质、全等三角形的判定与性质及旋转的性质，掌握其判定及性质，得出∵APO ∵∵COD 是正确解答本题的基础．6．如图，在ABC 中，30B ，90BAC ︒∠=，点P 是BC 的动点（不与点B ，C 重合），AI 、CI 分别是PAC ∠和PCA ∠的角平分线，AIC ∠的取值范围为m AIC n <∠<，则m =_______，n =________．【答案】105° 150°【分析】根据三角形内角和等于180°及角平分线定义即可表示出∵AIC ，从而得到m ，n 的值即可．【详解】解：设∵BAP=α，则∵APC=α+30°，∵∵BAC=90°，∵∵PCA=60°，∵PAC=90°-α，∵AI 、CI 分别平分∵PAC ，∵PCA ， ∵∵IAC=12∵PAC ，∵ICA=12∵PCA ， ∵∵AIC=180°-（∵IAC+∵ICA ）=180°-12（∵PAC+∵PCA ） =180°-12（90°-α+60°） =12α+105°， ∵0＜α＜90°，∵105°＜12α+105°＜150°，即105°＜∵AIC ＜150°， ∵m=105°，n=150°．故答案为：105°，150°．【点睛】本题考查了角平分线的定义，不等式的性质，熟练掌握角平分线的定义是解题的关键．三、解答题7．在平面直角坐标系中，已知A （a ，0），B （0，b ）．已知a ，b ()240b -=． （1）∠求出A ，B 两点的坐标；∠如图1，点P 为∠AOB 三个内角角平分线的交点，且AB=5，求点P 的坐标；（2）如图2．若点C 为点A 关于y 轴对称的点，∠DBE 是将∠ABC 绕点B 顺时针旋转后所得图形，连接AD 、CE 交于点F ．求证：BF 平分∠CFD ．（3）在（2）的基础上继续绕点B 旋转使得D 、B 、C 三点共线，若ABO α∠=，求∠CFD 的度数（用含α的式子表示）．【答案】（1）∵A(-3，0)，B(0，4)；∵(-1，1)；（2）∵证明见解析；∵90-α︒【分析】（1）∵根据非负性可求出a 和b ，即可得到A 、B 的坐标；∵从P 点分别向AB 、BO 、AO 作垂线，分别交D 、E 、F ，先证明∵BDP ∵∵BEP ，同理可证∵PFO ∵∵PEO ，∵PDA ∵∵PF A ，设PF =x ，则DP =PE =x ，可得到PAB POB PAO ABO S S S S ++=△△△△，即可求得PF ，进而得到P 点坐标；（2）∵根据∵DBE 是将∵ABC 绕点B 顺时针旋转后所得图形，点C 为点A 关于y 轴对称的点，可证得∵DBE ∵∵ABC ，进而可证得∵BDA ∵∵BCE ，得到∵BAF =∵BEC ，进而得到∵EFB ∵∵AFB ，即可证得BF 平分∵CFD ；∵连接BF ，可得∵BFC =∵ECA ，根据∵BFC =180°-∵FBC -∵BCF 即可求解．【详解】解：（1）()240b -=，∵a +3=0，b -4=0，∵a =-3，b =4，∵A (-3，0)，B (0，4)；∵∵点P 为∵AOB 三个内角角平分线的交点，且AB =5，∵∵DBP =∵EBP ，∵FOP =∵EOP ，∵DAP =∵F AP ，从P 点分别向AB 、BO 、AO 作垂线，分别交D 、E 、F ，如下图所示，∵DP =PE =PF ，在∵BDP 和∵BEP 中，BP BP DP DE BDP BEP =⎧⎪=⎨⎪∠=∠⎩，∵∵BDP ∵∵BEP ，同理可得∵PFO ∵∵PEO ，∵PDA ∵∵PF A ，设PF =x ，则DP =PE =x ，∵PAB POB PAO ABO S S S S ++=△△△△， 即()115433422x x x ++=⨯⨯， 解得：x =1，又∵点P 在第二象限，∵P点坐标为：(-1，1)；（2）∵∵点C为点A关于y轴对称的点，∵AB=BC，在∵BDA和∵BCE中，∵∵DBE是将∵ABC绕点B顺时针旋转后所得图形，∵∵DBE∵∵ABC，∵BD=AB=BE=BC，∵DBE=∵ABC，∵∵DBE+∵EBA=∵ABC+∵EBA，即∵DBA=∵EBC，∵∵BDA∵∵BCE，∵∵BAF=∵BEC，在∵EFB和∵AFB中，AB=EB，BF=BF，∵BAF=∵BEC，∵∵EFB∵∵AFB，∵BF平分∵CFD；∵如图，连接BF，由题可知，∵BFC=∵ECA，∵∵BFC=180°-∵FBC-∵BCF=180°-（∵ABC+∵FBA）-∵BCF=180°-∵ABC-（∵BCF+∵FBA）=180°-∵ABC-（∵BCF+∵FCA）=180°-2α-（90°-α）=90-α︒，∵∵CFD=90-α︒．【点睛】本题考查全等三角形的判定与性质、几何变换-旋转，解题的关键是综合运用相关知识．8．如图1，在平面直角坐标系中，AO＝AB，∠BAO＝90°，BO＝8cm，动点D从原点O出发沿x轴正方向以a cm/s的速度运动，动点E也同时从原点O出发在y轴上以b cm/s的速度运动，且a，b满足关系式a2+b2﹣4a﹣2b+5＝0，连接OD，OE，设运动的时间为t秒．（1）求a，b的值；（2）当t为何值时，∠BAD∠∠OAE；（3）如图2，在第一象限存在点P，使∠AOP＝30°，∠APO＝15°，求∠ABP．【答案】（1）a＝2，b＝1；（2）t＝83或t＝8；（3）∵ABP＝105°．【分析】（1）将a2+b2﹣4a﹣2b+5＝0用配方法得出（a﹣2）2+（b﹣1）2＝0，利用非负数的性质，即可得出结论；（2）先由运动得出BD＝|8﹣2t|，再由全等三角形的性质的出货BD＝OE，建立方程求解即可得出结论．（3）先判断出∵OAP∵∵BAQ（SAS），得出OP＝BQ，∵ABQ＝∵AOP＝30°，∵AQB＝∵APO ＝15°，再求出∵OAP＝135°，进而判断出∵OAQ∵∵BAQ（SAS），得出∵OQA＝∵BQA＝15°，OQ＝BQ，再判断出∵OPQ是等边三角形，得出∵OQP＝60°，进而求出∵BQP＝30°，再求出∵PBQ＝75°，即可得出结论．【详解】解：（1）∵a2+b2﹣4a﹣2b+5＝0，∵（a﹣2）2+（b﹣1）2＝0，∵a﹣2＝0，b﹣1＝0，∵a＝2，b＝1；（2）由（1）知，a＝2，b＝1，由运动知，OD＝2t，OE＝t，∵OB＝8，∵DB＝|8﹣2t|∵∵BAD∵∵OAE，∵DB＝OE，∵|8﹣2t|＝t，解得，t＝83（如图1）或t＝8（如图2）；（3）如图3，过点A作AQ∵AP，使AQ＝AP，连接OQ，BQ，PQ，则∵APQ＝45°，∵P AQ＝90°，∵∵OAB＝90°，∵∵P AQ＝∵OAB，∵∵OAB+∵BAP＝∵P AQ+∵BAP，即：∵OAP＝∵BAQ，∵OA＝AB，AD＝AD，∵∵OAP∵∵BAQ（SAS），∵OP＝BQ，∵ABQ＝∵AOP＝30°，∵AQB＝∵APO＝15°，在∵AOP中，∵AOP＝30°，∵APO＝15°，∵∵OAP＝180°﹣∵AOP﹣∵APO＝135°，∵∵OAQ＝360°﹣∵OAP﹣∵P AQ＝135°﹣90°＝135°＝∵OAP，∵OA＝AB，AD＝AD，∵∵OAQ∵∵BAQ（SAS），∵∵OQA＝∵BQA＝15°，OQ＝BQ，∵OP＝BQ，∵OQ ＝OP ，∵∵APQ ＝45°，∵APO ＝15°，∵∵OPQ ＝∵APO +∵APQ ＝60°，∵∵OPQ 是等边三角形，∵∵OQP ＝60°，∵∵BQP ＝∵OQP ﹣∵OQA ﹣∵BQA ＝60°﹣15°﹣15°＝30°，∵BQ ＝PQ ，∵∵PBQ ＝12（180°﹣∵BQP ）＝75°， ∵∵ABP ＝∵ABQ +∵PBQ ＝30°+75°＝105°．【点睛】本题是三角形综合题，主要考查了配方法、非负数的性质、三角形内角和定理、等边三角形的判定和性质、全等三角形的判定及性质，构造出全等三角形是解题的关键．9．在平面直角坐标系xOy 中，点P 和图形W 的中间点的定义如下：Q 是图形W 上一点，若M 为线段PQ 的中点，则称M 为点P 和图形W 的中间点．(2,3)C -，(1,3)D ，(1,0)E ，(2,0)F -．（1）点(2,0)A ，∠点A 和原点的中间点的坐标为________；∠求点A 和线段CD 的中间点的横坐标m 的取值范围；（2）点B 为直线2y x =上一点，在四边形CDEF 的边上存在点B 和四边形CDEF 的中间点，直接写出点B 的横坐标n 的取值范围．【答案】（1）∵（1，0）；∵0≤m≤32；（2）32-≤n≤0或1≤n≤3． 【分析】（1）∵由题意根据点A ，O 的坐标，利用中点坐标公式即可求出结论；∵根据题意先依据题意画出图形，观察图形可知点A 和线段CD 的中间点所组成的图形是线段C′D′，根据点A ，C ，D 的坐标，利用中点坐标公式可求出点C′，D′的坐标，进而可得出m 的取值范围；（2）根据题意利用一次函数图象上点的坐标特征可得出点B 的坐标为（n ，2n ），进而依据题意画出图形，观察图形可知：点B 和四边形CDEF 的中间点只能在边EF 和DE 上，当点B 和四边形CDEF 的中间点在边EF 上时，利用四边形CDEF 的纵坐标的范围，可得出关于n 的一元一次不等式组，解之即可得出n 的取值范围；当点B 和四边形CDEF 的中间点在边DE 上时，由四边形CDEF 的横、纵坐标的范围，可得出关于n 的一元一次不等式组，解之即可得出n 的取值范围．【详解】解：（1）∵∵点A 的坐标为（2，0），∵点A 和原点的中间点的坐标为()002202++，，即（1，0）． 故答案为：（1，0）； ∵如图1，点A 和线段CD 的中间点所组成的图形是线段C′D′．由题意可知：点C′为线段AC 的中点，点D′为线段AD 的中点．∵点A 的坐标为（2，0），点C 的坐标为（-2，3），点D 的坐标为（1，3），∵点C′的坐标为（0，32），点D′的坐标为（32，32）， ∵点A 和线段CD 的中间点的横坐标m 的取值范围为0≤m≤32． （2）∵点B 的横坐标为n ，∵点B 的坐标为（n ，2n ），当点B 和四边形CDEF 的中间点在边EF 上时，有023020n n ⎧⎨⎩-≤-≥， 解得：32-≤n≤0；当点B和四边形CDEF的中间点在边DE上时，有121 3220nn⎧⎨⎩⨯-≤⨯-≥，解得：1≤n≤3．综上所述，点B的横坐标n的取值范围为32-≤n≤0或1≤n≤3．【点睛】本题考查中点坐标公式和一次函数图象上点的坐标特征以及解一元一次不等式组，解题的关键是（1）∵利用中点坐标公式求出结论；∵通过画图找出点A和线段CD的中间点所组成的图形是线段C′D′；（2）分点B和四边形CDEF的中间点在边EF上及点B和四边形CDEF 的中间点在边DE上两种情况，找出关于n的一元一次不等式组．。

中考二次函数压轴题———解题法归类总结解决二次函数压轴题的通法，供大家参考。

几个自定义概念：①三角形基本模型：有一边在X轴或Y上，或有一边平行于X轴或Y轴的三角形称为三角形基本模型。

②动点（或不确定点）坐标“一母示”：借助于动点或不确定点所在函数图象的解析式，用一个字母把该点坐标表示出来，简称“设横表纵”。

如：动点P在y=2x+1上，就可设 P（t, 2t+1）.若动点Ｐ在ｙ＝2-+，则可x x321设为Ｐ（ｔ，2-+）当然若动点M 在X轴上，则设为（t, 0）.若动点M t t321在Ｙ轴上，设为（０，ｔ）．③动三角形：至少有一边的长度是不确定的，是运动变化的。

或至少有一个顶点是运动，变化的三角形称为动三角形。

④动线段：其长度是运动，变化，不确定的线段称为动线段。

⑤定三角形：三边的长度固定，或三个顶点固定的三角形称为定三角形。

⑥定直线：其函数关系式是确定的，不含参数的直线称为定直线。

如：ｙ＝３ｘ－６。

⑦X标，Y标：为了记忆和阐述某些问题的方便，我们把横坐标称为x标，纵坐标称为y标。

⑧直接动点：相关平面图形（如三角形，四边形，梯形等）上的动点称为直接动点，与之共线的问题中的点叫间接动点。

动点坐标“一母示”是针对直接动点坐标而言的。

1.求证“两线段相等”的问题：借助于函数解析式，先把动点坐标用一个字母表示出来；然后看两线段的长度是什么距离（即是“点点”距离，还是“点轴距离”，还是“点线距离”，再运用两点之间的距离公式或点到x轴（y轴）的距离公式或点到直线的距离公式，分别把两条线段的长度表示出来，分别把它们进行化简，即可证得两线段相等。

２、“平行于y轴的动线段长度的最大值”的问题：由于平行于y轴的线段上各个点的横坐标相等（常设为t），借助于两个端点所在的函数图象解析式，把两个端点的纵坐标分别用含有字母t的代数式表示出来，再由两个端点的高低情况，运用平行于y轴的线段长度计算公式-y y下上，把动线段的长度就表示成为一个自变量为t，且开口向下的二次函数解析式，利用二次函数的性质，即可求得动线段长度的最大值及端点坐标。

二次函数压轴题——线段问题解析类型一：距离最值常见模型1. “变动的两线段之和的最小值”时大都应用“两点之间的连线中，线段最短”这一模型．2. “变动的两线段之差的最大值”时大都应用“三角形两边之差小于第三边”这一模型．1. 如图，抛物线y ＝－14x 2＋bx ＋c 的图象过点A (4，0)，B (－4，－4)，且抛物线与y 轴交于点C ，连接AB ，BC ，AC .(1)求抛物线的解析式；(2)点P 是抛物线对称轴上的点，求△PBC 周长的最小值及此时点P 的坐标；答案：(1)y =−14x 2+12x +2;（2）2√13+6√22.如图，抛物线y ＝﹣x 2+bx +c 与x 轴交于A 、B 两点（A 在B 的左侧），与y 轴交于点N ，过A 点的直线l ：y ＝kx +n 与y 轴交于点C ，与抛物线y ＝﹣x 2+bx +c 的另一个交点为D ，已知A （﹣1，0），D （5，﹣6），P 点为抛物线y ＝﹣x 2+bx +c 上一动点（不与A 、D 重合）．（1）求抛物线和直线l 的解析式；（2）当点P 在直线l 上方的抛物线上时，过P 点作PE ∥x 轴交直线l 于点E ，作PF ∥y 轴交直线l 于点F ，求PE +PF 的最大值；答案（1）y=−x2+3x+4 ;（2）当x＝2时，其最大值为18；3.如图，抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0），点B（﹣3，0），且OB＝OC．（1）求抛物线的解析式；（2）抛物线上两点M，N，点M的横坐标为m，点N的横坐标为m+4．点D是抛物线上M，N之间的动点，过点D作y轴的平行线交MN于点E．求DE的最大值；【解答】解：（1）y=−x2−4x−3;（2）44.如图，抛物线y＝ax2+bx+c的图象过点A（﹣1，0）、B（3，0）、C（0，3）．（1）求抛物线的解析式；（2）在抛物线的对称轴上是否存在一点P，使得△PAC的周长最小，若存在，请求出点P 的坐标及△PAC的周长；若不存在，请说明理由；答案（1）y=−x2+2x+3;（2）p(1,2),√10+3√25.如图，抛物线y＝﹣x2+bx+c过点A（3，2），且与直线y＝﹣x+交于B、C两点，点B的坐标为（4，m）．（1）求抛物线的解析式；（2）点D为抛物线上位于直线BC上方的一点，过点D作DE⊥x轴交直线BC于点E，点P为对称轴上一动点，当线段DE的长度最大时，求PD+PA的最小值；答案：（1）y=−12x2+x+72;（2）32√56．直线132y x=-与抛物线2y x bx c=-++相交于A(),4m-和B（4，n）两点，点P是抛物线位于线段AB上方异于点A，B的一个动点，过点P作PQ⊥x轴，交线段AB于点Q．（1）求抛物线的解析式；（2）在P点运动过程中，线段PQ的长是否存在最大值？若存在，求出这个最大值，并求出此时P点的坐标；若不存在，请说明理由；答案（1）y=−x2+52x+5;（2）P(1,132),最大值9类型二距离和差积关系利用坐标的几何意义求距离1.已知抛物线y＝x2﹣bx+c（b，c为常数，b＞0）经过点A（﹣1，0），点M（m，0）是x轴正半轴上的动点．（Ⅰ）当b＝2时，求抛物线的顶点坐标；（Ⅱ）点D（b，y D）在抛物线上，当AM＝AD，m＝5时，求b的值；（Ⅲ）点Q（b+，y Q）在抛物线上，当AM+2QM的最小值为时，求b的值．【解答】解：（Ⅰ）（1，﹣4）；（Ⅱ）3√2−1（Ⅲ）42.抛物线y＝x2＋bx＋c过点A(3，0)，B(1，0)，交y轴于点C，点P是该抛物线上一动点，点P从C点沿抛物线向A点运动(点P不与点A重合)，过点P作PD∥y轴交直线AC于点D.(1)求抛物线的解析式；(2)求点P在运动的过程中线段PD长度的最大值；(3)在抛物线对称轴上是否存在点M，使|MA－MC|最大？若存在，请求出点M的坐标，若不存在，请说明理由．答案(1)y=x2−4x+3 (2)94；(3)存在.M(2，－3)3.抛物线与x轴交于A，B两点，与y轴交于点C（0，﹣2），点A的坐标是（2，0），P为抛物线上的一个动点，过点P作PD⊥x轴于点D，交直线BC于点E，抛物线的对称轴是直线x＝﹣1．（1）求抛物线的函数表达式；（2）若点P在第二象限内，且PE＝OD，求△PBE的面积．答案（1）14x2+12x−2 ;（2）58。

课题：二次函数背景下的几何问题------线段最值问题公开课教学设计1．教材分析二次函数是一次函数和反比例函数的继续和发展，它位居初中阶段三大函数中的首位，是初中数学学习的重点与难点，也为以后更高层次函数的学习奠定了基础.以二次函数为背景的试题常受中考命题者的青睐，能够全面考查用数析形的技能与计算能力，这也是学生将来学习高中数学知识所必备的.命题一般不会用以纯函数的形式出现，而是结合几何图形或点的运动使几何图形发生变化，从而让代数与几何有机结合起来.随着对《课程标准》基本理念被更为广泛和更为深入地认识，对“合情推理”与“数学活动过程”的考查也呈增强之势．而二次函数背景下的线段最值问题近年来屡屡出现在各地的中考试卷中，这类问题往往是利用重要的几何结论（如两点之间线段最短、三角形两边之和大于第三边、两边之差小于第三边、垂线段最短等）及二次函数的性质求最值.这类问题大多是“将军饮马”模型的变式应用，试题通过考查点在直线上运动时与它相关线段的最值情况，不但能了解学生综合运用数学知识解题能力，而且还能通过让学生对“动”与“定”之间的关系的思考，深入了解学生在图形的运动变化中探究几何元素之间位置关系和数量关系的能力与识别能力，体现新课程对学生几何探究活动过程、合情推理能力的要求.2.学情分析本节课是基于学生完成第一轮知识板块复习所进行的提高数学解题技能的专项复习，虽然学生在七年级时已经学习过最短路径问题，但很多学生对于从复杂图形中分离出基本图形仍有困难，通过本节课的学习，目的不仅是培养学生能正确、快速地分离基本图形，找到解决问题的突破口，而且通过几何模型、函数模型的逐渐深入地学习，学生能进一步体会到解决线段最值问题的实质.学生观察，操作，猜想能力较强，但演绎推理，归纳，运用数学意识的思想比较薄弱，自主探究和合作学习能力也需要在课堂教学中进一步引导.学生具有一定的探究精神和合作意识，能在一定的亲身经历和体验中获取一定的数学新知识，但在数学的说理上还不规范，集合演绎推理能力有待加强.3．教学目标分析1.知识与技能目标：（1）通过复习进一步落实用待定系数法求二次函数的解析式，掌握二次函数的图像和性质，会确定抛物线的顶点坐标、对称轴及最值等.（2）熟练掌握基本事实——两点之间线段最短、垂线段最短及三角形的三边关系，根据问题建构几何模型，解决因动点产生的二次函数背景下的线段最值问题.（3）能利用二次函数的图像和性质，根据问题建构函数模型，解决因动点产生的二次函数背景下的线段最值问题.2.过程与方法目标：（1）在探索用几何模型求线段最值问题中挖掘图形本质，最基本的原理、法则，实现多题归一.（2）经历探究用函数模型求线段最值问题，体会二次函数的应用价值和二次函数模型对解决最值问题的优越性.（3）让学生经历数学活动过程，并从中体会及感悟化归与转化、数形结合、函数与方程、数学建模等数学思想方法的具体体现和运用.3.情感、态度与价值观目标：（1）通过观察、分析、对比等方法，培养并提高学生的合情推理能力、分析问题、解决问题的能力.（2）由简单题入手逐渐提升，从而消除学生的畏难情绪，让学生有兴趣和积极性参与数学活动，从中体会及感悟科学的思想方法所蕴涵的意义和作用，并加强学生之间的合作交流，培养学生的问题意识，提高应用数学的能力.4.教学重难点重点：能运用几何模型和函数模型解决因动点产生的二次函数背景下的线段最值问题.难点：提高运用函数知识与几何知识解决数学综合题的能力，掌握模式识别的解题策略.5.教学策略（1）探究引导策略：探讨式学习；教师启发引导.（2）自主合作探究式学习策略：互相讨论、交流、合作的课堂氛围，使学生真正成为教学的主体.（3）问题串设计策略：运用有序的问题串有层次地灵活呈现问题，组织教学内容，提出有启发性的引申问题，激发学生的学习兴趣，积极地参与到探究规律的学习当中.（4）鼓励、激励策略：积极肯定学生的学习成果，及时评价学生的课堂表现，让学生体会成功的喜悦.6.设计理念：从近年的中考数学题型来看，经常考查二次函数背景下的线段最值问题，而这部分题目在中考分析中，失分率很高，应该引起我们的重视，线段最值问题在教课书虽然没有专题讲解，但却给出了它的模型.学生对线段最值模型的陌生由于当时的学生理解水平有限等条件下，教师在当时的教学中对教材例习题的拓展延伸程度相对低，因此在初三的综合复习中对此进行专题复习是很有必要的.所以我设计本节课的思路是想通过对此类题进行深层次的挖掘、拓展、再创造，利用例题、习题的潜在的价值，改变学生的学习方式由“重结论轻过程”向“过程与结果”并重的方向发展，使学生挖掘隐含问题的本质属性，从而达到“做一题，会一类，通一片”的解题境界.希望能通过此复习达到预想的目标.7.教学准备:（1）教学课件,导学练，教案（2）课前让学生分组合作交流,提前完成导学练,并让学生在小组内探讨如何充当小老师讲解导学练上的练习题.8.教学过程:一、导入课题：二次函数背景下的线段最值问题是历年中考压轴题的一个典型的考点，这类问题在近年中考试题中频繁现身，如2015年漳州第25题、2016年漳州第24题，在中考中，一些考生由于没有掌握此类试题的解题方法，在解题时往往不知所措，导致失分率很高.因此，今天我们将一起来学习如何解答此类问题.二、自主探究：探究一：1.活动：播放视频短片，让学生回顾下数学史上著名的“将军饮马”问题.设计意图：通过回顾“将军饮马“问题，烘托问题情境，利用视频短片吸引学生的注意力，在历史经典中唤起学生的兴趣，激发学生探究的欲望，定位了问题的取向，把学生引领到研究的航道上.2.教师活动：板书几何模型——线段和最小值（“将军饮马“问题）模型一：如图1，点P在直线l上运动，找出一点P使PA+PB取最小值.思路分析：特征：定点A、B（同侧）动点P（定直线）基本解法：轴对称法目标：和最小基本原理：两点之间线段最短操作：对称到异侧基本思想：转化（化同侧为异侧，化折为直）设计意图:为了落实好下面的模型应用，把知识背景归纳成一般化的数学模型.将归纳总结基本模型作为先行组织者，在温故中实现引新，为展开模型应用提供知识、方法及经验的支持.以此作为模型我们可以解决下列求线段和最小值的问题.3.学生活动：模型应用已知：如图，A （-1,0），B （3,0），C （0,3），抛物线经过点A 、B 、C ，抛物线的顶点为D ．⑴求解析式和抛物线的顶点D ；(2)点P 在对称轴上，PA+PC 取最小值时，求点P 的坐标；教学活动:请一位学生上台讲题,将他的解答过程通过投影仪展示出来.教师给予点评,并板演解答过程,规范书写格式.分析：（1）可设交点式或一般式，将点代入求解，求顶点坐标可用公式法或配方法；(2) 利用模型找出点P ，再求直线BC 的解析式，最后将P 点横坐标代入直线BC 的解析 式求它的纵坐标.板书规范写出解题过程：解：如图，连接BC A 、B 两点关于对称轴对称∴线段BC 与对称轴1=x 的交点即为使PA+PC 最小的点PPA=PB ∴PA+PC=PB+PC=BC设直线BC 的解析式为)0(≠+=k b kx y ，将B （3，0），C （0，3）代入，得：⎩⎨⎧==+303b b k 解得：⎩⎨⎧=-=31b k ∴直线BC 的解析式为3+-=x y 当1=x 时，231=+-=y此时，点P （1，2）能够使得PA+PC 的值最小.变式：点P 在对称轴上，△PAC 周长最小，求点P 的坐标.分析:要使△PAC 的周长最小，已知AC 为定值，只需求一点P 使得PA ＋PC 最小即可． 解题步骤归纳：1）找对称点 2）连线并求直线解析式 3）求点坐标设计意图：（1）二次函数类的压轴题第一问通常为求点坐标、解析式，本小问要求学生能够熟练地掌握待定系数法求函数解析式或利用函数解析式求点坐标，属于送分题.通过第一小问的解答增进学生解压轴题的信心.这个问题也是为下面的问题作铺垫的，这节课所要研究的一系列问题都是在这个二次函数背景下的展开的.（2）在具体的实例中学习把知识迁移应用并体会“将军饮马”问题中蕴含的数学本质：利用对称思想把复杂的问题简单化，它与抛物线（轴对称图形）相结合，在几何求最值问题中展现了特殊的魅力.变式与（2）属于等价问题，变式的设置对提高学生利用数形结合思想以及转化策略进行解题的能力起到了很好的作用.刚才我们研究了线段和的最值问题可以用几何模型解决，那么线段差的最值问题是否也有对应的几何模型呢？活动内容：1.问题:在一条直线l上，找一点P，使|P A－PB|的值最大师生合作交流:这时还需要作对称点吗？（不需要）那应该怎么解决这个问题？（先在直线l上任意取一点P’，连接AP’,BP’,AB,得到一个三角形，AP’,BP’是这个三角形的两条边，就要满足P’A-P’B＜AB，那么现在我们只要看P’A-P’B有没有可能等于AB，若能等于AB，AB就是这两条线段之差的最大值了？（有可能，当P、B、A三点共线时）若A、B两点异侧，你还能在一条直线l上，找一点P，使|P A－PB|的差最大吗？(能,利用轴对称化异侧为同侧)2.教师活动：板书几何模型——线段差最大值模型二：思路分析：特征：定点A、B（同侧）动点P（定直线）目标：差最大操作：连接AB并延长交l于P基本解法：使A、B、P三点共线基本原理：三角形两边之差小于第三边基本思想：转化（化折为直）设计意图：经历画图-观察-说理等活动，得出作图原理，将该问题归类建模，熟悉并理解该几何模型,培养学生的逻辑思维能力,为下面该模型的应用打下坚实基础..3.学生活动:模型应用最大，求点P的坐标；(3)点P在对称轴上，PA PC最小，求点P的坐标；变式： (4)点P在对称轴上，PA PC(5)点P在线段BC上，P A取最小值时，求点P的坐标；分析:（3）第一步，应用模型找到点P的位置；第二步，因为P点在直线AC上，所以求出直线AC的解析式；第三步，P点又在对称轴上，其横坐标已知，代入直线AC的解析式求其纵坐标.（4）第一步，找点P.要使|PA－PC|最小，只要PA=PC即可，由线段垂直平分线的逆定理可知：点P在线段AC的垂直平分线上，因此线段AC垂直平分线与对称轴的交点即为所求的点P.第二步，解析法或几何法求点P的坐标.（5）第一步，找点P，利用直线外一点与直线上各点连接的所有线段中，垂线段最短.第二步，解析法或几何法求点P的坐标.教师活动：板书几何模型——垂线段最短模型三：思路分析：特征：定点A 动点P（定直线）目标：线段AP值最小操作：过A作A P⊥l于P基本原理：直线外一点与直线上各点连接的所有线段中，垂线段最短设计意图：通过交流讨论、思维碰撞，得出作图原理，将该问题归类建模，熟悉并理解数学模型.强化模型的应用，通过变式训练来提高学生举一反三、触类旁通的能力.【链接中考】1．（2015•漳州）如图，抛物线y=﹣x2+2x+3与x轴交于A，B两点，与y轴交于点C，点D为抛物线的顶点，请解决下列问题．（1）填空：点C的坐标为（，），点D的坐标为（，）；（2）设点P的坐标为（a，0），当|PD﹣PC|最大时，求α的值并在图中标出点P的位置；设计意图：中考真题体验，使学生从解题过程中获取成功的喜悦，提升学习数学的信心.探究二：上面的第（5）个问题属单条线段最值问题，我们是从“形”的角度构造“垂线段最短”这种几何模型求解的，那么单条线段最值问题我们能不能从“数”的角度进行分析来解决问题呢？（建立函数模型）(6)点P 在第一象限的抛物线上，P Q ⊥x 轴交BC 于Q ，求PQ 的最大值；思路分析：第一步，设在抛物线中动点P 的横坐标为x,则该点纵坐标即可用含x 的式子表示；第二步，因为P Q ⊥x 轴交BC 于Q ，所以Q 点的横坐标也为x,又因为Q 在BC 上，因此求出直线BC 的解析式，即可用含x 的式子表示Q 点的纵坐标，接着就能确定PQ 的表达式；第三步，用配方法或公式法求最值，注意自变量的取值范围.活动：通过题目思路分析后，让学生自己纠正原来导学练上的问题，教师巡查，及时帮助学习困难的同学解决问题或者借助小组合作交流学习的方式让已经掌握的学生帮助他们.最后通过板书或多媒体展示的方式规范解题过程.解:设P ()()3032,2<<++-a a a a ,直线BC 的解析式为)0(≠+=k b kx y , 将B （3，0），C （0，3）代入，得：⎩⎨⎧==+303b b k 解得：⎩⎨⎧=-=31b k∴直线BC 的解析式为3+-=x y Q BC x PQ 于轴交⊥()3,+-∴a a Q ()()49)23(3332222+--=+-=+--++-=∴a a a a a a PQ ∴当23=a 时，()49max =PQ 变式：点P 在第一象限的抛物线上，求出△BCP 面积的这个最大值及此时P 点的坐标. 分析：如图，可将△BCP 分割为两个小三角形，两个小三角形的底都为PQ ，高分别为21,h h而21h h +始终等于OB 的长，那么△BCP 的面积就等于OB PQ •21，这实际上就是我们之前学习过的求三角形面积的的新方法水平宽铅垂高⨯21，此时PQ 为铅垂高，OB 为水平宽.而OB 长为定值，那么要求△BCP 的最大值实际上就是求线段PQ 的最大值.设计意图:问题（6）设置对培养学生会用不同角度分析问题解决问题的能力起到了很好的作用，求△BCP 面积的最大值是用函数模型求线段最值的变式应用，利用问题的潜在的价值，使学生挖掘隐含问题的本质属性，对学生的思维能力提出了较高的要求.【链接中考】(2016•漳州)如图，抛物线c bx x y ++=2与x 轴交于点A 和点B （3，0），与y 轴交于点C （0，3）.（1）求抛物线的解析式；（2）若点M 是抛物线在x 轴下方上的动点，过点M 作MN//y 轴交直线BC 于点N ，求线段MN 的最大值；设计意图：及时练习巩固，体现学以致用的理念，消除学生学无所用的思想顾虑，有效地促进学生对函数模型法的理解与掌握.三、归纳小结，整理反思问题：①本节课你学习了哪两种方法求线段最值问题？②对于线段最值问题，你认为还可以在哪些图形背景下研究呢？③本节课涉及到的数学思想方法有哪些？师生共议：①几何模型法：先确定几何模型，再利用模型找出点，最后求点坐标，函数模型法：把线段长用二次函数关系式表示出来再求最值（要注意自变量的取值范围）；②还可以在直线、角、三角形、菱形、矩形、正方形、梯形、圆等轴对称图形背景下来研究；③化归与转化、数形结合、函数与方程、数学建模思想. 数学建模是一种数学的思考方法，是运用数学的语言和方法，通过抽象、简化建立能近似刻画并“解决”实际问题的一种强有力的数学手段.用模型分析实际事物，锻炼我们的创新能力，建立的模型是分析事物的很好的方法.设计意图:对整个课堂的学习过程进行反思，能够促进理解，提高认识水平，从而促进数学观点的形成和发展．这是一次知识与情感的交流，浓缩知识要点，突出内容本质，渗透思想、方法．培养学生自我反馈、自主发展的意识．四、课后反馈作业：A组：《连接中考》P224第6题B组：《连接中考》P226第7题C组：《连接中考》P228第5题设计意图:作业分三类，让不同的学生在数学上得到不同的发展.五、板书设计1.“将军饮马”视频引入，学生很感兴趣。

线段差的最大值的原理线段差的最大值是指在一组给定的线段中，找出两条线段之间长度的差值的最大值。

这个问题在数学和计算几何中经常出现，对于解决实际问题具有重要意义。

在本文中，我们将介绍线段差的最大值的原理以及如何通过数学方法进行求解。

首先，我们来看一下线段差的最大值的定义。

给定一组线段，每个线段都有一个长度，我们需要找出其中两条线段之间长度的差值的最大值。

换句话说，我们需要找到两个线段的长度之差的最大值。

为了更直观地理解这个问题，我们可以通过一个简单的例子来说明。

假设我们有一组线段，它们的长度分别为3、5、7、9、11。

我们需要找出其中两条线段之间长度的差值的最大值。

在这个例子中，最大的差值显然是11-3=8，因此线段差的最大值为8。

接下来，我们将介绍线段差的最大值的原理。

假设我们有n条线段，它们的长度分别为L1、L2、L3、...、Ln。

我们需要找出其中两条线段之间长度的差值的最大值。

为了求解这个问题，我们可以采用以下方法：1. 首先，我们可以对给定的线段进行排序，从小到大排列。

这样可以方便我们找出最大值和最小值。

2. 然后，我们可以遍历所有的线段对，计算它们之间的长度差值，并找出其中的最大值。

3. 最后，我们得到的最大值就是线段差的最大值。

通过上述方法，我们可以比较容易地求解线段差的最大值。

当然，在实际问题中，我们可能会遇到更复杂的情况，例如线段不是按照长度排序的，或者线段的数量非常大。

针对这些情况，我们可以采用更高效的算法来求解线段差的最大值，例如动态规划算法或者贪心算法。

总之，线段差的最大值是一个重要的数学问题，它在实际问题中具有广泛的应用。

通过本文的介绍，我们了解了线段差的最大值的原理以及求解方法，希望能对读者有所帮助。

在实际问题中，我们可以根据具体情况选择合适的算法来求解线段差的最大值，从而更好地解决实际问题。

线段差的最大值与线段和的最小值问题有关线段差的最大值与线段和的最小值问题的主要应用原理是：1、两点这间线段最短。

2、三角形的任意两边之和大于第三边（找和的最小值）。

3、三角形的任意两边之差小于第三边（找差的最大值）。

作图找点的关键：充分利用轴对称，找出对称点，然后，使三点在一条直线上。

即利用线段的垂直平分线定理可以把两条线段、三条线段、四条线段搬在同一条直线上。

证明此类问题，可任意另找一点，利用以上原理来证明。

一两条线段差的最大值：（1）两点同侧：如图，点P在直线L上运动，画出一点P，使︱PA－PB︱取最大值。

作法：连结AB并延长AB交直线L于点P。

点P即为所求。

︱PA－PB︱=AB证明：在直线L上任意取一点P。

，连结PA、PB，︱PA－PB︱＜AB（2两点异侧：如图，如图，点P在直线L上运动，画出一点P，使︱PA－PB︱取最大值。

作法：1、作B关于直线L的对称点B。

2、连结AB并延长AB交直线L于点P。

点P即为所求。

︱PA－PB︱=AB证明：在直线L上任意取一点P。

，连结PA、PB、PB。

︱PA－PB︱=︱PA－PB︱＜AB（三角形任意两边之差小于第三边）二、两条线段和的最小值问题：（1））两点同侧：如图，点P在直线L上运动，画出一点P使P A＋PB取最小值。

（三角形的任意两边之和大于第三边（找和的最小值），P A＋PB=AB（2）两点异侧：如图，点P在直线L上运动，画出一点P使P A＋PB取最小值。

（两点之间线段最短）三、中考考点：08年林金钟老师的最后一题：如图，在矩形ABCO中，B（3，2），E（3，1），F（1，2）在X轴与Y轴上是否分别存在点M、N，使得四边形EFNM的周长最小？若存在，请求出周长的最小值，若不存在，请说明理由。

提示：EF长不变。

即求F N＋NM＋MF的最小值。

利用E关于X轴的对称点E，F的对称点F，把这三条线段搬到同一条直线上。

一、以正方形为载体，求线段和的最小值例1. 如图1，四边形ABCD是正方形，边长是4，E是BC上一点，且CE＝1，P是对角线BD上任一点，则PE＋PC的最小值是_____________。