《电路》考研邱关源版2021电路考研真题库

题 !!$ 图
$ %$: )$( )$; )$= %9-)!#-)<-)%-%$-- 6 即#元件 4 发出的总功率等于其余元件吸收的总功率#满足功率平衡! %!!%! 在指定的电压"和电流#参考方向下#写出各元件"和#的约束方程’元件的
组 成 关 系 (!
题 !!% 图
解 ! ’+(图为线性电阻元件#其电压"电流关系满足欧姆定律!’+(图电阻元件" 和
%!!# ! 若某元件端子上的电压和电流取关联参考方向#而" %!.-/01’!--!&(*## % .123’!--!&(4!求 $ ’!(该 元 件 吸 收 功 率 的 最 大 值 * ’#(该 元 件 发 出 功 率 的 最 大 值 !
解 ! !!!!!!!!!$’&(%"’&(#’&( % !.-/01’!--!&(’.123’!--!&( % &5&123’#--!&(6
#!-
&*- ’&* #1
"’&(% "-
# ’&* $1
!-&!%- $’&*%1
$应 用 "## 积 分 关 系 式 #有
&&%
&% !1时 #
) #’!(%#’-()
! ,
!
"’&(>&
-
) %
-)
! %
!
!->&%
-
! %
’
!
’!-&( -
% #+&4

第12章三相电路12.1复习笔记一、对称三相电源如图12-1-1所示，由同频率、等幅值、相位互差120°的三个正弦电压源连接成的电源被称为对称三相电源。

对称三相电源有星形（Y）和三角形（△）两种。

这3个电源依次称为A相、B相和C相，它们的电压瞬时表达式及相量如表12-1-1所示。

图12-1-1表12-1-1电压时域及相量表示二、三相电路的线电压（电流）与相电压（电流）的关系三相系统中，流经输电线中的电流称为线电流；电源端或是负载端各输电线线端之间的电压都称为线电压；三相电源和三相负载中每一相的电压、电流称为相电压和相电流。

三相系统中的线电压和相电压、线电流和相电流之间的关系都与连接方式有关，如表12-1-2所示。

表12-1-2线电压（电流）与相电压（电流）的关系三、对称三相电路的分析计算计算的一般步骤：①将△形电源和负载均变成Y形；②用短路线连接所有中性点，画出一相等效电路进行计算；③根据对称性推算其他两相电压和电流。

图12-1-2（a）的一相等效电路如图（b）所示。

图12-1-2四、三相电路的功率1．三相电路的功率计算有功功率：P＝P A ＋P B ＋P C 。

无功功率：Q＝Q A ＋Q B ＋Q C 。

视在功率：22Q P S +=若负载对称，则有A P P p p 33cos 3cos l l P P U I U I ϕϕ===A P P p p33sin 3sin l l Q Q U I U I ϕϕ===223l l S U I P Q ==+式中，φp 是指每相负载的阻抗角；对称三相电路的其他计算完全可以用正弦电流电路的相量分析方法。

2．三相电路有功功率的测量三相电路有功功率测量的三表法和两表法，如图12-1-3所示。

（2）若用二瓦计法测量电源端三相功率，试画出接线图，并求两个功率表的读数（S 闭合时）。
图 12-8 解： （1）开关 S 打开时，为对称的三相电路，令 如图 12-9（a）所示。
，电流方向
（a）
（b）
图 12-9
（2）开关 S 闭合时，用二瓦计测量电源端的三线功率的接线图如图 12-9（b）所示。
，
此时功率表上的读数为：
8．图 12-8 所示电路中，对称三相电源端的线电压 U1＝380 V，Z＝（50＋j50）Ω， Z1＝（100＋j100）Ω，ZA 为 R、L、C 串联组成，R＝50 Ω，XL＝314 Ω，XC＝－264 Ω。 试求：
7 / 16
圣才电子书 十万种考研考证电子书、题库视频学习平台
圣才电子书 十万种考研考证电子书、题库视频学习平台

第 12 章 三相电路
1．已知对称三相电路的星形负载阻抗 Z＝（165＋j84）Ω，端线阻抗 Z1＝（2＋j1）Ω，
中性线阻抗 ZN＝（1＋i1）Ω，线电压 U1＝380 V。求负载端的电流和线电压，并作电路的
相量图。
吸收的功率为原来的 /2 倍。
（5）如果加接零阻抗中性线，那么对于（3），电流表的读数为 317.2A，电压表的读
数为 660V；对于（4），电流表上的读数为 0，电压表上的读数为 1191.41V。
6．图 12-6 所示对称三相电路中， ＝380 V，三相电动机吸收的功率为 1.4 kW， 其功率因数 λ＝0.866（滞后），Z1＝－j55Ω。求 和电源端的功率因数 。
5．图 12-5 所示对称 Y-Y 三相电路中，电压表的读数为 1143.16V，Z＝（15＋j15 ） Ω，Z1＝（1＋j2）Ω。求：

第九章 正弦稳态电路的分析
BUCT
9. 1 阻抗和导纳 9. 2 阻抗（导纳）的串联和并联 9. 3 电路的相量图 9. 4 正弦稳态电路的分析 9. 5 正弦稳态电路的功率 9. 6 电路的谐振
1
9. 3 电路的相量图
一、RL、RC串联电路
IR
+
U _
+
_ UR +
jL
U_L
P188
U
j
0
8—11 BUCT
1, 纯电阻 0， 纯电抗
X<0, j < 0 , 容性负载， 超前功率因数
例：cos j = 0.5 (滞后)，则j =60o(电压领先电流60o)。
一般用户： 异步电机 空载 cosj =0.2~0.3 满载 cos j =0.7~0.85
日光灯
cosj =0.45~0.6
17
功率因数的提高
k
1
Qk
0
14
* 复功率守恒, 不等于视在功率守恒.
BUCT
I
+
U_
+ U 1 _
+
U_ 2
S UI* (U1 U 2 )I * U1I * U 2I* S1 S2
b
一般情况下： S Sk k 1
例：
S S2 Q2 S1 P2
Q1 P1
R2 UR2 I 33.9 1.73 19.6W
L UL2 I 72.45 1.73 41.88W
L2 41.88 314 0.133H
12
复功率
BUCT
为了用相量U和I来计算功率，引入“复功率”
I
+

谢谢！
55
《电路原理》第五版_邱关源_罗先觉 第五版
51、山气日夕佳，飞鸟相与还。 52、木欣欣以向荣，泉涓涓而始流。
53、富贵非吾愿，帝乡不可期。 54、雄发指危冠，猛气冲长缨。 55、土地平旷，屋舍俨然，有良田美 池桑竹 之属， 阡陌交 通，鸡 犬相闻 。
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
肩上。——叔本华

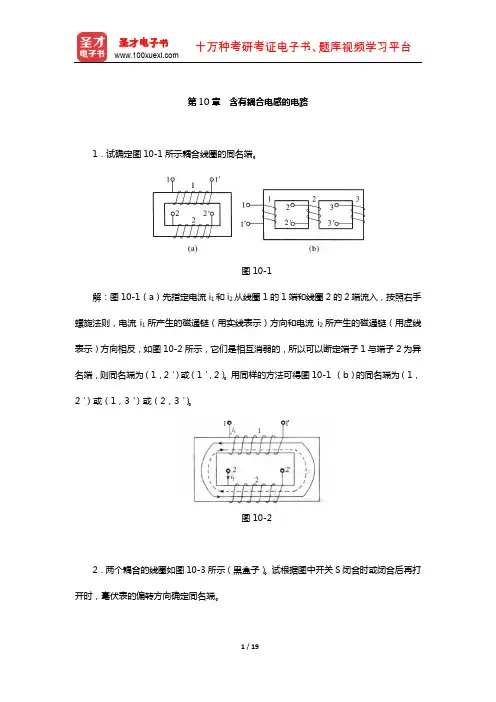
第10章含有耦合电感的电路1．试确定图10-1所示耦合线圈的同名端。

图10-1解：图10-1（a）先指定电流i1和i2从线圈1的1端和线圈2的2端流入，按照右手螺旋法则，电流i1所产生的磁通链（用实线表示）方向和电流i2所产生的磁通链（用虚线表示）方向相反，如图10-2所示，它们是相互消弱的，所以可以断定端子1与端子2为异名端，则同名端为（1，2＇）或（1＇，2）。

用同样的方法可得图10-1 （b）的同名端为（1，2＇）或（1，3＇）或（2，3＇）。

图10-22．两个耦合的线圈如图10-3所示（黑盒子）。

试根据图中开关S闭合时或闭合后再打开时，毫伏表的偏转方向确定同名端。

图10-3解：根据右手螺旋法可知，线圈的同名端为（1，2）。

当开关S闭合时，线圈1中随时间增大的电流i从电源正极流入线圈端子1，这时毫伏表的高电位与端子1为同名端；当开关S闭合后再打开时，电流i减小，毫伏表的低电位端与端子1为同名端。

3．若有电流i1＝2＋5cos（10t＋30°）A，i2＝10A，各从图10-4（a）所示线圈的1端和2端流入，并设线圈1的电感＝6H，线圈2的电感＝3H，互感为M＝4H。

试求：（1）各线圈的磁通链；（2）端电压和；（3）耦合因数k。

解：（1）（1，2）为异名端，两个线圈的磁通是相互消弱的，所以（2）根据电压和磁通的关系得：（3）耦合因数为：k＝＝0.943。

4．如图10-5所示电路中（1）＝8H，＝2H，M＝2H；（2）＝8H，＝2H，M＝4H；（3）＝＝M＝4H。

试求以上三种情况从端子1-1′看进去的等效电感。

图10-5解：（a）＝M＋（L1－M）//（L2－M）当L1＝8H，L2＝2H，M＝2H时，＝2H；当L1＝8H，L2＝2H，M＝4H时，＝0H；当L1＝L2＝M＝4H时，＝4H。

（b）＝－M＋（L1＋M）//（L2＋M）当L1＝8H，L2＝2H，M＝2H时，＝0.857H；当L1＝8H，L2＝2H，M＝4H时，＝0H；当L1＝L2＝M＝4H时，＝0H。

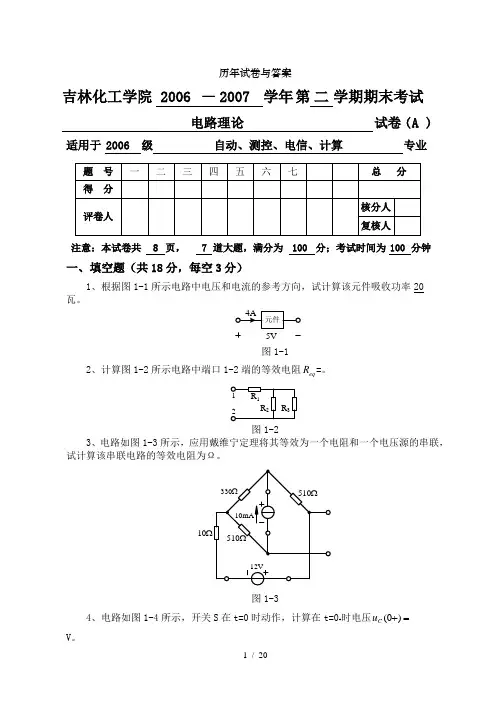
历年试卷与答案适用于 2006 级自动、测控、电信、计算专业注意：本试卷共 8 页， 7 道大题，满分为 100 分；考试时间为 100 分钟一、填空题（共18分，每空3分）1、根据图1-1所示电路中电压和电流的参考方向，试计算该元件吸收功率20 瓦。

5V图1-12、计算图1-2所示电路中端口1-2端的等效电阻eq R =。

图1-23、电路如图1-3所示，应用戴维宁定理将其等效为一个电阻和一个电压源的串联，试计算该串联电路的等效电阻为Ω。

10图1-34、电路如图1-4所示，开关S 在t=0时动作，计算在t=0+时电压=+)0(C u V 。

u C图1-45、电路如图1-5所示，试写出电压1u =。

图1-56、电路如图1-6所示，当电路发生谐振时，谐振的频率=0ω。

图1-6二、选择题（共33分，每题3分，答案填在答案卡内，填在别处无效）1、电路如图2-1所示，电路中的=X U A 。

A ． -5V ；B. 5V ；C. 10V ；D. -10V ；图2-12、电路如图2-2所示，电路一端口的输入电阻=ab R 。

A. 55Ω； B. 11Ω； C. 30Ω； D. 10V ；ab图2-23、电路如图2-3所示，电路中的电流=i。

A. 55Ω；B. 15A；C. 5A；D. 10A；图2-45、电路的图如图2-5所示，树的树枝数为。

A. 3；B. 4；C. 5；D. 6；图2-56、电路如图2-6所示，当=LRΩ时可获得最大功率。

A. 30；B. 25；C. 150；D. 180；360V RL图2-67、电路如图2-7所示，在0<t时电路处于稳态，0=t时闭合开关，求电感电流=+)0(Li A。

A. 10；B. 2.5；C. 2；D. 8；L u L图2-78、Z 参数方程是。

A. ⎩⎨⎧+=+=22212122121111U Y U Y I U Y U Y I ；B. ⎩⎨⎧-=-=221221I D U C I I B U A U ；C. ⎩⎨⎧+=+=22212122121111U H I H I U H I H U ；D. ⎩⎨⎧+=+=22212122121111I Z I Z U I Z I Z U ；9、单位阶跃函数的像函数是。

第14章线性动态电路的复频域分析14.1复习笔记一、拉氏变换及其基本性质对定义在[0，∞）上的函数f（t），其拉氏变换与拉氏反变换分别为()()0e d st F s f t t -∞-=⎰()()j j 1e d 2πj c st c f t F s s +∞-∞=⎰式中，s＝σ＋jω为复数，称为复频率。

其主要性质如下：（1）线性性质L[A 1f 1（t）＋A 2f 2（t）]＝A 1L[f 1（t）]＋A 2L[f 2（t）]＝A 1F 1（s）＋A 2F 2（s）（2）微分性质若L[f（t）]＝F（s），d ()()d f t f t t'=则L[f′（t）]＝sF（s）－f（0－）。

（3）积分性质若L[f（t）]＝F（s），则01()d ()t L f F s sξξ-⎡⎤=⎢⎥⎣⎦⎰（4）延迟性质若L[f（t）]＝F（s），则()()()000e st L f t t t t F s ε-⎡⎤--=⎣⎦（5）拉氏变换的卷积定理设f 1（t）和f 2（t）的象函数分别为F 1（s）和F 2（s），则有()()()()()()1212012*d t L f t f t L f t f F s F s ξξξ⎡⎤=-⎡⎤⎣⎦⎢⎥⎣⎦=⎰二、拉氏反变换的部分分式展开法1．部分分式展开法概述通常用两个实系数的s 的多项式之比来表示电路响应的象函数，有()()()()101101m m m n n n N s a s a s a F s m n D s b s b s b --+++==≤+++ 且均为正整数将有理分式F（s）用部分分式展开时，首先要把F（s）化为真分式，若n＞m，则F （s）为真分式；若n＝m，则将F（s）化为F（s）＝A＋N 0（s）/D（s）。

求反变换时，分情况讨论，如表14-1-1所示。

表14-1-12．部分分式展开法求拉氏反变换的步骤（1）n＝m时，将F（s）化成真分式和多项式之和；（2）求真分式分母的根，确定分解单元；（3）将真分式展开成部分分式，求各部分分式的系数；（4）对每个部分分式和多项式逐项求拉氏反变换。

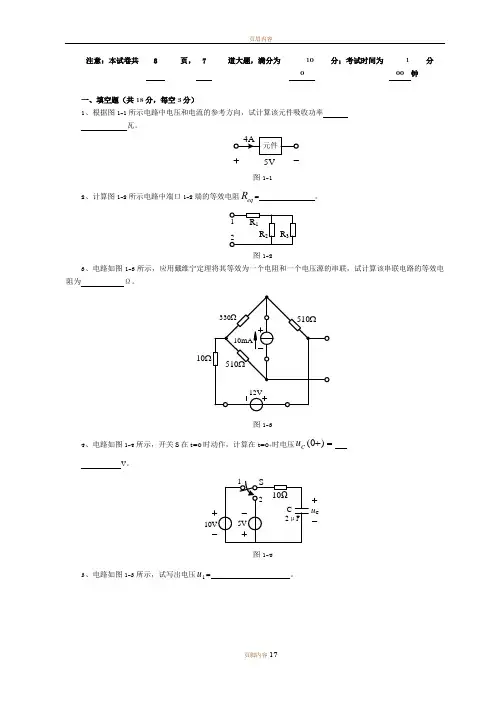
注意：本试卷共 8 页， 7 道大题，满分为 100分；考试时间为 100 分钟一、填空题（共18分，每空3分）1、根据图1-1所示电路中电压和电流的参考方向，试计算该元件吸收功率 瓦。

5V图1-12、计算图1-2所示电路中端口1-2端的等效电阻eq R = 。

图1-23、电路如图1-3所示，应用戴维宁定理将其等效为一个电阻和一个电压源的串联，试计算该串联电路的等效电阻为 Ω。

10图1-34、电路如图1-4所示，开关S 在t=0时动作，计算在t=0+时电压=+)0(C uV 。

u C图1-45、电路如图1-5所示，试写出电压1u = 。

图1-56、电路如图1-6所示，当电路发生谐振时，谐振的频率=ω。

图1-6二、选择题（共33分，每题3分，答案填在答案卡内，填在别处无效）1、电路如图2-1所示，电路中的=XU。

A．-5V； B. 5V； C. 10V； D. -10V；图2-12、电路如图2-2所示，电路一端口的输入电阻=abR。

A. 55Ω；B. 11Ω；C. 30Ω；D. 10V；ab图2-2A. 55Ω；B. 15A；C. 5A；D. 10A；图2-3A. 55Ω；B. 15A ；C. 5A ；D. 3A ；图2-45、电路的图如图2-5所示，树的树枝数为 。

A. 3； B. 4； C. 5； D. 6；图2-56、电路如图2-6所示，当=LR Ω时可获得最大功率。

A. 30；B. 25；C. 150；D. 180；360VR L图2-6A. 10；B. 2.5；C. 2；D. 8；L u L图2-78、Z 参数方程是 。

A. ⎩⎨⎧+=+=22212122121111U Y U Y I U Y U Y I ；B. ⎩⎨⎧-=-=221221I D U C I I B U A U ；C. ⎩⎨⎧+=+=22212122121111U H I H I U H I H U ；D. ⎩⎨⎧+=+=22212122121111I Z I Z U I Z I Z U ；9、单位阶跃函数的像函数是 。

6 / 81
圣才电子书 十万种考研考证电子书、题库视频学习平台

理想电压源的符号如图 1-1-4（a）所示。其特点是其两端电压总能保持一定或一定的 时间函数，且电压值大小由电压源本身决定，与流过它的电流值无关，如图 1-1-4（b）所 示。
图 1-1-4（a）
图 1-1-4（b） 说明：a．电压源为一种理想模型；b．与电压源并联的元件，其端电压为电压源的值； c．理想电压源的功率从理论上来说可以为无穷大。 ②理想电流源 理想电流源的符号如图 1-1-5（a）所示。其特点是输出电流总能保持一定或一定的时 间函数，且电流值大小由电流源本身决定，与外部电路及它的两端电压值无关，如图 1-1-5

电阻元件、电源元件和受控电源元件是常用的电路元件。电路元件可分为无源元件及有 源元件两大类。
1．无源元件及其伏安特性 表 1-1-2 无源元件及其伏安特性
功率和能量比较： （1）电阻元件 P＝ui＝Ri2＝u2/R≥0（关联参考方向）；
W t Ri2 d t0 电阻是耗能元件。 （2）电容元件
5 / 81
圣才电子书 十万种考研考证电子书Fra bibliotek题库视频学习平台

P＝ui＝Cu（du/dt）（u，i 取关联参考方向）；吸收功率，电容是无源元件。
WC C
ut2 udu 1 Cu 2
ut1
2
t2
1 Cu 2 2
t1
WC t2 WC t1
电容是储能元件。
2 / 81
圣才电子书 十万种考研考证电子书、题库视频学习平台

图 1-1-2 电压的参考方向 3．关联参考方向 对于一个元件或支路来说：如果指定元件的电流的参考方向是从电压参考极性的“＋” 指向“－”，即两者的参考方向一致，则把电流和电压的这种参考方向称为关联参考方向； 反之称为非关联参考方向。如图 1-1-3 所示，对 A 而言，u 和 i 为非关联方向；对 B 而言， u 和 i 为关联方向。

▪
（2）有效值相量：U＝U∠φu，复值常数的模表示有效值，由此可知
U U u u t = 2U ct i )
（3）正弦量的相量表示法：分为有效值相量和最大值相量。
例如，正弦量
i 10 2 cos(314t 50)A
▪
其有效值相量I＝10∠50°A。
图 8-1-5
8.2 课后习题详解
8-1 将下列复数化为极坐标形式： （1）F1＝－5－j5； （2）F2＝－4＋j3； （3）F3＝20＋j40； （4）F4＝j10； （5）F5＝－3； （6）F6＝2.78－j9.20。 解：复数 F 的坐标表示：F＝a＋jb＝|F|∠θ，其中θ＝arctan（b/a），
其对应的最大值相量
Im 10 250A
三、电路定律的相量形式
（1）KCL、KVL 定律的相量形式
▪
∑I＝0
▪
∑U＝0
（2）电路元件 VCR 的相量形式
4 / 108
圣才电子书

▪
▪
①电阻元件：U＝RI。
十万种考研考证电子书、题库视频学习平台
即电阻上的电压和电流同相位，相量图如图 8-1-3 所示。
（2）乘法运算
图 8-1-2 复数的加减运算
2 / 108
圣才电子书 十万种考研考证电子书、题库视频学习平台

F1F2 F1 e jθ1 F2 e jθ2 F1 F2 e j(θ1θ2 )
所以
|F1F2|＝|F1||F2|
arg（F1F2）＝arg（F1）＋arg（F2）
（3）除法运算
F1 F2
F1 θ1 F2 θ2
F1 F2
(θ1 θ2 )
所以
F1 F1 F2 F2

第12章三相电路一、选择题如图12-1所示为对称三相电路，电源线电压U1＝1OOV，线电流I1＝2A，负载功率因数λ＝cosφ＝0.8（感性），功率表接法也如图所示，则此时功率表读数为（）。

[上海交通大学2005研]图12-1A．208WB．120WC．173WD．0【答案】A【解析】选为参考相量，二、填空题1．在如图12-2所示的对称三相正弦交流电路中，所有三只安培表的读数都是10A，如果外加三相对称线电压保持不变，而将AB相负载断开，则电流表A1的读数为_____，电流表A2的读数为_____，电流表A3的读数为_____。

[浙江大学2004研]图12-2【答案】5.77A；5.77A；10A【解析】按一般正弦稳态电路分析方法即可得出结果。

2．图12-3所示三相对称电路中开关S合上时电流表A1的读数是A，则开关S 合上时电流表A2的读数是（）；A3的读数是（）；开关S断开时电流表A1的读数是（）；A2的读数是（）；A3的读数是（）。

[华南理工大学2010研]图12-3【答案】；；；10A；10A【解析】根据三相电路的对称性，在开关闭合后，三表读数是相同的，即都是；在开关打开之后，读数不变认为，和的电流表读数变化，线电流变为相电流，为10A。

3．某三角形联接的电力负载，线电压、及严重不对称且含有5、7次谐波，该三相负载线电压的零序分量为（）。

研]【解析】将不对称的三相线电压分解为三组对称的相量，分别为正序分量、负序分量和零序分量。

由于三相线电压中各相对应的正序分量相量和为0、负序分量相量和为0，并且各谐波分量只含有交流分量（即正序、零序分量），无零序分量。

则三相线电压的相量和即为三倍的零序分量。

即有：4．如图12-4所示对称三相电路中，已知星形连接负载（复）阻抗Z＝5＋j8.66Ω，若已测得电路无功功率则电路有功功率P＝_____。

[上海交通大学2006研]图12-4【答案】由Z＝5＋j8.66Ω可得阻抗角为于是有功功率为三、计算题1．线电压为的三相电源上接有两组对称三相负载：一组是三角形联结的电感性负载，每相阻抗；另一组是星形联结的电阻性负载，每相电阻，如图12-5所示。

第二章 电阻电路的等效变换一、是非题 (注:请在每小题后[ ]内用"√"表示对,用"×"表示错) .1. 如图所示电路的等效电阻为12122R R R R +- [√]解：212122122R R U U R R U R R U U R U I -+=-+=22221-+==R R R R I UR eq.2. 当Ｒ1 、Ｒ2与Ｒ3并联时等效电阻为:123123R R R R R R ++ [×].3. 两只额定电压为110V 的电灯泡串联起来总可以接到220V 的电压源上使用。

[×] 解：功率不同的不可以。

.4. 电流相等的两个元件必属串联,电压相等的两个元件必属并联。

[×].5. 由电源等效变换可知, 如图Ａ所示电路可用图Ｂ电路等效代替，其中/s s i u R =则图A 中的R i 和R L 消耗的功率与图Ｂ中R i 和R L 消耗的功率是不变的。

[×] 解：对外等效，对内不等效。

可举例说明。

.6. 一个不含独立源的电阻性线性二端网络（可以含受控源）总可以等效为一个线性电阻。

[√].7. 一个含独立源的电阻性线性二端网络（可以含受控源）总可以等效为一个电压源与一个电阻串联或一个电流源与一个电阻并联。

[√] .8.已知图示电路中Ａ、Ｂ两点电位相等，则ＡＢ支路中必然电流为零。

[×] 解：根据KVL 有： B A BA AB BA U U R I U R I E -+=+=55 5R EI BA =.9. 图示电路中, 既然ＡＢ两点电位相等, 即ＵAB =0,必有I AB =0 [×]解：A I AB 195459424=⨯+-⨯+=.10. 理想电压源不能与任何理想电流源等效。

[√] 二、选择题(注:在每小题的备选答案中选择适合的答案编号填入该题空白处,多选或不选按选错论) .1. 图示电路 ＡＢ间的等效电阻为_Ｃ_解：二个电阻并联等效成一个电阻，另一电阻断开。

第13章 非正弦周期电流电路和信号的频谱一、选择题1．某非正弦周期电流电路的电压为，电流为，则其三次谐波的功率为（ ）。

[南京航空航天大学2012研]A ．B ．C ．D ． 【答案】A【解析】由题目所给电压电流表达式，可知，三次谐波电压超前三次谐波电流60°，则三次谐波功率。

2．如图13-1所示电路中则电容C 2两端电压的有效值应为（ ）。

[上海交通大学2005研]12030)u t t V ωω=+++13930) 1.732sin(330)i t t A ωω=+++-25.95W 45W 51.9W 65W图13-1A．150VB．360VC．390VD．540V【答案】C【解析】分解u s＝u1＋u2＋u3，其中u1单独作用时，可得uu2单独作用时，由于L1，C1并联谐振，u3单独作用时，由于L2，C1串联谐振，等效为如图13-2所示。

图13-2从而得根据有效值的计算方法，可得u C2的有效值为。

二、填空题1．已知某无源二端网络的端口电压和电流分别为则此网络吸收的功率为（）W。

[北京交通大学2011研]【答案】43W【解析】（1）考虑直流分量可知其吸收的功率为0W（2）考虑频率为500的分量可知其吸收的功率为W （3）考虑频率为1000的分量可知其吸收的功率为0W（4）考虑频率为1500的分量可知其吸收的功率为。

因此，总功率为0＋25＋0＋18＝43W2．图13-3所示非正弦电路中，电源电压u S＝10＋cos3ωt V，R＝5Ω，ωL＝5Ω，＝45Ω，则电压表的读数为（）；电流表的读数为（）。

[华南理工大学2010研]图13-3【答案】10V；0.2A【解析】直流电压单独作用时，，三次谐波单独作用时，发生串联谐振，，所以电压表上读数为10V，电流表上读数为0.2A三、计算题1．图13-4所示非正弦电路中，已知，电流源。

试求：（1）图中ab两点间的电压u ab（t）及其有效值U ab；（2）电流源i S供出的有功功率P IS。

第一章 电路模型和电路定律电路理论主要研究电路中发生的电磁现象，用电流i 、电压u 和功率p 等物理量来描述其中的过程。

因为电路是由电路元件构成的，因而整个电路的表现如何既要看元件的联接方式，又要看每个元件的特性，这就决定了电路中各支路电流、电压要受到两种基本规律的约束，即：（1）电路元件性质的约束。

也称电路元件的伏安关系（VCR ），它仅与元件性质有关，与元件在电路中的联接方式无关。

（2）电路联接方式的约束（亦称拓扑约束）。

这种约束关系则与构成电路的元件性质无关。

基尔霍夫电流定律（KCL ）和基尔霍夫电压定律（KVL ）是概括这种约束关系的基本定律。

掌握电路的基本规律是分析电路的基础。

1-1 说明图（a ）,（b ）中,（1）,u i 的参考方向是否关联？（2）ui 乘积表示什么功率？（3）如果在图（a ）中0,0<>i u ；图（b ）中0,0u i <>，元件实际发出还是吸收功率？解：（1）当流过元件的电流的参考方向是从标示电压正极性的一端指向负极性的一端，即电流的参考方向与元件两端电压降落的方向一致，称电压和电流的参考方向关联。

所以（a ）图中i u ,的参考方向是关联的；（b ）图中i u ,的参考方向为非关联。

（2）当取元件的i u ,参考方向为关联参考方向时，定义ui p =为元件吸收的功率；当取元件的i u ,参考方向为非关联时，定义ui p =为元件发出的功率。

所以（a ）图中的ui 乘积表示元件吸收的功率；（b ）图中的ui 乘积表示元件发出的功率。

（3）在电压、电流参考方向关联的条件下，带入i u ,数值，经计算，若0>=ui p ，表示元件确实吸收了功率；若0<p ，表示元件吸收负功率，实际是发出功率。

（a ）图中，若0,0<>i u ，则0<=ui p ，表示元件实际发出功率。

在i u ,参考方向非关联的条件下，带入i u ,数值，经计算，若0>=ui p ，为正值，表示元件确实发出功率；若0<p ，为负值，表示元件发出负功率，实际是吸收功率。

《电路》考研邱关源版2021电路考研真题库第一部分考研真题精选一、选择题1图1-1-1所示电路中的电压源和电流源提供的功率分别为（）。

[南京航空航天大学2012年研]图1-1-1A．4W；6WB．－4W；－6WC．4W；－6WD．－4W；6W【答案】D查看答案【解析】由电流源发出电流可知，回路中电流为逆时针1A电流，电阻消耗功率为2×1＝2W，电压源发出功率为4×（－1）＝－4W。

电流源发出功率为2－（－4）＝6W。

2如图1-1-2所示二端网络的电压电流关系为（）。

[电子科技大学2012年研]图1-1-2A．U＝25＋IB．U＝25－IC．U＝－25－ID．U＝－25＋I【答案】C查看答案【解析】由节点KCL有流过1Ω电阻电流为（5＋I），则有：U＝－[（5＋I）×1＋20]＝－25－I。

3电路如图1-1-3所示，开关S自打开到闭合，电路内发生变化的是（）。

[电子科技大学2012年研]图1-1-3A．电压UB．电流IC．电压源的功率D．电流源的功率【答案】D查看答案【解析】开关S打开到闭合，左端干路上电流没有变化，电路上只有1Ω电阻的电流发生了变化，由2A变为0。

其消耗的功率仅由电流源提供，故电流源功率发生了变化。

4N A和N B均为含源线性电阻网络，在图1-1-4所示电路中3Ω电阻的端电压U应为（）。

[上海交通大学2005年研]图1-1-4A．不能确定B．－6VC．2VD．－2V【答案】C查看答案【解析】如图1-1-5所示。

图1-1-5a点的电流方程为i1＋i2＝2，网孔的电压方程为6i2－3i1－6＝0，可解出i1＝2/3 A，i2＝4/3 A，则U＝3×i1＝2V。

5如图1-1-6所示的电路中，影响U值的独立源应是（）。

[上海交通大学2005年研]图1-1-6A．I S1B．I S2D．U S2【答案】A查看答案【解析】由图1-1-7可得，在a点由KCL可得U ab/4＝U/3＋I S1＋0.5I，又U ab＝2×I－U，代入前式得U＝－12I S1/7。

邱关源《电路》（第5版）笔记和课后习题（含考研真题）详解完整版>精研学习wang>无偿试用20％资料全国547所院校视频及题库资料考研全套>视频资料>课后答案>往年真题>职称考试第1章电路模型和电路定律1.1复习笔记1.2课后习题详解1.3名校考研真题详解第2章电阻电路的等效变换2.1复习笔记2.2课后习题详解2.3名校考研真题详解第3章电阻电路的一般分析3.1复习笔记3.2课后习题详解3.3名校考研真题详解第4章电路定理4.1复习笔记4.2课后习题详解4.3名校考研真题详解第5章含有运算放大器的电阻电路5.1复习笔记5.2课后习题详解5.3名校考研真题详解第6章储能元件6.1复习笔记6.2课后习题详解6.3名校考研真题详解第7章一阶电路和二阶电路的时域分析7.1复习笔记7.2课后习题详解7.3名校考研真题详解第8章相量法8.1复习笔记8.2课后习题详解8.3名校考研真题详解第9章正弦稳态电路的分析9.1复习笔记9.2课后习题详解9.3名校考研真题详解第10章含有耦合电感的电路10.1复习笔记10.2课后习题详解10.3名校考研真题详解第11章电路的频率响应11.1复习笔记11.2课后习题详解11.3名校考研真题详解第12章三相电路12.1复习笔记12.2课后习题详解12.3名校考研真题详解第13章非正弦周期电流电路和信号的频谱13.1复习笔记13.2课后习题详解13.3名校考研真题详解第14章线性动态电路的复频域分析14.1复习笔记14.2课后习题详解14.3名校考研真题详解第15章电路方程的矩阵形式15.1复习笔记15.2课后习题详解15.3名校考研真题详解第16章二端口网络16.1复习笔记16.2课后习题详解16.3名校考研真题详解第17章非线性电路17.1复习笔记17.2课后习题详解17.3名校考研真题详解第18章均匀传输线18.1复习笔记18.2课后习题详解18.3名校考研真题详解。