空间几何证明

空间几何的证明与推理教学步骤和教学策略在数学教学中，空间几何的证明与推理是一个重要内容。

通过学习和运用几何证明和推理的方法，学生能够提高逻辑思维和问题解决能力。

本文将介绍空间几何的证明与推理的教学步骤和教学策略，帮助教师更好地引导学生进行几何推理。

一、教学步骤1.引入知识：教师可以通过提问和引导学生回顾已学知识，如平行线的性质、三角形的性质等，让学生建立起前后知识的联系。

2.概念解释：对于新学知识，教师应提供准确的定义和解释，让学生明确相关概念。

例如，在介绍平面内角的补、余角时，要给出相应的定义和示例。

3.定理陈述：教师可以从简单到复杂，逐步引入定理。

在陈述定理时，应给出合理的理由和证明方法，并鼓励学生思考和发现。

4.示例演练：引导学生通过具体的例子来巩固和应用所学知识。

教师可以设计一些典型的练习题，引导学生进行推理和证明。

5.概念联系：将学生已学的概念和定理联系起来，通过比较和分析不同概念之间的关系，帮助学生理解和应用知识。

6.问题拓展：提出一些拓展性问题，让学生运用所学知识进行解决。

教师可以组织小组讨论或个人思考，激发学生的想象力和创造力。

7.总结归纳：对于整个教学过程，教师应引导学生总结所学知识和解决问题的方法和思路，提高学生的思维能力和学习效果。

二、教学策略1.启发式教学：鼓励学生主动思考和探索，通过提出问题、观察现象和发现规律，引导学生形成自己的认知和理解。

2.互动合作：组织学生进行小组讨论、合作学习，促使学生相互交流、合作和互助，提高学生的学习效果和兴趣。

3.多样化教学：采用多种教学方法和教学资源，如演示、实物模型、电子课件等，激发学生的学习兴趣和积极性。

4.个性化辅导：注重学生的个别差异，根据学生的程度和需求给予针对性的辅导和指导，在教学过程中充分尊重学生的多样性。

5.形象化教学：通过图形、示意图等形象化方式来呈现抽象的几何概念和推理思路，有助于学生的理解和记忆。

6.巩固性训练：通过大量的练习和应用题，夯实学生对空间几何知识和推理方法的掌握，提高学生的解题能力和应用能力。

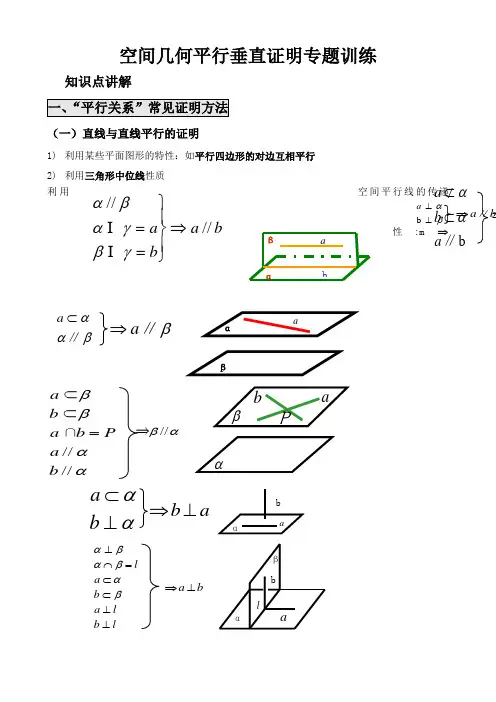
空间几何平行垂直证明专题训练知识点讲解一、“平行关系”常见证明方法（一）直线与直线平行的证明1) 利用某些平面图形的特性：如平行四边形的对边互相平行 2) 利用三角形中位线性质 利用空间平行线的传递性:m ⇒αα⊥⊂b a ab ⊥⇒αabβαaβαα∥⊂a β∥a ⇒ααββ////∩⊂⊂b a P b a b a =αβ//⇒αβbaPl abβαlb l a b a l ⊥⊥⊂⊂=⋂⊥βαβαβαba ⊥⇒a bαβb a b a ////⇒⎪⎭⎪⎬⎫==γβγαβαI I βα⊥⊥b a b a ∥⇒b∥a b a αα⊂⊄⇒αβ⊂⊥a a βα⊥⇒αβα⊥a ∥⇒图，在直三棱柱中，、分别是、的中点，求证： EF ∥平面ABC ； (两种方法证明)例2.如图，正三棱柱111ABC A B C -中，D 是BC 的中点， 求证：1A B //平面1ADC ．（两种方法证明） 方法一：方法二：3．如图，在底面为平行四边行的四棱锥P ABCD -中，点E 是PD 的中点.求证：//PB 平面AEC ；（两种方法证明）方法一：方法二：ca b a ⊥∥cb ⊥⇒balαAα⊥⇒⎪⎪⎭⎪⎪⎬⎫l bl a l A b a b a ⊥⊥=⊂⊂I ααβα⊥⇒la a l ⊥⊂=⋂⊥αβαβαα⊥b b a ∥α⊥⇒a αα∥b a ⊥ba ⊥⇒方法一：方法二：4.如图，E F O 、、分别为，，的中点，是的中点，求证：平面；（两种方法证明） 方法一：方法二：课后练习1.已知空间四边形ABCD 中，E,F,G,H 分别为AB,BC,CD,DA 的中点.求证：AC2.已知空间四边形ABCD 中，E,F,G,H 分别为AB,BC,CD,DA 的中点.求证：EF3.已知在四棱锥P-ABCD 中，ABCD 为平行四边形，E 为PC 的中点，O 为BD 的中点.求证：OE 知在四棱锥P-ABCD 中，ABCD 为平行四边形， E 为PC 的中点. 求证：PA 方体1111ABCD A B C D -中，,E G 分别是11,BC C D 中点.求证：//EG 平面11BDD B6.如图，在四棱锥O ABCD -中，底面ABCD 四边长为1的菱形， M 为OA 的中点，N 为BC 的中点 证明：直线MN ‖平面OCD ；7.在四棱锥P-ABCD 中，底面四边形ABCD 是平行四边形，E,F 分别是AB ，PD 的中点. 求证：//AF 平面PCE9．已知正方体ABCD —A 1B 1C 1D 1，O 是底ABCD 对角线的交点．求证： C 1O 图，在直三棱柱中，点在上，.求证：平面1A CD 平面.2.如图，正三棱柱111ABC A B C -中，D 是BC 的中点，．求证：直线111A D B C ⊥；3.如图，四棱锥的底面是正方形，，点E 在棱PB 上. 求证：平面；4.如图，直三棱柱中，AB=1，，∠ABC=︒60.求证：PBAC BD CA DE AFA5. 直三棱柱111ABC A B C -中，90BAC ∠=o ，12AB AC AA ===，M N 、分别是1BC CC 、的中点，求证：1B M ⊥平面AMN ；6.如图，在三棱锥中，⊿是等边三角形，∠PAC =∠PBC =90º。

∵ ，∴ ．
∵ ，∴ ．
又 ，∴ 平面CDF．
∵ 平面CDF，∴ ．
又 ， ，
∴ 平面ABE， ．
∵ ， ， ，
∴ 平面BCD．
考点：线面垂直的判定
考点：线面垂直的判定
7.证明：(1)由B1B∥DD1，得四边形BB1D1D是平行四边形，∴B1D1∥BD，
又BD平面B1D1C，B1D1 平面B1D1C，
∴BD∥平面B1D1C．
同理A1D∥平面B1D1C．
而A1D∩BD＝D，∴平面A1BD∥平面B1CD．
(2)由BD∥B1D1，得BD∥平面EB1D1．取BB1中点G，∴AE∥B1G．
6、如图，在正方体 中， 是 的中点.
（1）求证： 平面 ；
（2）求证：平面 平面 .
7、如图，在四棱锥 中，底面 是 且边长为 的菱形，侧面 是等边三角形，且平面 垂直于底面 ．
（1）若 为 的中点，求证： 平面 ；
3. 证明：连接 交 于 ，连接 ，
∵ 为 的中点， 为 的中点
∴ 为三角形 的中位线 ∴
又 在平面 ， 在平面 外
∴ 平面 。
考点：线面平行的判定
4.证明： °
又 面
面
又 面
考点：线面垂直的判定
5.证明：（1）连结 ，设 ，连结
∵ 是正方体 是平行四边形
∴A1C1∥AC且
又 分别是 的中点，∴O1C1∥AO且
是平行四边形
面 ， 面 ∴C1O∥面
（2） 面
又 ，
同理可证 ，又
面
考点：线面平行的判定（利用平行四边形），线面垂直的判定
从而得B1E∥AG，同理GF∥AD．∴AG∥DF．∴B1E∥DF．∴DF∥平面EB1D1．∴平面EB1D1∥平面FBD．

空间几何的位置关系与证明空间几何是研究空间中点、线、面等几何要素之间的位置关系的学科，广泛应用于建筑、工程、地理等领域。

在空间几何中，我们需要通过证明来得出准确的结论。

本文将介绍一些空间几何中的常见位置关系，并通过证明来解释它们。

一、点到点的位置关系在空间几何中，两个点之间可以存在不同的位置关系，常见的有以下几种情况：1. 两点重合：当两个点的坐标完全相同时，它们重合在同一个位置上。

我们可以通过计算两点的坐标来证明它们重合。

2. 两点重叠：当两个点的位置非常接近但不完全相同时，我们称它们为重叠。

通常我们需要通过测量两点之间的距离来证明它们的位置关系。

3. 两点相离：当两个点的位置远离并没有任何交集时，它们相离。

我们可以通过计算两点之间的距离来证明它们的位置关系。

二、线到线的位置关系在线到线的位置关系中，我们通常关注两条直线之间的相交情况。

下面是一些常见的情况：1. 直线相交：当两条直线在空间中相交于一个点时，我们称它们为相交。

要证明直线相交，我们可以找到它们的交点，并证明该交点在两条直线上。

2. 直线平行：当两条直线在空间中没有交点且始终保持相同的方向时，我们称它们为平行。

要证明直线平行，我们可以通过比较它们的斜率或者通过使用平行公理来证明。

3. 直线重合：当两条直线完全重合时，它们是同一条直线。

证明直线重合可以通过比较它们的方程或者通过验证它们上的两个点是否相同。

三、点到直线的位置关系点与直线之间的位置关系也是空间几何中的重要内容。

以下是一些常见的情况：1. 点在线上：当一个点与一条直线重合时，我们可以说该点在线上。

要证明一个点在线上，我们可以将该点的坐标代入直线的方程中，如果等式成立，则说明该点在线上。

2. 点在线上方或下方：对于一条直线，我们可以将它分为上方和下方两个区域。

对于一个点，如果它的纵坐标大于直线上所有点的纵坐标，我们称该点在直线上方；如果它的纵坐标小于直线上所有点的纵坐标，我们称该点在直线下方。

空间几何的计算与证明空间几何是研究三维空间中的物体形状、大小、位置等性质的数学学科。

在解决实际问题中，我们常常需要进行空间几何的计算与证明。

本文将介绍一些常见的空间几何计算方法和证明技巧。

一、空间几何计算1. 点到平面的距离计算对于三维空间中的一点P(x,y,z)，以及平面Ax+By+Cz+D=0，我们可以利用点P到平面的距离公式来计算二者的距离。

该公式为：d = |Ax+By+Cz+D| / √(A^2+B^2+C^2)例如，给定一个平面2x+y+3z-4=0，点P(1,2,3)到该平面的距离可以计算如下：d = |2*1+1*2+3*3-4| / √(2^2+1^2+3^2)= |2+2+9-4| / √14= 9 / √142. 直线和平面的交点计算对于直线和平面的交点计算，我们需要先求出直线的参数方程和平面的方程，然后解联立方程组即可得到交点的坐标。

例如，假设有一条直线L，其参数方程为：x = x_0 + lty = y_0 + mtz = z_0 + nt另外有一个平面P，其方程为：Ax + By + Cz + D = 0我们可以将直线的参数方程代入平面方程，得到一个关于t的一元二次方程，解该方程即可求得直线和平面的交点的坐标。

3. 多面体的表面积和体积计算对于多面体的表面积和体积计算，常用的方法是利用相应的公式进行计算。

例如，对于一个六面体，其表面积和体积的计算公式如下：六面体的表面积 S = 2(ab+ac+bc)六面体的体积 V = abc其中，a、b、c分别表示六面体的三个相邻棱长。

二、空间几何证明1. 平行线之间的角度在空间几何中，证明两条平行线之间的角度是一个重要问题。

一种常见的证明方法是利用平行线与平行线之间的交线来构造三角形，然后应用三角形的性质进行角度证明。

例如，我们希望证明两条平行直线L1和L2之间的夹角为90度。

我们可以构造一条与L1和L2都垂直的直线L3，然后证明L3与L1、L2之间的夹角都是90度，从而推出L1和L2之间的夹角也是90度。

空间几何的基本定理和证明空间几何是研究空间中点、线、面和体之间的位置、形态、大小、相对位置等性质的数学分支。

在空间几何中，有一些基本定理是我们必须要了解和掌握的。

本文将介绍几个常见的空间几何基本定理，并给出相应的证明。

一、平行线定理：平行线是位于同一平面内且不相交的两条直线。

在空间几何中，平行线间的关系有着重要的应用。

平行线定理如下：定理1：如果两条直线与第三条直线相交，且与第三条直线分别平行，则这两条直线互相平行。

证明：设直线l和m与直线n相交，且l与n平行，m与n平行。

我们需证明直线l与m平行。

根据平行线的定义，我们可以得到以下两组对应角相等关系：∠1 = ∠2，∠1 = ∠3；∠4 = ∠5，∠4 = ∠6。

现在我们来证明∠2 = ∠3 = ∠5 = ∠6，这样就证明了直线l与m平行。

根据同位角定理，我们可以得到：∠2 + ∠4 = 180°，∠3 + ∠6 = 180°。

将上述两个等式相加并整理得：∠2 + ∠4 + ∠3 + ∠6 = 360°。

由于∠2 = ∠3，∠4 = ∠5，∠5 = ∠6，代入上式我们可以得到：2∠2 + 2∠5 = 360°。

化简得：∠2 + ∠5 = 180°。

根据同位角的定义，∠2 + ∠5是直线l与m的内错角。

据直线外角定理，直线l与m的内错角相等，即∠2 + ∠5 = 180°。

因此，我们证明了直线l与m平行。

二、垂直定理：在空间几何中，垂直是指两个直线或线段相交时，交点的四个周围角都是直角（90°）。

垂直定理如下：定理2：直线和平面垂直的等价条件是直线上的任意一条直线垂直于平面。

证明：我们设直线l与平面P相交于点A，我们需要证明l上的任意一条直线垂直于平面P。

取直线l上任意一点B，连接OB。

构造平面Q，使得平面Q 过直线l且垂直于平面P。

则由垂直平面的性质得知，直线l就在平面Q内。

2023年高考数学考点复习——空间几何中的平行证明考点一、线线平行例1、如图，在四面体ABCD 中，E ，F 分别为DC ，AC 的中点，过EF 的平面与BD ，AB 分别交于点G ，H .求证：//EF GH证明：因为E ，F 分别为DC ，AC 的中点，所以//AD EF ，因为AD ⊄平面EFHG ，EF ⊂平面EFHG所以//AD 平面EFHG又平面EFHG ⋂平面ABD HG =，AD ⊂平面ABD所以//AD GH ，所以//EF GH .例2、如图，在四棱锥S -ABCD 中，底面ABCD 是菱形，60BAD ∠=︒，SAB ∆为等边三角形，G 是线段SB 上的一点，且SD //平面GAC .求证：G 为SB 的中点证明：证明：如图，连接BD 交AC 于点E ，则E 为BD 的中点，连接GE ，∵//SD 平面GAC ，平面SDB 平面=GAC GE ，SD ⊂平面SBD ，∵//SD GE ，而E 为BD 的中点，∵G 为SB 的中点.例3、在正四棱锥P ABCD -中，,E F 分别是,AB AD 的中点，过直线EF 的平面α分别与侧棱,PB PD 交于点,M N ，求证：//MN BD证明：证明：在ABD △中，因为E ，F 分别是,AB AD 的中点，所以EF BD ∕∕且12EF BD =， 又因为EF ⊄平面PBD ，BD ⊂平面PBD ，所以//EF 平面PBD因为EF ⊂平面,αα⋂平面PBD MN =，所以//EF MN ，所以//MN BD ．跟踪练习 1、如图，四边形ABCD 和三角形ADE 所在平面互相垂直，//AB CD ，AB BC ⊥，60DAB ∠=︒，4AB AD ==，AE DE ⊥，AE DE =，平面ABE 与平面CDE 交于EF ，求证：//CD EF证明：证明：因为//AB CD ，AB平面ABE ，CD ⊄平面ABE ，所以//CD 平面ABE ， 因为平面ABE 平面CDE EF =，CD ⊂平面CDE ，所以//CD EF .2、在四棱锥P ﹣ABCD 中，底面ABCD 为平行四边形E ，F 分别为BC ，AD 的中点，过EF 的平面与平面PCD 交于M ，N 两点，求证：//AB MN答案：证明见解析证明：∵底面ABCD 为平行四边形，E ，F 分别为BC ，AD 的中点，∵EF //CD ，∵EF //AB .EF ⊄平面PCD ，CD ⊂平面PCD ，所以//EF 平面PCD ，过EF 的平面与平面PCD 交于M ，N 两点，∵MN //EF ，∵AB //MN .3、如图，三棱锥P ABC -中，∵ABC 为正三角形，点1A 在棱PA 上，1B 、1C 分别是棱PB 、PC 的中点，直线11A B 与直线AB 交于点D ，直线11A C 与直线AC 交于点E ，求证：//DE BC证明：∵1B 、1C 分别是棱PB 、PC 的中点，∵11//B C BC ，∵11B C ⊄平面BCDE ，BC ⊂平面BCDE ，∵11//B C 平面BCDE ，∵11B C ⊂平面11B C DE ，平面BCDE ⋂平面11B C DE DE =，∵11//B C DE ，则//DE BC ；4、如图，四棱锥P ABCD -的底面是边长为8的正方形，点G.E.F .H 分别是棱PB ．AB ．DC ．PC 上共面的四点，//BC 平面GEFH.证明：//GH EF证明：∵//BC 平面GEFH ，又∵BC ⊂平面PBC 且平面PBC平面GEFH GH =，∵//BC GH .又∵//BC 平面GEFH ，又∵BC ⊂平面ABCD 且平面ABCD平面GEFH EF =，∵//BC EF ，∵//EF GH .5、如图，AE ⊥平面ABCD ，//BF 平面ADE ，//CF AE ，求证：//AD BC证明：依题意//CF AE ，CF ⊄平面ADE ，AE ⊂平面ADE ，∵//CF 平面ADE ，又//BF 平面ADE ，BF CF F ⋂=，∵平面//BCF 平面ADE ，∵平面BCF ⋂平面ABCD AD =，平面ADE平面ABCD BC =，∵//AD BC ；考点二、 线面平行例1、如图，正三棱柱ABC ﹣A 1B 1C 1中D 是AC 的中点，求证：B 1C ∵平面A 1BD证明：设AB 1与A 1B 相交于点P ，连接PD ，则P 为AB 1中点，∵D 为AC 中点，∵PD ∵B 1C ，又∵PD ∵平面A 1BD ，B 1C ⊄平面A 1BD ，∵B 1C ∵平面A 1BD例2、如图，在四棱锥A BCDE -中，底面BCDE 为矩形，M 为CD 中点，连接,BM CE 交于点,F G 为ABE △的重心，证明：//GF 平面ABC证明：延长EG 交AB 于N ，连接CN ，因为G 为ABE △的重心，则N 为AB 的中点，且2EG GN =， 因为//CM BE ，所以2EF BE FC CM ==，所以2EF EG FC GN==，因此//GF NC ， 又因为GF ⊄平面ABC ，NC ⊂平面ABC ，所以//GF 平面ABC ；例3、如图，四棱锥C ABED -中，四边形ABED 是正方形，若G ，F 分别是线段EC ，BD 的中点.（1）求证：//GF 平面ABC .证明：由四边形ABED 为正方形可知，连接AE 必与BD 相交于中点F ，又G 是线段EC 的中点，故//GF AC ，GF ⊄面ABC ，AC ⊂面ABC ，//GF ∴面ABC ；跟踪练习1、如图，在直三棱柱111ABC A B C -中，底面ABC 是等边三角形，D 是AC 的中点，证明：1//AB 平面1BC D证明：直三棱柱111ABC A B C -中，设1B C 与1BC 交于点E ，连接DE ，四边形11BCC B 是矩形，则E 为1B C 的中点，因D 是AC 的中点，所以1//DE AB ，又1AB ⊄平面1BC D ，DE ⊂平面1BC D ，所以1//AB 平面1BC D . 2、《九章算术》是我国古代的数学著作，是“算经十书”中最重要的一部，它对几何学的研究比西方要早1000多年.在《九章算术》中，将底面为直角三角形，且侧棱垂直于底面的三棱柱称为堑堵.如图，在堑堵111ABC A B C -中，，11AA AB AC ===，M ，N 分别是1CC ，BC 的中点，点P 在线段11A B 上，若P 为11A B 的中点，求证：//PN 平面11AAC C证明：证明：取11A C 的中点H ，连接PH ，HC .在堑堵111ABC A B C -中，四边形11BCC B 为平行四边形，所以11//B C BC 且11B C BC =.在111A B C △中，P ，H 分别为11A B ，11A C 的中点，所以11//PH B C 且1112PH B C =.因为N 为BC 的中点，所以12NC BC =， 从而NC PH =且//NC PH ， 所以四边形PHCN 为平行四边形，于是//PN CH .因为CH ⊂平面11AC CA ，PN ⊄平面11AC CA ，所以//PN 平面11AACC .3、如图，直四棱柱1111ABCD A B C D -的底面是菱形，12AA =，1AB =，E ，M ，N 分别是BC ，1BB ，1A D 的中点，证明：//MN 平面ABCD证明：连接1,ME B C ，,E M 分别为1,BC BB 中点，11//2ME B C ∴； 由直四棱柱特点知：11//A D B C ，11//2ME A D ∴，又N 为1A D 中点，//ME ND ∴， ∴四边形MNDE 为平行四边形，//MN DE ∴，又DE ⊂平面ABCD ，MN ⊄平面ABCD ，//MN ∴平面ABCD ；4、如图，在四棱锥P ABCD -中，四边形ABCD 是边长为2的菱形，M 是AB 的中点，N 是PD 的中点，PA AB =，求证：//MN 平面PBC证明：如图∵，取PC 的中点Q ，连接BQ ，NQ ，因为N 是PD 的中点，所以//NQ CD 且12NQ CD =.因为四边形ABCD 是菱形，M 是AB 的中点，所以//BM CD 且12BM CD =， 从而//BM NQ 且BM NQ =，所以四边形BMNQ 是平行四边形，从而//MN BQ .又MN ⊄平面PBC ，BQ ⊂平面PBC ，所以//MN 平面PBC . 5、如图，已知四边形ABCD 和BCEG 均为直角梯形，//AD BC ，//CE BG ，且2BCD BCE π∠=∠=，222BC CD CE AD BG =====，）求证：//AG 平面BDE答案：证明见解析证明：证明：过G 作GN CE ⊥于N ，交BE 于M ，连接DM ，如图所示：因为BC CE ⊥，且2CE BG =，所以N 为CE 中点，所以MG MN =，MNBC DA ，12MN AD BC ==， 所以MG AD ，MG AD =，所以四边形ADMG 为平行四边形，所以AG DM ，又DM ⊂平面BDE ，AG ⊄平面BDE ，所以AG 平面BDE .6、在四棱锥P —ABCD 中，AB //CD ，过CD 的平面分别交线段P A ，PB 于M ，N ，E 在线段DP 上(M ，N ，E 不同于端点)求证：CD //平面MNE证明：证明：∵//AB CD ，AB ⊂平面ABP ，CD ⊄平面ABP ∵//CD 平面ABP又∵CD ⊂平面CDMN ，平面CDMN 平面ABP MN =∵//CD MN又∵MN ⊂平面MNE ，CD ⊄平面MNE ∵//CD 平面MNE7、如图，在多面体ABCDEF 中，矩形BDEF 所在平面与正方形ABCD 所在平面垂直，1AB =，点M 为AE 的中点，求证：//BM 平面EFC证明：连接AC 交BD 于点N .连接MN .因为四边形ABCD 是正方形，所以N 为AC 的中点，由于M 为AE 的中点，所以//MN CE ， 又因为MN ⊄平面CEF ，CE ⊂平面CEF ，所以//MN 平面CEF ，易知//BN EF ，BN ⊄平面CEF ，EF ⊂平面CEF ，所以//BN 平面CEF ，因为MN BN N ⋂=，BN ⊂平面BMN ，MN ⊂平面BMN ，所以平面//BMN 平面CEF .又因为BM ⊂平面BMN ，所以//BM平面EFC ；8、在四棱锥P ABCD -中，底面ABCD 为梯形，//AB CD ，22AB CD ==，若Q 为AB 的中点，求证：//DQ 平面PBC证明：∵在梯形ABCD 中，//AB CD ，22AB CD ==，Q 为AB 的中点，所以//BQ CD 且BQ CD =，∵四边形BCDQ 为平行四边形，所以//DQ BC ，∵BC ⊂平面PBC ，DQ ⊄平面PBC ，所以//DQ 平面PBC ．9、如图所示，四面体P ABC 中，E ，F 分别为AB ，AC 的中点，过EF 作四面体的截面EFGH 交PC 于点G ，交PB 于点H ，证明：GH /平面ABC证明：∵E ，F 分别为AB ，AC 的中点,∵EF ∵BC ,又∵EF ∵平面PBC ,BC ∵平面PBC ,∵EF ∵平面PBC ,∵EF ∵平面EFGH ,平面EFGH ∩平面PBC =GH ,∵EF ∵GH ,又∵GH ∵平面ABC ,EF ∵平面ABC ,∵GH ∵平面ABC ;10、如图所示，在三棱柱111ABC A B C -中，D 为AC 的中点，求证：1//AB 平面1BC D证明：证明：如图，连接1B C 交1BC 于O ，连接OD ，∵四边形11BCC B 是平行四边形．∵点O 为1B C 的中点．∵D 为AC 的中点，∵OD 为1AB C 的中位线，∵1//OD AB ．∵OD ⊂平面1BC D ，1AB ⊄平面1BC D ，∵1//AB 平面1BC D ．11、如图，在四棱锥P ABCD -中，底面ABCD 是边长为2的正方形，PAB △为正三角形，且侧面PAB ⊥底面ABCD ，M 为PD 的中点，求证：//PB 平面ACM答案：证明见解析证明：证明：连接BD ，与AC 交于O ，在PBD △中，,O M 分别为,BD PD 的中点，//BP OM ∴,BP ⊄平面,ADE OM ⊂平面CAM ，//BP ∴平面CAM ；12、如图，在三棱柱111ABC A B C -中，侧面11ABB A 是菱形，E 是棱1BB 的中点，CA CB =，F 在线段AC 上，且2AF FC =，证明：1//CB 平面1A EF答案：证明见解析证明：连接1AB 交1A E 于点G ，连接FG ，因为四边形11ABB A 为菱形，则11//AA BB 且11AA BB =， E 为1BB 的中点，则11//B E AA 且1112B E AA =，故11112B G B E AG AA ==， 所以，1B G CF AG AF=，1//CB FG ∴， 1CB ⊄平面1A EF ，FG ⊂平面1A EF ，因此，1//CB 平面1A EF ；考点三、 面面平行例1、如图所示，四棱柱1111ABCD A B C D -的侧棱与底面垂直，12,,AC AA AD DC AC BD ====交于点E ，且,E F 分别为1,AC CC的中点，2BE =，求证：平面11//B CD 平面1A BD证明：如图，连接1AD ，设11AD A D H ⋂=，则H 为1AD 的中点，而E 为AC 的中点，连接EH ，则EH为1ACD △的中位线，所以1//EH CD ，又EH ⊄平面11B CD ，1CD ⊂平面11B CD ，所以//EH 平面11B CD ，又因为侧棱与底面垂直，所以1111//,=BB DD BB DD ，所以四边形11BB D D 为平行四边形，所以11//B D BD ，BD ⊄平面11B CD ，11B D ⊂平面11B CD ，所以//BD 平面11B CD ，又BD EH E ⋂=，,BD EH ⊂平面1A BD ，所以平面11//B CD 平面1A BD .例2、如图，在三棱锥P ABC -中，PAB △是正三角形，G 是PAB △的重心，D ，E ，H 分别是PA ，BC ，PC 的中点，点F 在BC 上，且3BF FC =，求证：平面//DFH 平面PGE证明：连结BG ，因为PAB △是正三角形，G 是PAB △的重心，D 为PA 的中点，所以BG 与GD 共线，且2BG GD =，因为E 为BC 的中点，3BF FC =，所以F 是CE 的中点， 所以2BG BE CD EF==，所以//GE DF ， 又GE平面PGE ，DF ⊄平面PGE ，所以//DF 平面PGE ， 因为H 是PC 的中点，所以FH //PE ，因为FH ⊄平面PGE ，PE ⊂平面PGE ，所以//FH 平面PGE ，因为FH DF F ⋂=，,FH DF ⊂平面DFH ，所以平面//DFH 平面PGE ；例3、如图，在多面体ABCDEF 中，ABCD 是正方形，2//AB DE BF BF DE ==，，，M 为棱AE 的中点，求证：平面//BMD 平面EFC证明：如图，连接AC ，交BD 于点N ，∵N 为AC 的中点，连接MN ，由M 为棱AE 的中点，则//MN EC ．∵MN ⊄面EFC ，EC ⊂面EFC ，∵//MN 平面EFC ．∵//BF DE BF DE =，，∵四边形BDEF 为平行四边形，∵//BD EF ．又BD ⊄平面EFC ，EF ⊂平面EFC ，∵//BD 平面EFC ，又MNBD N =， ∵平面//BMD 平面EFC ．跟踪练习1、如图，在几何体ABCDE 中，四边形ABCD 是矩形，2AB BE EC ===，G ，F ，M 分别是线段BE ，DC ，AB 的中点，求证：平面//GMF 平面ADE证明：如图，因为AB中点为M，连接MG，∥，又G是BE的中点，可知GM AE又AE⊆平面ADE，GM⊄平面ADE，所以GM平面ADE．在矩形ABCD中，由M，F分别是AB，CD的中点得MF AD．又AD⊆平面ADE，MF⊄平面ADE，所以MF平面ADE．⋂=，GM⊆平面GMF，MF⊆平面GMF，又因为GM MF M所以平面GMF平面ADE2、如图，四边形ABCD是边长为BB1＝DD1＝2，E，F分别是AD1，AB1的中点，证明：平面BDEF∵平面CB1D1证明：证明：连接AC ，交BD 于点O ，连接OE ，则O 为AC 的中点，∵E 是1AD 的中点，1//OE CD ∴OE ⊂平面BDEF ,1CD ⊄平面BDEF ,所以1//CD 平面BDEF又F 是1AB 的中点11//EF B D ∴EF ⊂平面BDEF ,11B D ⊄平面BDEF ,所以11//B D 平面BDEF又111,CD B D ⊂平面11CB D ,1111B D CD D ⋂=, 所以平面//BDEF 平面11CB D ．3、如图，已知矩形ABCD 所在的平面垂直于直角梯形ABPE 所在的平面，且EP =2BP =，1AD AE ==，AE EP ⊥，//AE BP ，F ，G 分别是BC ，BP 的中点，求证：平面//AFG 平面PEC证明：∵F ，G 分别是BC ，BP 的中点，∵FG CP ，且FG ⊄平面CPE ，则FG ∥平面CPE ，1BG PG AE ===，且//AE BP ，AE EP ⊥∵四边形AEPG 是矩形，则EP AG ∥，且AG ⊄平面CPE ，则AG平面CPE又GA GF G ⋂=，故平面//AFG 平面PEC4、如图，在四棱锥S -ABCD 中，底面ABCD 是直角梯形，AD //BC ，P ，Q 是AB ，CD 的中，点M ，N 分别是SB ，CB 的中点，求证∵平面AMN //平面SCD答案：证明见解析证明：因为M 、N 分别是SB ，CB 的中点，所以//MN SC ，MN ⊄面SCD ，SC ⊂面SCD ，所以//MN 面SCD ，又//AD CN 且AD CN =，所以ADCN 为平行四边形，所以//AN DC ，AN ⊄面SCD ，DC ⊂面SCD ，所以//AN 面SCD ，又AN MN N =，,AN MN ⊂面AMN ，所以面//AMN 面SCD ；5、如图，在三棱锥P ABC -中，PAB △是正三角形，G 是PAB △的重心，,,D E H 分别是,,PA BC PC 的中点，点F 在BC 上，且3BF FC =，求证：平面//DFH 平面PGE证明：证明：连结BG ，由题意可得BG 与GD 共线，且2BG GD =，∵E 是BC 的中点，3BF FC =，∵F 是CE 的中点，∵2BG BE GD EF==，∵//GE DF ，GE 平面PGE ；DF ⊄平面PGE ；∵//DF 平面PGE ， ∵H 是PC 的中点，∵//FH PE ，PE ⊂平面PGE ，FH ⊄平面PGE ；∵//FH 平面PGE ， ∵DF FH F =，DF ⊂平面DEF ，FH ⊂平面DEF ，∵平面//DFH 平面PGE ； 考点四 平行中的动点例1、直三棱柱111ABC A B C -所有棱长都为2，在AB 边上是否存在一点E ，使1//AC 平面1CEB ，若存在给出证明，若不存在，说明理由证明：存在，E 是AB 的中点，直三棱柱111ABC A B C -中，连接1BC 交1B C 于点O ，如图：则O 为1BC 中点，连接OE ，而E 为AB 的中点，则1//OE AC ，又1AC ⊄平面1CEB ，OE ⊂平面1CEB ，所以1//AC 平面1CEB ；例2、如图，在三棱柱111ABC A B C -中，1AA ⊥平面ABC ，90ACB ∠=︒，CA CB ==，1AA =D 是棱11A B 的中点，E 在棱1BB 上，且1AD EC ⊥，在棱BC 上是否存在点F ，满足//EF 平面1ADC ，若存在，求出BF 的值答案：存在，BF =证明：因为1AA ⊥面ABC ，故三棱柱111ABC A B C -为直三棱柱.故1AA ⊥面111A B C ，而1C D ⊂面111A B C ，故11AA C D ⊥，因为CA CB ==，故1111C A C B ==112B A =，因为D 是棱11A B 的中点，故111C D A B ⊥，因为1111AA A B A =， ∵直线1C D ⊥平面ADE ，而AD ⊂平面ADE ， ∵1C D AD ⊥，又1AD EC ⊥，111C D C E C ⋂=，∵AD ⊥平面1DEC ，而DE ⊂平面1DEC ，∵AD DE ⊥，在矩形11ABB A 中，11ADA DEB ∠=∠，11AA D DB E ∠=∠，故11ADA DEB ∠，故1111AA A D DB EB =11EB =即1=3EB ，故12BE EB =. 过E 作EG DE ⊥，交AB 于G ，取AB 的中点为L ，连接,DL CL ，则1DEB EGB ∠=∠，而190DB E EBG ∠=∠=︒，故1EBG DB E ， 所以11BG EB B E B D =31=，所以23BG =.在矩形11ABB A 中，因为11ADA DEB ∠=∠，故1ADA EGB ∠=∠，而1ADA DAL ∠=∠，所以EGB DAL ∠=∠，所以//AD EG ，而AD ⊂平面1ADC ，EG ⊄平面1ADC ，所以//EG 平面1ADC .在BC 上取点F ，使233BF BC ==，连GF ， 因为1BL =，故23BG BL =，故//GF CL . 在矩形11ABB A 中，因为,D L 为所在棱的中点，故11//,,DL AA DL AA =而1111//,,CC AA CC AA =故11//,CC DL CC DL =，故四边形1C DLC 为平行四边形，故1//DC CL ，故1//GF DC ，而1C D ⊂平面1ADC ，FG ⊄平面1ADC ，所以//FG 平面1ADC .因为GF EG G ⋂=，故平面以//EGF 平面1ADC ，因为EF ⊂平面EGF ，故//EF 平面1ADC .例3、如图，已知AD ⊥平面ABC ，EC ⊥平面ABC ，12AB AC AD BC ===，设P 是直线BE 上的点，当点P 在何位置时，直线//DP 平面ABC ？请说明理由证明：当点P 是BE 的中点时，//DP 平面ABC .理由如下：如下图，取BC 的中点O ，连接AO 、OP 、PD ，则//OP EC 且12OP EC =，因为AD ⊥平面ABC ，EC ⊥平面ABC ，所以//AD EC . 又12AD EC =，所以//OP AD 且OP AD =， 所以四边形AOPD 是平行四边形，所以//DP AO .因为AO ⊂平面ABC ，DP ⊄平面ABC ，所以//DP 平面ABC ；跟踪练习1、在三棱锥S ABC -中，AB ⊥平面SAC ，AS SC ⊥，1AB =，AC =，E 为AB 的中点，M 为CE 的中点，在线段SB 上是否存在一点N ，使//MN 平面SAC ？若存在，指出点N 的位置并给出证明，若不存在，说明理由证明：存在点N 为SB 上的靠近S 的四等分点即14SN SB =，//MN 平面SAC ， 证明如下：取AE 的中点F ，连接FN ，FM ，则//MF AC ，因为AC ⊂平面SAC ，MF ⊄平面SAC ，所以//MF 平面SAC ， 因为1124AF AE AB ==，14SN SB =， 所以FN //SA ，又SA ⊂平面SAC ，FN ⊄平面SAC ，所以//FN 平面SAC ，又MF FN F =，,MF FN ⊂平面MNF ，所以平面//MNF 平面SAC ，又MN ⊂平面MNF ，所以//MN 平面SAC ．2、在如图所示的五面体ABCDEF 中，∵ADF 是正三角形，四边形ABCD 为菱形，23ABC π∠=，EF //平面ABCD ，AB =2EF =2，点M 为BC 中点，在直线CD 上是否存在一点G ，使得平面EMG //平面BDF ，请说明理由证明：连接AC 交BD 于点O ，连接OM ，OF ，取CD 的中点G ，连接GM ，GE因为EF //平面ABCD ，EF ⊂平面ABEF ，平面ABEF ∩平面ABCD =AB ，所以EF //AB因为OM //AB //EF ，12OM AB EF ==，所以四边形OMEF 是平行四边形，所以OF //EM 因为EM ⊄平面BDF ，OF ⊂平面BDF ，所以EM //平面BDF因为点G 与点M 分别为CD 与BC 的中点，所以GM //BD因为GM ⊄平面BDF ，BD ⊂平面BDF ，所以GM //平面BDF而GM ∩EM =M ，平面EMG //平面BDF3、在长方体1111ABCD A B C D -中，已知AB AD =，E 为AD 的中点，）在线段11B C 上是否存在点F ，使得平面1//A AF 平面1ECC ？若存在，请加以证明，若不存在，请说明理由证明：存在，当点F 为线段11B C 的中点时，平面1//A AF 平面1ECC .证明：在长方体1111ABCD A B C D -中，11//AA CC ，11//AD B C .又因为1CC ⊂平面1ECC ，1AA ⊄平面1ECC ，所以1//AA 平面1ECC .又E 为AD 的中点，F 为11B C 的中点，所以1//AE FC ，且1AE FC =.故四边形1AEC F 为平行四边形，所以1//AF EC ，又因为1EC ⊂平面1ECC ，AF ⊄平面1ECC ，所以//AF 平面1ECC .又因为1AF AA A =，1AA ⊂平面1A AF ，AF ⊂平面1A AF ，所以平面1//A AF 平面1ECC .4、如图所示，在三棱柱ABC ﹣A 1B 1C 1中，平面ACC 1A 1∵平面ABC ，AA 1∵AC ，D ，D 1分别为AC ，A 1C 1的中点且AD =AA 1，在棱AA 1上找一点M ，使得1//D M 平面1DBC ，并说明理由答案：M 与A 重合时，1//D M 面1DBC ，理由见解析证明：当M 与A 重合时，D 1M ∵面DBC 1，理由如下：∵D 1C 1∵AD ，且D 1C 1=AD ，∵四边形D 1C 1DA 为平行四边形，∵D 1A ∵C 1D ，因为C 1D ∵面BDC 1，∵D 1M ∵面DBC 1.5、如图，在三棱锥P ABC -中，PA ⊥底面ABC ，ABC 是正三角形，E 是棱AB 的中点，如1AE =，在平面PAC 内寻找一点F 使得//BF 平面PEC ，并说明理由答案：答案见解析.证明：延长AC 至点G ，使得AC CG =，延长AP 至点H ，使得AP PH =，连接GH ，在直线GH 上任取一点F ，则点F 满足BF ∥平面PEC .理由如下： E 是线段AB 的中点，C 是线段AG 的中点，CE ∴是ABG 的中位线，∴BG CE ∥，BG ∴∥平面PEC .同理HG平面PEC ， 又BG HG G =，∴平面BHG平面PEC ， BF ⊂平面BHG ，BF ∴∥平面PEC .(注：若此题点F 直接取H 或G ，理由充分，给6分)6、已知四棱柱1111ABCD A B C D -的底面是边长为2的菱形，且BC BD =，1DD ⊥平面ABCD ，11AA =，BE CD ⊥于点E ，试问在线段11A B 上是否存在一点F ，使得//AF 平面1BEC ？若存在，求出点F 的位置；若不存在，请说明理由；证明：当F 为线段11A B 的中点时，//AF 平面1BEC .下面给出证明：取AB 的中点G ，连接EG ，1B G ，则1//FB AG ，且1FB AG =，所以四边形1AGB F 为平行四边形，所以1//AF B G .因为BC BD =，BE CD ⊥，所以E 为CD 的中点，又G 为AB 的中点，//AB CD ，AB CD =，所以//BG CE ，且BG CE =， 所以四边形BCEG 为平行四边形，所以//EG BC ，且EG BC =，又11//BC B C ，11BC B C =， 所以11//EG B C ，且11EG B C =，所以四边形11EGB C 为平行四边形， 所以11//B G C E ，所以1//AF C E ，又AF ⊄平面1BEC ，1C E ⊂平面1BEC ，所以//AF 平面1BEC ，7、在正三棱柱111ABC A B C -中，已知12,3AB AA ==，M ，N 分别为AB ，BC 的中点，P 为线段1CC 上一点．平面1ABC 与平面ANP 的交线为l ，是否存在点P 使得1//C M 平面ANP ？若存在，请指出点P 的位置并证明；若不存在，请说明理由证明：当2CP =时，1//C P 平面ANP证明如下：连接CM 交AN 于点G ，连接GP ，因为12CG CP GM PC ==，所以1//C M GP 又∵GP ⊂平面ANP ，1C M ⊄平面ANP ∵1C M 平面ANP。

l ml m
☺ 简称：线面垂直，线线垂直.
精选ppt
15
复习定理
空间中的垂直
3．平面与平面垂直判定
判定：如果一个平面经过另一个平面的一条垂线,则这两个 平面互相垂直.
b
b
b
☺ 简称：线面垂直，面面垂直.
精选ppt
16
复习定理
空间中的垂直
4．平面与平面垂直性质
性质：如果两个平面互相垂直，则其中一个平面内垂直于 交线的直线必垂直于另一个平面.
13
复习定理
空间中的垂直
1．直线与平面垂直判定
判定：如果一条直线和一个平面内的两条相交直线都垂 直,则称这条直线和这个平面垂直.
l P mn
m
n m
n
P
l .
l m
l n
☺ 简称：线线垂直，线面垂直.
精选ppt
14
复习定理
空间中的垂直
2．直线与平面垂直性质
判定：如果一条直线和一个平面垂直,则称这条直线和这 个平面内任意一条直线都垂直.
分析： (1)证明线面平行只需在平面内找一条和 该直线平行的直线即可，也可转化为经过这条直线 的平面和已知平面平行；(2)证明面面垂直，只需在 一个平面内找到另一个平面的垂线.
精选ppt
21
(1) 证明 如图所示，取线段 BC 的中点 F，
连接 EF、FD.
在△PBC 中，E、F 分别为 PC、CB 的中点，
∵AA1C1C为矩形，则E为AC1的中点． 又D是AB的中点，
∴在△ABC1中，DE∥BC1.
E
又DE⊂平面CA1D，
BC1⊄平面CA1D，
∴BC1∥平面CA1D.
精选ppt

空间几何导数证明一、课程目标知识目标：1. 让学生掌握空间几何导数的定义及其相关性质，理解导数在几何图形中的应用。

2. 使学生能够运用空间几何导数证明相关几何问题，如曲线、曲面的切线与法线等。

技能目标：1. 培养学生运用空间几何导数解决实际问题的能力，提高他们的几何直观和逻辑思维能力。

2. 培养学生通过团队合作，共同探讨和解决复杂几何问题的能力。

情感态度价值观目标：1. 培养学生对空间几何导数证明的兴趣，激发他们探索几何奥秘的热情。

2. 培养学生面对困难时，保持积极向上的心态，勇于克服挑战。

课程性质分析：本课程为高中数学课程，以空间几何为基础，重点探讨导数在空间几何中的应用和证明。

学生特点分析：高中学生已具备一定的空间想象能力和逻辑思维能力，但对空间几何导数证明可能仍感到陌生，需要引导和启发。

教学要求：1. 注重理论与实践相结合，引导学生通过具体实例理解空间几何导数的概念。

2. 鼓励学生积极参与讨论，培养他们的团队协作能力和创新意识。

3. 注重培养学生的几何直观，提高他们运用导数解决几何问题的能力。

二、教学内容本章节教学内容依据课程目标，结合教材《高中数学》相关章节，组织如下：1. 空间几何导数的定义与性质：讲解空间曲线、曲面的切线与法线概念，引入空间几何导数，阐述其相关性质。

2. 空间几何导数的计算方法：通过具体实例，教授空间几何导数的计算方法，包括求导法则、链式法则等。

3. 空间几何导数在几何问题中的应用：运用空间几何导数解决实际问题，如求曲线、曲面的切线方程、法线方程等。

4. 空间几何导数的证明方法：引导学生掌握空间几何导数证明的基本方法，包括直接证明、反证法、归纳法等。

教学大纲安排如下：第一课时：空间几何导数的定义与性质第二课时：空间几何导数的计算方法第三课时：空间几何导数在几何问题中的应用第四课时：空间几何导数的证明方法教学进度安排：第一周：第一、二课时第二周：第三课时第三周：第四课时教学内容关联教材章节：《高中数学》第四章 空间几何第四节 空间几何导数的概念与性质第五节 空间几何导数的计算与应用第六节 空间几何导数的证明方法三、教学方法针对本章节内容，采用以下多样化的教学方法，以激发学生学习兴趣和主动性：1. 讲授法：教师以清晰、生动的语言，系统讲解空间几何导数的定义、性质、计算方法和证明方法，为学生奠定坚实的理论基础。

空间几何的基本定理与证明在几何学中，空间几何是研究三维空间中的图形、点、线、面以及它们之间的关系的一个分支。

空间几何的基本定理是我们理解和解决复杂几何问题的基础。

本文将介绍一些空间几何的基本定理，并提供相应的证明，以帮助读者更好地理解这些重要概念。

### 定理一：平行线的平行公理在空间几何中，平行线的平行公理是一个基本的前提。

这个公理表明，如果在同一平面内有一条直线和一点，那么可以通过这一点引一条唯一的直线，与给定的直线平行。

**证明：**给定一条直线L和一点P，在L上选择一个任意点A。

现在，通过点P作一条线段AP，并且以A为中心，作一个半径为AP的圆，记作Γ。

该圆与直线L交于一点B。

我们要证明的是，直线PB与直线L平行。

首先，考虑三角形APB和三角形APB'，其中B'是直线L上的另一点，且与点A相距等于AP。

由于Γ是以A为中心，以AP为半径作的圆，因此AP和AP'是圆的两条半径，它们相等。

另外，AB和AB'分别是Γ的切线，因此它们与半径的夹角相等。

根据三角形的一侧和两个角相等，我们可以得出三角形APB与三角形APB'是全等的，这意味着∠APB和∠APB'相等。

又因为∠APB'是直线L上的角，所以∠APB与直线L平行。

因此，我们证明了通过点P引出的直线PB与给定的直线L平行，这证明了平行线的平行公理。

### 定理二：直线垂直平分线段这个定理表明，如果一条直线垂直于一段线段，并且将该线段平分成两等长的线段，那么这条直线通过线段的中点。

**证明：**给定一条线段AB，以及一条直线L，L垂直于线段AB并将其平分成两等长的线段。

我们要证明直线L通过线段AB的中点M。

首先，连接线段AB的两个端点A和B，并延长直线L，交线段AB的延长线于点P。

因为L垂直于线段AB，所以∠APB是直角。

现在，考虑三角形AMP和三角形BMP。

由于L平分了线段AB，所以AM和MB的长度相等，即AM = MB。

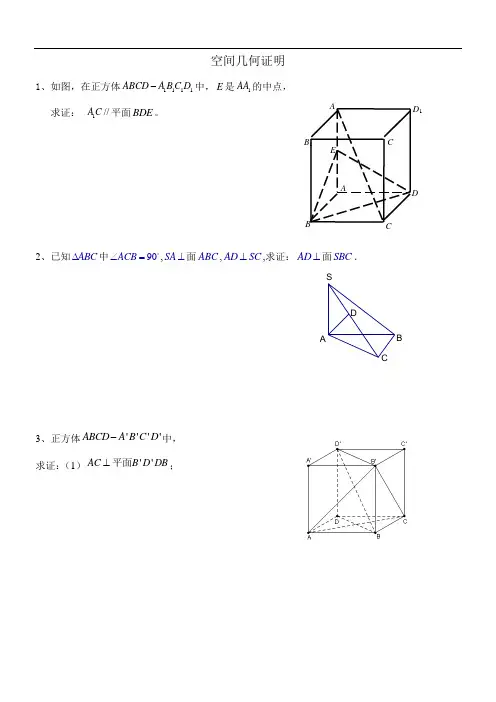
必修二空间几何证明经典练习题型一．解答题（共25小题）1．如图，在四棱锥P﹣ABCD中，AB∥CD，AB⊥AD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD．E 和F分别是CD和PC的中点，求证：（Ⅰ）BE∥平面PAD；（Ⅰ）PA⊥BC；（Ⅰ）平面BEF⊥平面PCD．【解答】解：（Ⅰ）∵PA⊥AD，平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，由平面和平面垂直的性质定理可得PA⊥平面ABCD．（Ⅰ）∵AB∥CD，AB⊥AD，CD=2AB，E和F分别是CD和PC的中点，故四边形ABED为平行四边形，故有BE∥AD．又AD⊂平面PAD，BE不在平面PAD内，故有BE∥平面PAD．（Ⅰ）平行四边形ABED中，由AB⊥AD可得，ABED为矩形，故有BE⊥CD．由PA⊥平面ABCD，可得PA⊥AB，再由AB⊥AD可得AB⊥平面PAD，∴CD⊥平面PAD，故有CD⊥PD．再由E、F分别为CD和PC的中点，可得EF∥PD，∴CD⊥EF．而EF和BE是平面BEF内的两条相交直线，故有CD⊥平面BEF．由于CD⊂平面PCD，∴平面BEF⊥平面PCD．2．如图，在三棱锥V﹣ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC=BC=，O，M分别为AB，VA的中点．（Ⅰ）求证：VB∥平面M OC；（Ⅰ）求证：平面MOC⊥平面VAB；（Ⅰ）求三棱锥A﹣MOC的体积．【解答】（Ⅰ）证明：∵O，M分别为AB，VA的中点，∴OM∥VB，∵VB⊄平面MOC，OM⊂平面MOC，∴VB∥平面MOC；（Ⅰ）证明：∵AC=BC，O为AB的中点，∴OC⊥AB，又∵平面VAB⊥平面ABC，平面ABC∩平面VAB=AB，且OC⊂平面ABC，∴OC⊥平面VAB，∵OC⊂平面MOC，∴平面MOC⊥平面VAB；（Ⅰ）解：在等腰直角三角形ACB中，AC=BC=，∴AB=2，OC=1，=，∴等边三角形VAB的边长为2，S△VAB∵O，M分别为AB，VA的中点．∴．又∵OC⊥平面VAB，∴三棱锥．3．如图，在三棱锥P﹣ABC中，PA⊥PC，AB=PB，E，F分别是PA，AC的中点．求证：（1）EF∥平面PBC；（2）平面BEF⊥平面PAB．【解答】证明：（1）在△APC中，因为E、F分别是PA、AC的中点，所以EF∥PC，…（3分）又PC⊂平面PAC，EF⊄平面PAC，所以EF∥平面PBC．…（6分）（2）因为AB=PB，且点E是PA的中点，所以PA⊥BE，…（9分）又PA⊥PC，EF∥PC，所以PA⊥EF，…（12分）因为BE⊂平面BEF，EF⊂平面BEF，BE∩EF=E，所以PA⊥平面BEF，又PA⊂平面PAB，所以平面PAB⊥平面BEF．…（14分）合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．【解答】证明：（1）因为AB⊥AD，EF⊥AD，且A、B、E、F四点共面，所以AB∥EF，又因为EF⊂平面ABC，AB⊂平面ABC，所以由线面平行判定定理可知：EF∥平面ABC；（2）在线段CD上取点G，连结FG、EG使得FG∥BC，则EG∥AC，因为BC⊥BD，FG∥BC，所以FG⊥BD，又因为平面ABD⊥平面BCD，所以FG⊥平面ABD，所以FG⊥AD，又因为AD⊥EF，且EF∩FG=F，所以AD⊥平面EFG，所以AD⊥EG，故AD⊥AC．5．已知四棱锥A﹣BCDE，其中AB=BC=AC=BE=1，CD=2，CD⊥面ABC，BE∥CD，F为AD的中点．（Ⅰ）求证：EF∥面ABC；（Ⅰ）求证：平面ADE⊥平面ACD；（Ⅰ）求四棱锥A﹣BCDE的体积．【解答】证明：（Ⅰ）取AC中点G，连接FG、BG，∵F，G分别是AD，AC的中点∴FG∥CD，且FG=DC=1．∵BE∥CD∴FG与BE平行且相等∴EF∥BG．EF⊄面ABC，BG⊂面ABC∴EF∥面ABC…（4分）（Ⅰ）∵△ABC为等边三角形∴BG⊥AC∴BG垂直于面ADC的两条相交直线AC，DC，∴BG⊥面ADC．…（6分）∵EF∥BG∴EF⊥面ADC∵EF⊂面ADE，∴面ADE⊥面ADC．…（8分）解：（Ⅰ）方法一：连接EC，该四棱锥分为两个三棱锥E﹣ABC和E﹣ADC．．…（12分）方法二：取BC的中点为O，连接AO，则AO⊥BC，又CD⊥平面ABC，∴CD⊥AO，BC∩CD=C，∴AO⊥平面BCDE，的高，，∴．∴AO为V A﹣BCDE6．如图，四棱柱ABCD﹣A1B1C1D1中，平面A1ABB1⊥平面ABCD，且∠ABC=．（1）求证：BC∥平面AB1C1；（2）求证：平面A1ABB1⊥平面AB1C1．【解答】证明：（1）∵BC∥B1C1，且B1C1⊂平面AB1C1，BC⊄平面AB1C1，∴BC∥平面AB1C1．（2）∵平面A1ABB1⊥平面ABCD，平面ABCD∥平面A1B1C1D1，∴平面A1ABB1⊥平面A1B1C1D1，∵平面A1ABB1∩平面A1B1C1D1=A1B1，A1B1⊥C1B1，∴C1B1⊂平面AB1C1，∴平面A1ABB1⊥平面AB1C1．7．如图，三角形ABC中，AC=BC=，ABED是边长为1的正方形，平面ABED⊥底面ABC，若G、F分别是EC、BD的中点．（Ⅰ）求证：GF∥底面ABC；（Ⅰ）求证：AC⊥平面EBC；（Ⅰ）求几何体ADEBC的体积V．【解答】解：（I）证法一：取BE的中点H，连接HF、GH，（如图）∵G、F分别是EC和BD的中点∴HG∥BC，HF∥DE，（2分）又∵ADEB为正方形∴DE∥AB，从而HF∥AB∴HF∥平面ABC，HG∥平面ABC，HF∩HG=H，∴平面HGF∥平面ABC∴GF∥平面ABC（5分）证法二：取BC的中点M，AB的中点N连接GM、FN、MN（如图）∵G、F分别是EC和BD的中点∴（2分）∴GM∥NF且GM=NF∴MNFG为平行四边形∴GF∥MN，又MN⊂平面ABC，∴GF∥平面ABC（5分）证法三：连接AE，∵ADEB为正方形，∴AE∩BD=F，且F是AE中点，（2分）∴GF∥AC，又AC⊂平面ABC，∴GF∥平面ABC（5分）（Ⅰ）∵ADEB为正方形，∴EB⊥AB，∴GF∥平面ABC（5分）又∵平面ABED⊥平面ABC，∴BE⊥平面ABC（7分）∴BE⊥AC又∵CA2+CB2=AB2∴AC⊥BC，∵BC∩BE=B，∴AC⊥平面BCE（9分）（Ⅰ）连接CN，因为AC=BC，∴CN⊥AB，（10分）又平面ABED⊥平面ABC，CN⊂平面ABC，∴CN⊥平面ABED．（11分）∵三角形ABC是等腰直角三角形，∴，（12分）∵C﹣ABED是四棱锥，∴V C==（14分）﹣ABED8．如图，在直三棱柱ABC﹣A1B1C1中，BC⊥AC，D，E分别是AB，AC的中点．（1）求证：B1C1∥平面A1DE；（2）求证：平面A1DE⊥平面ACC1A1．【解答】证明：（1）因为D，E分别是AB，AC的中点，所以DE∥BC，…（2分）又因为在三棱柱ABC﹣A1B1C1中，B1C1∥BC，所以B1C1∥DE…（4分）又B1C1⊄平面A1DE，DE⊂平面A1DE，所以B1C1∥平面A1DE…（6分）（2）在直三棱柱ABC﹣A1B1C1中，CC1⊥底面ABC，又DE⊂底面ABC，所以CC1⊥DE…（8分）又BC⊥AC，DE∥BC，所以DE⊥AC，…（10分）又CC1，AC⊂平面ACC1A1，且CC1∩AC=C，所以DE⊥平面ACC1A1…（12分）又DE⊂平面A1DE，所以平面A1DE⊥平面ACC1A1…（14分）9．如图，在多面体ABCDEF中，四边形ABCD是菱形，AC，BD相交于点O，EF∥AB，EF=AB，平面BCF⊥平面ABCD，BF=CF，G为BC的中点，求证：（1）OG∥平面ABFE；（2）AC⊥平面BDE．【解答】证明：（1）∵四边形ABCD是菱形，AC，BD相交于点O，∴O是AC中点，∵G为BC的中点，∴OG∥AB，∵OG⊄平面ABFE，AB⊂平面ABFE，∴OG∥平面ABFE．（2）∵四边形ABCD是菱形，AC，BD相交于点O，∴AC⊥BD，O是AC中点，∵G为BC的中点，∵EF∥AB，EF=AB，平面BCF⊥平面ABCD，BF=CF，∴FG⊥平面ABCD，∴EO⊥平面ABCD，∴EO⊥AC，∵EO∩BD=O，∴AC⊥平面BDE．10．如图所示，四棱锥P﹣ABCD的底面为直角梯形，AB⊥AD，CD⊥AD，CD=2AB．点E是PC的中点．（Ⅰ）求证：BE∥平面PAD；（Ⅰ）已知平面PCD⊥底面ABCD，且PC=DC．在棱PD上是否存在点F，使CF⊥PA？请说明理由．【解答】（1）证明：取PD中点Q，连结AQ、EQ．…（1分）∵E为PC的中点，∴EQ∥CD且EQ=CD．…（2分）又∵AB∥CD且AB=CD，∴EQ∥AB且EQ=AB．…（3分）∴四边形ABED是平行四边形，∴BE∥AQ．…（4分）又∵BE⊄平面PAD，AQ⊂平面PAD，∴BE∥平面PAD．…（5分）（2）解：棱PD上存在点F为PD的中点，使CF⊥PA，∵平面PCD⊥底面ABCD，平面PCD∩底面ABCD=CD，AD⊥CD，∴AD⊥平面PCD，∴DP是PA在平面PCD中的射影，∴PC=DC，PF=DF，∴CF⊥DP，∴CF⊥PA．11．如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的正方形，侧面PAD⊥底面ABCD，且PA=PD= AD，E、F分别为PC、BD的中点．（1）求证：EF∥平面PAD；（2）求证：面PAB⊥平面PDC．为PC中点．所以在△CPA中，EF∥PA，又PA⊂平面PAD，EF⊄平面PAD，所以EF∥平面PAD；（2）平面PAD⊥平面ABCD平面PAD∩面ABCD=AD⇒CD⊥平面PAD⇒CD⊥PA正方形ABCD中CD⊥ADPA⊂平面PADCD⊂平面ABCD又，所以PA2+PD2=AD2所以△PAD是等腰直角三角形，且，即PA⊥PD．因为CD∩PD=D，且CD、PD⊂面PDC所以PA⊥面PDC又PA⊂面PAB，所以面PAB⊥面PDC．12．在长方体ABCD﹣A1B1C1D1中，AB=BC=EC=．求证：（1）AC1∥平面BDE；（2）A1E⊥平面BDE．【解答】解：（1）ABCD﹣A1B1C1D1是长方体，AB=BC=EC=．可得平面ABCD和平面A1B1C1D1是正方形，E为CC1的中点．连接AC与DB交于O，连接OE，可得：AC1∥OE，OE⊂平面BDE．∴AC1∥平面BDE．（2）连接OA1，根据三垂线定理，可得OA1⊥DB，OE⊥DB，OA1∩OE=O，可得A1E⊥DB．∵E为CC1的中点．设AB=BC=EC=AA1=a∴，A1E=，A1B=∵A1B2=A1E2+BE2．∴A1E⊥EB．∵EB⊂平面BDE．BD⊂平面BDE．EB∩BD=B，∴A1E⊥平面BDE13．如图，ACQP所在的平面与菱形ABCD所在的平面相互垂直，交线为AC，若分别是PQ，CQ的中点．求证：（1）CE∥平面PBD；（2）平面FBD⊥平面PBD．【解答】证明：（1）设AC∩BD=O，连接PO，则∵O是AC的中点，E是PQ的中点，∴PE=OC，PE∥OC，∴四边形POCE是平行四边形，∴CE∥PO，∵CE⊄平面PBD，PO⊂平面PBD，∴CE∥平面PBD；（2）∵平面ACQP⊥平面ABCD，平面ACQP∩平面ABCD=AC，BD⊥AC，∴BD⊥平面ACQP，∵PO⊂平面ACQP，∴BD⊥PO，连接AQ，OF，则由三角形相似可AQ⊥PO，∵F是CQ中点，O是AC的中点，∴OF∥AQ，∴OF⊥PO，∵BD∩OF=O，∴PO⊥平面FBD，∴平面FBD⊥平面PBD．14．已知直四棱柱ABCD﹣A1B1C1D1的底面是菱形，F为棱BB1的中点，M为线段AC1的中点．求证：（Ⅰ）直线MF∥平面ABCD；（Ⅰ）平面AFC1⊥平面ACC1A1．【解答】（本小题满分12分）证明：（Ⅰ）延长C1F交CB的延长线于点N，连接AN．因为F是BB1的中点，所以，F为C1N的中点，B为CN的中点．又M是线段AC1的中点，故MF∥AN．又MF不在平面ABCD内，AN⊂平面ABCD，∴MF∥平面ABCD．（Ⅰ）连BD，由直四棱柱ABCD﹣A1B1C1D1 ，可知A1A⊥平面ABCD，又∵BD⊂平面ABCD，∴A1A⊥BD．∵四边形ABCD为菱形，∴AC⊥BD．又∵AC∩A1A=A，AC，A1A⊂平面ACC1A1，∴BD⊥平面ACC1A1．在四边形DANB中，DA∥BN且DA=BN，所以四边形DANB为平行四边形，故NA∥BD，∴NA⊥平面ACC1A1，又因为NA⊂平面AFC1，∴平面AFC1⊥ACC1A1．15．如图，四棱锥P﹣ABCD中，AD⊥平面PAB，AP⊥AB．（1）求证：CD⊥AP；（2）若CD⊥PD，求证：CD∥平面PAB．【解答】（本小题满分14分）证明：（1）因为AD⊥平面PAB，AP⊂平面PAB，所以AD⊥AP．…（2分）又因为AP⊥AB，AB∩AD=A，AB⊂平面ABCD，AD⊂平面ABCD，所以AP⊥平面ABCD．…（4分）因为CD⊂平面ABCD，所以CD⊥AP．…（6分）（2）因为CD⊥AP，CD⊥PD，且PD∩AP=P，PD⊂平面PAD，AP⊂平面PAD，所以CD⊥平面PAD．①…（8分）因为AD⊥平面PAB，AB⊂平面PAB，所以AB⊥AD．又因为AP⊥AB，AP∩AD=A，AP⊂平面PAD，AD⊂平面PAD，所以AB⊥平面PAD．②…（10分）由①②得CD∥AB，…（12分）因为CD⊄平面PAB，AB⊂平面PAB，所以CD∥平面PAB．…（14分）16．如图，四棱锥P﹣ABCD的底面是矩形，PA⊥平面ABCD，E，F分别是AB，PD的中点，且PA=AD．（Ⅰ）求证：AF∥平面PEC；（Ⅰ）求证：平面PEC⊥平面PCD．【解答】证明：（Ⅰ）取PC的中点G，连结FG、EG，∴FG为△CDP的中位线，FG∥CD，FG=CD．∵四边形ABCD为矩形，E为AB的中点，∴AE∥CD，AE=CD．∴FG=AE，FG∥AE，∴四边形AEGF是平行四边形，∴AF∥EG又EG⊂平面PCE，AF⊄平面PCE，∴AF∥平面PCE；（Ⅰ）∵PA=AD．∴AF⊥PDPA⊥平面ABCD，∴PA⊥CD，又因为CD⊥AB，AP∩AB=A，∴CD⊥面APD∴CD⊥AF，且PD∩CD=D，∴AF⊥面PDC由（Ⅰ）得EG∥AF，∴EG⊥面PDC又EG⊂平面PCE，∴平面PEC⊥平面PCD．17．如图，三棱柱ABC﹣A1B1C l中，M，N分别为CC1，A1B1的中点．CA⊥CB1，CA=CB1，BA=BC=BB1．（Ⅰ）求证：直线MN∥平面CAB1；（Ⅰ）求证：直线BA1⊥平面CAB1．【解答】证明：（Ⅰ）设A1B与AB1交于点O，连接CO，ON．因为四边形ABB1A1是平行四边形，所以是O是AB1的中点，又N是A1B1的中点，所以．ON又因为M是CC1的中点，所以．所以四边形CMNO是平行四边形，所以MN∥CO．又因为MN⊄平面CAB1，CO⊂CAB1平面，所以直线NM∥平面CAB1．…（6分）（Ⅰ）因为BA=BB1，所以平行四边形ABB1A1是菱形，所以BA1⊥AB1．因为CA=CB1，O是AB1的中点，所以CO⊥AB1，又CA⊥CB1，∴CO=AO．又因为BA=BC，所以△BOC≌△BOA，所以∠BOC=∠BOA，故BO⊥CO，即BA1⊥CO．又AB1∩CO=O，AB1⊂平面CAB1，CO⊂平面CAB1，所以直线BA1⊥平面CAB1．…（12分）18．如图，正三角形ABE与菱形ABCD所在的平面互相垂直，AB=2，∠ABC=60°，M是AB的中点，N是CE的中点．（I）求证：EM⊥AD；（II）求证：MN∥平面ADE；（III）求点A到平面BCE的距离．【解答】证明：（Ⅰ）∵EA=EB，M是AB的中点，∴EM⊥AB，（1分）∵平面ABE⊥平面ABCD，平面ABE∩平面ABCD=AB，EM⊂平面ABE，∴EM⊥平面ABCD，（4分）∵AD⊂平面ABCD，∴EM⊥AD．（5分）（Ⅰ）取DE的中点F，连接AF，NF，∵N是CE的中点．，∴NF CD，∵M是AB的中点，∴AM，∴NF AM，∴四边形AMNF是平行四边形，（7分）∴MN∥AF，（8分）∵MN⊄平面ADE，AF⊂平面ADE，∴MN∥平面ADE．（10分）解：（III）设点A到平面BCE的距离为d，由（I）知ME⊥平面ABC，BC=BE=2，MC=ME=，则CE=，BN==，（12分）∴，=，=V E﹣ABC，（13分）即，∵V A﹣BCE解得d=，故点A到平面BCE的距离为．（14分）19．在四棱锥P﹣ABCD中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，DC=2AB=2AD，BC⊥PD，E，F分别是PB，BC的中点．求证：（1）PC∥平面DEF；（2）平面PBC⊥平面PBD．【解答】证明：（1）∵E，F分别是PB，BC的中点，∴PC∥EF，又PC⊄平面DEF，EF⊂平面DEF，∴PC∥平面DEF．（2）取CD的中点M，连结BM，则AB DM，又AD⊥AB，AB=AD，∴四边形ABMD是正方形，∴BM⊥CD，BM=CM=DM=1，BD=，∴BC=，∴BD2+BC2=CD2，∴BC⊥BD，又BC⊥PD，BD∩PD=D，∴BC⊥平面PBD，又BC⊂平面PBC，∴平面PBC⊥平面PBD．20．如图，菱形ABCD与正三角形BCE的边长均为2，且平面ABCD⊥平面BCE，FD⊥平面ABCD，．（I）求证：EF∥平面ABCD；（II）求证：平面ACF⊥平面BDF．【解答】证明：（Ⅰ）如图，过点E作EH⊥BC于H，连接HD，∴．∵平面ABCD⊥平面BCE，EH⊂平面BCE，平面ABCD∩平面BCE=BC，∴EH⊥平面ABCD，又∵FD⊥平面ABCD，，∴FD∥EH，FD=EH．∴四边形EHDF为平行四边形．∴EF∥HD．∵EF⊄平面ABCD，HD⊂平面ABCD，∴EF∥平面ABCD．…（7分）（Ⅰ）∵FD⊥面ABCD，∴FD⊥AC，又四边形ABCD是菱形，∴AC⊥BD，又FD∩BD=D，∴AC⊥面FBD，又AC⊂面ACF，从而面ACF⊥面BDF．…（12分）21．如图，在直三棱柱ABC﹣A1B1C1中，AC⊥BC，A1B与AB1交于点D，A1C与AC1交于点E．求证：（1）DE∥平面B1BCC1；（2）平面A1BC⊥平面A1ACC1．【解答】证明：（1）由题意，D，E分别为A1B，A1C的中点，∴DE∥BC，∵DE⊄平面B1BCC1，BC⊂平面B1BCC1，∴DE∥平面B1BCC1；（2）∵AA1⊥平面ABC，BC⊂平面ABC，∴AA1⊥BC，∵AC⊥BC，AC∩AA1=A，∴BC⊥平面A1ACC1，∵BC⊂平面A1BC，∴平面A1BC⊥平面A1ACC1．22．如图，在多面体ABCDPE中，四边形ABCD和CDPE都是直角梯形，AB∥DC，PE∥DC，AD⊥DC，PD⊥平面ABCD，AB=PD=DA=2PE，CD=3PE，F是CE的中点．（1）求证：BF∥平面ADP（2）已知O是BD的中点，求证：BD⊥平面AOF．【解答】证明：（1）作FM⊥CD，垂足为M，连接BM，则DM=2PE=AB，EM∥PD∵DM∥AB，∴DMBA是平行四边形，∴BM∥AD，∵BM⊄平面ADP，AD⊂平面ADP∴BM∥平面ADP同理EM∥平面ADP∵BM∩EM=M．∴平面BFM∥平面ADP∵BF⊂平面BFM，∴BF∥平面ADP；（2）由（1）可知FM=PE，DM=BM=2PE，∴FD=FB=PE，∵O是BD的中点，∴FO⊥BD，∵AD=AB，O是BD的中点，∴AO⊥BD，∵AO∩FO=O，∴BD⊥平面AOF．23．如图，在几何体ABCDEF中，底面ABCD为矩形，EF∥CD，CD⊥EA，CD=2EF=2，ED=．M为棱FC上一点，平面ADM与棱FB交于点N．（Ⅰ）求证：ED⊥CD；（Ⅰ）求证：AD∥MN；（Ⅰ）若AD⊥ED，试问平面BCF是否可能与平面ADMN垂直？若能，求出的值；若不能，说明理由．【解答】（Ⅰ）证明：因为ABCD为矩形，所以VD⊥AD．[（1分）]又因为CD⊥EA，[（2分）]所以CD⊥平面EAD．[（3分）]所以ED⊥CD．[（4分）]（Ⅰ）证明：因为ABCD为矩形，所以AD∥BC，[（5分）]所以AD∥平面FBC．[（7分）]又因为平面ADMN∩平面FBC=MN，所以AD∥MN．[（8分）]（Ⅰ）解：平面ADMN与平面BCF可以垂直．证明如下：[（9分）]连接DF．因为AD⊥ED，AD⊥CD．ED∩CD=D，所以AD⊥平面CDEF．[（10分）]所以AD⊥DM．因为AD∥MN，所以DM⊥MN．[（11分）]因为平面ADMN∩平面FBC=MN，若使平面ADMN⊥平面BCF，则DM⊥平面BCF，所以DM⊥FC．[（12分）]在梯形CDEF中，因为EF∥CD，DE⊥CD，CD=2EF=2，ED=，所以DF=DC=2．所以若使DM⊥FC能成立，则M为FC的中点．所以=．[（14分）]24．如图，在三棱锥A﹣BCD中，E，F分别为BC，CD上的点，且BD∥平面AEF．（1）求证：EF∥平ABD面；（2）若AE⊥平面BCD，BD⊥CD，求证：平面AEF⊥平面ACD．【解答】证明：（1）∵BD∥平面AEF，BD⊂平面BCD，平面BCD∩平面AEF=EF，∴BD∥EF，又BD⊂平面ABD，EF⊄平面ABD，∴EF∥平ABD面．（2）∵AE⊥平面BCD，CD⊂平面BCD，∴AE⊥CD，由（1）可知BD∥EF，又BD⊥CD，∴EF⊥CD，又AE∩EF=E，AE⊂平面AEF，EF⊂平面AEF，∴CD⊥平面AEF，又CD⊂平面ACD，∴平面AEF⊥平面ACD．25．如图，四棱锥P﹣ABCD中，底面ABCD是平行四边形，且平面PAC⊥平面ABCD，E为PD的中点，PA=PC，AB=2BC=2，∠ABC=60°．（Ⅰ）求证：PB∥平面ACE；（Ⅰ）求证：平面PBC⊥平面PAC．【解答】证明：（Ⅰ）连接BD，交AC于点O，连接OE，∵底面ABCD是平行四边形，∴O为BD中点，又E为PD中点，∴OE∥PB，又OE⊂平面ACE，PB⊄平面ACE，∴PB∥平面ACE．（Ⅰ）∵PA=PC，O为AC中点，∴PO⊥AC，又平面PAC⊥平面ABCD，平面PAC∩平面ABCD=AC，PO⊂平面PAC，∴PO⊥平面ABCD，又BC⊂平面ABCD，∴PO⊥BC．在△ABC中，AB=2BC=2，∠ABC=60°，∴=，∴AC2=AB2+BC2，∴BC⊥AC．又PO⊂平面PAC，AC⊂平面PAC，PO∩AC=O，∴BC⊥平面PAC，又BC⊂平面PBC，∴平面PBC⊥平面PAC．。

P
M A
H D
B
N
C
空间中的平行
定理应用
构造平行平面
P
M
A
Q
D
B
N
C
空间中的平行
复习定理
空间中的垂直
解决空间直线与平面垂直的相关问题，特别要注意下面的 转化关系：
线线垂直
空间垂直之间的转化
①
③
②
线面垂直
④
面面垂直
复习定理
空间中的垂直
1．直线与平面垂直判定
判定：如果一条直线和一个平面内的两条相交直线都垂 直,则称这条直线和这个平面垂直.
a //
a


a
//
b
b
☺ 简称：线面平行，线线平行.
复习定理
空间中的平行
3.平面与平面平行的判定与性质
➳判定: 一个平面内的两条相交直线与另一个平面 平行，则这两个平面平行．
a,b
a a
//
b


A


//

b //
☺ 简称：线面平行，面面平行.
又AA1∩AB＝A， ∴CD⊥平面AA1B1B.
又CD⊂平面CA1D， ∴平面CA1D⊥平面AA1B1B.
例 2. 如图所示，在四棱锥 P—ABCD 中， △PAB 为正三角形，且面 PAB⊥面 ABCD， 四边形 ABCD 是直角梯形，且 AD∥BC， ∠BCD＝π4，AD＝1，BC＝2，E 为棱 PC 的中点． (1)求证：DE∥平面 PAB； (2)求证：平面 PAB⊥平面 PBC；
F
构造平面法
(1) 证明 如图所示，取线段 PB 的中点 H， 连接 EH、ＡＨ.

空间几何证明举例1．（典型例题）如图，在四棱锥P-ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD=DC ，E 是PC 的中点，作EF ⊥PB 于点F.（1）证明：PA//平面EDB ； （2）证明：BP ⊥平面EFD ；[对症下药]（1）如图，连接AC 、AC 交BD 于O ，连接EO 。

∵底面ABCD 为正方形，∴O 为AC 的中点，在△PAC 中，EO是中位线，∴PA//EO ，又EO ⊂平面EDB ，且PA ⊄平面EDB ，所以PA//平面EDB ；（2）∵PD ⊥平面ABCD ，∴平面PDC ⊥平面ABCD ，又底面ABCD 为正方形，∴BC ⊥CD ，∴BC ⊥平面PCD ，∴BC ⊥DE ，又DE ⊥PC ，∴DE ⊥平面PBC ，∴DF 在平面PBC 上的射影为EF ，又EF ⊥PB ，∴DF ⊥PB ，又PB ⊥EF ，∴PB ⊥平面DEF ；（3）由（2）知，PB ⊥DF ，故∠EFD 是二面角C —PB —D 的平面角。

由（2）知，DE ⊥EF ，PD ⊥DB ，设正方形ABCD 的边长为a 则PD=DC=a ，BD=2a ，PB=3a ，PC=2a,DE=21PC=a 22,在Rt △PDBk ,OF=a PB BD PD 36=∙.在Rt △EFD 中，sin ∠EFD=23=DF DE ,∴∠EFD=.3π所以二面角C —PB —D 的大小为.3π2.（典型例题）如图10-4所示，在正三棱锥A —BCD 中，∠BAC=30°，AB=a ，平行于AD 、BC 的截面EFGH 分别交AB 、BD 、DC 、CA 于E 、F 、G 、H 。

（1）判定四边形EFGH 的形状，并说明理由；（2）设P 是棱AD 上的点，当AP 为何值时，平面PBC ⊥平面EFGH ，请给出证明。

[专家把脉]正三棱锥的性质不熟悉而出错，正三棱锥的相对的棱互相垂直；正三棱锥的三个侧面是等腰三角形不是等边三角形。

高三文科数学复习资料一．选择题1.(2010湖北文数)用a、b、c表示三条不同的直线，y表示平面，给出下列命题：①若a∥b，b∥c，则a∥c；②若a⊥b，b⊥c，则a⊥c；③若a∥y，b∥y，则a∥b；④若a⊥y，b⊥y，则a∥b.A. ①②B. ②③C. ①④D.③④2．（2010山东文数）在空间，下列命题正确的是（）.A．平行直线的平行投影重合B．平行于同一直线的两个平面平行C．垂直于同一平面的两个平面平行D．垂直于同一平面的两条直线平行3、（2010年山东卷）在空间，下列命题正确的是（A）平行直线的平行投影重合 (B)平行于同一直线的两个平面（C）垂直于同一平面的两个平面平行（D）垂直于同一平面的两个平面平行二、解答题：1. （2011年高考山东卷文科19)（本小题满分12分）如图，在四棱台1111ABCD A B C D -中，1D D ⊥平面ABCD ，底面ABCD 是平行四边形，AB=2AD ，11AD=A B ，BAD=∠60°.（Ⅰ）证明：1AA BD ⊥； （Ⅱ）证明：11CC A BD ∥平面.2 （2011年高考全国新课标卷文科18)（本小题满分12分） 如图，四棱锥P-ABCD 中，底面ABCD 为平行四边形，︒=∠60DAB ，ABCD PD AD AB 底面⊥=,2， （1）证明：BD PA ⊥; (2) 设，1==AD PD 求三棱锥D-PBC 锥的高.3. （2011年高考福建卷文科20)（本小题满分12分）如图，四棱锥P-ABCD 中，PA ⊥底面ABCD ，AB ⊥AD ，点E 在线段AD 上，且CE ∥AB 。

（1） 求证：CE ⊥平面PAD ；（11）若PA =AB =1，AD =3，CDCDA =45°，求四棱锥P-ABCD 的体积4. （2011年高考湖北卷文科18)如图，已知正三棱柱111ABC A B C -的底面边长为2，侧棱长为E 在侧棱1AA 上，点F 在侧棱1BB 上，且222==BF ，AE .(Ⅰ)求证：E C CF 1⊥(Ⅱ)求二面角 1C CF E --的大小.5.(2010重庆文数)如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥底面ABCD，PA AB ==E 是棱PB 的中点.证明：AE ⊥平面PBC ；6．（2010湖南文数）如图所示，在长方体1111ABCD A B C D -中，AB =AD =1，AA 1=2，M 是棱CC 1的中点．证明：平面ABM ⊥平面A 1B 1M ．7、（2010年全国卷）如图，已知四棱锥P ABCD -的底面为等腰梯形，AB ∥CD ,AC BD ⊥,垂足为H ，PH 是四棱锥的高。

空间几何证明基本方法空间几何证明是几何学中的一个重要部分，旨在通过逻辑推理和数学推导来证明空间中的几何定理。

本文将介绍空间几何证明的基本方法，帮助读者更好地理解和运用这些方法。

一、引言在进行空间几何证明之前，我们需要了解一些基本概念和前提条件。

比如，我们需要熟悉空间中的点、线、面等基本要素，同时需要了解一些几何定理和性质。

在进行证明时，我们可以利用这些定理和性质来推导出需要证明的结论。

二、直线平行证明方法直线平行是几何中常见的证明题型之一。

下面将介绍两种常用的直线平行证明方法：方法一：使用等角定理在给定的平面中，首先找到一对平行线，并证明它们与另一条线的夹角相等。

然后以这个夹角为基础，通过角的关系推导出所需要证明的两条直线为平行关系。

方法二：使用垂直定理在给定的平面中，找到一条直线与给定的两条直线垂直相交。

然后通过证明两对垂直的对应角相等，进而推导出所需要证明的两条直线相互平行。

三、三角形相似证明方法三角形相似是空间几何中常见的证明题型之一。

下面将介绍两种常用的三角形相似证明方法：方法一：使用AAA相似定理如果两个三角形的对应角分别相等，那么这两个三角形是相似的。

在证明中，我们需要找到一组对应的角分别相等的三角形，并通过这些相等角的关系来推导出所需要证明的三角形是相似的。

方法二：使用AA相似定理如果两个三角形的其中两个角分别相等，那么这两个三角形是相似的。

在证明中，我们需要找到一组对应的角分别相等的三角形，并通过这些相等角的关系来推导出所需要证明的三角形是相似的。

四、圆相关证明方法在空间几何中，圆是一种特殊的几何形状，其证明方法也与其他几何形状有所不同。

下面将介绍两种常用的圆相关证明方法：方法一：使用切割定理如果一条直线与一个圆相切，那么切点与圆心的连线垂直于这条直线。

在证明中，我们可以通过找到与圆相切的某条直线，并证明其切点与圆心的连线垂直，从而得出所需要证明的结论。

方法二：使用弦切角定理在圆内部或外部，如果一条弦与一条切线相交，那么相交的角是半弧所对的角的一半。

一、空间几何证明八大定理1.直线与平面平行的判定定理(1)文字语言:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.(2)符号语言:ααα//,,//l l a a l ⇒⊄⊂.(3)图形语言:2.平面与平面平行的判定定理(1)文字语言:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.(2)符号语言:βαββ//,//,//⇒=P b a b a (3)图形语言:(1)文字语言:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.(2)符号语言:ba b a a //,,//⇒=⊂βαβα (3)图形语言:4.平面与平面平行的性质定理(1)文字语言:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.(2)符号语言:ba b a //,,//⇒==γβγαβα(3)图形语言:(1)文字语言:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.(2)符号语言:ααα⊥⇒=⊂⊂⊥⊥l P b a b a b l a l ,,,,(3)图形语言:6.平面与平面垂直的判定定理(1)文字语言:一个平面过另一个平面的垂线,则这两个平面垂直.(2)符号语言:βαβα⊥⇒⊂⊥,,l l (3)图形语言:(1)文字语言:垂直于同一个平面的两条直线平行.(2)符号语言:ba b a //,,⇒⊥⊥αα(3)图形语言:8.平面与平面垂直的性质定理(1)文字语言:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.(2)符号语言:βαβαβα⊥⇒⊥⊂=⊥a l a a l ,,, (3)图形语言:二、关于角的范围1.异面直线所成的角的范围是︒︒≤<900θ.2.直线与平面所成的角的范围是︒︒≤≤900θ.3.二面角的取值范围是︒︒≤≤1800θ.4.直线倾斜角的范围是︒︒<≤1800θ.。

AC1//AC,AB//CD1,BC1//AD1 AC1∩AB≠∅……所以得证
方法二：建立空间直角坐标系：两平面的法向量平行（不再举例）
证明线线平行
方法一：平行于同一直线的两直线平行
方法二：两平行平面，另一平面与这两平面相交，两条交线平行
方法三：建立空间直角坐标系
其实建立空间直角坐标系方法是万能的，不过用在有些题目中会比较麻烦，不如其他方法简便。
方法二：找到直线所在的平面与该平面平行
取点H使EH//AB,由题意可知B1E=C1F ,AE=BF,根据△AB1B≌△C1BB1,
有B1E/C1F =AE/BF=B1H/HB ,所以FH//
方法三：建立空间直角坐标系：平面的法向量与直线所在向量的数量积等于0
数学笔记：空间几何—证明平行
以下题为例讲解证明线面平行,面面平行的方法
证明线面平行
方法一：找到平面内一直线与该直线平行
作EG//B1B , FH//C1C
由题意可知AE=BF,且在正方体中△AB1B≌△BC1C
所以EG平行且等于FH ,EFHG是平行四边形
找到了面ABCD中的直线GH与EF平行,所以得证
以……为原点,……分别为X,Y,Z轴,设AB=1,E(0,t,1-t)
,F(1-t,0,1-t),得出EF(1-t,-t,0)
求出面ABCD的法向量（这题可直接看出来）n=（0,0,1）
n*EF=0 ,所以得证
证明面面平行
方法一：找到一个平面内的两条直线分别平行另一个平面内的两条直线
（如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。）