振动及频谱分析基础培训

振动分析培训计划下载温馨提示：该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help yousolve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts,other materials and so on, want to know different data formats and writing methods, please pay attention!振动分析在工程实践中扮演着重要的角色，它可以帮助工程师们深入了解结构的振动特性，从而指导设计和维护工作。

第二章简谐振动与频谱分析基础引子－混合动力汽车起步抖振简谐振动与频谱分析基础引子－混合动力汽车起步抖振2013-09-14简谐振动与频谱分析基础引子－混合动力汽车起步抖振2013-09-14简谐振动与频谱分析基础5 2.1简谐振动及其表示方法2013-09-14简谐振动与频谱分析基础2.1.1 简谐振动的正弦函数表示法sin()x A t ω=ATTt()x t 2013-09-14简谐振动与频谱分析基础2.1.1 简谐振动的正弦函数表示法sin()x A t ω=T Tsin(x A =t()x t Asin(x A =φω2.1.1 简谐振动的正弦函数表示法2.1.1 简谐振动的正弦函数表示法位移2.1.1 简谐振动的正弦函数表示法2013-09-14简谐振动与频谱分析基础2.1.1 简谐振动的正弦函数表示法简谐振动与频谱分析基础132.1.2 简谐振动的旋转矢量表示方法tφω=()x t ω角位移相位周期2π2.1.3 简谐振动的复数表示方法2.1.3 简谐振动的复数表示方法欧拉公式:2.1.3 简谐振动的复数表示方法虚部–sine wave实部–cosine wave2013-09-14简谐振动与频谱分析基础2.1.3 简谐振动的复数表示方法2.2周期振动的谐波分析2.2.1 谐波分析的概念2.2.2 周期振动的傅立叶级数2.2.2 周期振动的傅立叶级数（续）2.2.2 周期振动的傅立叶级数（续）2.2.2 周期振动的傅立叶级数（续）2.2.2 周期振动的傅立叶级数（续）例题：对图示周期方波作谐波分析，并绘制频谱图。

2.2.2 周期振动的傅立叶级数（续）2. 三要素:2.2.2 周期振动的傅立叶级数（续）2.2.2 周期振动的傅立叶级数（续）2013-09-14简谐振动与频谱分析基础2.2.2 周期振动的傅立叶级数（续）2013-09-14简谐振动与频谱分析基础2.2.2 周期振动的傅立叶级数（续）2013-09-14简谐振动与频谱分析基础2.2.2 周期振动的傅立叶级数（续）回顾周期振动的傅立叶级数回顾周期振动的傅立叶级数（续）2.2.3 傅立叶级数的复数形式2.2.3 傅立叶级数的复数形式(续)∞ax2.2.3 傅立叶级数的复数形式(续)a-ib2.2.3 傅立叶级数的复数形式(续)⎫⎛2.2.3 傅立叶级数的复数形式(续)2.2.3 傅立叶级数的复数形式(续)例题：求图示周期性矩形脉冲波的复数形式的傅立叶级数，并绘制频谱图。

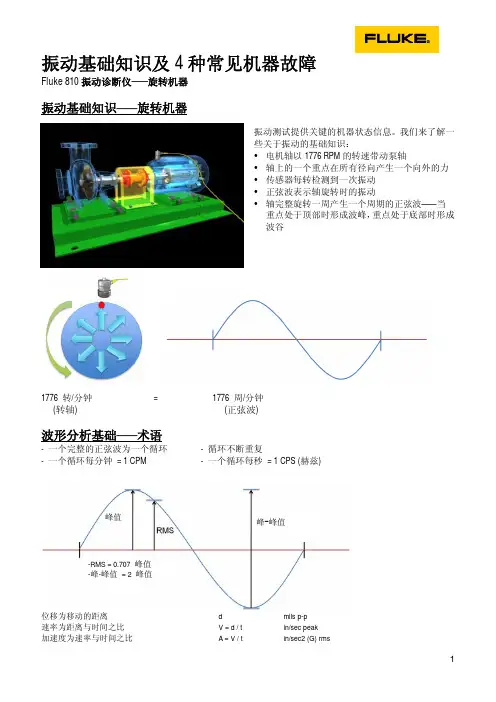
Fluke 810振动诊断仪——旋转机器振动基础知识——旋转机器振动测试提供关键的机器状态信息。

我们来了解一些关于振动的基础知识：y电机轴以1776 RPM的转速带动泵轴y轴上的一个重点在所有径向产生一个向外的力y传感器每转检测到一次振动y正弦波表示轴旋转时的振动y轴完整旋转一周产生一个周期的正弦波——当重点处于顶部时形成波峰，重点处于底部时形成波谷周/分钟1776 转/分钟 = 1776(转轴) (正弦波)波形分析基础——术语循环不断重复- 一个完整的正弦波为一个循环 -- 一个循环每分钟= 1 CPM - 一个循环每秒= 1 CPS (赫兹)峰值峰-峰值-RMS = 0.707 峰值-峰-峰值 = 2 峰值位移为移动的距离 d mils p-p速率为距离与时间之比V = d / t in/sec peak加速度为速率与时间之比 A = V / t in/sec2 (G) rmsFluke 810振动诊断仪——旋转机器机器部件y该泵有10个轮叶y轴每旋转一周，传感器检测到10次叶片振动y正弦波显示10次完整的循环，形成幅度较小的轴正弦波y振动水平较小意味着幅度低于轴振动y由于主轴的质量大，将导致振动强于叶轮10 次振动每转= 10 个循环每转(转轴) (正弦波)复合波形如果我们将两个正弦波(轴和泵轮)叠加在一起，将形成以下波形：- 1 次轴转动- 10 次泵轮振动但实际上振动彼此叠加，更像以下波形：真实旋转机器的20次或30次振动可能是如下波形：Fluke 810振动诊断仪——旋转机器频率(谱)分析y 波形含有关于被测机器的信息 y 但不同事件的模式相互叠加，杂乱无序——太复杂FFTy 采用快速傅里叶变换(FFT)方法，可将采集的波形从时域(幅值与时间关系)转换至频域(幅值与频率关系)。

幅值幅值y 由于特定的振动幅值可与机器的运行速度紧密相关，所以频谱简化了数据的理解。

事件 频率 • 由测试仪执行变换，简化波形 • 频谱是信号幅值(y 轴)与频率(x 轴)的关系曲线 • 这些尖峰处于特定的频率，表示机器正在发生的现象。