下载文档原格式
光的干涉和衍射练习题计算干涉和衍射的光强分布首先，让我们回顾一下光的干涉和衍射。
光的干涉是指两束或多束光波叠加在一起形成干涉图样的现象，而光的衍射是指光通过一个小孔或者绕过一个障碍物后产生的弯曲或扩散的现象。
我们将通过一些练习题来计算干涉和衍射的光强分布。
练习题1：单缝衍射设有一个宽度为a的单缝，缝宽为d，光波的波长为λ，观察屏幕与缝的距离为L。
求在屏幕上某一点的光强分布。
解答：根据夫琅禾费衍射公式，我们可以计算出在屏幕上某一点的光强分布。
公式如下：I(θ) = I0 * (sin(πd sinθ / λ)/(πd sinθ /λ))^2其中，I(θ)代表在观察屏幕上观察到的光强，I0代表缝的中央处光强的最大值，θ代表观察角度。
练习题2：双缝干涉设有两个宽度为a的缝，缝宽为d，两缝间距为D，光波的波长为λ，观察屏幕与缝的距离为L。
求在屏幕上某一点的光强分布。
解答：公式如下：I(θ) = 4I0 * cos^2(πd sinθ / λ) * cos^2(πD sinθ / λ) / (π^2 (d sinθ /λ)^2)其中，I(θ)代表在观察屏幕上观察到的光强，I0代表缝的中央处光强的最大值，θ代表观察角度。
练习题3：菲涅尔双棱镜干涉设有一对菲涅尔双棱镜，棱镜角为α，光波的波长为λ，观察屏幕与双棱镜的距离为L。
求在屏幕上某一点的光强分布。
解答：根据菲涅尔双棱镜干涉的理论，我们可以计算出在屏幕上某一点的光强分布。
公式如下：I = I0 * (sin(πα sinθ / λ)/(πα sinθ / λ))^2其中，I代表在观察屏幕上观察到的光强，I0代表双棱镜两个棱镜面的光强的最大值，θ代表观察角度。
练习题4：衍射光栅设有一个衍射光栅，光栅常数为d，光波的波长为λ，观察屏幕与光栅的距离为L。
求在屏幕上某一点的光强分布。
解答：公式如下：I(θ) = I0 * (sin(Nπd sinθ / λ)/(Nπd sinθ /λ))^2 * (sin(πd sinθ / λ)/(πd sinθ /λ))^2其中，I(θ)代表在观察屏幕上观察到的光强，I0代表光栅刻痕的光强的最大值，N代表光栅的阶数，θ代表观察角度。
推导光衍射光强分布公式新方法的探究05物理学江进指导老师余建立摘要：光的衍射是光学中的重要内容之一，而光具有波粒二象性。
分别从粒子性和波动性出发，采用量子力学中的几率波概念和傅立叶变换方法。
粒子性角度，首先给出微观粒子的归一化波函数，再对坐标表象下的波函数进行付氏变换，对变换后的函数求积分，得出夫琅和费单缝和多缝衍射光强分布规律；波动性角度，采用傅立叶变换给出光屏上某点光的振幅表达式，对振幅表达式求积分，得出夫琅和费单缝和多缝衍射光强分布规律。
两种方法所得的结果与大学物理教材中所采用的惠更斯-菲涅耳原理给出的结论一致，讨论的结果有助于更好的认识和理解光衍射的实质，对教学具有一定的指导意义。
关键词：衍射；物质波；傅立叶变换；单缝；多缝New method derivation of light diffraction intensitydistribution formula is explored05 Physics Jiang Jin Instructor Yu Jian LiAbstract: Diffraction of light is an important part in one of the optical with wave-particle duality. In my view, think of particles and volatility, we can use the method of the concept of probability wave and Fourier transform Particles in quantum mechanics. From the view of particle, first of all, we give wave function normalized of micro-particle and then do Fourier transform under the coordinate appearance of the wave function. To calculate the integral of transformed function, get the law of fraunhofer single-slit and multi-slit diffraction of light intensity distribution. From the view of volatility, use the Fourier Transform to get amplitude expression of one point on light of plane. And then we can solve the integration of amplitude expression, use this method, we could also get the law of fraunhofer single-slit and multi-slit diffraction of light intensity distribution. The result of two methods is the same as the results of Huygens-fresnel Principle in the college physics textbook. The result of discussion is better to help us to understand the light diffraction. It has a certain significance to teach.Keywords: diffraction; Matter wave; Fourier Transform; Single-slit; multi-seam1 引言光的衍射是波动光学中的重要内容之一[1]，衍射分为两类：一类是光源和观察点(或两者之一)到障碍物的距离为有限远，称为菲涅耳衍射；另一类是光源和观察点到障碍物的距离为无限远，称为夫琅和费衍射。
傅立叶变换光谱实验报告姓名：学号：专业：光电子一、实验目的(1 自组傅里叶变换光谱仪，掌握傅里叶变换光谱的原理；(2 测量常用光源的光谱分布。
二、实验原理傅里叶变换光谱仪是基于迈克尔逊干涉仪结构。
使两束相干光的光程差发生连续改变，干涉光强相应发生变化，记录下光强接收器输出中连续的变化部分，得到干涉光强随光程差的变化曲线，即干涉图函数。
然后计算出干涉图的傅里叶余弦变换，即可得到光源的光谱分布。
这样得到的光谱就被称为傅里叶变换光谱。
1、干涉光强的计算根据光波叠加原理，若有两束单色光，它们的波数都是σ，具有Δ的光程差，传播方向和偏振方向相同，光强都是I ’，这两束光相互叠加产生干涉，得到光强为：I =4I ' cos (πσ∆ =2I ' +2I ' cos(2πσ∆ 2从上式看，单色光的干涉图像包含一个直流分量和一个余弦函数分量，余弦函数分量的周期就是单色光的波长。
若光源不是单色光，光强随波长的分布为I(σ, 在光谱间隔d σ内光强是（σ）I d σ将此光源发出的光等强分成两束，相互干涉后光强是：dI =2I (σ d σ+2I (σ d σcos(2πσ∆在整个光谱范围内的干涉总光强为:I =c òI (s d s+c òI (scos(2psD d s00¥¥其中为常数，上式右侧第一项为常数，与光程差Δ无关；右边第二项是光程差的函数，将第二项单独写出：I (D =c òI (scos(2psD d s0¥两束光干涉所得光强是光束光谱分布的傅立叶余弦变换。
傅立叶余弦变换是可逆的，则有：∞I (σ =c ' ⎰I (∆ cos(2πσ∆ d ∆只要测出相干光束的干涉光强随光程差变化的干涉图函数曲线I(σ 进行傅立叶变换就可以得到相干光束的光谱分布。
2、实际应用的相关讨论将上述公式用于实际还需进行一下讨论：1. 公式中要求光程差测量范围为0到∞，但实际中光程差的测量范围有限。
光强分布一、实验目的１．观察单缝衍射现象，加深对衍射理论的理解。
２．会用光电元件测量单缝衍射的相对光强分布，掌握其分布规律。
３．学会用衍射法测量微小量。
4． 验证马吕斯定律。
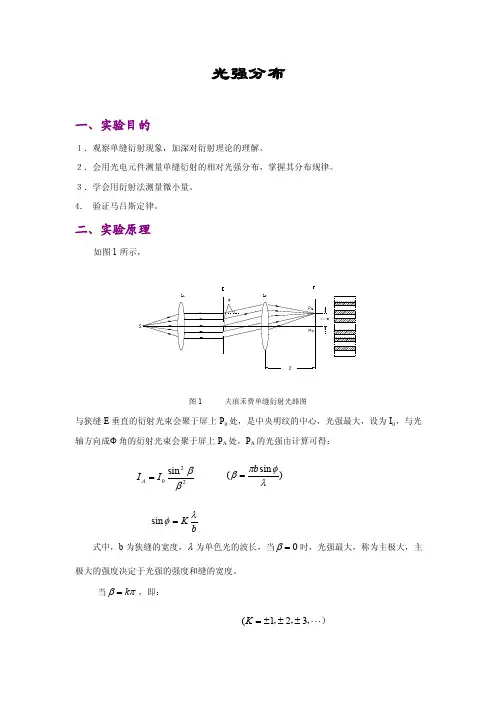
二、实验原理如图1所示，图1 夫琅禾费单缝衍射光路图与狭缝E 垂直的衍射光束会聚于屏上P 0处，是中央明纹的中心，光强最大，设为I 0，与光轴方向成Ф角的衍射光束会聚于屏上P A 处，P A 的光强由计算可得：式中，b 为狭缝的宽度，λ为单色光的波长，当0=β时，光强最大，称为主极大，主极大的强度决定于光强的强度和缝的宽度。
当πβk =，即：220sin ββI I A =)sin (λφπβb =b Kλφ=sin ），，，⋅⋅⋅±±±=321(K时，出现暗条纹。
除了主极大之外，两相邻暗纹之间都有一个次极大，由数学计算可得出现这些次极大的位置在β=±1.43π，±2.46π，±3.47π，…，这些次极大的相对光强I/I 0依次为0.047，0.017，0.008，…图2 夫琅禾费衍射的光强分布夫琅禾费衍射的光强分布如图2所示。
图3 夫琅禾费单缝衍射的简化装置用氦氖激光器作光源，则由于激光束的方向性好，能量集中，且缝的宽度b 一般很小，这样就可以不用透镜L 1，若观察屏（接受器）距离狭缝也较远（即D 远大于b ）则透镜L 2也可以不用，这样夫琅禾费单缝衍射装置就简化为图3，这时，由上二式可得三、实验装置激光器座、半导体激光器、导轨、二维调节架、一维光强测试装置、分划板 、可调狭缝、平行光管、起偏检偏装置、光电探头 、小孔屏、 数字式检流计、专用测量线等。
Dx /tan sin =≈φφxD K b /λ=图4 衍射、干涉等一维光强分布的测试四、实验步骤1. 接上电源（要求交流稳压220V ±11V ，频率50HZ 输出），开机预热15分钟；2. 量程选择开关置于“1”档，衰减旋钮顺时针置底，调节调零旋钮，使数据显示为－.000； 单缝衍射一维光强分布的测试1、 按图4搭好实验装置。
夫琅禾费衍射公式
公式的表达式如下：
I = I_0 * ( (sin(θ/2)) / (θ/2))^2
其中，I表示衍射光的强度，I_0表示入射光的强度，θ表示入射光
线和衍射光线的夹角。
夫琅禾费衍射公式是从亚波长单缝衍射的强度分布推导出来的。
对于
亚波长的单缝衍射，入射光线经过狭缝衍射后，会在屏幕上形成一系列明
暗相间的干涉条纹。
夫琅禾费衍射公式描述了这些干涉条纹的强度分布。
公式中的θ是入射光线与衍射光线的夹角，夹角越大，光线的干涉效应
越弱，干涉条纹的强度也相应减小。
夫琅禾费衍射公式的应用十分广泛。
除了单缝衍射，该公式还可以用
来描述其他几何形状的物体或孔隙的衍射现象，如双缝衍射、光栅衍射等。
通过该公式，可以计算出衍射光在不同夹角下的强度分布，进而研究光的
传播和干涉现象。
总之，夫琅禾费衍射公式是分析和描述衍射现象的重要数学工具。
通
过该公式，可以计算和预测衍射光的强度分布，深入理解光的波动性质和
光学系统的特性，进一步推动光学领域的研究和应用。
光学经典理论｜傅里叶光学基础2018-02-24 17:00今天的光学经典理论为大家带来的是傅里叶光学基础，傅里叶光学是现代光学的一个分支，将电信理论中使用的傅里叶分析方法移植到光学领域而形成的新学科。
光学人们可以看看！在电信理论中，要研究线性网络怎样收集和传输电信号，一般采用线性理论和傅里叶频谱分析方法。
在光学领域里，光学系统是一个线性系统，也可采用线性理论和傅里叶变换理论，研究光怎样在光学系统中的传播。
两者的区别在于，电信理论处理的是电信号，是时间的一维函数，频率是时间频率，只涉及时间的一维函数的傅里叶变换；在光学领域，处理的是光信号，它是空间的三维函数，不同方向传播的光用空间频率来表征，需用空间的三维函数的傅里叶变换。
包含内容60年代发明了激光器，使人们获得了新的相干光源后，傅里叶光学无论在理论和应用领域均得到了迅速发展。
傅里叶光学运用傅里叶频谱分析方法和线性系统理论对广泛的光学现象作了新的诠释。
其主要内容包括标量衍射理论、透镜成像规律以及用频谱分析方法分析光学系统性质等。
推导演示一个光学信息系统和一个电学信息系统有许多相同之处，它们都是收集信息和传递信息，它们都有共同的数学工具──线性系统理论和傅里叶分析。
从信息论角度,关心的是信息在系统中传递过程;同样，对一个光学系统来讲，物和像的关系，也可以根据标量衍射理论由系统中光场的传播来确定，因此光学系统可以看成一个通信信道。
这样，通信理论中已经成熟的线性系统理论可以用来描述大部分光学系统。
当物体用非相干光照射时，在系统像平面上强度分布与物体上强度分布成线性（正比）关系。
而用来描述电学系统的脉冲响应h(t，τ)概念，即系统对一窄脉冲δ(t)（狄喇克δ函数）的响应，也可以用来描述光学系统，即用光学系统对点光源δ(x，y)的响应(点光源的像)h(x,y；ξ，η)来描述系统的性质，两者的区别仅仅在于电学系统的脉冲响应是时间一维函数，光学系统的脉冲函数是空间二维函数，另外两者都具有位移不变性，前者分布不随时间位移而变，后者分布不随空间位移而变（即等晕条件）。
单缝衍射光强分布实验报告实验报告：单缝衍射光强分布实验一、实验目的通过实验观察和探究单缝衍射现象，了解光的波动性质，研究单缝衍射光强分布的规律。
二、实验原理单缝衍射是指当光线通过一个狭缝时，由于光的波动性质，光波会发生衍射现象，即光线会向周围扩散。
根据夫琅禾费衍射公式，单缝衍射光强分布的规律可以通过以下两个公式推导得出：1.衍射公式：θ=mλ/b其中，θ为衍射角，m为条纹的级次（m=0,±1,±2,...），λ为波长，b为狭缝宽度。
2. 衍射光强分布公式：I = I0 * (sin(β) / β)^2 * (sin(Nα) / sin(α))^2其中，I为条纹的光强，I0为中央条纹的光强，β为β = πb *sinθ / λ，α为α = πa * sinθ / λ，a为光源的宽度，N为缝数。
三、实验步骤1.将光源与被研究的缝隙间隔一定距离，并确保光源垂直照射缝隙。
2.使用光屏接收衍射光，并根据需要调整光屏距离缝隙的距离，以便更好地观察衍射条纹。
3.用CCD相机拍摄光屏上的衍射条纹，通过图像处理软件量化光强，得到光强分布曲线。
4.调整狭缝的宽度，观察并记录不同宽度下的光强分布情况。
5.重复实验多次，取平均值以减小误差。
四、实验结果与分析通过实验观察到的结果，我们可以得到以下结论：1.光强分布呈现明暗相间的条纹状，其中最中央的一条条纹最亮，两侧的条纹逐渐减弱。
2.随着波长λ的增大，条纹间距减小，光强分布也发生变化。
3.随着缝宽b的增大，条纹变得更为集中，光强分布呈现更明显的周期性变化。
4.当缝数N增加时，条纹的光强分布曲线会发生明显的变化，呈现出更多的衍射条纹。
五、实验注意事项1.实验过程中需要保证光源的稳定性，尽量避免光强波动引起的误差。
2.调整光屏与缝隙距离时，需注意确保垂直照射，并尽可能保持一定的距离以获得更清晰的图像。
3.使用CCD相机拍摄图像时，应注意调整曝光时间和对比度以获得最佳的图像质量。
傅里叶变换光谱实验原理中括号主题：傅里叶变换光谱实验原理傅里叶变换光谱实验是一项重要的光谱分析技术，能够将时间域中的信号转换成频域中的频谱信息，从而得到样品的光谱信息。
本文将以中括号为主题，分为以下步骤详细介绍傅里叶变换光谱实验的原理。
[步骤一：介绍傅里叶变换]傅里叶变换是一种数学方法，能够将一个函数表示成若干正弦函数和余弦函数的和。
它的原理是根据函数的周期性，通过积分运算将函数分解成多个频率的正弦和余弦函数的叠加，从而解析函数在不同频率下的振幅和相位信息。
傅里叶变换在信号处理、图像处理以及光谱分析等领域有广泛应用。
[步骤二：光谱分析的基本原理]光谱分析是通过测量目标物质在一定波长范围内的光强变化，从而获得目标物质的光谱信息。
光谱分析可以用于确定物质的组成、结构和各种化学过程的动力学等。
常见的光谱分析方法包括紫外可见吸收光谱、红外光谱、拉曼光谱、荧光光谱等。
[步骤三：傅里叶变换光谱仪的工作原理]傅里叶变换光谱仪主要由光源、样品室、光路系统、探测器和信号处理电路等组成。
其基本原理是通过光源发出连续谱或单色光，经过样品室与待测样品相互作用后，经过光路系统将光束引入探测器，再经过信号处理电路将光谱信息转换为频谱信息。
[步骤四：光纤和光栅的作用]光纤是傅里叶变换光谱仪中重要的光路系统组件之一，其作用是将样品室中接收到的光束引导到探测器进行信号测量。
光纤的选择要考虑其传输效率和波长范围等因素。
光栅是光谱仪中另一个关键的光学元件，其作用是将光束分散成不同波长的光，并将不同波长的光线按一定规律进行衍射。
光栅的特点是高色散性，能够将不同波长的光分离出来，实现波长的选择和测量。
[步骤五：信号的采集与处理]在傅里叶变换光谱实验中，探测器接收到的光信号经过放大、滤波等处理后，转换成电信号并传入信号处理电路。
信号处理电路中的放大器、低通滤波器等组件可以对信号进行进一步处理，消除噪声并增加信号的质量。
随后，经过模数转换器将信号转换为数字信号，利用计算机进行数据采集和存储。
光谱傅里叶变换
光谱傅里叶变换（spectral Fourier transform）是指将光谱信号从时域转换到频域的过程。
它在光谱分析、光学成像、光学通信等领域中得到广泛应用。
光谱傅里叶变换的基本原理是利用傅里叶变换的性质将时域的光强信号转换为频域的光谱信号。
在光学中，光谱信号通常包含了不同频率的光波成分。
通过对光谱信号进行傅里叶变换，可以将不同频率的光波成分分离出来，从而得到光谱中包含的频率信息。
光谱傅里叶变换的数学表达式为：
F(u) = ∫ f(x) * exp(-2πiux) dx
其中，F(u) 表示频域中的光谱信号，f(x) 表示时域中的光强信号，u 表示频率。
在实际应用中，可以通过光学器件，如光谱仪或光谱分析仪，来实现光谱傅里叶变换。
光谱仪将光信号转换为电信号后，再经过傅里叶变换操作，将光谱信号转换为频谱信号。
通过分析频谱信号，可以获取光谱中的频率信息，进而研究光波的特性和相互作用。
光谱傅里叶变换在光谱分析中的应用非常广泛，它可以用来研究光源的光谱特性、材料的吸收、反射和散射等光学性质，以及光波的干涉、衍射等现象。
此外，光谱傅里叶变换还被用于
光学成像、光学信号处理和光学通信等领域中的数据处理和信号处理。
实验 衍射光强的定量研究与单缝的测量【实验目的】1．掌握在光具座上组装、调整光路的实验技能；学习微机自动控制进行测量时相关参量的设定。
2．了解光强测量的一种方法，观察并定量测定衍射元件产生的光衍射图样；掌握一种单缝宽度的测量方法。
【实验原理】1．衍射光强分布谱光的衍射是人所共知的一种自然现象，光衍射的实验光路主要由光源、衍射元件和观察屏等三要素，在光具座或光学平台上组装而成。
根据三者间距离的大小，将光衍射效应大致分成两种典型的光衍射图样，一种是衍射元件与光源和观察屏都相距无穷远，产生这种类型的光衍射叫夫琅禾费衍射，另一种是上述三者间相距有限远，产生的光衍射叫做菲涅耳衍射。
由于激光光束平行度较佳，且三者间距离远大于元件的线度，故本实验着重研究更具有实际意义的夫琅禾费衍射。
根据光衍射理论分析，不同衍射元件产生的光衍射图样和光强分布是不同的。
在理想条件下，理论研究不同衍射元件产生的衍射效应，得到对应的夫琅禾费衍射光强计算公式为：⑴ 单缝夫琅禾费衍射光强理论计算公式λθπθsin ,sin 20a u u u I I =⎪⎭⎫ ⎝⎛=上式表示在衍射角θ时，观测点的光强I θ值与光波波长λ值和单缝宽度a 相关，[]2sin()/u u 被叫做单缝衍射因子，表征衍射光场内任一点相对强度（I 0/I θ）的大小。
若sin θ为横坐标，（I 0/I θ）为纵坐标，可得到单缝衍射光强分布谱（如图14-1）。
从图14-1可见，零衍射斑即主极大在中心，高级衍射斑即次极大，它们顺序出现在sin θ=±1.43a λ，±2.46a λ，±3.47aλ，…的位置，各级次极强的光强与入射光强比值分别是I 1/I 0≈4.7%，I 2/I 0≈1.7%，I 3/I 0≈0.08%，…。
此外，在单缝衍射光强分布谱上还有暗斑，依次出现在sin θ=±a λ，±2a λ，±3aλ，…的位置，分别称为±1、±2、±3、…级。
单缝衍射的光强分布实验报告实验报告：单缝衍射的光强分布一、实验目的通过实验，观察单缝衍射现象，了解其光强分布规律。
掌握光衍射实验的基本理论和实验方法。
二、实验原理单缝衍射是指当光线通过一块缝隙时，由于衍射作用，其出射光线方向发生偏转并交叉干涉形成衍射花样。
根据夫琅禾费衍射公式，单缝衍射中，d*sinθ=mλ，其中d为缝宽，θ为衍射角度，m为衍射级次，λ为光波长。
单缝衍射的光强分布可表示为I=I0 * sinc^2 (πd*sinθ/λ)，其中I0为中央亮度，sinc函数可由幅度衍射公式推导得出。
三、实验器材单色光源，光源支架，单缝，屏幕，卡尺。
四、实验步骤1. 将单色光源与单缝放置于透镜下方和光源支架上方，保持缝隙垂直于光路并尽量减小其宽度。
2. 将屏幕置于光源和单缝的正中央，在光路上设法使靠近光源的两侧与单缝对齐。
调整屏幕与单缝垂直，注意观察光芒的衍射现象。
3. 逐渐加宽缝隙的宽度，并观察光芒的衍射现象。
每增加一级，观察对应的条纹的亮度情况，记录下来。
4. 用卡尺测量两侧衍射花样亮条的距离，并计算衍射角度θ。
5. 用实验数据计算出衍射光强分布的函数图像。
五、实验结果当单缝宽度较小时，衍射现象并不显着。
随着单缝宽度的增加，衍射花样逐渐清晰，呈现出多级衍射的现象。
同时，每个级次的亮度会随着衍射角度的增大而逐渐减小。
最大亮度出现在中央，且亮度以一定规律逐渐减小。
通过记录和计算数据，得出了单缝衍射的光强分布函数图像。
六、实验结论通过单缝衍射实验，我们观察到了光线通过缝隙发生的衍射现象，并了解了其衍射级次、光强分布规律等基本知识。
实验结果表明，单缝衍射的亮条数目、亮条宽度、亮度以及衍射角度与单缝宽度、光波长等参数密切相关，通过计算可以得出与实验现象相符的衍射光强分布函数。
此外，通过实验还可以了解干涉、衍射、散射等基本光学现象，掌握基本的光学实验方法，有助于对光学知识的深入理解。
七、参考文献1. 杨生彦、齐玉福.《光学基础实验》. 北京：科学出版社，2015.2. 翁和兴、施永权.《光学实验讲义》. 北京：高等教育出版社，2014.。
夫琅禾费单缝衍射光强分析与探讨摘要：在夫琅禾费单缝衍射实验中,如果在透镜的物方焦面内沿着某一圆周改变光源S的位置,让透镜出射的单色平面光波都以相同的入射角H0入射到单缝衍射屏上,则单缝衍射光强分布均会发生改变,说明衍射图样的光强分布不仅和入射角H0以及衍射角H有关,而且和光源S的位置有关;考虑单缝衍射屏上光波相位的分布和平面光波的入射方位(即光源S的位置)的关系,采用矢量图解法对单缝衍射因子进行分析及计算,得到了全面的夫琅禾费单缝衍射光强公式。
关键词：单缝衍射;光强;光程差;斜入射目录1 夫琅禾费单缝衍射（一） (1)的物方焦点时的装置及现象 (1)1.1 单色点光源S位于透镜L11.2 用积分法来求夫琅禾费单缝衍射的光强………………………………（）1.3 衍射光强的极值分布条件及特点………………………………………（）2 夫琅禾费单缝衍射（二）……………………………………………………（）2.1 单色点光源S位于透镜L的物方焦面上时的装置……………………（）12.2 单缝衍射因子分析及计算………………………………………………（）3 总结…………………………………………………………………………（）1 夫琅禾费单缝衍射（一）1.1 单色点光源S位于透镜L的物方焦点时的装置及现象1如图1所示,单色点光源S置于凸透镜L1的物方焦平面上,从点光源发出的光经过透镜以后变成平行光,垂直射到宽度约为十分之几毫米的狭缝上。
缝后置一凸透镜L2,在L2象方焦平面上放置接收屏,则屏上显现出由一系列不连续的明亮短线组成的衍射图样,如图1[1]所示。
改变缝的宽度,衍射图样也发生变化,缝越宽,衍射图样越收缩,当缝宽足够大时(远大于波长),则衍射图样缩成一点,这就是点光源S在透镜中所成的象。
狭缝对光波在方向上的限制,使光在x方向上产生衍射,生成一系列沿x方向排列的明亮的短线,这些短线好像是点光源的一个扩展开的象。
如果用氮生在光器作为光源,则可以把透镜L1去掉,使激光直接照射在单缝上,并且去掉L2,在缝后足够远处(几米)屏上可观察到夫琅禾费衍射图样。
傅里叶光学衍射
傅里叶光学是一种基于傅里叶变换的光学分析方法，用于研究和描述光的传播、传输和干涉等现象。
衍射则是傅里叶光学中的一个重要概念，指的是光波在通过绕射物体或在光学衍射装置中遇到不同障碍物或孔径时发生的偏折、干涉和广泛分布的现象。
当光波通过一个物体或孔径时，由于光的波动性，光波在物体边缘处发生弯曲，并产生干涉、衍射效应。
这导致光波的幅度和相位在空间中发生变化，进而在接收屏幕上形成特定的光强和亮度分布。
衍射现象可以通过傅里叶光学的数学表达进行理解和描述。
根据傅里叶光学的原理，复杂的光波可以被分解成一系列具有不同频率的简单正弦波。
衍射可以被看作是这些不同频率的波在空间中互相干涉和综合的结果。
傅里叶光学提供了描述衍射现象的数学工具和方法，例如使用傅里叶变换分析光的传播和干涉，以及通过傅里叶光学的逆变换来重建或模拟复杂的光场。
衍射现象在许多光学应用中发挥着重要作用，例如在光学衍射实验中观察衍射图样，可用于分析和测量光源、物体的结构和特性。
此外，衍射也被广泛应用于光学显微镜、天文望远镜、激光技术等领域，为光学系统的设计和优化提供
重要参考。
---------------------------------------------------------------范文最新推荐------------------------------------------------------ 用傅里叶变换计算衍射的光强分布摘要：大学物理教程中关于衍射光强分布的内容，一般采用菲涅尔半波带法定性讨论；本论文采用了一种简单的方法，用傅里叶变换式计算光的单缝、圆孔衍射的光强分布，根据计算结果并用MATLAB软件仿真模拟单缝、圆孔衍射及其光强分布，分析计算结果和模拟结果得出衍射图样取决于缝宽或孔径的尺寸大小。
这种理论将衍射装置看成傅里叶分析器，这为光学提供了一种强有力的数学手段——傅里叶分析，同时也将抽象的数学运算变成了现实存在的物理实验过程。
8920关键词：傅里叶变换；衍射；光强分布The Calculation of Light Intensity Distribution of Diffraction by Fourier TransformationAbstract: On the light intensity distribution of1 / 6diffraction, the university physics course usually use the discussion of Final zone plate statutory; this paper presents a simple method, the calculation of light intensity distribution of Single slit and circular aperture diffraction by the Fourier transform calculation, the simulation using MATLAB software according to the results to the single slit and circular aperture diffraction and light intensity distribution, the analytical calculation and simulation results to know the diffraction pattern depends on slit width or aperture size.The theory looks diffraction device as Fu Fiye analyser, which provides a powerful mathematical tool - Fu Liye analysis for optical, also develops math abstract theory into physics experiment course which exists in reality.Key Words: Fourier transform; Diffraction; Intensity distribution目录摘要1---------------------------------------------------------------范文最新推荐------------------------------------------------------ 引言11.傅里叶变换21.1一维傅里叶变换式21.2二维傅里叶变换式31. 傅里叶变换1.1 一维傅里叶变换式设为一维周期函数，则其可以展开为下述形式：(1)其中k为空间频率，A(k)、B(k)由下式给出：3 / 6（2），（3）式代入（1）式得：(4)由于，中括号里为偶函数，改变外边积分范围得：与（7）式相加，再运用欧拉公式得：叫做的傅里叶变换式则：(11)在无线电通讯理论中，一维傅里叶变换把一个时间域中的信号变换成频率域中的信号[7]；在光学信息中，高亮度高强度的激光束通过衍射孔径，其夫琅和费衍射像是孔径的二维傅里叶变换，这个结论与通讯理论相似，通讯理论中的许多概念与方法可以移植到光学中来。
傅里叶衍射投影定理
傅里叶衍射投影定理是光学中的一个重要定理，它描述了在夫琅禾费衍射条件下，空间中任意一个物体的衍射图案可以通过对其傅里叶变换的投影来计算。
具体来说，该定理表明，对于一个在空间中具有非零光强度分布的物体，其夫琅禾费衍射图案可以通过将该物体的光强度分布进行傅里叶变换，并将得到的傅里叶谱在某个平面上进行投影来计算。
这个投影平面被称为衍射平面，它与物体的距离满足夫琅禾费衍射条件。
傅里叶衍射投影定理的意义在于，它提供了一种计算衍射图案的方法，使得我们可以通过对物体的光强度分布进行傅里叶变换来预测其衍射图案。
这对于许多光学应用，如光学成像、光学设计和光学信号处理等都非常重要。
需要注意的是，傅里叶衍射投影定理只适用于夫琅禾费衍射条件下，即光源和衍射平面距离无限远，并且衍射物体的尺寸远小于光源到衍射平面的距离。
在其他情况下，需要使用更复杂的衍射理论来计算衍射图案。
3.请用傅里叶变换法计算圆孔的夫琅和费衍射场分布，并与1进行比较。
在夫琅禾费圆孔衍射傅里叶分析装置图中，设衍射圆孔所在平面坐标为（x,y ），接收屏平面坐标为(),ξη，衍射屏上的圆孔是一个具有圆对称性函数，令单色光振幅为1，则()22=exp 2r x y U circ i x y dxdy a πξη∞∞-∞-∞⎛⎫+⎪-+⎡⎤⎣⎦⎪⎝⎭⎰⎰（） （1） 在（x,y ）和(),ξη平面上分别取极坐标(),ρϕ和(),r θ进行坐标代换：2222cos ,sin ,cos ,sin ,,x y x yr r r ρϕρϕρξθηθξη⎧===+⎪⎨===+⎪⎩ （2）得到衍射圆孔的透过率函数为： 221,0,a x y circ circ a a a ρρρ⎛⎫≤+⎧⎛⎫⎪==⎨ ⎪ ⎪>⎝⎭⎩⎝⎭（3）式中a 为圆孔半径，将（2）代入（1）得到 ()200exp 2cos r U circ d i r d aπρρρπρθϕθ∞=⎛⎫--⎡⎤ ⎪⎣⎦⎝⎭⎰⎰（） （4） 又因为零阶贝塞尔函数的积分表式式为()()2001exp -cos 2a ia d J πθϕθπ=-⎡⎤⎣⎦⎰（5）将（5）代入（4），得到 ()002r U circ J r d a ρρπρρ∞=⎛⎫⎪⎝⎭⎰（） （6） 上式即为傅里叶-贝塞尔变换。
再令'aρρ=， 得到()()12002'2''r a U circ J ra d πρπρρ=⎰（） （7）再令'''2ρπρar =，则()()()22122002222''''1''''''''2222raarr a J ra d U J J d a ar ar r raππππρρρρρρπππππ===⎰⎰（） （8）这样通过傅里叶变换分析法推导出夫琅禾费圆孔衍射接受屏上的光强强度分布为()()()()[]212222/22ra ra J a r U I πππ== （9）程序：p=500; %设置接收屏的大小 d=20; %设置圆孔的直径[x,y]=meshgrid(-p:p,-p:p);%设置X,Y 坐标轴都为[-500，500]的矩阵， for i=1:size(x,1) %设置循环数 for j=1:size(y,1)%设置循环数if x(i,j).^2+y(i,j).^2<=(d/2)^2%在半径为10内的圆 A(i,j)=1;%在圆内A=1 elseA(i,j)=0;%在圆外A=0 end end endfigure(1)imshow(A,[]) %画图，值等于1的亮，值等于0的暗 afft=fft2(A);%进行二维傅里叶变换转换 aabs=abs(afft);%求afft 的绝对值aabss=fftshift(aabs);% 正半轴部分和负半轴部分的图像分别关于各自的中心对称 figure(2)imshow(aabss,[])%画图colormap(gray);% 输出一个灰色系的曲面图 figure(3)[i,j]=size(aabss);%将aabss 矩阵的大小赋值给I,j c=(i+1)/2;B=aabss(c,:);%将X 坐标固定，只变化Y 坐标，从而导致abbss 的变化 y=-p:p;%设置y 的变化范围 plot(y,B)%画图 figure(4)mesh(x,y,aabss)%画出三维图当孔的半径为10当孔的半径为5当孔的半径为20总结：用夫琅禾费衍射积分公式求得的光强分布为()221022p p p J m A I A m I ⎡⎤===⎢⎥⎣⎦，其中s i n ()am πθλ=。
夫琅和费正交双缝衍射干涉光强分布的讨论双缝衍射干涉光强分布是原子物理学和光学等领域中重要的实验测量方法之一。
由英国物理学家立福（R.R.Fry）和英国物理学家莱克（W.H.Leake）在1960年首次提出。
目前，该方法被广泛地用于研究原子、分子、凝聚态物质和纳米结构等材料的光学和能谱特性。
立福和莱克在双缝衍射干涉实验中探究了双缝衍射光强分布的基础性质。
他们提出，在一个两个等尺度缝隙阵列中，距离相等的两个缝隙阵列之间对光线的散射射出的光强分布有一个正弦变化，随着两个等尺度缝隙阵列之间的水平距离的增加而变化。
之后，俄国科学家基斯洛夫（V.N.Kiselov）和芬兹（P.F.Fitz）在1962年提出了拟定双缝衍射光强分布的基斯洛夫（Kiselov）-费正（Fitz）方程。
该方程为原子物理学、凝聚态物理学和光学等学科以及微纳结构和声学散射等实验测量提供了有价值的数据。
基斯洛夫（Kiselov）-费正（Fitz）方程通过两个独立的变量描述了双缝衍射光强分布。
考虑干涉不可忽略的缝隙出射光子的概率，该方程的参数形式为：G(r)=1∕(r+r_0)sin[π*r∕(r+r_0)]其中r是双缝衍射阵列之间的水平距离，r_0是由缝隙出射光子的概率定义的参数，反映了双缝衍射样品表面反射率。
该式表明，较大的r_0值对应较小的双缝衍射干涉效应，较小的r_0值则表示较大的双缝衍射干涉效应。
随着r_0值增大，双缝衍射干涉曲线呈凹形，在r = 0处曲线最低点达到极小值。
从上述公式中可以看出，缝隙出射光子的概率是影响双缝衍射光强分布的关键参数。
如果适当控制双缝衍射材料的表面反射率，就可以改变r_0值，从而改变双缝衍射干涉光强分布的特性。
进而可以研究双缝衍射的各种物理特性。
基斯洛夫（Kiselov）-费正（Fitz）方程为这类光学实验提供了理论支撑，使得我们可以更加深入地探究和分析双缝衍射干涉光强分布。
编号 0810332毕业论文（ 2012 届本科）题目：用傅里叶变换计算衍射的光强分布学院：物理与机电工程学院专业：物理学作者姓名：王辉指导教师：马保宏职称：讲师完成日期： 2012 年 5 月 23 日二○一二年五月河西学院本科生毕业论文（设计）诚信声明本人郑重声明：所呈交的本科毕业论文（设计），是本人在指导老师的指导下，独立进行研究工作所取得的成果，成果不存在知识产权争议，除文中已经注明引用的内容外，本论文不含任何其他个人或集体已经发表或撰写过的作品成果。
对本文的研究做出重要贡献的个人和集体均已在文中以明确方式标明。
本人完全意识到本声明的法律结果由本人承担。
作者签名：（亲笔签名）二O 年月日（打印）河西学院本科生毕业论文（设计）开题报告用傅里叶变换计算衍射的光强分布摘要：利用傅里叶变换式计算光的单缝和圆孔衍射的光强分布，根据计算结果利用MATLAB软件仿真模拟单缝和圆孔衍射及光强分布，分析计算和模拟结果得知衍射图样取决于缝宽或孔径的大小。
关键词：傅里叶变换；单缝；圆孔；衍射；光强分布Abstract:Single slit and circular aperture diffraction of the Fourier transform calculation of light intensity distribution, the simulation using MATLAB software according to the results to the single slit and circular aperture diffraction and light intensity distribution, the analytical calculation and simulation results to know the diffraction pattern depends on slit width or aperture size.Key words：Fourier transform ;Single slit ;Hole ;Diffraction ;Intensity distribution 0 引言衍射现象是波动光学中的重要知识，光的衍射的定义从广义上说是光在传播过程中，遇到障碍物时产生的偏离几何光学规律从而引起光强重新分布的现象，也称为绕射。
龙岩学院学年论文（设计）论文题目用傅里叶变换计算衍射的光强分布学院物理与机电工程学院专业物理学（光电子技术方向）年级 2011级姓名徐武童学号 ********** 指导教师兑自强二0一三年四月十二日用傅里叶变换计算衍射的光强分布物理与机电工程学院 11物本2011042526徐武童指导老师：兑自强【摘要】：利用傅里叶变换式计算光的单缝和圆孔衍射的光强分布，根据计算结果利用MATLAB软件仿真模拟单缝和圆孔衍射及光强分布，分析计算和模拟结果得知衍射图样取决于缝宽或孔径的大小【关键词】：傅里叶变换；单缝；圆孔；衍射；光强分布目录前言1 1.傅里叶变换式 11.1一维变换式 21.2二维变换式 31.3三维傅里叶变换式 32. 用傅里叶变换计算衍射的光强分布 42.1计算圆孔衍射的光强分布 62.2计算单缝衍射的光强分布 73.光强分布曲线 83.1单缝衍射的光强分布曲线 83.2圆孔衍射的光强分布曲线 94.讨论104.1单缝衍射 104.2圆孔衍射 10总结11致谢110 前言衍射现象是波动光学中的重要知识，光的衍射的定义从广义上说是光在传播过程中，遇到障碍物时产生的偏离几何光学规律从而引起光强重新分布的现象，也称为绕射。
该定义指出光的衍射是一种区别于几何光学规律的光的传播现象。
当所选光学元件的尺度与波长相当时，光的传播现象明显不同于几何光学所描述的。
它也明确给出了产生衍射现象的条件“光波遇到障碍物”，对于任何一束光都会因在空间传播过程中遇到障碍物而使自由波面受损，从而改变波前后振幅，使光表现出衍射行为。
而傅里叶变换是一种特殊的积分变换，它能将满足一定条件的某个函数表示成正弦基函数的线性组合或者积分。
在不同的研究领域，傅里叶变换具有多种不同的变体形式，如连续傅里叶变换和离散傅里叶变换。
在数学领域，尽管最初傅立叶分析是作为热过程的解析分析的工具，但是其思想方法仍然具有典型的还原论和分析主义的特征。
从纯粹的数学意义上看，傅立叶变换是将一个函数转换为一系列周期函数来处理的。
从物理效果看，傅立叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。
在现代光学发展的今天，如何运用傅里叶方法解决干涉、衍射和成像等问题成了至关重要的部分。
1 傅里叶变换式1.1 一维变换式某个空间变量的一维函数()x f ，可以表示为无穷多个谐波分量的线性组合：()()⎪⎭⎫ ⎝⎛+=⎰⎰∞∞00sin cos 1)(kxdk k B kxdk k A x f π（1）其中决定各空间频率()k 的贡献的权重因子()k A 和()k B 分别是()x f 的傅里叶余弦和正弦变换式，由下式给出： ()()⎰+∞∞-'''=x d x k x f k A cos , ()()⎰+∞∞-'''=x d x k x f k B sin (2)将（2）式代入（1）式中()()()dk x d x k x f kx dk x d x k x f kx x f '''+'''=⎰⎰⎰⎰∞∞∞∞sin sin 1cos cos 1ππ（3）由于()x k kx x k kx x x k '+'=-'sin sin cos cos cos ，上式可改写为()()()⎰⎰∞+∞∞-⎥⎦⎤⎢⎣⎡'-''=cos 1dk x d x x k x f x f π（4）方括号中的量是k 的偶函数，因而改变外面的一个积分限得到()()⎰⎰+∞∞-+∞∞-⎥⎦⎤⎢⎣⎡-''=dk x x k x f x f cos 21)(π（5） 由于()()⎰⎰+∞∞-+∞∞-=⎥⎦⎤⎢⎣⎡'-''0sin 2dk x d x x k x f iπ，把它与上式相加，并应用欧拉公式，得()()⎰⎰+∞∞--+∞∞-'⎥⎦⎤⎢⎣⎡''=dk e x d e x f x f ikx x ik π21（6） 由于可以写为()()⎰+∞∞--=dk e k F x f ikxπ21（7） 只要 ()()dx e x f k F ikx ⎰+∞∞-=（8）式（8）中已令x x ='，函数()k F 叫做()x f 的傅里叶变换式，用下面的记号来表示：()()}{x f F k F = (9)常常把()x f 和()k F 称为傅里叶变换式。
如果f 是时间的函数而不是空间变量的函数，为了在时域中得到相应的变换式偶，我们只是把x 换成t ，再把空间角频率k 换成时间角频率w ，即()()⎰+∞∞--=dw e k F t f iwt π21（10）以及()()dt e t f w F iwt ⎰+∞∞-=（11）1.2 二维变换式光学中一般涉及的信号，例如孔上的光场或者象平面上的通量密度分布，将傅里叶变换式推广到二维情况有()()()()y x yk x k i y x dk dk ek k F y x f y x ⎰⎰∞+-=,21,2π（12）或者()()()dxdy ey x f y x F yk x k i y x ⎰⎰∞+=,,（13）其中x k 和y k 分别是沿坐标轴方向的空间角频率。
1.3 三维傅里叶变换式 将傅里叶变换推广到三维情况有()()()()z y x z k y k x k i z y x dk dk dk ek k k F z y x f z y x )3,,21,,++-∞⎰⎰⎰=π（14）以及()()()⎰⎰⎰∞++=dxdydz ez y x f z y x F yk y k x k i z y x ,,,,（15）其中x k ，y k 和z k 分别是沿坐标方向的空间角频率。
2 用傅里叶变换计算衍射的光强分布光是一种电磁波，按jwt e 的规律随时间传播，电光源发出的是一组球面波，设光源位于坐标原点处，以速度v 在电容率为ε的介质中传播，当光到达半径为r 的求面时，光的场强E 是t r ,的函数，可以表示为()()()()[]kr wt j r E r t jw r E t r E -=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=exp exp ,υ（16）其中λπυ2==w k 称为波数，()t r E , 为光矢量点光源从原点出发的球面波，能量密度为221E w ε=（17）以v 表示单位时间内光矢量所在空间的体积，则单位时间内通过整个球面的能量为V E W 221 ε=（18）而()0E k r E υ'= （19）式中0E 是与光源振动有关的常数，k '是与介质有关的常数，则()()[]kr wt j E rk t r E -'=exp ,0 （20）为简便，只考虑某时刻的振动，含时间的项jwt e 可省去。
在光学系统中，光从出射光瞳射出，取光瞳坐标为()00,y x ，观察平面的坐标为()y x ,，两坐标系相平行，原点在它们的公共垂线上，相距为z 。
见图（1）图（1）光瞳面上任意一点s ()00,y x 到观察面上的某点p ()y x ,的距离为()()[]2122020zy y x x r +-+-=（21）由（20）式知，光是从s 点以球面波jkre rk -'的形式传播到p 点的。
如果s 点振幅为E ()y x ,,则在P 点光的矢量为()()jkr e y x E rk y x E -'=00,, （22）为计算球面上p 点的光的场强，需要选取包含s 点在内的小面元00dy dx ，则()00001,),(dy dx e ry x E k y x E jkr -⎰⎰= （23）为便于计算，设光瞳与观察点面相距很远，取R r =,r 的近似值为()()[][]Ryy xx R y x R yy xx y x R zy y x x r x 0202021020222122020222+-++=--++=+-+-=（24）在远场衍射的情况下，即∞→R 时()Ry x k 222+-《1 且z R ≈，则()()()⎰⎰+=-ds zyy xx jk y x E zke y x E jkz]ex p[,,0000（25） 式（25）为远场近似情况下的衍射（也称之为夫琅禾费衍射）的公式。
式（25）与式（13）形式完全相同，级光源在p 点的E ()y x ,是光瞳函数E ()00,y x 的二维傅里叶变换式。
2.1 计算单缝衍射的光强分布当光源为线光源时，式（25）可以演化为()()000dx ex E zke x E zjkxx jkz⎰∞+∞--=（26）显然，式（26）和式（11）在形式上完全相同，切有以下对应关系：()()t f x E ↔0zkx w ↔式（24）可以记为()()}{0x E F zke x E jkz-=（27）可见，若要求观察平面上的光强分布，只要把表示出瞳光源的光强分布进行傅里叶变换，其中把傅里叶变换的w 用zkx置换即可。
也就是说只要计算出出瞳的傅里叶变换，就能求出观察面上的光强分布。
为简便，把式（26）前的常数省略，则()()000dx ex E x E zjkxx ⎰∞+∞-=（28）如果狭缝上有均匀照度，其值为A,则长度为a 2的狭缝上的振幅为()⎪⎩⎪⎨⎧>≤=ax ax A x E 000,0,则()()wa jwA e e jw A dx Ae x E jwa jwa aa jwx sin 00=-==-+-⎰（29） 所以，长为a 2的狭缝光源在观察面上所形成的光强分布为()()()222222sin 4sin 4⎪⎭⎫ ⎝⎛=-=•=*wa wa a A wa w A x E x E x I （30）2.2 计算圆孔衍射的光强分布圆孔上的夫琅禾费衍射，在光学仪器的研究中具有重要意义。
由（25）式知，在远场情况下，一个任意孔在p 点所产生的光的场强分布为()()()⎰⎰⎥⎦⎤⎢⎣⎡+=-000000exp ,,dy dx z yy xx jk y x E zke y x E jkz（36） 对于一个圆孔，由于对称性，所以在孔径平面和观察平面上都采用极坐标。
因此，令φρcos 0=x ，φρsin 0=y ，Φ=cos q x ，Φ=sin q y （37）因而微分面元现在是φρρd d dy dx =00（38）把（37）式和（38）式代入（36）式中，得()()φρρφρρπφφρd d ezke E a z q k j jkz⎰⎰==Φ-⎪⎭⎫ ⎝⎛-=20cos ,（39）由于问题是完全对称的，其解一定与Φ无关，这样可以令0=Φ求解（39）式。
