各个图形的基本特征

图形的归类与分类图形是我们日常生活中常见的一种表达方式，它可以传递信息、引起共鸣，也是艺术创作中常用的元素。

在视觉设计、信息传递等领域，图形的归类与分类是一项重要的任务。

本文将探讨图形的归类与分类的方法和应用。

一、图形的基本分类图形可以根据其形状、色彩、线条等属性进行基本的分类。

1. 形状分类：根据图形的形状，可以将其分为圆形、正方形、三角形、长方形等。

形状分类是最常见的一种分类方式，它能够帮助我们快速地辨识和识别不同的图形。

2. 色彩分类：图形的色彩是其表达和传递信息的重要手段。

我们可以根据图形所使用的颜色来进行分类，比如红色、蓝色、绿色等，也可以根据色彩的明暗、饱和度等属性来进行分类。

3. 线条分类：图形的线条也是其重要的表现方式之一。

线条可以分为直线、曲线、粗线、细线等。

线条的分类可以帮助我们更好地理解图形的结构和形态。

二、图形的高级分类除了基本分类外，图形还可以根据其在特定领域内的使用和特征进行高级分类。

1. 符号分类：在图形设计中，符号是一种常见的图形表达方式。

符号可以是文字、图案、标志等，它们往往具有较为固定的形态和意义。

根据符号的用途和特征，我们可以将其进行分类，比如标志性符号、表示性符号、象征性符号等。

2. 图形识别分类：在计算机视觉和人工智能领域，图形的分类和识别是一项重要的任务。

通过对图形的学习和分析，计算机可以自动识别和分类图像。

图形识别分类可以基于机器学习、深度学习等技术手段来实现，它在图像搜索、智能驾驶等领域有着广泛的应用。

3. 装饰性分类：在艺术和设计领域，图形的装饰性分类是一种常见的方式。

通过对图形元素的组合、重复和变化，可以创造出各种不同的装饰效果。

装饰性分类可以基于图形的样式、纹理、对比度等属性进行，它在室内设计、服装设计等领域有着广泛的应用。

三、图形分类的方法图形的分类可以通过人工进行，也可以通过计算机算法和技术进行。

1. 人工分类：人工分类是一种主观的分类方式，需要依靠专业人士的经验和认知来进行。

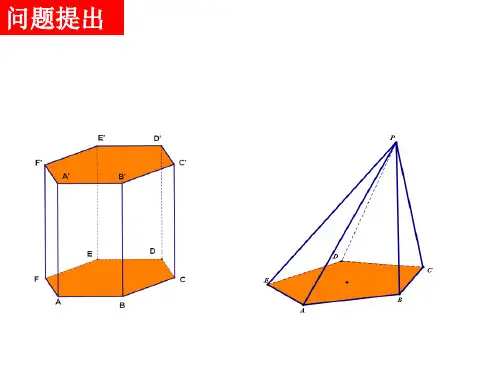
G F MCD A B EMD A PDA B C PADBC初三（上）数学辅导—“三垂足一线”基本图形的特征与应用一、“三垂足一线”基本图形及其基本特征如图1，AB ⊥BC ，DC ⊥BC ，AP ⊥PD ，且P 在直线BC 上． 由于三垂足B 、C 、P 在一条直线上，故命名为“三垂足一线”基本图形．不难看出图中有一对相似三角形，即△ABP ∽△PCD .由此我们得到如下 图1 性质：AB BP PCCD=，所以 AB CD PC PB ⋅=⋅．二、“三垂足一线”基本图形在解题中的应用例1．如图，在梯形ABCD 中，10AD BC ==，43tanD =，E 是腰AD 上 一点，且:1:3AE ED =．（1）当:1:3AB CD =时，求梯形ABCD 的面积； （2）当ABE BCE ∠=∠时，求线段BE 的长； （3）当BCE △是直角三角形时，求边AB 的长．例2．如图，在矩形ABCD 中，4AB =，2AD =，点M 是AD 的中点，点E 是边AB 上的一动点，联结EM 并延长交射线CD 于点F ，过M 作EF 的垂线交BC 的延长线于点G ，联结EG ，交边DC 于点Q 设AE 的长为x ，△EMG 的面积为y ． （1）求MEG ∠的正切值；（2）求y 关于x 的函数解析式，并写出x 的取值范围； （3）线段MG 的中点记为点P ，联结CP ，若△PGC ∽△EFQ ，求y 的值．A D C E B第 6 题图E F AB C D变式．已知9023ABC AB BC AD BC P ∠===°，，，∥，为线段BD 上的动点，点Q 在射线AB 上，且满足PQ AD PCAB=（如图1所示）．（1）当2AD =，且点Q 与点B 重合时（如图2所示），求线段PC 的长；（2）在图1中，联结AP ．当32AD =，且点Q 在线段AB 上时，设点B Q 、之间的距离为x ，APQ PBCS y S =△△，其中APQ S △表示APQ △的面积，PBC S △表示PBC △的面积，求y 关于x 的函数解析式，并写出函数定义域；（3）当AD AB <，且点Q 在线段AB 的延长线上时（如图3所示），求QPC ∠的大小．练 习 卷一、选择题：1．下列条件，不能判定ABC ∆与DEF ∆相似的是 （ ） A ︒=∠=∠90F C ，︒=∠55A ，︒=∠35D ； B ︒=∠=∠90F C ，10=AB ，6=BC ，15=DE ，9=EF ； C ︒=∠=∠90E B ，DFAC EFBC =； D ︒=∠=∠90E B ，ACDF EF AB =.2.在同一坐标系中，函数y mx m =+和函数222y mx x =-++（0m ≠是常数）的图象可能．．是 （ ）3．如图，在ABC △中，点D 是边BC 上任意一点，点E 、F 分别是ABD △和ACD △的重心．如果6BC =， 那么线段EF 的长为 （ ） A.2 B.3 C.4 D.5A D P CB Q 图1 D A PC B（Q ） 图2 图3C AD P B Q二、填空题：4. 矩形的周长是28，对角线与一边的夹角的正弦值为53，那么这个矩形的面积为 .5．在ABC ∆中，∠B=25°,AD 是BC 边上的高，且CD BD AD ⋅=2，则BAC ∠的度数是________．6.如图，EF 是△ABC 的中位线，将△AEF 沿中线AD 的方向平移到△A 1E 1F 1，使线段E 1F 1落在BC 边上，若△AEF 的面积为7cm 2，则图中阴影部分的面积是 cm 2.7. 如图，某公园入口处原有三级台阶，每级台阶高为20cm ，深为30c m ，为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A ，斜坡的起始点为C ，现设计斜坡的坡度1:5i =， 则AC 的长度是 cm .8.如图，在△ACB 中，∠CAB=90°,AC=AB ＝3,将△ABC 沿直线BC 平移，顶点A 、C 、B 平移后分别记为A 1、C 1、B 1，若△ACB 与△A 1C 1B 1重合部分的面积2，则CB 1= . 9.如图，平面直角坐标系中正方形ABCD ，已知()1,0A ，()0,3B ，则sin COA ∠= ．10如图1，把一张标准纸一次又一次对开，得到“2开”纸、“4开”纸、“8开”纸、 “16开”纸…．已知标准纸．．．的短边长为a ． （1）如图2，把这张标准纸对开得到的“16开”张纸按如下步骤折叠：第一步 将矩形的短边AB 与长边AD 对齐折叠，点B 落在AD 上的点B '处，铺平后得折痕AE ； 第二步 将长边AD 与折痕AE 对齐折叠，点D 正好与点E 重合，铺平后得折痕AF ． 则:AD AB 的值是 ，AD AB ，的长分别是 ， ．（2）“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等？若相等，直接写出这个比值；若不相等，请分别计算它们的比值．（3）如图3，由8个大小相等的小正方形构成“L ”型图案，它的四个顶点E F G H ，，，分别在“16开”纸的边AB BC CD DA ，，，上，求DG 的长．（4）已知梯形MNPQ 中，MN PQ ∥，90M =∠，2MN MQ PQ ==，且四个顶点M N P Q ，，，都在“4开”纸的边上，请直接写出2个符合条件且大小不同的直角梯形的面积．A B C D BC A DE G HF F EB ' 4开 2开 8开16图1 图2 图3 a AB C E F D A E F 第6题图A B 第7题图 C 3020 C B A 第8题图11.如图，在平面直角坐标系中，二次函数26y ax x c =++的图像经过点()4,0A 、()1,0B -，与y 轴交于点C ，点D 在线段OC 上，=OD t ，点E 在第二象限，∠=90ADE ，1=2tan DAE ∠，EF OD ⊥，垂足为F ．（1）求这个二次函数的解析式；（2）求线段EF 、OF 的长（用含t 的代数式表示）； （3）当∠ECA =∠OAC 时，求t 的值．自招题．已知42++=m m y ,若m 为整数，在使得y 为完全平方数的所有m 的值中，设m 的最大值为a ，最小值为b ，次小值为c ．（注：一个数如果是另一个整数的完全平方，那么我们就称这个数为完全平方数．） （1）求c b a 、、的值；（2）对c b a 、、进行如下操作：任取两个求其和再除以2，同时求其差再除以2，剩下的另一个数不变，这样就仍得到三个数．再对所得三个数进行如上操作，问能否经过若干次上述操作，所得三个数的平方和等于2008？证明你的结论．。

1.1 生活中的立体图形新知概览：知识要点课标要求中考考点生活中常见几何体的基本特征及其分类认识常见几何体的基本特征，能对这些几何体进行正确的识别和简单的分类识别柱体、锥体、球体棱柱的特征知道常见几何体的特征求棱柱的棱数，面数图形的构成要素认识点、线、面，理解“点动成线、线动成面、面动成体”探索平面图形旋转的旋转体知识全解知识点1生活中常见几何体的基本特征及其分类知识衔接：几何图形包括立体图形和平面图形．1.平面图形：数学上所说的平面没有边界，可以向四面八方无限延伸．如果一个图形的各个部分都在同一个平面内，那么这个图形是平面图形，常见的平面图形有三角形、正方形、长方形、平行四边形、梯形、圆等．2.如图1—1—1我们学过长方体,正方体等称为立体图形，这样的几何图形上的点不都在在同一平面内．长方体正方体知识详解：（1）几何体的分类：（2）几何体的基本特征：体是由面围成的；面有两种，平面和曲面．①柱体的相同点是上下两个面完全相同．不同点是圆柱的底面是圆，侧面是一个曲面，直棱柱底面是多边形，侧面都是长方形；②锥体相同点是都有一个顶点．不同点是圆锥的底面是一个圆，侧面是一个曲面，棱锥的底面是一个多边形，侧面都是三角形；③球体由一个曲面围成．知识警示：（1）立体图形是由一个或几个面围成的，如：球是有一个面围成的，而长方体是由六个面围成的，组成棱柱和棱锥的面都是平的，而组成圆锥、圆柱、球的面都是曲的．（2）我们直研究直棱柱，不作特殊说明，棱柱都指直棱柱；（3）长方体、正方体是棱柱；（4）几何体的分类可按“有无顶点”、“有无曲面”等不同的标准来区分．【试练例题1】如图1—1—2所示，请分别指出下列物体的形状分别类似于哪种几何体．思路导引：观察实物轮廓、分析轮廓特征、抽象几何体．直棱柱柱体棱柱圆柱锥体棱锥几何体圆锥球体斜棱柱1—1—2解：茶叶盒类似棱柱；地球仪类似球体；魔方类似棱柱；字典类似棱柱；金字塔类似棱锥；彩笔类似棱柱．方法：由实物的形状想象几何体是一个观察、体验、抽象的过程，解决此类问题应从实物的轮廓特征入手，抽象出几何体，进而确定是哪种几何体，即“有物悟形”、“由形命名”．【试练例题2】如图1—1—3将下列几何体进行分类，并说明理由.思路导引：把几何体进行分类，一定要注意根据不同的分类标准，分类情况不尽相同，切记不要混淆分类标准，分类要做到不重不漏．解：如一类是（1）（2）（4）（5）是柱体，另一类（3）（7）是椎体，第三类（6）是球体；或一类是（1）（4）（5）（7），有平面围成，另一类（2）（3）（6），有曲面参与围成．方法：几何体分类，先确定分类标准，按有无曲面来分较常用，在此标准下几何体可分为多面体（围成几何体的面都是平面）和旋转体（由平面图形旋转形成，围成几何体的面有曲面）．【试练例题3】如图1—1—4所示，陀螺是由下面哪两个几何体组合而成的（）A. 长方体和圆锥 B. 长方形和三角形C. 圆和三角形 D. 圆柱和圆锥1—1—41—1—3思路导引：根据立体图形的特征对图进行分析知：该图上部分是圆柱，下部分是圆锥．解：D.方法：先判断原几何体是曲面还是平面围成，再判断是否能分割为柱体、锥体还是球体.知识点2棱柱的相关概念及特征知识衔接：１．在小学里我们认识了六种常见的几何体，它们分别是长方体、正方体、圆柱、圆锥和球体．2．我们通过学习，已知道圆柱的侧面展开图是长方形．知识详解：（1）在棱柱里，任何相邻的两个面的交线都叫做棱，相邻两个侧面的交线交做侧棱，棱柱的所有侧棱都相等．棱柱的上、下底面是相同的图形，都是多边形，侧面都是长方形．（2）棱柱的特征是：①有两个面互相平行；②其余各面都是平行四边形；③每相邻两个四边形的公共边互相平行．知识警示：一般地，n棱柱有2n个顶点，3n条棱（其中有n条是侧棱），(n+2)个面（2个底面，n个侧面）．【试练例题4】如图1—1—5所示棱柱（1）这个棱柱的底面是____________边形．（2）这个棱柱有____________个侧面，侧面的形状是____________边形．1—1—5 （3）侧面的个数与底面的边数____________．（填“相等”或“不相等”）（4）这个棱柱有____________条侧棱，一共有____________条棱．（5）如果CC′=3 cm，那么BB′=____________cm．思路导引（１）观察图形，易知此棱柱为三棱柱；所以底面是3边形，这个棱柱有3个侧面，侧面形状是四边形；利用棱柱侧棱都相等，可求得BB′．答案：1.（1）三（2）3 四（3）相等（4）3 9 （5）3．方法：结合图形解决棱柱的问题，知识就显得较为容易．知识点3棱柱的分类知识详解：人们通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱、六棱柱……它们底面图形的形状分别为三角形、四边形、五边形、六边形……知识警示：（1）底面是n边形的棱柱称为n棱柱，长方体和正方体都是四棱柱．（2）正方体的六个面形状、大小都相同，都是正方形，正方体的12条棱都相等．【试练例题5】如图1—1—6请说出下面物体是哪种棱柱．思路导引根据棱柱的分类，观察这几个棱柱的底面，分别是三角形、四边形、六边形，所以这几个物体分别是：三棱柱、四棱柱、六棱柱．答案：三棱柱、四棱柱、六棱柱．方法：判断棱柱的种类，我们可以看棱柱底面是几边形，即可判断其是几棱柱．知识点4图形的构成要素知识详解：1.几何图形都是由点、线、面、体组成的.(1)点是构成图形的基本元素，是线与线相交的地方，即线与线相交成点.点无大小之分，只有位置之别；（2）线无粗细，可以有长度，它可分为直线、曲线，面与面相交成线；（3）面无厚薄，可分为平面、曲面.平面是向四周无限延伸的.2．用运动观点看几何基本图形之间的关系：点动成线，线动成面，面动成体.如：流星可以看作一个点，它划破夜空，就形成了线；直升飞机的螺旋桨快速旋转形成了一个圆面，这可以说线动成面；三角板绕它的一条直角边旋转一周，形成一个圆锥体.点动成线，线动成面，面动成体，这样就组合成了各种各样的几何图形，形成了1—1—6丰富多彩的图形世界.知识警示：（1）线、面、体都是由点组成的，即点是构成图形的基本元素；（2）面与面的交线可能是直线，也可能是曲线；（3）点是最简单的几何图形.【试练例题6】用数学的眼光去观察问题，你会发现很多图形都能看成是动静结合，舒展自如的．如图1—1—7绕虚线旋转得到的几何体是（）思路导引：根据旋转及线动成面的知识可得旋转后的图形为：两边为圆锥，中间为圆柱，结合实际生活经验此题易解．解：D.方法：长方形绕其一边所在直线旋转一周形成了一个圆柱; 半圆绕其直径所在直线旋转一周形成球;三角形形绕其一边所在直线旋转一周形成圆锥.1—1—7A B C D。

数学的分形几何分形几何是一门独特而迷人的数学领域，它研究的是自相似的结构和形态。

分形几何的概念由波蒂亚·曼德博（Benoit Mandelbrot）在1975年首次提出，之后得到了广泛应用和发展。

本文将介绍分形几何的基本概念和应用领域，旨在帮助读者更好地了解这一令人着迷的学科。

一、分形几何的基本概念分形（fractal）是一种非几何形状，具有自相似的特点。

简单来说，分形就是在各个尺度上都具有相似性的图形。

与传统的几何图形相比，分形图形更加复杂、细致，其形状常常无法用传统的几何方法进行描述。

分形几何的基本概念包括分形维度、分形特征和分形生成等。

1. 分形维度分形维度是分形几何中的重要概念之一。

传统的几何图形维度一般为整数，如直线的维度为1，平面的维度为2，而分形图形的维度可以是非整数。

分形维度能够描述分形的复杂程度和空间占据情况，是衡量分形图形特性的重要指标。

2. 分形特征分形几何的分形特征是指分形图形所具有的一些独特性质。

其中最著名的就是自相似性，即分形图形在不同尺度上具有相似的形态和结构。

此外，分形图形还具有无限的细节，无论放大多少倍都能够找到相似的结构。

3. 分形生成分形图形的生成是分形几何中的关键问题之一。

分形图形可以通过递归、迭代等方式进行生成，比如著名的分形集合——曼德博集合就是通过迭代运算得到的。

分形生成的过程常常需要计算机的辅助，对于不同的分形形状，生成算法也有所不同。

二、分形几何的应用领域分形几何的独特性质使其在许多领域中得到广泛应用。

以下列举了几个典型的应用领域。

1. 自然科学分形几何在自然科学中有着广泛的应用。

例如，分形理论可以用来研究自然界中的地形、云雾形态等。

通过分形几何的方法，我们能够更好地理解和描述自然界的复杂性，揭示出隐藏在表面之下的规律。

2. 经济金融分形几何在经济金融领域也有着重要的应用。

金融市场的价格走势往往具有分形特征，通过分形几何的方法可以更好地预测未来的市场走势和波动。

图像的三⼤特征（转）原⽂（⼀）HOG特征1、HOG特征：⽅向梯度直⽅图（Histogram of Oriented Gradient, HOG）特征是⼀种在计算机视觉和图像处理中⽤来进⾏物体检测的特征描述⼦。

它通过计算和统计图像局部区域的梯度⽅向直⽅图来构成特征。

Hog特征结合 SVM分类器已经被⼴泛应⽤于图像识别中，尤其在⾏⼈检测中获得了极⼤的成功。

需要提醒的是，HOG+SVM进⾏⾏⼈检测的⽅法是法国研究⼈员Dalal 在2005的CVPR上提出的，⽽如今虽然有很多⾏⼈检测算法不断提出，但基本都是以HOG+SVM的思路为主。

（1）主要思想：在⼀副图像中，局部⽬标的表象和形状（appearance and shape）能够被梯度或边缘的⽅向密度分布很好地描述。

（本质：梯度的统计信息，⽽梯度主要存在于边缘的地⽅）。

（2）具体的实现⽅法是：⾸先将图像分成⼩的连通区域，我们把它叫细胞单元。

然后采集细胞单元中各像素点的梯度的或边缘的⽅向直⽅图。

最后把这些直⽅图组合起来就可以构成特征描述器。

（3）提⾼性能：把这些局部直⽅图在图像的更⼤的范围内（我们把它叫区间或block）进⾏对⽐度归⼀化（contrast-normalized），所采⽤的⽅法是：先计算各直⽅图在这个区间（block）中的密度，然后根据这个密度对区间中的各个细胞单元做归⼀化。

通过这个归⼀化后，能对光照变化和阴影获得更好的效果。

（4）优点：与其他的特征描述⽅法相⽐，HOG有很多优点。

⾸先，由于HOG是在图像的局部⽅格单元上操作，所以它对图像⼏何的和光学的形变都能保持很好的不变性，这两种形变只会出现在更⼤的空间领域上。

其次，在粗的空域抽样、精细的⽅向抽样以及较强的局部光学归⼀化等条件下，只要⾏⼈⼤体上能够保持直⽴的姿势，可以容许⾏⼈有⼀些细微的肢体动作，这些细微的动作可以被忽略⽽不影响检测效果。

因此HOG特征是特别适合于做图像中的⼈体检测的。

2、HOG特征提取算法的实现过程：⼤概过程：HOG特征提取⽅法就是将⼀个image（你要检测的⽬标或者扫描窗⼝）：1）灰度化（将图像看做⼀个x,y,z（灰度）的三维图像）；2）采⽤Gamma校正法对输⼊图像进⾏颜⾊空间的标准化（归⼀化）；⽬的是调节图像的对⽐度，降低图像局部的阴影和光照变化所造成的影响，同时可以抑制噪⾳的⼲扰；3）计算图像每个像素的梯度（包括⼤⼩和⽅向）；主要是为了捕获轮廓信息，同时进⼀步弱化光照的⼲扰。