初一数学周末练习5

七年级数学第一周周练习一．判断题 答案正确的在括号内打“√”号，不正确的打“×”号 （1）单项式的次数是各字母的指数中最大的那个数. （ ） （2）组成多项式123423-++y y y 的项是y y y 2,3,423和1.（ ） （3）ba 33+是多项式. （ ） （4）多项式的次数是由组成多项式的各个单项式的次数相加得到的.（ ） （5）单项式26xy -减去2xy 3-的差是.32x y -（ ）０．（6）一个关于A ，B 的三次单项式与另一个关于A ，B 的三次单项式的和一定是关于A ，B 的三次单项式.（ ） （７）()().a 23a 6a 7a 3a 23a 6a 7a 3]a 23a 6a 7[a 3232322----=----=----（ ）二、选择题 1．在代数式bc a +21，2b ，1232--x x ，abc ，0，a b ，π，xyyx +中，下列结论正确的是 （ ）A ．有4个单项式，2个多项式B ．有5个单项式，3个多项式C ．有7个整式D ．有3个单项式，2个多项式 2．单项式－5x ，210x -，5x ，27x 的和，合并后的结果是 （ ） A ．二次二项式 B ．四次单项式 C ．二次单项式 D ．三次多项式3．下列四个算式：（1）22=-a a ；（2）633x x x =+；（3）n m n m 22523=+；（4）22232t t t =+，其中错误的个数为 （ ） A ．1 B ．2 C ．3 D ．4 4．下列各式计算正确的是（ ）A ．7232)(m m m =⋅B ．10232)(m m m =⋅C ．12232)(m m m =⋅D ．25232)(m m m =⋅5．第二十届电视剧飞天奖今年有a 部作品参赛，比去年增加了40%还多2部.设去年参赛作品有b 部，则b 是（ ）A ．%4012++a B ．2%)401(++aC ．%4012+-a D ．2%)401(-+a6．小华计算其整式减去ac bc ab 32+-时，误把减法看成加法，所得答案是ab ac bc 232+-，那么正确结果应为（ ） A ．ac bc 96+- B ．ac bc 96-C ．ab ac bc +-64D ．ab 3 7．下列结论中正确的是（ ）（A ）没有加减运算的代数式叫单项式（B ）单项式732xy 的系数是3，次数是2（C ）单项式M 既没有系数，也没有次数 （D ）单项式z xy 2-的系数是－1，次数是4 8．已知()()22205155,52x x x x --+--=则的值为（ ） （A ）2 （B ）-2 （C ）-10 （D ）-6 9．下列各式中，值一定为负的是（ ）（A ）b a - (B)22b a --（C ）12--a（D ）a -10．使()()2222229522cy xy x y bxy x y xy ax +-=++--+-成立的c b a ,,的值依次是（ ）（A ）4，－7，－1 （B ）－4，－7，－1 （C ）4，7，－1 （D ）4，7，1 三、填空题1．7323-+-x y x 的次数是_______. 2．单项式ab 4-，3ab ，2b -的和是______. 3．化简=-+--)x 2xy 2()x 2yx 4(3xy 3_______.4．若4353b a b a mn-所得的差是单项式，则这个单项式是_______. 5．200020014)212(⨯-=________.6．去掉下式的括号，再合并同类项.()()53466493434-+---++-x x xxx x=_____________________________=____________________________.7．已知多项式,234,2222222z y x B z y x A ++-=-+=且A+B+C=0，则多项式C 为__________.8．若代数式722++y y 的值为6，那么代数式5842-+y y 的值为= ________.9．. ();31329333⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛-⨯- ________.10．若N 为正整数，且72=nx ，则()()nn x x 222343-的值为________.四、解答题 1．计算：（1）]3)[()3(2222ab b a ab b a ++---；()()222(2) 325;x y xy x y xy x y +---（3）16145.02⨯； (4) 35768x x x x x x ⋅⋅+⋅⋅；(5)()()().52222344321044x x x x x ⋅+-+-２．解答下列问题（１）先化简，再求值()[]{}21，其中x 4x x 2x x 5x 3x 4x 2222-=+------.（2）．单项式my x 356-是六次单项式，求()m 2-的值.3．先化简，再求值：已知a C a a a A 4,32,16322=+-=+-=B . 计算()()[]C B A C B ---+.４．已知27，xy y x 22-==+.求22222711435y x xy y xy x +----的值.５．多项式()b x x x a b -+--34是关于x 的二次三项式，求,a b６．如图1－4，一块半圆形钢板，从中挖去直径分别为x 、y 的两个半圆： （1）求剩下钢板的面积：（2）若当x=4，y=2时，剩下钢板的面积是多少？（π取3.14）附加题：１．若243,25322+-=+-=m m B m m A ，试分析A 与B 的关系２．比较1002与753的大小.参考答案一、判断题（1）×（2）×（3）×（4）×（5）√（6）×（7）×二、选择题1-5 ACCBC 6-10 BDACC三、填空题 1．4 2．-b 2-ab 3. 4x-7xy 4. –2a 3b 4 5. –×1020006. –x+9+4x 4-6x 3-6x 4+4x 3-3x+5=-2x 4-2x 3-4x+147. 3x 2-5y 2-z 9. 8 10. 2891四、解答题 1．计算(1) 解：原式=a 2-b 2+3ab-a 2-b 2-3ab=-2b 2(2) 解：原式=3x 2y+3xy-2x 2y+2xy-5x 2y=-4x 2y+5xy(3) 解：原式=214×0.514×2= (2×0.5)14×2(4) 解：原式=x 3+5+7+x 1+6+8=x 15+x 15 =2x 15(5) 解：原式= (2x 4)4-2x 10(2x 2)3+2x 44×3=24. x 4×4-2x 10.23. x 2×3+2 x 4.5. x 4×3 =16x 16-16x 16+10x 16 =10x 162．解答下列问题(1) 解：原式=4x 2-[-3x 2-(5x-x 2-2x 2+x)+4x]=4x 2-(-3x 2-6x+3x 2+4x) =4x 2+2x把21-=x 代入其中，得： 0212414)21(2)21(42=⨯-⨯=-⨯+-⨯(2) 解：m+3=6m=3(-2)m =(-2)3=83. 解：原式=B+C-(A-B+C)=B+C-A+B-C =2B-A把A=3a 2-6a+1, B=-2a 2+3代入原式，得：2(-2a 2+3)-( 3a 2-6a+1)=-4a 2+6-3a 2+6a-1 =-7a 2+6a+54. 解：原式=-2x 2-2y 2-14xy=-2(x 2+y 2)-14xy把x 2+y 2=7, xy=-2, 带入原式，得： -2×7-14×(-2)=-14+28=14 5. 解：∵多项式为二次三项式∴ a-4=0, a=4 ∴ b=26. (1)xyxy xy xy y x xy y x y x y x y x y x 200157:2001574)42(21)42(21]444)([21)2(21)2(21]2)([21:2222222222剩下面积为答解==•=--++•=--+•=--+•πππππππ(2)28.6:28.620024157:,2,4:剩下面积为答得代入上式把解=⨯⨯==y x附加题 1．BA mB A m B A m m B A m m m m m m m m m B A <>==><-=--=-+-+-=+--+-=-,0,0,0243253)243(253:2222时当时当时当解2.10075252525253752525410023271627)3(316)2(2:>∴<==== 解七年级（下）数学周练习二一、填空题1、()()__________523=÷-⋅--x x x ，()()__________2552=-⋅--a a 2、55______a a =÷； ()()()3223________a a -=-÷3、________2121=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛--b a b a ；()224994________3223x y y x +-=⎪⎭⎫ ⎝⎛+- 4、；________322132213232=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--b a b a ；( )(—2x+3y)=9y 2—4x 25、．计算：54322c c c c c +⋅+⋅= .；（ ）－（x 2＋3xy ）=－xy －31y 2。

七年级数学周末练习题答案一、选择题1. 下列哪个选项是最小的正整数？A. -1B. 0C. 1D. 2答案：C2. 如果一个数的绝对值是5，那么这个数可能是：A. 5B. -5C. 5或-5D. 以上都不是答案：C3. 计算下列表达式的值：(-2) × (-3)：A. 6B. -6C. 3D. -3答案：A4. 一个数的平方是9，这个数可以是：A. 3B. -3C. 3或-3D. 9答案：C5. 以下哪个是偶数？A. 2B. 3C. 5D. 7答案：A二、填空题6. 一个数的相反数是-8，这个数是________。

答案：87. 如果一个数的立方是-27，那么这个数是________。

答案：-38. 一个数的绝对值是其本身，这个数是________。

答案：非负数9. 一个数的平方根是2，这个数是________。

答案：410. 一个数的立方根是-2，这个数是________。

答案：-8三、计算题11. 计算下列各题，并写出计算过程：(1) 5 + (-3) - 2答案：5 - 3 - 2 = 2 - 2 = 0(2) (-1) × 6 ÷ (-2)答案：-1 × 6 ÷ (-2) = -6 ÷ (-2) = 312. 化简下列表达式：(1) |-4| - |-6|答案：|-4| - |-6| = 4 - 6 = -2(2) √(-4)²答案：√(-4)² = √16 = 4四、解答题13. 一个数的3倍加上5等于这个数的5倍减去7，求这个数。

设这个数为x，根据题意可得方程：3x + 5 = 5x - 7解方程得：2x = 12所以 x = 614. 一个班级有40名学生，其中男生人数是女生人数的2倍，求男生和女生各有多少人。

设女生人数为x，则男生人数为2x。

根据题意可得方程：x + 2x = 40解方程得：3x = 40所以x = 40 ÷ 3 ≈ 13.33，但人数必须是整数，所以女生人数为13人，男生人数为40 - 13 = 27人。

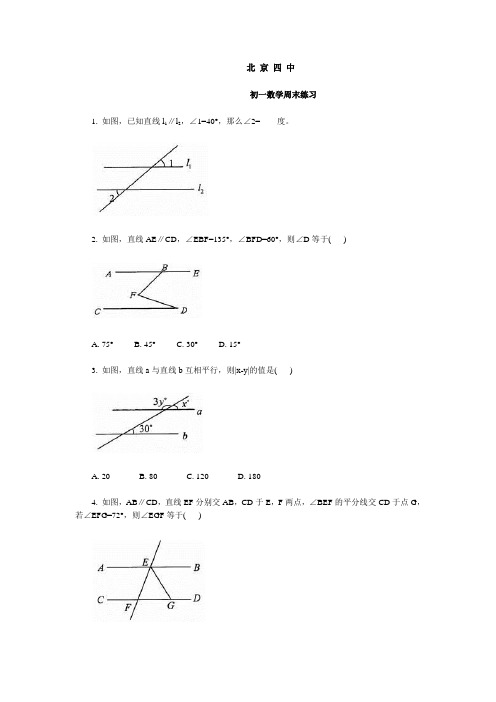
北京四中初一数学周末练习1. 如图，已知直线l1∥l2，∠1=40°，那么∠2=____度。

2. 如图，直线AE∥CD，∠EBF=135°，∠BFD=60°，则∠D等于()A. 75°B. 45°C. 30°D. 15°3. 如图，直线a与直线b互相平行，则|x-y|的值是()A. 20B. 80C. 120D. 1804. 如图，AB∥CD，直线EF分别交AB，CD于E，F两点，∠BEF的平分线交CD于点G，若∠EFG=72°，则∠EGF等于()A. 36°B. 54°C. 72°D. 108°5. 如图，AD∥BC，点E在BD的延长线上，若∠ADE=155°，则∠DBC的度数为( )A. 155°B. 50°C. 45°D. 25°6. 如图，以下条件能判定GE∥CH的是()A. ∠FEB=∠ECDB. ∠AEG=∠DCHC. ∠GEC=∠HCFD. ∠HCE=∠AEG7. 将直角三角尺的直角顶点靠在直尺上，且斜边与这根直尺直行，那么，在形成的这个图中与∠α互余的角共有()A. 4个B. 3个C. 2个D. 1个8. 如图，给出了过直线外一点作已知直线的平行线的方法，其依据是()A. 同位角相等，两直线平行B. 内错角相等，两直线平行C. 同旁内角互补，两直线平行D. 两直线平行，同位角相等9. 如图，AB∥CD，EG与AB，CD分别交F，G，∠EAB=31°，∠EGD=70°，则∠AEG=______10. 探照灯、锅形天线、汽车灯以及其它很多灯具都与抛物线形状有关，如图所示是一探照灯灯碗的纵剖面，从位于O点的灯泡发出的两束光线OB、OC经灯碗反射以后平行射出，如果图中∠ABO=α，∠DCO=β，则∠BOC的度数为( )(A)180°-α-β (B)α+β (C)(D)90°+(β-α)11. 如图，在甲、乙两地之间修一条笔直的公路，从甲地测得公路的走向是北偏东48°，甲、乙两地间同时开工，若干天后，公路准确接通，则乙地所修公路的走向是南偏西_____度。

七年级数学第五周周周练一、选择: （3分×4 =12分）1、在 , , , , , 中, 单项式的个数是 （ ）（A ）2个 （B ）3个 （C ）4个 （D ）5个2.下列各运算正确的是 （ ）（A ）2x 3·3x 2 = 6x 6 (B) 772)()(a a a =-⋅-（C ）[]633)2()2(-=- (D)44481)3(y x xy = 3.下列各组中的两项, 不是同类项的是 （ ）（A ） , （B ） , （C ） , （D ） ,4.下列计算正确的是 （ ）（A ）y x y x xy y x xy 3222)(-=⋅-（B ）2)2(322+--=-+-x x x x x（C ）x x x x x x 2329)1323(23243+-=+-（D ）232283)12()3241(b a b a ab b a a +-=-⋅- 填空: （2分×15=30分）5.用代数式表示: a 的平方与b 的3倍的和6、单项式 的次数是 次, 系数是7、多项式y y x xy x +-+3223534是 次 项式8、当 时, 求 的值9、去括号 =-+-)(21d c b a10、把42234263y y x y x x --+-按y 的降幂排列为11. =12. =13. =14. =15.计算: =16、已知, 求17、20042005)313()103(⋅-=18、若, , 则 =19、若与的乘积中不含项, 则=三、解答题: （5分×8=40分）20、化简 21.计算22.计算 23.计算24. 25.26.计算27、解方程 )2(2)2()1(-=++-x x x x x x四、简答题: （5分×2=10分）、28、先化简, 再求值： , 其中 ,29、化简 [][][]323223)()()(2y x x y y x ----+-五、拓展题（本题5分）30、（1）计算____________________)1)(1(=-+x x_______________________)1)(1(2=-++x x x_________________)1)(1(23=-+++x x x x（2）观察（1）的算式, 猜想： 与 之积等于什么, 并推导你的猜想是否正确。

七年级数学周末提优练习1.小明同学将28铅笔笔尖从原点0开始沿数轴进行连续滑动,先将笔尖沿正方向滑动1 个单位长度完成第一次操作：再沿负半轴滑动2个单位长度完成第二次操作：又沿正方向滑动3个单位长度完成第三次操作,再沿负方向滑4个单位长度完成第四次操作,…, 以此规律继续操作,经过第50次操作后笔尖停留在点尸处,那么点尸对应的数是〔〕A. 0B. - 10C. -25D. 502 .如下图,圆的周长为4个单位长度,在圆的4等分点处标上数字0, 1, 2, 3,先让圆周上数字0所对应的点与数轴上的数-2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数-2021将与圆周上的哪个数字重合〔〕3 .同学们都知道,15 - 〔-2〕 I表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.答复以下问题：（1）15 - 〔 -2〕 1=.〔2〕找出所有符合条件的整数x,使得k+5l+h -2l=7成立,这样的整数是.〔3〕对于任何有理数%, Lr-31+k - 61的最小值是.〔4〕对于任何有理数x, lx- ll+Lt-21+k+ll的最小值是,此时x的值是.4 .百子回归图是由1, 2, 3…,100无重复排列而成的正方形数表,它是一部数化的澳门简史,如：中央四位“19 99 12 20〞标示澳门回归日期,最后一行中间两位“23 50〞标示澳门而积,…,同时它也是十阶幻方,其每行10个数之和,每列10个数之和,每条对角线10个数之和均相等,那么这个和为.5 .符号“G 〞表示一种运算,它对一些数的运算结果如下：(1) G (1) =1, G (2) =3, G (3) =5, G (4) =7,-(2) G (i) =2, G (工)=4, G (1) =6, G (工)=8,… 2 3 4 5利用以上规律计算：G (2021) -G (―1―) -2021= 2021------------ 6 . 一电子跳蚤在数轴上从原点开始,第1次向右跳1个单位,紧接着第2次向左跳2个单 位,第3次向右跳3个单位,第4次向左跳4个单位,……,依此规律跳下去,当它跳 第2021次落下时,落点处离原点的距离是 个单位.7 .阅读以下材料：我们知道3的几何意义是在数轴上数x 对应的点与原点的距离：即lxl=lx -01,也就是说,卜1表示在数轴上数x 与数0对应点之间的距离：这个结论可以推广为M -.5表示在数轴上xi, 也对应点之间的距离：例1.kl=2,求x 的值.解：容易看出,在数轴上与原点距离为2点的对应数为-2和2,即x 的值为-2和2.例2.k-11=2,求x 的值.解：在数轴上与1的距离为2点的对应数为3和-1,即x 的值为3和-1.仿照阅读材料的解法,求以下各式中x 的值.(1) Lr-2I=3(2) lx+ll=4.8 .阅读以下材料：我们知道3的几何意义是在数轴上数x 对应的点与原点的距离；即Ld=k-0l ；这个结论 可以推广为M-X2I 表示在数轴上数也对应点之间的距离.绝对值的几何意义在解题 中有着广泛的应用：nMuMmMx “9luNullntt 35:31>:>|11 M;aM:“r44 UIN 二・eMA«■二他例1：解方程3=4.容易得出,在数轴上与原点距离为4的点对应的数为±4,即该方程的x= ±4：例2：解方程k+11+k-21=5.由绝对值的几何意义可知,该方程表示求在数轴上与-1和2的距离之和为5的点对应的x的值.在数轴上,-1和2的距离为3,满足方程的x对应的点在2的右边或在-1的左边.假设x对应的点在2的右边,如图(25-1)可以看出x=3：同理,假设x对应点在-1的左边,可得x=-2.所以原方程的解是x=3或工・=-2.例3：解不等式在数轴上找出k- 11=3的解,即到1的距离为3的点对应的数为-2, 4,如图〔25-2〕, 在-2的左边或在4的右边的x值就满足k - 11>3,所以k - 1>3的解为xV - 2或x>4. 参考阅读材料,解答以下问题：〔1〕方程卜+31=5的解为；〔2〕方程k - 2021l+Lx+ll=2021 的解为：〔3〕假设Lt+4l+k-3l2U,求x的取值范围.图1 图29 .根据给出的数轴及条件,解答下面的问题：-6 -5 -4「-2 -1 0-12~3 4 5〔1〕点A,B,.表示的数分别为1,一旦,-3观察数轴,与点A的距离为3的点2表示的数是,B, C两点之间的距离为:〔2〕假设将数轴折叠,使得A点与.点重合,那么与3点重合的点表示的数是；假设此数轴上M, N两点之间的距离为2021 〔M在N的左侧〕,且当A点与.点重合时,M 点与N点也恰好重合,那么M, N两点表示的数分别是：时, N:〔3〕假设数轴上P,.两点间的距离为小〔P在.左侧〕,表示数〃的点到尸,.两点的距离相等,那么将数轴折叠,使得尸点与.点重合时,P,.两点表示的数分别为：P, Q〔用含〃?,n的式子表示这两个数〕.10 .某一出租车一天下午以一中为出发地在东西方向运营,向东走为正,向西走为负,行车里程〔单位：加?〕依先后次序记录如下：+9, -3, -5, +4, -8, +6, -3, -6, -4, + 10.〔1〕将最后一名乘客送到目的地,出租车离一中出发点多远？在一中什么方向？〔2〕假设每千米的价格为3.5元,司机一个下午的营业额是多少？11 .从一批机器零件毛坯中取出10件,称的质量如下〔单位：/〕：205, 200, 185, 206, 214, 195, 192, 218, 187, 215,请用两种方法求这10 件毛坯的总质量.x 7 x>012 .阅读以下材料：lxl=・0, x=0 ,即当x>0时,-x, x<0 用这个结论可以解决下面问题:13 .某超市为了促销,推出两种促销方式:方式①：所有商品实行7.5折销售；方式②：一次购物满200元送60元现金.试解答以下问题：〔1〕杨师傅要购置标价为628元和788元的商品各一件,现有四种购置方案：方案一：628元和788元的商品均按促销方式①购置；方案二：628元的商品按促销方式①购置,788元的商品按促销方式②购置：方案三：628元的商品按促销方式②购置,788元的商品按促销方式①购置：方案四：628元和788元的商品均按促销方式②购置.请你帮杨师傅计算出四种购置方案所付金额,并给杨师傅提出省钱的购置方案. 〔2〕计算下表中标价在600元到800元之间商品的付款金额：商品标价〔元〕方式①方式② 根据上表计算的结果,你能总结出商品的购置规律吗？14 .：CaXb 〕 2=a 2Xb 2. 〔aXb 〕 3=a 3Xb\ 〔aXb 〕 4=t/4xM,〔l 〕用特例验证上述等式是否成立,〔取“=1, /7=-2〕 〔2〕通过上述验证,猜一猜：〔“X 〃〕,〔M,=,归纳得出：〔〃Xb 〕 〃=〔3〕上述性质可以用来进行积的乘方运算,反之仍然成立,即：〔“X 〃〕〞 应用上述等式计算：〔-L 〕 2.19义42叫15.商人小周于上周日买进某农产品10000 每斤2.4元,进入批发市场后共占5个摊位, 〔1〕己知如6是有理数,前嘀的值,〔2〕.、〃是有理数,当而cHO 时,〔3〕“、b 、c 是有理数,"Hc=0,求育土亩的值・…求皆嘀畤的值• 付款金额〔元〕628638 648 768 778 788-^=^=1：当 xVO 时,每个摊位最多能容纳2000斤该品种的农产品,每个摊位的市场治理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况〔购进当日该农产品的批发价格为每斤2.7元〕.星期—四五与前一天的价格涨跌情况〔元〕+0.3-0.1+0.25+0.2-0.5当天的交易量〔斤〕25002000300015001000〔1〕星期四该农产品价格为每斤多少元？〔2〕本周内该农产品的最高价格为每斤多少元？最低价格为每斤多少元？〔3〕小周在销售过程中采用逐步减少摊位个数的方法来降低本钱,增加收益,这样他在本周的买卖中共赚了多少钱？请你帮他算一算.16 .如图,数轴上一电子跳蚤.从原点.出发,第1次沿数轴向右跳4个单位长度落在点A,第2次从点A出发沿数轴向左跳3个单位长度落在点B,第3次从点B沿数轴向右跳4个单位长度落在点C,第4次从点.出发沿数轴向左跳3个单位长度落在点.,…, 按此规律继续跳动.〔1〕写出电子跳蚤.在第5、6次跳动后落在数轴上的点对应的数分别是多少？〔2〕写出电子跳蚤.在第〃次跳动后落在数轴上的点对应的数？〔3〕电子跳蚤.经过多少次跳动后落在数轴上的点对应数100?QQ一、^月 J ~ O 1 5^ 17 .阅读下面材料：点A、8在数轴上分别表示有理数〃、b, A、8两点之间的距离表示为L48I.当A、8两点中有一点在原点时,不妨设点儿在原点,如图1所示,\AB\ = \OB\=\b\ =1“ - 〃1：当A、8两点都不在原点时.〔1〕如图 2 所示,点A、5 都在原点右边,\AB\=\OB\ - \OA\=\b\ - la\=b - a=\a - bh 〔2〕如图 3 所示,点A、3 都在原点左边,\AB\=\OB\ - \OA\=\b\ - k/l= - b -〔-〃〕= h - Z?l；〔3〕如图 4 所示,点A、8在原点两边,\AB\=\OBMOA\=\b\+kA=a+〔 -//〕=\a - b\. 综上所述,数轴上A、B两点之间的距离表示为= 根据阅读材料答复以下问题：〔1〕数轴上表示-2和-5的两点之间的距离是,数轴上表示1和-3的两点之间的距离是: 〔2〕数轴上表示x和-3的两点A、B之间的距离是,如果IABI=2,那么X为.〔3〕当代数式k+11+lx- 21取最小值时,即在数轴上,表示x的动点到表示-1和2的两个点之间的距离和最小,这个最小值为,相应的x的取值范围是.18 .数学实验室：点A、8在数轴上分别表示有理数“、b, A、8两点之间的距离表示为A3,在数轴上4、8两点之间的距离利用数形结合思想答复以下问题：①数轴上表示2和6两点之间的距离是,数轴上表示1和-4的两点之间的距离是.②数轴上表示x和-3的两点之间的距离表示为.数轴上表示x和6的两点之间的距离表示为.③假设x表示一个有理数,那么lx - ll+k+41的最小值=.④假设x表示一个有理数,且lx+ll+k-3l=4,那么满足条件的所有整数x的是.⑤假设x表示一个有理数,当x为,式子k+21+k - 31+卜-41有最小值为.4 . 4 一答案与解析1 .小明同学将28铅笔笔尖从原点0开始沿数轴进行连续滑动,先将笔尖沿正方向滑动1 个单位长度完成第一次操作：再沿负半轴滑动2个单位长度完成第二次操作：又沿正方向滑动3个单位长度完成第三次操作,再沿负方向滑4个单位长度完成第四次操作,…, 以此规律继续操作,经过第50次操作后笔尖停留在点尸处,那么点尸对应的数是( )A. 0B. - 10C. -25D. 50【分析】取向右为正方向,那么向左为负,利用有理数的加减法可得结果.【解答】解：由题意得,1 - 2+3 - 4+5 - 6+…49 - 50=25X ( - 1) = - 25,应选：C.【点评】此题主要考查了正负数,数轴和有理数的加减法,理解正负数的意义是解答此题的关键.2 .如下图,圆的周长为4个单位长度,在圆的4等分点处标上数字0, 1, 2, 3,先让圆周上数字0所对应的点与数轴上的数-2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数-2021将与圆周上的哪个数字重合( )【分析】据圆在旋转的过程中,圆上的四个数,每旋转一周即循环一次,那么根据规律即可解答.【解答】解：圆在旋转的过程中,圆上的四个数,每旋转一周即循环一次,那么与圆周上的0重合的数是-2, -6, - 10-,即-(-2+4/?),同理与3重合的数是：-(-1+4/?),与2重合的数是-4%与1重合的数是-(1+4〞),其中〃是正整数.而- 2021= - ( - 1+4X505),・•・数轴上的数-2021将与圆周上的数字3重合.应选：O.【点评】此题综合考查了数轴、循环的有关知识,关键是把数和点对应起来,也就是把22“数〞和“形〞结合起来.3.同学们都知道,15- 〔-2〕 I表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.答复以下问题：（1）15 - 〔 -2〕 1= 7 ,〔2〕找出所有符合条件的整数必使得k+5l+h -2l=7成立,这样的整数是-5, -4,- 3. - 2, - 1, 0, 1, 2 ,〔3〕对于任何有理数%, Lr-31+k - 61的最小值是3 .〔4〕对于任何有理数x, LLll+Lr-21+k+ll的最小值是3 ,此时x的值是1 .【分析】〔1〕直接去括号,再根据去绝对值的方法去绝对值就可以了.〔2〕要x的整数值可以进行分段计算,令x+5=0或x-2=0时,分为3段进行计算, 最后确定x 的值.〔3〕根据〔2〕方法去绝对值,分为3种情况去绝对值符号,计算三种不同情况的值, 最后讨论得出最小值.〔4〕要使k- 21+Lr+ll的值最小,x的值只要取-1到2之间〔包括-1、2〕的任意一个数,要使Lr- II的值最小,x应取1,显然当x=l时能同时满足要求,把x=l代入原式计算即可得到最小值.【解答】解：〔1〕原式=15+21=7,故答案为：7：〔2〕令x+5=0 或x - 2=0 时,那么x=-5 或x=2当xV -5时,...-〔x+5〕 - 〔x-2〕 =7,-x - 5 - x+2=7,x=5〔范围内不成立〕；当-5WxW2 时,-•.〔A+5〕-〔A - 2〕 =7,x+5 - x+2=7,7=7,.*.x= - 5, - 4» - 3» - 2, - 1, 0, 1, 2：二(A+5) + (x-2) =7,2Y =4,x=2 (范围内不成立)；,综上所述,符合条件的整数x 有：-5, -4, -3, -2, - 1, 0, 1, 2： 故答案为：-5, -4, -3, -2, - 1, 0, 1, 2(3)当 xV3 时,k-3l+h -6l=9-2x>3,当 3WxW6 时,Lr-3l+k-6l=3, 当 x>6 时,k-3l+k-6l=2x-9>3,,k-3l+Lr-6l 的最小值是3,故答案为：3：(4)当 7WxW2 时,Lx -21+lx+ll 的值最小为 3,当尸1时,k- 11的值最小为0,,当 x=l 时,k- ll+k-21+Lr+ll 的最小值是 3, 故答案为：3, 1.【点评】此题考查了绝对值,两点间的距离,理解绝对值的几何意义是解题的关犍.4 .百子回归图是由1, 2, 3…,100无重复排列而成的正方形数表,它是一部数化的澳门简 史,如：中央四位“19 99 12 20〞标示澳门回归日期,最后一行中间两位“23 50〞 标示澳门面积,…,同时它也是十阶幻方,其每行10个数之和,每列10个数之和,每 条对角线10个数之和均相等,那么这个和为505.【分析】根据得:百子回归图是由1, 2, 3…,100无重复排列而成,先计算总和: 又由于一共有10行,且每行10个数之和均相等,所以每行10个数之和=总和=10. 【解答】解：1〜100的总和为：(1+100)乂 100=5050,»MI«〞M,» ■AilMavsieHM 〞2一共有10行,且每行10个数之和均相等,所以每行10个数之和为：5050・10=505,故答案为:505.【点评】此题是数字变化类的规律题,是常考题型；一般思路为：按所描述的规律从1 开始计算,从计算的过程中慢慢发现规律,总结出与每一次计算都符合的规律,就是最后的答案；此题非常简单,跟百子碑简介没关系,只考虑行、列就可以,同时,也可以利用列来计算.5 .符号“G〞表示一种运算,它对一些数的运算结果如下：(1) G (1) =1, G (2) =3, G (3) =5, G (4) =7,-(2) G (工)=2, G (工)=4, G (1)=6, G (1)=8, •••2 3 4 5利用以上规律计算：G (2021) -G(」一)- 2021= - 2021 .2021 ----------------【分析】此题是一道找规律的题目,通过观察可发现(1)中等号后面的数为前而括号中的数的2倍减1, (2)中等号后面的数为分母减去1再乘2,计算即可.【解答】解：G (2021) -G(―^) - 2021=2021X2- 1 - (2021- 1) X2-2021= 2021-2021.【点评】找到正确的规律是解答此题的关键.6 . 一电子跳蚤在数轴上从原点开始,第1次向右跳1个单位,紧接着第2次向左跳2个单位,第3次向右跳3个单位,第4次向左跳4个单位,……,依此规律跳下去,当它跳第2021次落下时,落点处离原点的距离是一1010个单位.【分析】根据题意可以直接写出前几次落点在数轴上对应的数据,从而可以发现变化的规律,从而可以解答此题.【解答】解：设向右为正,向左为负,所以1+ (-2) +3 (-4) +-+2021+ (-2021) +2021=[1+(-2) ]+[3(-4) ]+ -+[2021+ (-2021) ]+2021=-1009+2021=1010那么第2021次落点在数轴上对应的数是1010,故答案为：1010.【点评】此题考查数字的变化类、数轴,解答此题的关键是明确题意,发现数字的变化规律.7 .阅读以下材料：我们知道3的几何意义是在数轴上数x对应的点与原点的距离：即lxl=Lr -01,也就是说,卜1表示在数轴上数x与数0对应点之间的距离：这个结论可以推广为M--切表示在数轴上XI,X2对应点之间的距离：例1.Ld=2,求x的值.解：容易看出,在数轴上与原点距离为2点的对应数为-2和2,即x的值为-2和2.例2.k-11=2,求x的值.解：在数轴上与1的距离为2点的对应数为3和-1,即x的值为3和-1.仿照阅读材料的解法,求以下各式中x的值.（1）1A--21=3（2）I A+1I=4.【分析】〔1〕由例2可知在数轴上与2的距离为3点的对应数为5和-1；〔2〕由例2可知在数轴上与-1的距离为4点的对应数为3和-5.【解答】解：〔1〕在数轴上与2的距离为3点的对应数为5和-1,即x的值为5和一1.〔2〕在数轴上与-1的距离为4点的对应数为3和-5,即x的值为3和-5【点评】此题考查了在数轴上表示点与点的距离,同时考查了学生的阅读理解水平.8.阅读以下材料：我们知道3的几何意义是在数轴上数x对应的点与原点的距离：即Ld=k-OI；这个结论可以推广为M表示在数轴上数xi,电对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用：例1：解方程hl=4.容易得出,在数轴上与原点距离为4的点对应的数为±4,即该方程的x= ±4：例2：解方程k+11+k-21=5.由绝对值的几何意义可知,该方程表示求在数轴上与-1和2的距离之和为5的点对应的x的值.在数轴上,-1和2的距离为3,满足方程的%对应的点在2的右边或在-1的左边.假设x对应的点在2的右边,如图〔25-1〕可以看出x=3；同理,假设x对应点在- 1的左边,可得x=-2.所以原方程的解是x=3或x=-2.例3：解不等式lx-ll>3.在数轴上找出k - 11=3的解,即到1的距离为3的点对应的数为-2, 4,如图〔25 - 2〕, 22在-2的左边或在4的右边的x值就满足Lr - 11>3,所以k - 11>3的解为xV - 2或x>4.参考阅读材料,解答以下问题：〔1〕方程lx+31 = 5的解为x=2或x= - 8 ；〔2〕方程Lr - 2021l+h+ll=2021 的解为x=-2 或x=2O18 ；〔3〕假设3+4l+k-3l2U,求〉的取值范围.图L 图2【分析】〔1〕根据例1的方法,求出方程的解即可；〔2〕根据例2的方法,求出方程的解即可：〔3〕根据例3的方法,求出x的范围即可.【解答】解：〔1〕方程Lr+3I=5的解为x=2或x= - 8：故答案为：.*=2或x=8：〔2〕方程k-2021l+lx+ll=2021 的解为％= -2 或x=2021：故答案为：x= -2或尸2021：〔3〕・.・k+4l+k - 31表示的几何意义是在数轴上分别与-4和3的点的距离之和,而-4与3之间的距离为7,当x在-4和3时之间,不存在x,使k+41+k-31>11成立,当x在3的右边时,如下图,易知当x>5时,满足lx+4l+k-3l,ll,当x在-4的左边时,如下图,易知当xW-6时,满足k+41+k-31211,所以x的取值范围是或xW -6._____ z------ ----------- n ---- □——------- ►-6 -4 0 3 〕【点评】此题考查了含绝对值的一元一次方程,弄清题意是解此题的关键.9.根据给出的数轴及条件,解答下面的问题：।। 1 q % ।।। 4 ।।।।〕-6 -5 -4 -3 -2 -1 0~12~~3~~4 5〔1〕点A, B, C表示的数分别为1,-互,-3观察数轴,与点A的距离为3的点2表示的数是一4或-2 , B,.两点之间的距离为_1_：2〔2〕假设将数轴折卷,使得A点与C点重合,那么与5点重合的点表示的数是_1_：假设2此数轴上M, N两点之间的距离为2021 〔M在N的左侧〕,且当A点与.点重合时,M点与N点也恰好重合,那么M, N两点表示的数分别是：M - lOOS.S ?N 1006.5〔3〕假设数轴上P,.两点间的距离为小〔尸在.左侧〕,表示数〃的点到P,.两点的距离相等,那么将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:尸〃-典,Q〃但〔用含帆,〃的式子表示这两个数〕.一二【分析】〔1〕分点在A的左边和右边两种情况解答；利用两点之间的距离计算方法直接计算得出答案即可：〔2〕 A点与.点重合,得出对称点位-1,然后根据两点之间的距离列式计算即可得解: 〔3〕根据〔2〕的计算方法,然后分别列式计算即可得解.【解答】解：〔1〕点A的距离为3的点表示的数是1+3=4或1-3=-2：B, C两点之间的距离为一$-〔-3〕 =1：2 2〔2〕 8点重合的点表示的数是：〔-$〕］=!：2 2M= - 1 - - 1OO8.5, 〃= - 1006.5：2 2〔3〕尸=〃-四,.=〃目.2 2故答案为：4或-2,工：工,- 1008.5, 1006.5；史,〃目.2 2 2 2【点评】此题考查了数轴的运用.关键是利用数轴,数形结合求出答案,注意不要漏解.10 .某一出租车一天下午以一中为出发地在东西方向运营,向东走为正,向西走为负,行车里程〔单位：依先后次序记录如卜：+9, -3, - 5, +4» - 8, +6, -3, - 6, - 4, +10.〔1〕将最后一名乘客送到目的地,出租车离一中出发点多远？住一中什么方向？〔2〕假设每千米的价格为3.5元,司机一个下午的营业额是多少？【分析】〔1〕求出记录数据之和,即可作出判断：〔2〕求出各数据绝对值之和,乘以3.5即可得到结果.【解答】解：〔1〕根据题意得：+9-3-5+4-8+6-3-6-4+10=0,那么将最后一名乘客送到目的地,出租车在一中：〔2〕根据题意得：〔9+3+5+4+8+6+3+6+4+10〕 X3.5=58X3.5 = 203 〔元〕,那么司机一个下午的营业额是203元.【点评】此题考查了正数与负数,弄清题中的数据是解此题的关键.11 .从一批机器零件毛坯中取出10件,称的质量如下(单位：#)：205, 200, 185, 206, 214, 195, 192, 218, 187, 215,请用两种方法求这丘件毛坯的 总质量.【分析】(1)直接相加求出即可；(2)以每个毛坯重200g 为准,超过的记为正,缺乏的记为负,得到以下数据(单位：g)：5, 0, - 15, 6, 14, -5, -8, 18, - 13, 15.再计算即可.【解答】解：(1) 205+200+185+206+214+195+192+218+187+215=2021 (g)(2)以每个毛坯重200g 为准,超过的记为正,缺乏的记为负,得到以下数据(单位：g)：5, 0, - 15, 6, 14, -5, -8, 18, - 13, 15.5+0+ ( - 15) +6+14+ ( -5) + ( -8) +18+ ( - 13) +15 =5- 15+6+14-5-8+18- 13+15 = 5+6+14+18+15- 15-5-8-13 = 58-41=17(Q,200X10+17=2021 (g).答:这10件毛坯的总质量是2021g.【点评】此题主要考查有理数的混合运算,掌握混合运算的顺序是解题的关键.Xj x>012 .阅读以下材料：lxl= 0, x=0 ,即当x>0时,击了二「当XV0时,居二一1. 』X <01x1 X图 r用这个结论可以解决下面问题:(2).、〃是有理数,当而cHO 时,(3)“、b 、c 是有理数,"Hc=0,【分析】(1)分3种情况讨论即可求解:(2)分4种情况讨论即可求解;(3)根据得到"+c=-b, 〃+b=-c,八 氏c 两正一负,进一步计算即可求解.(1) 己知如〃是有理数,留神W0时,求前嘀的值,…求皆啮嘀的值.【解答】解：〔I 〕小〃是有理数,当帅W0时,〔2〕己知4, b, C 是有理数,当"cWO 时,①aVO, b<0, cVO, -Ar+ + R = - 1 - 1 - 1= - 3： 周 |bT |c| ②a>0, b>3 c>0,书-*^^-=1 + 1+1=3：|a| Ib| |c|故-f3r + J I + |G =± ］或±3;周 411cl(3) 〞,b, c 是有理数,a+b+c=O, "cVO,贝lj Hc= - a, a+c= - b, a+b= - c, a. b 、c 两正一负,a _bc _ i i i _ iM --N -¥T故答案为：±2或0； ±1或±3； - 1.【点评】此题考查了有理数的除法,以及绝对值,熟练掌握运算法那么是解此题的关键.13 .某超市为了促销,推出两种促销方式:方式①：所有商品实行7.5折销售; 方式②：一次购物满200元送60元现金. 试解答以下问题:〔1〕杨师傅要购置标价为628元和788元的商品各一件,现有四种购置方案：方案一：628元和788元的商品均按促销方式①购置；方案二：628元的商品按促销方式①购置,788元的商品按促销方式②购置： 方案三：628元的商品按促销方式②购置,788元的商品按促销方式①购置： 方案四：628元和788元的商品均按促销方式②购置.请你帮杨师傅冲算出四种购置方案所付金额,并给杨师傅提出省钱的购置方案.①aVO, b<0. ②a>0, b>0. 俞喻= 俞喻=-1 - 1= -2：1 + 1=2：=-1 - 1+1= - 1: =-1+1 + 1 = 1.③a 、b 异号,Ic|Icl c ③a 、b 、c 两负一正,④“、b 、c 两正一负,〔2〕计算下表中标价在600元到800元之间商品的付款金额:商品标价〔元〕方式① 方式②根据上表计算的结果,你能总结出商品的购置规律吗?【分析】〔1〕根据各种方案列式计算后再根据运算结果选择方案:〔2〕方式①直接乘以0.75,方式②有几个200就减掉几个60,【解答】解：〔1〕付款：方案一：〔628+788〕 X0.75=1062元; 方案二：628X0.75+788 - 3X60=471+608=1079 元； 方案三：628 - 3 X 60+788 X 0.75=448+591 = 1039 元； 方案四：628 - 3X60+788 - 3X60=448+608=1056 元. 所以选择方案三付款省钱.〔2〕正确填写下表:规律：商品标价接近600元的按促销方式②购置,标价接近800元的按促销方式①购买.或标价大于600元且小于720元按促销方式②购置,标价大于720元且小于800元 按促销方式①购置.〔其它表述正确,或能将两种购物方式抽象概括成一次函数并能正确解答的均可给分〕 【点评】此题信息量比拟大,读懂题意,仔细审题,不难求出答案.14 .：(aXb) 2=a 2Xh 2. CuXb) 3=a^Xb\ (aX 〃)4=a 4X//,〔1〕用特例验证上述等式是否成立,〔取.=1, b=-2〕〔2〕通过上述验证,猜一猜：〔aXb 〕 * J 00//00 ,归纳得出：〔＜/XZ ＞〕/r = g n h n ： 〔3〕上述性质可以用来进行积的乘方运算,反之仍然成立,即：〔aXb 〕 〃付款金额〔元〕628638 648 768 778 788分别计算后填入即可.付款金额 628 638 648 768 778 788〔元〕 商品标价 〔元〕 方式①方式② 471 478.5 486 576 583.5 591448 458 468 588 598 608应用上述等式计算：〔-[〕20,9X 42°,9.【分析】〔1〕分别令4=1,a=-2 代入〔〞X〃〕2=〃2乂//、〔"X〃〕3=t?X//、〔＜/ X /?〕4 = ,『X〃4进行计算即可；〔2〕根据〔1〕中的各数的值找出规律即可解答：〔3〕根据〔2〕中的规律计算出所求代数式的值即可.【解答】解：〔1〕令“=1, b= -2,那么：[IX 〔 -2〕 ]2=12X 〔 -2〕 2=4, [IX 〔 -2〕 ]3=13X 〔 -2〕3= -8, [IX 〔 -2〕 ]4 = 14X 〔 -2〕4=16,故〔“X.〕"=/〃：〔2〕由⑴ 可猜测：〔aXb〕100=«,00b100,归纳得出：〔“X〃〕"=1%〞：〔3〕由〔2〕中的规律可知,〔-±〕2021X42021 4=[〔-i〕 X4]20214=〔7〕2021=-1.【点评】此题考查数字的变化规律,从简单到复杂,从特殊到一般,探寻规律得出答案即可.15 .商人小周于上周日买进某农产品10000斤,每斤2.4元,进入批发市场后共占5个摊位, 每个摊位最多能容纳2000斤该品种的农产品,每个摊位的市场治理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况〔购进当日该农产品的批发价格为每斤2.7元〕.星期四五与前一天的价格涨跌情况〔元〕+0.3 -0.1+0.25+0.2-0.5当天的交易量〔斤〕2500 2000300015001000〔1〕星期四该农产品价格为每斤多少元？〔2〕本周内该农产品的最高价格为每斤多少元？最低价格为每斤多少元？〔3〕小周在销售过程中采用逐步减少摊位个数的方法来降低本钱,增加收益,这样他在本周的买卖中共赚了多少钱？请你帮他算一算.【分析】〔1〕根据价格的涨跌情况即可作出判断：〔2〕计算出每天的价格即可作出判断：〔3〕根据售价-进价-摊位费用=收益,即可进行计算.【解答】解：〔1〕 2.7+0.3-0.1+0.25+0.2=3.35 元:〔2〕星期一的价格是：2.7+03 = 3.0 7C；星期二的价格是：3.0-0.1 =2.9元：星期三的价格是：2.9+0.25=3.15元：星期四是：3.15+0.2=3.35元：星期五是：3.35 - 0.5 = 2.85元.因而本周内该农产品的最高价格为每斤3.35元,最低价格为每斤2.85元：〔3〕列式：〔2500X3 - 5X20〕 + 〔2000X2.9-4X20〕 + 〔3OOOX3.15-3X2O〕 + 〔1500 X3.35 - 2X20〕+ 〔1000X2.85 -20〕 - 10000X2.4 =7400+5720+9390+4985+2830 - 24000 = 30325 - 24000 =6325 〔元〕.答：小周在本周的买卖中共赚了6325元钱.【点评】解题关键是理解''正〞和“负〞的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,那么另一个就用负表示.16 .如图,数轴上一电子跳蚤.从原点.出发,第1次沿数轴向右跳4个单位长度落在点A,第2次从点A出发沿数轴向左跳3个单位长度落在点B,第3次从点B沿数轴向右跳4个单位长度落在点C,第4次从点.出发沿数轴向左跳3个单位长度落在点.,…, 按此规律继续跳动.〔1〕写出电子跳蚤.在第5、6次跳动后落在数轴上的点对应的数分别是多少？〔2〕写出电子跳蚤.在第〃次跳动后落在数轴上的点对应的数？〔3〕电子跳蚤.经过多少次跳动后落在数轴上的点对应数100?【分析】〔1〕根据左减右加的计算规律,计算得出答案即可；〔2〕分〃为奇数和偶数得出数轴上的对应点即可；〔3〕利用得出的规律列方程求得答案即可.【解答】解：〔1〕第5次跳动后落在数轴上的点对应的数是4 - 3+4 - 3+4=6：第6次跳动后落在数轴上的点对应的数是4 - 3+4 - 3+4 - 3 = 3：〔2〕当〃为偶数时,第〃次跳动后落在数轴上的点对应的数是反：2当〃为奇数时,第,,次跳动后落在数轴上的点对应的数是旦工4=纪工；2 2〔3〕由21=100, 2解得：〃 = 200：由过工=1002解得：〃=193.答：电子跳蚤Q经过193次或200次跳动后落在数轴上的点对应数100.【点评】此题考查了数轴及图形的变化规律,要注意数轴上点的移动规律是“左减右加〞.把数和点对应起来,也就是把“数〞和“形〞结合起来,二者互相补充,相辅相成, 把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.17.阅读下面材料：点A、8在数轴上分别表示有理数“、b, A、8两点之间的距离表示为L4BI.当A、8两点中有一点在原点时,不妨设点A在原点,如图1所示,\AB\ = \OB\=\b\ = 当A、B两点都不在原点时.〔1〕如图 2 所示,点A、8 都在原点右边,\AB\=\OB\ - \OA\=\b\ - \a\=b - a=\a - bh 〔2〕如图 3 所示,点A、B 都在原点左边,\AB\=\OB\ - \OA\=\b\ - k/l= - b -〔-〃〕= \ci - bl：〔3〕如图 4 所示,点A、5 在原点两边,lAB\=\OB\+\OA\=lb\+\al=a+〔- h〕 =\a - b\.综上所述,数轴上A、8两点之间的距离表示为= 乩根据阅读材料答复以下问题：〔1〕数轴上表示-2和-5的两点之间的距离是3 ,数轴上表示1和-3的两点之间的距离是4 :〔2〕数轴上表示x和-3的两点A、8之间的距离是k+31 ,如果A8I=2,那么x为-1 或-5 .〔3〕当代数式k+ll+k-21取最小值时,即在数轴上,表示x的动点到表示-1和2的两个点之间的距离和最小,这个最小值为3.相应的x的取值范闱是..0网」、.勾b。

七年级数学周末练习题答案七年级数学周末练习题答案数学是一门需要不断练习的学科，通过练习题的做题过程，我们可以更好地巩固所学的知识，提高解题能力。

下面是七年级数学周末练习题的答案，希望能够帮助同学们更好地理解和掌握数学知识。

一、选择题1. A2. C3. B4. D5. A6. B7. C8. D9. B10. A二、填空题1. 242. 363. 154. 185. 76. 97. 48. 129. 2010. 28三、解答题1. 解：设这个数为x，根据题意可得方程：(x + 5) / 3 = 9，解得x = 27。

所以这个数是27。

2. 解：设这个数为x，根据题意可得方程：(x - 2) / 4 = 5，解得x = 22。

所以这个数是22。

3. 解：设这个数为x，根据题意可得方程：(x + 3) / 2 = 8，解得x = 13。

所以这个数是13。

4. 解：设这个数为x，根据题意可得方程：(x - 4) / 3 = 7，解得x = 25。

所以这个数是25。

5. 解：设这个数为x，根据题意可得方程：(x + 2) / 5 = 6，解得x = 28。

所以这个数是28。

四、应用题1. 解：设这个数为x，根据题意可得方程：(x + 15) / 3 = 9，解得x = 12。

所以这个数是12。

2. 解：设这个数为x，根据题意可得方程：(x - 6) / 2 = 5，解得x = 16。

所以这个数是16。

3. 解：设这个数为x，根据题意可得方程：(x + 5) / 4 = 7，解得x = 23。

所以这个数是23。

4. 解：设这个数为x，根据题意可得方程：(x - 8) / 3 = 6，解得x = 26。

所以这个数是26。

5. 解：设这个数为x，根据题意可得方程：(x + 3) / 6 = 5，解得x = 27。

所以这个数是27。

通过以上的题目和答案，我们可以看到解题的思路和方法。

在解题过程中，我们要注意设变量、列方程、解方程等步骤，以及最后对答案的验证。

七年级数学周末练习2015.5.30一、填空题１．直接写出计算结果：)3()2(3xy xy -⋅= ；20)21()32(--= ． ２．不等式－4x≥－12的正整数解为 ；３．等腰三角形一边等于5，另一边等于8，则周长是 ． ４．如果04212=--++-y x y x ，则x+y 的值是 ．５．一本200页的书的厚度约为1．8cm ，用科学记数法表示每一页纸的厚度约等于 cm ． ６．方程032233=+--+-n m n y x 是二元一次方程，则，m = ，n =； ７．一个多边形的每一个外角都是60°，则这个多边形的内角和为 °８．已知三角形的两边长分别为2cm 和7cm ，第三边长为a cm ，则a 的取值范围是 ．９．关于x 、y 的方程组2421x y a x y a+=-+⎧⎨+=-⎩，则x ＋y 的值为 ． 10．因式分解a a 916)1(3-= ; =+-18122)2(2x x ．11．若关于x 的不等式组2x x m >⎧⎨>⎩的解集是x>2，则m 的取值范围是 ． 12．若,1,3==+xy y x 则=+22y x ．二、选择（ 每小题3分，共 24分）13．已知某种植物花粉的直径为0.00035米，用科学记数法表示该种花粉的直径是A ．3.5×104米B ．3.5×104-米C ．3.5×105-米D ．3.5×106-米 14．下列各组数不可能组成一个三角形的是 A ．3，4，5 B ．7，6，6 C ．7，6，13 D ．175，176，17715．如果关于x 的不等式x a )2(+＞2+a 的解集为1x <，那么a 的取值范围是A. 0>aB. 0<aC. 2->aD. 2-<a 16．下列运算正确的是A ．55)(ab ab =B ．538a a a =÷C ．532)(a a =D ．222)(b a b a -=- 17．若m ＞－1，则下列各式中错误的是A ．6m ＞－6B ．－5m ＜－5C ．m+1＞0D ．1－m ＜2 18. 下列等式由左边细若边的变形中，属于因式分解的是A ．x 2+5x －1=x(x+5)－1B ．x 2－4+3x=(x+2)(x －2)+3xC ．x 2－9=(x+3)(x －3)D ．(x+2)(x －2)=x 2－419．在△ABC 中,∠A=31∠B=41∠C,则△ABC 是 A ．锐角三角形B ．直角三角形C ．钝角三角形D ．都有可能 20．已知a ＞b ＞0，那么下列不等式组中无解的是A ．⎩⎨⎧-><b x a xB ．⎩⎨⎧-<->b x a xC ． ⎩⎨⎧-<>b x a xD ．⎩⎨⎧<->b x a x 三、解答题21．(本题共16分，每题4分)22．(本题6分)（1）已知1632793=⨯⨯m m ，求m 的值．（2）已知2,1==-xy y x ，求32232xy y x y x +-的值．23．如图，已知AB//DE ，BF 、EF 分别平分∠ABC 与∠CED ，若∠BCE ＝140°，求∠BFE 的度数．24.已知，关于x ，y 的方程组325x y a x y a -=+⎧⎨+=⎩解满足x>y>0． （1）求a 的取值范围；（2）化简2a a --．25. 如果关于x 、y 的方程组⎩⎨⎧-=-+=-562y x k x y 的解适合方程73-=+y x ，求k 的值.26某商场用3400元购进A 、B 两种新型节能台灯共60盏，这两种台灯的进价、标价如下表所示．（1）这两种台灯各购进多少盏？（2）在每种台灯销售利润不变的情况下，若该商场计划销售这批台灯的总利润不少于1400元，问至少需购进B 种台灯多少盏？27． “震灾无情人有情”．民政局将全市为四川受灾地区捐赠的物资打包成件，其中帐篷和食品共320件，帐篷比食品多80件．（1）求打包成件的帐篷和食品各多少件？（2）现计划租用甲、乙两种货车共8辆，一次性将这批帐篷和食品全部．．运往受灾地区． 已知甲种货车最多可装帐篷40件和食品10件，乙种货车最多可装帐篷和食品各20件．则民政局安排甲、乙两种货车时有几种方案？请你帮助设计出来．（3）在第（2）问的条件下，如果甲种货车每辆需付运输费4000元，乙种货车每辆需付运输费3600元．民政局应选择哪种方案可使运输费最少？最少运输费是多少元？28.阅读理解应用：我们在课本中学习过，要想比较a 和b 的大小关系，可以进行作差法，结果如下a-b ＞0，a ＞b ；a-b ＜0，a ＜b ；0,a b a b -==。

七年级（上）数学周末作业（五）一、一元一次方程的有关概念1、下列方程中，是一元一次方程的是（ ）A 、523=+y xB 、0562=+-y yC 、xx 1331=- D 、7423-=-x x 2、下列方程中，以2-=x 为解的一元一次方程为（ ）A 、x x 223=- B 、3214+=-x x C 、2635-=-x x D 、1213-=+x x 3、如果关于x 的方程3x ﹣5m=3与方程2x +10=2的解相同，那么m=（ ）A ．﹣2B ．﹣3C ．3D ．14、若()021=-+x k 是关于x 的一元一次方程，则k 应满足二、解一元一次方程（1）、解一元一次方程的一般步骤：①去分母：在方程两边都乘以合分母的 数。

②去括号：一般先去 ，再去中括号，最后去 。

③移项：把含有未知数的项都移到方程的 ，其他项都移到方程的 。

④合并同类项：把方程化成()0≠=a b ax 的形式⑤系数化为1：方程两边都除以未知数的系数a ，得到方程的解为ab x =（2）练习巩固1、下列结论错误的是（ ）A 、若b a =，则c b c a -=-B 、若b a =，则1122+=+c b c aC 、若x =2，则x x 22=D 、若ax =bx ，则b a =2、b ax =的解是ab x =的条件是 3、=x 时，代数式312+x 的值比615-x 的值大1 4、一个两位数的十位数字与个位数字之和是7，把这个两位数加上45后，结果恰好为数字对调后组成的两位数，则这个两位数是（ ）A 、16B 、25C 、34D 、615、化简①()[]1253---a a a ②()()14623522+----+x x x x ③63242+-+x x6、解下列方程①x x x x ++-=-21335 ②()()572685=--+x x③x ﹣（x ﹣9）=[x +（x ﹣9）] ④163242-=+-+x x⑤4131312-+=--y y y ⑥()()2.152103110=+--x x⑦6.15.032.04-=--+x x ⑧35.0102.02.01.0=+--x x⑨22143223=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-x ⑩﹣2=7、小华同学在解方程5x ﹣1=（ ）x +11时，把“（ ）”处的数字看成了它的相反数，解得x=2，则该方程的正确解应为x= ．8、若规定：[a ]表示小于a 的最大整数，例如：[5]=4，[﹣6.7]=﹣7，则方程3[﹣π]﹣2x=5的解是（ ）A ．x=7B ．x=﹣7C ．D ．三、一元一次方程的应用1、A、B两地相距450千米，甲、乙两车分别从A,B两地同时出发，相向而行，已知甲车速度为120km/h，乙车速度为80 km/h，经过t小时两车相距50km，则t的值是（）A、2或2.5B、2或10C、10或12.5D、2或12.53、用一个底面直径为0.1m的圆柱形储油器，油中浸有钢珠，若从中捞出546克钢珠，问液面下降了多少厘米？（13cm钢珠重7.8克）4、A、B两地相距70千米，甲从A地出发，每小时行15千米，乙从B地出发，每小时行20千米．（1）若两人同时出发，相向而行，则经过几小时两人相遇？（2）若甲在前，乙在后，两人同时同向而行，则几小时后乙超过甲10千米？（3）若两人同时出发，相向而行，则几小时后两人相距10千米？5、甲、乙两车同时从A城去B城，甲车每小时行35千米，乙车每小时行40千米，结果乙比甲提前半小时到达B城．问A、B两城间的路程有多少千米？6、星期日早晨，学校组织共青团员去参观雷锋纪念馆，小颖因故迟到没有赶上旅游车，于是她乘坐一辆出租车前往追赶，出租车司机说：“若以每小时80千米的速度，则需要1.5小时才能追上；若以每小时90千米的速度，则40分钟就能追上”．你知道出租车司机估计旅游车的速度是每小时多少千米吗？7、某工程交由甲、乙两个工程队来完成，已知甲工程队单独完成需要60天，乙工程队单独完成需要40天（1）若甲工程队先做30天后，剩余由乙工程队来完成，还需要用时天（2）若甲工程队先做20天，乙工程队再参加，两个工程队一起来完成剩余的工程，求共需多少天完成该工程任务？/8、我国古代数学著作《九章算术》中有这样一道题，原文是：“今有善行者行一百步，不善行者行六十步，今不善行者先行一百步，善行者追之，问几何步及之？”意思是：同样时间段内，走路快的人能走100步，走路慢的人只能走60步（两人的步长相同）．走路慢的人先走100步，走路快的人要走多少步才能追上走路慢的人（两人走的路线相同）？试求解这个问题．8、课外阅读课上．老师将一批书分给各小组．若每小组8本．则还剩余3本：若每小组9本．则还缺2本．问有几个小组．。

七年级数学第五周周末作业姓名一、填空题 1、化简：〔1〕()=-42x〔2〕()()=-•342a a 〔3〕()()=-÷-aa 42、等腰三角形的两边长为5cm ，10cm ，那么它的周长等于3、假设一个多边形的内角和是外角和的3．5倍，那么此多边形的边数是_____________．4、有棱长为4×103米的正方体容器5个，可以盛水最多为 立方米〔用科学记数法表示〕5、340________430〔 填“＞〞“＜〞或者“＝〞 〕 6、200820074)25.0(⨯-=______；323)4()5.2(a a -⋅-=7、41,4=-=y x ，那么4143)(+⋅⋅n n y x x = 8、推理填空，如图 ∵∠B ＝＿＿＿；∴AB ∥CD 〔＿＿＿＿＿＿＿＿＿＿＿＿〕； ∵∠DGF ＝＿＿＿；∴CD ∥EF 〔＿＿＿＿＿＿＿＿＿＿＿＿〕； ∵AB ∥EF ；∴∠B ＋＿＿＿＝180°〔＿＿＿＿＿＿＿＿＿＿＿〕；9、如以下图，根据图中的数据，计算阴影局部的面积为第9题 第10题 第11题 第32112题10、 如图，小明课间把教师的三角板的直角顶点放在黑板两条平行线a 、b 上，∠1=55°，那么∠2的度数为 。

11、 如图，把ΔABC 沿线段DE 折叠，使点A 落在点F 处，BC ∥DE ，假设∠B=80°，那么∠BDF=______12、 如图为6个边长相等 的正方形的组合图形，那么123∠+∠+∠= 。

二、选择题：13、有两根13cm 、15cm 的木棒，要想以这两根木棒做一个三角形，可以选用第三根木棒的长为〔 〕A 、2cmB 、11cmC 、28cmD 、30cm14、假设∠α+∠β=90°, ∠β+∠γ=90°，那么∠α与∠γ的关系是 ( ) A 、互余B 、互补C 、相等D 、没有关系15、假设两条直线被第三条直线所截，那么 〔 〕A 、同位角相等B 、内错角相等C 、同旁内角互补D 、以上结论都不对 16、如图，假设AD ∥BC ，那么 〔 〕 A 、∠DAC=∠BCA B 、∠BAC=∠DCA C 、∠DAC=∠BAC D 、∠B+∠BCD=180°17、具备以下条件的△ABC 中，不是直角三角形的是〔 〕A ．∠A ＋∠B=∠CB ．∠A －∠B=∠C C ．∠A ︰∠B ︰∠C =1︰2︰3D ．∠A=∠B=3∠C 18、以下计算中正确的选项是〔 〕A ．5322a a a =+B ．532a a a =⋅C ．632a a a =⋅D ．532a a a =+19、小明饶着一个五边形的花圃走了一圈，他一一共转了多少度〔 〕A ．180B. 36020、 如图，边长为(m +3)的正方形纸片剪出一个边长为m 的正方形之后余局部又剪拼成一个矩形(不重叠无缝隙)，假设拼成的矩形一边长为3，那么另一边长是〔 〕A ．2m +3B ．2m +6C ．m +3D ．m +621、计算：(1) (3a 2)3·(a 4) 2－(－a 5)2·(a 2) 2〔2〕()()43238422a ba b -+⋅-〔3〕 (－1)2021+()201020098125.0⨯-－|－3|；〔4〕999100100)1(5.02-⨯⨯-；(5) 假设23=m，43=n，那么求123-+n m 的值。

周末作业51．比较2-， 12-， 0， 0.02的大小，正确的是（ ） A ． 2-＜12-＜0＜0.02 B ． 12-＜2-＜0＜0.02 C ． 2-＜12-＜0.02＜0 D ． 0＜12-＜2-＜0.02 2．在数轴上表示﹣5的点离开原点的距离等于（ ）A ． 5B ． ﹣5C ． ±5 D． 103．若2011a+2012b=0，则ab 是（ ）A ． 正数B ． 非正数C ． 负数D ． 非负数4．有下列各数：，，，，，其中属于负数的共有（ ）A ． 个B ． 个C ． 个D ． 个5．下列计算不正确的是（ ）A ．B ．C ．D ． 6．若230m n -++=，则()2009m n +的值为( )A ． 1B ． 1-C ． 0D ． 1±7．下列说法正确的是（ ）A ． 最小的有理数是B ． 任何有理数都可以用数轴上的点表示C ． 绝对值等于它的相反数的数都是负数D ． 整数是正整数和负整数的统称8．下列不是具有相反意义的量是（ ）A ． 前进5米和后退5米B ． 收入30元和支出10元C ． 向东走10米和向北走10米D ． 超过5克和不足2克9．12017-的倒数是（ ） A ． 12017 B ． 2017 C ． -2017 D ． 12017- 10．温度从－2℃上升3℃后是（ ）A ． 1℃B ． －1℃C ． 3℃D ． 5℃11．若|a|＝3，|b|＝5，且ab ＜0，则a ＋b ＝ ．12．已知|x+1|+(y+3)2=0,则(x+y)2的值是_____.13．已知a 是有理数，设定[a ]表示不超过a 的最大整数，则[3]+[-51]2+[-3.4]-[0.7]的值为____.14．()21530______54-÷⨯-=； 15．若()2250a b -+-=，则点P (a ,b )关于x 轴对称的点的坐标为____.16．－2－3＝_____________.17．已知|x |＝2，|y |＝5，且x ＞y ，则x ＋y ＝________．18．已知取最小值，则____________。