匀变速直线运动公式的推导
- 格式:doc
- 大小:653.00 KB
- 文档页数:9

匀变速直线运动的比例式推导
一、平均速度
平均速度是指物体在一端到另一端用时相等的情况下运动时,所获得
的运动速度。
平均速度可以通过以下公式来推导:
三、均匀变速直线运动
均匀变速直线运动是一种物体在初始时间的速度和末端时间的速度都
是恒定的,但是中间的运动就需要以一定的变化速度(加速度)来实现。
推导均匀变速直线运动可以通过以下比例式:
1. 首先用Vd表示运动路径长度,V0表示初始速度,Vf表示结束速度,T表示持续时间。
2. 根据动力学定律和定理可以得到以下公式:Vd=(Vf-V0)/2*T;
3. 令期望的加速度a= (Vf-V0)/T;
4. 根据位移和时间的关系,可以得到以下比例关系:Vd= V0*T+
1/2*a*T²;
5. 将a进行代入,可以得到最终的比例:Vd= V0*T+ (Vf-V0)*T/2。
二、速度
速度是指在一定时间内物体能够移动的距离,也就是物体在一段时间
内移动距离所获得的平均速度。
速度的定义可以用以下公式表示:V=
S/T。
其中V表示速度,S表示路程,T表示持续的时间。

匀变速直线运动追及(避免撞车)基本公式:①速度公式:v t=v0+at;②位移公式:s=v0t+at2;③速度位移公式:v t2-v02=2as。
推导公式:①平均速度公式:V=。
②某段时间的中间时刻的瞬时速度等于该段时间内的平均速度:。
③某段位移的中间位置的瞬时速度公式:。
无论匀加速还是匀减速,都有。
④匀变速直线运动中,在任意两个连续相等的时间T内的位移差值是恒量,即ΔS=S n+l–S n=aT2=恒量。
⑤初速为零的匀变速直线运动中的比例关系(设T为相等的时间间隔,s为相等的位移间隔):推论1(持续时间-瞬时速度):T末、2T末、3T末……的瞬时速度之比为:v1:v2:v3:……:v n=1:2:3:……:n;推论2(持续时间-位移):T内、2T内、3T内……的位移之比为:s1:s2:s3:……:s n=1:4:9:……:n2;推论3(相等时间-位移):第一个T内、第二个T内、第三个T内……的位移之比为:sⅠ:sⅡ:sⅢ:……:s N=1:3:5:……:(2N-1);推论4(持续位移-所用时间)前一个s、前两个s、前三个s……所用的时间之比为:t1:t2:t3:……:t n=1:……:;推论5(相等位移-所用时间)第一个s、第二个s、第三个s……所用的时间之比为tⅠ、tⅡ、tⅢ:……:t N=1:……:。
相关运用:追及相遇问题①当两个物体在同一直线上运动时,由于两物体的运动情况不同,所以两物体之间的距离会不断发生变化,两物体间距会越来越大或越来越小,这时就会涉及追及、相遇或避免碰撞等问题。
②追及问题的两类情况:Ⅰ、速度大者减速(如匀减速直线运动)追速度小者(如匀速运动):Ⅱ、速度小者加速(如初速度为零的匀加速直线运动)追速度大者(如匀速运动):③相遇问题的常见情况:Ⅰ、同向运动的两物体追及即相遇;Ⅱ、相向运动的物体,当各自发生的位移大小和等于开始时两物体的距离时即相遇。
例题:A、B两列火车在同一轨道上同向行驶,A在前,速度为v A=10m/s,B车在后,速度v B=30m/s。

匀变速直线运动公式推论推导及规律总结v = v0 + at位移由速度的定义导出:s = v0t + 1/2at²在匀变速直线运动中,加速度是变化的,因此在不同的时间段内,可以得到不同的位移和速度的关系。
根据运动的规律,我们可以得到几个重要的推论:推论1:t=0时刻的速度为v0,t时刻的速度为v,则平均速度为(v0+v)/2根据速度的定义,可以得到:v = v0 + at从t=0到t时刻的时间段内,速度变化了v-v0,平均速度就是速度变化量的一半。
推论2:匀变速直线运动的位移与时间的关系可以由位移公式得出。
s = v0t + 1/2at²根据位移公式可以看出,位移与时间的平方成正比。
这说明,在匀变速直线运动中,物体的位移与时间的平方呈现出二次增长的规律。
推论3:匀变速直线运动的速度与时间的关系可以由加速度公式得出。
v = v0 + at在匀变速直线运动中,可以通过加速度的大小和方向的不同来改变速度的大小和方向。
加速度的大小和方向会影响速度的改变速率。
推论4:匀变速直线运动中,速度与位移的关系可以由速度公式和位移公式得出。
将速度公式和位移公式联立,并将速度v表示为位移s和时间t的函数,可以得到:v=(2/t)*(s-v0t)从上式中可以看出,速度与位移的关系呈现线性关系。
即速度与位移成正比,并且速度与时间的倒数成正比。
以上是对匀变速直线运动公式进行推论推导的过程,可以得出一些规律总结如下:1.在匀变速直线运动中,速度和位移与时间有关,速度与时间成一次函数关系,位移与时间成二次函数关系。
2.加速度的大小和方向会影响速度的改变速率,从而影响物体的运动轨迹和速度的变化。
3.速度与位移成正比,并且速度与时间的倒数成正比。
因此,在匀变速直线运动中,可以通过速度-时间图和位移-时间图来分析物体的运动情况。
4.在匀变速直线运动中,如果加速度为零,即物体的速度保持不变,则运动成为匀速直线运动;如果加速度为常数,即物体的速度随着时间的推移以恒定的速率加快或减慢,则运动成为等加速度运动。

匀变速直线运动的基本公式1.位移:物体在其中一时刻相对于参考点的位置变化量,用Δx表示。
2.速度:物体单位时间内移动的位移变化量,即位移对时间的导数。
可以分为瞬时速度和平均速度两种。
3.加速度:物体单位时间内速度的变化量,即速度对时间的导数。
同样可以分为瞬时加速度和平均加速度两种。
接下来,我们将对匀变速直线运动的位移、速度和加速度进行推导,并给出其基本公式。
一、位移的公式推导:对于匀变速直线运动,我们已知其加速度是一个常量a,即在任何时刻,物体的加速度都保持不变。
根据加速度定义可知:a=Δv/Δt其中,Δv表示速度的变化量,Δt表示时间的变化量。
由于物体的加速度是一个常量,我们可以将上述等式进行积分得到速度与时间的关系:∫a dt = ∫(Δv / Δt) dt由于a是一个常量,上式可以简化为:a*t=Δv其中,t表示时间。
接下来,我们再次对上式进行积分,得到位移与时间的关系:∫a t dt = ∫Δv dt化简可得:(1/2)*a*t^2=v其中,v表示速度。
此即为匀变速直线运动的位移公式。
二、速度的公式推导:根据上述位移公式可知:(1/2)*a*t^2=v将位移公式两边对时间t求导,得到速度与时间的关系:d((1/2) * a * t^2) / dt = dv / dt化简可得:a * t = dv / dt即:a = dv / dt此即为匀变速直线运动的速度公式。
三、加速度的公式推导:根据速度公式可知:a = dv / dt将速度公式两边对时间t求导,得到加速度与时间的关系:d(a * t) / dt = d^2x / dt^2化简可得:a = d^2x / dt^2此即为匀变速直线运动的加速度公式。
综上所述,匀变速直线运动的基本公式如下:位移公式:Δx=(1/2)*a*t^2速度公式:v=a*t加速度公式:a = dv / dt = d^2x / dt^2其中,Δx表示位移,v表示速度,a表示加速度,t表示时间。
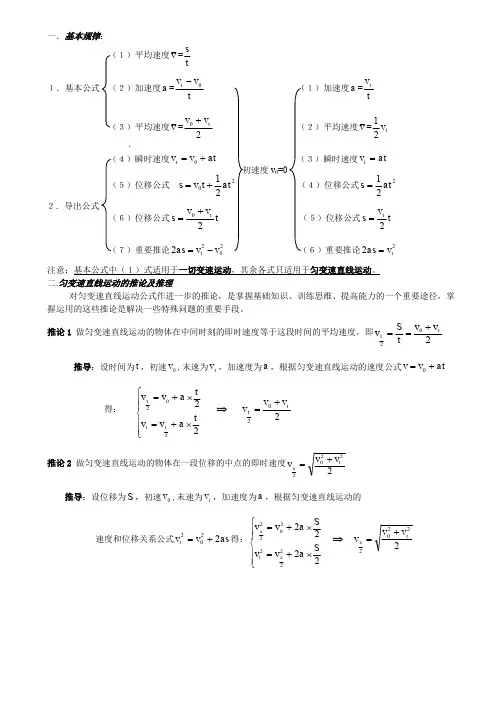
一.基本规律:v =ts 1.基本公式a =t v v t 0- a =tvtv =20t v v + v =t v 21at v v t +=0 at v t =021at t v s +=221at s =t v v s t 20+= t vs t 2=2022v v as t -= 22t v as =注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动。
二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
推论1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即202t t v v t S v +==推导:设时间为t ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度公式at v v +=0得: ⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22202t a v v t a v v t t t ⇒ 202t t v v v += 推论2 做匀变速直线运动的物体在一段位移的中点的即时速度22202t s v v v +=推导:设位移为S ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度和位移关系公式as v v t 2202+=得:⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22222222022S a v v Sa v v s t s ⇒ 22202t s v v v +=推论3 做匀变速直线运动的物体,如果在连续相等的时间间隔t 内的位移分别为1S 、2S 、 3S ……n S ,加速度为a ,则=-=-=∆2312S S S S S……21at S S n n =-=-推导:设开始的速度是0v经过第一个时间t 后的速度为at v v +=01,这一段时间内的位移为20121at t v S +=, 经过第二个时间t 后的速度为at v v +=022,这段时间内的位移为202122321at t v at t v S +=+=经过第三个时间t 后的速度为at v v +=023,这段时间内的位移为202232521at t v at t v S +=+=…………………经过第n 个时间t 后的速度为at nv v n +=0,这段时间内的位移为202121221at n t v at t v S n n -+=+=- 则=-=-=∆2312S S S S S……21at S S n n =-=-点拨:只要是匀加速或匀减速运动,相邻的连续的相同的时间内的位移之差,是一个与加速度a 与时间“有关的恒量”.这也提供了一种加速度的测量的方法:即2tSa ∆=,只要测出相邻的相同时间内的位移之差S ∆和t ,就容易测出加速度a 。

匀变速直线运动9个推论匀变速直线运动是物理学中的一种经典运动,其推论是通过对匀变速直线运动的研究和实验得出的。
以下是匀变速直线运动的九个推论:速度比例关系:在匀变速直线运动中,相邻相等的时间间隔内,速度的变化量相等,即Δv=aΔt\Delta v = a \Delta tΔv=aΔt。
因此,如果初始速度为v0v_0v0,则在时间间隔ttt内,速度的变化量为atatat。
速度与时间的关系:在匀变速直线运动中,速度与时间成线性关系,即v=v0+atv = v_0 + atv=v0+at。
这个公式表明,在匀变速直线运动中,速度的变化是线性增加或减少的。
位移与时间的关系:在匀变速直线运动中,位移与时间平方成正比关系,即x=v0t+12at2x = v_0t + \frac{1}{2}at^2x=v0t+21at2。
这个公式表明,在匀变速直线运动中,位移是由初始速度和加速度决定的。
相邻相等位移间的时间关系:在匀变速直线运动中,相邻相等位移间的时间与位移成正比关系,即t=2xat =\sqrt{\frac{2x}{a}}t=a2x。
这个公式表明,在匀变速直线运动中,相邻相等位移间的时间与位移成正比关系。
连续相等时间间隔内的位移差:在匀变速直线运动中,连续相等时间间隔内的位移差是恒定的,即Δx=aT2\Delta x = aT^2Δx=aT2。
这个公式表明,在匀变速直线运动中,位移差是由加速度决定的。
相对速度和相对加速度:在匀变速直线运动中,相对速度和相对加速度是不变的,即相对速度和相对加速度保持恒定。
匀减速运动:在匀变速直线运动中,如果加速度的方向与运动方向相反,那么物体将做匀减速运动。
此时,物体的速度将逐渐减小,直到停止。
静止和反向运动:在匀变速直线运动中,如果物体从静止开始运动或者以反向的速度运动,那么物体的速度将按照加速度的大小和方向进行变化。
初速度为零的匀加速直线运动:在匀变速直线运动中,如果物体的初速度为零,那么物体的速度将按照加速度的大小和方向进行变化,并且物体将在相同的时间内通过相同的位移。


匀变速六个推导公式匀变速直线运动是高中物理中非常重要的一个知识点,它有六个重要的推导公式。
下面咱就来好好唠唠这六个公式。
先说说匀变速直线运动的定义,物体沿着一条直线运动,且加速度不变的运动就叫匀变速直线运动。
在这个过程中,速度均匀变化。
咱来看看第一个推导公式,速度位移公式:$v^2 - v_0^2 = 2ax$ 。
这里的 $v$ 是末速度,$v_0$ 是初速度,$a$ 是加速度,$x$ 是位移。
我记得有一次给学生讲这个公式的时候,有个学生就迷糊了,怎么都理解不了。
我就给他举了个例子,假设你在骑自行车,刚出发的时候速度是 5 米每秒,这就是初速度 $v_0$ 。
然后你用力蹬,加速度是 2 米每二次方秒,骑了 10 米,这就是位移 $x$ 。
那最后你的速度是多少呢?通过这个公式就能算出来啦。
再看第二个公式,中间时刻速度公式:$v_{\frac{t}{2}} = \frac{v + v_0}{2}$ 。
这个公式说的是在匀变速直线运动中,中间时刻的瞬时速度等于初末速度的平均值。
有一回上课,我就问同学们:“假如你在跑步比赛,刚起跑的时候速度比较慢,跑着跑着速度快起来了,那跑到一半时间的时候,你的速度大概在什么位置?”同学们就七嘴八舌地讨论起来,通过这样的引导,大家对这个公式的理解就更深刻了。
接着是第三个公式,位移中点速度公式:$v_{\frac{x}{2}} =\sqrt{\frac{v_0^2 + v^2}{2}}$ 。
这个公式表示的是位移中点处的瞬时速度。
记得有一次做实验,让一个小车在水平面上做匀变速直线运动,通过测量不同位置的速度和位移,来验证这个公式。
同学们都特别认真,眼睛紧紧盯着小车,记录数据,那股子专注劲儿,真让人欣慰。
还有平均速度公式:$\bar{v} = \frac{v + v_0}{2}$ 。
这个公式大家应该比较好理解,平均速度就是初末速度的平均值。
有一次我在路上看到一辆汽车在加速行驶,我就在想,如果知道它的初速度和末速度,就能算出这段时间的平均速度,是不是还挺有意思的?第五个公式,连续相等时间内的位移差公式:$\Delta x = aT^2$ 。

匀变速直线运动6个推论推导过程一、推论一:速度 - 位移公式v^2-v_0^2=2ax1. 推导依据。
- 匀变速直线运动的速度公式v = v_0+at,位移公式x=v_0t+(1)/(2)at^2。
2. 推导过程。
- 由v = v_0+at可得t=frac{v - v_0}{a}。
- 将t=frac{v - v_0}{a}代入位移公式x = v_0t+(1)/(2)at^2中,得到:- x=v_0frac{v - v_0}{a}+(1)/(2)a(frac{v - v_0}{a})^2。
- 展开式子:x=frac{v_0v - v_0^2}{a}+(1)/(2)frac{(v - v_0)^2}{a}。
- 进一步化简:ax=v_0v - v_0^2+(1)/(2)(v^2-2vv_0+v_0^2)。
- ax = v_0v - v_0^2+(1)/(2)v^2-vv_0+(1)/(2)v_0^2。
- 整理可得v^2-v_0^2=2ax。
二、推论二:平均速度公式¯v=frac{v_0+v}{2}(适用于匀变速直线运动)1. 推导依据。
- 位移公式x = v_0t+(1)/(2)at^2,速度公式v = v_0+at,平均速度定义¯v=(x)/(t)。
2. 推导过程。
- 由位移公式x = v_0t+(1)/(2)at^2。
- 又因为v = v_0+at,则t=frac{v - v_0}{a}。
- 将t=frac{v - v_0}{a}代入位移公式得x=v_0frac{v - v_0}{a}+(1)/(2)a(frac{v - v_0}{a})^2。
- 平均速度¯v=(x)/(t),t=frac{v - v_0}{a},则¯v=frac{v_0frac{v -v_0}{a}+(1)/(2)a(frac{v - v_0}{a})^2}{frac{v - v_0}{a}}。

匀变速直线运动规律常见推论及推理过程本文对匀变速直线运动的常见推论、以及相关推理过程进行归纳总结,结合相关示意图将推理过程详细呈现给读者,适合高一学生学习参考。
匀变速直线运动基本公式如下: at v v +=02021at t v x +=()t v v x +=021ax v v 2202=-常用推论: 一.适用于任意匀变速直线运动的推论1. 某段匀变速直线运动中间时刻瞬时速度与该过程的平均速度相等,且都等于初、末速度和的一半,即:()v v t x v v t +===02212. 任意匀变速直线运动相邻相等时间间隔内的位移之差都相等,都等于2aT ,即:212312aT x x x x x x x n n =-==-=-=∆-拓展结论:x m −x n =(m −n)aT 23. 某段匀变速直线运动中间位置的瞬时速度:22202v v v x +=二. 仅适用于初速度为零的匀加速直线运动的推论1. 从开始运动起,前1个T 末、前2个T 末、前3个T 末……前n 个T 末的瞬时速度之比为:n v v v v n ::3:2:1::::321 =;2. 从开始运动起,前1个T 内、前2个T 内、前3个T 内……前n 个T 内的位移之比为:2222321::3:2:1::::n x x x x n =;3. 从开始运动起,第1个T 内、第2个T 内、第3个T 内……第n 个T 内的位移之比为:x Ⅰ:x Ⅱ:x Ⅲ: … :x N =1:3:5: … : (2n-1);4. 从开始运动起,前1个x 末、前2个x 末、前3个x 末……前n 个x 末的瞬时速度之比为:n v v v v n ::3:2:1::::321 =;5. 从开始运动起,第1个x 内、第2个x 内、第3个x 内……第n 个x 内所用时间之比为)1(::)23(:)12(:1::::321----=n n t t t t n 。
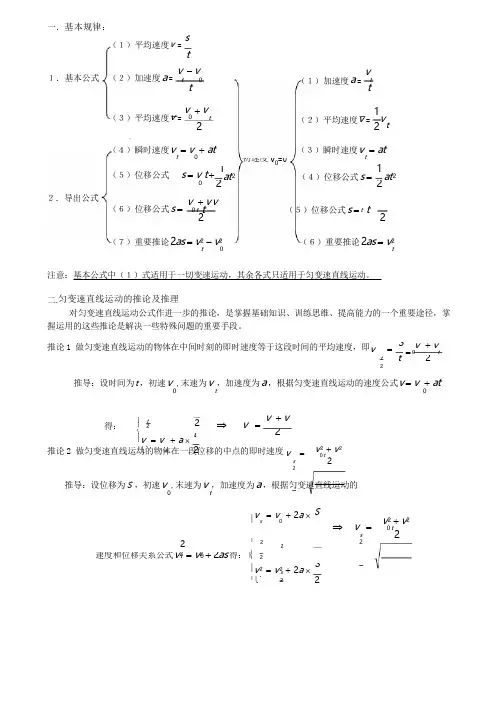
1.基本公式 (2)加速度 a = v - v初速度 v 0=0(5)位移公式 s = v t + 122推论 1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即v= St 2⇒ v = v + v ⎪ t 2 ⎪ 2 ⎨ 2 ⎪v = v + a ⨯ t ⎪⎩ t2 ⎧2速度和位移关系公式 v 2 = v 2 + 2as 得: ⎪ 2⎪v 2 = v 2+ 2 a ⨯ S⎪⎩ t 22一.基本规律:(1)平均速度 v =stvt 0(1)加速度 a = ttt(3)平均速度 v = v 0 +v2t1(2)平均速度 v = v2 t(4)瞬时速度 v = v + at(3)瞬时速度 v = attt1at 2(4)位移公式 s = at 22.导出公式(6)位移公式 s = v + v v0 t t (5)位移公式 s = t t2 2(7)重要推论 2as = v 2 - v 2t(6)重要推论 2as = v 2t注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动。
二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
t v + v = 0t2推导:设时间为 t ,初速 v ,末速为 v ,加速度为 a ,根据匀变速直线运动的速度公式 v = v + at0 t得:推论 2 做匀变速直线运动的物体在一段位移的中点的即时速度v=sv 2 + v 20 t22推导:设位移为 S ,初速 v ,末速为 v ,加速度为 a ,根据匀变速直线运动的0 t⎪vs = v 0+ 2 a ⨯2t 0 ⎨ s 2 S⇒ v =s2v 2 + v 20 t2经过第二个时间 t 后的速度为 v =2v +at ,这段时间内的位移为 S = v t + at 2 = v t + at 22 2 经过第三个时间 t 后的速度为 v =3v +at ,这段时间内的位移为 S = v t + at 2 = v t+ at 2 2 2 2 2 3 2 32 2 2 2t推论 3 做匀变速直线运动的物体,如果在连续相等的时间间隔 t 内的位移分别为 S 、 S 、 S …… S123n ,加速度为 a,则 ∆S =S 2- S 1 = S 3 - S 2= …… = S n - S推导:设开始的速度是 vn -1= at2经过第一个时间 t 后的速度为 v = v + a t ,这一段时间内的位移为 S = v t + 1 0 1 0 1 2 at 2,1 32 0 2 1 0 1 52 032…………………经过第 n 个时间 t 后的速度为 v =nv +at ,这段时间内的位移为 S =v t +1 a t 2 =v t + n 0 n n -1 02n -1 2at 2则 ∆S = S 2 - S 1 = S 3 - S 2 = …… = S n - Sn -1= at 2点拨:只要是匀加速或匀减速运动,相邻的连续的相同的时间内的位移之差,是一个与加速度 a 与时间 “有关的恒量”.这也提供了一种加速度的测量的方法: 即 a =∆S,只要测出相邻的相同时间内的位移之差 ∆S 和 t ,就容易测出加速度 a 。
匀速直线运动基本公式及推导1、 速度:物理学中将位移与发生位移所用的时间的比值定义为速度。
用公式表示为:V =ΔX Δt=x2−x1t2−t12、 瞬时速度:在某一时刻或某一位置的速度称为瞬时速度。
瞬时速度的大小称为瞬时速率,简称速率。
3、加速度:物理学中,用速度的改变量∆V 与发生这一改变所用时间∆t 的比值,定量地描述物体速度变化的快慢,并将这个比值定义为加速度。
α=ΔV Δt单位:米每二次方秒;m/S 2α即为加速度;即为一次函数图象的斜率;加速度的方向与斜率的正负一致。
速度与加速度的概念对比:速 度:位移与发生位移所用的时间的比值加速度:速度的改变量与发生这一改变所用时间∆t 的比值4、 匀变速直线运动:在物理学中,速度随时间均匀变化,即加速度恒定的运动称为匀变速直线运动。
1) 匀变速直线运动的速度公式:V t =V 0+αt推导:α=ΔV Δt=Vt− V0t……..速度改变量发生这一改变所用的时间2)匀变速直线运动的位移公式:x =V 0t+ 12 αt 2……….(矩形和三角形的面积公式) …推导:x =V0+Vt2∙t (梯形面积公式) 如图:3)由速度公式和位移公式可以推导出的公式:⑴V t 2-V 02=2αx (由来:V T 2-V 02=(V 0+αt)2 -V 02=2αV 0t +α2t 2=2α(V 0t+ 12αt 2)=2αx) ⑵V t 2=V0+Vt 2=V −(由来:V t 2=V 0+α t 2=2V0+αt 2=V0+(V0+αt)2=V0+Vt 2=V −)⑶V x 2=√V2+V t 22(由来:因为:V t 2-V 02=2αx 所以V x 22-V 02=2αx2=αx =VT2−V022)(V x 22-V 02=V t 2−V 022;V x 22=V t 2−V 022+V 02=V t 2+V 022)⑷∆x=αT 2(做匀变速直线运动的物体,在任意两个连续相等的时间内的位移差为定值。
匀变速直线运动常用公式(附匀变速直线运动的推论及推理过程)一、 基本公式速度公式at v vt+=0当00=v 时,atvt=位移公式2021at t v s+=221at s =二、 几个常用的推论1.位移推导公式222v vast-=,t v v st2+=2.平均速度v 、中间时刻的瞬时速度2/t v 、中间位置的瞬时速度2/s v 为:/22tt v vx v v t+===,2222/t s v v v +=3.做匀变速直线运动的物体,在各个连续相等的时间T 内的位移分别是s 1、s 2、s 3…s n ,则Δs =s 2-s 1=s 3-s 2=…=s n -s n-1=aT 22.4.V 0=0的匀加速直线运动中的几个常用的比例公式(1)等分运动时间,以T 为单位时间.为单位时间. ①1T 末,2T 末,末,33T 末…,末…,n n T 末的速度之比末的速度之比v 1:v 2:v 3:…:v n =1=1::2:3…:…:n n②1T 内、内、22T 内、内、33T 内…内…n n T 内通过的位移之比内通过的位移之比s 1:s 2:s 3:…:s n=1=1::4:9…:…:n n 2③第1个T 内、第2个T 内、第3个T 内…、第n 个T 内通过的位移之比内通过的位移之比s Ⅰ:s Ⅱ:s Ⅲ:…:s N =1=1::3:5…:(…:(2n 2n 2n——1)④第1个T 内、第2个T 内、第3个T 内…、第n 个T 内的平均速度之比内的平均速度之比v Ⅰ:v Ⅱ:v Ⅲ:…:v N =1=1::3:5…:(…:(2n 2n 2n——1) (2)等分位移,以x 为位移单位.为位移单位. ①通过1x 、2x 2x、、3x …、…、n n x 所需时间之比所需时间之比 t 1:t 2:t 3:…:t n =1=1::3:2…:n②通过第1个x 、第2个x 、第3个x 、…第n 个x 所需时间之比所需时间之比t Ⅰ:t Ⅱ:t Ⅲ:…:t N =1=1:::23:12--…:1--n n③1x 末,末,22x 末,末,33x 末…,末…,n n x 末的速度之比末的速度之比v 1:v 2:v 3:…:v n =1=1::3:2…:n对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
匀变速直线运动规律的公式总结与应用一、基本公式:1. 速度—时间公式:v t=v0+at;2.位移—时间公式: x v0t1at222-v2 4. 位移—平均速度公式:X V0V3. 位移—速度公式:v t0 =2ax2t t二、推导公式:v0v t X1.平均速度公式:v.=2Tv0v t2.某段的中刻的瞬速度等于段内的平均速度:v t223.某段位移的中位置的瞬速度公式:v 02v t2v x2。
无匀加或匀减速都有。
24.匀速直运中,在任意两个相等的T 内的位移差是恒量,即X=X n+l–X n=aT 2= 恒量。
5.初速零的匀速直运中的比例关系(T 相等的隔, x 相等的位移隔):⑴、 T 末、 2T 末、 3T 末⋯⋯的瞬速度之比: v1:v2:v3:⋯⋯:v n=1 :2 :3 :⋯⋯:n;⑵、 T 内、 2T 内、 3T 内⋯⋯的位移之比: x1: x2:x3:⋯⋯:x n=1 :4:9 :⋯⋯:n 2;⑶、第一个 T 内、第二个 T 内、第三个 T 内⋯⋯的位移之比: xⅠ:xⅡ: xⅢ:⋯⋯:s n=1 :3 :5 :⋯⋯:(2n-1) ;⑷、前一个 x、前两个 x、前三个 x⋯⋯所用的之比: t 1:t 2:t 3:⋯⋯:t n =1 :⋯⋯:;⑸、第一个 x、第二个 x、第三个 x⋯⋯所用的之比 tⅠ、 t Ⅱ、t Ⅲ:⋯⋯:t N =1 :⋯⋯:。
三、追及相遇问题:Ⅰ、速度大者减速(如匀减速直线运动)追速度小者(如匀速运动):Ⅱ、速度小者加速(如初速度为零的匀加速直线运动)追速度大者(如匀速运动):相遇问题的常见情况:1、同向运动的两物体追及即相遇;2、相向运动的物体,当各自发生的位移大小和等于开始时两物体的距离时即相遇。
匀变速直线运动的3个推导式【学习目标】1. 匀变速直线运动的三个推导式2. 匀变速直线运动推导式的应用推导1.匀变速直线运动中,相邻相等时间间隔的位移之差为一恒量,即:2x aT ∆=推导 2.匀变速直线运动中,某段时间内的平均速度等于初末速度的平均值,且等于中间时刻的瞬时速度。
即:推导3.做匀变速直线运动的物体,某段位移的中间位置的瞬时速度等于初、末速度的方均根。
22022x v v v +=推导一 2x aT ∆=例1.一质点做匀加速直线运动,速度变化△v =2m/s 时发生位移x 1=1m ;紧接着速度变化同样的△v 时发生位移x 2=73m ,则该质点的加速度为( ) A.21m/s 3 B.22m/s 3C.23m/sD.6m/s 2【答案】C【解析】设匀加速的加速度a ,物体的速度分别为v 1、v 2和v 3,据运动学公式可知222112v v ax -=223222v v ax -=且v 2-v 1=v 3-v 2=△v解得:221()v ax x ∆=-代入数据有:2222m/s 3m/s 713a ==- A.21m/s 3与分析不符,故A 项错误;B.22m/s 3与分析不符,故B 项错误; C.23m/s 与分析相符,故C 项正确; D.6m/s 2与分不符,故D 项错误。
例2.一小球(可视为质点)沿斜面匀加速滑下,依次经过A 、B 、C 三点,如图所示,已知AB =18m ,BC =30m ,小球经过AB 和BC 两段所用的时间均为2s ,则小球在经过A 、C 两点时的速度大小分别是( )A.6m/s 12m/sB.6m/s 18m/sC.3m/s 5m/sD.3m/s 7m/s【答案】B【解析】根据△x =at 2得:a ===3m/s 2,B 点的瞬时速度等于AC 段的平均速度,则有:v B ==m/s =12m/s则C 点的速度为:v C =v B +at =12+3×2=18m/s A 点的速度为:v A =v B ﹣at =12﹣3×2=6m/s 故B 正确,ACD 错误。
一.基本规律:v =ts a =t v v t 0- v =20t v v + at v v t +=0 021at t v s +=221att v v t 20+= t vt 22022v v as t -=注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动。
二.匀变速直线运动的推论与推理对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
推论1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即202t t v v t S v +==推导:设时间为t ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度公式at v v +=0得: ⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22202ta v v t a v v t t t ⇒202t t v v v +=推论2 做匀变速直线运动的物体在一段位移的中点的即时速度22202t s v v v +=推导:设位移为S ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度和位移关系公式as v v t 2202+=得:⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22222222022S a v v Sa v v s t s ⇒22202t s v v v +=推论3 做匀变速直线运动的物体,如果在连续相等的时间间隔t 内的位移分别为1S 、2S 、 3S ……n S ,加速度为a ,则=-=-=∆2312S S S S S……21at S S n n =-=-推导:设开始的速度是0v经过第一个时间t 后的速度为at v v +=01,这一段时间内的位移为20121at t v S +=, 经过第二个时间t 后的速度为at v v +=022,这段时间内的位移为202122321at t v at t v S +=+=经过第三个时间t 后的速度为at v v +=023,这段时间内的位移为202232521at t v at t v S +=+=…………………经过第n 个时间t 后的速度为at nv v n +=0,这段时间内的位移为202121221at n t v at t v S n n -+=+=- 则=-=-=∆2312S S S S S……21at S S n n =-=-点拨:只要是匀加速或匀减速运动,相邻的连续的一样的时间内的位移之差,是一个与加速度a 与时间“有关的恒量”.这也提供了一种加速度的测量的方法:即2t Sa ∆=,只要测出相邻的一样时间内的位移之差S ∆和t ,就容易测出加速度a 。
① 速度位移公式:202v v t -=as 2 ② 位移公式:s =2021at t v + ③ 位移中点的瞬时速度公式:2222v v v t s +=④ 中间时刻的瞬时速度:2t v =at v v v t 21200+=+=v (某段时间内的平均速度等于该段时间中间时刻的瞬时速度) ⑤ 末速度公式:at v v t +=0 ⑥ 加速度公式:tv v a t 0-=⑦ 任意两个连续相等的时间内的位移差公式:x ∆=2aT⑧ 初速度为0时,那么末速度v =at ,有1T 末、2T 末、3T 末……的瞬时速度比为自然数比⑨ 初速度为0时,那么位移221at s =,有1T 内、2T 内、3T 内……的位移比为自然数的平方比同时还有第1个T 内位的移比第2个T 内的位移比第3个T 内的位移……即位移差之比为奇数比⑩从静止开始通过连续相等的位移所用时间的比,有第1段位移的用时比第2段位移的用时比第3段位移的用时……即时差比为()1--n n 的比同时还有前一个位移所用时间比前二个位移所用时间比前三个位移所用时……即位移用时比为自然数开根比同时还有第一段位移未、第二段位移未、第三段位移未……的瞬时速度比为自然数开根比匀变速直线运动公式的推导加速度即为一次函数图象的斜率;加速度的方向与斜率的正负一致 1、由速度公式和位移公式可以推导出的公式①202v v t -=as 2202v v t -=()2020v at v -+=2202t a at v +=⎪⎭⎫ ⎝⎛+20212at t v a =as 2位移中点的瞬时速度 ∵202vv t-=as 2 ∴s =a v v t 2202-⇒2s =a v v t 422- ②设位移中点瞬时速度是2s v∵2022v v s -=22as =2202v v t- ∴22s v =2202v v t+⇒2s v =222v v t + ③设初速度是0v ,加速度a ,时间是t因为位移s =2021at t v +平均速度v =t s =at v 210+因为中间时刻的瞬时速度2t v =⎪⎭⎫⎝⎛+t a v 210=at v 210+=v 所以某段时间内的平均速度等于该段时间中间时刻的瞬时速度④x ∆=2aT (做匀变速直线运动的物体,在任意两个连续相等的时间内的位移差为定值。
设加速度为a ,连续相等的时间为T ,位移差为x ∆)证明:设第1个T 时间的位移为1x ;第2个T 时间的位移为2x ……第n 个T 时间的位移为n x由x =2021at t v + 得:1x =2021aT T v +2x =()2020212212aT T v T a T v --+=2023aT T v +n x =()()()[]2020121121T n a T n v nT a nT v ----+=20212aT n T v -+∴x ∆=12x x -=23x x -=1--n n x x =2aT ⇒a =2T x ∆ 2 ①因为初速度是0,那么末速度v =at1T 末、2T 末、3T 末……瞬时速度为aT,2aT,3aT …… 所以瞬时速度的比为v1:v2:v3……=1:2:3:……:n ②s =221at 所以1T 内、2T 内、3T 内……nT 内位移 为221at ,()2221t a , ()2321t a ……()221nt a 那么他们的比为S1:S2:S3:……:n s =12:22:32:……:n 2③第一个T 内位移=1s =221aT (初速度为0) 第二个T 内位移=12s s -=()2221221aT T a -=223aT (初速度为at )第三个T 内位移=23s s -=()()22221321T a T a -=225aT (初速度为2at )……第n 个T 内位移=1--n n s s =()()[]2212121T n a nT a --=2212aT n - [初速度为(2n-1)at] 所以第一个T 内、第二个T 内、第三个T 内……第n 个T 内的位移之比为: S Ⅰ:S Ⅱ:S Ⅲ:……:n s =1:3:5:……:12-n④从静止开始通过连续相等的位移所用时间的比 设每一个位移为s 对第一个s 有s =2121at ⇒1t =a s 2 对前两个s 有s 2=2221aT ⇒2T =a s 4=21t 因此2t =12t T -=()12-1t对前3个s ,有s 3=2321aT ⇒3T =a s 6=31t因此3t =23T T -=()23-1t对前4个s ,有s 4=2421aT ⇒4T =a s 8=41t因此4t =34T T -=41t -31t =()34-1t有第1段位移所用时间比第2段位移所用时间 得1t :2t :3t : (1)()12-:()23-:()34-:……()1--n n有前一个位移所用时间比前二个位移所用时间得1t :2T :3T :4T :……=1:2:3:……n对于从静止开始通过连续相等的位移有第一个s 末、第二个s 末、……第n 个s 末的速度之比:v1:v2:v3……=1:2:3:……n∵202v v t -=as 2 ∴21t v =as 2⇒1t v =as 2 22t v =as 4⇒2t v =as 4…… 逐差法是把连续的数据(必须是偶数个)s1、s2、s3……n s 从中间对半分成两组,每组有m=2n 个数据,前一半为s1、s2、s3……m s ,后一半为1+m s 、2+m s ……n s ,将后一半的第一个数据减去前一半的第一个数据得1s ∆=1+m s - s1,2s ∆=2+m s - s2……m s ∆=n s -m s ,则由这些差值求得加速度分别为:1a =21mT s ∆,2a =22mT s ∆……m a =2mT s m ∆取这样得到的加速度的平均值 a =m a a a m +++ 21=2221Tm s s s m∆++∆+∆ =()()()222211T m s s s s s s m n m m -++-+-++=()()222121Tm s s s s s s m n m m ++-++++逐差法的应用如果有数据三组:s1,s2,s3,则加速度表达式为a =()2132T s s -,即舍去第二组数据。
如果有四组数据s1,s2,s3,s4,则加速度表达式为a =()()2221432T s s s s +-+。
如果有五组数据s1,s2,s3,s4,s5,则加速度表达式为a =()()221436Ts s s s +-+,即舍去了中间一组数据。
有六组数据s1,s2,s3,s4,s5,s6,则加速度表达式为a =()()223216543T s s s s s s ++-++小结1、对于时间来说,有时间、时间段和时刻,研究时,其相邻差恒等①1T 内、2T 内是指连续时间内,对应的问题是连续时间内的位移,相邻时间差恒等,有s =2021at t v +当0v =0时,前后时间内的位移比等于自然数的平方比,(助记连续时间的位移比是自平比)②第1个T 时间、第2个T 时间或第1个T 时间内、第2个T 时间内,是指某1时间段,相邻时间段恒等。
对应的问题是位移,这一时间段的位移有x ∆=12x x -相邻位移比为奇数比即第一个t 秒内、第二个t 秒内、……第n 个t 秒内的位移比等于奇数比应用比较广泛,应熟记(时间段的位移比是奇数比)③1T 末、2T 末是指某1时刻,相邻时刻差恒等,对应的问题是瞬时速度,0v 、t v 即为瞬时速度,0v =0时,相邻瞬时速度比为自然数比(时刻速度比是自然比) 2、对于位移来说,研究时,位移由静止开始连续相等①第1段位移所用时间比第2段位移所用时间(孤立位移用时比根大减根小) 得1t :2t :3t : (1)()12-:()23-:()34-:……()1--n n②前一个位移所用时间比前二个位移所用时间(连续位移用时比根自比)得1t :2T :3T :4T :……=1:2:3:……n 此特点应用比较广泛,应熟记 ③第一个s 末、第二个s 末、……第n 个s 末的速度之比(位移末的速度比根自比) 得v1:v2:v3……=1:2:3:……n匀变速直线运动的解题思路1、加速度恒等不变,加速度等于0时,运动为匀速直线运动,速度、位移保持不变,问题简单,解题时应首先考虑加速度2、时间、时间段和时刻对应的相邻差恒等,解题时应理解所给的时间条件或所求时间条件是什么时间概念,涉及瞬时时间时应想到中间时刻瞬时速度和中心位移时刻瞬时速度,时刻比较好理解,时间是连续的,时间段是孤立的,速度只与时刻有关,时间和时间段与位移有关3、位移应分清是连续的还是孤立的,研究位移时初速度决定位移是连续的还是孤立的,应充分理解4、相同时间的位移不同,相同位移所用时间不同物体运动了10秒,前进了180米,最后1秒位移是多少?s =221at 180=50a a=3.6 前9秒位移=213.6×92=145.8m 所以最后1秒位移=180-145.8=35.2m竖直上抛运动竖直上抛的物体只受重力作用,竖直上抛运动的加速度大小为g ,方向竖直向下,初速度00≠v ,加速度为-g (通常规定以初速度0v 的方向为正方向)竖直上抛运动适应规律 速度公式:t v =gt v -0 位移公式:h =2021gt t v -速度位移关系式:202v v t -=gh 2-竖直上抛运动的处理方法 ①分段处理竖直上抛运动竖直上升过程:初速度为00≠v ,加速度为g 的匀减速直线运动 基本规律:t v =gt v -0 h =2021gt t v - 22v v t -=gh 2- 竖直下降过程:自由落体运动 基本规律:t v =gt h =221gt 2t v =gh 2 ②整体处理竖直上抛运动设抛出时刻t=0,向上的方向为下方向,抛出位置h=0,则有: 若t v >0表明物体处于上升阶段gt v v t -=0 若t v =0表明物体上升到最大高度若t v <0表明物体在抛出点下方。