当前位置：文档之家 › 习题答案(数电)

习题答案(数电)

  • 格式：ppt
  • 大小：1.79 MB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

习题数电参考答案(终)-图文

习题数电参考答案(终)-图文

习题数电参考答案（终）-图文第一章数字逻辑概论1.1数字电路与数制信号1.1.1试以表1.1.1所列的数字集成电路的分类为依据，指出下列IC器件属于何种集成度器件：（1）微处理器；（2）计数器；（3）加法器；（4）逻辑门；（5）4兆位存储器。

解：依照表1.1.1所示的分类，所列的五种器件：（1）、（5）属于大规模；（2）、（3）属于中规模；（4）属于小规模。

1.1.2一数字信号波形如图题1.1.2所示，试问该波形所代表的二进制数是什么？解：图题1.1.2所示的数字信号波形的左边为最高位（MSB），右边为最低位（LSB），低电平表示0，高电平表示1。

该波形所代表的二进制数为010110100。

1.1.3试绘出下列二进制数的数字波形，设逻辑1的电压为5V，逻辑0的电压为0V。

（1）001100110011（2）0111010（3）1111011101解：用低电平表示0，高电平表示1，左边为最高位，右边为最低位，题中所给的3个二进制数字的波形分别如图题 1.1.3（a）、（b）、（c）所示，其中低电平为0V，高电平为5V。

1.1.4一周期性数字波形如图1.1.4所示，试计算：（1）周期；（2）频率；（3）占空比。

解：因为图题1.1.4所示为周期性数字波，所以两个相邻的上升沿之间持续的时间为周期，T=10m。

频率为周期的倒数，f=1/T=1/0.01=100Hz。

占空比为高电平脉冲宽度与周期的百分比，q=1m/10m某100%=10%。

1.2数制1.2.1一数字波形如图1.2.1所示，时钟频率为4kHz，试确定：（1）它所表示的二进制数；（2）串行方式传送8位数据所需要的时间；（3）以8位并行方式传送的数据时需要的时间。

解：该波形所代表的二进制数为00101100。

时钟周期T=1/f=1/4kHz=0.25m。

串行方式传送数据时，每个时钟周期传送1位数据，因此，传送8位数据所需要的时间t=0.25m某8=2m。

数字电子技术课后习题答案（全部）

数字电子技术课后习题答案（全部）

第一章数制与编码1.1自测练习1.1.1、模拟量数字量1.1.2、（b）1.1.3、（c）1.1.4、（a）是数字量，（b）（c）（d）是模拟量1.2 自测练习1.2.1. 21.2.2.比特bit1.2.3.101.2.4.二进制1.2.5.十进制1.2.6.（a）1.2.7.（b）1.2.8.（c）1.2.9.（b）1.2.10.（b）1.2.11.（b）1.2.12.（a）1.2.13.（c）1.2.14.（c）1.2.15.（c）1.2.16.10010011.2.17.111.2.18.1100101.2.19.11011.2.20.8进制1.2.21.（a）1.2.22.0，1，2，3，4，5，6，71.2.23.十六进制1.2.24.0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F 1.2.25.（b）1.3自测练习1.3.1.1221.3.2.675.521.3.3.011111110.011.3.4.521.3.5.1BD.A81.3.6.1110101111.11101.3.7.38551.3.8.28.3751.3.9.100010.111.3.10.135.6251.3.11.570.11.3.12.120.51.3.13.2659.A1.4自测练习1.4.1.BCD Binary coded decimal 二—十进制码1.4.2.（a）1.4.3.（b）1.4.4.8421BCD码，4221BCD码，5421BCD1.4.5.（a）1.4.6.011001111001.10001.4.7.111111101.4.8.101010001.4.9.111111011.4.10.61.051.4.11.01011001.011101011.4.12.余3码1.4.13.XS31.4.14.XS31.4.15.1000.10111.4.16.1001100000111.4.17.521.4.18.110101.4.19.0101111.4.20.（b）1.4.21.ASCII1.4.22.（a）1.4.23.ASCII American Standard Code for Information Interchange美国信息交换标准码EBCDIC Extended Binary Coded Decimal Interchange Code 扩展二-十进制交换吗1.4.24.10010111.4.25.ASCII1.4.26.（b）1.4.27.(b)1.4.28.110111011.4.29.-1131.4.30.+231.4.31.-231.4.32.-861.5 自测练习 1.5.1 略1.5.2 11011101 1.5.3 010001011.5.4 11100110 补码形式 1.5.5 011111011.5.6 10001000 补码形式 1.5.7 11100010 补码形式习题1.1 （a ）（d ）是数字量，（b ）（c ）是模拟量，用数字表时（e ）是数字量，用模拟表时（e ）是模拟量 1.2 （a ）7, （b ）31, （c ）127, （d ）511, （e ）40951.3 （a ）22104108⨯+⨯+， （b ）26108108⨯+⨯+，（c ）321102105100⨯+⨯+⨯+（d ）322104109105⨯+⨯+⨯+ 1.4 （a ）212121⨯+⨯+, （b ）4311212121⨯+⨯+⨯+, （c ）64212+12+12+12+1⨯⨯⨯⨯（d ）9843212+12+12+12+12⨯⨯⨯⨯⨯ 1.5 2201210327.15310210710110510--=⨯+⨯+⨯+⨯+⨯,3210-1-221011.0112+02+12+12+02+12=⨯⨯⨯⨯⨯⨯,210-18437.448+38+78+48=⨯⨯⨯⨯, 10-1-2163A.1C 316+A 16+116+C 16=⨯⨯⨯⨯1.6 （a ）11110, （b ）100110,（c ）110010, （d ）1011 1.7 （a ）1001010110000, （b ）10010111111.8 110102 = 2610, 1011.0112 = 11.37510， 57.6438 = 71.81835937510， 76.EB 16= 118.91796875101.9 1101010010012 = 65118 = D4916，0.100112 = 0.468 = 0.9816，1011111.011012 = 137.328 = 5F.68161.10 168 = 1410，1728 = 12210，61.538 = 49.671875， 126.748 = 86.9375101.11 2A 16 = 4210 = 1010102 = 528， B2F 16 = 286310 = 1011001011112 = 54578， D3.E 16= 211.87510 = 11010011.11102 = 323.78， 1C3.F916 = 451.9726562510 = 111000011.111110012 = 703.76281.12 （a ）E, （b ）2E, （c ）1B3, （d ）349 1.13 （a ）22, （b ）110, （c ）1053, （d ）2063 1.14 （a ）4094, （b ）1386, （c ）49282 1.15（a ）23, （b ）440, （c ）27771.16 198610 = 111110000102 = 00011001100001108421BCD ， 67.31110 = 1000011.010012 =01100111.0011000100018421BCD ， 1.183410 = 1.0010112 = 0001.00011000001101008421BCD ，0.904710 = 0.1110012 = 0000.10010000010001118421BCD1.17 1310 = 000100118421BCD = 01000110XS3 = 1011Gray， 6.2510 = 0110.001001018421BCD=1001.01011000 XS3 = 0101.01Gray，0.12510= 0000.0001001001018421BCD= 0011.010*********XS3 = 0.001 Gray1.18 101102 = 11101 Gray，0101102 = 011101 Gray1.19 110110112 = 0010000110018421BCD，45610 = 0100010101108421BCD，1748=0010011101008421BCD，2DA16 = 0111001100008421BCD，101100112421BCD = 010*********BCD， 11000011XS3 = 100100008421BCD1.20 0.0000原= 0.0000反= 0.0000补，0.1001原= 0.1001反= 0.1001补，11001原= 10110反= 10111补1.21 010100原= 010100补，101011原= 110101补，110010原= 101110补，100001原=111111补1.22 1310 = 00001101补，11010 = 01101110补，-2510 = 11100111补，-90 =10100110补1.23 01110000补= 11210，00011111补= 3110，11011001补= -3910，11001000补= -56101.24 1000011 1000001 1010101 1010100 1001001 1001111 1001110 0100001 01000001001000 1101001 1100111 1101000 0100000 1010110 1101111 1101100 1110100 1100001 1100111 11001011.25 0100010 1011000 0100000 0111101 0100000 0110010 0110101 0101111 101100101000101.26 BEN SMITH1.27 00000110 100001101.28 01110110 10001110第二章逻辑门1.1 自测练习2.1.1. （b）2.1.2. 162.1.3. 32, 62.1.4. 与2.1.5. （b）2.1.6. 162.1.7. 32, 62.1.8. 或2.1.9. 非2.1.10. 12.2 自测练习=⋅2.2.1. F A B2.2.2. (b)2.2.3. 高2.2.4. 322.2.5. 16，52.2.6. 12.2.7. 串联2.2.8. (b)2.2.9. 不相同2.2.10. 高2.2.11. 相同2.2.12. (a)2.2.13. (c)2.2.14. 奇2.3 自测练习2.3.1. OC，上拉电阻2.3.2. 0，1，高阻2.3.3. （b）2.3.4. （c）2.3.5. F A B=⋅, 高阻2.3.6. 不能2.4 自测练习1.29 TTL，CMOS1.30 Transisitor Transistor Logic1.31 Complementary Metal Oxide Semicoductor1.32 高级肖特基TTL，低功耗和高级低功耗肖特基TTL1.33 高，强，小1.34 （c）1.35 （b）1.36 （c）1.37 大1.38 强1.39 （a）1.40 （a）1.41 （b）1.42 高级肖特基TTL1.43 （c）习题2.1 与，或，与2.2 与门，或门，与门2.3 （a）F=A+B, F=AB （b）F=A+B+C, F=ABC （c）F=A+B+C+D, F=ABCD2.4 （a ）0 （b ）1 （c ）0 （d ）0 2.5 （a ）0 （b ）0 （c ）1 （d ）0 2.6 （a ）1 （b ）1 （c ）1 （d ）1 2.7 （a ）4 （b ）8 （c ）16 （d ）32 2.8 （a ）3 （b ）4 （c ）5 （d ）62.9 （a ）（b ） A B C D F 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 1 1 0 1 0 0 0 0 1 0 1 1 0 1 1 0 1 0 1 1 1 0 1 0 0 0 0 1 0 0 1 1 1 0 1 0 1 1 0 1 1 0 1 1 0 0 1 1 1 0 1 0 1 1 1 0 0 1 11112.10 Y AB AC =+2.11A B C Y 0 0 0 0 0 0 1 0 011A B C F 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 0 11110 1 1 11 0 0 01 0 1 11 1 0 01 1 1 12.122.13F1 = A(B+C), F2=A+BCA B C F1F20 0 0 0 00 0 1 0 00 1 0 0 00 1 1 0 11 0 1 1 11 0 0 0 11 1 0 1 11 1 1 1 12.142.15 （a）0 （b）1 （c）1 （d）02.16 （a）1 （b）0 （c）0 （d）12.17 （a）0 （b）02.182.19 Y AB BC DE F=⋅⋅⋅2.20 Y AB CD EF=⋅⋅2.21 102.22 402.23 当TTL反相器的输出为3V，输出是高电平，红灯亮。

数电习题答案(一)

数电习题答案(一)


D 44H y 1 1 1 0 1 0 0 0 y 0 1 1 0 1 0 0 1 y 0 0 0 1 0 1 1 1
f 66H
# 23H
? 3FH
二章
y = abc + abc + abc + abc
y=~a&~b&~c|~a&~b&c|~a&b&~c|a&~b&~c
(2)
y = abc + abc + abc + abc
左边=右边
∴ 等式成立
(3) AB + BC + AC = ABC + A • B • C
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
AB + BC + AC
0 1 1 1 1 1 1 0
AB + BC + AC
ABC + A • B • C
y=~a&~b&c|~a&b&amamp;b&c
(3)
y = abc + abc + abc + abc
y=~a&b&c|~a&b&c|a&b&~c|a&b&c
2.8 (1) AB + AC + BC = ( A + C )( A + B )
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
;
F = AB C + A C D + AC = AB C + C ( A D + A) = AB C + C ( D + A) = AB C + AC + C D = A( B C + C ) + C D = A( B + C ) + C D = AB + AC + C D
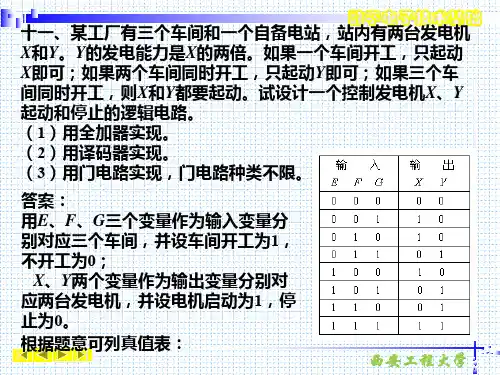
习题答案(数电)

习题答案(数电)


11. 在教材P469图10.3.5给出的积分型单稳态触发器电路中， 若G1和G2为74LS系列门电路，它们的VOH=3.4V ，VOL≈0V， VTH=1.1V ，R=1kΩ ，C=0.01μF，试求在触发信号作用下输 出负脉冲的宽度。设触发脉冲的宽度大于输出脉冲的宽度。
西安工程大学
数字电子技术基础
9. 在教材P467图10.3.1给出的微分型单稳态触发器电路中，已 知R=51kΩ ，C=0.01μF，电源电压VDD=10V ，试求在触发信号 作用下输出脉冲的宽度和幅度。 解：
tW=RCln2=51×103×0.01×10-6×0.69=0.35ms Vm=VOH-VOL≈10V
西安工程大学
令A2=E A1=F A0=G 则
数字电子技术基础 Y0 ~ Y7 m0 ~ m7
（3）用门电路实现，门电路种类不限。
X EFG EFG EFG EFG Y EFG EFG EFG EFG
G(EF EF) G(EF EF) G(EF EF) EF (G G)
西安工程大学
数字电子技术基础 21. 某石英晶体振荡器输出脉冲信号的频率为32768Hz，用 74161组成分频器，将其分频为频率为1Hz的脉冲信号。 解：因为32768=215，经15级二分频，就可获得频率为1Hz的脉 冲信号。因此将四片74161级联，从高位片（4）的Q2输出即 可。
西安工程大学
输入端 S、R 的电压波形如图中所示。 答案：
西安工程大学
数字电子技术基础 17.由或非门组成的触发器和输入端信号如图所示，设触发器
的初始状态为1，画出输出端Q的波形。 答案：
西安工程大学
数字电子技术基础 18. 在下图电路中，若CP、S、R的电压波形如图中所示，
数电-带答案

数电-带答案

第一章 逻辑代数基础 例题1.与(10000111)BCD 相等的十进制数是87， 二进制数是1010111 十六进制数是57，2.AB+CD=0（约束项）求 的最简与或表达式。

解：D C A C B A Z +=，见图1-1， 得3.若F(A,B,C,D)=∑m(0,1,2,3,4,7,15）的函数可化简为： 则可能存在的约束项为（ 3 ）。

见图1-21．逻辑函数式Y A B C D =++（）的反演式为 D C B A + 2. 在下列不同进制的数中，数值最大的数是（ D ）1051A.（） .101010B 2（） 163E C.（） D.（01011001）8421BCD 码 3、用卡诺图化简下式为最简与或式。

D C B A ++ Y(A,B,C,D)= ∑m(0,2,4,5,6,8,9)+ ∑d(10,11,12,13,14,15) 4.已知F ABC CD =+选出下列可以肯定使F=0的情况（ D )A. A=0，BC=1B. B=C=1C. D=0，C=1D. BC=1，D=1 5、是8421BCD 码的是（ B ）。

A 、1010 B C 、1100 D 、11016、欲对全班43个学生以二进制代码编码表示，最少需要二进制码的位数是（ B ）。

A 、5B 、6C 、8D 、437、逻辑函数F(A,B,C) = AB+B C+C A 的最小项标准式为（ D ）。

A 、F(A,B,C)=∑m(0,2,4)B 、F(A,B,C)=∑m(1,5,6,7)C 、F(A,B,C)=∑m (0,2,3,4)D 、F(A,B,C)=∑m(3,4,6,7)Z A BC A B AC D =++Z Z AC AC =+()B C D C D ++1..2..3..4..AC A DA C AB A D A B A B B C++++8、用代数法化简下式为最简与或式。

A+CC B BC C B A BCD A A F ++++=判断题1.若两个函数具有不同的真值表，则两个逻辑函数必然不相等。

数电课后习题及答案

数电课后习题及答案

（4）110,111,010
题1.8列出下面各函数的真值表
题1.9在举重比赛中，有甲、乙、丙三名裁判，其中甲为主裁判，乙、丙为副裁判，当主裁判和一名以上（包括一名）副裁判认为运动员上举合格后，才可发出合格信号。列出该函数的真值表。
设A为主裁判，真值表如下表所示。
题1.10一个对4逻辑变量进行判断的逻辑电路。当4变量中有奇数个1出现时，输出为1；其他情况，输出为0。列出该电路的真值表，写出函数式。
题1.11已知逻辑函数真值表如右表所示，写出对应的函数表达式。
将Y为1对应的最小项相加，就可以得到函数式。
Y=m1+m2+m4+m5+m7
=A'B'C+ A'BC'+ AB'C'+ AB'C+ ABC
同理可以得到题1.12的函数式：
Y= A'B'C'D+A'B'CD'+A'BC'D'+A'BCD+AB'C'D'+
题1.7在下列各个逻辑函数中，当变量A、B、C为哪些取值组合时，函数Y的值为1。
Y=AB+BC+A'C
= AB(C+C')+BC (A+A')+A'C(B+B')
=m7+m6+m1+m3
使以上四个最小项为1时，Y为1.
即：111；110；011；001
（2）000,001,011,100
（3）100,101,000,011,010,111
数字电子技术习题及答案

数字电子技术习题及答案

第一章 数字逻辑基础1-1. 将下列的二进制数转换成十进制数（1）、1011，（2）、10101，（3）、11111，（4）、1000011-2. 将下列的十进制数转换成二进制数（1）、8，（2）、27，（3）、31，（4）、1001-3. 完成下列的数制转换（1）、（255）10=（ ）2=（ ）16=（ ）8421BCD（2）、（11010）2=（ ）16=（ ）10=（ ）8421BCD（3）、（3FF ）16=（ ）2=（ ）10=（ ）8421BCD（4）、（1000 0011 0111）8421BCD =（）10=（）2=（）161-4. 完成下列二进制的算术运算（1）、1011+111，（2）、1000-11，（3）、1101×101，（4）、1100÷100 1-5. 设：AB Y 1=，B A Y 1+=，B A Y 1⊕=。

已知A 、B 的波形如图题1-5所示。

试画出Y 1、Y 2、Y 3对应A 、B 的波形。

图题1-51-6选择题1．以下代码中为无权码的为 。

A . 8421BCD 码B . 5421BCD 码C . 余三码D . 格雷码2．以下代码中为恒权码的为 。

A .8421BCD 码B . 5421BCD 码C . 余三码D . 格雷码3．一位十六进制数可以用 位二进制数来表示。

A . １B . ２C . ４D . 164．十进制数25用8421BCD码表示为。

A.10 101B.0010 0101C.100101D.101015．在一个8位的存储单元中，能够存储的最大无符号整数是。

A.（256）10B.（127）10C.（FF）16D.（255）106．与十进制数（53.5）10等值的数或代码为。

A.(0101 0011.0101)8421BCDB.(35.8)16C.(110101.1)2D.(65.4)87．矩形脉冲信号的参数有。

A.周期B.占空比C.脉宽D.扫描期8．与八进制数(47.3)8等值的数为：A. (100111.011)2B.(27.6)16C.(27.3 )16D. (100111.11)29. 常用的BCD码有。

数电习题及答案

数电习题及答案

数电习题及答案(总32页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一、时序逻辑电路与组合逻辑电路不同，其电路由组合逻辑电路和存储电路（触发器）两部分组成。

二、描述同步时序电路有三组方程，分别是驱动方程、状态方程和输出方程。

三、时序逻辑电路根据触发器的动作特点不同可分为同步时序逻辑电路和异步时序逻辑电路两大类。

四、试分析图时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图和时序图。

解：驱动方程：001101J KJ K Q====状态方程：100111010nnQ QQ Q Q Q Q++==+输出方程：10Y Q Q=状态图：功能：同步三进制计数器五、试用触发器和门电路设计一个同步五进制计数器。

解：采用3个D触发器，用状态000到100构成五进制计数器。

（1）状态转换图（2）状态真值表（3）求状态方程（4）驱动方程（5）逻辑图（略）[题] 分析图所示的时序电路的逻辑功能，写出电路驱动方程、状态转移方程和输出方程，画出状态转换图，并说明时序电路是否具有自启动性。

解：触发器的驱动方程2001021010211J Q K J Q J QQ K Q K ====⎧⎧⎧⎨⎨⎨==⎩⎩⎩ 触发器的状态方程120011010112210n n n Q Q Q Q Q Q Q Q Q Q Q Q +++==+=⎧⎪⎪⎨⎪⎪⎩输出方程 2Y Q = 状态转换图如图所示所以该电路的功能是：能自启动的五进制加法计数器。

[题] 试分析图时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，并检查电路能否自启动。

解：驱动方程输出方程 状态方程状态转换图如图 所示功能：所以该电路是一个可控的3进制计数器。

[题] 分析图时序电路的功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，并检查电路能否自启动。

数电习题答案..

数电习题答案..


• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
题3.1.4 将下列二进制数转换为十进制数 （1）(01101)2 （2）(10010111)2 （3）(0.1001)2 （4） (0.101101)2 解： （1）（01101）2=（2）（10010111）2 = （3）（0.1001）2=（4）（0.101101）2=题3.1.5 将下列二进制数转换为十进制数 （1）(101.011)2 （2）(110.101)2 （3）(1101.1001)2 （4） (1011.0101)2 解：（1）(101.011)2=(2) (110.101)2=（3）（1101.1001）2=(4) (1011.0101)2=题3.1.6 将下列二进制数转换为八进制数和十六进制数 （1）(101001)B （2）(11.01101)B 解： （1） （101001）2=（51）8=（29）16 （2）（11．01101）2=（3．32）8=（3．68）16 题3.1.7 将下列十六进制数转换为二进制数 （1）(23F.45)H （2）(A040.51)H 解：用四位二进制代替一位十六进制数码即可完成转换。 （1）（23F.45）16=(001000111111．01000101)2（2）（A040．51）16=（1010000001000000．01010001） 题3.1.8 将下列十进制数转换成8421 BCD码和余3码 （1）(468.32)10 （2）(127) 10 解： （1）（468．32）10=（0100 0110 1000．0011 0010）8421 =（0111 1001 1011．0110 0101）余三码 （2）（127）10=（0001 0010 0111）8421 =（0100 0101 1010）余三码题3.1.9 将下列数码作为自然二进制码和8421 BCD码时，分别求出相应的十进制数 （1）100010010011 （2）100110110.11001 解： 二进制数时：（100010010011）2= 8421BCD码时：（100010010011）8421=（893）10 （2） 二进制数时：（100110110.11001）2= 8421BCD码时：（100110110.11001）8421=（136.C8）10
数电习题答案（1）

数电习题答案（1）

数电习题答案（1）第⼀章数制和码制1．数字信号和模拟信号各有什么特点?答：模拟信号——量值的⼤⼩随时间变化是连续的。

数字信号——量值的⼤⼩随时间变化是离散的、突变的（存在⼀个最⼩数量单位△）。

2．在数字系统中为什么要采⽤⼆进制?它有何优点?答：简单、状态数少，可以⽤⼆极管、三极管的开关状态来对应⼆进制的两个数。

3.⼆进制：0、1；四进制：0、1、2、3；⼋进制：0、1、2、3、4、5、6、7；⼗六进制：0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。

4.(30.25)10=( 11110.01)2=( 1E.4)16。

(3AB6)16=( 0011101010110110)2=(35266)8。

(136.27)10=( 10001000.0100)2=( 88.4)16。

5. B E6.ABCD7.(432.B7)16=( 010*********. 10110111)2=(2062. 556)8。

8.⼆进制数的1和0代表⼀个事物的两种不同逻辑状态。

9.在⼆进制数的前⾯增加⼀位符号位。

符号位为0表⽰正数；符号位为1表⽰负数。

这种表⽰法称为原码。

10.正数的反码与原码相同，负数的反码即为它的正数原码连同符号位按位取反。

11.正数的补码与原码相同，负数的补码即为它的反码在最低位加1形成。

12.在⼆进制数的前⾯增加⼀位符号位。

符号位为0表⽰正数；符号位为1表⽰负数。

正数的反码、补码与原码相同，负数的反码即为它的正数原码连同符号位按位取反。

负数的补码即为它的反码在最低位加1形成。

补码再补是原码。

13.A:(+1011)2的反码、补码与原码均相同：01011；B: (-1101)2的原码为11101，反码为10010，补码为10011.14.A: (111011)2 的符号位为1，该数为负数，反码为100100，补码为100101. B: (001010)2的符号位为0，该数为正，故反码、补码与原码均相同：001010.15.两个⽤补码表⽰的⼆进制数相加时，和的符号位是将两个加数的符号位和来⾃最⾼有效数字位的进位相加，舍弃产⽣的进位得到的结果就是和的符号。

数电考试题及答案

数电考试题及答案

数电考试题及答案一、选择题（每题1分，共10分）1. 数字电路中最基本的逻辑关系是（）。

A. 与逻辑B. 或逻辑C. 非逻辑D. 异或逻辑2. 下列哪个不是数字电路的特点？（）A. 抗干扰能力强B. 功耗低C. 体积小D. 工作速度慢3. 一个二进制数1011转换为十进制数是（）。

A. 10B. 11C. 13D. 154. 在数字电路中，以下哪个不是基本的逻辑门？（）A. 与门B. 或门C. 非门D. 放大门5. 触发器的主要用途是（）。

A. 放大信号B. 存储信息C. 转换信号D. 滤波6. 一个完整的数字系统包括（）。

A. 逻辑电路B. 电源C. 输入设备D. 所有选项7. 以下哪个不是数字电路的分类？（）A. 组合逻辑电路B. 时序逻辑电路C. 模拟电路D. 存储电路8. 一个4位二进制计数器最多可以计数到（）。

A. 8B. 16C. 32D. 649. 以下哪个是数字电路的优点？（）A. 易受干扰B. 集成度高C. 功耗大D. 灵活性差10. 一个简单的数字钟至少需要多少个触发器？（）A. 1B. 2C. 4D. 6二、填空题（每空1分，共10分）1. 数字电路中，最基本的逻辑运算包括________、________和________。

2. 一个二进制数1101转换为十进制数是________。

3. 触发器的两个稳定状态是________和________。

4. 一个数字电路系统由________、________和________组成。

5. 一个4位二进制计数器的计数范围是________到________。

三、简答题（每题5分，共20分）1. 简述数字电路与模拟电路的区别。

2. 解释什么是组合逻辑电路和时序逻辑电路。

3. 描述数字电路中的触发器是如何工作的。

4. 什么是数字电路的抗干扰能力？四、计算题（每题10分，共20分）1. 给定一个二进制数101101，转换为十进制数是多少？2. 如果一个数字钟使用4位二进制计数器，计算它的计数周期是多少秒？（假设时钟频率为1Hz）五、综合题（每题15分，共30分）1. 设计一个简单的数字电路，实现两个输入信号A和B的异或逻辑功能。

《数电》教材习题答案 第1章习题答案

思考题与习题1-1 将下列二进制数转化为十进制数。

(1)（100101100）2=（300）10 (2)（101011）2=（43）10(3)（1111111）2=（127）10 (4)（1011110）2=（94）101-2 将下列十进制数转化为二进制数。

(1)（28）10=（11100）2 (2) （100）10=（1100100）2(3)（210）10=（11010010）2 (4)（321）10=（101000001）2 1-3 将八进制数34、567、4633转化为二进制数。

（34）8=（11100）2 （567）8=（101110111）2（4633）8=（100110011011）21-4 将二进制数转化为八进制数。

（1011010）2=（132）8 （11010011）2=（323）8 1-5 将二进制数转化为十六进制数。

（100100110101）2=（935）16 （1010110011）2=（2B3）16 1-6 将十六进制数转化为二进制数。

（7AF4）16=（ 111101*********）2 （F9DE ）16=（1111100111011110）2 1-7 将十进制数691用8421BCD 码表示。

（691）10=（0110 1001 0001）8421BCD1-8 写出如图T1-8所示逻辑函数的逻辑表达式。

图T1-8BC)C B (A C B )C B (A G CB A )C B (A H +⊕⋅=⋅+⊕⋅=⊕⊕=⊕⊕= 1-9 用真值表证明下列等式成立：（1）A B + A B = (A +B )(A+B)可见，左式＝右式，得证。

（2）A ⊕B =A ⊕B可见，左＝右，得证。

（3）A ⊕0 = A可见，左式＝右式，得证。

（4）A ⊕1 = A可见，左式＝右式，得证。

1-10 利用公式和运算规则证明下列等式：（1）ABC + A BC + A B C = BC + AC证明：左＝（ABC + A BC ） +（ A B C ＋ABC ）＝ BC + AC ＝右（2）C AB = AB + C证明：左＝C AB C AB +=+＝右（3）(A +B)(A + C)(B + C + D) = (A + B)(A + C)证明：将以上等式两边作对偶变换，可得到以下公式：AB ＋A C ＋BCD ＝AB ＋A C由常用公式四可知该式是成立的，则由对偶定理可知，对偶等式成立，则原等式也成立。

数电课后习题答案

部分习题答案第一章1.1(45)10=(101101)2=(55)8(129)10=(10000001)2=(201)8(538)10=(1000011010)2=(1032)8 (254.25)10=(11111110.01)2=(376.2)81.2 (1101)2=(13)10 (110101)2=(53)10 (1110101)2=(117)10 (10100110)2=(166)10 。

1.3 (27)10=(1B)16 ， (43)10=(2B)16 ， (125)10=(7D)16 ， (254)10=(15E)16 ，312=(138)16 ， (513)=(201)16 。

1.4 (1) (10100101)2=(425)8=(A5)16 。

(2) (10101111)2=(257)8=(AF)16 。

(3) (11001110111)2=(3167)8=(677)16 。

1.5 (1) (154)10=(10011010)2=(232)8=(9A)16 。

(2) (101011)2=(43)10=(53)8=(2B)16 。

(3) (7E)16=(126)10=(176)8=(1111110)2 。

1.6 (1) 1110，00001，0110101，110010，1110111，100001。

(2)＋0011，＋01010，－0001，－1111。

(3) 0111101，0001010，1000011，11010110。

(4) ＋1101,＋1010,－00101,－010110。

(5) 01011110，10010010。

(6) 0111000，001010，1000100，110100。

(7) ＋111101，＋001100，－01001，－01000。

1.7 (46)10=(1000110)8421BCD , (127)10=(100100111)8421BCD ， (254)10=(1001010100)8421BCD , (893)10=(10001010100)8421BCD ， (2.618)10=(10.011000011000)8421BCD 。

习题答案(数电)


总结：本题考察 了触发器的功能 和应用需要根据 题目要求选择合 适的触发器并理 解其工作原理。
第4题答案解析
答案：
解析：根据题目要求我们需要找到一个函数该函数在输入为0时输出为1在输入为1时 输出也为1。选项的函数f(x)=x恰好满足这一条件。
题目1内容
题目1：简述 二进制数的特
点
题目2：二进 制数的运算规
汇报人：
添加标题
答案：Y = 'BC + B'C + BC' + BC
添加标题
添加标题
注意事项：在化简过程中需要注意 避免出现多余的项和不必要的计算。
第3题答案
答案：
解析：根据题目要求需要选择一个能够实现异或逻辑功能的电路。选项中只有选项符合异或逻辑功能因此正确答 案为。
解题思路：首先分析题目要求然后根据逻辑功能选择合适的电路。在本题中需要选择一个能够实现异或逻辑功能 的电路因此应选择选项。
,
汇报人：
目录
第1题答案
题目：化简逻辑表 达式F=(+B)(C+D)
答案： F=C+D+BC+BD
解析：根据逻辑运 算的基本规则将表 达式展开即可得到 答案。
备注：注意区分逻 辑加和逻辑乘的优 先级。
题目：化简逻辑表达式
第2题答案
解析：利用逻辑代数的基本定律将 表达式化简为最简形式。
添加标题
总结：本题考查了异或逻辑功能和电路的选择要求考生掌握相关知识能够根据题目要求选择合适的电路。
题目：化简逻辑表达式 F='BC+B'C'+BC
第4题答案
答案： F=('+(B+C))(+(B'+C'))(+B

数电--数电习题答案

第1章习题答案1-1．按照集成度分类，试分析以下集成器件属于哪种集成度器件：（1）触发器；（2）中央处理器；（3）大型存储器；（4）单片计算机；（5）多功能专用集成电路；（6）计数器；（7）可编程逻辑器件。

解：（1）小规模；（2）大规模；（3）超大规模；（4）超大规模；（5）甚大规模；（6）中规模；（7）甚大规模。

1-2．将下列十进制数转换为二进制数、八进制数和十六进制数。

（1）45（2）78（3）（4）（5）65 （6）126解：（1）(45)10=(101101)2=(55)8=(2D)16（2）(78)10=(1111000)2=(170)8=(78)16（3）10=2=8=16（4）=2=8=16（5）(65)10=(1100101)2=(145)8=(65)16（6）(126)10=(1111110)2=(176)8=(7E)16101-3．将下列十六进制数转换为二进制数和十进制数。

解：（1）(49)16=(1001001)2=(73)10（2）(68)16=(1101000)2=(104)10（3）16=(1100101)2=(145)10（4）16=2=(84.)10（5）(35)16=(110101)2=(53)10（6）(124)16=(0)2=(292)101-4．将下列八进制数转换为二进制数和十进制数。

解：（1）(27)8=(010111)2=(23)10（2）(56)8=(101110)2=(46)10（3）8=2=10（4）8=2=10（5）(35)8=(11101)2=(29)10（6）(124)8=(1010100)2=(84)101-5．将下列二进制数转换为十六进制数、八进制和十进制数。

解：（1）(1110001)2=(71)16=(161)8=(113)10（2）2=16=8=10（3）2=16=8=10（4）(10001)2 =(11)16=(21)8=(17)10（5）(1010101)2=(55)16=(125)8=(85)101-6．试求出下列8421BCD码对应的十进制数。

数电习题答案

3）晶体三极管作为电子开关时，其工作状态必须为 饱和 状态或 截止 状态。
4） 74LSTTL电路的电源电压值和输出电压的高、低电平值依次约为 5V、2.7V、0.5V 。74TTL电路的电源电压值和输出电压的高、低电平值依次约为 5V、2.4V、0.4V 。
2. 对于T触发器，若原态 =1，欲使次态 =1，应使输入T=（ AD ）。
A.0 B.1 C.Q D.
3. 欲使JK触发器按 =0工作，可使JK触发器的输入端（ BCD ）。
A.J=K=1 B.J=Q,K=Q C.J=Q,K=1 D.J=0,K=1
7）TTL集电极开路门输出为１时由外接电源和电阻提供输出电流。（√ ）
8） CMOS OD门（漏极开路门）的输出端可以直接相连，实现线与。（ √ ）
9） CMOS或非门与TTL或非门的逻辑功能完全相同。（√ ）
1-4 试判断图1-50所示各电路中三极管工作处在什么状态，分别求出它们的基极电流 、集电极电流 ，并求出 。
1）三极管截止的条件是 UBE ≤0V 。三极管饱和导通的条件是 IB≥IBS 。三极管饱和导通的IBS是 IBS≥（VCC－UCES）/βRc 。
2）门电路输出为 高 电平时的负载为拉电流负载，输出为 低 电平时的负载为灌电流负载。
（2）构成一异步 进制加法计数器需要 n 个触发器，一般将每个触发器接成 计数或T’ 型触发器。计数脉冲输入端相连，高位触发器的 CP 端与 邻低位 端 相连。
（3） 一个4位移位寄存器，经过 4 个时钟脉冲CP后，4位串行输入数码全部存入寄存器；再经过 4 个时钟脉冲CP后可串行输出4位数码。
5）OC门称为 集电极开路门 门，多个OC门输出端并联到一起可实现 线与 功能。

数电习题(含答案)

一、选择题1．一位十六进制数可以用 C 位二进制数来表示。

A . １B . ２C . ４D . 162．十进制数25用8421BCD 码表示为 B 。

A .10 101B .0010 0101C .100101D .101013．以下表达式中符合逻辑运算法则的是 D 。

A.C ·C=C 2B.1+1=10C.0<1D.A+1=14. 当逻辑函数有n 个变量时，共有 D 个变量取值组合？A. nB. 2nC. n 2D. 2n5.F=A B +BD+CDE+A D= A 。

A.D B A + B.D B A )(+ C.))((D B D A ++ D.))((D B D A ++6.逻辑函数F=)(B A A ⊕⊕ = A 。

A.BB.AC.B A ⊕D. B A ⊕7．A+BC= C 。

A .A +B B.A +C C.（A +B ）（A +C ） D.B +C8．在何种输入情况下，“与非”运算的结果是逻辑0。

DA ．全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是19．在何种输入情况下，“或非”运算的结果是逻辑0。

BCDA ．全部输入是0 B.全部输入是1 C.任一输入为0，其他输入为1 D.任一输入为110. N 个触发器可以构成能寄存 B 位二进制数码的寄存器。

A.N -1B.NC.N +1D.2N 11．一个触发器可记录一位二进制代码，它有 C 个稳态。

A.0B.1C.2D.312．存储8位二进制信息要 D 个触发器。

A.2B.3C.4D.813．对于T触发器，若原态Qn=1，欲使新态Qn+1=1，应使输入T= A。

A.0B.1C.QD.Q14．对于D触发器，欲使Q n+1=Q n，应使输入D=C。

A.0B.1C.QD.Q15．对于J K触发器，若J=K，则可完成 C触发器的逻辑功能。

A.R SB.DC.TD.Tˊ16．为实现将J K触发器转换为D触发器，应使 A 。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

由真值表写出逻辑表达式：
X EFG EFG EFG EFG
Y EFG EFG EFG EFG
（1）用全加器实现 令CI=E A=F B=G 则S=X CO=Y
数字电子技术基础
（2）用译码器实现
X EFG EFG EFG EFG m1 m2 m4 m7 (m1 m2 m4 m7 ) Y EFG EFG EFG EFG m3 m5 m6 m7 (m3 m5 m6 m7 )
当X＝1时，状态变化为： 00→11→10→01→00→…
可见，该电路既具有递增计数功能，又具有递减计数功能，
是一个2位二进制同步可逆计数器。
西安工程大学
数字电子技术基础 8. 写出下图电路的驱动方程、特性方程和输出方程。
解：驱动方程 状态方程
输出方程
J1 Q3 J2 Q1 J3 Q1Q2
K1 1 K2 Q1 K3 1
答案：
西安工程大学
数字电子技术基础 19. 若主从结构RS触发器各输入端的电压波形如图中所示，试画
出 Q 、Q 端对应的电压波形。设触发器的初始状态为Q=0。 答案：
西安工程大学
数字电子技术基础 20. 已知主从结构JK触发器输入端J、K和CP的电压波形如图所示，
试画出 Q 、Q 端对应的波形。设触发器的初始状态为Q = 0。 答案：
西安工程大学
令A2=E A1=F A0=G 则
数字电子技术基础 Y0 ~ Y7 m0 ~ m7
（3）用门电路实现，门电路种类不限。
X EFG EFG EFG EFG Y EFG EFG EFG EFG
G(EF EF) G(EF EF) G(EF EF) EF (G G)
驱动方程：
T1 X Q0 T0 1
T触发器的特性方程： Q* T Q
将各触发器的驱动方程代入特性方程，
即得电路的状态方程：
QQ10**
T1 T0
Q1 Q0
X Q0 Q1
1 Q0 Q西0 安工程大学
列状态转换表
数字电子技术基础 画状态转换图和时序波形图
由状态图可以看出，
当输入X ＝0时，状态变化为： 00→01→10→11→00→…
QQ12**
Q3 Q1 Q1Q2 Q1Q2
Q1
Q2
Q3* Q1Q2 Q3
Y Q3
西安工程大学
数字电子技术基础
10. 输入信号波形如图所示， 试画出电路对应的输出Q2、Q1
的波形图。
西安工程大学
数字电子技术基础 11. 试分析下图所示时序逻辑电路的逻辑功能。
解：属同步时序电路，时钟方程省去。
输入端 S、R 的电压波形如图中所示。 答案：
西安工程大学
数字电子技术基础 17.由或非门组成的触发器和输入端信号如图所示，设触发器
的初始状态为1，画出输出端Q的波形。
答案：
西安工程大学
数字电子技术基础
18. 在下图电路中，若CP、S、R的电压波形如图中所示， 试画出Q的波形，假定触发器的初始状态为Q=0。
数字电子技术基础
《数字电子技术基础》习题答案
西安工程大学 房晔
西安工程大学
数字电子技术基础
第四章 组合逻辑电路
西安工程大学
数字电子技术基础 十一、某工厂有三个车间和一个自备电站，站内有两台发电机
X和Y。Y的发电能力是X的两倍。如果一个车间开工，只起动 X即可；如果两个车间同时开工，只起动Y即可；如果三个车 间同时开工，则X和Y都要起动。试设计一个控制发电机X、Y
西安工程大学
数字电子技术基础 21. 图示电路中，已知CP和输入信号T的电压波形，试画出触发
器输出端 Q 、Q 的电压波形，设触发器的起始状态为Q=0。 答案：
西安工程大学
数字电子技术基础
22. 已知上升沿触发的D触发器输入端的波形如图所示，画出 输出端Q的波形。若为下降沿触发，画出输出端Q的波形。设 初始状态为Q=0。
G(E F) G(E F)
G(E F) EF
EF G
西安工程大学
数字电子技术基础
第五章 触发器
西安工程大学
数字电子技术基础 15. 画出由与非门组成的SR锁存器输出端 Q 、Q的电压波形，
输入端 S 、R 的电压波形如图中所示。 答案：
西安工程大学
数字电子技术基础 16. 画出由或非门组成的SR锁存器输出端 Q 、Q的电压波形，
驱动方程：
J1
Q3
J2 Q1
J
3
Q2
K1 1 K2 Q1 K 3 Q2
将各触发器的驱动方程代 入特性方程，即得电路的 状态方程：
QQ12**
Q3 Q1 Q1Q2 Q1Q2
Q1
Q2
Q3* Q2 Q3 Q2Q3 Q2
西安工程大学
列状态转换表
数字电子技术基础 画状态转换图
由状态转换图可知： 该电路属同步五进制计数器，不具备自启动功能。
答案：
西安工程大学
数字电子技术基础 23. 已知 D 触发器各输入端的波形如图所示，试画出 Q 、Q
端的波形。 答案：
西安工程大学
数字电子技术基础
24. 如图所示为边沿D触发器构成的电路图，设触发器的初状态 Q1Q0=00，确定Q0 及Q1在时钟脉冲作用下的波形。
答案： 因为 D0 Q1 D1 Q0 所以 Q0* Q1 Q1* Q0
起动和停止的逻辑电路。 （1）用全加器实现。 （2）用译码器实现。 （3）用门电路实现，门电路种类不限。
答案：
用E、F、G三个变量作为输入变量分
别对应三个车间，并设车间开工为1， 不开工为0；
X、Y两个变量作为输出变量分别对
应两台发电机，并设电机启动为1，停 止为0。
根据题意可列真值表：
西安工程大学
即两个D触发器的输入信号分别为另一个D触发器的输出信
号，故在确定它们输出端波形时，应该分段交替画出其波形。
西安工程大学
数字电子技术基础
第六章 时序逻辑电路
西安工程大学
数字电子技术基础 7. 试分析下图所示时序逻辑电路的逻辑功能。
解：属同步时序电路，时钟方程省去。
输出方程：
Y XQ1 X Q1
西安工程大学
数字电子技术基础
12. 已知计数器的输出端Q2、Q1、Q 0的输出波该计数器为几进制计数器。
解：
由状态转换图可知：该电路属七进制计数器。 西安工程大学
数字电子技术基础 13. 分析图示时序电路的逻辑功能，假设电路初态为000，如