陕西省2018届高三教学质量检测

2018 年陕西省高三教学质量检测试题（三）理科综合一、选择题（本题包括13 小题。

每小题 6 分，每小题只有一个选项符合题意）1、脊髓灰质炎是由脊髓灰质炎病毒引起的急性传染病，主要症状是发热，全身不适，严重时肢体疼痛，发生瘫痰。

脊髓灰质炎病毒主要侵染脊髓中的传出神经元。

下列相关叙述正确的是（）A、通过被动运输进入细胞后，脊髓灰质炎病毒可在宿主细胞核糖体上合成蛋白质B、浆细胞在受到脊髓灰质炎病毒的直接刺激后，可产生能与该病毒特异性结合的抗体C、脊髓灰质炎患者的某些非条件反射可能消失，但通常不会出现感觉障砖D、脊髓灰质炎病毒属于寄生生物呼吸类型为无氧呼吸2、图 1 表示夏季晴朗的一天，某种绿色植物在 24 小时内 O2吸收和释放速率的变化示意图，A 、B 点对应时刻分别为 6 点和 19 点。

图 2 表示光照强度与植物光合速率的关系。

下列有关说法错误的是（）A 、图B、图C、图D、图1 中 24 小时内不进行光合作用的时段是0~5 点和 20~24 点1 的阴影部分可表示6~19 点有机物的积累量2 中限制 A~C 段光合速率的主要外界因素是光照强度2 的 C 点时，每个细胞合成ATP 的场所都有细胞质基质、线粒体、叶绿体3、甲、乙两人都表现为甲状腺激素水平低下，为找出病变的部位，现通过给两人注射适量的促状腺激素释放激素，分别测定每个人注射前30min 和注射后30min 的促甲状腺激素的浓度。

测定结果如下表。

下列推测合理的是A、甲病变的部位是下丘脑，乙病变的部位是垂体B、甲病变的部位是垂体，乙病变的部位是下丘脑C、甲病变的部位是下丘脑，乙病变的部位也是下丘脑D、甲病变的部位是垂体，乙病变的部位也是垂体4、分裂间期依次分为 G1 、S 和 G2 期，研究者将处于不同时期的细胞进行融合，实验如下图所示。

其中灰色的部分是细胞核，黑点代表中心体。

下列推测不合理的是A 、引发中心体复制的物质持续存在到G2 期B、中心体和DNA 的复制可能同时进行C、 S 期细胞中存在使G1 期细胞核进入S 期的物质D、中心体的复制始于G1 期，在 G 期复制完毕5、已知某女孩患有某种单基因遗传病，对其家系的其他成员进行调查后，记录如下：祖父祖母姑姑外祖父外祖母舅舅父亲母亲弟弟- + - + - - + + - （“＋”代表患者，“－”代表正常）下列有关分析错误的是（）A、该遗传病有可能属于常染色体显性遗传病B、调查该病的发病率应在自然人群中随机取样调查计算C、该患病女性的父母生一个正常孩子的概率为1/4D、该遗传病有可能属于细胞质遗传病6、下列有关生物的遗传、变异与进化的叙述，正确的是（）A、生物产生的变异个体都可以作为进化的原材料B、捕食者的存在客观上起到促进种群发展的作用，但不利于增加物种多样性C、地理隔离可阻止种群间的基因交流，种群基因库的差异导致种群间产生生殖隔离D、共同进化就是指生物与生物之间在相互影响中不断进化和发展29、（ 10 分）紫色洋葱是高中生物中常用的实验材料。

2018年陕西省高三教学质量检测试题（三）理科综合一、选择题（本题包括13小题。

每小题6分，每小题只有一个选项符合题意）1、脊髓灰质炎是由脊髓灰质炎病毒引起的急性传染病，主要症状是发热，全身不适，严重时肢体疼痛，发生瘫痰。

脊髓灰质炎病毒主要侵染脊髓中的传出神经元。

下列相关叙述正确的是（）A、通过被动运输进入细胞后，脊髓灰质炎病毒可在宿主细胞核糖体上合成蛋白质B、浆细胞在受到脊髓灰质炎病毒的直接刺激后，可产生能与该病毒特异性结合的抗体C、脊髓灰质炎患者的某些非条件反射可能消失，但通常不会出现感觉障砖D、脊髓灰质炎病毒属于寄生生物呼吸类型为无氧呼吸2、图1表示夏季晴朗的一天，某种绿色植物在24小时内O2吸收和释放速率的变化示意图，A、B点对应时刻分别为6点和19点。

图2表示光照强度与植物光合速率的关系。

下列有关说法错误的是（）A、图1中24小时内不进行光合作用的时段是0~5点和20~24点B、图1的阴影部分可表示6~19点有机物的积累量C、图2中限制A~C段光合速率的主要外界因素是光照强度D、图2的C点时，每个细胞合成ATP的场所都有细胞质基质、线粒体、叶绿体3、甲、乙两人都表现为甲状腺激素水平低下，为找出病变的部位，现通过给两人注射适量的促状腺激素释放激素，分别测定每个人注射前30min和注射后30min的促甲状腺激素的浓度。

测定结果如下表。

下列推测合理的是A、甲病变的部位是下丘脑，乙病变的部位是垂体B、甲病变的部位是垂体，乙病变的部位是下丘脑C、甲病变的部位是下丘脑，乙病变的部位也是下丘脑D、甲病变的部位是垂体，乙病变的部位也是垂体4、分裂间期依次分为G1、S和G2期，研究者将处于不同时期的细胞进行融合，实验如下图所示。

其中灰色的部分是细胞核，黑点代表中心体。

下列推测不合理的是A、引发中心体复制的物质持续存在到G2期B、中心体和DNA的复制可能同时进行C、S期细胞中存在使G1期细胞核进入S期的物质D、中心体的复制始于G1期，在G期复制完毕（“＋”代表患者，“－”代表正常）下列有关分析错误的是（）A、该遗传病有可能属于常染色体显性遗传病B、调查该病的发病率应在自然人群中随机取样调查计算C、该患病女性的父母生一个正常孩子的概率为1/4D、该遗传病有可能属于细胞质遗传病6、下列有关生物的遗传、变异与进化的叙述，正确的是（）A、生物产生的变异个体都可以作为进化的原材料B、捕食者的存在客观上起到促进种群发展的作用，但不利于增加物种多样性C、地理隔离可阻止种群间的基因交流，种群基因库的差异导致种群间产生生殖隔离D、共同进化就是指生物与生物之间在相互影响中不断进化和发展29、（10分）紫色洋葱是高中生物中常用的实验材料。

2018届陕西省高三教学质量检测语文试题WORD版含解析陕西省2018届高三教学质量检测语文试题第I卷阅读题一、现代文阅读(一)论述类文本阅读阅读下面的文字,完成下面小题。

近日,北京正研究试点建设全市首条封闭式的自行车高速路,连接天通苑至中关村,起到保障居住在天通苑、回龙观等地区的上班族往返上地、中关村的自行车骑行通勤需求。

与厦门的自行车高速路主要满足休闲、观光不同,线路连接的是工作区与居住区,首先要满足的是通行“刚需”。

多年来,一些城市新规划道路没有慢行系统,或配套设施不能满足公众所需,自行车道被占用等现象较为常见,骑车出行很不方便。

但随着共享单车的大量出现,自行车又重新进入公众生活,骑车出行逐渐变得普遍。

与之相对应的是,城市道路建设也日益重视慢行系統,新建道路多能确保自行丰的通行权。

“自行车高速公路”是指路面平坦宽阔、专门用于骑自行车的城区间交通线路。

这些专用通道两边虽然不是全封闭,但全程没有交叉路口,因此不设红绿灯。

该路段禁止行人行走及汽车行驶,这使得骑车人能以较快的速度在上面骑行。

自行车“高速路”对国人来说较为陌生。

当前,一些城市的管理者更多地偏向于机动车,使得城市道路没有专门的自行车道,这往往会造成交通的拥堵。

如果靠修建机动车道路去改变拥堵现状,提升出行效率,成本比自行车路要高很多。

无论是技术还是成本,自行车高速路相对来说要求都比较低,而且灵活,工程量比机动化快速路小很多。

除此之外,越来越多的人选择骑自行车出行,自行车“高速路”正好为这些人提供了方便,不仅能有效降低交通事故的发生率,还能缓解城市拥堵的压力。

但也有人对自行车高速路持谨慎态度,XXX副院长XXX 就认为,对于道路前提巳经根本构成的主体城区,就不适宜大规模建设自行车快速路。

不仅XXX,也有一些上班族心存疑虑,家住天通苑附近的XXX说,通行的很多自行车多是共享单车高速路修成之后,在早晚高峰使用时代,会不会面对调度上的难题?另外,电动自行车能不能上路?自行车“高速路”会不会成为另一个拥堵路段?有专家表示,这其中的车辆调度、安全管理、运营维护等方面都需要相关部门做好功课。

陕西省2018届高三教学质量检测（三）英语试题第—部分：听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第—节(共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有—个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下—小题。

每段对话仅读—遍。

例：How much is the shirt?A. ￡19.15.B. ￡9.18.C. ￡9.15.答案是C.1. What does the woman mean?A. She can mend the coat for the man.B. The coat is not worth mending.C. She will buy the man a new coat.2. What color are those glasses?A. Red.B. Blue.C. Brown.3. When is it suitable for the man to visit the woman?A. At 4：00 p. m. on Saturday.B. At 4：30 p. m. on Sunday.C. At 5：00 p. m. on Saturday.4. How much will the man pay for the computer if he buys one this weekend?A. 2,800 yuan.B. 2,850 yuan.C. 3,500 yuan.5. What does the man want to do?A. Check into the hotel.B. Change a room.C. Check out of the hotel第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

2018年陕西省高三教学质量检测试题（一）数学（理）第Ⅰ卷（选择题 共60分）一、选择题（本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.设集合2{|90}A x x =-<，{|}B x x N =∈，则A B 中元素的个数（ ） A ．0 B ．1 C ．2 D ．32.欧拉公式cos sin ix e x i x =+（i 为虚数单位）是由瑞士著名数学家欧拉发现的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数理论里非常重要，被誉为“数学中的天桥”，根据欧拉公式可知，2i e 表示的复数在复平面中位于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3.已知命题:p 对任意x R ∈，总有20x >；:q “1x >”是“2x >”的充分不必要条件，则下列命题为真命题的是（ ）A ．p q ∧B ．p q ⌝∧⌝C ．p q ⌝∧D ．p q ∧⌝4.已知等差数列{}n a 的前n 项和为n S ，且3512a a =，20a =.若10a >，则20S =（ ） A ．420 B ．340 C.-420 D ．-3405.设x R ∈，定义符号函数1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩，则函数()||sgn f x x x =的图像大致是（ ）A ．B ． C.D ．6.将2名教师、4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有（ ）A ．12种B ．10种 C.9种 D ．8种7.若变量,x y 满足约束条件1020y x y x y ≤⎧⎪+≥⎨⎪--≤⎩，则2z x y =-的最大值为（ ）A ．4B ．3 C.2 D ．18.已知ABC ∆与BCD ∆均为正三角形，且4AB =.若平面ABC 与平面BCD 垂直，且异面直线AB 和CD 所成角为θ，则cos θ=（ ） A． BC. 14- D ．149.运行如图所示的程序框图，设输出数据构成的集合为A ，从集合A 中任取一个元素a ，则函数a y x =，[0,)x ∈+∞是增函数的概率为（ ）A ．47 B ．45 C. 35 D ．3410.已知P 为ABC ∆所在平面内一点，0AB PB PC ++= ，||||||2AB PB PC ===，则ABC∆的面积等于（ ）A． C.D．11.过双曲线22221(0,0)x y a b a b-=>>的右焦点F 作圆222x y a +=的切线FM （切点为M ），交y 轴于点P .若M 为线段FP 的中点，则双曲线的离心率是（ ） A12.若函数2()ln f x ax x x =--存在极值，且这些极值的和不小于4ln2+，则a 的取值范围为（ ）A ．[2,)+∞B ．)+∞ C. )+∞ D ．[4,)+∞第Ⅱ卷（非选择题 共90分）二、填空题（本大题共4小题，每小题，每小题5分，共20分）13.若直线20x y c -+=是抛物线24x y =的一条切线，则c = ． 14.若函数()f x ax b =+，[4,]x a a ∈-的图像关于原点对称，则函数()a g x bx x=+，[4,1]x ∈--的值域为 ．15.在《九章算术》中，将四个面都为直角三角形的三棱锥称之为鳖臑（bie nao ）.已知在鳖臑M ABC -中，MA ⊥平面ABC ，2MA AB BC ===，则该鳖臑的外接球的表面积为 ．16.已知ABC ∆的内角,,A B C 的对边分别是,,a b c ，且222()a b c +-(cos cos )a B b A ⋅+abc =，若2a b +=，则c 的取值范围为 ．三、解答题（本大题分必考题和选择题两部分，满分70分.解答应写出文字说明、证明过程或演算过程）（一）必考题（共5小题，每小题12分，共60分）17.已知在递增等差数列{}n a 中，12a =，3a 是1a 和9a 的等比中项. （1）求数列{}n a 的通项公式； （2）若1(1)n nb n a =+，n S 为数列{}n b 的前n 项和，求100S 的值.18.如图，四棱柱1111ABCD A B C D -的底面ABCD 是菱形，AC BD O = ，1AO ⊥底面ABCD ，2AB =，13AA =.（Ⅰ）证明：平面1ACO ⊥平面11BB D D ； （Ⅱ）若60BAD ∠=︒，求二面角1B OB C --的余弦值.19.随着资本市场的强势进入，互联网共享单车“忽如一夜春风来”，遍布了一二线城市的大街小巷.为了解共享单车在A 市的使用情况，某调查机构借助网络进行了问卷调查，并从参与调查的网友中随机抽取了200人进行抽样分析，得到下表（单位：人）：（Ⅰ）根据以上数据，能否在犯错误的概率不超过0.15的前提下认为A 市使用共享单车情况与年龄有关？（Ⅱ）①现从所抽取的30岁以上的网民中，按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人，然后，再从这10人中随机选出3人赠送优惠券，求选出的3人中至少有2人经常使用共享单车的概率.②将频率视为概率，从A 市所有参与调查的网民中随机抽取10人赠送礼品，记其中经常使用共享单车的人数为X ，求X 的数学期望和方差.参考公式：22()()()()()n ad bc K a b c d a c b d -=++++，其中n a b c d =+++.参考数据：20.已知椭圆22221(0)x y a b a b+=>>的左右焦点分别为1F 和2F ，由4个点(,)M a b -，(,)N a b ，2F 和1F 的等腰梯形.（Ⅰ）求椭圆的方程；（Ⅱ）过点1F 的直线和椭圆交于两点,A B ，求2F AB ∆面积的最大值. 21.设函数()ln kf x x x=+，k R ∈. （Ⅰ）若曲线()y f x =在点(,())e f e 处的切线与直线20x -=垂直，求()f x 的单调递减区间和极小值（其中e 为自然对数的底数）；（Ⅱ）若对任何120x x >>，1212()()f x f x x x -<-恒成立，求k 的取值范围.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程在平面直角坐标系xOy 中，已知曲线C 的参数方程为cos sin x t y αα=⎧⎨=⎩，（0,t α>为参数）.以坐标原点O 为极点，x 轴的正半轴为极轴，取相同的长度单位建立极坐标系，直线l 的极坐标sin()34πθ+=.（Ⅰ）当1t =时，求曲线C 上的点到直线l 的距离的最大值； （Ⅱ）若曲线C 上的所有点都在直线l 的下方，求实数t 的取值范围. 23.选修4-5：不等式选讲 已知函数()|21||1|f x x x =-++. （Ⅰ）解不等式()3f x ≤.（Ⅱ）记函数()()|1|g x f x x =++的值域为M ，若t M ∈，证明2313t t t+≥+.试卷答案一、选择题1-5:DBDDC 6-10:ABDCB 11、12：AC二、填空题13.-4 14. 1[2,]2-- 15. 12π 16. [1,2)三、解答题17.解：（Ⅰ）由{}n a 为等差数列，设公差为d ，则1(1)n a a n d =+-. ∵3a 是1a 和9a 的等比中项，∴2319a a a =，即2(22)2(28)d d +=+，解之，得0d =（舍），或2d =. ∴1(1)2n a a n d n =+-=. （Ⅱ）11111()(1)2(1)21n n b n a n n n n ===-+++.12100n S b b b =+++=111111(1)2223100101-+-++- 1150(1)2101101=-=. 18.（Ⅰ）证明：∵1AO ⊥平面ABCD ，BD ⊂平面ABCD ，∴1AO BD ⊥. ∵ABCD 是菱形，∴CO BD ⊥.∵1AO CO O = ，∴BD ⊥平面1A CO . ∵BD ⊂平面11BB D D ，∴平面1ACO ⊥平面11BB D D . （Ⅱ）∵1AO ⊥平面ABCD ，CO BD ⊥，以O 为原点，OB ，OC ，1OA方向为,,x y z 轴正方向建立如图所示空间直角坐标系.∵2AB =，13AA =，60BAD ∠=︒，∴1OB OD ==，OA OC ==1OA = 则(1,0,0)B，C，(0,A，1A ，∴11BB AA ==，11(1OB OB BB ++=.设平面1OBB 的法向量为(,,)n x y z =， ∵(1,0,0)OB =，1(1OB =，∴0x x =⎧⎪⎨=⎪⎩.令y1)n =-.同理可求得平面1OCB的法向量为1)m =-.∴cos ,n m <>=19.解：（Ⅰ）由列联表可知，22200(70406030) 2.19813070100100K ⨯⨯-⨯=≈⨯⨯⨯.∵2.198 2.072>，∴能在犯错误的概率不超过0.15的前提下认为A 市使用共享单车情况与年龄有关. （Ⅱ）①依题意，可知所抽取的10名30岁以上网民中，经常使用共享单车的有60106100⨯=（人），偶尔或不用共享单车的有40104100⨯=（人）. 则选出的3人中至少2人经常使用共享单车的概率为21364633101023C C C P C C =+=.②由22⨯列联表，可知抽到经常使用共享单位的频率为1301320020=， 将频率视为概率，即从A 市市民中任意抽取1人，恰好抽到经常使用共享单车的市民的概率为1320. 由题意得13(10,)20X B ，∴1313()10202E X =⨯=；13791()10202040D X =⨯⨯=. 20.解：（Ⅰ）由条件，得b3a c +=.又223a c -=，解得2a =，1c =.∴椭圆的方程22143x y +=. （Ⅱ）显然，直线的斜率不能为0，设直线方程为1x my =-，直线与椭圆交于11(,)A x y ，22(,)B x y ，联立方程221431x y x my ⎧+=⎪⎨⎪=-⎩，消去x 得，22(34)690m y my +--=. ∵直线过椭圆内的点，无论m 为何值，直线和椭圆总相交. ∴122634m y y m +=+，122934y y m =-+. ∴21212121||||||2F ABS F F y y y y ∆=-=-==. 令211t m =+≥，设1()9f t t t =+，易知1(0,)3t ∈时，函数()f t 单调递减，1(,)3t ∈+∞函数单调递增，∴当211t m =+=，设0m =时，min 10()9f t =，2F AB S ∆的最大值为3. 21.解：（Ⅰ）由条件得21'()(0)kf x x x x=->， ∵曲线()y f x =在点(,())e f e 处的切线与直线20x -=垂直， ∴此切线的斜率为0，即'()0f e =，有210kex -=，得k e =. ∴221'()(0)e x ef x x x x x-=-=>，由'()0f x <得0x e <<，由'()0f x >得x e >. ∴()f x 在(0,)e 上单调递减，在(,)e +∞上单调递增.当x e =时，()f x 取得极小值()ln 2ef e e e=+=. 故()f x 的单调递减区间(0,)e ，极小值为2.（Ⅱ）条件等价于对任意120x x >>，1122()()f x x f x x -<-恒成立， 设()()ln (0)kh x f x x x x x x=-=+->， 则()h x 在(0,)+∞上单调递减.∴21'()10kh x x x=--≤在(0,)+∞上恒成立. 得2211()(0)24k x x x x ≥-+=--+>恒成立.∴14k ≥（对14k =，'()0h x =仅在12x =时成立）.故k 的取值范围是1[,)4+∞.22.解：（Ⅰ）直线l 的直角坐标方程为30x y +-=，曲线22:1C x y +=.∴曲线C 为圆，且圆心O 到直线l的距离d ==∴曲线C 上的点到直线l的距离的最大值为1+（Ⅱ）∵曲线C 上的所有点均在直线l 的下方， ∴对R α∀∈，有cos sin 30t αα+-<恒成立.)3αϕ-<（其中1tan tϕ=）恒成立.3.又0t >，∴解得0t << ∴实数t的取值范围为.23.解：（Ⅰ）依题意，得3,11()2,1213,2x x f x x x x x ⎧⎪-≤-⎪⎪=--<<⎨⎪⎪≥⎪⎩，于是得1()333x f x x ≤-⎧≤⇔⎨-≤⎩，或11223x x ⎧-<<⎪⎨⎪-≤⎩，或1233x x ⎧≥⎪⎨⎪≤⎩，解得11x -≤≤.即不等式()3f x ≤的解集为{|11}x x -≤≤.（Ⅱ）()()|1|g x f x x =++=|21||22||2122|3x x x x -++≥---=， 当且仅当(21)(22)0x x -+≤时，取等号，∴[3,)M =+∞. 原不等式等价于2331t t t-+-22233(3)(1)t t t t t t t-+--+==.∵t M ∈，∴30t -≥，210t +>.∴2(3)(1)0t t t -+≥. ∴2313t t t+≥+.。

绝密★启用前 试卷类型：A2018 年陕西省高三教学质量检测题库(二)数学(理)全卷满分 150 分，考试时间 120 分钟。

一、选择题(本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合 题目要求的)1．设集合 A ＝{x |x 2－3x ＋2≥0}，B ={x |2x ＜4}，则 A ∪B ＝()(A)∅(B){x |x ∈R}(C){x |x ≤1}(D){x |x ＞2} 2．若(1－mi )(m ＋i )＜0，其中 i 为虚数单位，则 m 的值为() (A)－1(B)－2(C)－3(D)－43．已知向量 a ＝(2，3)，b ＝(x ，4)，若 a ⊥(a －b )，则 x ＝ () (A)1 (B)12(C)2 (D)34．已知数列{a n }是等差数列，a 1 ＝2，其中公差 d ≠0，若 a 5 是 a 3 和 a 8 的等比中项，则S 18＝()(A)398(B)388(C)189(D)1995．已知函数 f (x )＝sin(ωx ＋3π)(ω＞0)的最小正周期为π，则该函数的图像() (A)关于点(12π，0)对称(B)关于点(6π，0)对称(C)关于直线 x ＝12π对称(D)关于直线 x ＝3π对称 6．某程序框图如右图所示，则该程序运行输出的 k 值是()(A)9(B)8(C)7(D)67．已知⊙C ：x 2＋y 2－4x －6y －3＝0，点 M (－2，0)是⊙C 外一点，则过点 M 的圆的切线的 方程是()(A)x ＋2＝0，7x －24y ＋14＝0(C)x ＋2＝0，7x ＋24y ＋14＝0 (B)y ＋2＝0，7x ＋24y ＋14＝0(D)y ＋2＝0，7x －24y＋14＝08．x －y ＋14≥0， ≤－3， ≥2，所确定的三角形区域内随机取一点，则该点到此三角形的三个顶点的距离均不．小．于．1 的概率是( )(A)9－2π (B)9π-(C)1－18π (D)1－9π9．已知函数 f (x )＝sin x sin(x ＋3θ)是奇函数，其中θ∈(0，2π)，则 f (x )的最大值( )(A)12 (B)(C)1 (D)10．已知三棱锥 S －ABC 中，SA ⊥平面 ABC ，且∠ACB ＝30°，AC ＝2AB ＝SA ＝1， 则该三棱锥的外接球的体积为( )(A)8 (B) 13π (C)6(D)6 11．已知 F 1、F 2 分别为双曲线2222-1x y a b = (a ＞0，b ＞0)的左、右两个焦点，点 P 是双曲线右支上一点，若 P 点的横坐标 x 0＝43a 时，F 1P ⊥F 2P ，则该双曲线的离心率 e 为( )(A) 2 (B) 32 (C)2 (D) 9212．已知函数 f (x )＝e x ＋2(x ＜0)与 g (x )＝ln(x ＋a )＋2 的图像上存在关于 y 轴对称的点，则 a 的取值范围是( )(A) 1(,)e -∞ (B) (,)e -∞ (C) 1(,)e e-(D)1(,)e e -二、填空题(本题共 4 小题，每小题 5 分，共 20 分)13．二项式－x 2)10 展开式中含 x 10 项的系数是 ． 14．设函数 f (x )＝2,3(1),3x x f x x ⎧≥⎨+⎩则函数 f (log 26)的值为 ． 15．已知函数 f (x )＝2ln x 和直线 l ：2x －y ＋6＝0，若点 P 是函数 f (x )图像上的一点，则点 P 到直线 l 的距离的最小值为 ． 16．在△ABC 中，内角 A ，B ，C 的对边分别是 a ，b ，c ，已知sin 1sin sin b Ca c A B=-++， 且 b ＝5且AC ·AB ＝5，则△ABC 的面积为．三、解答题(本大题分必考题和选考题两部分，第13 题~第21 题为必考题，每个考题考生必须作答．第22 题一第23 题为选考题，考生根据要求作答．满分70 分．解答应写出文字说明，证明过程或演算过程)(一)必考题(共5 小题，每小题12 分，共60 分)17．(本小题满分12 分)已知S n 为数列{a n}的前n 项和，且满足S n－2a n＝n－4．(1)证明{S n－n＋2}为等比数列；(2)求数列{S n}的前项n 和T n．18．(本小题满分12 分)某高中随机抽取部分高一学生调查其上学路上所需时间(单位：分钟)，并将所得数据绘制成频率分布直方图(如图)，其中上学路上所需时间的范围是[0，100]，样本数据分组为[0，20)，[20，40)，[40，60)，[60，80)，[80，100]．(1)求直方图中x 的值;(2)如果上学路上所需时间不少于1 小时的学生可申请在学校住宿，若招生1200 名，请估计新生中有多少名学生可以申请住宿；(3)从学校的高一学生中任选4 名学生，这4 名学生中上学路上所需时间少于40 分钟的人数记为X，求X 的分布列和数学期望．(以直方图中频率作为概率)19．(本小题满分 12 分)如图，在三棱柱 ABC －A 1B 1C 1 中，AA 1＝AB ，∠ABC ＝90°，侧面 A 1ABB 1⊥底面 ABC . (1)求证：AB 1⊥平面 A 1BC ；(2)若 AC ＝5，BC ＝3，∠A 1AB ＝60°，求二面角 B －A 1C －C 1 的余弦值．20．(本小题满分 12 分)已知 A (－2，0)，B (2，0)为椭圆 C 的左、右顶点，F 为其右焦点，P 是椭圆 C 上异于 A ，B 的动点，且△APB 面积的最大值为.(1)求椭圆 C 的方程;(2)直线 AP 与椭圆在点 B 处的切线交于点 D ，当点 P 在椭圆上运动时，求证：以 BD为直径的圆与直线 PF 恒相切．21．(本小题满分 12 分)设函数 f (x )＝ae x ＋x 2，g (x )＝sin x ＋bx ，直线 l 与曲线 C 1：y ＝f (x )切于点(0，f (0))且与曲线 C 2：y ＝g (x )切于点(2π，g (2π))． (1)求 a ，b 的值和直线 l 的方程；(2)证明：ae x ＋x 2－bx －sin x ＞0．(二)选考题(共 10 分．请考生在第 22、23 题中任选一题作答，如果多做，则按所做的第一 题记分．作答时请写清题号．)22．选修 4-4：坐标系与参数方程在平面直角坐标系中，直线 l x －y －0，以原点为极点，x 轴的正半 轴为极轴，建立极坐标系，曲线 C 极坐标方程为 2cos θ＝ρ(1－cos 2θ).(1)写出直线 l 的一个参数方程与曲线 C 的直角坐标方程；(2)已知直线 l 与曲线 C 交于 A ，B 两点，试求 AB 的中点 N 的坐标．23．选修 4-5：不等式选讲 已知不等式|x ＋2|－3|x |≥a . (1)当 a ＝0，解该不等式； (2)a 为何值时，该不等式成立.。

2018年陕西省高三教学质量检测试题（三）语文第Ⅰ卷（选择题共30分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷两部分。

满分150分。

考试用时150分钟。

2．答第Ⅰ卷前，请你务必在答卷纸的密封线内填写县（区）、学校、班级、姓名、考号。

3．第Ⅰ卷共10小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项符合题目要求。

每小题选出答案后，用铅笔把答卷纸上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不能答在试题卷上。

4．第Ⅱ卷共11小题，共120分。

请用0.5毫米黑色签字笔将答案写在答卷纸上。

不能直接答在试题卷上。

5．考试结束后，试题和答卷纸一并交由监考老师收回。

一、（12分，每小题3分）1．下列词语中加点的字，每对的字形书写完全正确的一组是（）A．报复．／抱负．吊．胃口／尾大不掉．鼎力．相助／再接再励．B．痉挛．／挛．生走捷．径／截．长补短言简意赅．／骇．人听闻C．宣．泄／渲．染炒鱿鱼．／竭泽而渔．蓝．天白云／筚路蓝．缕D．蛰．伏／海蜇．结伉．俪／吭．瀣一气矫．揉造作／骄．横跋扈2．下列各句中，加点的词语使用不恰当的一句是（）A．当下，网络上正对“虐猫事件”展开讨论，众口同声．．．．的现象反映了人们对现代社会道德重构的重视以及对都市人群心理健康问题的关注。

B．为配合中俄文化交流年活动，我国将在莫斯科举办汉唐文物展，俄罗斯投桃报李．．．．，以空军飞行队穿越张家界天门山的精彩表演打动了中国人民的心。

C．西安儿童医院医生收受医药回扣的行为属于商业贿赂，已触犯了我国法律不足为训．．．．，应教育广大医务工作者严格自律，遵守职业道德。

D．近日，民进党企图通过废除“国统纲领”来阻挠祖国统一，外交部发表严正声明警告陈水扁在台湾问题上的危．言危行．．．，只能搬起石头砸自己的脚。

3．下列各句中，没有语病的一句是A．去年冬季东南沿海发生咸潮灾害，许多城市为了解决用水不足的燃眉之急，只好将废水回收开展一水多用。

陕西部分重点中学2018—2018学年度高三第三次质量检测物理试题1．本试卷共8页，包含单项选择题(第1题一第6题，共6题)、多项选择题(第7题一第11题，共5题)、填空题(第12题－第13题，共2题)、计算和推导证明题(第14 题一第19题，共6题)四部分。

本次考试时间120分钟。

考试结束后，请将答题卡和答题纸一并交回。

2．答题前，请您务必将自己的姓名、考试证号等用书写黑色字迹的O．5毫米签字笔填写在答题纸及答题卡上。

3．作答非选择题必须使用书写黑色字迹的0．5毫米签字笔写在答题纸上的指定位置，作答选择题必须使用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，请用橡皮擦干净后，再选涂其它答案。

4．如有作图需要．可用2B铅笔作答．并请加黑加粗．描写清楚。

一、单项选择题：本题共6小题。

每小题3分。

共18分．每小题只有一个选项符合题意．1．下列说法中正确的是A．α射线与γ射线都是电磁波B．β射线为原子的核外电子电离后形成的电子流c．用升温、加压或改变其化学状态的方法都不能改变放射性元素的半衰期D．某原子核发生α衰变，生成的新核与放出的α粒子的质量之和一定等于原来核的质量2．如图甲所示，一矩形闭合线圈在匀强磁场中绕垂直于磁场方向的转轴00’以恒定的角速度ω转动，当线圈平面与磁场方向平行时开始计时，线圈中产生的交变电流按照图乙所示的余弦规律变化，在t=π/2ω时刻A．线圈中的电流最大B．线圈受到的安培力为零C．穿过线圈的磁通量为零D．穿过线圈磁通量的变化率最大3．根据玻尔理论，某原子从能量为E的状态跃迁到能量为E’的状态，辐射出波长为λ的光子．用h表示普朗克常量，c表示真空中的光速，则E’等于4．如图所示，在水平桌面上放置一个立方体容器，其中的S为一点光源，MN为一平面镜．点光源发出的光经平面镜反射后在天花板PM上形成一光斑，现要使这一光斑的面积变小些，下面措施中可行的是A．将点光源s向B移动一小段距离B．将点光源s向A移动一小段距离c．将点光源s向上移动一小段距离D．在容器中装进深度如虚线所示的水5．氧化锡传感器主要用于汽车尾气中一氧化碳浓度的检测，它的电阻随一氧化碳浓度的变化而变化．在如图甲所示的电路中，不同的一氧化碳浓度对应着传感器的不同电阻，这样，电压表的指针位置就与一氧化碳浓度有了对应关系，观察电压表指针就能判断一氧化碳浓度是否超标．有一种氧化锡传感器，其技术资料中给出的是电导(即电阻的倒数)一CO浓度曲线，如图乙所示．在下列表示一氧化碳浓度c与电压表示数U0之间关系的图象中正确的是6．如图所示，AB和BC是两段半径、长度及粗糙程度均相同的圆弧形路面，它们在B处相切平滑连在一起，且A、B、c在同一水平面上．一小物块以初速度v0从A端沿路面滑到C 端时的速度大小为v1；而以同样大小的初速度v0从c端沿路面滑到A端时的速度大小为v2．则二、多项选择题：本题共5小题。

2018年陕西省高三教学质量检测试题（一）数学本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，共4页。

满分150分。

考试时间120分钟。

第I 卷（选择题，共50分）注意事项：1． 在第I 卷的密封线内填写地（市）、县（区）、学校、班级、姓名、学号（或考号） 2． 答第I 卷前，请你务必将自己的姓名、准考证号、考试科目、试卷类型（A 或B ）用2B 铅笔和钢笔准确涂写在答题卡上。

3． 当你选出每小题的答案后，用2B 铅笔把答题卡上对应题目的选项标号涂黑。

如需改动，用橡皮擦干净后，再选其它选项，把答案写在试题卷上是不能得分的。

4． 考试结束后，本卷和答题卡一并交由监考老师收回。

一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．若,a R ∈(1)(3)ai i -+为纯虚数，则a 的值为A ．32-B ．32C ．23-D ．232．若集合{0,2}m M =，{,}N m n =，且M N ={2}，则M N =A ．{0,1,3}B ．{0,2,3}C ．{0,1,2}D ．{1,2,3}3．已知抛物线2:2C y x =，圆22:(2)1D x y -+=，若P 、Q 分别是曲线C 、D 上的点，则||PQ 的最小值为A ．2B1C1D4．（理）计算：22(sin 2)x dx -+⎰=（文）若锐角三角形ABC的面积为4,3BC CA ==，则C ∠的大小为5．定义在R 上的函数()f x 为奇函数(5)(),f x f x +=且(2)1f >，则A ．(3)3f <-B ．(3)3f >C ．(3)1f <-D ．(3)1f >6．在平面直角坐标系中，若不等式组101010x y x ax y +-≥⎧⎪-≤⎨⎪-+≥⎩，（a 为常数）所表示的平面区域内的面积等于2，则a 的值为A ．-5B ．1C ．2D ．37．如图，程序框图所进行的求和运算是 A ．1111...24620++++ B ．1111...3519++++C ．1111...24622++++D ．23501111 (2222)++++8．如图，一个几何体的主观图，左视图，俯视图为权等的等腰直角三角形，若该等要直角三角形的 直角边长为1，则这个几何体的表面积为A ．16B ．32C．3 D9．若点M 是ABC ∆所在平面内的一点，且满足53AM AB AC =+，则ABC ∆面积的比值为A ．15B ．25C ．35D ．4510．（理）若定义域为R 的函数log (1)()(3)(1)a x x f x a x a x >⎧=⎨--≤⎩对任意的12,,x x R ∈12x x ≠，都有1212()()f x f x x x --0>成立，则实数a 的取值范围是A ．3a <B ．1a >C ．13a <<D ．332a ≤< （文）若()f x 为偶函数，且当[0,)x ∈∞时，()1f x x =-，则不等式(1)1f x ->的解集为 A ．{|13}x x -<< B ．{|1x x <-，或3x >}C ．{|2}x x >D ．{|3}x x >第II 卷（非选择题，共100分）二、填空题（本大题共5小题，每小题5分，共25分）11．（理）在253()x x-的二项展开式中，4x 项的系数是 。

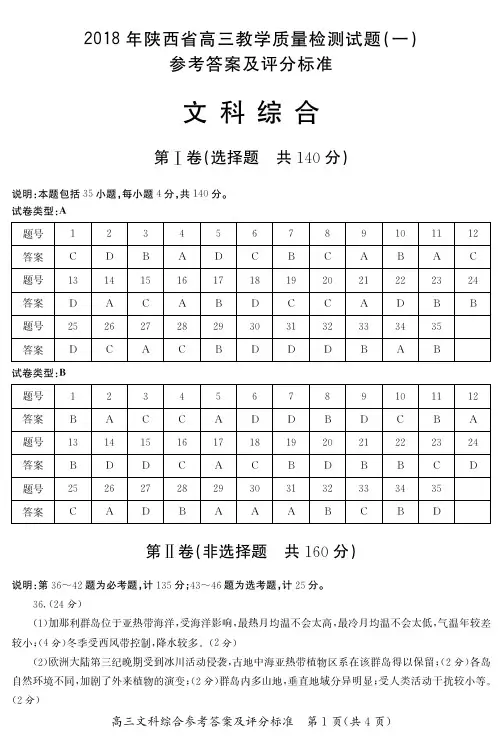
２０１８年陕西省高三教学质量检测试题（一）参考答案及评分标准文科综合第Ⅰ卷（选择题　共１４０分）说明：本题包括３５小题，每小题４分，共１４０分。

试卷类型：犃题号１２３４５６７８９１０１１１２答案ＣＤＢＡＤＣＢＣＡＢＡＣ题号１３１４１５１６１７１８１９２０２１２２２３２４答案ＤＡＣＡＢＤＣＣＡＤＢＢ题号２５２６２７２８２９３０３１３２３３３４３５答案ＤＣＡＣＢＤＤＤＢＡＢ试卷类型：犅题号１２３４５６７８９１０１１１２答案ＢＡＣＣＡＤＤＢＤＣＢＡ题号１３１４１５１６１７１８１９２０２１２２２３２４答案ＢＤＤＣＡＣＢＤＢＢＣＤ题号２５２６２７２８２９３０３１３２３３３４３５答案ＣＡＤＢＡＡＡＢＣＢＤ第Ⅱ卷（非选择题　共１６０分）说明：第３６～４２题为必考题，计１３５分；４３～４６题为选考题，计２５分。

３６．（２４分）（１）加那利群岛位于亚热带海洋，受海洋影响，最热月均温不会太高，最冷月均温不会太低，气温年较差较小；（４分）冬季受西风带控制，降水较多。

（２分）（２）欧洲大陆第三纪晚期受到冰川活动侵袭，古地中海亚热带植物区系在该群岛得以保留；（２分）各岛自然环境不同，加剧了外来植物的演变；（２分）群岛内多山地，垂直地域分异明显；受人类活动干扰较小等。

（２分）（３）可提高香蕉废料利用率；有利于节省矿物能源；可增加劳动力就业；可减少废料对环境的污染等。

（４分）（４）赞成。

（２分）加那利群岛是非洲、欧洲、美洲间来往轮船的重要燃料供应站，石油市场需求量大；在当地开发石油可以减少对进口石油的严重依赖；有利于促进当地经济的发展；有利于当地居民的就业等。

（答３点即得６分）不赞成。

（２分）加那利群岛距离非洲主要产油国近，方便进口石油；位于西亚至欧洲的石油运输线附近，便于石油的运进；沿岸有优良的港口，海运便利；当地开发石油易对环境造成破坏且不利于旅游业、渔业的发展。

（答３点即得６分）３７．（２２分）（１）位于阳坡，光照充足；（２分）位于山坡，排水条件好；（２分）海拔较高，夏季气温低，气候温和湿润。