数学建模优化问题经典练习

解 设分别购买饲料A B C D E 各i x 个单位，每单位营养成分为ij a ，单价为j c ，每天对营养成分的需要量为j b 。

⎪⎩⎪⎨⎧=≥===∑∑==5,4,3,2,1,03,2,1,..min 5151i x j b x a t s x c f ii ji ij i ii model : title ex1; sets :s1/1..5/:c,x; s2/1..3/:b; link(s1,s2):a; endsets data :c=2 7 4 3 8; b=700 30 100; a=; enddatamin =@sum (s1:c*x);@for (s2(j):@sum (s1(i):a(i,j)*x(i))>b(j));end每天购买饲料D 39.743kg,E 25.641k ，最少费用324.359元.解 设分别生产三种产品i x 个单位。

model : title ex2;max =3000*x1+2000*x2+2900*x3; 8*x1+2*x2+10*x3<300; 10*x1+5*x2+8*x3<400; 2*x1+13*x2+10*x3<420; end分别生产22.5,23.2,7.3个单位，利润最大，为135266.7元。

设备B 的单位租金为300元，高于影子价格266.67元，所以不合算。

产品Ⅰ的单位利润在（3000-1454.55,3000+333.33）上变化都不用改变生产计划。

3.队员选拔问题 某校篮球队准备从十名预备队员中选择五名作为正式队员，队员的各种情况如下表：队员号码 身高（厘米） 技术分 位置1 185 8.6 中锋2 186 9 中锋3 193 8.4 中锋 4 190 9.5 中锋5 182 9.1 前锋6 184 9 前锋7 188 8.1 前锋 8 186 7.8 后卫9 190 8.2 后卫 10 192 9.2 后卫队员的挑选要满足下面条件： （1）至少补充一名前锋。

练习1、求解下列线性规划问题。

（1）()131********max 43112.22233332436400,1,2,3,4i f x x x s tx x x x x x x x x x i =--++-=+=-+=≥= （2）()123123123max 23.2222320,1,2i f x x x x s tx x x x x x x i =---+≤-+-≤-≥=（3）()1231212312max 564.22553415100,1,2,3i f x x x x s tx x x x x x x x i =+++≤++≤+≤≥=（4）12312312312123min 33..25231612,,0x x x s t x x x x x x x x x x x -++-+≤-+≤+≤≥ （5）1212312412515max 2..506221,,0x x s t x x x x x x x x x x x +++=-++=++=≥ （6）()123412341234max 30354045..34647043658001,2,3,4i x x x x s t x x x x x x x x x i ++++++≤+++≤≥=2、建立线性规划模型，求解下列问题。

（1）某工厂生产甲、乙两种产品。

已知生产甲种产品t 1需耗A 种矿石t 10、B 种矿石t 5、煤t 4；生产乙种产品t 1需耗A 种矿石t 4、B 种矿石t 4、煤t 9。

每t 1甲种产品的利润是600元，每t 1乙种产品的利润是1000元。

工厂在生产这两种产品的计划中要求消耗A 种矿石不超过t 300、B 种矿石不超过t 200、煤不超过t 360。

甲、乙两种产品应各生产多少，能使利润总额达到最大？（2）设有A 1，A 2两个香蕉基地，产量分别为60吨和80吨，联合供应B 1，B 2，B 3三个销地的销售量经预测分别为50吨、50吨和40吨。

数学建模与优化考试试题题目一：某市的公交公司需要对公交车的发车时间进行调整，以满足市民的出行需求，并尽量减少公交车的等待时间和拥挤情况。

为了有效地解决这个问题，我们使用数学建模和优化的方法进行分析。

1. 问题描述某市公交车的运营时间为早上6点至晚上10点，每天间隔一段固定的时间发车。

公交车站点数量为M，每个站点的上下客时间为Ti。

现有数据显示，在早高峰时段（7点至9点）和晚高峰时段（17点至19点）市民出行需求较大，其他时间段市民出行需求较小。

公交公司希望尽量减少市民的等待时间和公交车的拥挤情况，提高出行效率。

因此，需要调整公交车的发车时间以适应市民的出行需求。

2. 模型建立建立一个数学模型来分析最优的公交车发车时间。

首先，我们将问题简化为一个最小化等待时间和最小化拥挤度的目标函数。

然后，通过对每个站点发车时间的调整，最大限度地优化这个目标函数。

3. 数据收集与分析为了准确建立模型，需要收集和分析以下数据：- 各个站点在早高峰时段和晚高峰时段的平均上下客时间；- 各个站点在各个时间段的客流量统计数据；- 公交车到站时间的统计数据。

4. 模型求解利用收集到的数据和已经建立的数学模型，可以通过数学优化算法求解最优的公交车发车时间。

该算法将最小化等待时间和拥挤度作为目标函数，并考虑到市民出行需求的变化。

5. 结果分析与改进根据模型求解的结果，可以进行结果分析，并对公交车发车时间进行进一步的调整和优化。

同时，还可以对模型进行改进，如引入更多的因素，如天气、节假日等。

题目二：某工厂需要优化生产线的排布和生产策略，以提高生产效率和降低成本。

为了完成这个任务，我们使用数学建模和优化的方法进行分析。

1. 问题描述该工厂的生产线包括多个工作站，每个工作站都有不同的生产能力和工作时间。

目前，生产线的排布和生产策略并不完善，导致生产效率低下和成本较高。

工厂希望通过优化生产线的排布和生产策略，提高生产效率，降低成本。

2. 模型建立建立一个数学模型来分析最优的生产线排布和生产策略。

《数学建模》课程作业题一13第五章优化模型•优化问题1、已知某工厂计划生产I, 11,111三种产品，各产品需要在A, B,C 设备上 加工，有模型得建立及求解：设生产I, 11,111产品xl, x2,x3件z 为所获得得利润。

于就是数学模型如下:利用mail a b 求解（附录一）得到最优值Z =1 3 5、2667（千元）, 生产方案如下表.生产I, I I, III 产品分别为2 3 , 23,7利润最大为125、2667千元.（2）若为了增加产量，可租用别得工厂设备B,每月可租用60台，租金1、8万 元，租用B 设备就是否划算？ 模型得建立及求解：租用别得工厂设备B 以后模型为：利用matlab 求解（附录二）得到最优值Z 二129（千元）， 生产方案如下表。

生产I, II, IH 产品分别为31, 28, 0利润最大为129千元.（3）若另有俩种新产品IV 、V,其中新产品IV 需用设备A 为12台时，B 为 5台时,C 为10台时,单位产品盈利2、1千元;新产品V 需用设备A 为4台时，B 为4台时，C 为12台时，单位产品盈利1、87千元，如A,B, C 得设备台时不 增加,这两种新产品投产在经济上就是否划算？ 模型得建立及求解：添加两个新产品IV 、V 后，IV 、V 对应得产品数分别为x4,x5,建立模型如下: 利用ma t lab 求解（附录三）得到最优值Z =136、96 2 5 （千元），生产方案如下告产I, II, III, IV, V产品分别为27, 16, 0, 0, 14利润最大为136、962 5千兀。

（4）对产品工艺重新进行设计，改进结构、改进后生产每件产品I需用设备A为9台时，设备B为12台时，设备C为4台时，单位盈利4、5千元,这时对原计划有何影响？模型得建立及求解：改进结构后，建立得模型如下：利用mat la b求解（附录四）得到最优值Z二1 53、1 618 （千元），生产方案如下表.生产I,II, III产品分别为23, 2 5, 0利润最大为153、1618千元。

即按照模式1、2、3分别切割10、10、8根原料钢管，使用 原料钢管总根数为28根。第一种切割模式下一根原料钢管 切割成3根4米钢管和1根6米钢管；第二种切割模式下一根 原料钢管切割成2根4米钢管、1根5米钢管和1根6米钢管； 第三种切割模式下一根原料钢管切割成2根8米钢管。 如果充分利用LINGO建模语言的能力，使用集合和属性 的概念，可以编写以下LINGO程序，这种方法更具有一 般的通用性，并有利于输入更大规模的下料问题的优化模 型：
优化建模
模型建立 决策变量 由于不同切割模式不能超过3种，可以用xi 表 示按照第i种模式（i=1, 2, 3）切割的原料钢管的根数， 显然它们应当是非负整数。设所使用的第i种切割模式 下每根原料钢管生产4米长、5米长、6米长和8米长的 钢管数量分别为r1i, r2i, r3i, r4i（非负整数）。 决策目标 以切割原料钢管的总根数最少为目标，即目标为
优化建模
问题1）的求解
问题分析 首先，应当确定哪些切割模式是可行的。 所谓一个切割模式，是指按照客户需要在原料钢管上 安排切割的一种组合。例如，我们可以将19米长的钢 管切割成3根4米长的钢管，余料为7米显然，可行的 切割模式是很多的。 其次，应当确定哪些切割模式是合理的。通常假设一 个合理的切割模式的余料不应该大于或等于客户需 要的钢管的最小尺寸。在这种合理性假设下，切割 模式一共有7种，如表1所示。
Reduced Cost 1.000000 1.000000 1.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
优化建模

Max z = 4.8( x11 + x21 ) + 5.6( x12 + x22 ) − (10 x1 + 8 x2 + 6 x3 )
(10)
应该注意到，只有当以 千元 千元/吨的价格购买 应该注意到，只有当以10千元 吨的价格购买 x1=500（吨）时，才能以8千元 吨的价格购买x2 （ 才能以 千元/吨的价格购买 千元 吨的价格购买 ），这个条件可以表示为 （>0），这个条件可以表示为 ），
§5.1.2建立模型 5.1.2建立模型
问题分析 安排原油采购、加工的目标是利润最大， 安排原油采购、加工的目标是利润最大，题目中给 出的是两种汽油的售价和原油A的采购价， 出的是两种汽油的售价和原油A的采购价，利润为 销售汽油的收入与购买原油A的支出之差。 销售汽油的收入与购买原油A的支出之差。这里的 难点在于原油A的采购价与购买量的关系比较复杂， 难点在于原油A的采购价与购买量的关系比较复杂， 是分段函数关系，能否及如何用线性规划、 是分段函数关系，能否及如何用线性规划、整数规 划模型加以处理是关键所在。 划模型加以处理是关键所在。
( x1 − 500) x 2 = 0
(11)
同理，只有当以8千元/ =500（ 同理，只有当以8千元/吨的价格购买x2=500（吨）时， >0）， ），于是 才能以6千元/ 才能以6千元/吨的价格购买x3（>0），于是
( x 2 − 500) x3 = 0
(12)
此外， 此外，x1，x2，x3的取值范围是
优化问题实例
• 例 某公司用两种原油（A和B）混合加工成两种汽 某公司用两种原油（ 甲和乙）。 ）。甲 乙两种汽油含原油A 油（甲和乙）。甲、乙两种汽油含原油A的最低比 例分别为50% 60%，每吨售价分别为4800 50%和 4800元和 例分别为50%和60%，每吨售价分别为4800元和 5600元 该公司现有原油A 的库存量分别为500 5600元。该公司现有原油A和B的库存量分别为500 吨和1000 1000吨 还可以从市场上买到不超过1500 1500吨 吨和1000吨，还可以从市场上买到不超过1500吨 的原油A 原油A的市场价为：购买量不超过500 500吨 的原油A。原油A的市场价为：购买量不超过500吨 时的单价为10000 10000元 购买量超过500 500吨但不超 时的单价为10000元/吨；购买量超过500吨但不超 1000吨时 超过500吨的部分8000 吨时， 500吨的部分8000元 过1000吨时，超过500吨的部分8000元/吨；购买 量超过1000吨时，超过1000吨的部分6000 1000吨时 1000吨的部分6000元 量超过1000吨时，超过1000吨的部分6000元/吨。 该公司应如何安排原油的采购和加工。 该公司应如何安排原油的采购和加工。

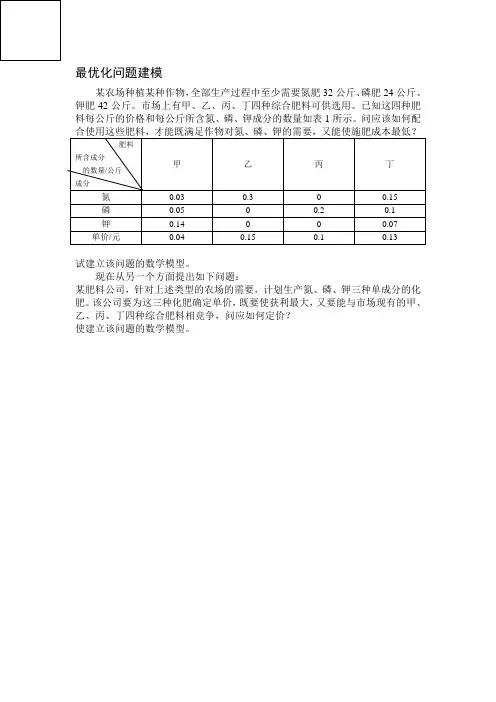
最优化问题建模
某农场种植某种作物，全部生产过程中至少需要氮肥32公斤、磷肥24公斤、钾肥42公斤。

市场上有甲、乙、丙、丁四种综合肥料可供选用。

已知这四种肥料每公斤的价格和每公斤所含氮、磷、钾成分的数量如表1所示。

问应该如何配
试建立该问题的数学模型。

现在从另一个方面提出如下问题：
某肥料公司，针对上述类型的农场的需要，计划生产氮、磷、钾三种单成分的化肥。

该公司要为这三种化肥确定单价，既要使获利最大，又要能与市场现有的甲、乙、丙、丁四种综合肥料相竞争，问应如何定价？
使建立该问题的数学模型。

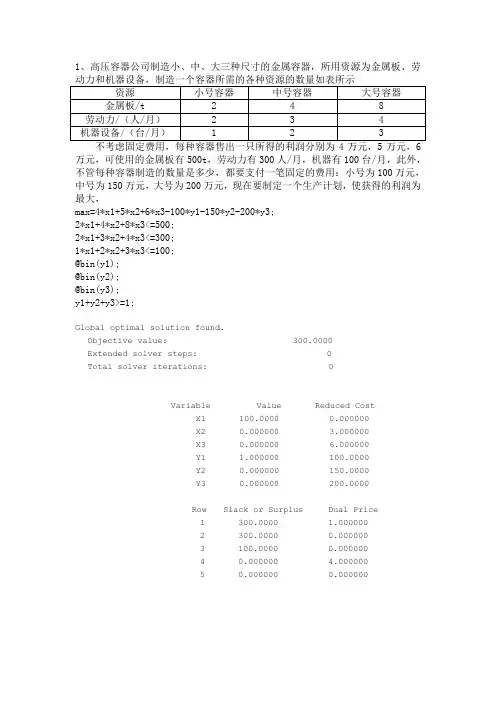
1、高压容器公司制造小、中、大三种尺寸的金属容器，所用资源为金属板、劳万元，可使用的金属板有500t，劳动力有300人/月，机器有100台/月，此外，不管每种容器制造的数量是多少，都要支付一笔固定的费用：小号为100万元，中号为150万元，大号为200万元，现在要制定一个生产计划，使获得的利润为最大，max=4*x1+5*x2+6*x3-100*y1-150*y2-200*y3;2*x1+4*x2+8*x3<=500;2*x1+3*x2+4*x3<=300;1*x1+2*x2+3*x3<=100;@bin(y1);@bin(y2);@bin(y3);y1+y2+y3>=1;Global optimal solution found.Objective value: 300.0000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX1 100.0000 0.000000X2 0.000000 3.000000X3 0.000000 6.000000Y1 1.000000 100.0000Y2 0.000000 150.0000Y3 0.000000 200.0000Row Slack or Surplus Dual Price1 300.0000 1.0000002 300.0000 0.0000003 100.0000 0.0000004 0.000000 4.0000005 0.000000 0.0000002、安排4个人去做4项不同的工作,每个工人完成各项工作所消耗的时间（单位：（2）如果在（1）中在增加一项工作E，甲、乙、丙、丁四人完成工作E的时间分别为17,20,15,16分钟，那么应指派这四人干哪四项工作，使得这四人总的消耗时间为最少？min=20*x11+19*x12+20*x13+28*x14+18*x21+24*x22+27*x23+20*x24+26*x31+16 *x32+15*x33+18*x34+17*x41+20*x42+24*x43+19*x44;x11+x12+x13+x14=1;x21+x22+x23+x24=1;x31+x32+x33+x34=1;x41+x42+x43+x44=1;x11+x21+x31+x41=1;x12+x22+x32+x42=1;x13+x23+x33+x43=1;x14+x24+x34+x44=1;@bin(x11);@bin(x12);@bin(x13);@bin(x14);@bin(x21);@bin(x22);@bin(x23);@bin(x24);@bin(x31);@bin(x32);@bin(x33);@bin(x34);@bin(x41);@bin(x42);@bin(x43);@bin(x44);Global optimal solution found.Objective value: 71.00000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX11 0.000000 20.00000X12 1.000000 19.00000X13 0.000000 20.00000X14 0.000000 28.00000X21 0.000000 18.00000X22 0.000000 24.00000X23 0.000000 27.00000X24 1.000000 20.00000X31 0.000000 26.00000X32 0.000000 16.00000X33 1.000000 15.00000X34 0.000000 18.00000X41 1.000000 17.00000X42 0.000000 20.00000X43 0.000000 24.00000X44 0.000000 19.00000Row Slack or Surplus Dual Price1 71.00000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.000000min=20*x11+19*x12+20*x13+28*x14+17*x15+18*x21+24*x22+27*x23+20*x24+20 *x25+26*x31+16*x32+15*x33+18*x34+15*x35+17*x41+20*x42+24*x43+19*x44+1 6*x45;x11+x12+x13+x14+x15=1;x21+x22+x23+x24+x25=1;x31+x32+x33+x34+x35=1;x41+x42+x43+x44+x45=1;x11+x21+x31+x41<=1;x12+x22+x32+x42<=1;x13+x23+x33+x43<=1;x14+x24+x34+x44<=1;x15+x25+x35+x45<=1;@bin(x11);@bin(x12);@bin(x13);@bin(x14);@bin(x15);@bin(x21);@bin(x22);@bin(x23);@bin(x24);@bin(x25);@bin(x31);@bin(x32);@bin(x33);@bin(x34);@bin(x35);@bin(x41);@bin(x42);@bin(x43);@bin(x44);@bin(x45);Objective value: 68.00000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced Cost X11 0.000000 20.00000 X12 1.000000 19.00000 X13 0.000000 20.00000 X14 0.000000 28.00000 X15 0.000000 17.00000 X21 1.000000 18.00000 X22 0.000000 24.00000 X23 0.000000 27.00000 X24 0.000000 20.00000 X25 0.000000 20.00000X31 0.000000 26.00000X32 0.000000 16.00000X33 1.000000 15.00000X34 0.000000 18.00000X35 0.000000 15.00000X41 0.000000 17.00000X42 0.000000 20.00000X43 0.000000 24.00000X44 0.000000 19.00000X45 1.000000 16.00000Row Slack or Surplus Dual Price1 68.00000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 1.000000 0.00000010 0.000000 0.0000003、一个公司考虑到北京、上海、广州和武汉四个城市设立库房，这些库房负责向华北、华中、华南三个地区供货，每个库房每月可处理货物1000件。

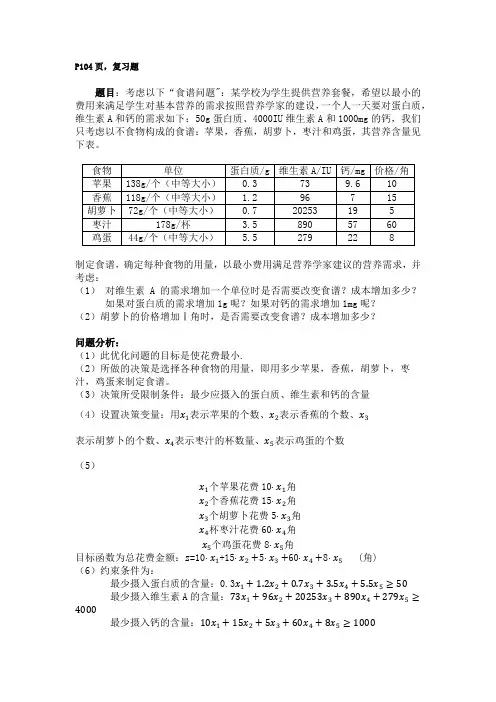
P104页，复习题题目：考虑以下“食谱问题"：某学校为学生提供营养套餐，希望以最小的费用来满足学生对基本营养的需求按照营养学家的建设，一个人一天要对蛋白质，维生素A和钙的需求如下：50g蛋白质、4000IU维生素A和1000mg的钙，我们只考虑以不食物构成的食谱：苹果，香蕉，胡萝卜，枣汁和鸡蛋，其营养含量见下表。

制定食谱，确定每种食物的用量，以最小费用满足营养学家建议的营养需求，并考虑：（1）对维生素A的需求增加一个单位时是否需要改变食谱？成本增加多少？如果对蛋白质的需求增加1g呢？如果对钙的需求增加1mg呢？（2）胡萝卜的价格增加Ⅰ角时，是否需要改变食谱？成本增加多少？问题分析：（1）此优化问题的目标是使花费最小.（2）所做的决策是选择各种食物的用量，即用多少苹果，香蕉，胡萝卜，枣汁，鸡蛋来制定食谱。

（3）决策所受限制条件：最少应摄入的蛋白质、维生素和钙的含量（4）设置决策变量：用x1表示苹果的个数、x2表示香蕉的个数、x3表示胡萝卜的个数、x4表示枣汁的杯数量、x5表示鸡蛋的个数（5）x1个苹果花费10·x1角x2个香蕉花费15·x2角x3个胡萝卜花费5·x3角x4杯枣汁花费60·x4角x5个鸡蛋花费8·x5角目标函数为总花费金额：z=10·x1+15·x2+5·x3+60·x4+8·x5 (角)（6）约束条件为：最少摄入蛋白质的含量：0.3x1+1.2x2+0.7x3+3.5x4+5.5x5≥50最少摄入维生素A的含量：73x1+96x2+20253x3+890x4+279x5≥4000最少摄入钙的含量：10x1+15x2+5x3+60x4+8x5≥1000非负约束：x 1,x 2,x 3,x 4,x 5≥0优化模型：minz =10x 1+15x 2+5x 3+60x 4+8x 5s.t. 0.3x 1+1.2x 2+0.7x 3+3.5x 4+5.5x 5≥5073x 1+96x 2+20253x 3+890x 4+279x 5≥4000 9.6x 1+7x 2+19x 3+57x 4+22x 5≥1000 x 1,x 2,x 3,x 4,x 5≥0由线性规划模型的定义，容易得到线性规划的性质：1. 比例性 每个决策变量的对目标函数的“贡献”与该决策变量的取值成正比；每个决策变量对每个约束条件右端项的“贡献”，与该决策变量的取值成正比.2. 可加性 各个决策变量对目标函数的“贡献”，与其他决策变量的取值无关；各个决策变量对每个约束条件右端项的“贡献”，与其他决策变量的取值无关.3. 连续性 每个决策变量的取值是连续的. 考察本题，实际上隐含下面的假设 ：1.购买苹果、香蕉、胡萝卜、枣汁、鸡蛋每个（杯）的花费是与各自的用量无关的常数；苹果、香蕉、胡萝卜、枣汁、鸡蛋每个（杯）所包含的蛋白质、维生素、钙的含量是与各自的用量无关的常数.（线性规划性质1—比例性）2.购买苹果、香蕉、胡萝卜、枣汁、鸡蛋每个（杯）的花费是与它们相互间用量无关的常数；苹果、香蕉、胡萝卜、枣汁、鸡蛋每个（杯）所包含的蛋白质、维生素A 、钙的含量是与它们相互间的用量无关的常数. （线性规划性质2—可加性）3. 购买苹果、香蕉、胡萝卜、枣汁、鸡蛋的数量都是实数. (线性规划性质3—连续性) 模型求解：（决策变量是5维的，不适用图解法求解模型）软件求解：线性规划模型：min z=10x1+15x2+5x3+60x4+8x5s.t. 0.3x1+1.2x2+0.7x3+3.5x4+5.5x5≥5073x1+96x2+20253x3+890x4+279x5≥40009.6x1+7x2+19x3+57x4+22x5≥1000x1,x2,x3,x4,x5≥0模型全局最优解：(Global optimal solution)x1=0x2=0x3=49.38272x4=0x5=2.805836z的最优值为269.3603角用LINGO 软件求解，得到如下输出：结果分析：1. 3个约束条件的右端项可视为3种资源：蛋白质含量、维生素A 含量、钙含量.LINGO 的输出项Row Slack or Surplus ，给出了3种资源在最优解下的剩余.2.目标函数可视为“支出（成本）”，紧约束的“资源”增加1单位时，“支出”的增加由LINGO 的输出项 Dual Price 给出。

路、公路运输，铺设一条
火车站 公路 管道
450 里程（km)
A1
钢管管道 A1 A2 A15 （沿管道建有公路）
优化建模
钢厂的产量和销价（1单位钢管=1km管道钢管）
钢厂i
1
2
3
4
产量上限 si 销价 pi （万元）
800 800 160 155
1000 155
2000 160
钢厂产量的下限：500单位钢管 1单位钢管的铁路运价
, tani

D yi0 xi0
or
i

3
2
, tani

yi0 xi0
,
,
yi0
v sin i
, if

i

3
2
, tani

yi0 xi0
or 3
2
i
2 , tani

yi0 D xi0
整理： 其中：
fij (t) zij 2 bij zij cij .
290 30 S7
S2
1200
S3
690 720
S4
690
170 520
160 130 88
A18
160
320 A20
100 70 30
70 260
A21
S6
A19
110
190
62
20 20
A15
500
1100
202
S1
A16
42
20
12
A17
462
70 10
S5 10
220
420

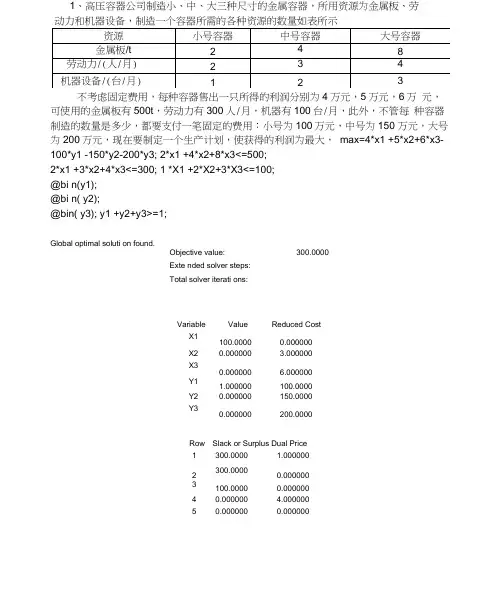
1、高压容器公司制造小、中、大三种尺寸的金属容器，所用资源为金属板、劳 动力和机器设备，制造一个容器所需的各种资源的数量如表所示不考虑固定费用，每种容器售出一只所得的利润分别为4万元，5万元，6万 元，可使用的金属板有500t ，劳动力有300人/月，机器有100台/月，此外，不管每 种容器制造的数量是多少，都要支付一笔固定的费用：小号为100万元，中号为150 万元，大号为200万元，现在要制定一个生产计划，使获得的利润为最大， max=4*x1 +5*x2+6*x3-100*y1 -150*y2-200*y3; 2*x1 +4*x2+8*x3<=500; 2*x1 +3*x2+4*x3<=300; 1 *X1 +2*X2+3*X3<=100; @bi n(y1); @bi n( y2);@bin( y3); y1 +y2+y3>=1; Global optimal soluti on found.Objective value: Exte nded solver steps: Total solver iterati ons:Variable Value Reduced Cost X1 100.0000 0.000000 X2 0.000000 3.000000 X3 0.000000 6.000000 Y1 1.000000 100.0000 Y2 0.000000 150.0000 Y30.000000200.0000Row 1 Slack or Surplus Dual Price 300.0000 1.000000 2 300.0000 0.000000 3 100.0000 0.000000 4 0.000000 4.000000 50.0000000.000000300.00002、安排4个人去做4项不同的工作，每个工人完成各项工作所消耗的时间(单位：分钟)如表：(2) 如果在(1)中在增加一项工作E,甲、乙、丙、丁四人完成工作E的时间分别为17,20,15,16分钟，那么应指派这四人干哪四项工作，使得这四人总的消耗时间为最少？min =20*x11 + 19*x12+20*x13+28*x14+18*x21 +24*x22+27*x23+20*x24+26*x31 +16*x32+15*x33+18*x34+17*x41 +20*x42+24*x43+19*x44;x11+x12+x13+x14=1;x21+x22+x23+x24=1;x31+x32+x33+x34=1;x41+x42+x43+x44=1;x11+x21+x31+x41=1;x12+x22+x32+x42=1;x13+x23+x33+x43=1;x14+x24+x34+x44=1;@bin (x11);@bin (x12);@bin (x13);@bin (x14);@bin (x21);@bin (x22);@bin (x23);@bin (x24);@bin (x31);@bin (x32);@bin (x33);@bin (x34);@bin (x41);@bin (x42);@bin (x43); @bin (x44);Global optimal solution found. Objective value: 71.00000Extended solver steps 0 Total solver iterations:Variable Value Reduced Cost X11 0.000000 20.00000 X12 1.000000 19.00000 X13 0.000000 20.00000 X14 0.000000 28.00000 X21 0.000000 18.00000 X22 0.000000 24.00000 X23 0.000000 27.00000 X24 1.000000 20.00000 X31 0.000000 26.00000 X32 0.000000 16.00000 X33 1.000000 15.00000 X34 0.000000 18.00000 X41 1.000000 17.00000 X42 0.000000 20.00000 X430.000000 24.00000 X440.00000019.00000Row Slack or Surplus Dual Price 1 71.00000 2 0.000000 3 0.000000 4 0.000000 5 0.000000 6 0.000000 7 0.000000 8 0.000000 90.000000min =20*x11 +19*x12+20*x13+28*x14+17*x15+18*x21 +24*x22+27*x23+20*x24+20 *x25+26*x31 +16*x32+15*x33+18*x34+15*x35+17*x41 +20*x42+24*x43+19*x44+1 6*x45; x11+x12+x13+x14+x15=1; x21+x22+x23+x24+x25=1; x31+x32+x33+x34+x35=1;-1.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000x41+x42+x43+x44+x45=1;x11 +x21 +x31 +x41 <=1;x12+x22+x32+x42<=1;x13+x23+x33+x43v=1;x14+x24+x34+x44<=1;x15+x25+x35+x45<=1;@bin (x11);@bin (x12);@bin (x13);@bin (x14);@bin (x15);@bin (x21);@bin (x22);@bin (x23);@bin (x24);@bin (x25);@bin (x31);@bin (x32);@bin (x33);@bin (x34);@bin (x35);@bin (x41);@bin (x42);@bin (x43);@bin (x44);@bin (x45);Objective value: 68.00000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX11 0.000000 20.00000X12 1.000000 19.00000X13 0.000000 20.00000X14 0.000000 28.00000X15 0.000000 17.00000X21 1.000000 18.00000X22 0.000000 24.00000X23 0.000000 27.00000X24 0.000000 20.00000X25 0.000000 20.00000X31 0.000000 26.00000X320.000000 16.00000X33 1.000000 15.00000X340.000000 18.00000X35 0.000000 15.00000X41 0.000000 17.00000X42 0.000000 20.00000X43 0.000000 24.00000X44 0.000000 19.00000X451.000000 16.00000DualRow Slack or Surplus Prii1 68.00000 -1.0000002 0.000000 0.0000003 0.000000 0.00000040.000000 0.00000050.000000 0.0000006 0.000000 0.00000070.000000 0.0000008 0.000000 0.0000009 1.000000 0.00000010 0.000000 0.0000003、一个公司考虑到北京、上海、广州和武汉四个城市设立库房，这些库房负责向华北、华中、华南三个地区供货，每个库房每月可处理货物1000件。

数学建模动态优化模型例题例题：动态投资组合优化假设有一个投资者，在每年初都需要重新配置其投资组合。

该投资者面临两个主要问题：首先，选择在哪些资产上进行投资；其次，在每个资产上分配多少资金。

假设该投资者有n个不同的资产可供选择，每个资产的预期收益率和风险不同。

此外，该投资者还有一个总共可投资的资金总额B。

为了最大化预期收益并控制风险，投资者希望找到一个最优的投资组合。

假设每年初的投资组合决策可以视为一个动态优化问题。

投资者可以在每个年初选择不同的投资组合来适应市场的变化。

投资者需要考虑以下因素：1. 资产的预期收益率和风险。

2. 投资组合的总收益率和风险。

3. 投资组合在不同时间点的波动。

数学建模：1. 定义变量：- x(i, t): 在第t年开始时投资于第i个资产的金额。

- r(i): 第i个资产的预期年收益率。

- σ(i): 第i个资产的年波动率。

- R(t): 第t年的总投资组合收益率。

- Σ(t): 第t年的总投资组合波动率。

2. 约束条件：- ∑(i=1 to n) x(i, t) = B，总投资金额等于可投资的资金总额。

3. 目标函数：- max ∑(t=1 to T) R(t)，总收益最大化。

4. 模型建立：- 目标函数为最大化投资组合的总收益。

- 约束条件为总投资金额等于可投资的资金总额。

- 根据预期收益率和波动率，计算每一年投资组合的收益率和波动率。

- 使用动态规划等方法，通过逐年调整投资组合来找到最优解。

以上是一个简化的动态投资组合优化模型。

在实际应用中，还需要考虑更多的因素，例如纳税规则、市场交易成本等。

此外，还需要根据实际情况进行数据收集、参数估计和模型求解。

(1) s.t
(2-1)
(2-2)
(2-3)
(2-4)
(3)
(4) 以上目标函数（1）是对包括生产费和库存费在内的总费用求最 小，约束（2-1）、（2-2）、（2-3）、（2-4）描述了需求、产量和库 存之间的关系（通常称为物流平衡条件），（3）表示的是生产能力限 制，（4）是非负限制。 将以上模型输入matlab求解，可以得到最优解如下：
，
，
，并且合理地设
（为什么？）。简单地假设每个型号的成本与本型号的产量服从负指数 关系，且有渐进值，即
，
，
。于是总利润为
问题化为求解
。 设定如下一组数据：
，
，输入MatLab求解，得到结果为：甲的产量为23.9025，乙的产量为
62.4977，最大利润为6413.5。
查看程序代码
function y=fun(x)
由于在投资时购买股票的数量必须是整数（手），我们简单将上述 结果取整（上整数或下整数）。例如： x1=132，x2=15，x3=22。该投资 人应投资股票1、2、3的数量分别为 13200、1500和2200(股)。所用去 的资金为13200′20+1500′25+2200′30 = 367500（元），期望利润为 13200′5+1500′8+2200′10 = 100000 （元），此时的风险（方差） 为 68116 (均方差约为261（百元）)。 2. 投资回报与风险之间的关系图：
B2=d;
x0=[zeros(1,12) 5 1 2 7]; % 取料场位置的初值
v1=zeros(1,16);
v2=[d',d',[10,10,10,10]];
opt=optimset('LargeScale','off','MaxFunEvals',1000,'MaxIter',100);

数学建模优化类问题例子
1.最佳生产计划：有一家汽车零部件制造公司，需要决定该如何安排生产计划以最大化利润。

该公司需要考虑每个零部件的生产成本、供应链的延迟和运输成本等因素，以确定最佳的生产数量和交付时间。

2.最优投资组合：一位投资者有一定资金，希望通过合理的资产配置来最大化投资回报。

该投资者需要考虑不同资产类别的风险和回报率，并使用数学建模优化方法来确定最佳的资产配置比例。

3.旅行销售员问题：一位旅行销售员需要在多个城市之间进行访问，并希望以最小的总行驶距离完成所有访问任务。

通过使用数学建模和优化算法，销售员可以确定最佳的访问顺序，从而减少总行驶距离和时间。

4.最佳路径规划：在一个迷宫中，有一只小老鼠需要找到从起点到终点的最短路径。

通过将迷宫与数学模型相关联，可以使用图论和最短路径算法来确定小老鼠应该采取的最佳行动策略。

以上只是一些例子中的几个，实际上数学建模和优化方法可以应用于各种不同的问题领域，包括金融、物流、能源管理、医疗决策等。

通过数学建模和优化，可以帮助人们做出更明智的决策，提高效率和效果。

数学建模竞赛用到优化的赛题摘要：一、数学建模竞赛简介1.数学建模竞赛的概念2.数学建模竞赛的意义和价值3.数学建模竞赛的分类二、优化问题的概述1.优化问题的定义2.优化问题的分类3.优化问题的应用领域三、数学建模竞赛中的优化赛题1.历届数学建模竞赛中的优化赛题举例2.优化赛题的解题思路和方法3.优化赛题的挑战和难点四、优化方法在数学建模竞赛中的应用1.优化方法的选择和运用2.优化方法在数学建模竞赛中的实际案例3.优化方法对竞赛结果的影响和意义五、数学建模竞赛中优化赛题的启示1.对优化问题的深入理解2.提高优化方法的应用能力3.团队合作和沟通的重要性正文：数学建模竞赛是面向全球范围内的高校大学生的一项重要赛事，旨在通过对现实世界中的问题进行抽象、建模和求解，培养学生的创新意识、团队协作精神和实际问题解决能力。

其中，优化问题是一类非常重要的赛题，涉及到众多领域的核心问题。

本文将围绕数学建模竞赛中的优化赛题展开讨论，分析优化问题在数学建模竞赛中的地位和作用，探讨优化方法在数学建模竞赛中的应用和挑战。

首先，我们需要了解什么是优化问题。

优化问题是指在给定一定约束条件下，寻找一个目标函数的最优解或次优解的问题。

它具有广泛的应用价值，涉及到诸如经济学、工程、管理、生物学等诸多领域。

根据优化问题的具体性质和特点，可以将其分为线性规划、非线性规划、动态规划、随机规划等多种类型。

在数学建模竞赛中，优化问题是一类具有挑战性的赛题。

以历届数学建模竞赛为例，我们可以发现许多涉及优化问题的赛题，如在“网络优化”、“生产调度”、“供应链管理”等题目中，都需要运用优化方法来求解。

解这类问题通常需要具备扎实的数学基础、丰富的建模经验和灵活的思维方式。

通过对优化问题的深入理解，能够找到问题的本质特征，从而选择合适的优化方法进行求解。

优化方法在数学建模竞赛中的应用具有重要意义。

在竞赛过程中，优化方法的选择和运用直接影响到建模成果的质量和水平。

第五节生活中的优化问题举例(数学建模二)A组基础题组1.已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=-x3+81x-234,则使该生产厂家获得最大年利润的年产量为()A.13万件B.11万件C.9万件D.7万件答案C由题意得,y'=-x2+81,令y'=0,解得x=9或x=-9(舍去).当0<x<9时,y'>0;当x>9时,y'<0.故当x=9时,y取最大值.2.(2019孝感模拟)某品牌小汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/时)的函数解析式为y=x3-x+18(0<x≤120).要使该汽车行驶200千米时的油耗最低,则汽车匀速行驶的速度应为()A.60千米/时B.80千米/时C.90千米/时D.100千米/时答案C当速度为x千米/小时时,该汽车行驶200千米时行驶了小时,设耗油量为h(x)升,y=x3-x+18(0<x≤120).依题意得h(x)=-·=x2+-20(0<x≤120),h'(x)=x-=-(0<x≤120).令h'(x)=0,得x=90.当x∈(0,90)时,h'(x)<0,h(x)是减函数;当x∈(90,120]时,h'(x)>0,h(x)是增函数.所以当x=90时,h(x)取得极小值h(90)=18.因为h(x)在(0,120]上只有一个极值,所以当x=90时取得最小值.故选C.3.设底面为正三角形的直棱柱的体积为V,那么其表面积最小时,底面正三角形的边长为()A. B. C. D.2答案C设底面正三角形的边长为x,侧棱长为l,则V=x2·sin60°·l,∴l=,∴S表=2S底+S侧=x2sin60°+3xl=x2+.令S'表=x-=0,得x=,又当x∈(0,)时,S'表<0;x∈(,+∞)时,S'表>0,∴当x=时,表面积最小.4.在半径为r的半圆内作一内接梯形,使其下底为直径,其他三边为圆的弦,则梯形的面积最大时,梯形的上底长为()A. B.r C.r D.r答案D设梯形的上底长为2x,高为h,面积为S,∵h=-,∴S=-=(r+x)·-.∴S'=---=-=-.令S'=0,得x=(x=-r舍去),∴h=r.当x∈时,S'>0;当x∈时,S'<0,∴当x=时,S取最大值,即当梯形的上底长为r 时,它的面积最大.5.某厂生产某种产品x件的总成本c(x)=1200+x3(万元),已知产品单价的平方与产品件数x 成反比,生产100件这样的产品单价为50万元,则产量定为件时,总利润最大.答案25解析设产品的单价为p万元,根据已知,可设p2=,其中k为比例系数.因为当x=100时,p=50,所以k=250000,所以p2=,p=(x>0).设总利润为y万元,则y=·x-1200-x3=500-x3-1200.y'=-x2.令y'=0,得x=25.当0<x<25时,y'>0;当x>25时,y'<0.因此当x=25时,函数y取得极大值,也是最大值.6.要做一个圆锥形的漏斗,其母线长为20cm,要使其体积最大,则高为cm.答案解析设该漏斗的高为x cm,则其底面半径为-cm,体积V=π(202-x2)x=π(400x-x3)(0<x<20),则V'=π(400-3x2).令V'=0,解得x1=,x2=-(舍去).当0<x<时,V'>0;当<x<20时,V'<0,所以当x=时,V取得最大值.7.统计表明,某种型号的汽车在匀速行驶过程中的耗油量y(L/h)关于行驶速度x(km/h)的解析式可以表示为y=x3-x+8(0<x≤120).已知甲、乙两地相距100km.(1)当汽车以40km/h的速度匀速行驶时,从甲地到乙地要耗油多少升?(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少?解析(1)汽车以40km/h的速度从甲地匀速行驶到乙地需=2.5(h),要耗油-×2.5=17.5(L).(2)当匀速行驶速度为x km/h时,汽车从甲地行驶到乙地需h,设耗油量为h L,依题意得h(x)=-=-+(0<x≤120),则h'(x)=-=-(0<x≤120).令h'(x)=0,得x=80.当x∈(0,80)时,h'(x)<0,h(x)是减函数;当x∈(80,120]时,h'(x)>0,h(x)是增函数.所以当x=80时,h(x)取得极小值h(80)=11.25.因为h(x)在(0,120]上只有一个极小值,所以它也是最小值.所以当汽车以80km/h的速度匀速行驶时,从甲地到乙地耗油最少,为11.25L.8.某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h 米,体积为V立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).(1)将V表示成r的函数V(r),并求该函数的定义域;(2)讨论函数V(r)的单调性,并确定r和h为何值时,该蓄水池的体积最大.解析(1)因为蓄水池侧面的总成本为100·2πrh=200πrh元,底面的总成本为160πr2元,所以蓄水池的总成本为(200πrh+160πr2)元.又据题意知200πrh+160πr2=12000π,所以h=(300-4r2),从而V(r)=πr2h=(300r-4r3).又由r>0,h>0可得r<5,故函数V(r)的定义域为(0,5).(2)因V(r)=(300r-4r3),故V'(r)=(300-12r2).令V'(r)=0,解得r1=5,r2=-5(舍去).当r∈(0,5)时,V'(r)>0,故V(r)在(0,5)上为增函数;当r∈(5,5)时,V'(r)<0,故V(r)在(5,5)上为减函数.由此可知,V(r)在r=5处取得最大值,此时h=8.即当r=5,h=8时,该蓄水池的体积最大.B组提升题组1.某商店经销一种奥运纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务部门上交a(a为常数,4≤a≤5)元的税收,设每件产品的日售价为x(35≤x≤41)元,根据市场调查,日销售量与e x(e为自然对数的底数)成反比.已知每件产品的日售价为40元时,日销量为10件.(1)求该商店的日利润L(x)元与每件产品的日售价x元的函数关系式;(2)当每件产品的日售价为多少元时,该商品的日利润L(x)最大?并求出L(x)的最大值.解析(1)设日销售量为,则=10,所以k=10e40,则日销售量为件.则日利润L(x)=(x-30-a)=--(35≤x≤41).(2)由(1)可得L'(x)=-,因为4≤a≤5,所以35≤a+31≤36.令L'(x)=0,得x=a+31,故L(x)在[35,a+31]上为增函数,在(a+31,41]上为减函数.所以当x=a+31时,L(x)取得最大值,最大值为10e9-a.2.某种商品的成本为5元/件,开始按8元/件销售,销售量为50件,为了获得最大利润,商家先后采取了提价与降价两种措施进行试销.经试销发现:销售单价每上涨1元,每天的销售量就减少10件,而降价后,日销售量Q(单位:件)与实际销售单价x(单位:元)满足关系:Q(x)=---(1)试写出该商家的销售利润y与销售单价x的函数关系式;(利润=销售额-成本)(2)当实际销售单价为多少元时,日销售利润最大?并求出最大利润.解析(1)根据题意得y=--------=-----(2)由(1)得当5<x<7时,y=39(2x3-39x2+252x-535),y'=39(6x2-78x+252),令y'=0,则6x2-78x+252=0,解得x=6或x=7(舍去).当5<x<6时,y'>0;当6<x<7时,y'<0,故当x=6时,y max=195.当7≤x<8时,y=6(33-x),故当x=7时,y max=156.当8≤x≤13时,y=-10x2+180x-650=-10(x-9)2+160,故当x=9时,y max=160.综上可知,当实际销售单价定为6元时,日销售利润最大,最大利润为195元.3.如图,点C为某沿海城市的高速公路出入口,直线BD为海岸线,∠CAB=,AB⊥BD,是以A 为圆心,半径为1km的圆弧形小路.该市拟修建一条从C通往海岸的观光专线-PQ,其中P 为上异于B,C的一点,PQ与AB平行,设∠PAB=θ.(1)证明:观光专线-PQ的总长度随θ的增大而减小;(2)已知新建道路PQ的单位成本是翻新道路的单位成本的2倍,当θ取何值时,观光专线-PQ的修建总成本最低?请说明理由.解析(1)证明:由题意,∠CAP=-θ,所以=-θ.又PQ=AB-APcosθ=1-cosθ,所以观光专线的总长度f(θ)=-θ+1-cosθ=-θ-cosθ++1,0<θ<.因为当0<θ<时,f'(θ)=-1+sin θ<0,所以f(θ)在上单调递减,即观光专线-PQ的总长度随θ的增大而减小.(2)设翻新道路的单位成本为a(a>0),则总成本g(θ)=a--=a(-θ-2cosθ++2),0<θ<,g'(θ)=a(-1+2sinθ),令g'(θ)=0,得sinθ=,因为0<θ<,所以θ=.当0<θ<时,g'(θ)<0;当<θ<时,g'(θ)>0.所以,当θ=时,g(θ)最小,即当θ=时,观光专线-PQ的修建总成本最低.。

习题六1、某工厂生产四种不同型号的产品，而每件产品的生产要经过三个车间进行加工，根据该厂现有的设备和劳动力等生产条件，可以确定各车间每日的生产能力（折合成有效工时来表示）。

现将各车间每日可利用的有效工时数，每个产品在各车间加工所花费的工时数及每件产品可获得利润列成下表：试确定四种型号的产品每日生产件数,,,,4321x x x x 使工厂获利润最大。

2、在车辆拥挤的交叉路口，需要合理地调节各车道安置的红绿灯时间，使车辆能顺利、有效地通过。

在下图所示的十字路口共有6条车道，其中d c b a ,,,是4条直行道，f e ,是两条左转弯道，每条车道都设有红绿灯。

按要求制定这6组红绿灯的调节方案。

首先应使各车道的车辆互不冲突地顺利驶过路口，其次希望方案的效能尽量地高。

即各车道总的绿灯时间最长，使尽可能多的车辆通过。

da bc提示：将一分钟时间间隔划分为4321,,,d d d d 共4个时段，()()()f J b J a J ,,, 为相应车道的绿灯时间。

()d J3、某两个煤厂A 和B 每月进煤量分别为60吨和100吨，联合供应三个居民区C 、D 、E 。

这三个居民区每月对煤的需求量依次分别是50吨、70吨、40吨。

煤厂A 与三个居民区C 、D 、E 的距离分别为10公里、5公里和6公里。

煤厂B 与三个居民区C 、D 、E 的距离分别为4公里、8公里和12公里。

问如何分配供煤量可使运输总量达到最小？4、某工厂制造甲、乙两种产品，每种产品消耗煤、电、工作日及获利润如下表所示。

现有煤360吨，电力200KW.h ，工作日300个。

请制定一个使总利润最大的生产计划。

5、棉纺厂的主要原料是棉花，一般要占总成本的70%左右。

所谓配棉问题，就是要根据棉纱的质量指标，采用各种价格不同的棉花，按一定的比例配制成纱，使其既达到质量指标，又使总成本最低。

棉纱的质量指标一般由棉结和品质指标来决定。

这两项指标都可用数量形式来表示。