一年级-等量代换

一年级等量代换在数学的世界里，有一个非常重要的概念叫做等量代换。

这是我们在学习加法和减法之后，进一步理解数学的基础之一。

这个概念对于我们理解更复杂的数学概念，如代数和几何，也是至关重要的。

等量代换是指用一种量来代替与其相等的另一种量。

例如，我们可以说10个苹果等于5个橙子。

在这个例子中，我们用10个苹果的重量来代替5个橙子的重量。

这就是等量代换。

在一年级的数学课程中，我们通常会学习如何使用等量代换。

我们会用数字来代替量，比如用10来代替10个苹果，用5来代替5个橙子。

然后我们可以通过简单的算术运算来找出两种量之间的关系。

例如，如果我们有10个苹果和5个橙子，我们可以通过等量代换来找出1个橙子等于多少个苹果。

如果我们设1个橙子等于x个苹果，那么我们可以建立如下方程：10 = 5x，解这个方程可以得到x=2。

所以，1个橙子等于2个苹果。

通过这样的学习，我们可以更好地理解数量的概念，掌握基本的算术运算，提高我们的数学素养。

我们也可以了解到数学在现实生活中的应用，比如在购物和做交易时如何进行数量的比较和转换。

等量代换是数学学习中一个非常基础但非常重要的概念。

通过学习等量代换，我们可以更好地理解数学的基础知识，为以后的学习打下坚实的基础。

在人生中，有些看似复杂的难题，其实可以用简单的等量代换来解答。

今天，我想和大家分享一个我在一年级时学到的重要概念——等量代换。

在一年级的数学课上，我们开始学习用数字来描述世界。

老师让我们认识数字，学习加减法，这都很有趣。

但最让我印象深刻的，是老师给我们讲的一个故事。

老师告诉我们，有一个古老的村庄，村子里的人们非常善良。

每当有外来人来到村子里，村民们都会给他们一些食物。

但这个村子的食物非常特别，它叫做“公平食”。

每份公平食都是用两个苹果和三个橘子做成的。

有一天，一个外来人来到了村子里，他非常饿。

村民们给了他一份公平食。

这个人吃了一半的公平食，发现自己已经饱了。

他看着剩下的食物，想把它们带走。

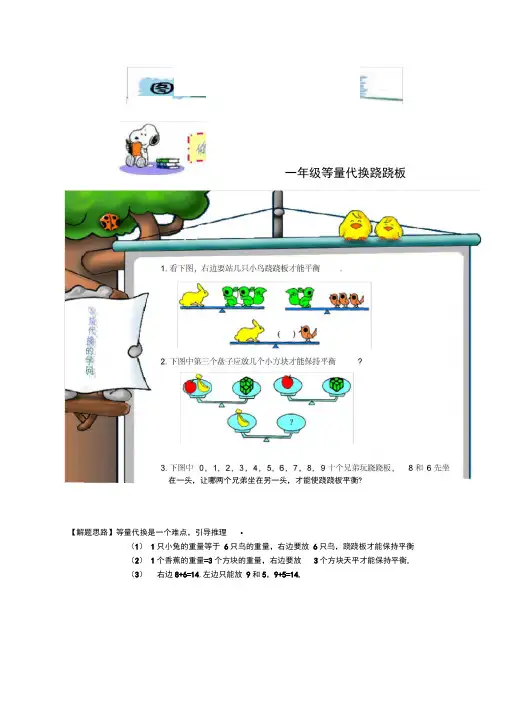
【解题思路】等量代换是一个难点，引导推理 •
（1） 1只小兔的重量等于 6只鸟的重量，右边要放 6只鸟，跷跷板才能保持平衡
（2） 1个香蕉的重量=3个方块的重量，右边要放
3个方块天平才能保持平衡. （3） 右边8+6=14,左边只能放 9和5，9+5=14.
一年级等量代换跷跷板
在一头，让哪两个兄弟坐在另一头，才能使跷跷板平衡?
£
有一天，小狗老师要在动物学校挑选队员参加数学竞赛，小松鼠很高兴也
跑来了•小狗老师说：“那我就来考考你！你把下面的题做对了就可以参加了
小松鼠看了半天说：“老师，你写的这是什么？”小狗老师说：“哈哈！看
心―———
哈哈！水果兄弟们也组成了各种不同的图文算式，它们各代表一个数，你能猜出它们各代表几吗?
20 ! 0=5 0 …
e 十€ - 6=15+10
8
=
H A +
F面的符号各代表一个数，相同的符号代表相同的数，它们各代表几呢?
F面这些由美丽花朵组成的算式，你能猜岀这些花朵都表示什么数吗
?
! - 矽+ ◎匸■
[△*△ + △｝桃| 竇=14,
1* + ^iA + A=is f
[A = ( ) - ★=()；'V/ R
I；6p
根F面的算式，你知
道冃、、Ml各代表数字几?
F面的符号各表示几?。

《等量代换》知识清单一、什么是等量代换等量代换是数学中一种基本的思想方法，指的是用一种量（或一种量的一部分）来代替和它相等的另一种量（或另一种量的一部分）。

简单来说，就是两个相等的量可以互相替换。

例如，如果我们知道 1 个苹果的重量等于 2 个橘子的重量，而现在有 3 个苹果，那么就相当于有 6 个橘子。

这里就是用橘子的数量替换了苹果的数量，因为它们之间存在着等量关系。

二、等量代换的重要性等量代换在数学学习和日常生活中都具有极其重要的作用。

在数学学习中，它是解决很多数学问题的关键方法。

比如在代数运算中，通过等量代换可以将复杂的式子简化，从而更方便地进行计算和求解。

在几何图形中，也经常会用到等量代换的思想来证明一些定理和求解图形的面积、周长等问题。

在日常生活中，等量代换的思想也无处不在。

比如在购物时，我们会根据商品的价格和数量进行等量代换，计算出总花费；在比较不同物品的价值时，也会通过等量代换来做出更明智的选择。

三、等量代换的应用场景1、货币兑换当我们出国旅游或者进行国际贸易时，需要进行货币兑换。

例如，1 美元可以兑换 65 元人民币，如果我们有 50 美元，那么就可以通过等量代换计算出相当于 325 元人民币。

2、物品交换假设你有 3 本书，而你的朋友有 5 支笔，并且你们约定 1 本书可以换 2 支笔。

那么通过等量代换，你可以算出 3 本书可以换 6 支笔，而朋友的 5 支笔相当于 25 本书。

3、面积计算在计算不规则图形的面积时，我们常常会将其分割成几个规则的图形，然后通过等量代换，将不规则图形的面积转化为规则图形面积的组合。

4、重量衡量比如在市场上，知道 1 斤猪肉的价格和 1 斤牛肉的价格，当我们要比较买一定量的猪肉和牛肉哪个更划算时，就会用到等量代换。

四、等量代换的解题步骤1、找出等量关系这是等量代换的关键步骤。

需要仔细观察题目中给出的条件，找出两个或多个量之间的相等关系。

2、表示等量关系可以用等式、图表或者文字描述等方式，将找出的等量关系清晰地表示出来。

《等量代换》知识清单一、什么是等量代换等量代换是数学中一种基本的思想方法，它指的是用一种量（或一种量的一部分）来代替和它相等的另一种量（或另一种量的一部分）。

简单来说，如果两个量是相等的，那么在一定的条件下，它们可以相互替换。

例如，我们知道 1 个苹果的重量等于 2 个橘子的重量，如果有 3 个苹果，那么就相当于 6 个橘子。

这里就是用橘子的重量代替了苹果的重量，这就是等量代换。

二、等量代换的重要性1、解决数学问题等量代换在解决数学问题中经常用到。

比如在计算图形的面积或体积时，如果已知某些部分的等量关系，就可以通过代换来简化计算。

2、培养逻辑思维通过等量代换的练习，可以帮助我们锻炼逻辑推理能力，让我们更加清晰地理解事物之间的关系，从而更有条理地思考问题。

3、为后续学习打下基础等量代换是代数学习的重要前置知识，为以后学习方程、函数等内容做好铺垫。

三、等量代换的常见类型1、重量等量代换就像前面提到的苹果和橘子的例子，在比较不同物体的重量时，经常会用到等量代换。

2、长度等量代换比如，已知 1 米的绳子等于 3 尺，那么 5 米的绳子就等于 15 尺。

3、面积等量代换在计算几何图形的面积时，如果两个图形的面积相等，就可以相互代换进行计算。

4、货币等量代换不同国家的货币之间存在汇率，通过汇率进行货币的等量代换。

四、等量代换的应用实例1、简单算术题例如：已知 1 只鸡加 1 只鸭等于 10 斤，1 只鸡等于 3 斤，那么 1 只鸭是多少斤？我们可以用等量代换的思想，因为 1 只鸡加 1 只鸭等于 10 斤，而 1 只鸡等于 3 斤，所以 1 只鸭的重量就是 10 3 ＝ 7 斤。

2、几何图形问题在一个三角形中，如果已知其中一条边的长度是另一条边的两倍，而另一条边的长度又已知，就可以通过等量代换来求出第一条边的长度。

3、实际生活中的问题比如在购物时，如果知道 1 瓶饮料的价格等于 2 包薯片的价格，而薯片的价格已知，就可以算出饮料的价格。

一年级数学等量代换训练题题目 1已知 1 个苹果 = 2 个橘子，1 个橘子 = 3 颗草莓，那么 1 个苹果 = （）颗草莓解析：因为 1 个橘子 = 3 颗草莓，1 个苹果 = 2 个橘子，所以 1 个苹果 = 2×3 = 6 颗草莓。

题目 21 只兔子的重量等于2 只小鸡的重量，1 只小鸡的重量等于3 只小鸭的重量，1 只兔子的重量等于（）只小鸭的重量解析：因为 1 只小鸡的重量等于 3 只小鸭的重量，1 只兔子的重量等于 2 只小鸡的重量，所以 1 只兔子的重量 = 2×3 = 6 只小鸭的重量。

题目 31 个菠萝 = 3 个苹果，1 个苹果 =2 个香蕉，1 个菠萝 = （）个香蕉解析：因为 1 个苹果 = 2 个香蕉，1 个菠萝 = 3 个苹果，所以 1 个菠萝 = 3×2 = 6 个香蕉。

题目 41 只大象的重量等于 4 只熊的重量，1 只熊的重量等于 3 只猴子的重量，1 只大象的重量等于（）只猴子的重量解析：因为 1 只熊的重量等于 3 只猴子的重量，1 只大象的重量等于 4 只熊的重量，所以 1 只大象的重量 = 4×3 = 12 只猴子的重量。

题目 51 辆汽车的价格 =2 辆摩托车的价格，1 辆摩托车的价格 =3 辆自行车的价格，1 辆汽车的价格 = （）辆自行车的价格解析：因为 1 辆摩托车的价格 = 3 辆自行车的价格，1 辆汽车的价格 = 2 辆摩托车的价格，所以 1 辆汽车的价格 = 2×3 = 6 辆自行车的价格。

题目 61 个西瓜 = 4 个哈密瓜，1 个哈密瓜 =2 个桃子，1 个西瓜 = （）个桃子解析：因为 1 个哈密瓜 = 2 个桃子，1 个西瓜 = 4 个哈密瓜，所以 1 个西瓜 = 4×2 = 8 个桃子。

题目 71 只老虎的体重 = 3 只狮子的体重，1 只狮子的体重 =2 只羊的体重，1 只老虎的体重 = （）只羊的体重解析：因为 1 只狮子的体重 = 2 只羊的体重，1 只老虎的体重 = 3 只狮子的体重，所以 1 只老虎的体重 = 3×2 = 6 只羊的体重。

一年级数学上册重难点之《等量代换》，分类，方法，技巧
昨天，一位一年级的家长让我给她找几个数学题目，孩子平常考试，其余的题目都达成得
很好，计算能力也不错，这周还去参加计算竞赛。

可是呢，有个题总是弄不好，以下列图：
这是一个等量代换的题目，一年级的奥数里面也有这样的题型。

同时，这个题还会出此刻试卷后边的较难的题中，属于需要动脑筋的题。

关于一年级的孩子来说，这个数学题目需要必定的理解力。

由于波及到推理能力！
等量代换的重点是推理：
4 个苹果，这个时候，就知道1 个桃子等于 4 个苹果，那么右侧的式子中，就把桃子换成
右侧是 6 个苹果啦。

因此答案是 6.
这题属于形象化的，仍是比较好理解的。

比如：
练习 1：
练习题
来了（ 4 道）：。

等量代换一年级教学设计引言：等量代换是一种重要的数学概念，在数学学科中起着至关重要的作用。

等量代换是指通过替换在一个等式中的变量，以便使等式保持成立。

了解等量代换的概念对学生们的数学能力发展至关重要。

在本文中，将设计一节适用于一年级学生的等量代换教学课程，以帮助他们理解和应用这一概念。

一、教学目标：1. 学生能够理解等量代换的概念。

2. 学生能够应用等量代换解决简单的数学问题。

3. 学生能够分辨出等量代换在数学题中的应用场景。

二、教学准备：1. 打印有关等量代换的数学例题和练习题。

2. 准备幻灯片或白板，用于演示和解释等量代换的概念。

3. 准备设计好的教学课件和学生练习册。

三、教学过程：1. 引入概念：使用幻灯片或白板演示等量代换的概念，并与学生一起讨论，解释等量代换在数学中的重要性。

解释等量代换的定义，以及如何通过替换变量来保持等式的平衡。

2. 示例演示：在幻灯片或白板上给出一个简单的等式，例如：3 + x = 7，然后引导学生通过等量代换的方式解决该等式。

让学生逐步思考如何通过替换变量来找到等式的解。

3. 合作学习：将学生分成小组，每个小组分发一份练习册。

在练习册中，给出一些涉及等量代换的简单数学问题。

要求学生在小组内合作，并使用等量代换的方法解决问题。

教师应给予足够的时间和机会供学生互相讨论和分享解决方法。

4. 分享和讨论：每个小组在完成练习后，教师引导学生们向全班分享他们的解决方法。

其他学生可以提出问题或建议，促进学生之间的互动和思维碰撞。

5. 拓展练习：在小组合作的基础上，教师提供一些更具挑战性的问题，让学生通过等量代换解决。

这些问题可以是实际生活中的数学问题，从而鼓励学生将所学的数学概念应用到实际情境中。

6. 结束：教师总结今天的教学内容，并鼓励学生对等量代换的理解和应用做个总结。

提问学生们他们是如何理解等量代换的，以及他们如何将其应用到解决实际问题中。

四、教学评价：1. 观察学生在课堂上的参与程度和合作学习的活跃度。

一年级数学上册重难点之等量代换
《等量代换》；分类；方法；技巧昨天；一位一年级的家长让我给她找几个数学题目；孩子平时考试；其它的题目都完成得很好；计算能力也不错；这周还去参加计算比赛。

但是呢；有个题老是弄不好；如下图：
这是一个等量代换的题目；一年级的奥数里面也有这样的题型。

同时；这个题还会出现在试卷后面的较难的题中；属于需要动脑筋的题。

对于一年级的孩子来说；这个数学题目需要一定的理解力。

因为涉及到推理能力！等量代换的关键是推理：
1个桃子等于4个苹果；那么右边的式子中；就把桃子换成4个苹果；这个时候；就知道右边是6个苹果啦。

所以答案是6.
这题属于形象化的；还是比较好理解的。

例如：
练习1：
练习题来了（4道）：。

《等量代换》知识清单一、什么是等量代换等量代换是数学中一种基本的思想方法，指的是用一种量（或一种量的一部分）来代替和它相等的另一种量（或另一种量的一部分）。

简单来说，就是在等式中，如果两个量相等，那么可以用其中一个量去替换另一个量。

例如，如果我们知道 2 个苹果的重量等于 1 个西瓜的重量，那么当需要计算 4 个苹果的重量时，就可以通过等量代换，得出 4 个苹果的重量等于 2 个西瓜的重量。

等量代换的核心在于找到两个相等的量，并明确它们之间的替换关系。

二、等量代换的应用场景1、解决数学运算问题在加减法运算中，等量代换可以帮助我们简化计算。

比如，已知 A ＋ B ＝ 10，B ＝ 3，那么我们可以通过等量代换，将 B 的值代入第一个式子，得出 A ＋ 3 ＝ 10，从而计算出 A ＝ 7。

在乘法运算中，也经常用到等量代换。

例如，若 3×C ＝ 18，那么通过等量代换，可以得出 C ＝ 6。

2、几何图形中的应用在几何图形中，等量代换常用于求图形的面积、周长等。

比如，两个三角形等底等高，那么它们的面积相等。

如果已知一个三角形的面积和相关条件，就可以通过等量代换求出另一个与之等底等高三角形的面积。

3、实际生活中的运用在购物时，如果知道不同商品之间的价格等价关系，就可以通过等量代换来比较不同组合商品的价值。

在工程测量中，当无法直接测量某个长度或距离时，可以通过与已知长度或距离建立等量关系，从而间接得出所需测量的值。

三、等量代换的原则1、相等性原则进行等量代换的两个量必须是相等的，这是最基本的前提。

2、可替换性原则等量的量必须是在相同的条件和环境下可以相互替换的。

3、等量传递原则如果 A ＝ B，B ＝ C，那么 A ＝ C。

通过这种传递关系，可以进行多次等量代换。

四、等量代换的步骤1、观察与分析首先要仔细观察题目中给出的条件和关系，确定哪些量是相等的，以及它们之间的联系。

2、确定替换量根据观察和分析的结果，明确要进行替换的量。