下载文档原格式
教学设计：2024秋季人教版高中物理必修第二册第八章机械能守恒定律《动能和动能定理》教学目标（核心素养）1.物理观念：理解动能的定义及其表达式，掌握动能与速度的关系，能够运用动能概念描述物体的运动状态。
2.科学思维：通过实例分析，理解动能定理的物理意义，能够运用动能定理分析解决简单的物理问题，培养逻辑推理和批判性思维能力。
3.科学探究：通过实验或模拟实验，观察动能变化与外力做功的关系，体验科学探究的过程，培养观察、记录、分析数据的能力。
4.科学态度与责任：激发学生对物理学的兴趣，培养严谨的科学态度和实事求是的科学精神，认识动能定理在日常生活和工程技术中的应用价值。
教学重点•动能的定义、表达式及物理意义。
•动能定理的表述、理解及应用。
教学难点•动能定理中功与动能变化关系的理解。
•运用动能定理解决复杂物理问题的能力培养。
教学资源•多媒体课件（含动画演示动能变化、动能定理应用实例）。
•实验器材（如斜面、小车、弹簧、打点计时器等，用于演示动能定理实验）。
•教材、教辅资料及网络资源。
教学方法•讲授法：通过教师讲解，明确动能和动能定理的基本概念。
•演示法：利用实验或多媒体演示，直观展示动能变化与外力做功的关系。
•讨论法：组织学生讨论动能定理的应用实例，促进思维碰撞。
•探究法：引导学生设计实验方案，探究动能定理的适用性。
教学过程导入新课•情境导入：播放一段运动员冲刺的视频，提问：“为什么运动员跑得越快，越难停下来？”引导学生思考速度与质量对物体运动状态的影响，引出动能的概念。
新课教学1.动能的概念•定义：物体由于运动而具有的能量称为动能。
•表达式：Ek=21mv2，解释各符号含义。
•讨论：动能与速度、质量的关系，通过举例加深理解。
2.动能定理的引入•通过分析实例（如滑块沿斜面下滑），引导学生思考外力做功与动能变化的关系。
•引出动能定理：外力对物体做的总功等于物体动能的变化量。
•表达式：W=ΔEk=21mv22−21mv12。
听课记录：2024秋季人教版高中物理必修第二册第八章机械能守恒定律《动能和动能定理》一、教学目标（核心素养）•物理观念：使学生理解动能的概念，掌握动能表达式，并能应用动能公式进行简单计算。
•科学思维：通过推导动能定理的过程，培养学生的逻辑推理能力和问题解决能力。
•科学探究：引导学生通过实验观察或理论探讨，探索动能变化与外力做功之间的关系。
•科学态度与责任：激发学生对物理学的兴趣，培养严谨的科学态度和实事求是的精神。
二、导入•教师行为：教师首先展示一段视频，内容为不同质量的物体从同一高度自由落体，落地时产生的不同效果（如沙坑凹陷程度不同）。
提问：“为什么不同质量的物体落地效果不同？这背后隐藏着什么物理规律？”•学生活动：学生观看视频，积极思考教师提出的问题，讨论并尝试提出初步假设。
•过程点评：通过直观的视频引入，激发学生的好奇心和求知欲，为后续学习动能和动能定理做铺垫。
三、教学过程3.1 动能概念的引入•教师行为：结合视频中的现象，引导学生分析物体运动状态与能量变化的关系，引出动能的概念，并解释动能是描述物体运动状态的物理量。
•学生活动：学生跟随教师思路，理解动能定义，尝试用自己的话解释动能的意义。
•过程点评：通过逐步引导，使学生从具体现象中抽象出物理概念，加深对动能的理解。
3.2 动能表达式的推导•教师行为：利用牛顿第二定律和匀变速直线运动公式，逐步推导出动能表达式（Ek=21mv2），过程中强调物理公式的推导逻辑。
•学生活动：学生跟随教师推导过程，记录关键步骤，尝试自行推导动能表达式。
•过程点评：通过推导过程，不仅让学生掌握动能公式，更重要的是培养学生的逻辑推理能力。
3.3 动能定理的讲解与应用•教师行为：介绍动能定理，即外力对物体做的功等于物体动能的变化量（W=ΔEk ），并通过实例讲解如何应用动能定理解决问题。
•学生活动：学生认真听讲，理解动能定理的含义，通过例题练习巩固所学知识，尝试独立解决问题。
第7节动能和动能定理一、动能1．大小：E k ＝12mv 2。
2．单位：国际单位制单位为焦耳，1 J ＝1N·m＝1 kg·m 2/s 2。
3．标矢性：动能是标量，只有大小，没有方向，只有正值，没有负值。
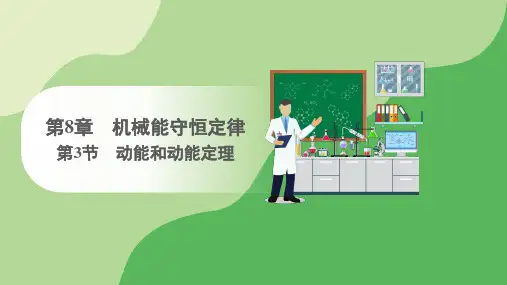
二、 动能定理1．推导：如图所示，物体的质量为m ，在与运动方向相同的恒力F 的作用下发生了一段位移l ，速度由v 1增加到v 2，此过程力F 做的功为W 。
1．物体由于运动而具有的能量叫做动能，表达式为E k ＝12mv 2。
动能是标量，具有相对性。
2．力在一个过程中对物体做的功，等于物体在这个过 程中动能的变化，这个结论叫动能定理，表达式为 W ＝E k2－E k1。
3．如果物体同时受到几个力的共同作用，则W 为合力 做的功，它等于各个力做功的代数和。
4．动能定理既适用于恒力做功，也适用于变力做功， 既适用于直线运动，也适用于曲线运动。
2．内容：力在一个过程中对物体做的功，等于物体在这个过程中动能的变化。
3．表达式：W＝E k2－E k1。
4．适用范围：既适用于恒力做功也适用于变力做功；既适用于直线运动也适用于曲线运动。
1．自主思考——判一判(1)速度大的物体动能也大。
(×)(2)某物体的速度加倍，它的动能也加倍。
(×)(3)合外力做功不等于零，物体的动能一定变化。
(√)(4)物体的速度发生变化，合外力做功一定不等于零。
(×)(5)物体的动能增加，合外力做正功。
(√)2．合作探究——议一议(1)歼15战机是我国自主研发的第一款舰载战斗机，如图所示：①歼15战机起飞时，合力做什么功？速度怎么变化？动能怎么变化？②歼15战机着舰时，动能怎么变化？合力做什么功？增加阻拦索的原因是什么？提示：①歼15战机起飞时，合力做正功，速度、动能都不断增大。
②歼15战机着舰时，动能减小，合力做负功。
高中物理必修二动能和动能定理
【知识整合】
1、动能：物体由于_____________而具有的能量叫动能。
⑴动能的大小：_________________
⑵动能是标量。
⑶动能是状态量，也是相对量。
2、动能定理：
⑴动能定理的内容和表达式：____________________________________________
⑵物理意义：动能定理指出了______________________和_____________________的关系，即外力做的总功，对应着物体动能的变化，变化的大小由________________来度量。
我们所说的外力，既可以是重力、弹力、摩擦力，又可以是电场力、磁场力或其他力。
物体动能的变化是指_____________________________________________。
⑶动能定理的适用条件：动能定理既适用于直线运动，也适用于________________。
既适用于恒力做功，也适用于______________________。
力可以是各种性质的力，既可以同时做用，也可以____________________，只要求出在作用过程中各力做功的多少和正负即可，这些正是动能定理解题的优越性所在。
【重难点阐释】
1、应用动能定理解题的基本步骤：
⑴选取研究对象，明确它的运动过程。
⑵分析研究对象的受力情况和各力做功的情况：受哪些力？每个力是否做功？做正功还是负功？做多少功？然后求各力做功的代数和。
⑶明确物体在过程的始末状态的动能E k1和E k2
⑷列出动能定理的方程W合＝E k2-E k1及其它必要的解题方程，进行求解。
2、动能定理的理解和应用要点：
（1）动能定理的计算式为W合＝E k2-E k1，v和s是想对于同一参考系的。
（2）动能定理的研究对象是单一物体，或者可以看做单一物体的物体系。
（3）动能定理不仅可以求恒力做功，也可以求变力做功。
在某些问题中由于力F的大小发生变化或方向发生变化，中学阶段不能直接利用功的公式W=FS来求功，，此时我们利用动能定理来求变力做功。
（4）动能定理不仅可以解决直线运动问题，也可以解决曲线运动问题，而牛顿运动定律和运动学公式在中学阶段一般来说只能解决直线运动问题（圆周和平抛有自己独立的方法）。
（5）在利用动能定理解题时，如果物体在某个运动过程中包含有几个运动性质不同的分过程（如加速和减速的过程），此时可以分段考虑，也可整体考虑。
如能对整个过程列动能定理表达式，则可能使问题简化。
在把各个力代入公式：W1﹢W2﹢……﹢Ｗｎ＝E k2-E k1时，要把它们的数值连同符号代入，解题时要分清各过程各力做功的情况。
【典型例题】
另一端施加大小为F1的拉力作用，在水平面上
做半径为R1的匀速圆周运动今将力的大小改变
为F 2，使小球仍在水平面上做匀速圆周运动，
但半径变为R 2，小球运动的半径由R 1变为R 2过程中拉力对小球做的功。
例题2：物体从高出地面H 米处由静止开始
自由落下，不考虑空气阻力，落至地面进入沙
坑h 米停止，求物体在沙坑中受到的平均阻 力是其重力的多少倍？
例题3：如图所示，物体从倾斜角为θ的斜面上
由A 点从静止滑下，最后停在水平面上的C 点，
物体与斜面和地面间的动摩擦因数都是μ，并且 物体在滑经斜面与水平面的连接点B 时无机械能
损失，试求物体在斜面上滑动的距离s 1和在地面
上滑行的距离s 2的比值。
例题4：如图所示：在光滑的水平面上有一平板小车M 正以速度v 向右运动，现将一质量为m 的木块无初速度的放在小车上。
由于木块和小车之间的摩擦力作用，小车的速度将会发生变化，为使小车保持原来的运动速度不变，必须及时对小车施加一个向右的水平力F ，当F 作用一段时间后，小车与木块刚好相对静止时，把它撤开，木块与小车的动摩擦因数为μ，求在上述过程中，水平恒力F
【课堂练习】
1、汽车在平直公路上行驶，在它的速度从零增至v 的过程中，汽车发动机做的功为W 1，在它的速度从v 增大至2v 的过程中，汽车所做的功为W 2，设汽车在行驶过程中发动机的牵引力和所受阻力不变，则有（ ）
A.W 2=2W 1
B. W 2=3W 1
C. W 2=4W 1
D.仅能判断W 2＞W 1
2、如图所示，一块长木版B 放在光滑的水平面上，在B 上放一物体A ，现以恒定的外力拉B ，由于A 、B 间摩擦力的作用，A 将在B
在此过程中（
） A 、外力F 做的功等于A 和B 动能的增量 B 、B 对A 的摩擦力所做的功，等于A 的动能的增量
C 、A 对B 的摩擦力所做的功，等于B 对A 的摩擦力所做的功
D 、外力F 对B 做的功等于B 的动能的增量与B 克服摩擦力所做的功之和
3、试在下列简化情况下，从牛顿定律出发，导出动能定理的表达式：物体为质点，作用力是恒力，运动轨迹为直线。
要求写出每个符号及所得结果中每项的意义。
4、如图所示，一弹簧振子，物块的质量为 m ，它与水平桌面间的动摩擦因数为 μ。
起初，用手按住物块，物块的速度为零，弹簧的伸长量为x 。
然后放手，当弹簧的长度回到原长时，物块的速度为v 。
试用动能定理求此过程中弹力所做的功。
5、跳高运动员从地面起跳后上升到一定的高度，越过横杆后落下，为了避免对运动员的伤害，在运动员落下的地方设置一片沙坑。
某运动员质量为60.0kg ，身高为1.84m 。
运动员从距地高度为1.90m 的横杆上落下，设运动员开始下落的初速度为零。
他的身体直立落地，双脚在沙坑里陷下去的深度为10cm ，落地过程重心下落的高度为1.25m 。
忽略他下落过程受到的空气阻力。
（重力加速度g 取10m/ ）。
求
（1）运动员在接触沙坑表面时的速度大小；
（2）沙坑对运动员平均阻力的大小。
6、额定功率80kW 的无轨电车，最大速度是72km/h ，质量是2×103 kg 。
如果汽车从静止开
始作匀加速直线运动，加速度大小为２ｍ／ｓ２，阻力大小一定，则电车匀加速运动行使能
维持多长时间？又知电车从静止驶出到增至最大速度共经历了21s ，在此过程中，电车通过的位移是多少？
7、竖直固定在桌面上的轻质弹簧，原长为L0，质量为 m的小球从弹簧上端正上方H 处自由落下，碰到弹簧后，使弹簧发生的最大缩短量为△Ｌ，求小球具有最大速度时离桌面的高度（弹簧劲度系数为 k），以及此后弹簧可能具有的最大弹性势能。
８、质量为M的机车，牵引质量为m 的车箱在水平轨道上匀速前进，某时刻车箱与机车脱节，机车前进了 L后，司机才发现，便立即关闭发动机让机车滑行。
假定机车与车厢所受阻力与其重力成正比且恒定。
试求车厢与机车都停止时两者的距离。
参考答案
例一：
解析：此题中，绳的拉力作为小球圆周运动的向心力，是变力，求变力做功应使用动能定理，设半径为R1和R2时小球的圆周运动的线速度大小分别为v1和v2，由向心力公式得
F1＝mv12/R1……①
F2＝mv22/R2……②
由动能定理得：
W＝mv22/2－mv12/2……③
由①②③得：W＝（F2R2－F1R1）/2
例二：
解法一：由牛顿定律和运动学公式求解
解法二：利用动能定理，将物体运动分为两个物理过程，先自由落体后匀减速运动，设物体落至地面时速度为v,则由动能定理可得：
mgH=mv2/2
第二个过程中物体受重力和阻力，同理可得：
mgh－fh=0－mv2/2
解得：f/mg＝(H+h)/h
解法三：视全过程为一整体，由于物体的初末动能均为零，
由动能定理得：mg(H+h)-fh=0
解得：f/mg＝(H+h)/h
例三：
解法一：
由牛顿第二定律和运动学公式求解。
解法二：应用动能定理：取物体在A、C两点为始末状态mgsinθ·s1-μmgcosθ·s1-μmgs2=0
解得:s1/s2=μ/(sinθ-μcosθ)
例四：
解析：本题中的m和M是通过摩擦相互联系的。
由于S车＝vt,S木＝vt=vt/2
所以S车/ S木=2/1
根据动能定理，对木块有：
μmg S木＝mv2/2-0
对于车有：W F-μmg S车＝Mv2/2- Mv2/2=0
将上述式子联立可得：W＝mv2
课堂练习：
１、Ｂ２、Ｂ、Ｄ３、略
４、μｍｇｘ＋ｍｖ２／２
５、５ｍ／ｓ８１００Ｎ
６、５ｓ２７０ｍ
７、Ｌ０－ｍｇ／Ｋｍｇ（Ｈ＋△Ｌ）
８、（Ｍ＋ｍ）Ｌ／Ｍ。
