中考数学压轴题抛物线及动点精选

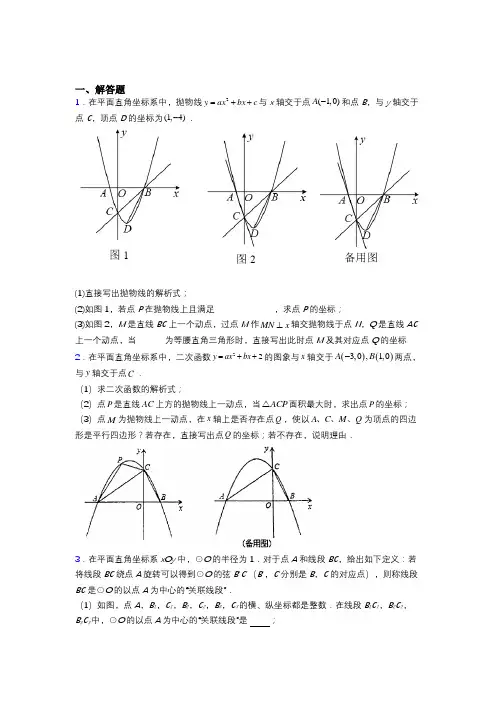
一、解答题1．在平面直角坐标系中，抛物线2y ax bx c =++与x 轴交于点(1,0)A -和点B ，与y 轴交于点C ，顶点D 的坐标为(1,4)-．(1)直接写出抛物线的解析式；(2)如图1，若点P 在抛物线上且满足，求点P 的坐标； (3)如图2，M 是直线BC 上一个动点，过点M 作MN x ⊥轴交抛物线于点N ，Q 是直线AC 上一个动点，当为等腰直角三角形时，直接写出此时点M 及其对应点Q 的坐标2．在平面直角坐标系中，二次函数22y ax bx =++的图象与x 轴交于()()3,0,1,0A B -两点，与y 轴交于点C ．（1）求二次函数的解析式；（2）点P 是直线AC 上方的抛物线上一动点，当ACP △面积最大时，求出点P 的坐标；（3）点M 为抛物线上一动点，在x 轴上是否存在点Q ，使以A C M Q 、、、为顶点的四边形是平行四边形？若存在，直接写出点Q 的坐标；若不存在，说明理由．3．在平面直角坐标系xOy 中，⊙O 的半径为1．对于点A 和线段BC ，给出如下定义：若将线段BC 绕点A 旋转可以得到⊙O 的弦B ′C ′（B ′，C ′分别是B ，C 的对应点），则称线段BC 是⊙O 的以点A 为中心的“关联线段”．（1）如图，点A ，B 1，C 1，B 2，C 2，B 3，C 3的横、纵坐标都是整数．在线段B 1C 1，B 2C 2，B 3C 3中，⊙O 的以点A 为中心的“关联线段”是 ；（2）△ABC 是边长为1的等边三角形，点A （0，t ），其中t ≠0．若BC 是⊙O 的以点A 为中心的“关联线段”，求t 的值；（3）在△ABC 中，AB ＝1，AC ＝2．若BC 是⊙O 的以点A 为中心的“关联线段”，直接写出OA 的最小值和最大值，以及相应的BC 长．4．综合与探究如图，在平面直角坐标系中，点()0,10A ，点B 是x 轴的正半轴上的一个动点，连接AB ，取AB 的中点M ，将线段MB 绕着点B 按顺时针方向旋转90°，得到线段BC ．过点B 作x 轴的垂线交直线AC 于点D ．设点B 坐标是(),0t（1）当6t =时，点M 的坐标是 ；（2）用含t 的代数式表示点C 的坐标；（3）是否存在点B ，使四边形AOBD 为矩形？若存在，请求出点B 的坐标；若不存在，请说明理由；（4）在点B 的运动过程中，平面内是否存在一点N ，使得以A 、B 、N 、D 为顶点的四边形是菱形？若存在，请直接写出点N 的纵坐标（不必要写横坐标）；若不存在，请说明理由．5．如图（1），在菱形ABCD 中，∠ABC ＝60°，点E 在边CD 上（不与点C ，D 重合），连结AE ，交BD 于点F ．（1）如图（2），若点M 在BC 边上，且DE ＝CM ，连结AM ，EM ．求证：三角形AEM 为等边三角形；（2）设DF x BF=，求tan ∠AFB 的值（用x 的代数式表示）； （3）如图（3），若点G 在线段BF 上，且FG ＝2BG ，连结AG 、CG ，DF x BF =，四边形AGCE 的面积为S 1，ABG 的面积为S 2，求12S S 的最大值．6．如图，在平面直角坐标系中，ABC 的边AB 在x 轴上，且OB OA >，以AB 为直径的圆过点C ．若点C 的坐标为()0,4，10AB =，（1）求抛物线的解析式；（2）点P 为该函数在第一象限内的图象上一点（不与BC 重合)，过点P 作PQ BC ⊥，垂足为点Q ，连接PC ．若以点P 、C 、Q 为顶点的三角形与COA 相似，求点P 的坐标；（3）若ACB ∠平分线所在的直线l 交x 轴与点E ，过点E 任作一直线l '分别交射线CA ，CB （点C 除外）于点M ，N ．则11CM CN+的是否为定值？若是，求出该定值；若不是，请说明理由．7．如图1，⊙I 与直线a 相离，过圆心I 作直线a 的垂线，垂足为H ，且交⊙I 于P 、Q 两点（Q 在P 、H 之间）．我们把点Q 称为⊙I 关于直线a 的“近点”，点P 称为⊙I 关于直线a 的“远点”把PQ ·QH 的值称为⊙I 关于直线a 的“特征数”．（1）如图2，在平面直角坐标系xOy 中，点E 的坐标为（0，3）．半径为1的⊙O 与两坐标轴交于点A 、B 、C 、D ．①过点E 画垂直于y 轴的直线m ，则⊙O 关于直线m 的“近点”“远点”分别是点_____和_____（填“A ”、“B ”、“C ”或“D ”），⊙O 关于直线m 的“特征数”为_____；②若直线n 的函数表达式为33y x =-+．求⊙O 关于直线n 的“特征数”；（2）在平面直角坐标系xOy 中，直线l 经过点M （1，2），点F 是坐标平面内一点，以F 5为半径作⊙F ．若⊙F 与直线l 相离，点N （1-，0）是⊙F 关于直线l 的“近点”．且⊙F 关于直线l 的“特征数”是6，求直线l 的函数表达式．8．如图，抛物线y＝－x2＋bx＋c与x轴交于A，B两点，其中A（3，0），B（－1，0），与y轴交于点C，抛物线的对称轴交x轴于点D，直线y＝kx＋b1经过点A、C，连接CD．（1）分别求抛物线和直线AC的解析式；（2）在直线AC下方的抛物线上，是否存在一点P，使得△ACP的面积是△ACD面积的2倍，若存在，请求出点P的坐标；若不存在，请说明理由；（3）在抛物线的对称轴上是否存在一点Q，使线段AQ绕Q点顺时针旋转90°得到线段QA1，且点A1恰好落在该抛物线上？若存在，求出点Q的坐标；若不存在，请说明理由．9．已知：如图，在平面直角坐标系中，点O为坐标原点，直线y＝﹣x+b（b＞0）交x轴于点A，交y轴于点C，以OA，OC为边作矩形ABCO，矩形ABCO的面积是36．（1）求直线AC的解析式．（2）点P为线段AB上一点，点Q为第一象限内一点，连接PO，PQ，∠OPQ＝90°，且OP＝PQ，设AP的长为t，点Q的横坐标为d，求d与t的函数关系式．（不要求写出自变量t的取值范围）（3）在（2）的条件下，过点Q作QE∥PO交AB的延长线于点E，作∠POC的平分线OF 交PE于点F，交PQ于点K，若KQ＝2EF，求点Q的坐标．10．如图，平面直角坐标系中，点O为原点，抛物线交x轴于()2,05,0B两点，交y轴于点C．A-、()（1）求抛物线解析式；（2）点P在第一象限内的抛物线上，过点P作x轴的垂线，垂足为点H，连AP交y轴于点E，设P点横坐标为t，线段EC长为d，求d与t的函数解析式；（3）在（2）条件下，点M在CE上，点Q在第三象限内抛物线上，连接PC、PQ、PM，PQ与y轴交于W，若，，，求点Q的坐标．11．已知：如图1，点A（a，b），AB x⊥轴于点B2++-+=．a b a b24(8)0（1）试判断△AOB的形状，并说明理由；（2）如图2，若点C为线段AB的中点，连OC并作OD OC⊥，且OD OC=，连AD交x轴于点E，试求点E的坐标；（3）如图3，若点M为点B的左边x轴负半轴上一动点，以AM为一边作45∠=︒交MANy轴负半轴于点N，连MN，在点M运动过程中，试猜想式子OM MN ON+-的值是否发生变化？若不变，求这个不变的值；若发生变化，试求它变化的范围．12．直角三角板ABC的斜边AB的两个端点在⊙O上，已知∠BAC=30°，直角边AC与⊙O 相交于点D，且点D是劣弧AB的中点．(1)如图1，判断直角边BC所在直线与⊙O的位置关系，并说明理由；(2)如图2，点P是斜边AB上的一个动点（与A、B不重合），DP的延长线交⊙O于点Q，连接QA、QB．①AD=6，PD=4，则AB= ；PQ= ；②当点P在斜边AB上运动时，求证：QA+QB=3QD．13．如图，已知四边形ABCD内接于⊙O，直径DF交BC于点G．(1)如图1，求证：∠BAD－∠BCF＝90°；(2)如图2，连接AC，当∠BAC＝∠CFD＋∠ACD时，求证：CA＝CB；(3)如图3，在（2）的条件下，AC交DF于点H，∠BAC＝∠DGB，45CGBG，AC＝9，求△CDH的面积．14．同学们学过正方形与等腰三角形发现它们都是轴对称图形，它们之间有很多相似，在正边形ABCD中，E是对角线AC上一点（不与点A、C重合），以AD、AE为邻边作平行四边形AEGD，GE交CD于点M，连接CG．(1)如图1，当12AE AC<时，过点E作EF BE⊥交CD于点F，连接GF并延长交AC于点H．求证：EB EF=；(2)在ABC中，AB AC=，90BAC∠=︒．过点A作直线AP，点C关于直线AP的对称点为点D，连接BD，CD直线BD交直线AP于点E．如图2，①依题意补全图形；②请用等式表示线段EB，ED，BC之间的数量关系，并予以证明．15．如图，在平面直角坐标系中，抛物线y＝x2+bx+c与x轴交于点A和点B（1，0），与y轴交于点C（0，﹣3）．(1)求抛物线的函数表达式．(2)若点P为第三象限内抛物线上一动点，作PD⊥x轴于点D，交AC于点E，过点E作AC 的垂线与抛物线的对称轴和y轴分别交于点F、G，设点P的横坐标为m．①求PE2的最大值；②连接DF、DG，若∠FDG＝45°，求m的值．16．【问题提出】如图①，在△ABC中，若AB＝8，AC＝4，求BC边上的中线AD的取值范围．【问题解决】解决此问题可以用如下方法：延长AD 到点E ，使DE ＝AD ，再连结BE （或将△ACD 绕着点D 逆时针旋转180°得到△EBD ），把AB 、AC ，2AD 集中在△ABE 中，利用三角形三边的关系即可判断．由此得出中线AD 的取值范围是__________【应用】如图②，如图，在△ABC 中，D 为边BC 的中点、已知AB ＝10，AC ＝6，AD ＝4，求BC 的长．【拓展】如图③，在△ABC 中，∠A ＝90°，点D 是边BC 的中点，点E 在边AB 上，过点D 作D F⊥DE 交边AC 于点F ，连结EF ．已知BE ＝5，CF ＝6，则EF 的长为__________.17．已知二次函数()20y x bx c a =++≠的图象与x 轴的交于A 、B （1，0）两点，与y 轴交于点()03C -，．(1)求二次函数的表达式及A 点坐标；(2)D 是二次函数图象上位于第三象限内的点，若点D 的横坐标为m ，ACD △的面积为S ，求S 与m 之间的函数关系式，并写出ACD △的面积取得最大值时点D 的坐标；(3)M 是二次函数图象对称轴上的点，在二次函数图象上是否存在点N ．使以M 、N 、B 、O 为顶点的四边形是平行四边形？若有，请写出点N 的坐标（不写求解过程）．18．如图，在平面直角坐标系中，已知二次函数图像222(1)2y x a x a a =-+++的顶点为P ，点B 39(2,)16- 是一次函数5119216y x =+上一点．(1)当a ＝0时，求顶点P 坐标；(2)若a ＞0，且一次函数2y x b =-+的图象与此抛物线没有交点，请你写出一个符合条件的一次函数关系式（只需写一个，不必写出过程）；(3)作直线OC ：12y x =与一次函数5119216y x =+交于点C ．连结OB ，当抛物线与△OBC 的边有两个交点时，求a 的取值范围．19．已知O 为ABC ∆的外接圆，AC BC =，点D 是劣弧AB 上一点（不与点A ，B 重合），连接DA ，DB ，DC ．(1)如图1，若AB 是直径，将ACD ∆绕点C 逆时针旋转得到BCE ∆．若4CD =，求四边形ADBC 的面积；(2)如图2，若AB AC =，半径为2，设线段DC 的长为x ．四边形ADBC 的面积为S ． ①求S 与x 的函数关系式；②若点M ，N 分别在线段CA ，CB 上运动（不含端点），经过探究发现，点D 运动到每一个确定的位置．DMN ∆的周长有最小值t ，随着点D 的运动，t 的值会发生变化．求所有t 值中的最大值，并求此时四边形ADBC 的面积S ．20．如图，在ABCD 中，90ABD ∠=︒，5cm AD =，8cm BD =．点P 从点A 出发，沿折线AB BC -向终点C 运动，点P 在AB 边、BC 边上的运动速度分别为1cm/s 、5cm /s ．在点P 的运动过程中，过点P 作AB 所在直线的垂线，交边AD 或边CD 于点Q ，以PQ 为一边作矩形PQMN ，且2QM PQ =，MN 与BD 在PQ 的同侧．设点P 的运动时间为t （秒），矩形PQMN 与ABCD 重叠部分的面积为()2cm S ．（1）求边AB 的长．（2）当04t <<时，PQ = ，当48t <<时，PQ = ．（用含t 的代数式表示）（3）当点M 落在BD 上时，求t 的值．（4）当矩形PQMN 与ABCD 重叠部分图形为四边形时，求S 与t 的函数关系式．【参考答案】参考答案**科目模拟测试一、解答题1．(1)223y x x =--；(2)，； (3)，；，；，；，； ，；，． 【解析】【分析】（1）根据顶点的坐标，设抛物线的解析式为y ＝a （x ﹣1）2﹣4，将点A （﹣1，0）代入，求出a 即可得出答案；（2）利用待定系数法求出直线BD 解析式为y ＝2x ﹣6，过点C 作CP 1∥BD ，交抛物线于点P 1，再运用待定系数法求出直线CP 1的解析式为y ＝2x ﹣3，联立方程组即可求出P 1（4，5），过点B 作y 轴平行线，过点C 作x 轴平行线交于点G ，证明△OCE ≌△GCF（ASA），运用待定系数法求出直线CF解析式为y＝12x﹣3，即可求出P2（52，﹣74）；（3）利用待定系数法求出直线AC解析式为y＝﹣3x﹣3，直线BC解析式为y＝x﹣3，再分以下三种情况：①当△QMN是以NQ为斜边的等腰直角三角形时，②当△QMN是以MQ为斜边的等腰直角三角形时，③当△QMN是以MN为斜边的等腰直角三角形时，分别画出图形结合图形进行计算即可．(1)解：∵顶点D的坐标为（1，﹣4），∴设抛物线的解析式为y＝a（x﹣1）2﹣4，将点A（﹣1，0）代入，得0＝a（﹣1﹣1）2﹣4，解得：a＝1，∴y＝（x﹣1）2﹣4＝x2﹣2x﹣3，∴该抛物线的解析式为y＝x2﹣2x﹣3；(2)解：∵抛物线对称轴为直线x＝1，A（﹣1，0），∴B（3，0），设直线BD解析式为y＝kx+e，∵B（3，0），D（1，﹣4），∴，解得：，∴直线BD解析式为y＝2x﹣6，过点C作CP1∥BD，交抛物线于点P1，设直线CP1的解析式为y＝2x+d，将C（0，﹣3）代入，得﹣3＝2×0+d，解得：d＝﹣3，∴直线CP1的解析式为y＝2x﹣3，结合抛物线y＝x2﹣2x﹣3，可得x2﹣2x﹣3＝2x﹣3，解得：x1＝0（舍），x2＝4，故P1（4，5），过点B作y轴平行线，过点C作x轴平行线交于点G，∵OB＝OC，∠BOC＝∠OBG＝∠OCG＝90°，∴四边形OBGC是正方形，设CP1与x轴交于点E，则2x﹣3＝0，解得：x＝32，∴E（32，0），在x轴下方作∠BCF＝∠BCE交BG于点F，∵四边形OBGC是正方形，∴OC＝CG＝BG＝3，∠COE＝∠G＝90°，∠OCB＝∠GCB＝45°，∴∠OCB﹣∠BCE＝∠GCB﹣∠BCF，即∠OCE＝∠GCF，∴△OCE≌△GCF（ASA），∴FG＝OE＝32，∴BF＝BG﹣FG＝3﹣32＝32，∴F（3，﹣32），设直线CF解析式为y＝k1x+e1，∵C（0，﹣3），F（3，﹣32），∴，解得：，∴直线CF解析式为y＝12x﹣3，结合抛物线y＝x2﹣2x﹣3，可得x2﹣2x﹣3＝12x﹣3，解得：x1＝0（舍），x2＝52，∴P2（52，﹣74），综上所述，符合条件的P点坐标为：（4，5）或（52，﹣74）；(3)解：（3）设直线AC解析式为y＝m1x+n1，直线BC解析式为y＝m2x+n2，∵A（﹣1，0），C（0，﹣3），∴，解得：，∴直线AC解析式为y＝﹣3x﹣3，∵B（3，0），C（0，﹣3），∴，解得：，∴直线BC解析式为y＝x﹣3，设M（t，t﹣3），则N（t，t2﹣2t﹣3），∴MN＝|t2﹣2t﹣3﹣（t﹣3）|＝|t2﹣3t|，①当△QMN是以NQ为斜边的等腰直角三角形时，此时∠NMQ＝90°，MN＝MQ，如图2，∵MQ∥x轴，∴Q（﹣13t，t﹣3），∴|t2﹣3t|＝|t﹣（﹣13t）|，∴t2﹣3t＝±43t，解得：t＝0（舍）或t＝53或t＝133，∴，；，；②当△QMN是以MQ为斜边的等腰直角三角形时，此时∠MNQ＝90°，MN＝NQ，如图3，∵NQ∥x轴，∴Q（，t2﹣2t﹣3），∴NQ＝|t﹣|＝13|t2+t|，∴|t2﹣3t|＝13|t2+t|，解得：t＝0（舍）或t＝5或t＝2，∴M3（5，2），Q3（﹣5，12）；M4（2，﹣1），Q4（0，﹣3）；③当△QMN是以MN为斜边的等腰直角三角形时，此时∠MQN＝90°，MQ＝NQ，如图4，过点Q作QH⊥MN于H，则MH＝HN，∴H（t，），∴Q（，），∴QH＝|t﹣|＝16|t2+5t|，∵MQ＝NQ，∴MN＝2QH，∴|t2﹣3t|＝2×16|t2+5t|，解得：t＝7或1，∴M5（7，4），Q5（﹣7，18）；M6（1，﹣2），Q6（0，﹣3）；综上所述，点M及其对应点Q的坐标为：，；，；M3（5，2），Q3（﹣5，12）；M4（2，﹣1），Q4（0，﹣3）；M5（7，4），Q5（﹣7，18）；M6（1，﹣2），Q6（0，﹣3）．【点睛】本题是二次函数综合题，主要考查了待定系数法求一次函数和二次函数解析式，求一次函数与二次函数图象交点坐标，全等三角形判定和性质，正方形判定和性质，等腰直角三角形性质等，本题属于中考压轴题，综合性强，难度较大，熟练掌握待定系数法、等腰直角三角形性质等相关知识，运用数形结合思想、分类讨论思想是解题关键．2．（1）224233y x x =--+；（2）35(,)22P -（3）存在，12(1,0),(5,0)Q Q --，34(27,0),(27,0)Q Q ．【解析】【分析】（1）根据待定系数法求抛物线解析式；（2）设224(,)33P t t --根据（1）的结论求得C 的坐标，进而求得AC 的解析式，过P 作PD ⊥x 轴交AC 于点D ，进而求得PD 的长，根据12APC C A S PD x x =⋅⋅-△求得APC S 的表达式，进而根据二次函数的性质求得取得最大值时，t 的值，进而求得P 点的坐标；（3）分情况讨论，①//CM AQ ，②//AC MQ ，根据抛物线的性质以及平行四边形的性质先求得M 的坐标进而求得Q 点的坐标．【详解】（1）二次函数22y ax bx =++的图象与x 轴交于()()3,0,1,0A B -两点，则093202a b a b =-+⎧⎨=++⎩解得2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴抛物线解析式为224233y x x =--+ （2）抛物线224233y x x =--+与y 轴交于点C ，令0x =，则2y = (0,2)C ∴设直线AC 的解析式为y kx b =+，由(3,0)A -，(0,2)C ，则302k b b -+=⎧⎨=⎩解得232k b ⎧=⎪⎨⎪=⎩ ∴直线AC 的解析式为223y x =+， 如图，过P 作PD ⊥x 轴交AC 于点D ，设224(,)33P t t --，则2(,2)3D t t +， 2224222223333PD t t t t t ⎛⎫∴=--+-+=-- ⎪⎝⎭∴12APC C A S PD x x =⋅⋅-△212(2)323t t =⨯--⨯2239324t t t ⎛⎫=--=-++ ⎪⎝⎭ ∴当32t =-时，APC S 取得最大值，此时222423435223332322t t ⎛⎫⎛⎫--+=-⨯--⨯-+= ⎪ ⎪⎝⎭⎝⎭ ∴35(,)22P - （3）存在，理由如下抛物线解析式为224233y x x =--+()228133x =-++ ∴抛物线的对称轴为直线1x =①如图，当//CM AQ 时，Q 点在x 轴上，//CM x 轴∴,M C 关于抛物线的对称轴直线1x =对称，(0,2)C(2,2)M ∴-2CM ∴=122AQ AQ ∴==(3,0)A -12(1,0),(5,0)Q Q ∴--②当//AC MQ 时，如图，设M 的纵坐标为n ，四边形ACQM 是平行四边形，点A ,Q 在x 轴上，则,AQ MC 的交点也在x 轴上， 202n +∴= 解得2n =-设(,2)M m -，2242233x x ∴-=--+ 解得17x =-(17,2)M ∴--A 点到C 点是横坐标加3，纵坐标加2∴M 点到Q 点也是横坐标加3，纵坐标加2 即(173,0)Q -±34(27,0),(27,0)Q Q ∴综上所述，存在点Q ，使得以A C M Q 、、、为顶点的四边形是平行四边形，Q 点的坐标为12(1,0),(5,0)Q Q --，34(27,0),(27,0)Q Q ．【点睛】本题考查了二次函数综合，待定系数法，二次函数最值，二次函数的图象与性质，平行四边形的性质，综合运用以上知识是解题的关键．3．（1）B 2C 2；（233-3）OA 最小值为1，相应的3BC =OA 最大值为2，相应的6BC =【解析】【分析】（1）结合题意，根据旋转和圆的性质分析，即可得到答案；（2）根据题意，分B C ''在x 轴上方和x 轴上方两种情况；根据等边三角形、勾股定理、全等三角形的性质，得32AD OD ==，从而完成求解； （3）结合题意，得当AC '为⊙O 的直径时，OA 取最小值；当A 、B '、O 三点共线时，OA 取最大值；根据勾股定理、等腰三角形的性质计算，即可得到答案．【详解】（1）线段B 1C 1绕点A 旋转得到的11B C ''，均不能成为⊙O 的弦∴线段B 1C 1不是⊙O 的以点A 为中心的“关联线段”；线段B 2C 2绕点A 旋转得到的22B C ''，如下图：∴线段B 2C 2是⊙O 的以点A 为中心的“关联线段”；线段B 3C 3绕点A 旋转得到的33B C ''，均不能成为⊙O 的弦∴线段B 3C 3不是⊙O 的以点A 为中心的“关联线段”；故答案为：B 2C 2；（2）∵△ABC 是边长为1的等边三角形，点A （0，t ），⊙O 的半径为1 ∴//B C x ''轴分B C ''在x 轴上方和x 轴上方两种情况：当B C ''在x 轴上方时，B C ''与y 轴相交于点D ，见下图：∵1OB OC ''==∴1122B D B C '''== ∴2232OD OB B D ''=-=∵△ABC 是边长为1的等边三角形，即△AB C ''是边长为1的等边三角形， ∴AC D OC D ''∠=∠，AD B C ''⊥ ∴AC D OC D ''△≌△∴32AD OD == ∴3AO AD OD =+=∴3t =；当B C ''在x 轴上方时，B C ''与y 轴相交于点D ，见下图：同理，3AO AD OD =+=∴()0,3A -；∴t 3=-；∴3t =或3-；（3）当AC '为⊙O 的直径时，OA 取最小值，如下图：∴OA 最小值为1，90AB C ''∠=︒ ∴223BC B C AC AB ''''==-=；当A 、B '、O 三点共线时，OA 取最大值，2OA AC '== ，如下图：作AE OC '⊥交OC '于点E ，作C F AO '⊥交AO 于点F ，如下图∵2OA AC '==∴1122OE OC '==∴2215AE AO OE - ∵11222AE OC OB C F '''⨯=⨯⨯ ∴1152C F AE '==∴2214OF OC C F ''=-=∴34B F OB OF ''=-=∴262BC B C C F B F ''''==+=∴OA 最小值为1，相应的3BC =；OA 最大值为2，相应的62BC =． 【点睛】本题考查了旋转、圆、等边三角形、勾股定理、全等三角形、等腰三角形的知识；解题的关键是熟练掌握旋转、圆周角、等腰三角形三线合一、勾股定理的性质，从而完成求解．4．（1）(3,5)M ，（2）1(5,)2C t t +；（3）(20,0)B ；（4）154或10． 【解析】 【分析】（1）利用中点坐标公式计算即可．（2）如图1中，作ME OB ⊥于E ，CF x ⊥轴于F ．证明()MEB BFC AAS ∆≅∆，利用全等三角形的性质即可解决问题．（3）如图2中，存在．由题意当CF OA =时，可证四边形AOBD 是矩形，构建方程即可解决问题．（4）分三种情形：①如图3中，当AD BD =时，以AB 为对角线可得菱形ADBN ，此时点N 在y 轴上．②如图4中，当AD AB =时，以BD 为对角线可得菱形ABND ．此时点N 的纵坐标为6．③因为BD AB ≠，所以不存在以AD 为对角线的菱形． 【详解】解：（1）如图1中，(0,10)A ，(6,0)B ，AM BM =， (3,5)M ∴，（2）如图1中，作ME OB ⊥于E ，CF x ⊥轴于F ．//ME OA ，AM BM =， 12OE EB t ∴==，152ME OA ==，90MEB CFB CBM ∠=∠=∠=︒，90MBE CBF ∴∠+∠=︒，90MBE BME ∠+∠=︒， BME CBF ∴∠=∠，()MEB BFC AAS ∴∆≅∆，5BF ME ∴==，12CF BE t ==，5OF OB BF t ∴=+=+， 1(5,)2C t t ∴+．（3）存在．如图2中，作ME OB ⊥于E ，CF x ⊥轴于F ．理由：由题意当=10CF OA =时，//OA CF ， ∴四边形AOFC 是平行四边形，90AOF ∠=︒，∴四边形AOFC 是矩形，90DAO AOB DBO ∴∠=∠=∠=︒，∴四边形AOBD 是矩形，又∵由（2）得12CF BE t ==， 即：1102t =，解得：20t =．(20,0)B ∴．（4）①如图3中，当AD BD =时，以AB 为对角线可得菱形ADBN ，此时点N 在y 轴上．AD BD =， BAD ABD ∴∠=∠，OAB ABD ∴∠=∠，OAB BAD ∴∠=∠． tan tan OAB BAD ∴∠=∠， ∴12OB BC OA BA ==，即1102t =，5t ∴=，5OB ∴=，设AN NB m ==，在Rt OBN △中，则有2225(10)m m =+-， 解得254m =， 25151044ON OA AN ∴=-=-=， ∴点N 的纵坐标为154． ②如图4中，当AD AB =时，以BD 为对角线可得菱形ABND ．此时点N 的纵坐标为10．③BD AB ≠，∴不存在以AD 为对角线的菱形． 综上所述，满足条件的点N 的纵坐标为154或10． 【点睛】本题属于四边形综合题，考查了矩形的判定和性质，菱形的判定和性质，翻折变换，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．5．（1）证明见解析；（23333xx；（3）194【解析】 【分析】（1）如图，连接,AC 证明,ACB ACD 都为等边三角形，可得,AC AD = 再证明,ACM ADE ≌从而可得答案；（2）如图，记,AC BD 交于点,O 设,,DFa OFb 四边形ABCD 为菱形，60,ABC ∠=︒表示33,33OA OB a b 利用,2DF ax BF a b则2,1a xb x再利用三角函数的定义可得答案；（3）如图，设,DFESn 证明,DFE BFA ∽ 2,BFAnSx 再表示2222,,33ABGAGFn nSS S x x 结合菱形的轴对称的性质可得：2=,3CBG nS x 表示,AFDn S x可得2=,BCD ABDn n S Sxx 可得2212243334,3nn n S x x x x n S x 再利用二次函数的性质可得答案.【详解】证明：（1）如图，连接,AC 菱形ABCD 中，∠ABC ＝60°，,60,120,60,AB BC CDAD ABC ADC BAD BCD BAC CAD ACB,ACB ACD 都为等边三角形，,AC AD ∴=,60,DE CM ACM ADE,ACM ADE ≌ ,,AMAE MAC EAD 60,MACCAECAEEADAME ∴是等边三角形（2）如图，记,AC BD 交于点,O设,,DF a OF b 四边形ABCD 为菱形，60,ABC ∠=︒,,30,ACBD OB OD a b ABO33,33OAOB a b ,2DF a x BFa b1221,a b bx a a 11,22b ax 则2,1ax bx333tan 13a b OAa AFBOFbb32331,3133xxxx（3）如图，设,DFESn四边形ABCD 是平行四边形，,DFE BFA ∽22=,BFAn DF x S BF2,BFAn SxFG ＝2BG ， 2222,,33ABGAGFn n SS S xx根据菱形的轴对称的性质可得：2=,3CBG n S x ,AFD ABFS DF x SBF2,AFDn n S x x x 2=,BCDABD n n SSxx1222224=333n n n n n nS nn x x x x x x， 2212243334,3n n n S x x x x n S x 30,a所以12S S 有最大值， 当31232x时，最大值为：1119334.424【点睛】本题考查的是菱形的性质，全等三角形的判定与性质，等边三角形的判定与性质，相似三角形的判定与性质，列二次函数关系式，二次函数的性质，锐角三角函数的应用，灵活运用以上知识解题是解本题的关键.6．（1）213442y xx =-++；（2）点P 的坐标为：（6，41，2）；（3）11NC MC +=【解析】 【分析】（1）根据题意，先证明AOC ∆∽COB ∆，得到AO OCCO OB=，求出点A 、B 的坐标，然后利用待定系数法，即可求出抛物线解析式；（2）根据题意，可分为两种情况：AOC ∆∽PQC ∆或AOC ∆∽CQP ∆，结合解一元二次方程，相似三角形的判定和性质，分别求出点P 的坐标，即可得到答案；（3）过点E 作EI ⊥AC 于I ，EJ ⊥CN 于J ，然后由角平分线的性质定理，得到EI =EJ ，再证明△MEI ∽△MNC ，△NEJ ∽△NMC ，得到111NC MC EI+=，然后求出EI 一个定值，即可进行判断． 【详解】解：（1）∵以AB 为直径的圆过点C ， ∴∠ACB =90°， ∵点C 的坐标为()0,4， ∴CO ⊥AB ，∴∠AOC =∠COB =90°，∴∠ACO +∠OCB =∠ACO +∠OAC =90°， ∴∠OCB =∠OAC , ∴AOC ∆∽COB ∆，∴AO OCCO OB=， ∵4CO =，10AO BO AB +==， ∴10AO OB =-， ∴1044OB OB-=， 解得：2OB =或8OB =， 经检验，满足题意， ∵OB OA >， ∴8OB =，∴点A 为（2-，0），点B 为（8，0）．设抛物线的解析式为2y ax bx c =++，把点A 、B 、C 三点的坐标代入，有44206480c a b c a b c =⎧⎪-+=⎨⎪++=⎩，解得：14324a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩，∴抛物线的解析式为213442y x x =-++；（2）根据题意，如图：当AOC ∆∽PQC ∆时， ∴ACO PCQ ∠=∠， ∵90ACO OCB ∠+∠=︒， ∴90PCQ OCB ∠+∠=︒， ∴PC ⊥OC ， ∴点P 的纵坐标为4，当4y =时，有2134442x x -++=，解得：16x =或20x =（舍去）； ∴点P 的坐标为（6，4）；当AOC ∆∽CQP ∆时，则此时BC 垂直平分OP ，作PG ⊥y 轴，垂足为G ，如上图， ∴90CQP AOC ∠=∠=︒，∴AC ∥OP ， ∴∠ACO =∠POG ， ∵90PGO AOC ∠=∠=︒， ∴AOC ∆∽PGO ∆， ∴AO OCPG GO=， 设点P 为（x ，213442x x -++）， ∴PG x =，213442GO x x =-++，∴22413442x x x =-++， 解得：171x =±-， ∵点P 在第一象限， ∴171x =-，∴2134217242x x -++=-，∴点P 的坐标为（171-，2172-）；综合上述，点P 的坐标为：（6，4）或（171-，2172-）； （3）过点E 作EI ⊥AC 于I ，EJ ⊥CN 于J ，如图：∵CE 是∠ACB 的角平分线， ∴EI =EJ ，∵EI ∥CN ，EJ ∥CM ，∴△MEI ∽△MNC ，△NEJ ∽△NMC ， ∴EI ME NC MN =，EJ NE MC MN =， ∴1EI EJ ME NENC MC MN MN +=+=， ∴1EI EI NC MC +=， ∴111NC MC EI+=， ∵△ACO ∽△AEI ，∴12AI AO EI CO ==，∵AC = ∵AC AI IC AI EI =+=+，12=，解得：EI =∴111NC MC EI +==∴11NC MC+是一个定值． 【点睛】本题考查了二次函数的综合应用，求二次函数的解析式，二次函数的性质，相似三角形的判定和性质，解一元二次方程，角平分线的性质定理等知识，解题的关键是熟练掌握题意，正确的作出辅助线，运用数形结合的思想进行解题．7．（1）①B ；D ；4；②1；（2）1522y x =-+或24y x =-+【解析】 【分析】（1）①根据“近点”、“远点”以及“ 特征数”的定义判断即可；②过点O 作OH ⊥直线n 于点H ，交O 于点Q ，P ．先分别求得点E 、F 的坐标，进而可求得EF 的长，再利用等积法求得OH 的长，进而即可解决问题；（2）如图，先求得“近点”N 到直线l 的距离NH AOB AHN △∽△即可求得答案． 【详解】解：（1）①由题意，点B 是O 关于直线m 的“近点”， 点D 是O 关于直线m 的“远点”， ∵点E 的坐标为（0，3）．⊙O 的半径为1， ∴OE ＝3，OB ＝OD ＝1，∴BE ＝OE －OB ＝2，DB ＝OB ＋OD ＝2，O 关于直线m 的特征数224DB BE =⋅=⨯=， 故答案为：B ；D ；4；②如图，过点O 作OH ⊥直线n 于点H ，交O 于点Q ，P ，设直线33y x =-+交x 轴于点F ，交y 轴于点E ， 令y ＝0，则x ＝3；令x ＝0，则y ＝3， ∴(3F ，0)，(0,3)E ，3OE ∴=，3OF =，22223(3)23EF OE OF ∴=+=+=，∵1122EOF S OE OF EF OH =⋅=⋅△， ∴11332322OH ⨯⨯=⨯⋅， 解得：32OH =， 12QH OH OQ ∴=-=， 又∵2PQ OQ OP =+=，O ∴关于直线n 的“特征数” 1212PQ QH =⋅=⨯=；（2）如图，设直线l 交x 轴于点A ，交y 轴于点B ，过点F 作FH ⊥直线l ，垂足为点H ，交⊙F 于N ，G ，∵⊙F 5，∴FN ＝FG 5，∴GN ＝FN ＋FG 5∵⊙F 关于直线l 的“特征数”是6， ∴GN·NH ＝6，NH ＝6， 解得：NH设直线l 的解析式是y kx b =+， ∵直线l 经过点M （1，2），∴将（1，2）代入y kx b =+，得：2k b +=， 2b k ∴=-，(2)y kx k ∴=+-，∴当0x =时，2y k =-，∴点B 坐标为（0，2－k ），|2|OB k ∴=-，当0y =时，(2)0kx k +-=， 解得：2k x k-=， ∴点A 坐标为（2k k-，0）， 2||k OA k -∴=，22|(1)||1|k k AN k k--=--=+，AB ∴2||k k-= BAO NAH ∠=∠，90AOB AHN ∠=∠=︒， AOB AHN ∴△∽△，∴NH ANOB AB=，∴|2|522|1|||k k k k k-=--+， 整理，得：22520k k ++=，解得：12k =-或2k =-，∴直线l 的解析式为1522y x =-+或24y x =-+．【点睛】本题属于圆综合题，考查了一次函数的性质，相似三角形的判定和性质运用以及勾股定理的运用，远点，近点，特征数等新定义等知识，解题的关键是理解题意，学会用分类讨论的思想思考问题，属于中考压轴题．8．（1）y ＝－x 2+2x +3，y ＝-x +3；（2）存在，（－1，0）或（4，－5）；（3）存在，（1，2）或（1，－3） 【解析】 【分析】（1）将点A ，B 坐标代入抛物线解析式中，求出b ，c 得出抛物线的解析式，进而求出点C 的坐标，再将点A ，C 坐标代入直线AC 的解析式中，即可得出结论；（2）利用抛物线的对称性得出BD AD =，进而判断出ABC 的面积和ACP △的面积相等，即可得出结论；（3）分点Q 在x 轴上方和在x 轴下方，构造全等三角形即可得出结论． 【详解】（1）把(30)A ，、(10)B -，代入2y x bx c =-++， 解得2b =、3c =∴抛物线的解析式为2y x 2x 3=-++则C 点为（0，3），又(30)A ，，代入1y kx b =+， 得1k =-，13b =， ∴直线AC 的解析式为3y x =-+， （2）如图，连接BC ，∵点D 是抛物线的对称轴与x 轴的交点， ∴AD BD =， ∴2ABCACDSS=，∵2ACP ACD S S =△△，∴ACP ABC S S =△△，此时，点P 与点B 重合， 即：(10)P -，， 过B 点作PB AC ∥交抛物线于点P ，则直线BP 的解析式为1y x =--①， ∵抛物线的解析式为2y x 2x 3=-++②，联立①②解得，10x y =-⎧⎨=⎩或45x y =⎧⎨=-⎩，∴P （4，﹣5），∴即点P 的坐标为（﹣1，0）或（4，﹣5）； （3）由（1）可知，抛物线解析式为()214y x =--+ 把1x =代入直线AC 解析式3y x =-+得AC 与抛物线对称轴的交点(1,2)M ，如下图所示：22222BM AM ==+，4AB =即222BM AM AB +=则MAB △是等腰直角三角形，符合题意，M 点即为所求Q 点的一种情况，当Q 点在x 轴下方时，设Q 为(1,)m ，0m ＜， 因为线段AQ 绕Q 点顺时针旋转90°得到线段1QA 过A1作直线DQ 的垂线于E 点，则1ADQ QEA ≌ ∴2AD QE ==，1DQ EA m ==- ∴12(1)A m m --，∵点A1恰好落在抛物线2y x 2x 3=-++上， 代入，解得m=－3或2m = (舍去) ∴Q （1，－3）综上，Q 点坐标为（1,2）或（1，－3）， 【点睛】本题考查的是二次函数的综合题，涉及解析式的求解，与三角形面积有关的问题，全等三角形的判定与性质，解题的关键是利用数形结合的思想，设点坐标并结合几何图形的性质列式求解．9．（1）直线AC 的解析式为y ＝﹣x +6；（2）d =4-t ；（3）Q （212，1）． 【解析】 【分析】（1）先由解析式求出得A 、C 点的坐标，得OA =OC ，得四边形ABCO 为正方形，再根据正方形的面积求得边长，便可得b 的值；（2）过点Q 作QG ⊥AB 交AB 延长沿于点G ，证明Rt △AOP ≌Rt △GPQ （AAS ），得到AP =GQ ，进而求得结论便可；（3）过点P 作PH ⊥OF 于点H ，延长PH 交EQ 的延长线于点R ，EQ 的延长线与x 轴交于点N ，过Q 作QM ⊥x 轴于点M ．证明Rt △AOP ≌Rt △GPQ （CCS ），得PK =QR ，∠R=∠OKP，再证明∠R=∠FPR，得EP=ER，再证FE=NR，设FE=NR=k，NQ=m，在Rt△PQE中，由勾股定理列出方程，得到k与m的关系，解Rt△PQE得tan∠PEQ，进而把这个函数值运用到△OAP中，求得t的值，再运用（2）中结论得Q的纵坐标d的值，再运用到△QNM中求得NM，NQ的值，进而求得ON，便可得Q的横坐标的值．【详解】解：（1）∵直线y＝﹣x+b（b＞0）交x轴于点A，交y轴于点C，A b C b，∴(,0),(0,)∴OA=OC=b，∴矩形ABCO为正方形，∵矩形ABCO的面积是36．∴b=6，即直线AC的解析式为y＝﹣x+6；（2）如图，过点Q作QG⊥AB交AB延长沿于点G，∵∠OPQ=90°，∴∠APO+∠GPQ=90°，∵∠APO+∠AOP=90°，∴∠AOP=∠GPQ，∵在矩形ABCO，∠OAP=90°，QG⊥AB,∴∠QGP=∠OAP=90°，∵PQ=OP，∴Rt△AOP≌Rt△GPQ（AAS），∴AP=GQ，∵AP=t，∴GQ=t，∴d=4-t；（2）过点P作PH⊥OF于点H，延长PH交EQ的延长线于点R，EQ的延长线与y轴交于点N，过Q作QM⊥y轴于点M．则AP=t，QM=d，且d=6-t．∵OF 平分∠POC ， ∴∠POF =∠COF =∠PFO ， ∴PF =PO ，∵PH ⊥OF ，∠OPQ ＝90°， ∴∠OPH =∠FPH ，∠KPH =∠POH ， 在△OPK 和△PQR 中， 90OPK PQR PO QP POK QPR ∠∠︒⎧⎪⎨⎪∠∠⎩＝＝＝＝， ∴△OPK ≌△PQR （ASA ）， ∴PK =QR ，∠R =∠OKP ，∵∠OKP +∠POK =∠POK +∠OPH =90°， ∴∠OKP =∠OPH ， ∴∠R =∠OPH ， ∵PO =PF ，PH ⊥OF ， ∴∠OPH =∠FPH ， ∴∠R =∠FPR ， ∴EP =ER ，∵PE ∥ON ，OP ∥EN ， ∴四边形OPEN 是平行四边形， ∴EN =PO =PF ， ∴PE -PF =ER -EN ， ∴FE =NR ，设FE =NR =k ，则KQ =2FE =2k ， 又设NQ =m ，∴PK=QR=m+k，∴PQ=m+3k，∴PO=EN=PF=m+3k，∴QE=EN-QR=m+3k-m=3k，PE=PF+FE=4k+m，在Rt△PQE中，∵PE2=PQ2+QE2，∴（4k+m）2=（3k+m）2+（3k）2，∴k1=0（舍去），k2=m，∴PQ=4m，QE=3m，∴tan∠PEN=43 PQQE=，∵OP∥EN，∴∠OPA=∠PEN，∴tan∠APO=43，∵AO=6，∴AP=4.5，∴t=4.5，∴QM=d=6-t=1.5，∵PE∥OC，∴∠QNM=∠PEN，∴tan∠QNM=tan∠PEN=43，∴NM=9 tan8QMQNM=∠，∴m=NQ158 =，∴PE=ON=4k+m=5m=758，∴OM=ON+NM=212，∴Q（212，1）．【点睛】本题是一次函数与四边形的综合题，主要考查了一次函数的图象与性质，全等三角形的性质与判定，正方形的性质，旋转的性质，解直角三角形的应用，等腰三角形的性质与判定，平行四边形的性质与判定，是一道综合性极强的题目，解决这类问题常用到数形结合、方程和转化等数学思想方法．构造全等三角形是解题的关键，也是问题的突破口．10．（1）；（2）；（3）【解析】 【分析】（1）由抛物线的二次项系数 再根据交点式可得抛物线为从而可得答案；（2）先画好图形，证明利用相似三角形的性质求解从而可得答案；（3）如图，过P 作轴于,K 过M 作于,N 证明即再求解则，再解方程可得 4,t = 再求解的解析式，再联立解析式解方程可得答案. 【详解】 解：（1） 抛物线交x 轴于()2,0A -、()5,0B 两点，所以可得抛物线为：（2）如图，过P 作于,H 连AP 交OC 于则，x 则令0,（3）如图，过P作轴于,K过M作于,N 由（2）得：，，轴，则轴，，即结合（1）可得：四边形为矩形，。

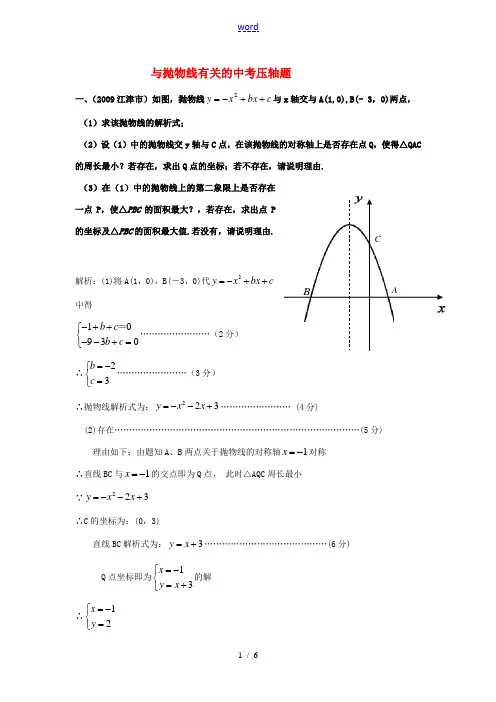
与抛物线有关的中考压轴题一、（2009江津市）如图，抛物线c bx x y ++-=2与x 轴交与A(1,0),B(- 3，0)两点， （1）求该抛物线的解析式；（2）设（1）中的抛物线交y 轴与C 点，在该抛物线的对称轴上是否存在点Q ，使得△QAC 的周长最小？若存在，求出Q 点的坐标；若不存在，请说明理由. （3）在（1）中的抛物线上的第二象限上是否存在一点P ，使△PBC 的面积最大？，若存在，求出点P 的坐标及△PBC 的面积最大值.若没有，请说明理由.解析：(1)将A(1，0)，B(－3，0)代2y x bx c =-++中得10930b c b c -++⎧⎨--+=⎩＝……………………（2分） ∴23b c =-⎧⎨=⎩……………………（3分）∴抛物线解析式为：223y x x =--+…………………… (4分)(2)存在…………………………………………………………………………(5分) 理由如下：由题知A 、B 两点关于抛物线的对称轴1x =-对称 ∴直线BC 与1x =-的交点即为Q 点， 此时△AQC 周长最小 ∵223y x x =--+ ∴C 的坐标为：(0，3)直线BC 解析式为：3y x =+……………………………………(6分)Q 点坐标即为13x y x =-⎧⎨=+⎩的解∴12x y =-⎧⎨=⎩ABC∴Q(－1，2)…………………………………………………………………(7分)（3）答：存在。

…………………………………………………………………(8分)理由如下：设P 点2(23) (30)x x x x --+-<<，∵92BPC BOC BPCO BPCO S S S S ∆∆=-=-四边形四边形若BPCO S 四边形有最大值，则BPC S ∆就最大，∴BPE BPCO PEOC S S S ∆+Rt 四边形直角梯形＝……………………………………………(9分)11()22BE PE OE PE OC =⋅++ ＝2211(3)(23)()(233)22x x x x x x +--++---++＝233927()2228x -+++当32x =-时，BPCO S 四边形最大值＝92728+∴BPC S ∆最大＝9279272828+-=………………………………………(10分) 当32x =-时，215234x x --+=∴点P 坐标为315( )24-，………………………………………(11分)二、（2009某某）如图，在直角坐标系中，点A 的坐标为（－2，0），连结OA ，将线段OA 绕原点O 顺时针旋转120°，得到线段OB .（1）求点B 的坐标；（2）求经过A 、O 、B 三点的抛物线的解析式；（3）在（2）中抛物线的对称轴上是否存在点C ，使△BOC 的周长最小？若存在，求出点C 的坐标；若不存在，请说明理由.（4）如果点P 是（2）中的抛物线上的动点，且在x 轴的下方，那么△PAB 是否有最大面积？若有，求出此时P 点的坐标及△PAB 的最大面积；若没有，请说明理由.解析：（1）B （1（2）设抛物线的解析式为y =ax (x+a )，代入点B （，得a =，因此2y =+ （3）如图，抛物线的对称轴是直线x =—1，当点C 位于对称轴与线段AB 的交点时，△BOC 的周长最小.设直线AB 为y =kx +b .所以20.k k b k b b ⎧⎪⎧+=⎪⎪⎨⎨-+=⎪⎩⎪=⎪⎩解得因此直线AB 为y x =， 当x =－1时，y =， 因此点C 的坐标为（－1.（4）如图，过P 作y 轴的平行线交AB 于D . 2221()()213212PAB PAD PBD D P B A S S S y y x x x x x ∆∆∆=+=--⎡⎤⎫=+-⨯⎢⎥⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦=⎫=+⎪⎝⎭当x =－12时，△PAB ，此时1,2P ⎛- ⎝⎭. 三 、（2007某某某某）．已知抛物线y ＝ax 2＋bx ＋c 与x 轴交于A 、B 两点，与y 轴交于点C ，其中点B 在x 轴的正半轴上，点C 在y 轴的正半轴上，线段OB 、OC 的长（OB <OC ）是方程x 2－10x ＋16＝0的两个根，且抛物线的对称轴是直线x ＝－2． （1）求A 、B 、C 三点的坐标； （2）求此抛物线的表达式；（3）连接AC 、BC ，若点E 是线段AB 上的一个动点 （与点A 、点B 不重合），过点E 作EF ∥AC 交BC 于点F ，连接CE ，设AE 的长为m ，△CEF 的面积为S ，求S 与m 之间的函数关系式，并写出自变量m 的取值X 围；（4）在（3）的基础上试说明S 是否存在最大值，若存在，请求出S 的最大值，并求出此时点E 的坐标，判断此时△BCE 的形状；若不存在，请说明理由． 解析（1）点B （2，0），点C （0，8），点A （－6，0），（2）抛物线的表达式为y ＝－23x 2－83x ＋8 ，（3）由EF AC ＝BE AB ，因为AC=2268+=10，BE=8-m ，AB=8.所以EF ＝40－5m4.作FG ⊥AB ，垂足为G ，则sin ∠FEG=sin ∠CAB=54108=.所以在Rt △EGF 中， FG ＝EF ·sin ∠FEG=45·40－5m4=8-m ，所以S ＝BFE BCE S S ∆∆-=()8821⨯-m -()()m m --8821=－12m 2＋4m ， m 的取值X 围是0＜m ＜8 （4）存在．因为S ＝－12m 2＋4m ，又a=21-<0，当m=ab2-=⎪⎭⎫ ⎝⎛-⨯-2124=4时，a4b ac 42-=最大S =8.因为m=4，所以点E 的坐标为（－2，0），△BCE 为等腰三角形．四（2006·某某市）施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM 为12米.现以O 点为原点，OM 所在直线为X 轴建立直角坐标系（如图所示）. （1）直接写出点M 及抛物线顶点P 的坐标； （2）求出这条抛物线的函数解析式；（3）施工队计划在隧道门口搭建一个矩形“脚手架”CDAB ，使A 、D 点在抛物线上，B 、C 点在地面OM 上．为了筹备材料，需求出“脚手架”三根木杆AB 、AD 、DC 的长度之和．．．．的最大值是多少？请你帮施工队计算一下.解:⑴()()12,0,6,6M P⑵（法1）设这条抛物线的函数解析式 为:()266y a x =-+ ∵抛物线过O(0,0) ∴06)60(2=+-a 解得16a =-∴这条抛物线的函数解析式为:()21666y x =--+ 即2126y x x =-+. （法2）设这条抛物线的函数解析式 为:c bx ax y ++=2∵抛物线过O(0,0),()()12,0,6,6M P 三点，∴⎪⎩⎪⎨⎧=+⋅+⋅=+⋅+⋅=01212666022c b a c b a c 解得：⎪⎪⎩⎪⎪⎨⎧==-=0261c b a ∴这条抛物线的函数解析式为:2126y x x =-+.⑶设点A 的坐标为21,26m m m ⎛⎫-+ ⎪⎝⎭∴OB=m ，AB=DC=m m 2612+-根据抛物线的轴对称,可得:OB CM m == ∴122BC m =- 即AD=12－2m ∴l ＝AB+AD+DC=m m m m m 26121226122+--++-=122312++-m m =15)3(312+--m∴当m=3，即OB=3米时，三根木杆长度之和l的最大值为15米.。

在中考数学中，抛物线是一个常见的考点，经常以压轴题的形式出现。

以下是一个关于抛物线的中考压轴题的示例：题目：已知抛物线y=ax^2+bx+c(a,b,c是常数，a≠0)经过点(-1,-1)，(0,1)，当x=-2时，与其对应的函数值y>1。

1. 请你求出abc的值，并判断抛物线的开口方向。

2. 设直线y=kx+d(k≠0)经过点(1,-1)，且与抛物线的对称轴平行。

请你求出该直线的解析式。

3. 设E(m,n)是抛物线y=ax^2+bx+c上的一个动点，且满足∠APE=90°，请你求出m的值。

解析：1. 根据题目条件，抛物线经过点(-1,-1)，(0,1)，可得到方程：$a-b+c=-1$ ①$c=1$ ②将x=-2，y>1代入解析式得：$4a-2b+1>1$化简得：$2a-b>0$ ③由①②③解得：$a>0$$b>0$$c=1$所以，abc=1。

由于a>0，抛物线开口向上。

2. 由题意知：直线y=kx+d经过点(1,-1)，则有：k+d=-1 ④又因为直线与对称轴平行，所以其斜率等于对称轴的斜率，即：k=-b/2a=-1/2 ⑤由④⑤解得：d=-3/2所以，直线的解析式为：y=-x/2-3/2。

3. 根据题意知：E(m,n)在抛物线上，则有：$n=am^2+bm+c$ ⑥由于∠APE=90°，所以AE与PE垂直。

根据两直线垂直的条件：斜率之积等于-1。

即：$(m-1)/(n+1)=-1$ ⑦由⑥⑦解得：m=0或m=-2综上所述，m的值为0或-2。

中考压轴题专项训练1——抛物线专题考点分析：命题预测：函数是数形结合的重要体现，是每年中考的必考内容，函数的概念主要用选择、填空的形式考查自变量的取值范围，及自变量与因变量的变化图像、平面直角坐标系等，一般占2%左右．一次函数与一次方程有紧密地联系，是中考必考内容，一般以填空、选择、解答题及综合题的形式考查，占5%左右．反比例函数的图像和性质的考查常以客观题形式出现，要关注反比例函数与实际问题的联系，突出应用价值，3—6分；二次函数是初中数学的一个十分重要的内容，是中考的热点，多以压轴题出现在试卷中．要求：能通过对实际问题情景分析确定二次函数的表达式，并体会二次函数的意义；会用描点法画二次函数图像，能丛图像上分析二次函数的性质；会根据公式确定图像的顶点、开口方向和对称轴，并能解决复杂的图形综合问题。

二次函数常考点汇总：1. 两点间的距离公式：22)()(AB B A B A x x y y -+-=2. 中点坐标公式：已知A ),(A A y x ，B ),(B B y x ，则线段AB 的中点C 的坐标为⎪⎭⎫⎝⎛++2,2B A B A y y x x 。

3. 在平面直角坐标系中求面积的方法：公式法、割补法（做铅垂高或水平宽） 4. 几何分析法：特别是构造“平行四边形”、“梯形”、“相似三角形”、“直角三角形”、“等腰三角形”等图形时，利用几何分析法能给解题带来方便。

例题精讲：1.如图，直线y＝﹣x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y＝﹣x2+bx+c 经过点A，B．（1）求点B的坐标和抛物线的解析式；（2）M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．①点M在线段OA上运动，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标；②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点（三点重合除外），则称M，P，N三点为“共谐点”．请直接写出使得M，P，N三点成为“共谐点”的m的值．2．如图①，抛物线y＝﹣x2+（a+1）x﹣a与x轴交于A，B两点（点A位于点B的左侧），与y轴交于点C．已知△ABC的面积是6．（1）求a的值；（2）求△ABC外接圆圆心的坐标；（3）如图②，P是抛物线上一点，Q为射线CA上一点，且P、Q两点均在第三象限内，Q、A是位于直线BP同侧的不同两点，若点P到x轴的距离为d，△QPB的面积为2d，且∠P AQ＝∠AQB，求点Q的坐标．3.已知，在平面直角坐标系xoy 中，点A 的坐标为（0，2），点P （m ，n ）是抛物线2114y x =+上的一个动点．（1）①如图1，过动点P 作PB ⊥x 轴，垂足为B ，连接PA ，求证：PA=PB ； ②如图2，设C 的坐标为（2，5），连接PC ，AP+PC 是否存在最小值？如果存在，求点P 的坐标；如果不存在，请说明理由；（2）如图3，过动点P 和原点O 作直线交抛物线于另一点D ，若AP=2AD ，求直线OP 的解析式．4.【变式】在平面直角坐标系xOy 中，抛物线21124y x =+的顶点为M ，直线2y x =，点()0P n ，为x 轴上的一个动点，过点P 作x 轴的垂线分别交抛物线21124y x =+和直线2y x =于点A ，点B.（1）直接写出A ，B 两点的坐标（用含n 的代数式表示）；⑵设线段AB 的长为d ，求d 关于n 的函数关系式及d 的最小值，并直接写出此时线段OB 与线段PM 的位置关系和数量关系；(3) 已知二次函数2y ax bx c =++（a ，b ，c 为整数且0a ≠），对一切实数x 恒有x ≤y ≤2124x +，求a ，b ，c 的值.5．如图，已知二次函数()21y x m x m =+--（其中0＜m ＜1）的图像与x 轴交于A 、B 两点（点A在点B 的左侧），与y 轴交于点C ，对称轴为直线l ．设P 为对称轴l 上的点，连接P A 、PC ，P A =PC ． （1）∠ABC 的度数为 °；（2）求P 点坐标（用含m 的代数式表示）；（3）在坐标轴上是否存在点Q （与原点O 不重合），使得以Q 、B 、C 为顶点的三角形与△P AC 相似，且线段PQ 的长度最小？如果存在，求出所有满足条件的点Q 的坐标；如果不存在，请说明理由．6.（本题满分10分）如图，二次函数2y x bx c =++的图像与x 轴交于A 、B 两点，与y 轴交于点C ，C OB =O ．点D 在函数图像上，CD//x 轴，且CD 2=，直线l 是抛物线的对称轴，E 是抛物线的顶点．（1）求b 、c 的值；（2）如图①，连接BE ，线段C O 上的点F 关于直线l 的对称点F '恰好在线段BE 上，求点F 的坐标； （3）如图②，动点P 在线段OB 上，过点P 作x 轴的垂线分别与C B 交于点M ，与抛物线交于点N ．试问：抛物线上是否存在点Q ，使得Q ∆P N 与∆APM 的面积相等，且线段Q N 的长度最小？如果存在，求出点Q 的坐标；如果不存在，说明理由．7．（8分）如图，已知抛物线y=x2﹣4与x轴交于点A，B（点A位于点B的左侧），C 为顶点，直线y=x+m经过点A，与y轴交于点D．（1）求线段AD的长；（2）平移该抛物线得到一条新拋物线，设新抛物线的顶点为C′．若新抛物线经过点D，并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD，求新抛物线对应的函数表达式．答案解析1.【解答】解：（1）∵y＝﹣x+c与x轴交于点A（3，0），与y轴交于点B，∴0＝﹣2+c，解得c＝2，∴B（0，2），∵抛物线y＝﹣x2+bx+c经过点A，B，∴，解得，∴抛物线解析式为y＝﹣x2+x+2；（2）①由（1）可知直线解析式为y＝﹣x+2，∵M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N，∴P（m，﹣m+2），N（m，﹣m2+m+2），∴PM＝﹣m+2，AM＝3﹣m，PN＝﹣m2+m+2﹣（﹣m+2）＝﹣m2+4m，∵△BPN和△APM相似，且∠BPN＝∠APM，∴∠BNP＝∠AMP＝90°或∠NBP＝∠AMP＝90°，当∠BNP＝90°时，则有BN⊥MN，∴N点的纵坐标为2，∴﹣m2+m+2＝2，解得m＝0（舍去）或m＝2.5，∴M（2.5，0）；当∠NBP＝90°时，过点N作NC⊥y轴于点C，则∠NBC+∠BNC＝90°，NC＝m，BC＝﹣m2+m+2﹣2＝﹣m2+m，∵∠NBP＝90°，∴∠NBC+∠ABO＝90°，∴∠ABO＝∠BNC，∴Rt△NCB∽Rt△BOA，∴＝，∴＝，解得m＝0（舍去）或m＝，∴M（，0）；综上可知当以B，P，N为顶点的三角形与△APM相似时，点M的坐标为（2.5，0）或（，0）；②由①可知M（m，0），P（m，﹣m+2），N（m，﹣m2+m+2），∵M，P，N三点为“共谐点”，∴有P为线段MN的中点、M为线段PN的中点或N为线段PM的中点，当P为线段MN的中点时，则有2（﹣m+2）＝﹣m2+m+2，解得m＝3（三点重合，舍去）或m＝；当M为线段PN的中点时，则有﹣m+2+（﹣m2+m+2）＝0，解得m＝3（舍去）或m＝﹣1；当N为线段PM的中点时，则有﹣m+2＝2（﹣m2+m+2），解得m＝3（舍去）或m＝﹣；综上可知当M，P，N三点成为“共谐点”时m的值为或﹣1或﹣．2．【解答】解：（1）∵y＝﹣x2+（a+1）x﹣a令y＝0，即﹣x2+（a+1）x﹣a＝0解得x1＝a，x2＝1由图象知：a＜0∴A（a，0），B（1，0）∵s△ABC＝6∴解得：a＝﹣3，（a＝4舍去）（2）设直线AC：y＝kx+b，由A（﹣3，0），C（0，3），可得﹣3k+b＝0，且b＝3∴k＝1即直线AC：y＝x+3，A、C的中点D坐标为（﹣，）∴线段AC的垂直平分线解析式为：y＝﹣x，线段AB的垂直平分线为x＝﹣1代入y＝﹣x，解得：y＝1∴△ABC外接圆圆心的坐标（﹣1，1）（3）作PM⊥x轴，则＝∵∴A、Q到PB的距离相等，∴AQ∥PB设直线PB解析式为：y＝x+b∵直线经过点B（1，0）所以：直线PB的解析式为y＝x﹣1联立解得：∴点P坐标为（﹣4，﹣5）又∵∠P AQ＝∠AQB可得：△PBQ≌△ABP（AAS）∴PQ＝AB＝4设Q（m，m+3）由PQ＝4得：解得：m＝﹣4，m＝﹣8（当m＝﹣8时，∠P AQ≠∠AQB，故应舍去）∴Q坐标为（﹣4，﹣1）3.【解答】解：（1）①设P（m，n）∴n=m2+1，∵PB⊥x 轴，∴PB=m2+1，∵A（0，2）∴AP==m2+1，∴PB=PA；②过点P作PB⊥x轴于B，由（1）得PA=PB，所以要使AP+CP最小，只需当BP+CP最小，因此当C，P，B共线时取得，此时点P的横坐标等于点C（2，5）的横坐标，所以点P的坐标为（2，2），（2）如图，作DE⊥x轴于E，作PF⊥x轴于F，由（1）得：DA=DE，PA=PF∵PA=2DA，∴PF=2DE，∵△ODE∽△OPF，∴==，设P（m，m2+1），则D（m，m2+）∵点D在抛物线y=x2+1上，∴m2+=（m）2+1，解得m=±2，∴P 1（，3），直线OP 的解析式为y=x ， P 2（﹣，3）直线OP 的解析式为y=﹣x ， 综上所求，所求直线OP 的解析式为y=x 或y=﹣x ．4.【解答】解：(1)21(2)4A n n +，，()B n n ，. (2) d =AB=A B y y -=2124n n -+.∴ d =2112()48n -+=2112()48n -+.∴ 当14n =时，d 取得最小值18. 当d 取最小值时，线段OB 与线段PM 的位置 关系和数量关系是OB ⊥PM 且OB=PM. (如图)(3) ∵对一切实数x 恒有 x ≤y ≤2124x +， ∴对一切实数x ，x ≤2ax bx c ++≤2124x +都成立. (0a ≠) ①当0x =时，①式化为 0≤c ≤14.xy111APBMO∴整数c 的值为0.此时，对一切实数x ，x ≤2ax bx +≤2124x +都成立.(0a ≠) 即 222,12.4x ax bx ax bx x ⎧≤+⎪⎨+≤+⎪⎩ 对一切实数x 均成立. 由②得 ()21ax b x +-≥0 (0a ≠) 对一切实数x 均成立.∴()210,10.a b >⎧⎪⎨∆=-≤⎪⎩ 由⑤得整数b 的值为1.此时由③式得，2ax x +≤2124x +对一切实数x 均成立. (0a ≠) 即21(2)4a x x --+≥0对一切实数x 均成立. (0a ≠) 当a=2时，此不等式化为14x -+≥0，不满足对一切实数x 均成立.当a≠2时，∵ 21(2)4a x x --+≥0对一切实数x 均成立，(0a ≠)∴2220,1(1)4(2)0.4a a ->⎧⎪⎨∆=--⨯-⨯≤⎪⎩∴由④，⑥，⑦得 0 <a ≤1.∴整数a 的值为1.∴整数a ，b ，c 的值分别为1a =，1b =，0c =.5．【解答】解：（1）45．理由如下：令x =0，则y =-m ，C 点坐标为（0，-m ）．令y =0，则()210x m x m +--=，解得11x =-，2x m =． ∵0＜m ＜1，点A 在点B 的左侧，∴B 点坐标为（m ，0）．∴OB =OC =m ．∵∠BOC ＝90°，∴△BOC 是等腰直角三角形，∠OBC ＝45°． （2）如图①，作PD ⊥y 轴，垂足为D ，设l 与x 轴交于点E ，由题意得，抛物线的对称轴为12mx -+=． 设点P 坐标为（12m-+，n ）． ∵P A = PC ， ∴P A 2= PC 2，即AE 2+ PE 2=CD 2+ PD 2．∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭．解得12m n -=．∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭． ④⑤② ③ ⑥ ⑦图①图②（3）存在点Q 满足题意．∵P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭， ∴P A 2+ PC 2=AE 2+ PE 2+CD 2+ PD 2=222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． ∵AC 2=21m +，∴P A 2+ PC 2=AC 2．∴∠APC ＝90°． ∴△P AC 是等腰直角三角形．∵以Q 、B 、C 为顶点的三角形与△P AC 相似， ∴△QBC 是等腰直角三角形．∴由题意知满足条件的点Q 的坐标为（-m ，0）或（0，m ）． ①如图①，当Q 点的坐标为（-m ，0）时，若PQ 与x 轴垂直，则12m m -+=-，解得13m =，PQ =13． 若PQ 与x 轴不垂直， 则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭． ∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ ．＜13， ∴当25m =，即Q 点的坐标为（25-，0）时， PQ 的长度最小．②如图②，当Q 点的坐标为（0，m ）时，若PQ 与y 轴垂直，则12m m -=，解得13m =，PQ =13． 若PQ 与y 轴不垂直， 则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭． ∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ ．＜13， ∴当25m =，即Q 点的坐标为（0，25）时， PQ 的长度最小．综上：当Q 点坐标为（25-，0）或（0，25）时，PQ 的长度最小．6. 【解答】解：（1）.3)(03,20.0,c -),,0(,.2,12.1x 2CD x //2-=∴=-=++=∴∴=-==-∴=∴=c c c c c c B c C OC OB b bl CD ，舍去或解得）点坐标为（：抛物线对称轴为直线，轴，（2）设点F 坐标为（0，m ）.∵对称轴是直线,1:=x l ∴点F 关于直线l 的对称点’F 的坐标为（2，m ）. ∵直线BE 经过点B （3,0），E （1，-4），∴利用待定系数法可得直线BE 的表达式为y=2x-6. ∵点’F 在BE 上，∴m=2⨯2-6=-2,即点F 的坐标为（0，-2）. （3）存在点Q 满足题意。

动点与抛物线专题复习一、平行四边形与抛物线1、（2012•钦州）如图甲，在平面直角坐标系中，A、B的坐标分别为（4，0）、（0，3），抛物线y=x2+bx+c经过点B，且对称轴是直线x=﹣．（1）求抛物线对应的函数解析式；（2）将图甲中△ABO沿x轴向左平移到△DCE（如图乙），当四边形ABCD是菱形时，请说明点C和点D都在该抛物线上；（3）在（2）中，若点M是抛物线上的一个动点（点M不与点C、D重合），经过点M作MN∥y轴交直线CD于N，设点M的横坐标为t，MN的长度为l，求l与t之间的函数解析式，并求当t为何值时，以M、N、C、E为顶点的四边形是平行四边形．（参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标为（﹣，），对称轴是直线x=﹣．）2、（2012•鸡西）如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x2﹣7x+12=0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点0运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒．（1）求A、B两点的坐标．（2）求当t为何值时，△APQ与△AOB相似，并直接写出此时点Q的坐标．（3）当t=2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．3.（2012•恩施州）如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N．其顶点为D．（1）抛物线及直线AC的函数关系式；（2）设点M（3，m），求使MN+MD的值最小时m的值；（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD 交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；（4）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．二、梯形与抛物线1、已知，在Rt△OAB中，∠OAB=90°，∠BOA=30°，AB=2．若以O为坐标原点，OA所在直线为x轴，建立如图所示的平面直角坐标系，点B在第一象限内．将Rt△OAB沿OB折叠后，点A落在第一象限内的点C处．（1）求点C的坐标；（2）若抛物线y=ax2+bx（a≠0）经过C、A两点，求此抛物线的解析式；（3）若上述抛物线的对称轴与OB交于点D，点P为线段DB上一动点，过P作y轴的平行线，交抛物线于点M，问：是否存在这样的点P，使得四边形CDPM为等腰梯形？若存在，请求出此时点P的坐标；若不存在，请说明理由．2、（2012•泉州）如图，O为坐标原点，直线l绕着点A（0，2）旋转，与经过点C（0，1）的二次函数y=x2+h的图象交于不同的两点P、Q．（1）求h的值；（2）通过操作、观察，算出△POQ的面积的最小值（不必说理）；（3）过点P、C作直线，与x轴交于点B，试问：在直线l的旋转过程中，四边形AOBQ是否为梯形？若是，请说明理由；若不是，请指出四边形的形状．3.（2012•玉林）如图，在平面直角坐标系xOy中，矩形AOCD的顶点A的坐标是（0，4），现有两动点P，Q，点P从点O出发沿线段OC（不包括端点O，C）以每秒2个单位长度的速度匀速向点C运动，点Q从点C出发沿线段CD（不包括端点C，D）以每秒1个单位长度的速度匀速向点D运动．点P，Q同时出发，同时停止，设运动时间为t（秒），当t=2（秒）时，PQ=2．（1）求点D的坐标，并直接写出t的取值范围．（2）连接AQ并延长交x轴于点E，把AE沿AD翻折交CD延长线于点F，连接EF，则△AEF的面积S是否随t的变化而变化？若变化，求出S与t的函数关系式；若不变化，求出S的值．（3）在（2）的条件下，t为何值时，四边形APQF是梯形？三、等腰三角形、菱形与抛物线1、（2012•龙岩）在平面直角坐标系xOy中，一块含60°角的三角板作如图摆放，斜边AB在x轴上，直角顶点C在y轴正半轴上，已知点A（﹣1，0）．（1）请直接写出点B、C的坐标：B、C；并求经过A、B、C三点的抛物线解析式；（2）现有与上述三角板完全一样的三角板DEF（其中∠EDF=90°，∠DEF=60°），把顶点E放在线段AB上（点E是不与A、B两点重合的动点），并使ED所在直线经过点C．此时，EF所在直线与（1）中的抛物线交于点M．①设AE=x，当x为何值时，△OCE∽△OBC；②在①的条件下探究：抛物线的对称轴上是否存在点P使△PEM是等腰三角形？若存在，请写出点P的坐标；若不存在，请说明理由．3、（2012•湛江）如图，在平面直角坐标系中，直角三角形AOB的顶点A、B分别落在坐标轴上．O为原点，点A的坐标为（6，0），点B的坐标为（0，8）．动点M从点O出发．沿OA向终点A以每秒1个单位的速度运动，同时动点N从点A出发，沿AB向终点B以每秒个单位的速度运动．当一个动点到达终点时，另一个动点也随之停止运动，设动点M、N运动的时间为t秒（t＞0）．（1）当t=3秒时．直接写出点N的坐标，并求出经过O、A、N三点的抛物线的解析式；（2）在此运动的过程中，△MNA的面积是否存在最大值？若存在，请求出最大值；若不存在，请说明理由；（3）当t为何值时，△MNA是一个等腰三角形？4、如图，直线l 1经过点A（﹣1，0），直线l2经过点B（3，0），l1、l2均为与y轴交于点C（0，），抛物线y=ax2+bx+c（a≠0）经过A、B、C三点．（1）求抛物线的函数表达式；（2）抛物线的对称轴依次与x轴交于点D、与l2交于点E、与抛物线交于点F、与l1交于点G．求证：DE=EF=FG；（3）若l1⊥l2于y轴上的C点处，点P为抛物线上一动点，要使△PCG为等腰三角形，请写出符合条件的点P的坐标，并简述理由．5、如图，在平面直角坐标系中，直角梯形OABC的边OC、OA分别与x轴、y轴重合，AB∥OC，∠AOC=90°，∠BCO=45°，BC=12，点C的坐标为（﹣18，0）．（1）求点B的坐标；（2）若直线DE交梯形对角线BO于点D，交y轴于点E，且OE=4，OD=2BD，求直线DE 的解析式；（3）若点P是（2）中直线DE上的一个动点，在坐标平面内是否存在点Q，使以O、E、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．6、（2012•铁岭）如图，已知抛物线经过原点O和x轴上一点A（4，0），抛物线顶点为E，它的对称轴与x轴交于点D．直线y=﹣2x﹣1经过抛物线上一点B（﹣2，m）且与y轴交于点C，与抛物线的对称轴交于点F．（1）求m的值及该抛物线对应的解析式；（2）P（x，y）是抛物线上的一点，若S△ADP=S△ADC，求出所有符合条件的点P的坐标；（3）点Q是平面内任意一点，点M从点F出发，沿对称轴向上以每秒1个单位长度的速度匀速运动，设点M的运动时间为t秒，是否能使以Q、A、E、M四点为顶点的四边形是菱形？若能，请直接写出点M的运动时间t的值；若不能，请说明理由．四、直角三角形与抛物线1、（2012•广州）如图，抛物线y=与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．（1）求点A、B的坐标；（2）设D为已知抛物线的对称轴上的任意一点，当△ACD的面积等于△ACB的面积时，求点D的坐标；（3）若直线l过点E（4，0），M为直线l上的动点，当以A、B、M为顶点所作的直角三角形有且只有三个时，求直线l的解析式．2、（2012•河池）如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=﹣x2+x+4经过A、B两点．（1）写出点A、点B的坐标；（2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接P A、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的最大面积；（3）在（2）的条件下，抛物线上是否存在一点P，使得△P AM是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．3.（2012•海南）如图，顶点为P（4，﹣4）的二次函数图象经过原点（0，0），点A在该图象上，OA交其对称轴l于点M，点M、N关于点P对称，连接AN、ON，（1）求该二次函数的关系式；（2）若点A在对称轴l右侧的二次函数图象上运动时，请解答下面问题：①证明：∠ANM=∠ONM；②△ANO能否为直角三角形？如果能，请求出所有符合条件的点A的坐标；如果不能，请说明理由．4、（2012•云南）如图，在平面直角坐标系中，直线y=x+2交x轴于点P，交y轴于点A．抛物线y=x2+bx+c的图象过点E（﹣1，0），并与直线相交于A、B两点．（1）求抛物线的解析式（关系式）；（2）过点A作AC⊥AB交x轴于点C，求点C的坐标；（3）除点C外，在坐标轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M的坐标；若不存在，请说明理由．五、相似三角形与抛物线1、（2012•福州）如图1，已知抛物线y=ax2+bx（a≠0）经过A（3，0）、B（4，4）两点．（1）求抛物线的解析式；（2）将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个公共点D，求m 的值及点D的坐标；（3）如图2，若点N在抛物线上，且∠NBO=∠ABO，则在（2）的条件下，求出所有满足△POD∽△NOB的点P坐标（点P、O、D分别与点N、O、B对应）．3、（2012•遵义）如图，已知抛物线y=ax2+bx+c（a≠0）的图象经过原点O，交x轴于点A，其顶点B的坐标为（3，﹣）．（1）求抛物线的函数解析式及点A的坐标；（2）在抛物线上求点P，使S△POA=2S△AOB；（3）在抛物线上是否存在点Q，使△AQO与△AOB相似？如果存在，请求出Q点的坐标；如果不存在，请说明理由．4.（2012•黄冈）如图，已知抛物线的方程C1：y=﹣（x+2）（x﹣m）（m＞0）与x轴相交于点B、C，与y轴相交于点E，且点B在点C的左侧．（1）若抛物线C1过点M（2，2），求实数m的值；（2）在（1）的条件下，求△BCE的面积；（3）在（1）条件下，在抛物线的对称轴上找一点H，使BH+EH最小，并求出点H的坐标；（4）在第四象限内，抛物线C1上是否存在点F，使得以点B、C、F为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．5、（2012•常德）如图，已知二次函数的图象过点A（﹣4，3），B（4，4）．（1）求二次函数的解析式：（2）求证：△ACB是直角三角形；（3）若点P在第二象限，且是抛物线上的一动点，过点P作PH垂直x轴于点H，是否存在以P、H、D为顶点的三角形与△ABC相似？若存在，求出点P的坐标；若不存在，请说明理由．6（2012•鞍山）如图，直线AB交x轴于点B（4，0），交y轴于点A（0，4），直线DM⊥x 轴正半轴于点M，交线段AB于点C，DM=6，连接DA，∠DAC=90°．（1）直接写出直线AB的解析式；（2）求点D的坐标；（3）若点P是线段MB上的动点，过点P作x轴的垂线，交AB于点F，交过O、D、B三点的抛物线于点E，连接CE．是否存在点P，使△BPF与△FCE相似？若存在，请求出点P的坐标；若不存在，请说明理由．7.（2012•阜新）在平面直角坐标系中，二次函数y=ax2+bx+2的图象与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C．（1）求这个二次函数的关系解析式；（2）点P是直线AC上方的抛物线上一动点，是否存在点P，使△ACP的面积最大？若存在，求出点P的坐标；若不存在，说明理由；考生注意：下面的（3）、（4）、（5）题为三选一的选做题，即只能选做其中一个题目，多答时只按作答的首题评分，切记啊！（3）在平面直角坐标系中，是否存在点Q，使△BCQ是以BC为腰的等腰直角三角形？若存在，直接写出点Q的坐标；若不存在，说明理由；（4）点Q是直线AC上方的抛物线上一动点，过点Q作QE垂直于x轴，垂足为E．是否存在点Q，使以点B、Q、E为顶点的三角形与△AOC相似？若存在，直接写出点Q的坐标；若不存在，说明理由；（5）点M为抛物线上一动点，在x轴上是否存在点Q，使以A、C、M、Q为顶点的四边形是平行四边形？若存在，直接写出点Q的坐标；若不存在，说明理由．六、抛物线中的翻折问题1、（2012•天门）如图，抛物线y=ax2+bx+2交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点．（1）求抛物线解析式及点D坐标；（2）点E在x轴上，若以A，E，D，P为顶点的四边形是平行四边形，求此时点P的坐标；（3）过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点为Q′．是否存在点P，使Q′恰好落在x轴上？若存在，求出此时点P的坐标；若不存在，说明理由．2、（2010•恩施州）如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．（1）求这个二次函数的表达式．（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．（3）当点P运动到什么位置时，四边形ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积．动点与抛物线专题复习答案一、平行四边形与抛物线1、解：（1）由于抛物线y=x2+bx+c与y轴交于点B（0，4），则c=4；∵抛物线的对称轴x=﹣=﹣，∴b=5a=；即抛物线的解析式：y=x2+x+4．（2）∵A（4，0）、B（3，0）∴OA=4，OB=3，AB==5；若四边形ABCD是菱形，则BC=AD=AB=5，∴C（﹣5，3）、D（﹣1，0）．将C（﹣5，3）代入y=x2+x+4中，得：×（﹣5）2+×（﹣5）+4=3，所以点C在抛物线上；同理可证：点D也在抛物线上．（3）设直线CD的解析式为：y=kx+b，依题意，有：，解得∴直线CD：y=﹣x﹣．由于MN∥y轴，设M（t，t2+t+4），则N（t，﹣t﹣）；①t＜﹣5或t＞﹣1时，l=MN=（t2+t+4）﹣（﹣t﹣）=t2+t+；②﹣5＜t＜﹣1时，l=MN=（﹣t﹣）﹣（t2+t+4）=﹣t2﹣t﹣；若以M、N、C、E为顶点的四边形是平行四边形，由于MN∥CE，则MN=CE=3，则有：t2+t+=3，解得：t=﹣3±2；﹣t2﹣t﹣=3，解得：t=﹣3；综上，l=且当t=﹣3±2或﹣3时，以M、N、C、E为顶点的四边形是平行四边形．2、解：（1）解方程x2﹣7x+12=0，得x1=3，x2=4，∵OA＜OB，∴OA=3，OB=4．∴A（0，3），B（4，0）．（2）在Rt△AOB中，OA=3，OB=4，∴AB=5，∴AP=t，QB=2t，AQ=5﹣2t．△APQ与△AOB相似，可能有两种情况：（I）△APQ∽△AOB，如图（2）a所示．则有，即，解得t=．此时OP=OA﹣AP=，PQ=AP•tanA=，∴Q（，）；（II）△APQ∽△ABO，如图（2）b所示．则有，即，解得t=．此时AQ=，AH=AQ•cosA=，HQ=AQ•sinA=，OH=OA﹣AH=，∴Q（，）．综上所述，当t=秒或t=秒时，△APQ与△AOB相似，所对应的Q点坐标分别为（，）或（，）．（3）结论：存在．如图（3）所示．∵t=2，∴AP=2，AQ=1，OP=1．过Q点作QE⊥y轴于点E，则QE=AQ•sin∠QAP=，AE=AQ•cos∠QAP=，∴OE=OA﹣AE=，∴Q（，）．∵▱APQM1，∴QM1⊥x轴，且QM1=AP=2，∴M1（，）；∵▱APQM2，∴QM2⊥x轴，且QM2=AP=2，∴M2（，）；如图（3），过M3点作M3F⊥y轴于点F，∵▱AQPM3，∴M3P=AQ，∠QAE=∠M3PF，∴∠PM3F=∠AQE；在△M3PF与△QAE中，∵∠QAE=∠M3PF，M3P=AQ，∠PM3F=∠AQE，∴△M3PF≌△QAE，∴M3F=QE=，PF=AE=，∴OF=OP+PF=，∴M3（﹣，）．∴当t=2时，在坐标平面内，存在点M，使以A、P、Q、M为顶点的四边形是平行四边形．点M的坐标为：M1（，），M2（，），M3（﹣，）．3.解：（1）由抛物线y=﹣x2+bx+c过点A（﹣1，0）及C（2，3）得，，解得，故抛物线为y=﹣x2+2x+3又设直线为y=kx+n过点A（﹣1，0）及C（2，3）得，解得故直线AC为y=x+1；（2）作N点关于直线x=3的对称点N′，则N′（6，3），由（1）得D（1，4），故直线DN′的函数关系式为y=﹣x+，当M（3，m）在直线DN′上时，MN+MD的值最小，则m=﹣×=；（3）由（1）、（2）得D（1，4），B（1，2）∵点E在直线AC上，设E（x，x+1），①当点E在线段AC上时，点F在点E上方，则F（x，x+3），∵F在抛物线上，∴x+3=﹣x2+2x+3，解得，x=0或x=1（舍去）∴E（0，1）；②当点E在线段AC（或CA）延长线上时，点F在点E下方，则F（x，x﹣1）由F在抛物线上∴x﹣1=﹣x2+2x+3解得x=或x=∴E（，）或（，）综上，满足条件的点E为E（0，1）、（，）或（，）；（4）过点P作PQ⊥x轴交AC于点Q，交x轴于点H；过点C作CG⊥x轴于点G，如图2，设Q（x，x+1），则P（x，﹣x2+2x+3）又∵S△APC=S△APH+S直角梯形PHGC﹣S△AGC=（x+1）（﹣x2+2x+3）+（﹣x2+2x+3+3）（2﹣x）﹣×3×3=﹣x2+x+3=﹣（x﹣）2+∴△APC的面积的最大值为．二、梯形与抛物线1、解：（1）过点C作CH⊥x轴，垂足为H；∵在Rt△OAB中，∠OAB=90°，∠BOA=30°，AB=2，∴OB=4，OA=2；由折叠的性质知：∠COB=30°，OC=AO=2，∴∠COH=60°，OH=，CH=3；∴C点坐标为（，3）．（2）∵抛物线y=ax2+bx（a≠0）经过C（，3）、A（2，0）两点，∴，解得；∴此抛物线的函数关系式为：y=﹣x2+2x．（3）存在．因为y=﹣x2+2x的顶点坐标为（，3），即为点C，MP⊥x轴，垂足为N，设PN=t；因为∠BOA=30°，所以ON=t，∴P（t，t）；作PQ⊥CD，垂足为Q，ME⊥CD，垂足为E；把x=t代入y=﹣x2+2x，得y=﹣3t2+6t，∴M（t，﹣3t2+6t），E（，﹣3t2+6t），同理：Q（，t），D（，1）；要使四边形CDPM为等腰梯形，只需CE=QD，即3﹣（﹣3t2+6t）=t﹣1，解得t=，t=1（舍），∴P点坐标为（，），∴存在满足条件的P点，使得四边形CDPM为等腰梯形，此时P点坐标为（，）．2、解：（1）∵抛物线y=x2+h经过点C（0，1），∴+h=1，解得h=1．（2）依题意，设抛物线y=x2+1上的点，P（a，a2+1）、Q（b，b2+1）（a＜0＜b）过点A的直线l：y=kx+2经过点P、Q，∴a2+1=ak+2…①b2+1=bk+2…②①×b﹣②×a得：（a2b﹣b2a）+b﹣a=2（b﹣a），化简得：b=﹣；∴S△POQ=OA•|x Q﹣x P|=•OA•|﹣﹣a|=（﹣）+（﹣a）≥2•=4 由上式知：当﹣=﹣a，即|a|=|b|（P、Q关于y轴对称）时，△POQ的面积最小；即PQ∥x轴时，△POQ的面积最小，且POQ的面积最小为4．（3）连接BQ，若l与x轴不平行（如图），即PQ与x轴不平行，依题意，设抛物线y=x2+1上的点，P（a，a2+1）、Q（b，b2+1）（a＜0＜b）直线BC：y=k1x+1过点P，∴a2+1=ak1+1，得k1=﹣a，即y=ax+1．令y=0得：x B=﹣，同理，由（2）得：b=﹣∴点B与Q的横坐标相同，∴BQ∥y轴，即BQ∥OA，又∵AQ与OB不平行，∴四边形AOBQ是梯形，据抛物线的对称性可得（a＞0＞b）结论相同．故在直线l旋转的过程中：当l与x轴不平行时，四边形AOBQ是梯形；当l与x轴平行时，四边形AOBQ是正方形．3.解：（1）由题意可知，当t=2（秒）时，OP=4，CQ=2，在Rt△PCQ中，由勾股定理得：PC===4，∴OC=OP+PC=4+4=8，又∵矩形AOCD，A（0，4），∴D（8，4）．点P到达终点所需时间为=4秒，点Q到达终点所需时间为=4秒，由题意可知，t的取值范围为：0＜t＜4．（2）结论：△AEF的面积S不变化．∵AOCD是矩形，∴AD∥OE，∴△AQD∽△EQC，∴，即，解得CE=．由翻折变换的性质可知：DF=DQ=4﹣t，则CF=CD+DF=8﹣t．S=S梯形AOCF+S△FCE﹣S△AOE=（OA+CF）•OC+CF•CE﹣OA•OE=[4+（8﹣t）]×8+（8﹣t）•﹣×4×（8+）化简得：S=32为定值．所以△AEF的面积S不变化，S=32．（3）若四边形APQF是梯形，因为AP与CF不平行，所以只有PQ∥AF．由PQ∥AF可得：△CPQ∽△DAF，∴，即，化简得t2﹣12t+16=0，解得：t1=6+2，t2=6﹣2，由（1）可知，0＜t＜4，∴t1=6+2不符合题意，舍去．∴当t=（6﹣2）秒时，四边形APQF是梯形．三、等腰三角形、菱形与抛物线1、解：（1）∵点A（﹣1，0），∴OA=1，由图可知，∠BAC是三角板的60°角，∠ABC是30°角，所以，OC=OA•tan60°=1×=，OB=OC•cot30°=×=3，所以，点B（3，0），C（0，），设抛物线解析式为y=ax2+bx+c，则，解得，所以，抛物线的解析式为y=﹣x2+x+；（2）①∵△OCE∽△OBC，∴=，即=，解得OE=1，所以，AE=OA+OE=1+1=2，即x=2时，△OCE∽△OBC；②存在．理由如下：抛物线的对称轴为x=﹣=﹣=1，所以，点E为抛物线的对称轴与x轴的交点，∵OA=OE，OC⊥x轴，∠BAC=60°，∴△ACE是等边三角形，∴∠AEC=60°，又∠DEF=60°，∴∠FEB=60°，∴∠BAC=∠FEB，∴EF∥AC，由A（﹣1，0），C（0，）可得直线AC的解析式为y=x+，∵点E（1，0），∴直线EF的解析式为y=x﹣，联立，解得，（舍去），∴点M的坐标为（2，），EM==2，分三种情况讨论△PEM是等腰三角形，当PE=EM时，PE=2，所以，点P的坐标为（1，2）或（1，﹣2），当PE=PM时，∵∠FEB=60°，∴∠PEF=90°﹣60°=30°，PE=EM÷cos30°=×2÷=，所以，点P的坐标为（1，），当PM=EM时，PE=2EM•cos30°=2×2×=2，所以，点P的坐标为（1，2），综上所述，抛物线对称轴上存在点P（1，2）或（1，﹣2）或（1，）或（1，2），使△PEM是等腰三角形．3、解：（1）由题意，A（6，0）、B（0，8），则OA=6，OB=8，AB=10；当t=3时，AN=t=5=AB，即N是线段AB的中点；∴N（3，4）．设抛物线的解析式为：y=ax（x﹣6），则：4=3a（3﹣6），a=﹣；∴抛物线的解析式：y=﹣x（x﹣6）=﹣x2+x．（2）过点N作NC⊥OA于C；由题意，AN=t，AM=OA﹣OM=6﹣t，NC=NA•sin∠BAO=t•=t；则：S△MNA=AM•NC=×（6﹣t）×t=﹣（t﹣3）2+6．∴△MNA的面积有最大值，且最大值为6．（3）Rt△NCA中，AN=t，NC=AN•sin∠BAO=t，AC=AN•cos∠BAO=t；∴OC=OA﹣AC=6﹣t，∴N（6﹣t，t）．∴NM==；又：AM=6﹣t，AN=t（0＜t＜6）；①当MN=AN时，=t，即：t2﹣8t+12=0，t1=2，t2=6（舍去）；②当MN=MA时，=6﹣t，即：t2﹣12t=0，t1=0（舍去），t2=；③当AM=AN时，6﹣t=t，即t=；综上，当t的值取2或或时，△MAN是等腰三角形．4、解：（1）抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（3，0），C（0，）三点，∴，解得a=，b=，c=，∴抛物线的解析式为：y=x2x．（2）设直线l1的解析式为y=kx+b，由题意可知，直线l1经过A（﹣1，0），C（0，）两点，∴，解得k=，b=，∴直线l1的解析式为：y=x；直线l2经过B（3，0），C（0，）两点，同理可求得直线l2解析式为：y=x．∵抛物线y=x2x=（x﹣1）2，∴对称轴为x=1，D（1，0），顶点坐标为F（1，）；点E为x=1与直线l2：y=x的交点，令x=1，得y=，∴E（1，）；点G为x=1与直线l1：y=x的交点，令x=1，得y=，∴G（1，）．∴各点坐标为：D（1，0），E（1，），F（1，），G（1，），它们均位于对称轴x=1上，∴DE=EF=FG=．（3）如右图，过C点作C关于对称轴x=1的对称点P1，CP1交对称轴于H点，连接CF．△PCG为等腰三角形，有三种情况：①当CG=PG时，如右图，由抛物线的对称性可知，此时P1满足P1G=CG．∵C（0，），对称轴x=1，∴P1（2，）．②当CG=PC时，此时P点在抛物线上，且CP的长度等于CG．如右图，C（1，），H点在x=1上，∴H（1，），在Rt△CHG中，CH=1，HG=|y G﹣y H|=|﹣（）|=，∴由勾股定理得：CG==2．∴PC=2．如右图，CP1=2，此时与①中情形重合；又Rt△OAC中，AC==2，∴点A满足PC=2的条件，但点A、C、G在同一条直线上，所以不能构成等腰三角形．③当PC=PG时，此时P点位于线段CG的垂直平分线上．∵l1⊥l2，∴△ECG为直角三角形，由（2）可知，EF=FG，即F为斜边EG的中点，∴CF=FG，∴F为满足条件的P点，∴P2（1，）；又cos∠CGE==，∴∠CGE=30°，∴∠HCG=60°，又P1C=CG，∴△P1CG为等边三角形，∴P1点也在CG的垂直平分线上，此种情形与①重合．综上所述，P点的坐标为P1（2，）或P2（1，）．5、解：（1）过点B作BF⊥x轴于F在Rt△BCF中∵∠BCO=45°，BC=6∴CF=BF=12∵C的坐标为（﹣18，0）∴AB=OF=6∴点B的坐标为（﹣6，12）．（2）过点D作DG⊥y轴于点G∵AB∥DG∴△ODG∽△OBA∵===，AB=6，OA=12∴DG=4，OG=8∴D（﹣4，8），E（0，4）设直线DE解析式为y=kx+b（k≠0）∴∴∴直线DE解析式为y=﹣x+4．（3）结论：存在．设直线y=﹣x+4分别与x轴、y轴交于点E、点F，则E（0，4），F（4，0），OE=OF=4，EF=4．如答图2所示，有四个菱形满足题意．①菱形OEP1Q1，此时OE为菱形一边．则有P1E=P1Q1=OE=4，P1F=EF﹣P1E=4﹣4．易知△P1NF为等腰直角三角形，∴P1N=NF=P1F=4﹣2；设P1Q1交x轴于点N，则NQ1=P1Q1﹣P1N=4﹣（4﹣2）=2，又ON=OF﹣NF=2，∴Q1（2，﹣2）；②菱形OEP2Q2，此时OE为菱形一边．此时Q2与Q1关于原点对称，∴Q2（﹣2，2）；③菱形OEQ3P3，此时OE为菱形一边．此时P3与点F重合，菱形OEQ3P3为正方形，∴Q3（4，4）；④菱形OP4EQ4，此时OE为菱形对角线．由菱形性质可知，P4Q4为OE的垂直平分线，由OE=4，得P4纵坐标为2，代入直线解析式y=﹣x+4得横坐标为2，则P4（2，2），由菱形性质可知，P4、Q4关于OE或x轴对称，∴Q4（﹣2，2）．综上所述，存在点Q，使以O、E、P、Q为顶点的四边形是菱形；点Q的坐标为：Q1（2，﹣2），Q2（﹣2，2），Q3（4，4），Q4（﹣2，2）．6、解：（1）∵点B（﹣2，m）在直线y=﹣2x﹣1上∴m=3 即B（﹣2，3）又∵抛物线经过原点O∴设抛物线的解析式为y=ax2+bx∵点B（﹣2，3），A（4，0）在抛物线上∴，解得：．∴设抛物线的解析式为．（2）∵P（x，y）是抛物线上的一点，∴，若S△ADP=S△ADC，∵，，又∵点C是直线y=﹣2x﹣1与y轴交点，∴C（0，1），∴OC=1，∴，即或，解得：．∴点P的坐标为．（3）结论：存在．∵抛物线的解析式为，∴顶点E（2，﹣1），对称轴为x=2；点F是直线y=﹣2x﹣1与对称轴x=2的交点，∴F（2，﹣5），DF=5．又∵A（4，0），∴AE=．如右图所示，在点M的运动过程中，依次出现四个菱形：①菱形AEM1Q1．∵此时DM1=AE=，∴M1F=DF﹣DE﹣DM1=4﹣，∴t1=4﹣；②菱形AEOM2．∵此时DM2=DE=1，∴M2F=DF+DM2=6，∴t2=6；③菱形AEM3Q3．∵此时EM3=AE=，∴DM3=EM3﹣DE=﹣1，∴M3F=DM3+DF=（﹣1）+5=4+，∴t3=4+；④菱形AM4EQ4．此时AE为菱形的对角线，设对角线AE与M4Q4交于点H，则AE⊥M4Q4，∵易知△AED∽△M4EH，∴，即，得M4E=，∴DM4=M4E﹣DE=﹣1=，∴M4F=DM4+DF=+5=，∴t4=．综上所述，存在点M、点Q，使得以Q、A、E、M四点为顶点的四边形是菱形；时间t的值为：t1=4﹣，t2=6，t3=4+，t4=．四、直角三角形与抛物线1、解：（1）令y=0，即=0，解得x1=﹣4，x2=2，∴A、B点的坐标为A（﹣4，0）、B（2，0）．（2）S△ACB=AB•OC=9，在Rt△AOC中，AC===5，设△ACD中AC边上的高为h，则有AC•h=9，解得h=．如答图1，在坐标平面内作直线平行于AC，且到AC的距离=h=，这样的直线有2条，分别是l1和l2，则直线与对称轴x=﹣1的两个交点即为所求的点D．设l1交y轴于E，过C作CF⊥l1于F，则CF=h=，∴CE==．设直线AC的解析式为y=kx+b，将A（﹣4，0），B（0，3）坐标代入，得到，解得，∴直线AC解析式为y=x+3．直线l1可以看做直线AC向下平移CE长度单位（个长度单位）而形成的，∴直线l1的解析式为y=x+3﹣=x﹣．则D1的纵坐标为×（﹣1）﹣=，∴D1（﹣4，）．同理，直线AC向上平移个长度单位得到l2，可求得D2（﹣1，）综上所述，D点坐标为：D1（﹣4，），D2（﹣1，）．（3）如答图2，以AB为直径作⊙F，圆心为F．过E点作⊙F的切线，这样的切线有2条．连接FM，过M作MN⊥x轴于点N．∵A（﹣4，0），B（2，0），∴F（﹣1，0），⊙F半径FM=FB=3．又FE=5，则在Rt△MEF中，ME==4，sin∠MFE=，cos∠MFE=．在Rt△FMN中，MN=MN•sin∠MFE=3×=，FN=MN•cos∠MFE=3×=，则ON=，∴M点坐标为（，）直线l过M（，），E（4，0），设直线l的解析式为y=kx+b，则有，解得，所以直线l的解析式为y=x+3．同理，可以求得另一条切线的解析式为y=x﹣3．综上所述，直线l的解析式为y=x+3或y=x﹣3．2、解：（1）抛物线y=﹣x2+x+4中：令x=0，y=4，则B（0，4）；令y=0，0=﹣x2+x+4，解得x1=﹣1、x2=8，则A（8，0）；∴A（8，0）、B（0，4）．（2）△ABC中，AB=AC，AO⊥BC，则OB=OC=4，∴C（0，﹣4）．由A（8，0）、B（0，4），得：直线AC：y=﹣x+4；依题意，知：OE=2t，即E（2t，0）；∴P（2t，﹣2t2+7t+4）、Q（2t，﹣t+4），PQ=（﹣2t2+7t+4）﹣（﹣t+4）=﹣2t2+8t；S=S△ABC+S△P AB=×8×8+×（﹣2t2+8t）×8=﹣8t2+32t+32=﹣8（t﹣2）2+64；∴当t=2时，S有最大值，且最大值为64．（3）∵PM∥y轴，∴∠AMP=∠ACO＜90°；而∠APM是锐角，所以△P AM若是直角三角形，只能是∠P AM=90°；由A（8，0）、C（0，﹣4），得：直线AC：y=x﹣4；所以，直线AP可设为：y=﹣2x+h，代入A（8，0），得：﹣16+h=0，h=16∴直线AP：y=﹣2x+16，联立抛物线的解析式，得：，解得、∴存在符合条件的点P，且坐标为（3，10）．3.解：（1）∵二次函数的顶点坐标为（4，﹣4），∴设二次函数的解析式为y=a（x﹣4）2﹣4，又二次函数过（0，0），∴0=a（0﹣4）2﹣4，解得：a=，∴二次函数解析式为y=（x﹣4）2﹣4=x2﹣2x；（2）①证明：过A作AH⊥l于H，l与x轴交于点D，如图所示：设A（m，m2﹣2m），又O（0，0），∴直线AO的解析式为y=x=（m﹣2）x，则M（4，m﹣8），N（4，﹣m），H（4，m2﹣2m），∴OD=4，ND=m，HA=m﹣4，NH=ND﹣HD=m2﹣m，在Rt△OND中，tan∠ONM==，在Rt△ANH中，tan∠ANM====，∴tan∠ONM=tan∠ANM，则∠ANM=∠ONM；②△ANO不能为直角三角形，理由如下：分三种情况考虑：（i）若∠ONA为直角，由①得：∠ANM=∠ONM=45°，∴△AHN为等腰直角三角形，∴HA=NH，即m﹣4=m2﹣m，整理得：m2﹣8m+16=0，即（m﹣4）2=0，解得：m=4，此时点A与点P重合，故不存在A点使△ONA为直角三角形；（ii）若∠AON为直角，根据勾股定理得：OA2+ON2=AN2，∵OA2=m2+（m2﹣2m）2，ON2=42+m2，AN2=（m﹣4）2+（m2﹣2m+m）2，∴m2+（m2﹣2m）2+42+m2=（m﹣4）2+（m2﹣2m+m）2，整理得：m（m﹣4）2=0，解得：m=0或m=4，此时A点与P点重合或与原点重合，故∠AON不能为直角；（iii）若∠NAO为直角，可得∠NAM=∠ODM=90°，且∠AMN=∠DMO，∴△AMN∽△DMO，又∠MAN=∠ODN=90°，且∠ANM=∠OND，∴△AMN∽△DON，∴△AMN∽△DMO∽△DON，∴=，即=，整理得：（m﹣4）2=0，解得：m=4，此时A与P重合，故∠NAO不能为直角，综上，点A在对称轴l右侧的二次函数图象上运动时，△ANO不能为直角三角形4、解：（1）直线解析式为y=x+2，令x=0，则y=2，∴A（0，2），∵抛物线y=x2+bx+c的图象过点A（0，2），E（﹣1，0），∴，解得．∴抛物线的解析式为：y=x2+x+2．（2）∵直线y=x+2分别交x轴、y轴于点P、点A，∴P（6，0），A（0，2），∴OP=6，OA=2．∵AC⊥AB，OA⊥OP，∴Rt△OCA∽Rt△OP A，∴，∴OC=，又C点在x轴负半轴上，∴点C的坐标为C（，0）．（3）抛物线y=x2+x+2与直线y=x+2交于A、B两点，令x2+x+2=x+2，解得x1=0，x2=，∴B（，）．如答图①所示，过点B作BD⊥x轴于点D，则D（，0），BD=，DP=6﹣=．点M在坐标轴上，且△MAB是直角三角形，有以下几种情况：①当点M在x轴上，且BM⊥AB，如答图①所示．设M（m，0），则MD=﹣m．∵BM⊥AB，BD⊥x轴，∴，即，解得m=，∴此时M点坐标为（，0）；②当点M在x轴上，且BM⊥AM，如答图①所示．设M（m，0），则MD=﹣m．∵BM⊥AM，易知Rt△AOM∽Rt△MDB，∴，即，化简得：m2﹣m+=0，解得：x1=，x2=，∴此时M点坐标为（，0），（，0）；（说明：此时的M点相当于以AB为直径的圆与x轴的两个交点）③当点M在y轴上，且BM⊥AM，如答图②所示．此时M点坐标为（0，）；④当点M在y轴上，且BM′⊥AB，如答图②所示．设M′（0，m），则AM=2﹣=，BM=，MM′=﹣m．易知Rt△ABM∽Rt△MBM′，∴，即，解得m=，∴此时M点坐标为（0，）．综上所述，除点C外，在坐标轴上存在点M，使得△MAB是直角三角形．符合条件的点M有5个，其坐标分别为：（，0）、（，0）、（，0）、（0，）或（0，）．五、相似三角形与抛物线1、解：（1）∵抛物线y=y=ax2+bx（a≠0）经过A（3，0）、B（4，4）∴，解得：∴抛物线的解析式是y=x2﹣3x．（2）设直线OB的解析式为y=k1x，由点B（4，4），得：4=4k1，解得：k1=1∴直线OB的解析式为y=x，∴直线OB向下平移m个单位长度后的解析式为：y=x﹣m，∵点D在抛物线y=x2﹣3x上，∴可设D（x，x2﹣3x），又点D在直线y=x﹣m上，∴x2﹣3x=x﹣m，即x2﹣4x+m=0，∵抛物线与直线只有一个公共点，∴△=16﹣4m=0，解得：m=4，此时x1=x2=2，y=x2﹣3x=﹣2，∴D点的坐标为（2，﹣2）．（3）∵直线OB的解析式为y=x，且A（3，0），∴点A关于直线OB的对称点A′的坐标是（0，3），设直线A′B的解析式为y=k2x+3，过点（4，4），∴4k2+3=4，解得：k2=，∴直线A′B的解析式是y=，∵∠NBO=∠ABO，∴点N在直线A′B上，∴设点N（n，），又点N在抛物线y=x2﹣3x上，∴=n2﹣3n，解得：n1=﹣，n2=4（不合题意，舍去）∴N点的坐标为（﹣，）．方法一：如图1，将△NOB沿x轴翻折，得到△N1OB1，则N1（，），B1（4，﹣4），∴O、D、B1都在直线y=﹣x上．∵△P1OD∽△NOB，∴△P1OD∽△N1OB1，∴，∴点P1的坐标为（，）．将△OP1D沿直线y=﹣x翻折，可得另一个满足条件的点P2（，），综上所述，点P的坐标是（，）或（，）．2、解：（1）设函数解析式为：y=ax2+bx+c，由函数经过点A（﹣4，0）、B（1，0）、C（﹣2，6），可得，解得：，故经过A、B、C三点的抛物线解析式为：y=﹣x2﹣3x+4；（2）设直线BC的函数解析式为y=kx+b，由题意得：，解得：，即直线BC的解析式为y=﹣2x+2．故可得点E的坐标为（0，2），从而可得：AE==2，CE==2，故可得出AE=CE；（3）相似．理由如下：设直线AD的解析式为y=kx+b，则，解得：，即直线AD的解析式为y=x+4．联立直线AD与直线BC的函数解析式可得：，解得：，即点F的坐标为（﹣，），则BF==，AF==，又∵AB=5，BC==3，∴=，=，∴=，又∵∠ABF=∠CBA，∴△ABF∽△CBA．故以A、B、F为顶点的三角形与△ABC相似．3、解：（1）由函数图象经过原点得，函数解析式为y=ax2+bx（a≠0），又∵函数的顶点坐标为（3，﹣），∴，解得：，故函数解析式为：y=x2﹣x，由二次函数图象的对称性可得点A的坐标为（6，0）；（2）∵S△POA=2S△AOB，∴点P到OA的距离是点B到OA距离的2倍，即点P的纵坐标为2，代入函数解析式得：2=x2﹣x，解得：x1=3+，x2=3﹣，即可得满足条件的有两个，P1（3+，2），P2（3﹣，2）．（3）存在．过点B作BP⊥OA，则tan∠BAP==，故可得∠BOA=60°，设Q1坐标为（x，x2﹣x），过点Q1作Q1F⊥x轴，∵△OAB∽△OQ1A，∴∠Q1OA=30°，故可得OF=Q1F，即x=（x2﹣x），解得：x=9或x=0（舍去），即可得Q1坐标为（9，3），根据函数的对称性可得Q2坐标为（﹣3，3）．4.解：（1）依题意，将M（2，2）代入抛物线解析式得：2=﹣（2+2）（2﹣m），解得m=4．（2）令y=0，即（x+2）（x﹣4）=0，解得x1=﹣2，x2=4，∴B（﹣2，0），C（4，0）在C1中，令x=0，得y=2，∴E（0，2）．∴S△BCE=BC•OE=6．（3）当m=4时，易得对称轴为x=1，又点B、C关于x=1对称．如答图1，连接BC，交x=1于H点，此时BH+CH最小（最小值为线段CE的长度）．设直线EC：y=kx+b，将E（0，2）、C（4，0）代入得：y=x+2，当x=1时，y=，∴H（1，）．（4）分两种情形讨论：①当△BEC∽△BCF时，如答图2所示．则，∴BC2=BE•BF．由（2）知B（﹣2，0），E（0，2），即OB=OB，∴∠EBC=45°，∴∠CBF=45°，作FT⊥x轴于点F，则BT=TF．∴可令F（x，﹣x﹣2）（x＞0），又点F在抛物线上，∴﹣x﹣2=﹣（x+2）（x﹣m），∵x+2＞0（∵x＞0），∴x=2m，F（2m，﹣2m﹣2）．。

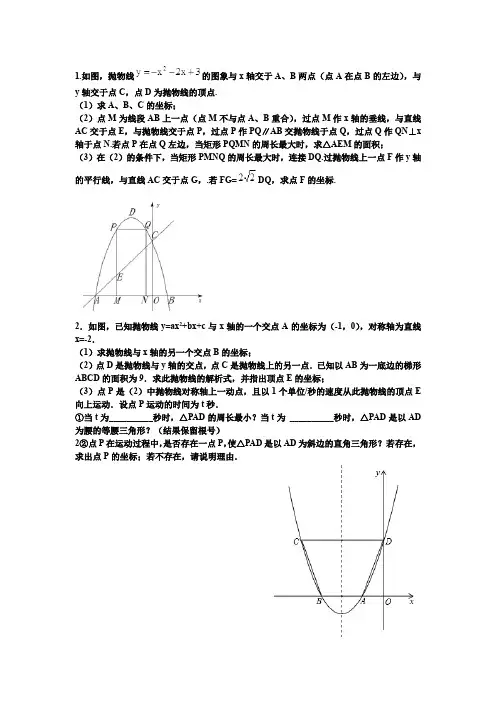
1.如图，抛物线的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点.（1）求A、B、C的坐标；（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x 轴于点N.若点P在点Q左边，当矩形PQMN的周长最大时，求△AEM的面积；（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ.过抛物线上一点F作y轴的平行线，与直线AC交于点G，.若FG=DQ，求点F的坐标.2．如图，已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为（-1，0），对称轴为直线x=-2．（1）求抛物线与x轴的另一个交点B的坐标；（2）点D是抛物线与y轴的交点，点C是抛物线上的另一点．已知以AB为一底边的梯形ABCD的面积为9．求此抛物线的解析式，并指出顶点E的坐标；（3）点P是（2）中抛物线对称轴上一动点，且以1个单位/秒的速度从此抛物线的顶点E 向上运动．设点P运动的时间为t秒．①当t为__________秒时，△PAD的周长最小？当t为__________秒时，△PAD是以AD 为腰的等腰三角形？（结果保留根号）2②点P在运动过程中，是否存在一点P，使△PAD是以AD为斜边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．3.如图，已知抛物线2y ax bx c =++的顶点坐标为Q （2，-1），且与轴交于点C （0,3），与轴交于A 、B 两点（点A 在点B 的右侧），点P 是该抛物线上一动点，从点C 沿抛物线向点A 运动（点P 与A 不重合），过点P 作PD ∥轴， 交AC 于点D ．(1)求该抛物线的函数关系式；(2)当△ADP 是直角三角形时，求点P 的坐标；(3)在问题(2)的结论下，若点E 在轴上，点F 在抛物线上，问是否存在以A 、P 、E 、F 为顶点的平行四边形？若存在，求点F 的坐标；若不存在，请说明理由．4.如图，在平面直角坐标系中，点A 的坐标为（m ，m ），点B 的坐标为（n ，-n ），抛物线经过A 、O 、B 三点，连接OA 、OB 、AB ，线段AB 交y 轴于点C ．已知实数m 、n （m ＜n ）分别是方程x 2-2x-3=0的两根． （1）求抛物线的解析式；（2）若点P 为线段OB 上的一个动点（不与点O 、B 重合），直线PC 与抛物线交于D 、E 两点（点D 在y 轴右侧），连接OD 、BD ． ①当△OPC 为等腰三角形时，求点P 的坐标；②求△BOD 面积的最大值，并写出此时点D 的坐标．y x y x 图165．如图，抛物线y=a（x-h）2+k经过点A（0，1），且顶点坐标为B（1，2），它的对称轴与x轴交于点C．（1）求此抛物线的解析式．（2）在第一象限内的抛物线上求点P，使得△ACP是以AC为底的等腰三角形，请求出此时点P的坐标．（3）上述点是否是第一象限内此抛物线上与AC距离最远的点？若是，请说明理由；若不是，请求出第一象限内此抛物线上与AC距离最远的点的坐标．6．如图，已知抛物线y=14x2+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知A点的坐标为A（-2，0）．（1）求抛物线的解析式及它的对称轴方程；（2）求点C的坐标，连接AC、BC并求线段BC所在直线的解析式；（3）试判断△AOC与△COB是否相似？并说明理由；（4）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若不存在，求出符合条件的Q点坐标；若不存在，请说明理由．7.已知抛物线y=ax 2-2ax+c 与y 轴交于C 点，与x 轴交于A 、B 两点，点A 的坐标是（-1,0），O 是坐标原点，且．（1 ）求抛物线的函数表达式；（2 ）直接写出直线BC 的函数表达式；（3 ）如图1 ，D 为y 轴的负半轴上的一点，且OD=2，以OD 为边作正方形ODEF.将正方形ODEF 以每秒1个单位的速度沿x 轴的正方向移动，在运动过程中，设正方形ODEF与△OBC 重叠部分的面积为s ，运动的时间为t 秒（0＜t ≤2）.求： ①s 与t 之间的函数关系式；②在运动过程中，s 是否存在最大值？如果存在，直接写出这个最大值；如果不存在，请说明理由．（4 ）如图2 ，点P （1，k ）在直线BC 上，点M 在x 轴上，点N 在抛物线上，是否存在以A 、M 、N 、P 为顶点的平行四边形？若存在，请直接写出M 点坐标；若不存在，请说明理由。

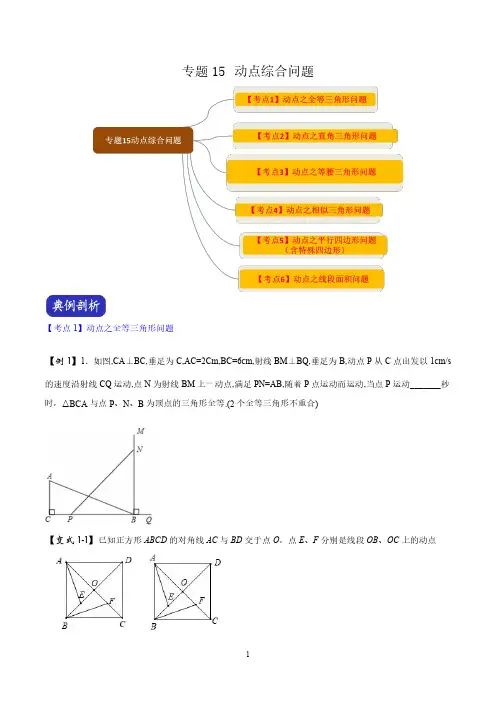
专题15动点综合问题【考点1】动点之全等三角形问题【例1】1．如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s 的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时，△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)【变式1-1】已知正方形ABCD的对角线AC与BD交于点O，点E、F分别是线段OB、OC上的动点（1）如果动点E 、F 满足BE ＝OF （如图），且AE ⊥BF 时，问点E 在什么位置？并证明你的结论；（2）如果动点E 、F 满足BE ＝CF （如图），写出所有以点E 或F 为顶点的全等三角形（不得添加辅助线）．【变式1-2】如图①，将长方形纸片沿对角线剪成两个全等的直角三角形ABC 、EDF ，其中AB ＝8cm ，BC ＝6cm ，AC ＝10cm ．现将△ABC 和△EDF 按如图②的方式摆放（点A 与点D 、点B 与点E 分别重合）．动点P 从点A 出发，沿AC 以2cm /s 的速度向点C 匀速移动；同时，动点Q 从点E 出发，沿射线ED 以acm /s （0＜a ＜3）的速度匀速移动，连接PQ 、CQ 、FQ ，设移动时间为ts （0≤t ≤5）．（1）当t ＝2时，S △AQF ＝3S △BQC ，则a ＝；（2）当以P 、C 、Q 为顶点的三角形与△BQC 全等时，求a 的值；（3）如图③，在动点P 、Q 出发的同时，△ABC 也以3cm /s 的速度沿射线ED 匀速移动，当以A 、P 、Q 为顶点的三角形与△EFQ 全等时，求a 与t 的值．【考点2】动点之直角三角形问题【例2】如图，在四边形纸片ABCD 中，//AB CD ，60A ∠=︒，30B ∠=︒，2CD =，4BC =，点E 是AB 边上的动点，点F 是折线A D C --上的动点，将纸片ABCD 沿直线EF 折叠，使点A 的对应点A '落在AB 边上，连接A C '，若A BC ' 是直角三角形，则AE 的长为________．【变式2-1】（2019·辽宁中考模拟）如图，已知二次函数y ＝ax 2+bx+4的图象与x 轴交于点A(4，0)和点D(﹣1，0)，与y 轴交于点C ，过点C 作BC 平行于x 轴交抛物线于点B ，连接AC(1)求这个二次函数的表达式；(2)点M 从点O 出发以每秒2个单位长度的速度向点A 运动；点N 从点B 同时出发，以每秒1个单位长度的速度向点C 运动，其中一个动点到达终点时，另一个动点也随之停动，过点N 作NQ 垂直于BC 交AC 于点Q ，连结MQ.①求△AQM 的面积S 与运动时间t 之间的函数关系式，写出自变量的取值范围；当t 为何值时，S 有最大值，并求出S 的最大值；②是否存在点M ，使得△AQM 为直角三角形？若存在，求出点M 的坐标；若不存在，说明理由．【变式2-2】如图，在矩形OAHC 中，8,12OC OA ==，B 为CH 中点，连接AB .动点M 从点O 出发沿OA 边向点A 运动，动点N 从点A 出发沿AB 边向点B 运动，两个动点同时出发，速度都是每秒1个单位长度，连接,,CM CN MN ，设运动时间为t （秒）(010)t <<.则t =_____时，CMN ∆为直角三角形【考点3】动点之等腰三角形问题【例3】如图，AB 是⊙O 的直径，BC 是弦，10cm AB =，6cm BC =．若点P 是直径AB 上一动点，当PBC 是等腰三角形时，AP =__________cm ．【变式3-1】如图①，已知正方形ABCD 边长为2，点P 是AD 边上的一个动点，点A 关于直线BP 的对称点是点Q ，连结PQ 、DQ 、CQ 、BQ .设AP=x.（1）当1x =时，求BP 长；（2）如图②，若PQ 的延长线交CD 边于E ，并且90CQD ∠=o ，求证：CEQ ∆为等腰三角形；（3）若点P 是射线AD 上的一个动点，则当CDQ ∆为等腰三角形时，求x 的值.【变式3-2】（2019·河南中考模拟）如图，抛物线y=ax 2+bx+3交y 轴于点A ，交x 轴于点B （-3，0）和点C （1，0），顶点为点M ．（1）求抛物线的解析式；（2）如图，点E 为x 轴上一动点，若△AME 的周长最小，请求出点E 的坐标；（3）点F 为直线AB 上一个动点，点P 为抛物线上一个动点，若△BFP 为等腰直角三角形，请直接写出点P 的坐标．【变式3-3】（2019·广西中考真题）已知抛物线2y mx =和直线y x b =-+都经过点()2,4M -，点O 为坐标原点，点P 为抛物线上的动点，直线y x b =-+与x 轴、y 轴分别交于A B 、两点．（1）求m b 、的值；（2）当PAM ∆是以AM 为底边的等腰三角形时，求点P 的坐标；（3）满足（2）的条件时，求sin BOP ∠的值．【考点4】动点之相似三角形问题【例4】如图，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC 是相似三角形，求AP的长．【变式4-1】已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB＝90°，点A，C的坐标分别为A（﹣3，0），C（1，0），BC＝3 4AC（1）求过点A，B的直线的函数表达式；（2）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP＝DQ＝m，问是否存在这样的m，使得△APQ与△ADB相似？如存在，请求出m的值；如不存在，请说明理由．【变式4-2】如图，正方形ABCD，点P为射线DC上的一个动点，点Q为AB的中点，连接PQ，DQ，过点P作PE⊥DQ于点E．（1）请找出图中一对相似三角形，并证明；（2）若AB＝4，以点P，E，Q为顶点的三角形与△ADQ相似，试求出DP的长．【考点5】动点之平行四边形问题（含特殊四边形）【例5】如图，抛物线23y ax bx =++与x 轴交于(3,0),(1,0)A B -两点，与y 轴交于点C ．（1）求抛物线的解析式；（2）点P 是抛物线上的动点，且满足2PAO PCO S S ∆∆=，求出P 点的坐标；（3）连接BC ，点E 是x 轴一动点，点F 是抛物线上一动点，若以B 、C 、E 、F 为顶点的四边形是平行四边形时，请直接写出点F 的坐标．备用图【变式5-1】（2019·江西中考真题）在图1，2，3中，已知，，点为线段上的动点，连接，以为边向上作菱形，且．（1）如图1，当点与点重合时，________°；（2）如图2，连接．①填空：_________（填“>”，“<”，“=”）；②求证：点在的平分线上；（3）如图3，连接，，并延长交的延长线于点，当四边形是平行四边形时，求的值．【变式5-2】（2019·湖南中考真题）如图，二次函数213y x bx c =-++的图象过原点，与x 轴的另一个交点为()8,0（1）求该二次函数的解析式；（2）在x轴上方作x轴的平行线1y m=，交二次函数图象于A、B两点，过A、B两点分别作x轴的垂线，垂足分别为点D、点C．当矩形ABCD为正方形时，求m的值；（3）在（2）的条件下，动点P从点A出发沿射线AB以每秒1个单位长度匀速运动，同时动点Q以相同的速度从点A出发沿线段AD匀速运动，到达点D时立即原速返回，当动点Q返回到点A时，P、Q两点同时停止运动，设运动时间为t秒（0t>）．过点P向x轴作垂线，交抛物线于点E，交直线AC于点F，问：以A、E、F、Q四点为顶点构成的四边形能否是平行四边形．若能，请求出t的值；若不能，请说明理由．【变式5-3】．如图，在平面直角坐标系中，AOB∆的顶点O是坐标原点，点A坐标为()1,3，A、B两点关于直线y x=对称，反比例函数()0ky xx=>图象经过点A，点P是直线y x=上一动点.（1）B点的坐标为______；（2）若点C是反比例函数图象上一点，是否存在这样的点C，使得以A、B、C、P四点为顶点的四边形是平行四边形？若存在，求出点C坐标；若不存在，请说明理由；（3）若点Q 是线段OP 上一点（O 不与O 、P 重合），当四边形AOBP 为菱形时，过点Q 分别作直线OA 和直线AP 的垂线，垂足分别为E 、F ，当QE QF QB ++的值最小时，求出Q 点坐标.【考点6】动点之线段面积问题【例6】如图，在平面直角坐标系中，平行四边形如图放置，将此平行四边形绕点O 顺时针旋转90°得到平行四边形．抛物线经过点A 、C 、A′三点．（1）求A 、A′、C 三点的坐标；（2）求平行四边形和平行四边形重叠部分的面积；（3）点M 是第一象限内抛物线上的一动点，问点M 在何处时，的面积最大？最大面积是多少？并写出此时M 的坐标．【变式6-1】（1）发现：如图1，点A 为线段BC 外一动点，且BC =α，AB b =(0)a b >>，当点A 位于时，线段AC 的长取得最大值，最大值为（用含,a b 的式子表示）；（2）应用：如图2，点A 为线段BC 外一动点，4BC =，2AC =，以AB 为边作等边ABD ∆，连接CD ，求线段CD 的最大值；（3）拓展：如图3，线段3AB =，点P 为线段AB 外一动点，且2AP =，PM PB =，90BPM ∠=︒，求线段AM 长的最大值及此时PBM ∆的面积．【变式6-2】如图，矩形ABCD 中，3,4AD AB ==，点P 是对角线AC 上一动点（不与A C 、重合），连接PB ，过点P 作PE PB ⊥，交射线DC 于点E ，以线段,PE PB 为邻边作矩形BPEF ，过点P 作GH CD ⊥。

中考数学抛物线动点题秒杀技巧全文共四篇示例，供读者参考第一篇示例：抛物线是数学中一个非常重要的概念，也是中考数学考试中常常会出现的题型之一。

抛物线的性质不仅仅是个别的知识点，更是一个整体的系统性知识。

在解题过程中，我们需要灵活运用抛物线的相关知识，抓住关键点，掌握一些技巧，才能在考试中取得更好的成绩。

本文将为大家介绍一些中考数学抛物线动点题的秒杀技巧，希望能够帮助大家顺利解答相关题目。

我们需要了解抛物线的基本性质。

抛物线是一种特殊的二次曲线，其一般方程为y=ax^2+bx+c，其中a、b、c为常数，a≠0。

抛物线开口的方向取决于a的正负性：当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

在抛物线上，我们常常遇到顶点、焦点、准线等概念，这些都是解题过程中需要重点关注的内容。

在解决抛物线动点题时，我们首先要确定动点的位置。

动点通常是抛物线上的一个点，在运动过程中其坐标会发生变化。

设抛物线的方程为y=ax^2+bx+c，动点的坐标为(x,y)，我们需要根据题目中的条件，确定动点的位置。

我们需要利用抛物线的性质，建立动点坐标变化的关系式。

在解题过程中，我们常常需要根据已知条件列方程，利用抛物线的性质建立动点坐标变化的关系式，从而求解动点的轨迹、移动方向等。

如果动点在抛物线上以匀速运动，我们可以利用速度的定义建立关于动点坐标的变化式。

我们需要灵活运用数学知识，解题过程中要注意化繁为简。

在解决抛物线动点题时，我们可能会遇到复杂的条件和问题，这时我们需要善于化繁为简，抓住关键点，简化问题。

可以通过几何、代数等不同的方法，灵活运用数学知识，解题过程中要注意逻辑性，不要陷入死胡同。

中考数学抛物线动点题并不是难题，关键在于掌握抛物线的基本性质，灵活运用数学知识，化繁为简，善于建立关系式，抓住关键点。

通过不断练习，积累经验，相信大家能够在考试中轻松应对抛物线动点题，取得好成绩。

希望以上的技巧能够帮助大家更好地掌握抛物线动点题的解题方法，祝大家在中考数学考试中取得优异成绩！第二篇示例：中考数学中，抛物线动点题是考生普遍认为比较难的题型之一。

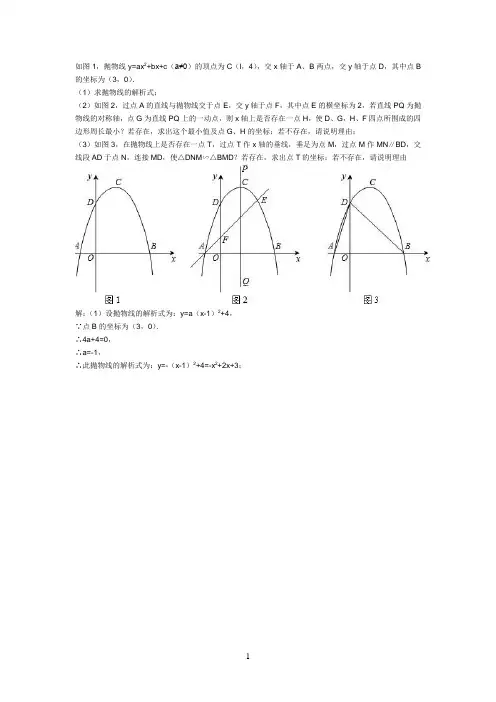
如图1，抛物线y=ax2+bx+c（a≠0）的顶点为C（l，4），交x轴于A、B两点，交y轴于点D，其中点B 的坐标为（3，0）．（1）求抛物线的解析式；（2）如图2，过点A的直线与抛物线交于点 E，交y轴于点F，其中点E的横坐标为2，若直线PQ为抛物线的对称轴，点G为直线 PQ上的一动点，则x轴上是否存在一点H，使D、G，H、F四点所围成的四边形周长最小？若存在，求出这个最小值及点G、H的坐标；若不存在，请说明理由；（3）如图3，在抛物线上是否存在一点T，过点T作x轴的垂线，垂足为点M，过点M作MN∥BD，交线段AD于点N，连接MD，使△DNM∽△BMD？若存在，求出点T的坐标；若不存在，请说明理由解：（1）设抛物线的解析式为：y=a（x-1）2+4，∵点B的坐标为（3，0）．∴4a+4=0，∴a=-1，∴此抛物线的解析式为：y=-（x-1）2+4=-x2+2x+3；如图1，在直角坐标系中，O是坐标原点，点A在y轴正半轴上，二次函数的图象F交x轴于B、C两点，交y轴于M点，其中B（-3，0），M（0，-1）．已知AM=BC．（1）求二次函数的解析式；（2）证明：在抛物线F上存在点D，使A、B、C、D四点连接而成的四边形恰好是平行四边形，并请求出直线BD的解析式；（3）在（2）的条件下，设直线l过D且分别交直线BA、BC于不同的P、Q两点，AC、BD相交于N．①若直线l⊥BD，如图1，试求的值；②若l为满足条件的任意直线．如图2．①中的结论还成立吗？若成立，证明你的猜想；若不成立，请举出反例．四边形OABC是等腰梯形，OA∥BC，在建立如图的平面直角坐标系中，A（10，0），B（8，6），直线x=4与直线AC交于P点，与x轴交于H点；（1）直接写出C点的坐标，并求出直线AC的解析式；（2）求出线段PH的长度，并在直线AC上找到Q点，使得△PHQ的面积为△AOC面积的1/5，求出Q 点坐标；（3）M点是直线AC上除P点以外的一个动点，问：在x轴上是否存在N点，使得△MHN为等腰直角三角形？若有，请求出M点及对应的N点的坐标，若没有，请说明理由．如图1，平面直角坐标系xOy中，抛物线y= x2+bx+c与x轴交于A、B两点，点C是AB的中点，CD ⊥AB且CD=AB．直线BE与y轴平行，点F是射线BE上的一个动点，连接AD、AF、DF．（1）若点F的坐标为（9/2，1），AF=①求此抛物线的解析式；②点P是此抛物线上一个动点，点Q在此抛物线的对称轴上，以点A、F、P、Q为顶点构成的四边形是平行四边形，请直接写出点Q的坐标；（2）若2b+c=-2，b=-2-t，且AB的长为kt，其中t＞0．如图2，当∠DAF=45°时，求k的值和∠DFA的正切值．如图，在平面直角坐标系中，已知点A、B、C的坐标分别为（-1，0），（5，0），（0，2）．（1）求过A、B、C三点的抛物线解析式；（2）若点P从A点出发，沿x轴正方向以每秒1个单位长度的速度向B点移动，连接PC并延长到点E，使CE=PC，将线段PE绕点P顺时针旋转90°得到线段PF，连接FB．若点P运动的时间为t秒，（0≤t≤6）设△PBF的面积为S；①求S与t的函数关系式；②当t是多少时，△PBF的面积最大，最大面积是多少？（3）点P在移动的过程中，△PBF能否成为直角三角形？若能，直接写出点F的坐标；若不能，请说明理由．如图1，在直角坐标系中，已知点A（0，2）、点B（-2，0），过点B和线段OA的中点C作直线BC，以线段BC为边向上作正方形BCDE．（1）填空：点D的坐标为（），点E的坐标为（）．（2）若抛物线y=ax2+bx+c（a≠0）经过A、D、E三点，求该抛物线的解析式．（3）若正方形和抛物线均以每秒个单位长度的速度沿射线BC同时向上平移，直至正方形的顶点E落在y轴上时，正方形和抛物线均停止运动．①在运动过程中，设正方形落在y轴右侧部分的面积为s，求s关于平移时间t（秒）的函数关系式，并写出相应自变量t的取值范围．②运动停止时，求抛物线的顶点坐标．如图，矩形OABC中，A（6，0），C（0，），D（0，），射线l过点D且与x轴平行，点P、Q分别是l和x轴的正半轴上的动点，满足∠PQO=60°．（1）①点B的坐标是（）；②∠CAO= 度；③当点Q与点A重合时，点P的坐标为（）；（直接填写答案）（2）设点P的横坐标为x，△OPQ与矩形OABC的重叠部分的面积为S，试求S与x的函数关系式和相应的自变量x的取值范围．已知抛物线y=a（x+1）2+c（a＞0）与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，其顶点为M，已知直线MC的函数表达式为y=kx-3，与x轴的交点为N，且cos∠BCO=（1）求抛物线的解析式；（2）在此抛物线上是否存在异于点C的点P，使以N、P、C为顶点的三角形是以NC为一条直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．（3）如图2，过点A作x轴的垂线，交直线MC于点Q，若将抛物线沿其对称轴上下平移，使抛物线与线段NQ总有公共点，则抛物线向上最多可平移多少单位长度？向下最多可平移多少个单位长度？。

考点二十二 动点与抛物线问题典型例题：（如图，已知抛物线2(1)33(0)y a x a =-+≠经过点A(－2，0)，抛物线的顶点为D ，过0作射线OM∥AD．过顶点D 平行于x 轴的直线交射线OM 于点C ，B 在x 轴正半轴上，连结BC ．(1)求该抛物线的解析式； (2)若动点P 从点0出发，以每秒l 个长度单位的速度沿射线OM 运动，设点P 运动的时间为t(s)．问：当t 为何值时，四边形DAOP 分别为平行四边形?直角梯形?等腰梯形?(3)若OC=OB ，动点P 和动点Q 分别从点O 和点B 同时出发，分别以每秒l 个长度单位和2个长度单位的速度沿OC 和B0运动，当其中一个点停止运动时另一个点也随之停止运动设它们运动的时间为t(s)，连接PQ ，当t 为何值时，四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长．解：（1）抛物线2(1)33(0)y a x a =-+≠经过点(20)A -，， 30933a a ∴=+= ·············································································· 1分 ∴二次函数的解析式为：232383y x x =++··········································· 3分 （2）D 为抛物线的顶点(133)D ∴，过D 作DN OB ⊥于N ，则33DN = 2233(33)660AN AD DAO =∴=+=∴∠=，° ············································ 4分 OM AD ∥①当AD OP =时，四边形DAOP 是平行四边形66(s)OP t ∴=∴= ·········································· 5分 ②当DP OM ⊥时，四边形DAOP 是直角梯形过O 作OH AD ⊥于H ，2AO =，则1AH =xyM CDPQO AB N E H（如果没求出60DAO ∠=°可由Rt Rt OHA DNA △∽△求1AH =）55(s)OP DH t ∴=== ················································································ 6分 ③当PD OA =时，四边形DAOP 是等腰梯形26244(s)OP AD AH t ∴=-=-=∴=综上所述：当6t =、5、4时，对应四边形分别是平行四边形、直角梯形、等腰梯形． · 7分（3）由（2）及已知，60COB OC OB OCB ∠==°，，△是等边三角形 则6262(03)OB OC AD OP t BQ t OQ t t =====∴=-<<，，，过P 作PE OQ ⊥于E ，则PE =······························································· 8分116(62)22BCPQ S t ∴=⨯⨯⨯-232t ⎫-⎪⎝⎭··················································································· 9分当32t =时，BCPQ S ························································· 10分∴此时33393324444OQ OP OE QE PE ==∴=-==，=，PQ ∴===············································· 11分名题精练1.（2009河南）如图，在平面直角坐标系中，已知矩形ABCD 的三个顶点B （4，0）、C （8，0）、D （8，8）.抛物线y=ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标，并求出抛物线的解析式；(2)动点P 从点A 出发．沿线段AB 向终点B 运动，同时点Q 从点C 出发，沿线段CD 向终点D 运动．速度均为每秒1个单位长度，运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E①过点E 作EF ⊥AD 于点F ，交抛物线于点G.当t 为何值时，线段EG 最长?②连接EQ ．在点P 、Q 运动的过程中，判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值.2． 已知二次函数c bx ax y ++=2的图象经过点A (3，0)，B (2，-3)，C (0，-3)．(1)求此函数的解析式及图象的对称轴；(2)点P 从B 点出发以每秒0.1个单位的速度沿线段BC 向C 点运动，点Q 从O 点出发以相同的速度沿线段OA 向A 点运动，其中一个动点到达端点时，另一个也随之停止运动．设运动时间为t 秒．①当t 为何值时，四边形ABPQ 为等腰梯形；②设PQ 与对称轴的交点为M ，过M 点作x 轴的平行线交AB 于点N ，设四边形ANPQ 的面积为S ，求面积S 关于时间t 的函数解析式，并指出t 的取值范围；当t 为何值时，S 有 最大值或最小值．3．如图，二次函数2y ax bx c =++（0a ≠）的图象与x 轴交于A B 、两点，与y 轴相交于点C ．连结AC BC A C 、，、两点的坐标分别为(30)A -，、(03)C ，，且当4x =-和2x =时二次函数的函数值y 相等．（1）求实数a b c ，，的值；xyO A BCP Q M N第23题图（2）若点M N 、同时从B 点出发，均以每秒1个单位长度的速度分别沿BA BC 、边运动，其中一个点到达终点时，另一点也随之停止运动．当运动时间为t 秒时，连结MN ，将BMN △沿MN 翻折，B 点恰好落在AC 边上的P 处，求t 的值及点P 的坐标；（3）在（2）的条件下，二次函数图象的对称轴上是否存在点Q ，使得以B N Q ，，为项点的三角形与ABC △相似？如果存在，请求出点Q 的坐标；如果不存在，请说明理由．考点二十二 答案1．解.(1)点A 的坐标为（4，8） …………………1 将A (4,8)、C （8，0）两点坐标分别代入y=ax 2+bx8=16a +4b得0=64a +8b解 得a =-12,b =4 ∴抛物线的解析式为：y =-12x 2+4x …………………3分（2）①在Rt △APE 和Rt △ABC 中，tan ∠PAE =PE AP =BC AB ,即PE AP =48∴PE =12AP =12t ．PB=8-t ．∴点Ｅ的坐标为（4+12t ，8-t ）.∴点G 的纵坐标为：-12（4+12t ）2+4(4+12t ）=-18t 2+8. …………………5分∴EG=-18t 2+8-(8-t )=-18t 2+t .∵-18＜0，∴当t =4时，线段EG 最长为2. …………………7分②共有三个时刻. …………………8分t 1=163， t 2=4013，t 3= 8525+． …………………11分2.解：(1)∵二次函数c bx ax y ++=2的图象经过点C (0，-3)，∴c =-3．将点A (3，0)，B (2，-3)代入c bx ax y ++=2得⎩⎨⎧-+=--+=.32433390b a b a ，解得：a =1，b =-2．∴322--=x x y ．-------------------2分配方得：412--=）（x y ，所以对称轴为x =1．-------------------3分 (2) 由题意可知：BP = OQ =0.1t ． ∵点B ，点C 的纵坐标相等， ∴BC ∥OA ．过点B ，点P 作BD ⊥OA ，PE ⊥OA ，垂足分别为D ，E ． 要使四边形ABPQ 为等腰梯形，只需PQ =AB ．xyO A BC P QDE GM N F即QE =AD =1．又QE =OE －OQ =(2-0.1t )-0.1t =2-0.2t ， ∴2-0.2t =1． 解得t =5．即t=5秒时，四边形ABPQ 为等腰梯形．-------------------6分 ②设对称轴与BC ，x 轴的交点分别为F ，G ． ∵对称轴x =1是线段BC 的垂直平分线， ∴BF =CF =OG =1． 又∵BP =OQ ， ∴PF =QG ．又∵∠PMF =∠QMG ， ∴△MFP ≌△MGQ ． ∴MF =MG ．∴点M 为FG 的中点 -------------------8分 ∴S=BPN ABPQ S -S ∆四边形， =BPN ABFG S -S ∆四边形．由=ABFG S 四边形FG AG BF )(21+=29．t FG BP S BPN 4032121=⋅=∆．∴S=t 40329-．-------------------10分 又BC =2，OA =3，∴点P 运动到点C 时停止运动，需要20秒． ∴0<t ≤20．∴当t =20秒时，面积S 有最小值3．------------------113、（1）由题意，得93016442a b c a b c a b c c ⎧-+=⎪-+=++⎨⎪=⎩，，解之得3a b c ⎧=-⎪⎪⎪⎪=⎨⎪⎪=⎪⎪⎩··········································································· 3分 （2）由（1）得3332332+--=x x y ，当y =0时，3x =-或1． ∴B （1，0），A （3-，0），C （0，3）．∴OA =3，OB =1，OC =3. 易求得AC =23，24BC AB ==，． ∴△ABC 为Rt △，且∠ACB =90°，∠A =30°，∠B =60°．又由BM BN PN PM ===知四边形PMBN 为菱形， ∴PN ∥AB ，∴CB CN AB PN =，即224tt -=． ∴34=t ． ···························································································· 5分过P 作PE ⊥AB 于E ，在Rt △PEM 中，∠PME =∠B =60°，PM =34． ∴332233460sin =⨯=⋅=PM PE ． 3260tan ==PE ME ． 又31=-=OB BM OM 故，∴(1P -． ·················································································· 7分 （3）由（1）、（2）知抛物线3332332+--=x x y 的对称轴为直线1x =-， 且∠ACB =90°．①若∠BQN =90°，∵BN 的中点到对称轴的距离大于1， 而13221<=BM ， ∴以BN 为直径的圆不与对称轴相交， ∴∠BQN ≠90°，即此时不存在符合条件的Q 点． ②若∠BNQ =90°，当∠NBQ =60°，则Q 、E 重合，此时90BNQ ∠≠°； 当∠NBQ =30°，则Q 、P 重合，此时90BNQ ∠≠°．即此时不存在符合条件的Q 点．③若∠QBN =90°时，延长NM 交对称轴于点Q ， 此时，Q 为P 关于x 轴的对称点． ∴Q （1-，332-）为所求． 10分。

1.（08福建莆田）如图：抛物线经过A （-3，0）、B （0，4）、C （4，0）三点. （1） 求抛物线的解析式.（2）已知AD = AB （D 在线段AC 上），有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动；同时另一个动点Q 以某一速度从点B 沿线段BC 移动，经过t 秒的移动，线段PQ 被BD 垂直平分，求t 的值；（3）在（2）的情况下，抛物线的对称轴上是否存在一点M ，使MQ+MC 的值最小？若存在，请求出点M 的坐标；若不存在，请说明理由。

（注：抛物线2y ax bx c =++的对称轴为2b x a=-）4.（08广东深圳）如图9，在平面直角坐标系中，二次函数)0(2>++=a c bx ax y 的图象的顶点为D 点，与y 轴交于C 点，与x 轴交于A 、B 两点， A 点在原点的左侧，B 点的坐标为（3，0），OB ＝OC ，tan∠ACO＝31． （1）求这个二次函数的表达式．（2）经过C 、D 两点的直线，与x 轴交于点E ，在该抛物线上是否存在这样的点F ，使以点A 、C 、E 、F 为顶点的四边形为平行四边形？若存在，请求出点F 的坐标；若不存在，请说明理由．（3）若平行于x 轴的直线与该抛物线交于M 、N 两点，且以MN 为直径的圆与x 轴相切，求该圆半径的长度．（4）如图10，若点G （2，y ）是该抛物线上一点，点P 是直线AG 下方的抛物线上一动点，当点P 运动到什么位置时，△APG 的面积最大？求出此时P 点的坐标和△APG 的最大面积.y x O E D CB A GA BCD O xy7.（08湖北荆门）已知抛物线y =ax 2+bx +c 的顶点A 在x 轴上，与y 轴的交点为B （0，1），且b =－4ac ． (1) 求抛物线的解析式；(2) 在抛物线上是否存在一点C ，使以BC 为直径的圆经过抛物线的顶点A ？若不存在说明理由；若存在，求出点C 的坐标，并求出此时圆的圆心点P 的坐标；(3) 根据(2)小题的结论，你发现B 、P 、C 三点的横坐标之间、纵坐标之间分别有何关系?10.（08湖北武汉）如图 1，抛物线y=ax2-3ax+b 经过A （-1,0），C （3,2）两点，与y 轴交于点D ，与x 轴交于另一点B.（1）求此抛物线的解析式；（2）若直线y=kx-1（k≠0）将 四 边 形ABCD 面积二等分，求k 的值；（3）如图2，过点 E （1，-1）作EF ⊥x 轴于点F ，将△AEF 绕平面内某点旋转 180°后得△MNQ （点M ，N ，Q 分别与 点 A ，E ，F 对应），使点M ，N 在抛物线上，求点M ，N 的坐标.3（08湖南益阳）我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线.如图，点A 、B 、C 、D 分别是“蛋圆”与坐标轴的交点，已知点D 的坐标为(0，-3)，AB 为半圆的直径，半圆圆心M 的坐标为(1,0)，半圆半径为2.(1) 请你求出“蛋圆”抛物线部分的解析式，并写出自变量的取值范围； (2)你能求出经过点C 的“蛋圆”切线的解析式吗？试试看；O x y ABO x y A C B P P 1 D P 2 PAOBMDCyx(3)开动脑筋想一想，相信你能求出经过点D 的“蛋圆”切线的解析式.14.（08江苏常州）如图,抛物线24y x x =+与x 轴分别相交于点B 、O ,它的顶点为A ,连接AB,把AB 所的直线沿y 轴向上平移,使它经过原点O,得到直线l ,设P 是直线l 上一动点.(1) 求点A 的坐标;(2) 以点A 、B 、O 、P 为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P 的坐标;(3) 设以点A 、B 、O 、P 为顶点的四边形的面积为S,点P 的横坐标为x,当462682S +≤≤+,求x 的取值范围.15、（08江苏淮安）如图所示，在平面直角坐标系中．二次函数y=a(x-2)2-1图象的顶点为P ，与x 轴交点为 A 、B ，与y 轴交点为C ．连结BP 并延长交y 轴于点D. (1)写出点P 的坐标；(2)连结AP ，如果△APB 为等腰直角三角形，求a 的值及点C 、D 的坐标； (3)在(2)的条件下，连结BC 、AC 、AD ，点E(0，b)在线段CD(端点C 、D 除外)上,将△BCD 绕点E 逆时针方向旋转90°，得到一个新三角形．设该三角形与△ACD 重叠部分的面积为S ，根据不同情况，分别用含b 的代数式表示S ．选择其中一种情况给出解答过程，其它情况直接写出结果；判断当b 为何值时,重叠部分的面积最大?写出最大值．27、（08江西南昌）如图，抛物211y ax ax =--+经过点19(,)28P -，且与抛物线221y ax ax =--相交于A 、B 两点（1）求a 值；（2）设211y ax ax =--+与x 轴分别交于M N ，两点（点M 在点N 的左边），221y ax ax =--与x 轴分别交于E F ，两点（点E 在点F 的左边），观察M N E F ，，，四点的坐标，写出一条正确的结论，并通过计算说明；（3）设A B ，两点的横坐标分别记为A B x x ，，若在x 轴上有一动点(0)Q x ，，且A B x x x ≤≤，过Q 作一条垂直于x 轴的直线，与两条抛物线分别交于C ，D 两点，试问当x为何值时，线段CD 有最大值？其最大值为多少？33、（08山东临沂）如图，已知抛物线与x 轴交于A （－1，0）、B （3，0）两点，与y 轴交于点C （0，3）。

中考数学压轴题100题精选【含答案】【001】如图，已知抛物线y a(x 3 3( a z 0)经过点A2 °)，抛物线的顶点为D , 过O作射线OM // AD •过顶点D平行于x轴的直线交射线OM于点C , B在x轴正半轴上，连结BC •(1)求该抛物线的解析式；(2)若动点P从点0出发，以每秒1个长度单位的速度沿射线OM运动，设点P运动的时间为t(s) •问当t为何值时，四边形DAOP分别为平行四边形？直角梯形？等腰梯形？(3)若0C °B，动点P和动点Q分别从点0和点B同时出发，分别以每秒1个长度单位和2 个长度单位的速度沿OC和BO运动，当其中一个点停止运动时另一个点也随之停止运动•设它们的运动的时间为t (s)，连接PQ，当t为何值时，四边形BCPQ的面积最小？并求出最小值及此时PQ的长.【002】如图16,在Rt A ABC中，/ C=90 , AC = 3 , AB = 5 .点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动，DE保持垂直平分PQ,且交PQ于点D，交折线QB-BC-CP于点E.点P、Q同时出发，当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t >0).(1) 当t = 2时，AP = ，点Q到AC的距离是:(2) 在点P从C向A运动的过程中，求△ APQ的面积S与t的函数关系式；(不必写出t的取值范围)(3) 在点E从B向C运动的过程中，四边形QBED能否成为直角梯形？若能，求t的值.若不能，请说明理由；(4) 当DE经过点C时，请直接写出t的值.【003】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B (4, 0)、C ( 8, 0)、D ( 8,8) •抛物线y=ax2+bx过A、C两点.(1) 直接写出点A的坐标，并求出抛物线的解析式；(2) 动点P从点A出发.沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD 向终点D运动.速度均为每秒1个单位长度，运动时间为t秒•过点P作PE丄AB交AC于点E,①过点E作EF丄AD于点F，交抛物线于点G.当t为何值时，线段EG最长?②连接EQ.在点P、Q运动的过程中，判断有几个时刻使得△ CEQ是等腰三角形？请直接写出相应的t值。

中考数学复习高频考点提升《抛物线压轴题中的动点问题》（五大必考题型汇编）专题练习考型一：平移型动点问题1. 如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B,且过点C(5,4).(1)求a的值和该抛物线顶点P的坐标.(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的表达式.2.如图，抛物线y＝x2＋(m＋2)x＋4的顶点C在x轴正半轴上，直线y＝x＋2与抛物线交于A，B两点(点A在点B的左侧)．(1)求抛物线的函数表达式；(2)将直线AB上下平移，平移后的直线y＝x＋t与抛物线交于A′、B′两点(A′在B′的左侧)，当以点A′、B′、(2)中第二象限的点P为顶点的三角形是直角三角形时，求t的值．3. 如图，二次函数y＝ax2＋bx＋4的图象与x轴交于点A(－1．0)，B(4．0)，与y轴交于点C，抛物线的顶点为D，其对称轴与线段BC交于点E．垂直于x 轴的动直线l分别交抛物线和线段BC于点P和点F，动直线l在抛物线的对称轴的右侧（不含对称轴）沿x轴正方向移动到B点．（1）求出二次函数y＝ax2＋bx＋4和BC所在直线的表达式；（2）连接CP，CD，在移动直线l移动的过程中，抛物线上是否存在点P，使得以点P，C，F为顶点的三角形与△DCE相似，如果存在，求出点P的坐标，如果不存在，请说明理由．考型二：动点与面积问题1. 如图,抛物线经过A(-2,0),B,C(0,2)三点.(1)求抛物线的解析式;(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标.CA O EFBPDlxy2.如图，在平面直角坐标系中，直线y＝mx＋3与抛物线交于点A(9，－6)，与y 轴交于点B，抛物线的顶点C的坐标是(4，－11)．(1)分别求该直线和抛物线的函数表达式；(2)D是抛物线上位于对称轴左侧的点，若△ABD的面积为812，求点D的坐标；3.如图，抛物线y＝x2＋(m＋2)x＋4的顶点C在x轴正半轴上，直线y＝x＋2与抛物线交于A，B两点(点A在点B的左侧)．(1)求抛物线的函数表达式；(2)点P是抛物线上一点，若S△PAB＝2S△ABC，求点P的坐标；4. 已知抛物线y=ax2+bx-4经过点A(2,0),B(-4,0),与y轴交于点C.(1)求这条抛物线的表达式.(2)如图1,点P是第三象限内抛物线上的一个动点,当四边形ABPC的面积最大时,求点P的坐标.考型三：动点与角度变换问题1. 如图,已知点A(-1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.(1)求抛物线解析式;(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点坐标;若不存在,说明理由.2. 如图，已知抛物线y＝ax2+bx+6经过两点A（﹣1，0），B（3，0），C是抛物线与y轴的点．（1）求抛物线的解析式；（2）点P（m，n）在平面直角坐标系第一象限内的抛物线上运动，设△PBC的面积为S，求S关于m的函数表达式（指出自变量m的取值范围）和S的最大值；（3）点M在抛物线上运动，点N在y轴上运动，是否存在点M、点N使得∠CMN＝90°，且△CMN与△OBC相似，如果存在，请求出点M和点N的坐标．3. 如图，在平面直角坐标系中，直线y＝mx＋3与抛物线交于点A(9，－6)，与y轴交于点B，抛物线的顶点C的坐标是(4，－11)．(1)分别求该直线和抛物线的函数表达式；(2)在y轴上是否存在一点P，使∠APC＝45°？若存在，求出满足条件的点P的坐标；若不存在，请说明理由．考型四：动点与图形周长问题1. 如图,抛物线y=x2-bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.(1)求抛物线的表达式.(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.2. 如图，抛物线y＝x2＋(m＋2)x＋4的顶点C在x轴正半轴上，直线y＝x＋2与抛物线交于A，B两点(点A在点B的左侧)．(1)求抛物线的函数表达式；(2)点P是抛物线上一点，若S△PAB＝2S△ABC，求点P的坐标；3. 已知抛物线y=ax2+bx-4经过点A(2,0),B(-4,0),与y轴交于点C.(1)求这条抛物线的解析式;(2)如图2,线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.4. 已知抛物线y=ax2+bx-4经过点A(2,0),B(-4,0),与y轴交于点C.(1)求这条抛物线的表达式.(2)如图2,线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.考型五：动点与图形存在问题1. 如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,-2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=-1.(1)求抛物线的函数表达式;(2)若点P在第二象限内,且PE=2OD,求△PBE的面积;(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM 是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.2. 如图1所示,直线y=x+c与x轴交于点A(-4,0),与y轴交于点C,抛物线y=-x2+bx+c经过点A,C.(1)求抛物线的解析式;(2)点E在抛物线的对称轴上,求CE+OE的最小值;(3)如图2所示,M是线段OA上的一个动点,过点M垂直于x轴的直线与直线AC 和抛物线分别交于点P,N.若点P恰好是线段MN的中点,点F是直线AC上的一个动点,在坐标平面内是否存在点D,使以点D,F,P,M为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.3. 如图，已知在平面直角坐标系xOy中，抛物线y＝﹣x2+bx+c（c＞0）的顶点为D，与y轴的交点为C．过点C的直线CA与抛物线交于另一点A（点A在对称轴左侧），点B在AC的延长线上，连结OA，OB，DA和DB．（1）如图1，当AC∥x轴时，①已知点A的坐标是（﹣2，1），求抛物线的解析式；②若四边形AOBD是平行四边形，求证：b2＝4c．（2）如图2，若b＝﹣2，BCAC =35，是否存在这样的点A，使四边形AOBD是平行四边形？若存在，求出点A的坐标；若不存在，请说明理由．4. 如图，在平面直角坐标系xOy中，直线y＝kx＋3分别交x轴、y轴于A，B 两点，经过A，B两点的抛物线y＝－x2＋bx＋c与x轴的正半轴相交于点C (1，0)．(1)求抛物线的解析式;(2)若P为线段AB上一点，∠APO＝∠ACB，求AP的长;(3)在(2)的条件下，设M是y轴上一点，试问:抛物线上是否存在点N，使得以A，P，M，N为顶点的四边形为平行四边形?若存在，求出点N的坐标;若不存在，请说明理由．。

中考300压轴题第7部分抛物线1．如图，点A是x轴正半轴上的动点，点B的坐标为（0，4），将线段AB的中点绕点A按顺时针方向旋转90°得点C，过点C作x轴的垂线，垂足为F，过点B作y轴的垂线与直线CF相交于点E，点D是点A 关于直线CF的对称点，连接AC、BC、CD，设点A的横坐标为t．（I）线段AB与AC的数量关系是，位置关系是．（II）当t=2时，求CF的长；（III）当t为何值时，点C落在线段BD上？求出此时点C的坐标；（IV）设△BCE的面积为S，求S与t之间的函数关系式．2．如图，在平面直角坐标系xOy中，顶点为M的抛物线y=ax2+bx（a＞0），经过点A和x轴正半轴上的点B，AO=OB=2，∠AOB=120°．（1）求这条抛物线的表达式；（2）连接OM，求∠AOM的大小；（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．3．如图，已知△ABC的三个顶点坐标分别为A（﹣4，0）、B（1，0）、C（﹣2，6）．（1）求经过A、B、C三点的抛物线解析式；（2）设直线BC交y轴于点E，连接AE，求证：AE=CE；（3）设抛物线与y轴交于点D，连接AD交BC于点F，试问以A、B、F为顶点的三角形与△ABC相似吗？（4）若点P为直线AE上一动点，当CP+DP取最小值时，求P点的坐标．4．如图，抛物线y=ax2+b与x轴交于点A、B，且A点的坐标为（1，0），与y轴交于点C（0，1）．（1）求抛物线的解析式，并求出点B坐标；（2）过点B作BD∥CA交抛物线于点D，连接BC、CA、AD，求四边形ABCD的周长；（结果保留根号）（3）在x轴上方的抛物线上是否存在点P，过点P作PE垂直于x轴，垂足为点E，使以B、P、E为顶点的三角形与△CBD相似？若存在请求出P点的坐标；若不存在，请说明理由．5．如图，已知抛物线经过原点O，顶点为A（1，1），且与直线y=x﹣2交于B，C两点．（1）求抛物线的解析式及点C的坐标；（2）求证：△ABC是直角三角形；（3）若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．6．如图，在平面直角坐标系中，抛物线y=ax2+x+c（a≠0）与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C，点A的坐标为（4，0），抛物线的对称轴是直线x=．（1）求抛物线的解析式；（2）M为第一象限内的抛物线上的一个点，过点M作MG⊥x轴于点G，交AC于点H，当线段CM=CH 时，求点M的坐标；（3）在（2）的条件下，将线段MG绕点G顺时针旋转一个角α（0°＜α＜90°），在旋转过程中，设线段MG 与抛物线交于点N，在线段GA上是否存在点P，使得以P、N、G为顶点的三角形与△ABC相似？如果存在，请求出点P的坐标；如果不存在，请说明理由．7．如图，抛物线经过A（4，0），B（1，0），C（0，﹣2）三点．（1）求出抛物线的解析式；（2）P是抛物线上一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；（3）在直线AC上方的抛物线上有一点D，使得△DCA的面积最大，求出点D的坐标．8．如图，在平面直角坐标系中，抛物线y=mx2﹣8mx+4m+2（m＞0）与y轴的交点为A，与x轴的交点分别为B（x1，0），C（x2，0），且x2﹣x1=4，直线AD∥x轴，在x轴上有一动点E（t，0）过点E作平行于y 轴的直线l与抛物线、直线AD的交点分别为P、Q．（1）求抛物线的解析式；（2）当0＜t≤8时，求△APC面积的最大值；（3）当t＞2时，是否存在点P，使以A、P、Q为顶点的三角形与△AOB相似？若存在，求出此时t的值；若不存在，请说明理由．9．如图，在平面直角坐标系xOy中，直线y=x+2与x轴交于点A，与y轴交于点C．抛物线y=ax2+bx+c 的对称轴是x=﹣且经过A、C两点，与x轴的另一交点为点B．（1）①直接写出点B的坐标；②求抛物线解析式．（2）若点P为直线AC上方的抛物线上的一点，连接PA，PC．求△PAC的面积的最大值，并求出此时点P 的坐标．（3）抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A、M、N为顶点的三角形与△ABC 相似？若存在，求出点M的坐标；若不存在，请说明理由．10．如图已知：直线y=﹣x+3交x轴于点A，交y轴于点B，抛物线y=ax2+bx+c经过A、B、C（1，0）三点．（1）求抛物线的解析式；（2）若点D的坐标为（﹣1，0），在直线y=﹣x+3上有一点P，使△ABO与△ADP相似，求出点P的坐标；（3）在（2）的条件下，在x轴下方的抛物线上，是否存在点E，使△ADE的面积等于四边形APCE的面积？如果存在，请求出点E的坐标；如果不存在，请说明理由．11．如图1，已知抛物线y=ax2+bx（a≠0）经过A（3，0）、B（4，4）两点．（1）求抛物线的解析式；（2）将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个公共点D，求m的值及点D的坐标；（3）如图2，若点N在抛物线上，且∠NBO=∠ABO，则在（2）的条件下，求出所有满足△POD∽△NOB 的点P坐标（点P、O、D分别与点N、O、B对应）．12．在平面直角坐标系中，抛物线y=ax2+bx+3与x轴的两个交点分别为A（﹣3，0）、B（1，0），过顶点C 作CH⊥x轴于点H．（1）直接填写：a=，b=，顶点C的坐标为；（2）在y轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH 相似时，求点P的坐标．13．如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．（1）求直线BD和抛物线的解析式．（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．（3）在抛物线上是否存在点P，使S△PBD=6？若存在，求出点P的坐标；若不存在，说明理由．14．如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（4，0），C（0，2）三点．（1）求这条抛物线的解析式；（2）E为抛物线上一动点，是否存在点E，使以A、B、E为顶点的三角形与△COB相似？若存在，试求出点E的坐标；若不存在，请说明理由；（3）若将直线BC平移，使其经过点A，且与抛物线相交于点D，连接BD，试求出∠BDA的度数．15．已知抛物线y=x2+c与x轴交于A（﹣1，0），B两点，交y轴于点C．（1）求抛物线的解析式；（2）点E（m，n）是第二象限内一点，过点E作EF⊥x轴交抛物线于点F，过点F作FG⊥y轴于点G，连接CE、CF，若∠CEF=∠CFG．求n的值并直接写出m的取值范围（利用图1完成你的探究）．（3）如图2，点P是线段OB上一动点（不包括点O、B），PM⊥x轴交抛物线于点M，∠OBQ=∠OMP，BQ交直线PM于点Q，设点P的横坐标为t，求△PBQ的周长．16．如图，在平面直角坐标系中，顶点为A（1，﹣1）的抛物线经过点B（5，3），且与x轴交于C，D两点（点C在点D的左侧）．（1）求抛物线的解析式；（2）求点O到直线AB的距离；（3）点M在第二象限内的抛物线上，点N在x轴上，且∠MND=∠OAB，当△DMN与△OAB相似时，请你直接写出点M的坐标．17．如图，已知抛物线y=﹣（x+2）（x﹣m）（m＞0）与x轴相交于点A、B，与y轴相交于点C，且点A在点B的左侧．（1）若抛物线过点G（2，2），求实数m的值；（2）在（1）的条件下，解答下列问题：①求出△ABC的面积；②在抛物线的对称轴上找一点H，使AH+CH最小，并求出点H的坐标；（3）在第四象限内，抛物线上是否存在点M，使得以点A、B、M为顶点的三角形与△ACB相似？若存在，求m的值；若不存在，请说明理由．18．已知抛物线y=x2﹣2mx+m2+m﹣1（m是常数）的顶点为P，直线l：y=x﹣1（1）求证：点P在直线l上；（2）当m=﹣3时，抛物线与x轴交于A，B两点，与y轴交于点C，与直线l的另一个交点为Q，M是x轴下方抛物线上的一点，∠ACM=∠PAQ（如图），求点M的坐标；（3）若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形，请直接写出所有符合条件的m的值．19．如图，已知抛物线y=（x+2）（x﹣4）与x轴交于点A、B（点A位于点B的左侧），与y轴交于点C，CD∥x轴交抛物线于点D，M为抛物线的顶点．（1）求点A、B、C的坐标；（2）设动点N（﹣2，n），求使MN+BN的值最小时n的值；（3）P是抛物线上一点，请你探究：是否存在点P，使以P、A、B为顶点的三角形与△ABD相似（△PAB 与△ABD不重合）？若存在，求出点P的坐标；若不存在，说明理由．20．设抛物线的解析式为y=ax2，过点B1（1，0）作x轴的垂线，交抛物线于点A1（1，2）；过点B2（，0）作x轴的垂线，交抛物线于点A2；…；过点B n（（）n﹣1，0）（n为正整数）作x轴的垂线，交抛物线于点A n，连接A n B n+1，得Rt△A n B n B n+1．（1）求a的值；（2）直接写出线段A n B n，B n B n+1的长（用含n的式子表示）；（3）在系列Rt△A n B n B n+1中，探究下列问题：①当n为何值时，Rt△A n B n B n+1是等腰直角三角形？②设1≤k＜m≤n（k，m均为正整数），问：是否存在Rt△A k B k B k+1与Rt△A m B m B m+1相似？若存在，求出其相似比；若不存在，说明理由．21．如图，直线y=kx+b（b＞0）与抛物线相交于点A（x1，y1），B（x2，y2）两点，与x轴正半轴相交于点D，与y轴相交于点C，设△OCD的面积为S，且kS+32=0．（1）求b的值；（2）求证：点（y1，y2）在反比例函数的图象上；（3）求证：x1•OB+y2•OA=0．22．如图，在平面直角坐标中，点O为坐标原点，直线y=﹣x+4与x轴交于点A，过点A的抛物线y=ax2+bx 与直线y=﹣x+4交于另一点B，且点B的横坐标为1．（1）求a，b的值；（2）点P是线段AB上一动点（点P不与点A、B重合），过点P作PM∥OB交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，过点P作PF⊥MC于点F，设PF的长为t，MN的长为d，求d 与t之间的函数关系式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，当S△ACN=S△PMN时，连接ON，点Q在线段BP上，过点Q作QR∥MN交ON于点R，连接MQ、BR，当∠MQR﹣∠BRN=45°时，求点R的坐标．23．如图1，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是（0，4），点B在第一象限，点P是x轴上的一个动点，连接AP，并把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，得到△ABD．（1）求直线AB的解析式；（2）当点P运动到点（，0）时，求此时DP的长及点D的坐标；（3）是否存在点P，使△OPD的面积等于？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．24．在矩形ABCD中，点P是边AD上的动点，连接BP，线段BP的垂直平分线交边BC于点Q，垂足为点M，联结QP（如图）．已知AD=13，AB=5，设AP=x，BQ=y．（1）求y关于x的函数解析式，并写出x的取值范围；（2）当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时，求x的值；（3）点E在边CD上，过点E作直线QP的垂线，垂足为F，如果EF=EC=4，求x的值．25．如图，在平面直角坐标系中，直线l：y=﹣2x+b（b≥0）的位置随b的不同取值而变化．（1）已知⊙M的圆心坐标为（4，2），半径为2．当b=时，直线l：y=﹣2x+b（b≥0）经过圆心M；当b=时，直线l：y=﹣2x+b（b≥0）与⊙M相切；（2）若把⊙M换成矩形ABCD，其三个顶点坐标分别为：A（2，0）、B（6，0）、C（6，2）．设直线l扫过矩形ABCD的面积为S，当b由小到大变化时，请求出S与b的函数关系式．26．如图，在Rt△ABC中，∠ACB=90°，AC=，BC=3，△DEF是边长为a（a为小于3的常数）的等边三角形，将△DEF沿AC方向平移，使点D在线段AC上，DE∥AB，设△DEF与△ABC重叠部分的周长为T．（1）求证：点E到AC的距离为一个常数；（2）若AD=，当a=2时，求T的值；（3）若点D运动到AC的中点处，请用含a的代数式表示T．27．如图，Rt△ABC中，∠C=90°，AB=15，BC=9，点P，Q分别在BC，AC上，CP=3x，CQ=4x（0＜x＜3）．把△PCQ绕点P旋转，得到△PDE，点D落在线段PQ上．（1）求证：PQ∥AB；（2）若点D在∠BAC的平分线上，求CP的长；（3）若△PDE与△ABC重叠部分图形的周长为T，且12≤T≤16，求x的取值范围．1.解：（I）∵如图，将线段AB的中点绕点A按顺时针方向旋转90°得点C，∵AB=2AC，∠BAC=90°，∴AB⊥AC．故答案是：AB=2AC，AB⊥AC；（II）由题意，易证Rt△ACF∽Rt△BAO，∴=．∵AB=2AM=2AC，∴CF=OA=t．当t=2时，CF=1；（III）由（1）知，Rt△ACF∽Rt△BAO，∴=，∴AF=OB=2，∴FD=AF=2，．∵点C落在线段BD上，∴△DCF∽△DBO，∴=，即=，整理得t2+4t﹣16=0解得t=2﹣2或t=﹣2﹣2（不合题意，舍去）∴当t=2﹣2时，点C落在线段BD上．此时，CF=t=﹣1，OF=t+2=2，∴点C的坐标为（2，﹣1+）；（IV）①当0＜t≤8时，如题图1所示：S=BE•CE=（t+2）•（4﹣t）=﹣t2+t+4；②当t＞8时，如答图1所示：CE=CF﹣EF=t﹣4S=BE•CE=（t+2）•（t﹣4）=t2﹣t﹣4；③如答图2，当点C与点E重合时，CF=OB=4，可得t=OA=8，此时S=0．2.解：（1）过点A作AE⊥y轴于点E，∵AO=OB=2，∠AOB=120°，∴∠AOE=30°，∴OE=，AE=1，∴A点坐标为：（﹣1，），B点坐标为：（2，0），将两点代入y=ax2+bx得：，解得：，∴抛物线的表达式为：y=x2﹣x；（2）过点M作MF⊥OB于点F，∵y=x2﹣x=（x2﹣2x）=（x2﹣2x+1﹣1）=（x﹣1）2﹣，∴M点坐标为：（1，﹣），∴tan∠FOM==，∴∠FOM=30°，∴∠AOM=30°+120°=150°；（3）当点C在x轴负半轴上时，则∠BAC=150°，而∠ABC=30°，此时∠C=0°，故此种情况不存在；当点C在x轴正半轴上时，∵AO=OB=2，∠AOB=120°，∴∠ABO=∠OAB=30°，∴AB=2EO=2，当△ABC1∽△AOM，∴=，∵MO==，∴=，解得：BC1=2，∴OC1=4，∴C1的坐标为：（4，0）；当△C2BA∽△AOM，∴=，∴=，解得：BC2=6，∴OC2=8，∴C2的坐标为：（8，0）．综上所述，△ABC与△AOM相似时，点C的坐标为：（4，0）或（8，0）．3.方法一：解：（1）设函数解析式为：y=ax2+bx+c，由函数经过点A（﹣4，0）、B（1，0）、C（﹣2，6），可得，解得：，故经过A、B、C三点的抛物线解析式为：y=﹣x2﹣3x+4；（2）设直线BC的函数解析式为y=kx+b，由题意得：，解得：，即直线BC的解析式为y=﹣2x+2．故可得点E的坐标为（0，2），从而可得：AE==2，CE==2，故可得出AE=CE；（3）相似．理由如下：设直线AD的解析式为y=kx+b，则，解得：，即直线AD的解析式为y=x+4．联立直线AD与直线BC的函数解析式可得：，解得：，即点F的坐标为（﹣，），则BF==，又∵AB=5，BC==3，∴=，=，∴=，又∵∠ABF=∠CBA，∴△ABF∽△CBA．故以A、B、F为顶点的三角形与△ABC相似．方法二：（1）略．（2）略．（3）若△ABF∽△ABC，则，即AB2=BF×BC，∵A（﹣4，0），D（0，4），∴l AD：y=x+4，l BC：y=﹣2x+2，∴l AD与l BC的交点F（﹣，），∴AB=5，BF=，BC=3，∴AB2=25，BF×BC=×3=25，∴AB2=BF×BC，又∵∠ABC=∠ABC，∴△ABF∽△ABC．（4）由（3）知：K AE=，K CE=﹣2，∴K AE×K CE=﹣1，∴AE⊥CE，过C点作直线AE的对称点C，点E为CC′的中点，∴，，∵C（﹣2，6），E（0，2），∴C′X=2，C′Y=﹣2，∵D（0，4），∴l C′D：y=﹣3x+4，∵l AE：y=x+2，∴l C′D与l AE的交点P（，）．4.方法一：解：（1）∵点A（1，0）和点C（0，1）在抛物线y=ax2+b上，∴，解得：a=﹣1，b=1，∴抛物线的解析式为：y=﹣x2+1，抛物线的对称轴为y轴，则点B与点A（1，0）关于y轴对称，∴B（﹣1，0）．（2）设过点A（1，0），C（0，1）的直线解析式为y=kx+b，可得：，解得k=﹣1，b=1，∴y=﹣x+1．∵BD∥CA，∴可设直线BD的解析式为y=﹣x+n，∵点B（﹣1，0）在直线BD上，∴0=1+n，得n=﹣1，∴直线BD的解析式为：y=﹣x﹣1．将y=﹣x﹣1代入抛物线的解析式，得：﹣x﹣1=﹣x2+1，解得：x1=2，x2=﹣1，∵B点横坐标为﹣1，则D点横坐标为2，D点纵坐标为y=﹣2﹣1=﹣3，∴D点坐标为（2，﹣3）．如答图①所示，过点D作DN⊥x轴于点N，则DN=3，AN=1，BN=3，在Rt△BDN中，BN=DN=3，由勾股定理得：BD=；在Rt△ADN中，DN=3，AN=1，由勾股定理得：AD=；又OA=OB=OC=1，OC⊥AB，由勾股定理得：AC=BC=；∴四边形ABCD的周长为：AC+BC+BD+AD=+++=+．（3）假设存在这样的点P，则△BPE与△CBD相似有两种情形：（I）若△EPB∽△BDC，如答图②所示，则有，即，∴PE=3BE．设OE=m（m＞0），则E（﹣m，0），BE=1﹣m，PE=3BE=3﹣3m，∴点P的坐标为（﹣m，3﹣3m）．∵点P在抛物线y=﹣x2+1上，∴3﹣3m=﹣（﹣m）2+1，解得m=1或m=2，当m=1时，点E与点B重合，故舍去；当m=2时，点E在OB左侧，点P在x轴下方，不符合题意，故舍去．因此，此种情况不存在；（II）若△EBP∽△BDC，如答图③所示，则有，即，∴BE=3PE．设OE=m（m＞0），则E（m，0），BE=1+m，PE=BE=（1+m）=+m，∴点P的坐标为（m，+m）．∵点P在抛物线y=﹣x2+1上，∴+m=﹣（m）2+1，解得m=﹣1或m=，∵m＞0，故m=﹣1舍去，∴m=，点P的纵坐标为：+m=+×=，∴点P的坐标为（，）．综上所述，存在点P，使以B、P、E为顶点的三角形与△CBD相似，点P的坐标为（，）．方法二：（1）略．（2）∵A（1，0），C（0，1），∴l AC：y=﹣x+1，∵BD∥CA，∴K BD=K AC=﹣1，∴l BD：y=﹣x﹣1，∴，∴x1=2，x2=﹣1（舍），∴D（2，﹣3），∴AC==，CB==，BD==3，DA==，∴四边形ABCD的周长为：5+．（3）∵C（0，1），B（﹣1，0），∴K BC==1，∵K BD=﹣1，∴K BC×K BD=﹣1，∴BD⊥BC，若△EPB∽△BDC，则或，①设点P（t，﹣t2+1），E（t，0），B（﹣1，0），PE=P Y=﹣t2+1，BE=E X﹣B X=t+1，∵BD=3，CB=，，∴，∴t=﹣2（此时点P位于x轴下方，故舍去）②∵，∴，∴t=，∴P（，）．5.解：（1）∵顶点坐标为（1，1），∴设抛物线解析式为y=a（x﹣1）2+1，又抛物线过原点，∴0=a（0﹣1）2+1，解得a=﹣1，∴抛物线解析式为y=﹣（x﹣1）2+1，即y=﹣x2+2x，联立抛物线和直线解析式可得，解得或，∴B（2，0），C（﹣1，﹣3）；（2）如图，分别过A、C两点作x轴的垂线，交x轴于点D、E两点，则AD=OD=BD=1，BE=OB+OE=2+1=3，EC=3，∴∠ABO=∠CBO=45°，即∠ABC=90°，∴△ABC是直角三角形；（3）假设存在满足条件的点N，设N（x，0），则M（x，﹣x2+2x），∴ON=|x|，MN=|﹣x2+2x|，由（2）在Rt△ABD和Rt△CEB中，可分别求得AB=，BC=3，∵MN⊥x轴于点N∴∠ABC=∠MNO=90°，∴当△ABC和△MNO相似时有=或=，①当=时，则有=，即|x||﹣x+2|=|x|，∵当x=0时M、O、N不能构成三角形，∴x≠0，∴|﹣x+2|=，即﹣x+2=±，解得x=或x=，此时N点坐标为（，0）或（，0）；②当=时，则有=，即|x||﹣x+2|=3|x|，∴|﹣x+2|=3，即﹣x+2=±3，解得x=5或x=﹣1，此时N点坐标为（﹣1，0）或（5，0），综上可知存在满足条件的N点，其坐标为（，0）或（，0）或（﹣1，0）或（5，0）．6.解：（1）∵x=﹣=，b=，∴a=﹣，把A（4，0），a=﹣代入y=ax2+x+c，可得（）×42+×4+c=0，解得c=2，则抛物线解析式为y=﹣x2+x+2．（2）如图1，连接CM，过C点作CE⊥MH于点E，，∵y=﹣x2+x+2，∴当x=0时，y=2，∴C点的坐标是（0，2），设直线AC解析式为y=kx+b（k≠0），把A（4，0）、C（0，2）代入y=kx+b，可得，解得：，∴直线AC解析式为y=﹣x+2，∵点M在抛物线上，点H在AC上，MG⊥x轴，∴设点M的坐标为（m，﹣m2+m+2），H（m，﹣m+2），∴MH=﹣m2+m+2﹣（﹣m+2）=﹣m2+2m，∵CM=CH，OC=GE=2，∴MH=2EH=2×[2﹣（﹣m+2）]=m，又∵MH=﹣m2+2m，∴﹣m2+2m=m，即m（m﹣2）=0，解得m=2或m=0（不符合题意，舍去），∴m=2，当m=2时，y=﹣×22+×2+2=3，∴点M的坐标为（2，3）．（3）存在点P，使以P，N，G为顶点的三角形与△ABC相似，理由为：∵抛物线与x轴交于A、B两点，A（4，0），A、B两点关于直线x=成轴对称，∴B（﹣1，0），∵AC==2，BC==，AB=5，∴AC2+BC2=+=25，AB2=52=25，∵AC2+BC2=AB2=25，∴△ABC为直角三角形，∴∠ACB=90°，线段MG绕G点旋转过程中，与抛物线交于点N，当NP⊥x轴时，∠NPG=90°，设P点坐标为（n，0），则N点坐标为（n，﹣n2+n+2），①如图2，当=时，∵∠N1P1G=∠ACB=90°，∴△N1P1G∽△ACB，∴=，解得：n1=3，n2=﹣4（不符合题意，舍去），∴P的坐标为（3，0）．②当=时，∵∠N2P2G=∠BCA=90°，∴△N2P2G∽△BCA，∴，解得：n1=1，n2=1﹣（不符合题意，舍去），∴P的坐标为（1+，0）．∴存在点P（3，0）或（1，0），使以P，N，G为顶点的三角形与△ABC相似．7.解：（1）∵该抛物线过点C（0，﹣2），设该抛物线的解析式为y=ax2+bx﹣2．将A（4，0），B（1，0）代入，得，解得，∴此抛物线的解析式为y=﹣x2+x﹣2．（2）存在．如图，设P点的横坐标为m，则点P的纵坐标为，当1＜m＜4时，AM=4﹣m，PM=，又∵∠COA=∠PMA=90°，∴①当==2时，△APM∽△ACO，∴=2，即|4﹣m|=2（），∴4﹣m=m2+5m﹣4，∴m2﹣6m+8=0，∴（m﹣2）（m﹣4）=0，解得：m1=2，m2=4（舍去）∴P（2，1）②当，△APM∽△CAO，那么有：2|4﹣m|=，∴2（4﹣m）=﹣m2+m﹣2，∴m2﹣9m+20=0，∴（m﹣4）（m﹣5）=0，解得：m1=4（舍去），m2=5（舍去），∴当1＜m＜4时，P（2，1），类似地可求出当m＞4时，P（5，﹣2），当m＜1时，P（﹣3，﹣14），当P，C重合时，△APM≌△ACO，P（0，﹣2）．综上所述，符合条件的点P为（2，1）或（5，﹣2）或（﹣3，﹣14）或（0，﹣2）；（3）如图，设D点的横坐标为t（0＜t＜4），则D点的纵坐标为﹣t2+t﹣2．过D作y轴的平行线交AC于E．由题意可求得直线AC的解析式为y=x﹣2．∴E点的坐标为（t，t﹣2）．∴DE=﹣t2+t﹣2﹣（t﹣2）=﹣t2+2t．∴S△DAC=×（﹣t2+2t）×4=﹣t2+4t=﹣（t﹣2）2+4．∴当t=2时，△DAC面积最大．∴D（2，1）．8.解：（1）由题意知x1、x2是方程mx2﹣8mx+4m+2=0的两根，∴x 1+x2=8，由解得：∴B（2，0）、C（6，0）则4m﹣16m+4m+2=0，解得：m=，∴该抛物线解析式为：y=；（2）可求得A（0，3）设直线AC的解析式为：y=kx+b，∵∴∴直线AC的解析式为：y=﹣x+3，要构成△APC，显然t≠6，分两种情况讨论：①当0＜t＜6时，设直线l与AC交点为F，则：F（t，﹣），∵P（t，），∴PF=，∴S=S△APF+S△CPF===，此时最大值为：，②当6＜t≤8时，设直线l与AC交点为M，则：M（t，﹣），∵P（t，），∴PM=，∴S △APC=S△APM﹣S△CPM===，当t=8时，取最大值，最大值为：12，综上可知，当0＜t≤8时，△APC面积的最大值为12；（3）方法一：如图，连接AB，则△AOB中，∠AOB=90°，AO=3，BO=2，Q（t，3），P（t，），①当2＜t＜8时，AQ=t，PQ=，若：△AOB∽△AQP，则：，即：，∴t=0（舍），或t=，若△AOB∽△PQA，则：，即：，∴t=0（舍）或t=2（舍），②当t＞8时，AQ′=t，PQ′=，若：△AOB∽△AQP，则：，即：，∴t=0（舍），或t=，若△AOB∽△PQA，则：，即：，∴t=0（舍）或t=14，方法二：若以A、P、Q为顶点的三角形与△AOB相似，则或，设P（t，）（t＞2）∴Q（t，3）①||=，∴||=，∴t1=2（舍），t2=14，②||=，∴||=，∴t1=，t2=，9.解：（1）①y=当x=0时，y=2，当y=0时，x=﹣4，∴C（0，2），A（﹣4，0），由抛物线的对称性可知：点A与点B关于x=﹣对称，∴点B的坐标为1，0）．②∵抛物线y=ax2+bx+c过A（﹣4，0），B（1，0），∴可设抛物线解析式为y=a（x+4）（x﹣1），又∵抛物线过点C（0，2），∴2=﹣4a∴a=∴y=x2x+2．（2）设P（m，m2m+2）．过点P作PQ⊥x轴交AC于点Q，∴Q（m，m+2），∴PQ=m2m+2﹣（m+2）=m2﹣2m，∵S△PAC=×PQ×4，=2PQ=﹣m2﹣4m=﹣（m+2）2+4，∴当m=﹣2时，△PAC的面积有最大值是4，此时P（﹣2，3）．（3）方法一：在Rt△AOC中，tan∠CAO=在Rt△BOC中，tan∠BCO=，∴∠CAO=∠BCO，∵∠BCO+∠OBC=90°，∴∠CAO+∠OBC=90°，∴∠ACB=90°，∴△ABC∽△ACO∽△CBO，如图：①当M点与C点重合，即M（0，2）时，△MAN∽△BAC；②根据抛物线的对称性，当M（﹣3，2）时，△MAN∽△ABC；③当点M在第四象限时，设M（n，n2n+2），则N（n，0）∴MN=n2+n﹣2，AN=n+4当时，MN=AN，即n2+n﹣2=（n+4）整理得：n2+2n﹣8=0解得：n1=﹣4（舍），n2=2∴M（2，﹣3）；当时，MN=2AN，即n2+n﹣2=2（n+4），整理得：n2﹣n﹣20=0解得：n1=﹣4（舍），n2=5，∴M（5，﹣18）．综上所述：存在M1（0，2），M2（﹣3，2），M3（2，﹣3），M4（5，﹣18），使得以点A、M、N为顶点的三角形与△ABC相似．方法二：∵A（﹣4，0），B（1，0），C（0，2），∴K AC×K BC=﹣1，∴AC⊥BC，MN⊥x轴，若以点A、M、N为顶点的三角形与△ABC相似，则，，设M（2t，﹣2t2﹣3t+2），∴N（2t，0），①||=，∴||=，∴2t1=0，2t2=2，②||=，∴||=2，∴2t1=5，2t2=﹣3，综上所述：存在M1（0，2），M2（﹣3，2），M3（2，﹣3），M4（5，﹣18），使得以点A、M、N为顶点的三角形与△ABC相似．10.解：（1）由题意得，A（3，0），B（0，3）∵抛物线经过A、B、C三点，∴把A（3，0），B（0，3），C（1，0）三点分别代入y=ax2+bx+c，得方程组解得：∴抛物线的解析式为y=x2﹣4x+3（2）由题意可得：△ABO为等腰三角形，如答图1所示，若△ABO∽△AP1D，则∴DP1=AD=4，∴P1（﹣1，4）若△ABO∽△ADP2 ，过点P2作P2 M⊥x轴于M，AD=4，∵△ABO为等腰三角形，∴△ADP2是等腰三角形，由三线合一可得：DM=AM=2=P2M，即点M与点C重合，∴P2（1，2）综上所述，点P的坐标为P1（﹣1，4），P2（1，2）；（3）不存在．理由：如答图2，设点E（x，y），则S△ADE=①当P1（﹣1，4）时，S四边形AP1CE=S△ACP1+S△ACE==4+|y|∴2|y|=4+|y|，∴|y|=4∵点E在x轴下方，∴y=﹣4，代入得：x2﹣4x+3=﹣4，即x2﹣4x+7=0，∵△=（﹣4）2﹣4×7=﹣12＜0∴此方程无解②当P2（1，2）时，S四边形AP2CE=S△ACP2+S△ACE==2+|y|，∴2|y|=2+|y|，∴|y|=2∵点E在x轴下方，∴y=﹣2，代入得：x2﹣4x+3=﹣2，即x2﹣4x+5=0，∵△=（﹣4）2﹣4×5=﹣4＜0∴此方程无解综上所述，在x轴下方的抛物线上不存在这样的点E．11.解：（1）∵抛物线y=ax2+bx（a≠0）经过A（3，0）、B（4，4）∴将A与B两点坐标代入得：，解得：，∴抛物线的解析式是y=x2﹣3x．（2）设直线OB的解析式为y=k1x，由点B（4，4），得：4=4k1，解得：k1=1∴直线OB的解析式为y=x，∴直线OB向下平移m个单位长度后的解析式为：y=x﹣m，∵点D在抛物线y=x2﹣3x上，∴可设D（x，x2﹣3x），又∵点D在直线y=x﹣m上，∴x2﹣3x=x﹣m，即x2﹣4x+m=0，∵抛物线与直线只有一个公共点，∴△=16﹣4m=0，解得：m=4，此时x1=x2=2，y=x2﹣3x=﹣2，∴D点的坐标为（2，﹣2）．（3）∵直线OB的解析式为y=x，且A（3，0），∴点A关于直线OB的对称点A′的坐标是（0，3），根据轴对称性质和三线合一性质得出∠A′BO=∠ABO，设直线A′B的解析式为y=k2x+3，过点（4，4），∴4k2+3=4，解得：k2=，∴直线A′B的解析式是y=，∵∠NBO=∠ABO，∠A′BO=∠ABO，∴BA′和BN重合，即点N在直线A′B上，∴设点N（n，），又点N在抛物线y=x2﹣3x上，∴=n2﹣3n，解得：n1=﹣，n2=4（不合题意，舍去）∴N点的坐标为（﹣，）．方法一：如图1，将△NOB沿x轴翻折，得到△N1OB1，则N 1（，），B1（4，﹣4），∴O、D、B1都在直线y=﹣x上．∵△P 1OD∽△NOB，△NOB≌△N1OB1，∴△P1OD∽△N1OB1，∴，∴点P1的坐标为（，）．将△OP1D沿直线y=﹣x翻折，可得另一个满足条件的点P2（，），方法二：如图2，将△NOB绕原点顺时针旋转90°，得到△N2OB2，则N2（，），B2（4，﹣4），∴O、D、B1都在直线y=﹣x上．∵△P 1OD∽△NOB，△NOB≌△N2OB2，∴△P1OD∽△N2OB2，∴，∴点P1的坐标为（，）．将△OP1D沿直线y=﹣x翻折，可得另一个满足条件的点P2（，），方法三：∵直线OB：y=x是一三象限平分线，∴A（3，0）关于直线OB的对称点为A′（0，3），∴得：x1=4（舍），x2=﹣，∴N（﹣，），∵D（2，﹣2），∴l OD：y=﹣x，∵l OD：y=x，∴OD⊥OB，∵△POD∽△NOB，∴N（﹣，）旋转90°后N1（，）或N关于x轴对称点N2（﹣，﹣），∵OB=4，OD=2，∴，∵P为ON 1或ON2中点，∴P1（，），P2（，）．12.解：（1）a=﹣1，b=﹣2，顶点C的坐标为（﹣1，4）；（2）假设在y轴上存在满足条件的点D，过点C作CE⊥y轴于点E．由∠CDA=90°得，∠1+∠2=90°．又∠2+∠3=90°，∴∠3=∠1．又∵∠CED=∠DOA=90°，∴△CED∽△DOA，∴．设D（0，c），则．变形得c2﹣4c+3=0，解之得c1=3，c2=1．综合上述：在y轴上存在点D（0，3）或（0，1），使△ACD是以AC为斜边的直角三角形．（3）①若点P在对称轴右侧（如图①），只能是△PCQ∽△CAH，得∠QCP=∠CAH．延长CP交x轴于M，∴AM=CM，∴AM2=CM2．设M（m，0），则（m+3）2=42+（m+1）2，∴m=2，即M（2，0）．设直线CM的解析式为y=k1x+b1，则，解之得，．∴直线CM的解析式．联立，解之得或（舍去）．∴．②若点P在对称轴左侧（如图②），只能是△PCQ∽△ACH，得∠PCQ=∠ACH．过A作CA的垂线交PC于点F，作FN⊥x轴于点N．由△CFA∽△CAH得，由△FNA∽△AHC得．∴AN=2，FN=1，CH=4，HO=1，则AH=2，∴点F坐标为（﹣5，1）．设直线CF的解析式为y=k2x+b2，则，解之得．∴直线CF的解析式．联立，解之得或（舍去）．∴．∴满足条件的点P坐标为或．13.解：（1）∵直线l：y=3x+3与x轴交于点A，与y轴交于点B，∴A（﹣1，0），B（0，3）；∵把△AOB沿y轴翻折，点A落到点C，∴C（1，0）．设直线BD的解析式为：y=kx+b，∵点B（0，3），D（3，0）在直线BD上，∴，解得k=﹣1，b=3，∴直线BD的解析式为：y=﹣x+3．设抛物线的解析式为：y=a（x﹣1）（x﹣3），∵点B（0，3）在抛物线上，∴3=a×（﹣1）×（﹣3），解得：a=1，∴抛物线的解析式为：y=（x﹣1）（x﹣3）=x2﹣4x+3．（2）抛物线的解析式为：y=x2﹣4x+3=（x﹣2）2﹣1，∴抛物线的对称轴为直线x=2，顶点坐标为（2，﹣1）．直线BD：y=﹣x+3与抛物线的对称轴交于点M，令x=2，得y=1，∴M（2，1）．设对称轴与x轴交点为点F，则CF=FD=MF=1，∴△MCD为等腰直角三角形．∵以点N、B、D为顶点的三角形与△MCD相似，∴△BND为等腰直角三角形．如答图1所示：（I）若BD为斜边，则易知此时直角顶点为原点O，∴N1（0，0）；（II）若BD为直角边，B为直角顶点，则点N在x轴负半轴上，∵OB=OD=ON2=3，∴N2（﹣3，0）；（III）若BD为直角边，D为直角顶点，则点N在y轴负半轴上，∵OB=OD=ON3=3，∴N3（0，﹣3）．∴满足条件的点N坐标为：（0，0），（﹣3，0）或（0，﹣3）．（3）方法一：假设存在点P，使S△PBD=6，设点P坐标为（m，n）．（I）当点P位于直线BD上方时，如答图2所示：过点P作PE⊥x轴于点E，则PE=n，DE=m﹣3．S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE=（3+n）•m﹣×3×3﹣（m﹣3）•n=6，化简得：m+n=7 ①，∵P（m，n）在抛物线上，∴n=m2﹣4m+3，代入①式整理得：m2﹣3m﹣4=0，解得：m1=4，m2=﹣1，∴n1=3，n2=8，∴P1（4，3），P2（﹣1，8）；（II）当点P位于直线BD下方时，如答图3所示：过点P作PE⊥y轴于点E，则PE=m，OE=﹣n，BE=3﹣n．S△PBD=S梯形PEOD+S△BOD﹣S△PBE=（3+m）•（﹣n）+×3×3﹣（3﹣n）•m=6，化简得：m+n=﹣1 ②，∵P（m，n）在抛物线上，∴n=m2﹣4m+3，代入②式整理得：m2﹣3m+4=0，△=﹣7＜0，此方程无解．故此时点P不存在．综上所述，在抛物线上存在点P，使S△PBD=6，点P的坐标为（4，3）或（﹣1，8）．方法二：假设存在点P，使S△PBD=6，过点P作直线l平行BD，则l与BD的距离为d，∵BD==3，∴S△PBD=BD×d，∴d=2，∵BD与y轴夹角为45°，∴BB′=4，∴将BD上移或下移4个单位，①上移4个单位，l解析式为：y=﹣x+7，∵y=x2﹣4x+3，∴x2﹣3x﹣4=0，∴x1=4，x2=﹣1，②下移4个单位，l解析式为y=﹣x﹣1，∵y=x2﹣4x+3，∴x2﹣3x+4=0，△＜0，∴此方程无解，综上所述，点P的坐标为（4，3）或（﹣1，8）．14.方法一：解：（1）∵该抛物线过点C（0，2），∴可设该抛物线的解析式为y=ax2+bx+2．将A（﹣1，0），B（4，0）代入，得，解得，∴抛物线的解析式为：y=﹣x2+x+2．（2）存在．由图象可知，以A、B为直角顶点的△ABE不存在，所以△ABE只可能是以点E为直角顶点的三角形．在Rt△BOC中，OC=2，OB=4，∴BC==．在Rt△BOC中，设BC边上的高为h，则×h=×2×4，∴h=．∵△BEA∽△COB，设E点坐标为（x，y），∴=，∴y=±2将y=2代入抛物线y=﹣x2+x+2，得x1=0，x2=3．当y=﹣2时，不合题意舍去．∴E点坐标为（0，2），（3，2）．（3）如图2，连结AC，作DE⊥x轴于点E，作BF⊥AD于点F，∴∠BED=∠BFD=∠AFB=90°．设BC的解析式为y=kx+b，由图象，得，∴，y BC=﹣x+2．由BC∥AD，设AD的解析式为y=﹣x+n，由图象，得0=﹣×（﹣1）+n ∴n=﹣，y AD=﹣x﹣．∴﹣x2+x+2=﹣x﹣，解得：x1=﹣1，x2=5∴D（﹣1，0）与A重合，舍去；∴D（5，﹣3）．∵DE⊥x轴，∴DE=3，OE=5．由勾股定理，得BD=．∵A（﹣1，0），B（4，0），C（0，2），∴OA=1，OB=4，OC=2．∴AB=5在Rt△AOC中，Rt△BOC中，由勾股定理，得AC=，BC=2，∴AC2=5，BC2=20，AB2=25，∴AC2+BC2=AB2∴△ACB是直角三角形，∴∠ACB=90°．∵BC∥AD，∴∠CAF+∠ACB=180°，∴∠CAF=90°．∴∠CAF=∠ACB=∠AFB=90°，∴四边形ACBF是矩形，∴AC=BF=，在Rt△BFD中，由勾股定理，得DF=，∴DF=BF，∴∠ADB=45°．方法二：（1）略．（2）∵以A、B、E为顶点的三角形与△COB相似，∴AE⊥BE且或，∵E为抛物线上一动点，∴设E（t，﹣），A（﹣1，0），B（4，0），∴，∴t2﹣3t=0，解得：t1=0，t2=3，∴E1（0，2），E2（3，2），①当E1（0，2）时，AE=，BE=，∴，∵，∴，∴△ABE∽△COB，②当E2（3，2）时，同理△ABE∽△COB，∴E1（0，2），E2（3，2）．（3）过B点作AD的垂线，垂足为H，∵B（4，0），C（0，2），∴K BC==﹣，∵BC∥AD，∴K AD=﹣，l AD：y=﹣x﹣，∵BH⊥AD，∴K BH×K AD=﹣1，∴K BH=2，l BH：y=2x﹣8，∴l AD与l BH的交点H（3，﹣2），∴，解得x1=﹣1（舍），x2=5，∴D（5，﹣3），∵B（4，0），H（3，﹣2），∴BH=，BD=，∴sin∠BDH=，∴∠BDA=45°．15.解：（1）把A（﹣1，0）代入得c=﹣，∴抛物线解析式为（2）如图1，过点C作CH⊥EF于点H，∵∠CEF=∠CFG，FG⊥y轴于点G∴△EHC∽△FGC∵E（m，n）∴F（m，）又∵C（0，﹣）∴EH=n+，CH=﹣m，FG=﹣m，CG=m2又∵，则∴n+=2∴n=当F点位于E点上方时，则∠CEF＞90°；又∠CFG肯定为锐角，故这种情形不符合题意．由此当n=时，代入抛物线解析式，求得m=±2，又E点位于第二象限，所以﹣2＜m＜0．（3）由题意可知P（t，0），M（t，）∵PM⊥x轴交抛物线于点M，∠OBQ=∠OMP，∴△OPM∽△QPB．∴．其中OP=t，PM=，PB=1﹣t，∴PQ=．BQ=∴PQ+BQ+PB=．∴△PBQ的周长为2．16.解：（1）设抛物线的解析式为y=a（x﹣1）2﹣1，将B点坐标代入函数解析式，得（5﹣1）2a﹣1=3，解得a=．故抛物线的解析式为y=（x﹣1）2﹣1；（2）由勾股定理，得OA2=11+12=2，OB2=52+32=34，AB2=（5﹣1）2+（3+1）2=32，OA2+AB2=OB2，∴∠OAB=90°，O到直线AB的距离是OA=；（3）设M（a，b），N（a，0）当y=0时，（x﹣1）2﹣1=0，解得x1=3，x2=﹣1，D（3，0），DN=3﹣a．①当△MND∽△OAB时，=，即=，化简，得4b=a﹣3 ①M在抛物线上，得b=（a﹣1）2﹣1 ②联立①②，得，解得a1=3（不符合题意，舍），a2=﹣2，b=，M1（﹣2，），当△MND∽△BAO时，=，即=，化简，得b=12﹣4a ③，联立②③，得，解得a1=3（不符合题意，舍），a2=﹣17，b=12﹣4×（﹣17）=80，M2（﹣17，80）．综上所述：当△DMN与△OAB相似时，点M的坐标（﹣2，），（﹣17，80）．17.解：（1）∵抛物线过G（2，2），∴把G坐标代入抛物线解析式得：2=﹣（2+2）（2﹣m），解得：m=4；（2）①令y=0，得到﹣（x+2）（x﹣m）=0，解得：x1=﹣2，x2=m，∵m＞0，∴A（﹣2，0），B（m，0），把m=4代入得：B（4，0），∴AB=6，令x=9，得到y=2，即C（0，2），∴OC=2，则S△ABC=×6×2=6；②∵A（﹣2，0），B（4，0），∴抛物线解析式为y=﹣（x+2）（x﹣4）的对称轴为x=1，如图1，连接BC交对称轴于点H，由对称轴的性质和两点之间线段最短的性质可得：此时AH+CH=BH+CH=BC 最小，设直线BC的解析式为y=kx+b，把B与C坐标代入得：，解得：，∴直线BC解析式为y=﹣x+2，令x=1，得到y=，即H（1，）；（3）在第四象限内，抛物线上存在点M，使得以点A、B、M为顶点的三角形与△ACB相似，分两种情况考虑：（i）当△ACB∽△ABM时，则有=，即AB2=AC•AM，∵A（﹣2，0），C（0，2），即OA=OC=2，∴∠CAB=45°，∠BAM=45°，如图2，过M作MN⊥x轴，交x轴于点N，则AN=MN，∴OA+ON=2+ON=MN，设M（x，﹣x﹣2）（x＞0），把M坐标代入抛物线解析式得：﹣x﹣2=﹣（x+2）（x﹣m），∵x＞0，∴x+2＞0，∵m＞0，∴x=2m，即M（2m，﹣2m﹣2），∴AM==2（m+1），∵AB2=AC•AM，AC=2，AB=m+2，∴（m+2）2=2•2（m+1），解得：m=2±2，∵m＞0，∴m=2+2；（ii）当△ACB∽△MBA时，则=，即AB2=CB•MA，∵∠CBA=∠BAM，∠ANM=∠BOC=90°，∴△ANM∽△BOC，∴=，∵OB=m，设ON=x，∴=，即MN=（x+2），令M（x，﹣（x+2））（x＞0），把M坐标代入抛物线解析式得：﹣（x+2）=﹣（x+2）（x﹣m），∵x＞0，∴x+2＞0，∵m＞0，∴x=m+2，即M（m+2，﹣（m+4）），∵AB2=CB•MA，CB=，AN=m+4，MN=（m+4），∴（m+2）2=•，整理得：=0，显然不成立，18.（1）证明：∵y=x2﹣2mx+m2+m﹣1=（x﹣m）2+m﹣1，∴点P的坐标为（m，m﹣1），∵当x=m时，y=x﹣1=m﹣1，∴点P在直线l上；（2）解：当m=﹣3时，抛物线解析式为y=x2+6x+5，当y=0时，x2+6x+5=0，解得x1=﹣1，x2=﹣5，则A（﹣5，0），当x=0时，y=x2+6x+5=5，则C（0，5），可得解方程组，解得或，则P（﹣3，﹣4），Q（﹣2，﹣3），作ME⊥y轴于E，PF⊥x轴于F，QG⊥x轴于G，如图，∵OA=OC=5，∴△OAC为等腰直角三角形，∴∠ACO=45°，∴∠MCE=45°﹣∠ACM，∵QG=3，OG=2，∴AG=OA﹣OG=3=QG，∴△AQG为等腰直角三角形，∴∠QAG=45°，∵∠APF=90°﹣∠PAF=90°﹣（∠PAQ+45°）=45°﹣∠PAQ，∵∠ACM=∠PAQ，∴∠APF=∠MCE，∴Rt△CME∽Rt△PAF，∴=，设M（x，x2+6x+5），∴ME=﹣x，CE=5﹣（x2+6x+5）=﹣x2﹣6x，∴=，整理得x2+4x=0，解得x1=0（舍去），x2=﹣4，∴点M的坐标为（﹣4，﹣3）；（3）解：解方程组得或，则P（m，m﹣1），Q（m+1，m），∴PQ2=（m+1﹣m）2+（m﹣m+1）2=2，OQ2=（m+1）2+m2=2m2+2m+1，OP2=m2+（m﹣1）2=2m2﹣2m+1，当PQ=OQ时，2m2+2m+1=2，解得m1=，m2=；当PQ=OP时，2m2﹣2m+1=2，解得m1=，m2=；当OP=OQ时，2m2+2m+1=2m2﹣2m+1，解得m=0，综上所述，m的值为0，，，，．19.解：（1）令y=0得x1=﹣2，x2=4，∴点A（﹣2，0）、B（4，0）令x=0得y=﹣，∴点C（0，﹣）（2）将x=1代入抛物线的解析式得y=﹣∴点M的坐标为（1，﹣）∴点M关于直线x=﹣2的对称点M′的坐标为（﹣5，）设直线M′B的解析式为y=kx+b将点M′、B的坐标代入得：解得：所以直线M′B的解析式为y=．将x=﹣2代入得：y=﹣，所以n=﹣．（3）过点D作DE⊥BA，垂足为E．由勾股定理得：AD==3，BD=，如下图，①当P1AB∽△ADB时，即：∴P1B=6过点P1作P1M1⊥AB，垂足为M1．∴即：解得：P1M1=6，∵即：解得：BM1=12∴点P1的坐标为（﹣8，6）∵点P1不在抛物线上，所以此种情况不存在；②当△P2AB∽△BDA时，即：∴P2B=6过点P2作P2M2⊥AB，垂足为M2．∴，即：∴P2M2=2∵，即：∴M2B=8∴点P2的坐标为（﹣4，2）将x=﹣4代入抛物线的解析式得：y=2，∴点P2在抛物线上．由抛物线的对称性可知：点P2与点P4关于直线x=1对称，∴P4的坐标为（6，2），当点P3位于点C处时，两三角形全等，所以点P3的坐标为（0，﹣），综上所述点P的坐标为：（﹣4，2）或（6，2）或（0，﹣）时，以P、A、B为顶点的三角形与△ABD相似．20.解：（1）∵点A1（1，2）在抛物线的解析式为y=ax2上，∴a=2；（2）A n B n=2x2=2×[（）n﹣1]2=，B n B n+1=；（3）由Rt△A n B n B n+1是等腰直角三角形得A n B n=B n B n+1，则：=，2n﹣3=n，n=3，∴当n=3时，Rt△A n B n B n+1是等腰直角三角形，②依题意得，∠A k B k B k+1=∠A m B m B m+1=90°，有两种情况：i）当Rt△A k B k B k+1∽Rt△A m B m B m+1时，=，=，=，所以，k=m（舍去），ii）当Rt△A k B k B k+1∽Rt△B m+1B m A m时，=，=，=，∴k+m=6，∵1≤k＜m≤n（k，m均为正整数），∴取或；当时，Rt△A1B1B2∽Rt△B6B5A5，相似比为：==64，当时，Rt△A2B2B3∽Rt△B5B4A4，相似比为：==8，所以：存在Rt△A k B k B k+1与Rt△A m B m B m+1相似，其相似比为64：1或8：1．。

九年级中考数学动点问题压轴题专题训练1. 如图1，在平面直角坐标系中，四边形OABC各顶点的坐标分别为O(0，0)，A(3，33)，B(9，53)，C(14，0)．动点P与Q同时从O点出发，运动时间为t秒，点P沿OC方向以1单位长度/秒的速度向点C运动，点Q沿折线OA－AB－BC运动，在OA，AB，BC上运动的速度分别为3，3，52(单位长度/秒)．当P，Q中的一点到达C点时，两点同时停止运动．(1)求AB所在直线的函数表达式．(2)如图2，当点Q在AB上运动时，求△CPQ的面积S关于t的函数表达式及S 的最大值．(3)在P，Q的运动过程中，若线段PQ的垂直平分线经过四边形OABC的顶点，求相应的t值．图1 图22. 如图，抛物线y=-x2+bx+c与x轴交于A，B两点(A在B的左侧)，与y轴交于点N，过A点的直线l:y=kx+n与y轴交于点C，与抛物线y=-x2+bx+c的另一个交点为D，已知A(-1，0)，D(5，-6)，P点为抛物线y=-x2+bx+c上一动点(不与A，D重合).(1)求抛物线和直线l的解析式;(2)当点P在直线l上方的抛物线上时，过P点作PE∥x轴交直线l于点E，作PF∥y轴交直线l于点F，求PE+PF的最大值;(3)设M为直线l上的点，探究是否存在点M，使得以点N，C，M，P为顶点的四边形为平行四边形.若存在，求出点M的坐标;若不存在，请说明理由.3. 如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋c经过A(－2, －4 )、O(0, 0)、B(2, 0)三点．（1）求抛物线y＝ax2＋bx＋c的解析式；（2）若点M是该抛物线对称轴上的一点，求AM＋OM的最小值．4. 设直线l1：y＝k1x＋b1与l2：y＝k2x＋b2，若l1⊥l2，垂足为H，则称直线l1与l2是点H的直角线．（1）已知直线①122y x =-+；②2y x =+；③22y x =+；④24y x =+和点C (0，2)，则直线_______和_______是点C 的直角线（填序号即可）；（2）如图，在平面直角坐标系中，直角梯形OABC 的顶点A (3，0)、B (2，7)、C (0，7)，P 为线段OC 上一点，设过B 、P 两点的直线为l 1，过A 、P 两点的直线为l 2，若l 1与l 2是点P 的直角线，求直线l 1与l 2的解析式．5. 如图①，在平面直角坐标系xOy 中，已知抛物线y=ax 2-2ax -8a 与x 轴相交于A ，B 两点(点A 在点B 的左侧)，与y 轴交于点C (0，-4).(1)点A 的坐标为 ，点B 的坐标为 ，线段AC 的长为 ，抛物线的解析式为 .(2)点P 是线段BC 下方抛物线上的一个动点.如果在x 轴上存在点Q ，使得以点B ，C ，P ，Q 为顶点的四边形是平行四边形，求点Q 的坐标.①6. 如图，已知抛物线211(1)444by x b x =-++（b 是实数且b ＞2）与x 轴的正半轴分别交于点A 、B （点A 位于点B 是左侧），与y 轴的正半轴交于点C ．（1）点B 的坐标为______，点C 的坐标为__________（用含b 的代数式表示）； （2）请你探索在第一象限内是否存在点P ，使得四边形PCOB 的面积等于2b ，且△PBC 是以点P 为直角顶点的等腰直角三角形？如果存在，求出点P 的坐标；如果不存在，请说明理由；（3）请你进一步探索在第一象限内是否存在点Q ，使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似（全等可看作相似的特殊情况）？如果存在，求出点Q 的坐标；如果不存在，请说明理由．7. 如图，已知A 、B 是线段MN 上的两点，4=MN ，1=MA ，1>MB ．以A 为中心顺时针旋转点M ，以B 为中心逆时针旋转点N ，使M 、N 两点重合成一点C ，构成△ABC ，设x AB =． （1）求x 的取值范围；（2）若△ABC 为直角三角形，求x 的值； （3）探究：△ABC 的最大面积？8. 如图，已知抛物线y＝－x2＋bx＋c经过A(0, 1)、B(4, 3)两点．（1）求抛物线的解析式；（2）求tan∠ABO的值；（3）过点B作BC⊥x轴，垂足为C，在对称轴的左侧且平行于y轴的直线交线段AB于点N，交抛物线于点M，若四边形MNCB为平行四边形，求点M的坐标．9. 在平面直角坐标系中，反比例函数与二次函数y＝k(x2＋x－1)的图象交于点A(1,k)和点B(－1,－k)．（1）当k＝－2时，求反比例函数的解析式；（2）要使反比例函数与二次函数都是y随x增大而增大，求k应满足的条件以及x的取值范围；（3）设二次函数的图象的顶点为Q，当△ABQ是以AB为斜边的直角三角形时，求k的值．10. 如图，已知抛物线y＝ax2＋bx＋4(a≠0)的对称轴为直线x＝3，抛物线与x轴相交于A，B两点，与y轴相交于点C，已知B点的坐标为(8，0)．(1)求抛物线的解析式；(2)点M为线段BC上方抛物线上的一点，点N为线段BC上的一点，若MN∥y 轴，求MN的最大值；(3)在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．11. 如图，直线y＝2x＋6与反比例函数y＝kx(k＞0)的图象交于点A(m，8)，与x轴交于点B，平行于x轴的直线y＝n(0＜n＜6)交反比例函数的图象于点M，交AB于点N，连接BM.(1)求m的值和反比例函数的解析式；(2)观察图象，直接写出当x＞0时不等式2x＋6－kx＞0的解集；(3)直线y＝n沿y轴方向平移，当n为何值时，△BMN的面积最大？最大值是多少？12. 如图，在平面直角坐标系xOy中，顶点为M的抛物线y＝ax2＋bx（a＞0）经过点A和x轴正半轴上的点B，AO＝BO＝2，∠AOB＝120°．（1）求这条抛物线的表达式；（2）连结OM，求∠AOM的大小；（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．13. 在直角梯形OABC中，CB//OA，∠COA＝90°，CB＝3，OA＝6，BA＝35．分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系．（1）求点B的坐标；（2）已知D、E分别为线段OC、OB上的点，OD＝5，OE＝2EB，直线DE交x轴于点F．求直线DE的解析式；（3）点M是（2）中直线DE上的一个动点，在x轴上方的平面内是否存在另一点N，使以O、D、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．14. 如图，已知一次函数y ＝－x ＋7与正比例函数43y x 的图象交于点A ，且与x 轴交于点B ．（1）求点A 和点B 的坐标；（2）过点A 作AC ⊥y 轴于点C ，过点B 作直线l //y 轴．动点P 从点O 出发，以每秒1个单位长的速度，沿O —C —A 的路线向点A 运动；同时直线l 从点B 出发，以相同速度向左平移，在平移过程中，直线l 交x 轴于点R ，交线段BA 或线段AO 于点Q ．当点P 到达点A 时，点P 和直线l 都停止运动．在运动过程中，设动点P 运动的时间为t 秒．①当t 为何值时，以A 、P 、R 为顶点的三角形的面积为8？②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形？若存在，求t 的值；若不存在，请说明理由．15. 如图，二次函数y ＝a (x 2－2mx －3m 2)（其中a 、m 是常数，且a ＞0，m ＞0）的图像与x 轴分别交于A 、B （点A 位于点B 的左侧），与y 轴交于点C (0,－3)，点D 在二次函数的图像上，CD //AB ，联结AD ．过点A 作射线AE 交二次函数的图像于点E ，AB 平分∠DAE ． （1）用含m 的式子表示a ；（2）求证：AD为定值；AE（3）设该二次函数的图像的顶点为F．探索：在x轴的负半轴上是否存在点G，联结GF，以线段GF、AD、AE的长度为三边长的三角形是直角三角形？如果存在，只要找出一个满足要求的点G即可，并用含m的代数式表示该点的横坐标；如果不存在，请说明理由．16. 如图，二次函数y=-x2+4x+5的图象的顶点为D，对称轴是直线l，一次函数y=x+1的图象与x轴交于点A，且与直线DA关于l的对称直线交于点B.(1)点D的坐标是.(2)直线l与直线AB交于点C，N是线段DC上一点(不与点D，C重合)，点N 的纵坐标为n.过点N作直线与线段DA，DB分别交于点P，Q，使得△DPQ与△DAB 相似.①当n=时，求DP的长;②若对于每一个确定的n的值，有且只有一个△DPQ与△DAB相似，请直接写出n的取值范围.17. 已知直线y ＝3x －3分别与x 轴、y 轴交于点A ，B ，抛物线y ＝ax 2＋2x ＋c 经过点A ，B ．（1）求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐标；（2）记该抛物线的对称轴为直线l ，点B 关于直线l 的对称点为C ，若点D 在y 轴的正半轴上，且四边形ABCD 为梯形． ①求点D 的坐标；②将此抛物线向右平移，平移后抛物线的顶点为P ，其对称轴与直线y ＝3x －3交于点E ，若73tan =∠DPE ，求四边形BDEP 的面积．18. 如图，在平面直角坐标系xOy 中，二次函数y ＝－x 2＋2x ＋8的图象与一次函数y ＝－x ＋b 的图象交于A 、B 两点，点A 在x 轴上，点B 的纵坐标为－7.点P是二次函数图象上A 、B 两点之间的一个动点(不与点A 、B 重合)，设点P 的横坐标为m ，过点P 作x 轴的垂线交AB 于点C ，作PD ⊥AB 于点D . (1)求b 及sin ∠ACP 的值；(2)用含m 的代数式表示线段PD 的长；(3)连接PB ，线段PC 把△PDB 分成两个三角形，是否存在适合的m 值，使这两个三角形的面积之比为1∶2？如果存在，直接写出m 的值；如果不存在，请说明理由．19. 如图，抛物线233384y x x =--+与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ． （1）求点A 、B 的坐标；（2）设D 为已知抛物线的对称轴上的任意一点，当△ACD 的面积等于△ACB 的面积时，求点D 的坐标；（3）若直线l 过点E (4, 0)，M 为直线l 上的动点，当以A 、B 、M 为顶点所作的直角三角形有且只有．．．．三个时，求直线l 的解析式．20. 已知平面直角坐标系中两定点A(－1, 0)、B(4, 0)，抛物线y＝ax2＋bx－2（a≠0）过点A、B，顶点为C，点P(m, n)（n＜0）为抛物线上一点．（1）求抛物线的解析式和顶点C的坐标；（2）当∠APB为钝角时，求m的取值范围；（3）若m＞32，当∠APB为直角时，将该抛物线向左或向右平移t（0＜t＜52）个单位，点C、P平移后对应的点分别记为C′、P′，是否存在t，使得顺次首尾连接A、B、P′、C′所构成的多边形的周长最短？若存在，求t的值并说明抛物线平移的方向；若不存在，请说明理由．2021中考数学压轴专题训练之动点问题-答案一、解答题（本大题共20道小题）1. 【答案】【思维教练】(1)设一次函数解析式，将已知点A、B的坐标值代入求解即可；(2)S△CPQ＝12·CP·Q y，CP＝14－t，点Q在AB上，Q y即为当x＝t时的y值，代入化简得出S与t的函数关系式，化为顶点式得出最值；(3)垂直平分线过顶点需以时间为临界点分情况讨论，当Q在OA上时，过点C；当Q在AB上时，过点A；当Q在BC上时，过点C和点B，再列方程并求解．解图1解：(1)把A(3，33)，B(9，53)代入y ＝kx ＋b ，得⎩⎪⎨⎪⎧3k ＋b ＝33，9k ＋b ＝53，解得⎩⎨⎧k ＝33，b ＝23， ∴y ＝33x ＋23；(3分) (2)在△PQC 中，PC ＝14－t ，∵OA ＝32＋（33）2＝6且Q 在OA 上速度为3单位长度/s ， AB ＝62＋（23）2＝43且Q 点在AB 上的速度为3单位长度/s ， ∴Q 在OA 上时的横坐标为t ，Q 在AB 上时的横坐标为32t ， PC 边上的高线长为33t ＋2 3.(6分)所以S ＝12(14－t )(32t ＋23)＝－34t 2＋532t ＋143(2≤t ≤6)．当t ＝5时，S 有最大值为8134.(7分)解图2(3)①当0＜t ≤2时，线段PQ 的中垂线经过点C(如解图1)． 可得方程(332t )2＋(14－32t )2＝(14－t )2. 解得t 1＝74，t 2＝0(舍去)，此时t ＝74.(8分)解图3②当2＜t ≤6时，线段PQ 的中垂线经过点A(如解图2)． 可得方程(33)2＋(t －3)2＝[3(t －2)]2.解得t 1＝3＋572，∵t 2＝3－572(舍去)，此时t ＝3＋572. ③当6＜t ≤10时，(1)线段PQ 的中垂线经过点C(如解图3)． 可得方程14－t ＝25－52t ，解得t ＝223.(10分)解图4(2)线段PQ 的中垂线经过点B(如解图4)． 可得方程(53)2＋(t －9)2＝[52(t －6)]2. 解得t 1＝38＋2027，t 2＝38－2027(舍去)．此时t ＝38＋2027.(11分)综上所述，t 的值为74，3＋572，223，38＋2027.(12分)【难点突破】解决本题的关键点在于对PQ 的垂直平分线过四边形顶点的情况进行分类讨论，在不同阶段列方程求解．2. 【答案】[分析] (1)将点A，D的坐标分别代入直线表达式、抛物线的表达式，即可求解;(2)设出P点坐标，用参数表示PE，PF的长，利用二次函数求最值的方法.求解;(3)分NC是平行四边形的一条边或NC是平行四边形的对角线两种情况，分别求解即可.解:(1)将点A，D的坐标代入y=kx+n得:解得:故直线l的表达式为y=-x-1.将点A，D的坐标代入抛物线表达式，得解得故抛物线的表达式为:y=-x2+3x+4.(2)∵直线l的表达式为y=-x-1，∴C(0，-1)，则直线l与x轴的夹角为45°，即∠OAC=45°，∵PE∥x轴，∴∠PEF=∠OAC=45°.又∵PF∥y轴，∴∠EPF=90°，∴∠EFP=45°.则PE=PF.设点P坐标为(x，-x2+3x+4)，则点F(x，-x-1)，∴PE+PF=2PF=2(-x2+3x+4+x+1)=-2(x-2)2+18，∵-2<0，∴当x=2时，PE+PF有最大值，其最大值为18.(3)由题意知N(0，4)，C(0，-1)，∴NC=5，①当NC是平行四边形的一条边时，有NC∥PM，NC=PM.设点P 坐标为(x ，-x 2+3x +4)，则点M 的坐标为(x ，-x -1)， ∴|y M -y P |=5，即|-x 2+3x +4+x +1|=5， 解得x=2±或x=0或x=4(舍去x=0)，则点M 坐标为(2+，-3-)或(2-，-3+)或(4，-5);②当NC 是平行四边形的对角线时，线段NC 与PM 互相平分. 由题意，NC 的中点坐标为0，，设点P 坐标为(m ，-m 2+3m +4)， 则点M (n'，-n'-1)， ∴0==，解得:n'=0或-4(舍去n'=0)， 故点M (-4，3).综上所述，存在点M ，使得以N ，C ，M ，P 为顶点的四边形为平行四边形，点M 的坐标分别为: (2+，-3-)，(2-，-3+)，(4，-5)，(-4，3).3. 【答案】（1）212y x x =-+。

抛物线压轴题考点及解决技巧摘要：1.抛物线压轴题概述2.抛物线压轴题的考点a.抛物线的性质b.抛物线与直线的关系c.抛物线与坐标轴的关系d.抛物线的顶点3.解决抛物线压轴题的技巧a.利用抛物线的性质b.利用抛物线与直线的关系c.利用抛物线与坐标轴的关系d.利用抛物线的顶点4.例题解析5.总结与建议正文：抛物线是中学数学中的重要内容，其在压轴题中的出现频率相当高。

对于许多学生来说，抛物线压轴题往往显得难度较大，因此掌握一定的解决技巧显得尤为重要。

本文将为大家介绍抛物线压轴题的考点及解决技巧，希望能为大家带来帮助。

首先，我们来了解一下抛物线压轴题的概述。

抛物线压轴题通常涉及抛物线的性质、抛物线与直线的关系、抛物线与坐标轴的关系以及抛物线的顶点等多个方面。

要解决这类问题，关键是熟练掌握抛物线的各种性质和公式。

接下来，我们来详细了解一下抛物线压轴题的考点。

1.抛物线的性质：包括抛物线的开口方向、对称轴、焦距等。

这些性质在解决抛物线与直线的关系时尤为重要。

2.抛物线与直线的关系：掌握抛物线与直线的交点、切线等知识点，能够帮助我们解决抛物线与直线相交、相切等问题。

3.抛物线与坐标轴的关系：了解抛物线与坐标轴的交点、对称性等知识点，能够帮助我们解决抛物线与坐标轴的位置关系问题。

4.抛物线的顶点：掌握顶点的求法及顶点坐标，能够帮助我们快速找到抛物线的最值、对称轴等信息。

在了解了抛物线压轴题的考点后，我们来看看解决抛物线压轴题的技巧。

1.利用抛物线的性质：在解决抛物线问题时，可以充分利用抛物线的性质，例如对称性、单调性等，简化问题。

2.利用抛物线与直线的关系：当抛物线与直线相交时，可以利用解析几何知识求解交点坐标；当抛物线与直线相切时，可以利用导数求解切线方程。

3.利用抛物线与坐标轴的关系：解决抛物线与坐标轴的位置关系问题时，可以利用对称性快速求解。

4.利用抛物线的顶点：在解决抛物线问题时，可以尝试寻找顶点，从而找到最值、对称轴等信息。

1 / 5数学中考题精选----------抛物线1、在平面直角坐标系中，已知抛物线经过A （－4，0），B （0，－4），C （1）求抛物线的解析式；（2）若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ， △AMB 的面积为S ．求S 关于m 的函数关系式，并求出S 的最大值． （3）若点P 是抛物线上的动点，点Q 是直线y ＝－x 上的动点，判断有几个位置能够使得点P 、Q 、B 、O 直接写出相应的点Q 的坐标．2、已知抛物线y ＝－x 2＋bx ＋c 经过点A （0，4），且抛物线的对称轴为直线x ＝2． （1）求该抛物线的解析式；（2）若该抛物线的顶点为B ，在抛物线上是否存在点C ，使得A 、B 、O 、C 点构成的四边形为梯形？若存在，请求出点C （3）试问在抛物线上是否存在着点P ，使得以3为半径的⊙P 既与x 又与对称轴相交？若存在，请求出点P 的坐标，并求出对称轴被⊙P 的弦EF 的长度；若不存在，请说明理由．3、如图，已知抛物线y ＝ax 2＋bx ＋c （a ≠0）的顶点坐标为Q （2，－1），且与y 轴交于点C （0，3），与x 轴交于A 、B 两点（点A 在点B 的右侧），点P 是该抛物线上一动点，从点C 沿抛物线向点A 运动（点P 与A 不重合），过点P 作PD ∥y 轴，交AC 于点D ．（1）求该抛物线的函数关系式；（2）当△ADP 是直角三角形时，求点P 的坐标；（3）在题（2）的结论下，若点E 在x 轴上，点F 在抛物线上，问是否存在以A 、P 、E 、F 为顶点的平行四边形？若存在，求点F 的坐标；若不存在，请说明理由． ．4、如图，平面直角坐标系中，点A 、B 、C 在x 轴上，点D 、E 在y 轴2 / 5上，OA ＝OD ＝2，OC ＝OE ＝4，DB ⊥DC ，直线AD 与经过B 、E 、C 三点的抛物线交于F 、G 两点，与其对称轴交于M .点，P 为线段FG 上一个动点（与F 、G 不重合），PQ ∥y 轴与抛物线交于点Q ． （1）求经过B 、E 、C 三点的抛物线的解析式；（2）是否存在点P ，使得以P 、Q 、M 为顶点的三角形与△AOD 相似？若存在，求出满足条件的点P 的坐标；若不存在，请说明理由；（3）若抛物线的顶点为N ，连接QN ，探究四边形PMNQ 的形状：①能否成为菱形；②能否成为等腰梯形？若能，请直接写出点P 的坐标；若不能，请说明理由．5、如图，把抛物线y ＝－x 2（虚线部分）向右平移1个单位长度，再向上平移1个单位长度，得到抛物线l 1，抛物线l 2与抛物线l 1关于y 轴对称．点A 、O 、B 分别是抛物线l 1、l 2与x 轴的交点，D 、C 分别是抛物线l 1、l 2的顶点，线段CD 交y 轴于点E ．（1）分别写出抛物线l 1与l 2的解析式；（2）设P 是抛物线l 1上与D 、O 两点不重合的任意一点，Q 点是P点关于y 轴的对称点，试判断以P 、Q 、C 、D 为顶点的四边形是什么特殊的四边形？说明你的理由．（3）在抛物线l 1上是否存在点M ，使得S △ABM ＝S 四边形AOED ，如果存在，求出M 点的坐标；如果不存在，请说明理由．6、已知二次函数y ＝ax 2＋bx ＋c 的图象经过点A （3，0），B （2，－3），C （0，－3）．（1）求此函数的解析式及图象的对称轴；（2）点P 从B 点出发以每秒个单位的速度沿线段BC 向C 点运动，点Q 从O 点出发以相同的速度沿线段OA 向A 点运动，其中一个动点到达端点时，另一个也随之停止运动．设运动时间为t 秒．①当t 为何值时，四边形ABPQ 为等腰梯形；②设PQ 与对称轴的交点为M ，过M 点作x 轴的平行线交AB 于点N ，设四边形ANPQ 的面积为S ，求面积S 关于时间t 的函数解析式，并指出t 的取值X 围；当t 为何值时，S 有最大值或最小值． 说明理由．7、如图，二次函数y ＝－x 2＋ax ＋b 的图象与x 轴交于A （－21，0），B （2，0）两点，且与y 轴交于点C ． （1）求该抛物线的解析式，并判断△ABC 的形状；3 / 5（2）在x 轴上方的抛物线上有一点D ，且以A 、C 、D 、B 四点为顶点的四边形是等腰梯形，请直接写出D 点的坐标；（3）在此抛物线上是否存在点P ，使得以A 、C 、B 、P 四点为顶点的四边形是直角梯形？若存在，求出P 点的坐标；若不存在，说明理由．8、如图，Rt △ABC 的顶点坐标分别为A （0，3），B （－21，23），C （1，0），∠ABC ＝90°，BC 与y 轴的交点为D ，D 点坐标为（0，33），以点D 为顶点、y 轴为对称轴的抛物线过点B ．（1）求该抛物线的解析式；（2）将△ABC 沿AC 折叠后得到点B 的对应点B ′，求证：四边形AOCB ′是矩形，并判断点B ′是否在（1）的抛物线上；（3）延长BA 交抛物线于点E ，在线段BE 上取一点P ，过P 点作x 轴的垂线，交抛物线于点F ，是否存在这样的点P ，使四边形PADF 是平行四边形？若存在，求出点P 的坐标，若不存在，说明理由．9、如图，矩形OABC 的两边OA 、OC 分别在x 轴和y 轴上，A （－3，0），过点C 的直线y ＝－2x ＋4与x 轴交于点D ，二次函数y ＝－21x 2＋bx ＋c 的图象经过B 、C 两点． （1）求B 、C 两点的坐标； （2）求二次函数的解析式；（3）若点P 是CD 的中点，求证：AP ⊥CD ；（4）在二次函数的图象上是否存在这样的点M ，使以A 、P 、C 、M 为顶点的四边形为矩形？若存在，求出点M 的坐标；若不存在，请说明理由．10、如图，在平面直角坐标系中，以点A (－3，0)为圆心、5为半径的圆与x 轴相交于点B 、C 两点（点B 在点C 的左边），与y 轴相交于D 、M 两点（点D 在点M 的下方）．（1）求以直线x ＝－3为对称轴、且经过D 、C 两点的抛物线的解析式； （2）若点P 是这条抛物线对称轴上的一个动点，求PC ＋PD 的取值X 围；（3）若点E E 、F 为顶点的四边形是平行四边形？若存在，求出点F4 / 511、如图，已知抛物线y ＝ax 2－2ax －b （a ＞0）与x 轴的一个交点为B (－1，0)，与y 轴的负半轴交于点C ，顶点为D ．（1）直接写出抛物线的对称轴及抛物线与x 轴的另一个交点A 的坐标； （2）以AD 为直径的圆经过点C ．①求抛物线的解析式；②点E 在抛物线的对称轴上，点F 在抛物线上，且以B ，A ，F ，E四点为顶点的四边形为平行四边形，求点F 的坐标．12、如图，已知抛物线与x 轴交于点A (－1，0)和点B (1，0)，与y 轴交于点C (0，－2)，直线x ＝m (m ＞1)与x 轴交于点D ．（1）求该抛物线的解析式；（2）在直线x ＝m (m ＞1)上有一点P （点P 在第一象限），使得以P 、D 、B 为顶点的三角形与以B 、C 、O 为顶点的三角形相似，求点P 的坐标（用含m 的代数式表示）；（3）在（2）成立的条件下，在抛物线上是否存在点Q ，使得四边形ABPQ 为平行四边形？若存在，请求出点Q 的坐标；若不存在，请说明理由．13、已知抛物线：x x y 22121+-= （1）求抛物线y 1的顶点坐标；（2）将抛物线y 1向右平移2个单位，再向上平移1个单位，得到抛物线y 2，求抛物线y 2的解析式；（3）如下图，抛物线y 2的顶点为P ，x 轴上有一动点M ，在y 1、y 2这两条抛物线上是否存在点N ，使O （原点）、P 、M 、N 四点构成以OP 为一边的平行四边形？若存在，求出N 点的坐标；若不存在，请说明理由．x ＝m5 / 514如图，在水平地面点A 处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B ．有人在直线AB 上点C （靠点B 一侧）竖直向上摆放无盖的圆柱形桶，试图让网球落入桶内．已知AB ＝4米，AC ＝3米，网球飞行最大高度OM =5米，圆柱形桶的直径为，高为（网球的体积和圆柱形桶的厚度忽略不计）．（1）如果竖直摆放5个圆柱形桶时，网球能不能落入桶内？ （2）当竖直摆放圆柱形桶多少个时，网球可以落入桶内？15、已知抛物线y ＝x 2＋bx ＋c 交y 轴于点A ，点A 关于抛物线对称轴的对称点为B （3，－4），直线y ＝41x 与抛物线在第一象限的交点为C ，连结OB ．（1）求抛物线的解析式；（2）如图（1），点P 在射线．．OC ．．上运动，连结BP ，设点P 的横坐标为x ，△OBP 的面积为y ，求y 与x 之间的函数关系式；（3）如图（2），点P 在直线．．OC ．．上运动，点Q在抛物线上运动，试问点P 、Q 在运动过程中是否存在以O 、B 、P 、Q 为顶点的四边形是平行四边形的情况，若存在，请求出点P 的坐标；若不存在，请说明理由．图（1） 图（2） 备用图。