2016年初三下册数学第27章知识点：图形的相似

=A′C′:AC=B′C′:BC.求证:△ABC∽△A′B′C′.
A′
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
过点D作DE∥BC交AC于点E.
B′
C′
∴AD:AB=AE:AC=DE:BC,△ADE∽△ABC
A
∵AD=A′B′∴AD:AB=A′B′:AB
又A′B′:AB=B′C′:BC=C′A′:CA
A
D
E
∵ DE∥BC，
A
D
E ∴ △ADE∽△ABC.
B
C
B
C
思考:有没有其他简单的办法判断两个三角形相似?
九年级数学第27章相似三角形
A
三边对应成
A′
比例
B
C
B′
C′
A' B' B'C' A'C' AB BC AC
是否有△ABC∽△A′B′C′？
九年级数学第27章相似三角形
已知:如图△ABC和△A′B′C′中A′B′:AB
成的三角形与原三角形相似.
九年级数学第27章相似三角形
平行于三角形一边的直线与其他两边(或延长线)相交,所得 的三角形与原三角形___相__似___.
“A”型 A
D
E
“X”型
D
E
O
B
C
（图1）
B
（图2）
C
九年级数学第27章相似三角形
已知：如图，AB∥EF ∥CD，
图中共有__3__对相似三角形.
AB∥EF
△AOB∽△FOE
AB∥CD
△AOB∽△DOC
EF∥CD
△EOF∽△COD
A E C

∠A=∠A′,∠B=∠B′,∠C=∠C′,∠D=∠D′,∠E=∠E′
对应角相等，对应边成比例 的两个多边形相似。
只满足对应角相等的两个 多边形相似吗？为什么？
只满足对应边成比例的两 个多边形呢？
相似多边形对应边的比叫做相似比
相似多边形的对应角相等，对应边成 比例.
例： 在如图所示的相似四边形中, 求未知边x、 y的长度和角度a的大小．
§27.1 图形的相似
• 1、了解图形相似的意义。
• 2、理解相似多边形的定义和性 质。
• 3、理解相似多边形的相似比的 意义。
请欣赏下面几组图片，观察每组图片有 怎样的共同特点？
你从上述几组图片发现了什么？
它们的形状相同，但大小不一定 相等。
判断下列图形，哪些是相似形？
(1)
(2)
(3)
5
α╭
图1
3
15
20
x
图2
谈一谈，通过本节课的 学习你有哪些收获？
• 相似图形 ——相同形状的图形
• 判断两个图形是否相似 • 利用相似放大或缩小图形
•相似多边形的特征和识别：
特征 对应角相等 相似多边形
识别 对应边成比例
• 如图：矩形草坪长30米，宽20米。沿草坪 四周有1米宽的环形小路，小路内外边缘形
(4)
(5)
(6)
(7)
(8)
•想一想
为什么有些图形是相似的， 而有些不相似呢？
那么两个图形满足什么条件时， 它们才是相似的？
AB BC CD DA AB BC CD DA
A A,B B,C C,D D
AB BC CD DE EA A' B' B'C' C' D' D' E' E' A'

九年级数学下册第二十七章【相似】重要知识点总结27.1 图形的相似1、相似的定义如果两个图形形状相同,但大小不一定相等,那么这两个图形相似。

（相似的符号：∽）2、相似的判定如果两个多边形满足对应角相等，对应边的比相等，那么这两个多边形相似。

3、相似比相似多边形的对应边的比叫相似比。

相似比为1时，相似的两个图形全等相似多边形的对应角相等，对应边的比相等。

相似多边形的周长比等于相似比。

相似多边形的面积比等于相似比的平方。

27.2相似三角形1、相似三角形的判定（★重难点）（1）.平行于三角形一边的直线和其他两边或两边延长线相交，所构成的三角形与原三角形相似（2）三边对应成比例（3）两边对应成比例,且夹角相等（4）两个三角形的两个角对应相等★常考题型：利用三角形的相似测量塔高、河宽2、相似三角形判定的常用模型A字型、8字型、三等角模型3、相似的性质1.相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比。

2.相似三角形周长的比等于相似比。

3.相似三角形面积的比等于相似比的平方4.多边形的面积的比等于相似比的平方，周长比等于相似比。

27.3位似1、定义：如果两个图形不仅是相似图形，而且每组对应点的连线交于一点，对应边互相平行，那么这两个图形叫做位似图形，这个点叫做位似中心，这时的相似比又称为位似比。

2、位似的相关性质（1）位似图形的对应点和位似中心在同一直线上，它们到位似中心的距离之比等于相似比。

（2）位似多边形的对应边平行或共线。

（3）位似可以将一个图形放大或缩小。

（4）位似图形的中心可以在任意的一点，不过位似图形也会随着位似中心的位变而位变。

（5）根据一个位似中心可以作两个关于已知图形一定位似比的位似图形,这两个图形分布在位似中心的两侧,并且关于位似中心对称。

★易错点1、位似是一种具有位置关系的相似，所以两个图形是位似图形，必定是相似图形，而相似图形不一定是位似图形；2、两个位似图形的位似中心只有一个；3、两个位似图形可能位于位似中心的两侧，也可能位于位似中心的一侧；4、位似比就是相似比．利用位似图形的定义可判断两个图形是否位似；5、平行于三角形一边的直线和其它两边相交，所构成的三角形与原三角形位似。

九年级下册数学第27章知识点汇总（人教
版）
27.1图形的相似
gt;gt;gt;gt;图形的相似知识点
27.2相似三角形
相似三角形定理：平行于三角形一边的直线和其他两边(或两边的延长线)相交，所构成的三角形与原三角形相似。

相似三角形判定定理1：两角对应相等，两三角形相似(ASA)
gt;gt;gt;gt;相似三角形知识点
27.3位似
位似图形(Homothetic figures)的任意一对对应点与位似中心在同一直线上，它们到位似中心的距离之比等于相似比。

把幻灯片上的图形放大到屏幕上，形成的新图形和原图形就是典型的位似图形。

两个多边形不仅相似，而且对应顶点的连线相交于一点，像这样的两个图形叫做位似图形(homothetic figures)，这个交点叫做位似中心，这时的相似比又称为位似比。

gt;gt;gt;gt;位似图形知识点
九年级下册数学第27章知识点整理的很及时吧，提高学习成绩离不开知识点和练习的结合，因此大家想要取得更好的成绩一定要注重从平时中发现问题查缺补漏~请关注数学知识点。

相似图形图形相似的定义：我们把形状相同的图形叫作相似图形。

注意：1、相似图形只针对形状，不谈大小；2、两个图形相似，其中一个图形可以看作由另一个图形放大或缩小得到；3、相似图形的形状相同，大小不一定相同，全等图形是特殊的相似图形；4、图形的相似与图形的位置无关。

特殊图形——相似多边形：如果它们的角对应相等，对应边成比例，那么这两个多边形叫相似多边形。

图文说明：如图所示，在四边形ABCD 和四边形1111D C B A ，1A A ∠=∠,1B B ∠=∠,1C C ∠=∠1D D ∠=∠,11111111D A ADD C CD C B BC B A AB === 则四边形ABCD 相似于四边形1111D C B A 相似； 记作：四边形ABCD ∽四边形1111D C B A(注意要把表示对应角顶点的字母写在对应的位置上！！！)相似多边形的性质：对应角相等，对应边成比例。

注意： 1、相似多边形对应边的比称为相似比,一般用 k 表示；2、若已知四边形ABCD 与四边形1111D C B A 的相似是k ,那么四边形1111D C B A 与四边形ABCD 的相似比是k1。

比例线段定义：对于四条线段a 、b 、c 、d ，如果其中两条线段的比（即它们的长度的比)与另两条线段的比相等，如dcb a =（即bc ad =），我们就说这四段线段是成比例线段，简称比例线段。

其中a 、b 、c 、d 叫组成比例的项；a 、d 叫比的外项，b 、c 叫比的内项， 当比的内项相等时，即cbb a =或c b b a ::=，线段 b 叫做线段a 和c 的比例中项。

解题策略：1、抓住比的内项乘积等于比的外项乘积，进行一些比的变换； 2、判断四条线段是否成比例，需要将这四条线段从小到大先排列，再判断前两条线段的比与后两条线段的比是否相等即可；3、成比例的线段是有顺序的，比如：a 、b 、c 、d 是成比例的线段，则只能写成d c b a =，而不能写成cd b a =。

求证：AC2=AD·AB
而∠AFC=∠BFA，
解析：此题考查了相似三角形的性质，通过构造相似 的面积之比为
.
◑两直角三角形的斜边和一条直角边成比例的两三角形相似。
1下2三面给出角C.了一形些关．于相似利的命用题，相其中真似命题三有（角形）对应边成比例解答即可．
(2)
；
解：过A点作AH⊥DE，交CF于G，交DE于H． 如图，△ABC 是一块锐角三角形材料，边 BC＝120 mm，高 AD＝80 mm，要把它加工成正方形零件，使正方形的一边在 BC 上，其余两个顶点分别在 AB、AC 上，这个正方形零
答：电视塔的高DE是33.6 m。
小题热身
要点梳理（五、位似的性质及应用）
1. 在如图所示的四个图形中，位似图形的个数为 ( C)
A. 1个
B. 2个
C. 3个
D. 4个
知识要点5 5.位似的性质及应用
(1)如果两个图形不仅相似，而且对应顶点的连线相交于一点，那么这样的两
个图形叫做位似图形，这个点叫做位似中心。(这时的相似比也称为位似比)。 (2)性质：位似图形上任意一对对应点到位似中心的距离之比等于位似比；对
件的边长是多少？
由题意可得△AFG∽△AEH = _________。
◑周长比等于相似比，面积比等于相似比的平方
下列图形中，属于相似图形的是（ ）
要点梳理（四、相似三角形的应用）
∴ AG FG 即 下列图形中，属于相似图形的是（ ）
如图（1），在 □ABCD 中，点 E 在边 BC 上，BE : EC =
上，已知此人眼睛距地面1.6 ∴ AC2=AD·AB
故球能碰到墙面离地 5.
m，标杆为3.2
m，且BC=1

则△ABC与△ A′B′C′的相似比是 △ A′B′C′与△ABC的相似比是
2，
1． 2
第十八页，共二十七页。
分层教学
做一做下面的题目(tímù)，看谁做得又快又准确。
1、2组
3、4组
如图所示的各组图形(túxíng)
中，不相似的图形(túxíng)有 组
下列图形(túxíng)中是 与
相似的.
第十九页，共二十七页。
相似多边形的对应边的比叫作相似比.
第十二页，共二十七页。
新知讲解
议一议 任意(rènyì)两个等边三角形相似吗？任意(rènyì)两个正方形呢？任意(rènyì)两个正n边形呢？
…
a1
a2
a3
an
分析：已知等边三角形的每个角都为60°, 三边都相等. 所以(suǒyǐ)满足边数相等，对应角相等， 以及对应边的比相等.
β
E 24cm
78°
83° C
F
x 118°
第十六页，共二十七页。
H
α G
新知讲解
四边形ABCD和EFGH相似，它们的对应(duìyìng)边的比相等．由此可得
EHEF,即x =24, AD AB 21 18
解得 x＝28cm.
21cm
D
A
β
18cm 78°
B
83° C
E 24cm
x 118°
F
H
则x= 2.5，y = 1，.5 α= ；90° ⑵如图2是两个相似的矩形，x= . 22.5
3
800 x
╮1250 y
6 650╰ 800
5
α╭
图1
3
30
15
20

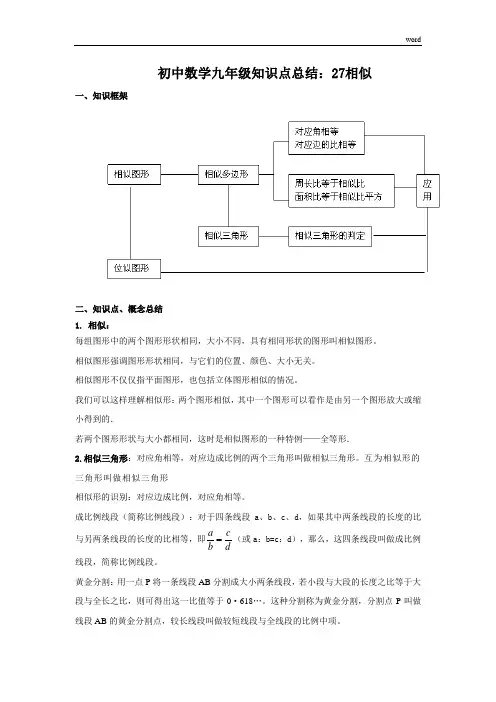
初中数学九年级知识点总结：27相似一、知识框架二、知识点、概念总结 1. 相似：每组图形中的两个图形形状相同，大小不同，具有相同形状的图形叫相似图形。

相似图形强调图形形状相同，与它们的位置、颜色、大小无关。

相似图形不仅仅指平面图形，也包括立体图形相似的情况。

我们可以这样理解相似形：两个图形相似，其中一个图形可以看作是由另一个图形放大或缩小得到的．若两个图形形状与大小都相同，这时是相似图形的一种特例——全等形．2.相似三角形：对应角相等，对应边成比例的两个三角形叫做相似三角形。

互为相似形的三角形叫做相似三角形相似形的识别：对应边成比例，对应角相等。

成比例线段（简称比例线段）：对于四条线段a 、b 、c 、d ，如果其中两条线段的长度的比与另两条线段的长度的比相等，即dcb a （或a ：b=c ：d ），那么，这四条线段叫做成比例线段，简称比例线段。

黄金分割：用一点P 将一条线段AB 分割成大小两条线段，若小段与大段的长度之比等于大段与全长之比，则可得出这一比值等于0·618…。

这种分割称为黄金分割，分割点P 叫做线段AB 的黄金分割点，较长线段叫做较短线段与全线段的比例中项。

3.相似三角形的判定方法:根据相似图形的特征来判断。

（对应边成比例，对应角相等）○1.平行于三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似；○2.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似；3.如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似；○4.如果两个三角形的三组对应边的比相等,那么这两个三角形相似；○4.直角三角形相似判定定理:○1.斜边与一条直角边对应成比例的两直角三角形相似。

○2.直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似，并且分成的两个直角三角形也相似。

5. 一定相似的三角形（1）两个全等的三角形一定相似。

九年级第二十七章相似知识点在九年级数学课程中，相似是一个重要的概念。

在第二十七章中，我们学习了一些与相似相关的知识点。

本文将深入探讨这些知识点，并为读者提供更多的理解。

相似是指两个或多个图形的形状相似，但大小可能不同。

我们可以通过以下几个方面来判断图形是否相似：比例是否相等、形状是否相同、边对应是否成比例。

此外，还有一些特殊情况需要特别注意，比如全等图形一定是相似的，但相似图形不一定是全等的。

在相似三角形方面，我们学习了一些重要的定理。

首先是“相似三角形的对应角相等”。

这一定理告诉我们，如果两个三角形的对应角相等，那么它们一定是相似的。

而如果两个三角形是相似的，它们的对应角也一定相等。

另一个重要的定理是“相似三角形的边比例相等”。

这一定理告诉我们，如果两个三角形的边对应成比例，那么它们一定是相似的。

而如果两个三角形是相似的，它们的边对应成比例。

这个定理为我们解决相似三角形的问题提供了一个重要的方法，即通过设立比例等式来求解未知量。

在实际问题中，我们可以利用相似三角形的性质解决一些实际的测量问题。

比如，在测量高楼的高度时，我们可以利用相似三角形的性质以及一个测得的长度和相应角度来计算高楼的高度。

这一应用使我们能够在没有直接测量的情况下获取一些有用的信息。

除了相似三角形，我们还学习了相似多边形的知识。

相似多边形指的是边对应成比例的多边形。

我们学习了两个重要的定理，即“相似多边形的对应角相等”和“相似多边形的边比例相等”。

这两个定理与相似三角形的定理类似，对于判断和求解相似多边形都非常有用。

相似的概念不仅仅出现在几何学中，在实际生活中也有很多与相似相关的现象。

比如，我们可以发现一些事物之间的相似之处，比如大树和小树的形状相似，山川和河流的形状也相似。

通过观察和比较，我们可以深入理解相似的概念，并将其应用到更广泛的领域中。

总而言之，在九年级数学课程中，相似是一个重要的概念。

我们学习了相似三角形和相似多边形的性质与定理，并应用这些知识解决了一些实际问题。

通过这次教学，我深感教学反思的重要性。在今后的工作中，我会继续努力，以学生为中心，关注他们的学习需求，提高教学质量，让每个学生都能在数学的世界里找到乐趣。
-难点二：在实际图形中找出相似图形。教师可以设计一些具有挑战性的题目，如多边形内含相似三角形等，引导学生通过观察、分析找到相似图形。
-难点三：相似性质与其他几何知识的综合应用。例如，在求解复杂图形的线段长度时，需要运用相似性质与勾股定理。教师需引导学生逐步分析，将复杂问题分解为简单步骤，便于学生理解。
三、教学难点与重点
1.教学重点
-理解并掌握相似图形的定义：相似图形的对应角相等，对应边成比例。
-掌握相似图形的性质及其应用，如相似三角形的判定（AA、SAS等）。
-学会运用相似性质解决实际问题，如求线段长度、角度等。
-通过实例，让学生理解相似在实际生活中的应用，提高学生的实际应用能力。
举例解释：
-通过比较两个三角形，强调对应角相等、对应边成比例的相似定义。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《图形的相似》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过两个物体形状相似但大小不同的情况？”（如两个不同大小的三角形装饰品）这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索图形相似的奥秘。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解相似图形的基本概念。相似图形是指对应角相等，对应边成比例的图形。它在几何学中有着广泛的应用，如解决实际问题中的长度、面积等计算。
2.案例分析：接下来，我们来看一个具体的案例。通过分析两个相似三角形，展示相似在实际中的应用，以及如何利用相似性质解决问题。

典例剖析
例2 （2013•枣庄）已知矩形ABCD中，AB=1， 在BC上取一点E，将△ABE沿AE向上折叠，使B 点落在AD上的F点．若四边形EFDC与矩形ABCD 相似，则AD= ． 解：∵AB=1， 设AD=x，则FD=x﹣1，FE=1，
∵四边形 EFDC 与矩形 ABCD 相似， ∴ = ， = ，
对应角：∠A＝∠A′，∠B＝∠B′，∠C＝∠C′， ∠D＝∠D′，
对应角相等
新知探究
对应边成比例．
l问题1 相似图形有什么特征？并请结合下面下 图中两个四边形是相似图形，分别从对应角和对 应边进行说明. 对应边有什么关系？
AB BC CD DA 对应边: ＝ ＝ ＝ A′B′ B′C′ C′D′ D′A′
新知探究
l问题1 相似图形有什么特征？并请结合下面下 图中两个四边形是相似图形，分别从对应角和对 应边进行说明.
两个相似多边形的特征：对应角相等， 对应边成比例．
对应边的比 相等
新知探究
l问题2 相似？ 什么叫做相似图形？如何识别两个图形
形状相同的多边形是相似多边形
什么样才算形 状相同呢？
新知探究
A．
B．
C．
D．
总结结课
（一）学生总结 这节课学习了什么？你有什么收获？ （小组说--组内总结--组间交流） 1．相似多边形的概念，相似比、相似多边形的特征． 2．相似与全等既有联系，又有区别．首先，从它们各 自具备的特征来说：(1)它们都具备“形状相同”的本质 特征，对应角都相等．(2)全等形的大小相同，对应边相 等；而相似三角形大小不一定相同，对应边成比例．(3) 全等形可以看作是相似形的特殊情况，其相似比k＝1； 反过来，当相似比k＝1时，两个相似形全等．

九年级数学下册第二十七章相似知识点总结(超全)单选题1、△DEF和△ABC是位似图形，点O是位似中心，点D，E，F分别是OA，OB，OC的中点，若△DEF的面积是2，则△ABC的面积是( )A．2B．4C．6D．8答案：D分析：先根据三角形中位线的性质得到DE=12AB，从而得到相似比，再利用位似的性质得到△DEF∽△ABC，然后根据相似三角形的面积比是相似比的平方求解即可．∵点D，E分别是OA，OB的中点，∴DE=12AB，∵△DEF和△ABC是位似图形，点O是位似中心，∴△DEF∽△ABC，∴SΔDEFSΔABC =1 4，∴△ABC的面积=2×4=8故选D．小提示：本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．2、下列图形中不一定相似的是（）A．两个矩形B．两个圆C．两个正方形D．两个等边三角形答案：A分析：两个多边形相似，是指边数相同的两个多边形，对应角相等，对应边成比例，根据此定义即可判断．A、两个矩形不一定相似，由于对应边不一定成比例，故符合题意；B、两个圆一定相似，故不满足题意；C、根据两个图形相似的定义，两个正方形相似，故不满足题意；D、根据两个图形相似的定义，两个等边三角形相似，故不满足题意；故选：A．小提示：本题考查两个图形的相似，关键是掌握两个图形相似的概念．3、如图所示，网格中相似的两个三角形是（）A．①与②B．①与③C．③与④D．②与③答案：B分析：分别根据网格的特点求得各三角形三边的长，根据三边对应成比例判断两三角形相似即可．解：根据网格的特点，①号三角形的三边长分别为：√2，2，√10，②号三角形的三边长分别为：√2，√5，3，③号三角形的三边长分别为：2，2√2，2√5，④号三角形的三边长分别为：√2，3，√17，∵√22=2√2=√102√5√22，∴①与③相似，故B选项正确，符合题意；其他选项不正确故选：B．小提示：本题考查了网格中判断相似三角形，分别求得各三角形的边长是解题的关键．4、如图所示，某校数学兴趣小组利用标杆BE测量建筑物的高度，已知标杆BE高1.5m，测得AB=1.2m，BC=12.8m，则建筑物CD的高是( )A ．17.5mB ．17mC ．16.5mD ．18m答案：A分析：先求得AC ，再说明△ABE ∽△ACD ，最后根据相似三角形的性质列方程解答即可．解：∵AB =1.2m ，BC =12.8m∴AC=1.2m+12.8m=14m∵标杆BE 和建筑物CD 均垂直于地面∴BE//CD∴△ABE ∽△ACD∴AB BE =AC CD ,即1.21.5=14CD ,解得CD=17.5m ． 故答案为A ．小提示：本题考查了相似三角形的应用，正确判定相似三角形并利用相似三角形的性质列方程计算是解答本题的关键．5、已知线段AB 的长为2厘米，点P 是AB 的黄金分割点，线段PB 的长是（ ）A ．√5−12B ．√5−1或3−√5C ．3−√5D ．√5−1答案：B分析：根据黄金分割的定义和黄金比值√5−12，分PB 为较长线段和PB 为较短线段求解即可．解：∵线段AB 的长为2厘米，点P 是AB 的黄金分割点，∴PB = √5−12AB = √5−12×2=√5−1，或PB =2－（√5−1）=3−√5，故选：B ．小提示：本题考查黄金分割的定义：把线段AB 分成两条线段AC 和CB （AC ＞BC ），且AC 为AB 和BC 的比例中项（即AB：AC=AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点，其中AC= √5−12AB，熟记黄金比值√5−12是解答的关键．6、如图，△ABC与△A1B1C1位似，位似中心是点O，若OA:OA1=1:2，则△ABC与△A1B1C1的周长比是（）A．1:2B．1:3C．1:4D．1:√2答案：A分析：根据位似图形的概念得到ΔABC∽△A1B1C1，AC//A1C1，进而得出ΔAOC∽△A1OC1，根据相似三角形的性质解答即可．解：∵ΔABC与△A1B1C1位似，∴ΔABC∽△A1B1C1，AC//A1C1，∴ΔAOC∽△A1OC1，∴ACA′C′=OAOA′=12，∴ΔABC与△A1B1C1的周长比为1:2，故选：A．小提示：本题考查的是位似图形的概念、相似三角形的性质，掌握位似图形是相似图形、位似图形的对应边平行是解题的关键．7、如图，在等腰△ABC中，∠ABC＝∠ACB＝α，BC＝12，点D是边AB上一点，且BD＝4，点P是边BC上一动点，作∠DPE＝α，射线PE交边AC于点E，当CE＝9时，则满足条件的P点的个数是（）A．1B．2C．3D．以上都有可能答案：A分析：由已知得∠ABC＝∠ACB＝α，再证明∠EPC＝∠PDB，则可判断△PDB∽△EPC，利用相似比得到BD：PC ＝PB：CE，设PB＝x，则PC＝10﹣x，CE＝9时，所以x2﹣12x+36＝0，根据判别式的意义得到Δ＝0，即原方程只有一个实数根即可选出答案．解：∵△ABC为等腰三角形，∴∠ABC＝∠ACB＝α，∵∠DPC＝∠B+∠PDB，即∠DPE+∠EPC＝∠B+∠PDB，而∠DPE＝α，∴∠EPC＝∠PDB，而∠ABC＝∠ACB，∴△PDB∽△EPC，∴BDPC =PBCE，设PB＝x，则PC＝12﹣x，当CE＝9时，∴412−x =x9，∴x2﹣12x+36＝0，∵Δ＝（﹣12）2﹣4×36＝0，原方程只有一个实数根，∴点P有且只有一个，故选A．小提示：本题主要考查了三角形外角的性质，等腰三角形的性质，相似三角形的性质与判定，一元二次方程根的判别式，解题的关键在于能够熟练掌握相关知识进行求解．8、如图，直线AB ∥CD ∥EF ，若AC =3，CE =4，则BD BF 的值是（ ）A ．34B ．43C ．37D ．47 答案：C分析：由平行线分线段成比例直接得到答案．解：∵AB ∥CD ∥EF∴BD BF =AC AE ∵AC =3，CE =4∴BD BF =37， 故选C ．小提示：本题考查的是平行线分线段成比例，解题的关键在于能够熟练掌握平行线分线段成比例．9、神奇的自然界处处蕴含着数学知识．动物学家在鹦鹉螺外壳上发现，其每圈螺纹的直径与相邻螺纹直径的比约为0.618．这体现了数学中的（ ）A ．平移B ．旋转C ．轴对称D ．黄金分割答案：D分析：根据黄金分割的定义即可求解．解：动物学家在鹦鹉螺外壳上发现，其每圈螺纹的直径与相邻螺纹直径的比约为0.618．这体现了数学中的黄金分割．故选：D小提示：本题考查了黄金分割的定义，黄金分割是指将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值，其比值为√5−12，约等于0.618，这个比例被公认为是最能引起美感的比例，因此被称为黄金分割．熟知黄金分割的定义是解题关键．10、若ab =cd=−2，则a−cb−d＝（）A．−2B．2C．−12D．12答案：A分析：根据ab =cd=−2，可知a＝﹣2b，c＝﹣2d，将a和c的值代入求值的代数式化简即可．解：∵ab =cd=−2，∴a＝﹣2b，c＝﹣2d，∴a−cb−d =−2b+2db−d=−2(b−d)(b−d)=−2．故选：A．小提示：本题考查了比例的性质，解题的关键是根据已知将a和c用b和d正确表示．填空题11、如图，已知△ABC与△DEF位似，位似中心为O，且△ABC的面积与△DEF的面积之比是16：9，则AO：OD＝_____．答案：4:3##43分析：根据位似图形具有相似三角形的性质即可得出结果．解：∵△ABC与△DEF位似，位似中心为O，且△ABC的面积与△DEF的面积之比是16：9，∴AO：OD=4：3，所以答案是：4：3．小提示：本题考查了位似变换，正确掌握位似变换的性质是解题的关键．12、如图，已知一组平行线a//b//c，被直线m、n所截，交点分别为A、B、C和D、E、F，且AB＝3，BC＝4，EF＝4.8，则DE的长为__．答案：3.6分析：根据平行线分线段成比例定理列出比例式，代入数据进行计算即可得到答案．解：∵a∥b∥c，∴DEEF =ABBC，即DE4.8=34，∴DE＝3.6，所以答案是：3.6．小提示：本题考查了平行线分线段成比例，根据题目特点，灵活选择比例式计算是解题的关键．13、如图，在△ABC中，AB=8cm，BC=16cm，动点P从点A开始沿AB边运动，速度为2cm/s；动点Q 从点B开始沿BC边运动，速度为4cm/s；如果P、Q两动点同时运动，那么经过______秒时△QBP与△ABC 相似．答案：0.8或2##2或0.8分析：设经过t秒时，△QBP与△ABC相似，则AP=2tcm,BP=(8−2t)cm,BQ=4tcm,利用两组对应边的比相等且夹角对应相等的两个三角形相似进行分类讨论：BPBA =BQBC时，△BPQ∽△BAC，即8−2t8=4t16；当BPBC=BQ BA 时，△BPQ∽△BCA，即8−2t16=4t8，然后解方程即可求出答案．解：设经过t秒时，△QBP与△ABC相似，则AP=2tcm,BP=(8−2t)cm,BQ=4tcm, ∵∠PBQ=∠ABC，∴当BPBA =BQBC时，△BPQ∽△BAC，即8−2t8=4t16，解得：t=2；当BPBC =BQBA时，△BPQ∽△BCA，即8−2t16=4t8，解得：t=0.8；综上所述：经过0.8s或2s秒时，△QBP与△ABC相似，小提示：本题考查了相似三角形的判定：两组对应边成比例且夹角相等的两个三角形相似，解题的关键是准确分析题意列出方程求解．14、已知a2=b3=c5，则a+bc的值为_____．答案：1分析：由比例的性质，设a2=b3=c5=k，则a=2k，b=3k，c=5k，然后代入计算，即可得到答案．解：根据题意，设a2=b3=c5=k，∴a=2k，b=3k，c=5k，∴a+bc =2k+3k5k=1，所以答案是：1．小提示：本题考查了比例的性质，解题的关键是掌握比例的性质进行解题．15、如图，在△ABC中，点D，E分别在边AB，AC上，且ADDB =32，AEEC=12，射线ED和CB的延长线交于点F，则FBFC的值为________．答案：13分析：过B作BG∥AC交EF于G，得到△DBG∽△ADE，由相似三角形的性质得到BGAE =BDAD=23，推出BG：CE=13，根据相似三角形的性质即可得到结论．解：过B作BG∥AC交EF于G，∴△DBG∽△DAE，∴BGAE =BDAD=23，∵AEEC =12，∴BGCE =13，∵BG∥AC，∴△BFG∽△CFE，∴BFFC =BGCE=13．故答案是：13．小提示：本题考查了平行线分线段成比例定理，相似三角形的判定和性质，正确的作出辅助线构造相似三角形是解题的关键．解答题16、如图，BD，AC相交于点P，连接AB，BC，CD，DA，∠DAP＝∠CBP．(1)求证：△ADP∽△BCP；(2)直接回答△ADP与△BCP是不是位似图形；(3)若AB＝8，CD＝4，DP＝3，求AP的长．答案：(1)见解析；(2)不是位似图形；(3)6分析：（1）根据两角对应相等的两个三角形相似证明；（2）根据位似图形的定义判断，即可；（3）根据△ADP∽△BCP，得到APDP =BPCP，再证明△APB∽△DPC，根据相似三角形的性质列出比例式，代入计算得到答案．（1）证明：∵∠DAP＝∠CBP，∠DPA＝∠CPB，∴△ADP∽△BCP．（2）解：△ADP与△BCP不是位似图形．理由是：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，那么这样的两个图形叫做位似图形，这个点叫做位似中心．△ADP与△BCP的对应点的连线交于一个点，∴△ADP与△BCP不是位似图形．（3）解：∵△ADP∽△BCP，∴APDP =BPCP，∵∠APB＝∠DPC，∴△APB∽△DPC，∴APPD =ABCD，∴AP3=84，解得AP＝6．小提示：本题考查的是位似变换的概念、相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理是解题的关键．17、已知线段a、b满足a：b＝3：2，且a＋2b＝28（1）求a、b的值．（2）若线段x是线段a、b的比例中项，求x的值．答案：（1）a＝12，b＝8；（2）x＝4√6．分析：（1）利用a:b=3:2，可设a=3k，b=2k，则3k+4k=28，然后解出k的值即可得到a、b的值；（2）根据比例中项的定义得到x2=ab，即x2=96，然后根据算术平方根的定义求解．解：（1）∵a:b=3:2∴设a=3k，b=2k，∵a+2b=28，∴3k+4k=28，∴k=4，∴a=12，b=8；（2）∵x是a:b的比例中项，∴x2=ab=96，∵x是线段，x>0，∴x=4√6．小提示：本题考查了比例线段，解题的关键是掌握对于四条线段a、b、c、d，如果其中两条线段的比（即它们的长度比）与另两条线段的比相等，如a:b=c:d（即ad=bc)，我们就说这四条线段是成比例线段，简称比例线段．注意利用代数的方法解决较为简便．18、已知△OAB在平面直角坐标系中的位置如图所示．(1)将△ABO绕原点O顺时针旋转90°得△OA1B1；(2)以原点O为位似中心，将△OA1B1在原点异侧按位似比2：1进行放大得到△OA2B2．答案：(1)见解析(2)见解析分析：（1）先找到A、B的对应点A1、B1，然后顺次连接O、A1、B1即可；（2）先找到A1、B1的对应点A2、B2，然后顺次连接O、A2、B2即可；．（1）解：如图所示，△OA1B1即为所求；（2）解：如图所示，△OA2B2即为所求．小提示：本题主要考查了再坐标系中画旋转图形，画位似图形，熟知画旋转图形和画位似图形的方法是解题的关键．。

＝12·AE·DF＝EACE＝2. 2·EC·DF
∴AACE＝23.
又∵DE∥BC，∴△ADE∽△ABC.
∴
S△ ADE S△ ABC
＝AACE2＝232＝49.
即 S△ADE∶S△ABC＝4∶9
第二十一页，共二十四页。
课堂小结
相似三角形对应线段(xiànduàn)的 比等于相似比
相似(xiānɡ sì)三角形的性质
做一做下面的题目(tímù)，看谁做得又快又准确。
1、2组
3、4组
正方形ABCD的边长为3，点E在边CD的
延长线上，连接(liánjiē)BE交边AD于F，如果
9
DE=1，那么AF=
．
4
在平行四边形ABCD中，点E是边AB的中点(zhōnɡ
diǎn)，AC、DE交于点F，则AF：FC= 1：2．
第十八页，共二十四页。
2.如图，AD=DF=FB，DE∥FG∥BC，则SⅠ：SⅡ：SⅢ=
．1：3：5
3.如图，▱ABCD中，E是CD的延长线上一点(yī diǎn)，BE与AD交于点F，CD=2DE．若△DEF
的面积为1，则▱ABCD的面积为
．
12
第四页，共二十四页。
新知讲解
一 相似三角形对应线段的比
合作(hézuò)探究
AP＝2，则DQ的值为( ) C
A．2 B．4
C．1
D.
1
2
3.连接三角形两边中点的线段把三角形截成的一个(yī ɡè)小三角形与原三角形的周长
比等于_____1_:2,面积比等于_____. 1:4
4.两个(liǎnɡ ɡè)相似三角形对应的中线长分别是6cm和18cm，若较大三角形的周长是42cm，面积是