第六章 投影变换

投影变换投影变换就是要确定一个取景体积，其作用有两个：1). 确定物体投影到屏幕的方式，即是透视投影还是正交投影。

2). 确定从图象上裁剪掉哪些物体或物体的某些部分。

投影变换包括透视投影和正交投影（平行投影）。

●透视投影透视投影的示意图如下，其取景体积是一个截头锥体，在这个体积内的物体投影到锥的顶点，用glFrustum()函数定义这个截头锥体，这个取景体积可以是不对称的，计算透视投影矩阵M，并乘以当前矩阵C，使C=CM。

void glFrustum(GLdouble left,GLdouble right,GLdouble bottom,GLdouble top,GLdouble near,GLdouble far);该函数以透视矩阵乘当前矩阵left, right 指定左右垂直裁剪面的坐标。

bottom,top 指定底和顶水平裁剪面的坐标。

near,far 指定近和远深度裁剪面的距离，两个距离一定是正的。

程序函数gluPerspective()可以创建一个与调用glFrustum()所得到的同样形状的视图体，它创建的是一个沿视线关于x和y轴均对称的平截台体，在很多实际应用中都采用函数gluPerspective()。

void gluPerspective(GLdouble fovy,GLdouble aspect, GLdouble zNear,GLdouble zFar)；fovy是在x-z平面内视区的角度，其值必须在区间【0.0，180.0】内。

Aspect为长宽比，是平截台体的宽度与高度之比。

zNear和zFar的值是视点（沿z轴负向）与两个裁剪平面的距离。

参数恒为正。

图1透视投影示意图●正交投影正交投影的示意图见下：其取景体积是一个各面均为矩形的六面体，用glOrtho()函数创建正交平行的取景体积，计算正交平行取景体积矩阵M，并乘以当前矩阵C，使C=CM。

void glOrtho(Gldouble left,Gldouble right,Gldouble bottom,Gldouble top,Gldoublenear,Gldouble far);该函数以正交投影矩阵乘当前矩阵。

AD C B a≡b≡d ≡ ≡ P X V H
b′ ′
a′ ′
d′ ′ b 距离 b’1. a2≡b2≡d2 c2
c a
.
d
. a’1 d’1
H X1 V 1
c
如何确定d 如何确定 1 c’1 点的位置？ 点的位置？ 过c1作线平行于x2轴。
V1 H2 X2
例：已知两交叉直线AB和CD的公垂线的长度 为MN， 已知两交叉直线 和 的公垂线的长度 ， N 为水平线， 的投影。 且AB为水平线，求CD及MN的投影。 M 为水平线 及 的投影
●
a′ ′ XV H a c
m′ ′
b′ ′
● ●
m
n
d b
d’1
.
●
a1≡b1≡m1
●
c1
n1
.
d1
n’1 圆半径=MN 圆半径
请注意各点的投 H V 1 影如何返回？ 影如何返回？ X1 求m点是难点。 点是难点。 点是难点
c’1
●
点作直线CD与 相交成 相交成60º角 例: 过C点作直线 与AB相交成 角。 点作直线
的实长及与H面的夹角 例：求直线AB的实长及与 面的夹角。 求直线 的实长及与 面的夹角。
面代替V面 投影体系中， 用 面代替 投影体系中 。 空间分析： V1面代替 面，在V1/H投影体系中，AB//V1。 b′ ′ 作图： 作图： a′′ V1 a′ ′ a’1
V
b′ ′ a
A
X
V
B
b’1
H
b a
4
6.2.1基本条件 基本条件
a'1 V1
6.2 换面法
X1
α
α b'1 O1

b d c
b d c
b1
a1(d1)
c1
4、 投影面垂直面变换为投影面平行面
换H面
正垂面
“水平面”（实形）
换V面
b
铅垂面
“正平面”（实形）
V V1
a1
X1
b1
c1
A a
b
a
B
V X
a
H
c
C
X
a
b(c)
H
c
b(c) c1
b1
a1
实形
5、 一般位置线变换为投影面垂直线:二次换面
b a
a2 (b2) H2
（2）轨迹圆在旋转轴所平行面上的投影，为平行于投影轴的直线。
三、 换面法的投影规律
1. 换面法的投影规律（1）以点的一次变换为例-替换V面
替换投影面
V a
新投影面
V a 替换投影
A
a1 V1
X ax
新投影
旧轴
X ax
新投影
a1
a
ax1
X1 H
a
ax1
保留投影面
H
保留投影
新轴
X1
新投影到不变投影连线垂直于新投影轴:a1a ⊥ X1
新投影到新投影轴的距离等于旧投影到旧投影轴的距
V1称为新投影面；V称为被更换的投影面；H称为被保留的 投影面。 X1称为新投影轴；X称为被更换的投影轴。
二、 新投影面的选择原则
V1
a1
X1
b1
c1
A a
V
b
B
a
c
C
b(c) H
V1∥ABC
V1┴H
新投影面的选择必须符合以下两个基本条件： (1) 新投影面必须和空间几何元素处于有利解题的位置(平行或垂直) (2) 新投影面必须垂直于于原投影体系中的一个被保留的投影面。

a’
a
a1‘
一般位置平面经过二次变换成为投影面平行面
（选择一条投影面平行线作为辅助线）
旋转轴
旋转平面
点在旋转轴垂直的投影面上做圆周运动； 在旋转轴平行的投影面上做直线运动。
不指明轴的旋转
A a’
a
• 小结： 一、 变换投影面法 新投影到新轴的距离等于老投影到老轴的距离。 二、旋转法 在旋转轴垂直的投影面上作圆周运动； 在另一投影面上作平行于投影轴的直线运动，形状、 大小不变。 一般位置直线一次变换成投影面平行线； 投影面平行线一次变换成投影面垂直线。 一般位置直线一次变换成投影面垂直面（取平面上的平行线 变换）； 投影面垂直面一次变换成投影面平行面。
V V1
V
H
H
投影体系仍然保持相互垂直的关系，每次变换一个投影面。
V V V1 V H2 V1
H
H
H
V
V H1
V V2 H1
H
H
H
V a‘ A O ax a XX1 ax1 H O1 a1‘ V1 O
a‘
XX1 ax ax1 a O1 a1‘
V a’ a’ ax1 A a1 O ax XX1 a a H O1 H1 O ax O1 a1 ax1 X1
O2 a’ V X ax O a2 H2 ax2 V1 X2 a1‘ A X1 ax1 a H O1 O
a’
X
X2
a2
X1 O2 a1‘ a O1
一般位置直线经过一次变面垂直线
一般位置直线经过两次变换成为投影面垂直线
投影面垂直面经过一次变换成为投影面平行面

步骤二
步骤三
增加的投影面称为新投影面 或辅助投影面(如V1面) ，新 投影面上的投影称为新投影 或辅助投影（如a1’）。
与新投影面垂直的投影面，称 为保留投影面（如H），投影 称为保留投影,新投影面与保 留投影面交得的投影轴称为新 投影轴或辅助投影轴（如OX）
原来与保留投影面垂直的投 影面，称为替换投影面或旧 投影面(如V面)，投影称为替 换投影或旧投影（如a’）。
1.一般位置平面变换为投影面垂直面
(单击play按钮)
一般位置平面变换为投影面垂直面：只要将该一般位置平面上的任一直线变换成投 影面的垂直线，则此一般位置平面就成为该投影面的垂直面。
平面的换面法
一般位置平面变换为投影面垂直面—求α角
c’
a’
X
V H
d' b’

取水平线AD；作V1⊥AD，则△ABC⊥V1， △ABC在V1面的积聚投影与X1轴的夹角α 即为其与H面的夹角
a c d b b '1
作X1轴垂直于ad
α a'（ 1 d '1 ）
c'1
平面的换面法
2.投影面垂直面变换为投影面平行面
b’
X1轴平行于ac
V a’ X
ax bx
b’ c’
cx
B
b’1
V1
X1 A c’1 cx1 bx1 ax1 a’1
a’
X
V H
c’
O
C
b a
O1
c
c’1
c b
a
H
a’1
b’1
实形
平面的换面法
3.一般位置平面变换为投影面平行面 a’ 投影面 平行面
X V H

投影变换由于数据源的多样性，当数据与我们研究、分析问题的空间参考系统（坐标系统、投影方式）不一致时，就需要对数据进行投影变换。

同样，在对本身有投影信息的数据采集完成时，为了保证数据的完整性和易交换性，要对数据定义投影。

空间数据与地球上的某个位置相对应。

对空间数据进行定位，必须将其嵌入到一个空间参照系中。

因为GIS 描述的是位于地球表面的信息，所以根据地球椭球体建立的地理坐标（经纬网）可以作为空间数据的参照系统。

而地球是一个不规则的球体，为了能够将其表面的内容显示在平面的显示器或纸面上，就必须将球面的地理坐标系统变换成平面的投影坐标系统当系统使用的数据取自不同地图投影的图幅时，需要将一种投影的数字化数据转换为所需要投影的坐标数据。

投影转换的方法可以采用：1.正解变换通过建立一种投影变换为另一种投影的严密或近似的解析关系式，直接由一种投影的数字化坐标x、y 变换到另一种投影的直角坐标X、Y。

2.反解变换即由一种投影的坐标反解出地理坐标(x、y→B、L)，然后再将地理坐标代入另一种投影的坐标公式中(B、L→X、Y)，从而实现由一种投影的坐标到另一种投影坐标的变换(x、y→X、Y)。

3.数值变换根据两种投影在变换区内的若干同名数字化点，采用插值法，或有限差分法，最小二乘法、或有限元法，或待定系数法等，从而实现由一种投影的坐标到另一种投影坐标的变换。

目前，大多数GIS 软件是采用正解变换法来完成不同投影之间的转换，并直接在GIS 软件中提供常见投影之间的转换。

借助ArcToolbox 中Projections and Transformations工具集中的工具，可以实现对数据定义空间参照系统、投影变换，以及对栅格数据进行多种转换，例如翻转（Flip）、旋转（Rotate）和移动（Shift）等操作。

1. 定义投影定义投影（Define Projection），指按照地图信息源原有的投影方式，为数据添加投影信息。

图6-4 点的一次变换（变换H面）
如果变换H面，则用一个垂直于V面的新投影面H1代替H面，构成V/ H1投影体系。如图6-4所示， 可作出点B在H1面上的新投影，其作图步骤与变换V面时相似，此时点B的Y坐标不变。
9
6.2.2 点的换面规律
2．点的二次换面
画法几何
在工程中，有些问题经过一次换面还不能解决，需要经过两次或两 次以上的连续换面。二次换面是在一次换面的基础上再进行换面，每次 换面都按照点的换面规律。但应注意，在换面时，先换哪一个面应根据 解题需要而定，然后按顺序依次更换各个投影面，V，H面必须交替变 换，即以V/H→V/ H1 → V2/ H1的顺序变换或以V/H→ V1 /H→ V1 / H2的 顺序变换。
画法几何
将一般位置直线变换成铅垂线，作图步骤如下： ① 作新投影轴O1X1// ab ，得到AB在V1 / H体系中的新投影 a1′ b1′ ； ② 再作另一新投影轴O2X2⊥ a1′ b1′ ，得到AB在V1 / H2体系中的新 投影 a2(b2) 。
图6-9 一般位置直线变换成投影面垂直线
15
③ ∠ b2c2 d2 为△ABC与△ACD两平面间的夹角a。
图6-15 两平面间的夹角分析
19
6.2.4 应用实例
【例6-3】 如图6-16所示，在直线BC上取一点E，使AE=20mm 。
画法几何
分析： 直线BC与点A组成一般位置平面△ABC，利用两次换面可求出 △ABC的实形，在实形中可作出AE=20mm 。
画法几何
作图步骤如下： ① 作新投影轴O1X1平行于△ABC的积聚性投影acb； ② 在V1投影面上得到△ABC的新投影△ a1′ b1′ c1′ ，△ a1′ b1′ c1′反映△ABC实形。

sinφ 1]
• z轴上C点［0 0 1 1］。
• 变换后为： ［0 0 1 1］·H = [sinθ -
cosθ·sinφ cosθ·cosφ 1]
2021/6/29
13
6.2.2 正轴测投影
•
在观察坐标系中的正投影是去掉z分量，上
述三点到坐标原点的长度是
,按正等轴测投
影的要求，原用户坐标系中x、y和z方向单位长
平面与二个坐标轴相交，这种投影被称为二点透
视。
二点透视示意图
2021/6/29
27
6.4 透视投影
• 3、三点透视 • 三点透视：按照投影面的方向可对在
用户坐标系中正放的矩形体产生三主消失 点，即投影平面与三个坐标轴相交，这种 投影被称为三点透视。
2021/6/29
28
ቤተ መጻሕፍቲ ባይዱ题
1.为什么需要做投影变换？
2.什么叫投影变换?
3.试述投影变换的分类
4.沿Z方向正投影的变换矩阵是什么样的？
5.若给出投影方向矢量［A，B，C］，且以Z=0的 平面作为投影平面，则斜平行投影变换矩阵是什 么样的？
6.若投影中心处于观察坐标系的原点，投影平面与Z 轴垂直并距原点的距离为d，则透视投影变换矩阵 是什么样的？
2021/6/29
2、平行投影变换：平行投影可以看成投影中
心在无限远处的投影。见下图（b）。
2021/6/29
3
6.1 投影概念分类
a透视投影变换示意图 b平行投影变换示意图
2021/6/29
4
6.1 投影概念分类
• 二、投影的分类
2021/6/29
5
6.2 正平行投影
• 正平行投影的投影中心是在无限远处， 且投影射线与投影平面垂直。

投影变换
生活感知
中午的太阳光下,一排排的树木的影子会 投影到各自的树根
排球中场休息时,工作人员用平地 拖把拖扫比赛场地.要求同时同向推动拖 把,把垃圾推到边界线停止
图2垃圾推到边界线 图1树在中午的阳光下形成影子
提出问题
这两个生活中事情，实质反映了平 面上的点在某一直线上的投影，能否用 矩阵来表示？
•
12、越是无能的人，越喜欢挑剔别人 的错儿 。2021/3/12021/3/12021/3/1M onday, March 01, 2021
•
13、知人者智，自知者明。胜人者有 力，自 胜者强 。2021/3/12021/3/12021/3/12021/3/13/1/2021
•
14、意志坚强的人能把世界放在手中 像泥块 一样任 意揉捏 。2021年3月1日星期 一2021/3/12021/3/12021/3/1
谢谢观赏
You made my day!
我们，还在路上……
理解应用
研究线段AB在矩阵
作用下变换
得到的图形,其中A(0,0),B(1,2)
例题深化
矩阵
的变换作用如何?并说
明这种变换的几何意义.
变式1
A(0,0),B(1,2) 在投影矩阵M矩阵 作 用下分别变换为点A/(0,0),B/(1.5,1.5)
求变换对应的矩阵M
解决问题
方案1:以直线为X轴,建立直角坐标系,
设平面上的任一点的坐标为(x,y),则 投影后的点坐标为(x,0)故所求矩阵为
y
P(x,y)
o
p/(x,0) x
方案2:以直线为y轴,建立直角坐标系.
设平面上的任一点的坐标为(x,y),则投 影后的点坐标为(0,y)

意义
意义
随着计算机地图制图的发展，研究地图投影变换的理论和方法日益重要和迫切，因为在采用制图自动化作业 中，必须首先提供从一种地图投影点的坐标变换为另一种地图投影点的坐标的关系式，即数学模式，才能进行这 种作业。因为如果没有这两种不同投影点的坐标变换关系式，就无法编制出合乎变换要求的，适用于电子计算机 进行变换所需要的程序设计。所以，地图投影变换已成为计算机地图制图的一个组成部分。
种类
种类
ArcGIS投影变换 ArcToolBox投影变换 ArcToolBox -> Data Management Tools -> Projections and Transformations a) Define Projection b) Feature -> Project c) Raster -> Project Raster d) Create Custom Geographic Transformation 当数据没有任何空间参考显示为Unknown时 (1)利用Define Projection给数据定义一个Coordinate System (2)利用Feature -> Project或 Raster -> Project Raster对数据进行投影变换 我国经常使用的投影坐标系统为北京54、西安80，由这两个坐标系统变换到其他坐标系统下时，通常需要提 供
投影变换
研究投影点坐标变换的理论和方法
01 简介
03 种类 05ห้องสมุดไป่ตู้意义
目录
02 基本方法 04 方法发展
基本信息
投影变换（projection transformation）是将一种地图投影点的坐标变换为另一种地图投影点的坐标的过 程。研究投影点坐标变换的理论和方法。

第六章投影变换§6-1 概述前面介绍过特殊位置直线和平面可在投影图上直接求得实长或实形，而一般位置直线和平面在投影图上就不能直接得到它们的实长、实形、距离和夹角。

要解决一般位置几何元素的度量和定位问题时，可想办法把它们由一般位置改变为特殊位置，以达到简化解题的目的。

采用方法如下：1．空间几何元素的位置保持不动，用新的投影面来代替旧的投影面，使空间几何元素对新投影面的相对位置变成有利解题的位置，然后找出其在新投影面上的投影。

这种方法叫换面法。

2．投影面保持不动，使空间几何元素绕某一轴旋转到有利解题的位置，然后找出其旋转后的新投影，这种方法叫旋转法。

§6-2 换面法一、换面法基本概念如图6-1（a）表示一个铅垂面ΔABC，该三角形在V面和H面的投影体系（以后简称H／V 体系）中的两个投影都不反映实形。

为使新投影反映实形，取一个平行于三角形且垂直于H面的V1面来代替V面，则新的V1面和不变的H面构成了一个新的两面投影体系（H／V1）。

三角形在（H／V1）体系中V1面上的投影Δa1′b1′c1′就反映三角形的实形。

再以V1面和H面的交线X1为轴，使V1面旋转至和H面重合，就得出（H／V1）体系的投影图，如图6-1（b）所示。

（a）（b）图6-1 V／H体系变为V1／H体系新投影面不能任意选择，用换面法解题时应遵守下列两条原则：(1)新投影面必须和空间几何元素处于有利于解题的位置。

(2)新投影面必须垂直于原投影体系中的一个投影面，并与它组成新投影面体系。

必要时可连续变换。

二、点的投影变换规律点是最基本的几何元素。

因此在更换投影面时必须首先掌握点的投影变换规律。

1．变换正立投影面变换投影面V时，新投影面——用符号 V1表示——必须垂直于被保留的H面，从而得新体系（H、V1），如图6-2（a）。

（a） （b）图6-2 变换V面时，点的新投影的作法设原体系中有一个点A，它的原投影是a和a′，为作出A点在新投影面V1上的投影，经过A 向V1引垂线，所得垂足a1′就是A点的新投影。

3N
6
cos (1 tg )
3
5N
120
cos5 (5 18tg 2 4tg 4 4 ) ......
（6-7）
16
经纬线形状：
本投影通常是按一定的经差分带投影，每带的经差一般不大（6或3）。
17
图6-2 高斯-克吕格投影全球经纬格网
18
x s
y x
x
-dy
N
由于对取导数比较复杂，以下利用等角 条件加以变换，得：
x x r M y y r M
o
-dy
-dx F 图6-3 子午线收敛角

A’
y
y tg x
25
或利用下式
x x x x d d d dx tg y y y y dy d d d
同理可得：
考虑到H=（EG-F2）=(x/)(y/)-(y/)(x/) 是一个面积元素， 恒为正，在上面两式的开方中，只有当第一个式子取负号，第二个式子 取正号时，才恒成立。所以等角条件还可以表示为：
x r y M
y r x M
10
第六章
高斯-克吕格投影
（Gauss-Krüger Projection）
§6-1 高斯-克吕格投影的原理和公式
投影性质
等角横切椭圆柱投影
名称由来
德国数学家、物理学家、天文学家高斯于19世纪20年 代拟定，后经德国大地测量学家克吕格于1912年对投 影公式加以补充，故称为高斯-克吕格投影。
2
概念
2 2 2 2 2 2
15
高斯—克吕格投影的直角坐标公式：
将以上求得的各个系数a代入前面的方程，加以整理，有：

的变换下
的曲线方程。
y
y=x
x
南京东山外国语学校高三数学组 2019/8/16
课堂练习
选修4－2 矩阵与变换
(1)
说明矩阵

1 1
0 0

的变换作用，哪些
变换是一一映射？
(2)
矩阵

1 1
0 0

把椭圆
x



y
变成了
什么图形?其方程是什么?
选修4－2 矩阵与变换
L
南京东山外国语学校高三数学组 2019/8/16
南京东山外国语学校高三数学组 2019/8/16
建构数学
选修4－2 矩阵与变换
像

1 0
0 1
0


1
0 0

这类将平面内图形投影到某条直线
(或某个点) 上的矩阵,我们称之为投影变换矩阵,
相应的变换称做投影变换.
(1)投影变换的几何要素: 投影方向, 投影到的某条直线L. (2)投影变换矩阵能反映投影变换的几何要素 (3)与投影方向平行的直线投影于L的情况是某个点 (4)投影变换是映射,但不是一一映射
南京东山外国语学校高三数学组 2019/8/16
解决问题
选修4－2 矩阵与变换
方案1:以直线为x轴,建立直角坐标系,
设平面上的任一点的坐标为(x,y),则投
影后的点坐标为(x,0).
y P(x,y)
故所求矩阵为

1 0
0
0

o P/(x,0) x
南京东山外国语学校高三数学组 2019/8/16

c
先换V面 再换H面
X
a
V H
b
b2●
●
●
a2
a b c
.
●
.
a1 （b1）
H V 1 X1
c2
c1
●
［例1］试求平面△ＡＢＣ的实形 和 角
先换H面 再换V面
b
d a b2 d2 c2 a2
实形
c
b
X V H
a
d c
例2
已知一般位置平面ABC的V、H投影，
●
b1
换H面行吗？ 不行！
新投影轴的位置？
与ab平行。
［例2］已知：直线AB的两投影ａｂ、ａ′ｂ′， 试求：直线AB的实长和对V面的夹角。
2.把投影面平行线变换为新投影面的垂直线
把投影面平行线变换为投影面垂直线， 是为了使直线投影成为一个点，从而解 决与直线有关的度量问题(如求两直线间 的距离)和定位问题(如求线面交点)。
4）返回求得内切圆中心的投影G、G。
本
章
结
束
(2)换H面
X1 H 1 V
.
a1
a XV H ax a
ax1
O1
O
求新投影的作图方法 更换V面 更换H面
a
X1 H 1 V
.
a1
V X H
ax
ax1
.
●
a 1
XV H
a
ax a
ax1
H
V1
X1
a
作图规律： 由点的不变投影向新投影轴作垂线， 并在垂线上量取一段距离，使这段距离等 于被代替的投影到原投影轴的距离。
5）ａ2即为变换后的新投影。
a 2 a ax1 H X1 V1

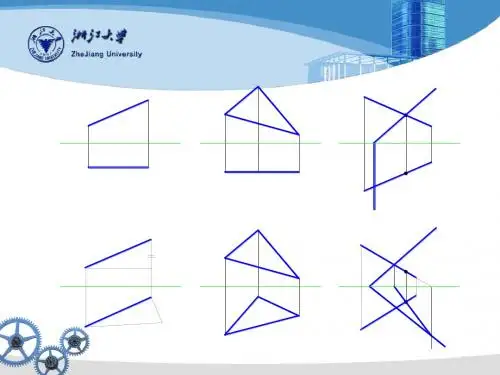
第六章投影变换§6-1 概述§6-2 换面法基本要求基本要求§6-1 概述a'a bb'两点之间距离a'a bb'c'c三角形实形a'abb'c'cdd'直线与平面的交点a'b'c'd'abcd两平面夹角§6-2 换面法一、换面法的基本概念二、新投影面的选择原则三、点的投影变换规律四、六个基本问题一、换面法的基本概念a 1'c 1'b 1'V 1X 1X 1换面法—空间几何元素的位置保持不动，用新的投影面来代替旧的投影面，使对新投影面的相对位置变成有利解题的位置，然后V /H 体系变为V 1/H 体系c 1'b 1'a 1'bcab 'a 'c 'X二、新投影面的选择原则（二）、新投影面的选择必须符合以下两个基本条件：1．新投影面必须和空间几何元素处于有利解题的位置。

三、点的投影变换规律1．点的一次变换2．点的投影变换规律3．点的两次变换1．点的一次变换V1a1X1a1'V1a1'2．点的投影变换规律（1）点的新投影和不变投影的连线，必垂直于新投影轴。

（2）点的新投影到新投影轴的距离等于点的旧投影到旧投影轴的距离。

点在V/H1体系中的投影a1a1四、六个基本问题（一）把一般位置直线变为投影面平行线例题1（二）把投影面平行线变为投影面垂直线（三）把一般位置直线变为投影面垂直线例题2例题3（四）把一般位置平面变为投影面垂直面例题4例题5（五）把投影面垂直面变为投影面平行面（六）把一般位置平面变为投影面平行面例题6（一）把一般位置直线变为投影面平行线a1'b1'αa1'b1'α[例题1] 把一般位置直线变为H1投影面平行线a1b1a 1b 1（二）把投影面平行线变为投影面垂直线b ba 1b 1（三）把一般位置直线变为投影面垂直线V 1X 1a 1'b 1'a 2 b 2把一般位置直线变为投影面垂直线a2 b2[例题2] 求点C到直线AB的距离提示c'2作图c 1b 1a 1kk'k 1b'2 k'2a'2距离2'1'1'12'11222a 2b 2d 2c 2d'1c'121b '[例题3] 求两直线AB 与CD 的公垂线。