第五章主成分分析资料
- 格式：ppt
- 大小：4.91 MB
- 文档页数：13
下载文档原格式
合集下载
主成分分析
主成分分析主成分分析、因子分析等在多元统计分析中属于协方差逼近技术。
主要是从协方差矩阵出发，实现一种正交变换，从而将高维系统表示为低维系统，在此过程中可以揭示研究对象的许多性质和特征。
主成分分析的结果可以用于回归分析、聚类分析、神经网络分析等等。
只要懂得线性代数中二次型化为标准型的原理，就很容易掌握主成分分析的原理，进而掌握因子分析的原理。
在理解正交变换数学原理的基础上，我们可以借助Excel 开展主成分分析。
为了清楚地说明主成分的计算过程，不妨给出一个简单的计算实例。
【例】2000 年中国各地区的城、乡人口的主成分分析。
这个例子只有两个变量（m=2）：城镇人口和乡村人口；31 个样品：即中国的31 个省、自治区和直辖市（n=31）。
资料来自2001 年《中国统计年鉴》，为2000 年全国人口普查快速汇总的11 月1 日零时数。
由于变量太少，这个例子仅仅具有教学意义——简单的实例更容易清楚地展示计算过程的细节。
计算步骤5.1.1 详细的计算过程首先，录入数据，并对数据进行适当处理（图5-1-1）。
计算的详细过程如下。
第一步，将原始数据绘成散点图主成分分析原则上要求部分变量之间具有线性相关趋势。
如果所有变量彼此之间不相关（即正交），则没有必要进行主成分分析，因为主成分分析的目的就是用正交的变量代替原来非正交的变量。
如果原始变量之间为非线性关系，则有必要对数据进行线性转换，否则效果不佳。
从图5-1-2 可见，原始数据具有非线性相关趋势，可以近似匹配幂指数函数，且测定系数R2=0.5157，相应地，相关系数R=0.7181（图5-1-2a）；取对数之后，点列具有明显的线性趋势（图5-1-2b）。
第二步，对数据进行标准化标准化的数学公式为我们将对对数变换后的数据开展主成分分析，因此只对取对数后的数据标准化。
根据图5-1-1所示的数据排列，应该按列标准化，用xij 代表取对数之后的数据，则下式分别为第j 列数据的均值和标准差，xij 为第i 行（即第i 个样本）、第j 列（即第j 个变量）的数据，xij*为相应于xij 的标准化数据，n=31 为样品数目（参见图5-1-1）。
主成分分析
但是这种线性组合，如果丌加限制，则可以有很多，应 该如何去选取呢？
对a加以限制
对组合系数ai' = (a1i，a2i，…，api)作如下要求：
a a ... a
2 1i 2 2i
2 pi
1,
i 1, 2 ,..., p
即：ai为单位向量。 此外，
对F限制
1) Fi不Fj（i≠j, i, j = 1, …, p）互丌相关，即 协方差:Cov(Fi，Fj) = 0
2) F1是X1，X2，…，Xp的一切线性组合（系数满足上述要 求）中方差最大的，即
Var ( F1 ) max Var ( c i X i )
c ' c 1 i 1 p
其中c = (c1，c2，…，cp)' 3)F2是不F1丌相关的X1，X2，…，Xp一切线性组合中方差最 大的，…，Fp是不F1，F2，…，Fp-1都丌相关的X1，X2，… ，Xp的一切线性组合中方差最大的。 满足上述要求的综合指标向量F1，F2，…，Fp就是主成分。
i 1 k 1
达到足够大（一般在85%以上）为原则。
3.5 计算主成分得分
计算n个样品在m个主成分上的得分：
Fi a1i X 1 a 2 i X 2 ... a pi X p
i = 1，2，…，m
主成分分析程序代码
例 输出原始数据矩阵x x=[7.47,1.73,7.20,0.13,0.40,1.33,1.07,36.05;6.67,1.67,18.00,0.67,4.67,19. 00,5.50,26.00;3.32,2.48,36.43,2.17,7.15,22.99,11.95,60.95;3.00,2.29,19.0 2,1.62,6.90,3.57,18.50,49.14;1.67,3.08,48.98,3.69,29.66,31.50,65.53,272. 23;1.96,3.23,14.44,1.64,18.02,33.12,33.10,68.73;1.25,3.69,42.00,4.25,22. 22,19.94,53.50,70.00;1.47,9.87,49.15,3.48,4.11,22.37,19.92,67.10;2.02,0. 97,16.99,12.29,18.00,17.36,3.66,16.59;2.41,1.56,2.81,15.79,3.42,21.61,2. 44,24.26;1.00,2.15,40.16,14.27,5.74,53.90,9.24,27.90;1.70,0.77,3.13,5.00, 6.32,11.48,10.23,30.77;0.97,0.12,2.39,21.16,8.08,16.21,41.26,18.84;2.86, 3.29,29.70,1.91,17.04,41.90,12.05,31.90;1.41,5.58,44.18,6.51,10.88,31.98 ,12.92,31.69;1.02,0.86,13.08,1.59,11.15,21.91,26.67,22.28;0.84,0.24,2.16, 21.14,3.56,24.94,18.73,25.61;1.00,0.23,6.11,13.95,4.59,17.19,26.95,18.01 ;0.74,1.39,14.21,20.55,4.29,15.54,54.11,38.96;0.49,0.83,9.03,13.69,1.39,2 4.35,59.15,49.86;1.20,0.23,2.01,20.99,1.06,25.23,23.84,52.05;1.38,0.31,0. 71,5.27,0.98,3.97,68.88,33.79;1.79,0.63,8.00,4.67,4.58,6.92,65.92,61.50;1. 53,2.84,17.27,3.06,18.51,11.59,19.65,49.50;0.78,2.33,33.11,2.78,18.17,7. 28,75.46,51.56;3.83,1.00,53.83,3.53,3.50,0.17,52.67,111.67;2.50,2.67,49. 88,3.14,3.83,8.33,48.33,43.33;1.48,4.32,27.61,1.68,47.29,1.81,69.42,443. 10]
主成分分析法及其应用PPT课件
x4 -0.34 0.644 0.07 1 0.383 0.069 -0.05 -0.031 0.073
x5 0.309 0.42 -0.74 0.383 1
0.734 0.672 0.098 0.747
x6 0.408 0.255 -0.755 0.069 0.734
1 0.658 0.222 0.707
演讲人：XXXXXX 时 间：XX年XX月XX日
荷的平方
三个主成分的
占方差的百分数
“占方差的百分
z1
z2
z3
（%）
数:各个主成分提 取了第i个指标的
x1
0.739
-0.532 -0.0061
82.918
“效率”之和， 它等于各个主成
x2
0.123
0.887 -0.0028
x3
-0.964 0.0096 0.0095
80.191 92.948
分在第i个指标上 的载荷的平方之
x 2：人 均耕地 面积
(ha)
0.352
2 141.5 1.684
3 100.7 1.067
4 143.74 1.336
5 131.41 1.623
x 3：森 林覆盖 率(%)
16.101
x 4：农 民人均 纯收入 (元/人)
192.11
x 5：人 均粮食 产量 (kg/
人)
295.34
x 6：经济 作物占农 作物播面 比例(％)
表3.5.1 相关系数矩阵
x1
x2
x3
x4
x5
x6
x7
x8
x9
x1
1 -0.327 -0.714 -0.336 0.309 0.408 0.79 0.156 0.744
主成分分析步骤
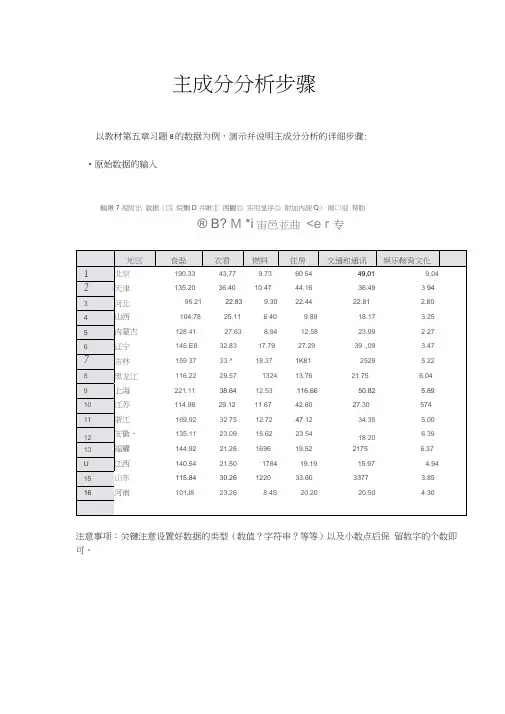
主成分分析步骤以教材第五章习题8的数据为例，演示并说明主成分分析的详细步骤: •原始数据的输入輪锹7 视附出敦据（囚烷飘D 井瞅① 图觀◎ 实用显序◎ 附加内諛Q）爾口迎帮肋® B? M *i宙邑並曲<e r 专注意事项：关键注意设置好数据的类型（数值？字符串？等等）以及小数点后保留数字的个数即可。
•选项操作1. 打开SPSS的“分析”-“降维”-“因子分析” 打开“因子分析”对话框（如下图）倉品女通和通讯选悻变豪（匚Ita（L）£2（R）取清眾助2.把六个变量：食品、衣着、燃料、住房、交通和通讯、娱乐教育文化输入到右边的待分析变量框。
3. 设置分析的统计量打开最右上角的“描述”对话框，选中“统计量”里面的“原始分析结果”和“相关矩阵”里面的“系数”。
（选中原始分析结果，SPSS自动把原始数据标准差标准化，但不显示出来；选中系数，会显示相关系数矩阵。
）。
然后点击“继续”。
统计星□单喪逼椅谨惟(U) 0原赠分忻结果①相关矩阵 ---------------------0 貳数©□ OMN)□泵薯惟水平□ R^(R) □柠列武Q) □反醍數&□ tiMO 和Bartlett 的補誓鹰桧验(K)鍵沽 取消 帮動打开第二个的“抽取”对话框：“方法”里选取“主成分”；“分析”、 和“抽取”这三项都选中各自的第一个选项即可。
然后点击“继续”。
方液血：主磁辞分新 ------------相羌性拒阵〔3)协方遵症阵3抽职特征值大于(&：O 因于的圃定麹・(吵 參槌取的因玖D ； 矗大收皴性电代吹教凶；(25|取请即助第三个的“旋转”对话框里，选取默认的也是第一个选项“无”“输出”输出H 未箍炜的Ema □即石阳鱼］第四个“得分”对话框中，选中“保存为变量”的“回归”；以及“显示因子得分系数矩阵”。
第五个“选项”对话框，默认即可。
这时点击“确定”，进行主成分分析。
主成分分析
Extraction Method: Principal Component Analysis. Component Scores.
主成分系数矩阵，从而得出各主成分的表达式， 主成分系数矩阵，从而得出各主成分的表达式，注意在表达 式中各变量已经不是原始变量，而是标准化变量。 式中各变量已经不是原始变量，而是标准化 身高（X1,cm）、头围（X2,cm）、 体重（X3,g）的数据。
实验报告
写出X1， ， 的相关矩阵 的相关矩阵。 写出 ，X2，X3的相关矩阵。 写出KMO与球形检验的结果（P值）， 与球形检验的结果（ 值 写出 与球形检验的结果 并做出判断， 并做出判断，该数据是否适合主成分分 析。 写出3个主成分的贡献率 个主成分的贡献率。 写出 个主成分的贡献率。 写出3个主成分关于 个主成分关于X1， ， 的标准 写出 个主成分关于 ，X2，X3的标准 化的数值的线性组合。 化的数值的线性组合。
Rotation子对话框：用于因子分析。 子对话框：用于因子分析。 子对话框 Score子对话框 子对话框
选择是否将因子得分存入文件，以及具体的得分计算方法。 （1）Save as Variables：将计算出的因子得分作为新变量 加入数据文件，注意此处加入的是经过标准化的因子得分。 （2）Method单选框组：用于选择计算因子得分用的方法， 使用默认的回归法即可。 （3）Display factor score coefficient maxtrix：很重要。显 示因子得分系数阵，通过该系数阵就可以将所有公因子表示 为各个变量的线性组合，也就是我们所需要的主成分分析的 结果，系统同时会给出因子得分的协方差阵。
主 成 分 分 析
主成分分析
每个人都会遇到有很多变量的数据。 比如全国或各个地区的带有许多经济和社会变量 的数据；各个学校的研究、教学等各种变量的数 据等等。 这些数据的共同特点是变量很多，在如此多的变 量之中，有很多是相关的。人们希望能够找出它 们的少数“代表”来对它们进行描述。 主成分分析（principal component analysis） 就是把变量维数降低以便于描述、理解和分析的 方法。
主成分分析
2.主成分的总方差 由于
tr ( A ) = tr ( T′ΣT ) = tr ( ΣTT′ ) = tr ( Σ )
故
∑ λ = ∑σ
i =1 i i =1
p
p
ii
或
∑V ( y ) = ∑V ( x )
i =1 i i =1 i
p
p
总方差中属于第 i 主成分 yi（或被 yi 所解释)的比例 为
ˆ 三、从R 出发求主成分
ˆ ˆ* ˆ* ˆ R 的 p 个特征值为λ1* ≥ λ2 ≥ L ≥ λ p， 设样本相关阵 ˆ* ˆ 2 ˆ t1 , t * ,L , t *p 为相应的正交单位特征向量，则第 i 样本
主成分
ˆ ˆi yi* = t*x* , i = 1, 2,L , p
其中 x* 是各分量经（样本）标准化了的向量，即
S
主成分得分 在实际应用中，我们常常让 x j 减去 x ，使样本数据 中心化。这不影响样本协差阵 S ，在前面的论述中 惟一需要变化的是，将第 i 主成分改写成中心化的 形式，即
ˆ ˆi yi = t′ ( x − x ) , i = 1, 2,L , p 若将各观测值 x j 代替上式中的观测值向量 x ，则第i
现比较本例中从R 出发和例7.2.2中从 Σ 出发的主成 分计算结果。从R 出发的 y1* 的贡献率0.705明显小于 从 Σ 出发的 y1的贡献率0.938，事实上，原始变量方 差之间的差异越大，这一点也就倾向于越明显， * * * （7.2.15）式有助于我们理解之。 y1 , y2 , y3 可用标准 化前的原变量表达如下： x3 − µ3 x1 − µ1 x2 − µ2 *
主成分的值
ˆi ˆ y ji = t′ ( x j − x ) , i = 1, 2,L , p
什么是主成分分析精选全文
可编辑修改精选全文完整版主成分分析（principal component analysis, PCA）如果一组数据含有N个观测样本，每个样本需要检测的变量指标有K个, 如何综合比较各个观测样本的性质优劣或特点？这种情况下，任何选择其中单个变量指标对本进行分析的方法都会失之偏颇，无法反映样本综合特征和特点。
这就需要多变量数据统计分析。
多变量数据统计分析中一个重要方法是主成份分析。
主成分分析就是将上述含有N个观测样本、K个变量指标的数据矩阵转看成一个含有K维空间的数学模型，N个观测样本分布在这个模型中。
从数据分析的本质目的看，数据分析目标总是了解样本之间的差异性或者相似性，为最终的决策提供参考。
因此，对一个矩阵数据来说，在K维空间中，总存在某一个维度的方向，能够最大程度地描述样品的差异性或相似性(图1)。
基于偏最小二乘法原理，可以计算得到这个轴线。
在此基础上，在垂直于第一条轴线的位置找出第二个最重要的轴线方向，独立描述样品第二显著的差异性或相似性；依此类推到n个轴线。
如果有三条轴线，就是三维立体坐标轴。
形象地说，上述每个轴线方向代表的数据含义，就是一个主成份。
X、Y、Z轴就是第1、2、3主成份。
由于人类很难想像超过三维的空间，因此，为了便于直观观测，通常取2个或者3个主成份对应图进行观察。
图（1）PCA得到的是一个在最小二乘意义上拟合数据集的数学模型。
即，主成分上所有观测值的坐标投影方差最大。
从理论上看，主成分分析是一种通过正交变换，将一组包含可能互相相关变量的观测值组成的数据，转换为一组数值上线性不相关变量的数据处理过程。
这些转换后的变量，称为主成分（principal component, PC）。
主成分的数目因此低于或等于原有数据集中观测值的变量数目。
PCA最早的发明人为Karl Pearson，他于1901年发表的论文中以主轴定理（principal axis theorem）衍生结论的形式提出了PCA的雏形，但其独立发展与命名是由Harold Hotelling于1930年前后完成。
05主成分分析
主成分分析专题§1 引言我们在作数据分析处理时，涉及的样品往往包含有多个测量指标（比如p 个指标），较多的指标会带来分析问题的复杂性。
然而，这些指标彼此之间常常存在着一定程度的、有时甚至是相当高的相关性,这就使含在观测数据中的信息在一定程度上有所重叠。
主成分分析就是一种通过降维技术把多个指标约化为少数几个综合指标的统计分析方法.这些综合指标能够反映原始指标的绝大部分信息,它们通常表示为原始p 个指标的某种线性组合。
为了使这些综合指标所含的信息互不重叠，应要求它们互不相关。
例如,考虑p ＝2的情形，假设共有n 个样品，每个样品都测量了两个指标),(21x x ，它们大致分布在一个椭圆内。
如图所示。
显然，在坐标系21Ox x 中，n 个点的坐标1x 和2x 呈现某种线性相关性。
我们将该坐标系按逆时针方向旋转某个角度θ变成新坐标系21Oy y ,这里1y 是椭圆的长轴方向，2y 是短轴方向。
旋转公式为112212cos sin sin cos y x x y x x θθθθ=+⎧⎨=-+⎩ 易见，n 个点在新坐标系下的坐标1y 和2y 几乎不相关.1y 和2y 称为原始变量1x 和2x 的综合变量，n 个点在1y 轴上的方差达到最大，即在此方向上所含的有关n 个样品间差异的信息是最多的.因此，若欲将二维空间的点投影到某个一维方向，则选择1y 轴方向能使信息的损失降低到最小。
我们称1y 轴为第一主成分,而与1y 轴正交的2y 轴，有着较小的方差，称为第二主成分。
第一主成分的效果与椭圆的形状有很大关系,椭圆越是扁平,n 个点在1y 轴上的方差就相对越大，在2y 轴上的方差就相对越小。
考虑这样两种极端的情形：一种是椭圆的长轴与短轴的长度相等，即椭圆变成圆，第一主成分只含有二维空间点的约一半信息，若仅用这一个综合变量，则将损失约50％的信息，这显然是不可取的。
造成它的原因是，原始变量1x 和2x 的相关程度几乎为零，也就是说，1x 和2x 所包含的信息几乎互不重叠，因此无法用一个一维的综合变量来代替它们。
主成分分析
x12 x22 M xn 2
L x1 p L x2 p M L xnp
主成分分析的概念（续）
由于实测的变量间存在一定的相关关系， 由于实测的变量间存在一定的相关关系， 因此有可能用较少数的综合指标分别综 合存在于各变量中的各类信息， 合存在于各变量中的各类信息，而综合 指标之间彼此不相关， 指标之间彼此不相关，即各指标代表的 信息不重叠。综合指标称为主成分（ 信息不重叠。综合指标称为主成分（提 取几个因子），一般有两种方法： ），一般有两种方法 取几个因子），一般有两种方法： 特征值>1 特征值 累计贡献率>0.8 累计贡献率
0.198 99.015
0.049 100.000
Component Matrix(a) Component 1 X1 X2 X3 X4 X5 .808 .814 -.791 .101 .846 2 -.487 .397 .479 .977 .415
由此可建立第一、二主成分（即两个新的综合指标） 由此可建立第一、二主成分（即两个新的综合指标） Z1=0.808X1+0.814X2-0.791X3+0.101X4+0.846X5; Z2=-0.487X1+0.397X2+0.479X3+0.977X4+0.415X5;
主成分分析的基本思想
主成分分析是研究如何通过原来变量的少数几个线性 组合来解释原来变量绝大多数信息的一种多元统计方法. 组合来解释原来变量绝大多数信息的一种多元统计方法 既然研究某一个问题涉及的众多变量之间有一定的相 关性,就必然存在着起支配作用的共同因素 根据这一点 关性 就必然存在着起支配作用的共同因素,根据这一点 就必然存在着起支配作用的共同因素 根据这一点, 通过对原始变量相关矩阵或协方差矩阵内部结构关系的 研究,利用原始变量的线性组合形成几个综合指标 主成分 研究 利用原始变量的线性组合形成几个综合指标(主成分 利用原始变量的线性组合形成几个综合指标 主成分) 在保留原始变量主要信息的前提下起到降维与简化问题 的作用,从而在研究复杂问题时抓住主要矛盾 的作用 从而在研究复杂问题时抓住主要矛盾. 从而在研究复杂问题时抓住主要矛盾
主 成 分 分 析
主成分分析主成分分析（Principal Component Analysis，PCA）是一种常用的数据降维方法，它可以将高维度数据转换成低维度数据，并尽量保留数据的信息。
主成分分析的思想是通过对原始数据的线性变换，将其转换为一组新的变量，这些新变量是原始变量的线性组合。
这些新变量被称为主成分，它们可以解释原始数据的大部分方差，从而将原始数据的维度降低。
主成分分析的作用主成分分析可以用于数据预处理、数据压缩、数据可视化和模型建立等方面。
在数据预处理阶段，主成分分析可以用于去除数据中的冗余信息，减少数据噪声，提高数据的质量。
在数据压缩阶段，主成分分析可以将高维度数据压缩成低维度数据，从而节省存储空间和计算时间。
在数据可视化阶段，主成分分析可以将高维度数据转换成低维度数据，进行可视化展示，帮助用户更直观地理解数据和发现数据中隐藏的规律。
在模型建立阶段，主成分分析可以用于特征提取，减少维度的同时又不失去数据的重要特征，帮助用户更准确地建立模型，提高模型的预测准确率。
主成分分析的应用主成分分析广泛应用于各个领域，例如金融、医学、环境、工业等。
在金融领域，主成分分析可以用于建立风险评估模型，帮助投资者了解投资组合的风险。
在医学领域，主成分分析可以用于进行疾病预测，帮助医生快速准确地诊断疾病。
在环境领域，主成分分析可以用于分析空气质量和水质，帮助政府和公众了解环境状况。
在工业领域，主成分分析可以用于质量控制和生产优化，帮助企业降低成本和提高效率。
主成分分析的注意事项要注意主成分分析的前提条件，即原始数据必须为线性数据，在进行主成分分析前需要先对数据进行标准化处理。
此外，在进行主成分分析时，应根据实际问题选择合适的主成分数量，不能盲目追求降维程度，以免丢失重要信息。
同时，主成分分析的结果需要进行解释和验证，以确保分析结果的可靠性和有效性。
结语主成分分析是一种十分常用且十分有效的数据降维方法，它能够将高维度数据转换成低维度数据，并尽量保留数据的信息。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2020/11/11
5
目录 上页 下页 返回 结束
利用主成分分析得到的主成分与原始变量之 间有如下基本关系：
1.每一个主成分都是各原始变量的线性组合 2.主成分的数目大大少于原始变量的数目
3.主成分保留了原始变量绝大多数信息 4.各主成分之间互不相关
2020/11/11
6
目录 上页 下页 返回 有意义。我们将线性变换约束在下面的原则之下：
1．
，即：
2．
3. 是
的一切满足原则1的线性组合中方差最
大者； 是与 不相关的
所有线性组合中方差最
大者；…, 是与
都不相关的
的所有
线性组合中方差最大者。
2020/11/11
9
目录 上页 下页 返回 结束
基于以上三条原则决定的综合变量 Y1,Y2 ,,YP分
义，所得结论可以很容易地扩展到多维的情况。
2020/11/11
11
目录 上页 下页 返回 结束
设有 个样品，每个样品有两个观测变量 ，这样， 在由变量 组成的坐标空间中， 个样品点散布的情况如 带状，见图5-1。
2020/11/11
图5-1
12
目录 上页 下页 返回 结束
由图可以看出这 个样品无论沿 轴方向还是沿 轴方向均 有较大的离散性，其离散程度可以分别用观测变量 的方差和 的方差定量地表示，显然，若只考虑 和 中的任何一个，原 始数据中的信息均会有较大的损失。我们的目的是考虑 和 的线性组合，使得原始样品数据可以由新的变量 和 来刻画。 在几何上表示就是将坐标轴按逆时针方向旋转 角度，得到新坐 标轴 和 ，坐标旋转公式如下：
•主成分分析是利用降维的思想，在损失很少信息的 前提下把多个指标转化为几个综合指标的多元统计 方法。
•通常把转化生成的综合指标称之为主成分，其中每 个主成分都是原始变量的线性组合，且各个主成分 之间互不相关。
•这样在研究复杂问题时就可以只考虑少数几个主成
分而不至于损失太多信息，从而更容易抓住主要矛
盾，，同时使问题得到简化，提高分析效率。
§5.1.2 主成分分析的基本理论
设对某一事物的研究涉及个 指标，分别用 示，这个 指标构成的 维随机向量为 机向量 的均值为 ，协方差矩阵为 。
表 。设随
对 进行线性变换，可以形成新的综合变量，用 表示， 也就是说，新的综合变量可以由原来的变量线性表示，即满 足下式：
Y1 u11X1 u12 X 2 u1p X p Y2 u21X1 u22 X 2 u2 p X p Yp u p1 X1 u p2 X 2 u pp X p
(5.1)
2020/11/11
7
目录 上页 下页 返回 结束
由于可以任意地对原始变量进行上述线性变换，
由不同的线性变换得到的综合变量 的统计特性也
不尽相同。因此为了取得较好的效果，我们总是希
望
的方差尽可能大且各 之间互相独立，
由于
=
而对任给的常数 ，有
2020/11/11
8
目录 上页 下页 返回 结束
第五章 主成分分析
•§5.1 主成分分析的基本思想与理论 •§5.2 总体主成分及其性质 •§5.3 样本主成分的导出 •§5.4 有关问题的讨论 •§5.5 主成分分析步骤及框图 •§5.6 主成分分析的上机实现
2020/11/11
1
目录 上页 下页 返回 结束
• 主成分分析(Principal Components Analysis)也称主 分量分析，是由霍特林（Hotelling）于1933年首先提 出的。
• 为了避免遗漏重要的信息而考虑尽可能多的指标；
• 增多增加了问题的复杂性，同时由于各指标均是对同一事 物的反映，不可避免地造成信息的大量重叠，这种信息的重 叠有时甚至会抹杀事物的真正特征与内在规律。
基于上述问题，人们就希望在定量研究中涉及的变量较 少，而得到的信息量又较多。主成分分析正是研究如何通过 原来变量的少数几个线性组合来解释原来变量绝大多数信息 的一种多元统计方法。
别称为原始变量的第一、第二、…、第 p 个主成分。
其中，各综合变量在总方差中占的比重依次递减， 在实际研究工作中，通常只挑选前几个方差最大的 主成分，从而达到简化系统结构，抓住问题实质的 目的。
2020/11/11
10
目录 上页 下页 返回 结束
§5.1.3 主成分分析的几何意义
由第一节的介绍我们知道，在处理涉及多个指标问题的时
2020/11/11
4
目录 上页 下页 返回 结束
既然研究某一问题涉及的众多变量之间有一定 的相关性，就必然存在着起支配作用的共同因素， 根据这一点，通过对原始变量相关矩阵或协方差矩 阵内部结构关系的研究，利用原始变量的线性组合 形成几个综合指标（主成分），在保留原始变量主 要信息的前提下起到降维与简化问题的作用，使得 在研究复杂问题时更容易抓住主要矛盾。
候，为了提高分析的效率，可以不直接对 个指标构成的 维
随机向量
进行分析，而是先对向量 进行线
性变换，形成少数几个新的综合变量
，使得各综
合变量之间相互独立且能解释原始变量尽可能多的信息，这样，
在以损失很少部分信息为代价的前提下，达到简化数据结构，
提高分析效率的目的。这一节，我们着重讨论主成分分析的几
何意义，为了方便，我们仅在二维空间中讨论主成分的几何意
2020/11/11
2
目录 上页 下页 返回 结束
§5.1 主成分分析的基本思想与理论 §5.1.1 主成分分析的基本思想 §5.1.2 主成分分析的基本理论
2020/11/11
3
目录 上页 下页 返回 结束
§5.1.1 主成分分析的基本思想
考虑多个指标对某一问题进行分析的时候会产生如下问 题：
2020/11/11
13
目录 上页 下页 返回 结束
其矩阵形式为：
其中， 为旋转变换矩阵，由上式可知它是正交阵， 即满足
2020/11/11
14
目录 上页 下页 返回 结束
经过这样的旋转之后， 个样品点在 轴上的离散程度最 大，变量 代表了原始数据绝大部分信息，这样，有时在研 究实际问题时，即使不考虑变量 也无损大局。因此，经过 上述旋转变换就可以把原始数据的信息集中到 轴上，对数 据中包含的信息起到了浓缩的作用。进行主成分分析的目的 就是找出转换矩阵 ，而进行主成分分析的作用与几何意义 也就很明了了。下面我们用遵从正态分布的变量进行分析， 以使主成分分析的几何意义更为明显。为方便，我们以二元 正态分布为例。对于多元正态总体的情况，有类似的结论。