《新编基础物理学答案解析》_第11章

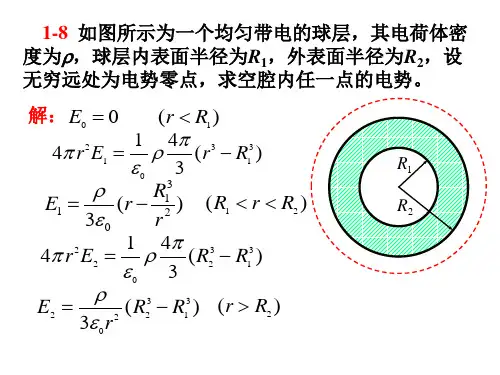
题图10-1题10-1解图 d 第十章习题解答10-1 如题图10-1所示，三块平行的金属板A ，B 和C ，面积均为200cm 2,A 与B 相距4mm ，A 与C 相距2mm ，B 和C 两板均接地，若A 板所带电量Q =3.0×10-7C ，忽略边缘效应,求：（1）B 和C 上的感应电荷？（2）A 板的电势（设地面电势为零）。

分析：当导体处于静电平衡时，根据静电平衡条件和电荷守恒定律，可以求得导体的电荷分布，又因为B 、C 两板都接地，所以有ACAB U U =。

解：（1）设B 、C 板上的电荷分别为B q 、C q 。

因3块导体板靠的较近，可将6个导体面视为6个无限大带电平面。

导体表面电荷分布均匀，且其间的场强方向垂直于导体表面。

作如图中虚线所示的圆柱形高斯面。

因导体达到静电平衡后，内部场强为零，故由高斯定理得：1A C q q =- 2A B q q =-即 ()A B C q q q =-+ ①又因为： ACAB U U =而: 2AC ACdU E =⋅ AB AB U E d =⋅∴ 2AC AB E E =于是：002C B σσεε =⋅ 两边乘以面积S 可得： 002C B S S σσεε =⋅ 即： 2C B q q = ②联立①②求得: 77210,110C B q C q C --=-⨯=-⨯题图10-2(2) 00222C C A AC C AC AC q d d d U U U U E S σεε =+==⋅=⋅=⋅ 733412210210 2.2610()200108.8510V ----⨯=⨯⨯=⨯⨯⨯⨯ 10-2 如题图10-2所示，平行板电容器充电后，A 和B 极板上的面电荷密度分别为+б和－б，设P 为两极板间任意一点，略去边缘效应，求： （1）A,B 板上的电荷分别在P 点产生的场强E A ,E B ;（2）A,B 板上的电荷在P 点产生的合场强E ； (3)拿走B 板后P 点处的场强E ′。

新编物理基础学(上、下册)课后习题详细答案王少杰，顾牡主编第一章1-1.质点运动学方程为：cos()sin(),r a t i a t j btk ωω=++r r r r其中a ，b ，ω均为正常数，求质点速度和加速度与时间的关系式。

分析：由速度、加速度的定义，将运动方程()r t r对时间t 求一阶导数和二阶导数，可得到速度和加速度的表达式。

解：/sin()cos()==-++r r r r rv dr dt a t i a t j bk ωωωω2/cos()sin()a dv dt a t i t j ωωω⎡⎤==-+⎣⎦r r r r1-2. 一艘正在沿直线行驶的电艇，在发动机关闭后，其加速度方向与速度方向相反，大小与速度平方成正比，即2/d d v v K t -=， 式中K 为常量．试证明电艇在关闭发动机后又行驶x 距离时的速度为 0Kx v v e -= 。

其中0v 是发动机关闭时的速度。

分析：要求()v v x =可通过积分变量替换dxdvvdt dv a ==，积分即可求得。

证：2d d d d d d d d v x vv t x x v t v K -==⋅= d Kdx v =-v⎰⎰-=x x K 0d d 10v v v v , Kx -=0ln v v0Kx v v e -=1-3．一质点在xOy 平面内运动，运动函数为22,48x t y t ==-。

（1）求质点的轨道方程并画出轨道曲线；（2）求t =1 s t =2 s 和时质点的位置、速度和加速度。

分析：将运动方程x 和y 的两个分量式消去参数t ，便可得到质点的轨道方程。

写出质点的运动学方程)(t r ρ表达式。

对运动学方程求一阶导、二阶导得()v t r 和()a t r ，把时间代入可得某时刻质点的位置、速度、加速度。

解：（1）由2,x t =得：,2x t =代入248y t =-可得：28y x =-，即轨道曲线。

新编基础物理学上册答案【篇一：新编基础物理学上册1-2单元课后答案】class=txt>王少杰，顾牡主编第一章????1-1.质点运动学方程为：r?acos(?t)i?asin(?t)j?btk,其中a，b，?均为正常数，求质点速度和加速度与时间的关系式。

?分析：由速度、加速度的定义，将运动方程r(t)对时间t求一阶导数和二阶导数，可得到速度和加速度的表达式。

?????解：v?dr/dt??a?sin(?t)i?a?cos(?t)j?bk????2a?dv/dt??a???cos(?t)i?sin(?t)j??1-2. 一艘正在沿直线行驶的电艇，在发动机关闭后，其加速度方向与速度方向相反，大小与速度平方成正比，即dv/dt??kv2，式中k为常量．试证明电艇在关闭发动机后又行驶x距离时的速度为v?v0e?kx 。

其中v0是发动机关闭时的速度。

dvdv分析：要求v?v(x)可通过积分变量替换a?，积分即可求得。

?vdtdxdvdvdxdv???v??kv2dtdxdtdxdv??kdxvv1xvv???v0v?0kdx ,lnv0??kx证：v?v0e?kx1-3．一质点在xoy平面内运动，运动函数为x?2t,y?4t2?8。

（1）求质点的轨道方程并画出轨道曲线；（2）求t=1 s和t=2 s 时质点的位置、速度和加速度。

分析：将运动方程x和y的两个分量式消去参数t，便可得到质点的轨道方程。

写出质点的???运动学方程r(t)表达式。

对运动学方程求一阶导、二阶导得v(t)和a(t)，把时间代入可得某时刻质点的位置、速度、加速度。

解：（1）由x?2t,得：t?,代入y?4t2?8可得：y?x2?8，即轨道曲线。

画图略???（2）质点的位置可表示为：r?2ti?(4t2?8)j?????由v?dr/dt则速度：v?2i?8tj????由a则加速度：a?8j ?dv/dt????????则：当t=1s时，有r?2i?4j,v?2i?8j,a?8j????????当t=2s时，有r?4i?8j,v?2i?16j,a?8j1-4．一质点的运动学方程为x?t2，y?(t?1)2，x和y均以m为单位，t以s为单位。

窗体顶端测试题（第9章）（一）单项选择题1.在传染病区内属于半污染区的是（）。

A.办公室B.病区走廊C.值班室D.库房E.盥洗室2.对芽胞无作用的化学消毒剂是（）。

A.环氧乙烷B.过氧乙酸C.碘酊D.乙醇E.甲醛3.执行隔离技术不妥的是（）。

A.用一次性口罩不超过4hB.刷手时应从指尖开始C.冲洗手时应腕部低于肘部D.隔离衣应每日更换E.取避污纸从页面抓取4.下列不符合无菌技术操作要求的是（）。

A.铺好的无菌盘有效时限为8hB.已开启的溶液瓶内溶液可保存24hC.无菌包打开后包内物品使用时限为24hD.无菌包的有效期一般为7天E.一份无菌物品只能供一个病人使用5.医院内一般病室适宜的环境是（）。

A.温度18～22℃，湿度50%～60%，噪音强度45～55dBB.温度22～24℃，湿度50%～60%，噪音强度35～45dBC.温度18～22℃，湿度50%～60%，噪音强度35～45dBD.温度22～24℃，湿度40%～50%，噪音强度45～55dBE.温度24～28℃，湿度40%～50%，噪音强度45～55dB6.以下关于热力消毒灭菌法的叙述中，错误的是（）。

A.利用热力破坏微生物的蛋白质、核酸，从而导致其死亡B.燃烧灭菌法适用于锐利刀剪的消毒灭菌C.湿热法的优点是传热快，穿透力强，可释放潜热D.煮沸消毒法可用于金属、搪瓷、玻璃、橡胶类物品的消毒E.预真空压力蒸汽灭菌器在5min左右即可灭菌7.下列关于隔离技术的说法中，正确的是（）。

A.传染性分泌物二次培养结果均为阴性后可解除隔离B.脱隔离衣前应用清洁液洗手C.艾滋病患者应采用保护性隔离D.对于严密隔离的患者，可以出病室，但必须戴好口罩和帽子E.接触隔离适用于破伤风和气性坏疽8.使用紫外线灯进行消毒，不妥的是（）。

A.照射时间应从开灯5～7min后开始计算B.用于物品消毒时，有效距离为25～60cmC.用于空气消毒时，有效照射距离不应超过2mD.当灯管强度低于60w/cm2时应予以更换E.消毒效果最好的相对湿度为40%～60%（二）多项选择题1.传染病区内属清洁区的是（）。

新编物理基础学全册课后习题详细答案王少杰，顾牡主编第一章1-1.质点运动学方程为：cos()sin(),r a t i a t j btk ωω=++其中a ，b ，ω均为正常数，求质点速度和加速度与时间的关系式。

分析：由速度、加速度的定义，将运动方程()r t 对时间t 求一阶导数和二阶导数，可得到速度和加速度的表达式。

解：/sin()cos()==-++v dr dt a t i a t j bk ωωωω2/cos()sin()a dv dt a t i t j ωωω⎡⎤==-+⎣⎦1-2. 一艘正在沿直线行驶的电艇，在发动机关闭后，其加速度方向与速度方向相反，大小与速度平方成正比，即2/d d v v K t -=， 式中K 为常量．试证明电艇在关闭发动机后又行驶x 距离时的速度为 0Kxv v e -= 。

其中0v 是发动机关闭时的速度。

分析：要求()v v x =可通过积分变量替换dxdvv dt dv a ==，积分即可求得。

证：2d d d d d d d d v x vv t x x v t v K -==⋅= d Kdx v =-v⎰⎰-=x x K 0d d 10v v v v , Kx -=0ln v v0Kxv v e -=1-3．一质点在xOy 平面内运动，运动函数为22,48x t y t ==-。

（1）求质点的轨道方程并画出轨道曲线；（2）求t =1 s t =2 s 和时质点的位置、速度和加速度。

分析：将运动方程x 和y 的两个分量式消去参数t ，便可得到质点的轨道方程。

写出质点的运动学方程)(t r表达式。

对运动学方程求一阶导、二阶导得()v t 和()a t ，把时间代入可得某时刻质点的位置、速度、加速度。

解：（1）由2,x t =得：,2x t =代入248y t =-可得：28y x =-，即轨道曲线。

画图略 （2）质点的位置可表示为：22(48)r ti t j =+- 由/v dr dt =则速度：28v i tj =+ 由/a dv dt =则加速度：8a j =则：当t=1s 时，有24,28,8r i j v i j a j =-=+=当t=2s 时，有48,216,8ri j v i j a j =+=+=1-4．一质点的运动学方程为22(1)x t y t ==-，，x 和y 均以m 为单位，t 以s 为单位。

习题二2-1．两质量分别为m 和M ()M m ≠的物体并排放在光滑的水平桌面上，现有一水平力F 作用在物体m 上，使两物体一起向右运动，如题图2-1所示，求两物体间的相互作用力。

若水平力F 作用在M 上，使两物体一起向左运动，则两物体间相互作用力的大小是否发生变化？解：以m 、M 整体为研究对象，有()F m M a =+…①以m 为研究对象，如解图2-1（a ），有Mm F F ma -=…②由①、②两式，得相互作用力大小若F 作用在M 上，以m 为研究对象，如题图2-1（b ）有Mm F ma =…………③由①、③两式，得相互作用力大小MmmFF m M=+发生变化。

2-2.在一条跨过轻滑轮的细绳的两端各系一物体，两物体的质量分别为M 1和M 2，在M 2上再放一质量为m 的小物体，如题图2-2所示，若M 1=M 2=4m ，求m 和M 2之间的相互作用力，若M 1=5m ，M 2=3m ，则m与M 2之间的作用力是否发生变化？解：受力图如解图2-2，分别以M 1、M 2和m 为研究对象，有111T M g M a -=又12T T =，则2M m F =1122M mgM M m++当124M M m ==时 当125,3M m M m ==时2109M m mg F =，发生变化。

2-3.质量为M 的气球以加速度a v匀加速上升，突然一只质量为m 的小鸟飞到气球上，并停留在气球上。

若气球仍能向上加速，求气球的加速度减少了多少？题图2-2题图2-1解图2-1解图2-2解：设f r为空气对气球的浮力，取向上为正。

分别由解图2-3（a ）、(b)可得 由此解得2-4．如题图2-4所示，人的质量为60kg ，底板的质量为40kg 。

人若想站在底板上静止不动，则必须以多大的力拉住绳子？ 解：设底板和人的质量分别为M ，m ，以向上为正方向，受力图如解图2-4（a ）、(b)所示，分别以底板、人为研究对象，则有3'0T F mg +-=F 为人对底板的压力，'F 为底板对人的弹力。

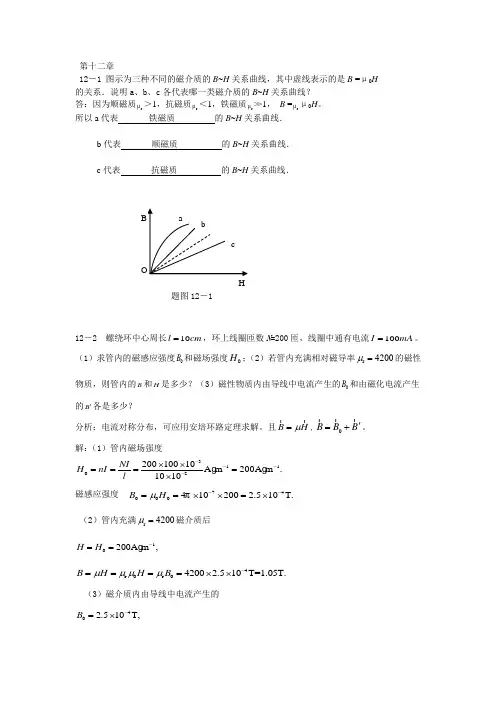
第十二章12－1 图示为三种不同的磁介质的B ~H 关系曲线，其中虚线表示的是B =μ0H 的关系．说明a 、b 、c 各代表哪一类磁介质的B ~H 关系曲线？ 答：因为顺磁质r μ＞1，抗磁质r μ＜1，铁磁质r μ>>1， B =r μμ0H 。

所以a 代表 铁磁质 的B ~H 关系曲线．b 代表 顺磁质 的B ~H 关系曲线．c 代表 抗磁质 的B ~H 关系曲线．12－2 螺绕环中心周长10l cm =，环上线圈匝数N =200匝，线圈中通有电流100I mA =。

（1）求管内的磁感应强度0B 和磁场强度0H ；（2）若管内充满相对磁导率r 4200μ=的磁性物质，则管内的B 和H 是多少？（3）磁性物质内由导线中电流产生的0B 和由磁化电流产生的B '各是多少？分析：电流对称分布，可应用安培环路定理求解。

且B H μ= ,0B B B '=+。

解：（1）管内磁场强度3110220010010A m 200A m .1010NI H nI l ----⨯⨯====⨯ 磁感应强度 740004π10200 2.510T.B H μ--==⨯⨯=⨯ （2）管内充满r 4200μ=磁介质后10200A m ,H H -==4r 0r 04200 2.510T=1.05T.B H H B μμμμ-====⨯⨯（3）磁介质内由导线中电流产生的40 2.510T,B -=⨯则40(1.05 2.510)T 1.05T.B B B -'=-=-⨯≈12－3 一铁制的螺绕环，其平均圆周长为30cm ，截面积为1cm 2，在环上均匀绕以300匝导线，当线圈内的电流为0.032A 时，环内的磁通量为6210wb -⨯.试计算（1）环内的磁通量密度；（2）环圆截面中心的磁场强度；（3）磁化面电流；（4）环内材料的磁导率、相对磁导率及磁化率；（5）环芯内的磁化强度.分析：可应用介质中安培环路定理求磁场强度。

专业班级 学号 姓名机械振动本章知识点：简谐振动的特征及其运动方程，简谐振动的旋转矢量表示法，振动的能量，简谐运动的合成，阻尼振动，受迫振动，共振本章重点：简谐振动的特征及其运动方程，简谐振动的旋转矢量表示法，振动的能量，同方向同频率简谐运动的合成 一、填空题1．一个给定系统做简谐振动时，其振幅和初相位决定于 、 和 ；弹簧振子做简谐振动时，其频率决定于 和 ．2．一弹簧振子，弹簧的劲度系数为0.32 N/m ，重物的质量为0.02 kg ，则这个系统的固有角频率为 rad/s ，相应的振动周期为 s ．3．在两个相同的弹簧下各悬挂一物体，两物体的质量比为4：1，则两者做简谐运动的周期之比为 ． 4．质点做简谐运动的位移和时间关系如图1所示，则其运动方程为 ． 5．两个同频率的简谐运动曲线如图2所示，则2x 的相位比1x 的相位落后 ．6．两个简谐振动曲线如图3所示，两个简谐振动的频率之比12:νν= ，加速度最大值之比a 1m ：a 2m = ，初始速率之比1020:=v v ．7．简谐振动的方程为)cos(ϕω+=t A x ，势能最大时位移x= ，此时动能E k = ．8．已知一质点做简谐运动曲线如图4所示，由图可确定振子在t= s 时速度为零；在t= s 时弹性势能最小；在(__________)s 时加速度取正的最大值．9．两个同方向同频率的简谐振动，其合振动的振幅为0.20m ，合振动与第一分振动的相位差为60度，已知第一分振动的振幅为0.10m ，则第二分振动的振幅为 m ，第二分振动与第一分振动的相位差为 ．10．某谐振子同时参与两个同方向的简谐运动，其运动方程分别为))(3/4cos(10321m t x ππ+⨯=-；))(4cos(10422m t x ϕπ+⨯=-当ϕ= 时合振动的振幅最大，其值max A = ；当ϕ= 时合振动的振幅最小，其值min A = ．11．图5中所示为两个简谐振动的振动曲线，若以余弦函数表示这两个振动的合成结果，则合振动的方程为=+=11x x xt/s7x/m0.050.10 图1x 1xx 2to图32 1xt/s图4图5x 2x 1 xt图2(____________________)。

第1章 质点运动学1-1. 一质点沿x 轴运动，坐标与时间的变化关系为x ＝8t 3－6t （m ），试计算质点 (1) 在最初2s 内的平均速度，2s 末的瞬时速度；(2) 在1s 末到3s 末的平均加速度，3s 末的瞬时加速度. 分析：平均速度和瞬时速度的物理含义不同，分别用x t ∆=∆v 和d d xt=v 求得；平均加速度和瞬时加速度的物理含义也不同，分别用a t∆=∆v和d d a t =v 求得.解：(1) 在最初2s 内的平均速度为31(2)(0)(8262)026(m s )2x x x t t -∆-⨯-⨯-====⋅∆∆v2s 末质点的瞬时速度为212d 24690(m s )d xt t-==-=⋅v (2) 1s 末到3s 末的平均加速度为22(3)(1)(2436)(246)96(m s )2a t t -∆-⨯---====⋅∆∆v v v3s 末的瞬时加速度23d 48144(m s )d a t t-===⋅v1-2．一质点在xOy 平面内运动，运动方程为22(m),48(m)x t y t ==-. （1）求质点的轨道方程并画出轨道曲线；（2）求=1 s =2 s t t 和时质点的位置、速度和加速度.分析：将运动方程x 和y 的两个分量式消去参数t ，便可得到质点的轨道方程.写出质点的运动学方程)(t r表达式.对运动学方程求一阶导、二阶导得()t v 和()a t ，把时间代入可得某时刻质点的位置、速度、加速度.解：（1） 由2,x t = 得：,2xt =代入248y t =- 可得：28y x =-，即轨道方程. 画图略（2）质点的位置矢量可表示为22(48)r ti t j =+-则速度d 28d ri t j t==+v 加速度d 8d a j t==v当t =1s 时，有1224(m),28(m s ),8m s r i j i j a j --=-=+⋅=⋅v当t =2s 时，有1248(m),216(m s ),8m s r i j i j a j --=+=+⋅=⋅v1-3．一质点的运动学方程为22(1)x t y t ==-，，x 和y 均以m 为单位，t 以s 为单位. 求： （1）质点的轨迹方程；（2）在2s t =时质点的速度和加速度. 分析： 同1-2.解：（1）由题意可知：x ≥ 0，y ≥ 0，由2x t =，可得t =,代入2(1)y t =- 整理得：1=即轨迹方程（2）质点的运动方程可表示为22(1)r t i t j =+-则d 22(1)d rti t j t ==+-v d 22d a i j t==+v因此, 当2s t =时，有1242(m s ),22(m s )i j a i j --=+⋅=+⋅v1-4．一枚从地面发射的火箭以220m s -⋅的加速度竖直上升后，燃料用完，于是像一个自由质点一样运动. 略去空气阻力并设g 为常量，试求： （1）火箭达到的最大高度；（2）它从离开地面到再回到地面所经过的总时间.分析：分段求解：030s t ≤≤时，220m s a -=⋅，可求出11,x v ；t ＞30s 时，g a -=.可求出2()t v ，2()x t .当20=v 时，火箭达到的最大高度, 求出t 、x . 再根据0x =，求出总时间.解：（1）以地面为坐标原点，竖直向上为x 轴正方向建立一维坐标系，设火箭在坐标原点时，t =0s ，且=30s.则当0≤ t ≤30s，由d d xx a t=v ,得 3020d d xx t =⎰⎰v v ， 解得 20x t =v当130s =v 时11600m s -=⋅v由d d x xt=v ， 得 13020d d x t t x =⎰⎰，则19000m x =当火箭未落地, 且t ＞30s, 又有221309.8d d x tx t -=⎰⎰v v v解得28949.8x t =-v同理由d d x x t=v 得 130(8949.8)d d txx t t x -=⎰⎰解得24.989413410x t t =-+- … ①由20x =v ，得91.2s t =，代入①得max 27.4km x ≈（2）由①式可知，当0x =时，解得1166s t ≈216s<30s t ≈（舍去）1-5．质点沿直线运动，加速度24a t =-，式中a 的单位为2m s -⋅，t 的单位为s ，如果当t =3s时，x =9m ，12m s -=⋅v ，求质点的运动方程.分析 本题属于第二类运动学问题，可通过积分方法求解. 解 由分析可知0200d d (4)d tta t t t ==-⎰⎰⎰vv v 积分得30143t t =+-v v 由030001d d (4)d 3xt tx x t t t t ==+-⎰⎰⎰v v 得24001212x x t t t =+-+v 将t =3s 时，x =9m ，12m s -=⋅v 代入上两式中得101m s -=-⋅v ，x 0=0.75m所以质点的运动方程为2410.752(m)12x t t t =-+-1-6. 一艘正在沿直线行驶的电艇，在发动机关闭后，其加速度方向与速度方向相反，大小与速度大小平方成正比，即2d /d t k =-v v ， 式中k 为常量．试证明电艇在关闭发动机后又行驶x 距离时的速度大小为 0kxe-=v v . 其中0v 是发动机关闭时的速度大小.分析：要证明~x v 关系，可通过积分变量替换将时间变量替换掉，即d d d d a t x==v vv ，积分即可证明. 证： 2d d d d d d d d k =⋅==-v v vv v x t x t x分离变量得d d k x =-vv两边积分001d d x k x =-⎰⎰vv v v , 0lnkx =-v v 证得0kxe -=v v1-7．一质点沿半径为R 做圆周运动，运动学方程为2012s t bt =+v ，其中v 0，b 都是大于零的常量.求：（1）t 时刻质点的加速度大小及方向； （2）在何时加速度大小等于；分析：由质点在自然坐标系下的运动学方程()t s s =，求导可求出质点的运动速率d d st=v ，而切向加速度d d t a t=v ，法向加速度2n a ρ=v ，总加速度22n a a a +=τ，当a =时，即可求出t .解：（1）质点的运动速率0d d sbt t==+v v 切向加速度d d t a b t ==v 法向加速度220()n bt a Rρ+==v v 加速度大小a ==方向()211tantan ntbt a a bRθ--+==v（2）当a =时，可得22220()2bt b b R ⎡⎤++=⎢⎥⎣⎦v解出t b=v 1-8. 物体以初速度120m s -⋅被抛出，抛射仰角60°，略去空气阻力，问： （1）物体开始运动后的末，运动方向与水平方向的夹角是多少 末的夹角又是多少 （2）物体抛出后经过多少时间，运动方向才与水平成45°角这时物体的高度是多少 （3）在物体轨迹最高点处的曲率半径有多大 （4）在物体落地点处，轨迹的曲率半径有多大分析：（1）建立坐标系，写出初速度0v ，求出()t v 、θtan ，代入t 求解.（2）由（1）中的θtan 关系，求出时间t ；再根据y 方向的运动特征写出()t y ，代入t 求y . （3）根据物体在轨迹最高点处，0y =v ，且加速度2n a a g ρ===v ，可求出ρ.（4）由对称性，落地点与抛射点的曲率相同 2cos n a g θρ==v ，求出ρ.解：以水平向右为x 轴正向，竖直向上为y 轴正向建立二维坐标系 （1）初速度001020cos6020sin6010103(m s )i j i j -=+=+⋅v ，加速度29.8(m s ),a j -=-⋅则任一时刻10(1039.8)at i t j =+=+-v v ………………①与水平方向夹角有1039.8tan 10tθ-=……………………………②当t =时tan 0.262,1441'θθ==︒当t =时tan 0.718,3541'θθ=-=-︒（2）此时tan 1θ=, 由②得t =物体的高度22111030.759.80.7510.23(m)22yo y t gt =-=⨯-⨯⨯=v （3）在最高处2110m s ,n a g ρ-=⋅==v v得210.2m gρ==v （4）由对称性可知，落地点的曲率与抛射点的曲率相同. 由解图1-8得210cos cos 4.9(m s )20x n a a g gg θθ-=====⋅v v240082(m)4.9n a ρ===v1-9．汽车在半径为400m 的圆弧弯道上减速行驶，设在某一时刻，汽车的速率为110m s -⋅，切向加速度的大小为20.2m s -⋅.求汽车的法向加速度和总加速度的大小和方向. 分析：由某一位置的ρ、v 求出法向加速度n a ，再根据已知切向加速度τa 求出总加速度a 的大小和方向.解：法向加速度的大小222100.25(m s ),400n a ρ-===⋅v 方向指向圆心 总加速度的大小222220.20.250.32(m s )n a a a τ-=+=+=⋅由解图1-9得tan 0.8,3840'na a ταα===︒ 则总加速度与速度夹角9012840'θα=︒+=︒1-10. 质点在重力场中作斜上抛运动，初速度的大小为0v ，与水平方向成α角．求质点到达抛出点的同一高度时的切向加速度、法向加速度以及该时刻质点所在处轨迹的曲率半径（忽略空解图1-8解图1-9气阻力）．已知法向加速度与轨迹曲率半径之间的关系为2n a ρ=v .分析：在运动过程中，质点的总加速度 a g =.由于无阻力作用，所以回落到抛出点高度时， 质点的速度大小0=v v ，其方向与水平线夹角也是α.可求出n a ，如解图1-10所示.再根据法向加速度与轨迹曲率半径之间的关系2n a ρ=v ，解出曲率半径.解：切向加速度t sin a g a =法向加速度a g a n cos =因为2n a ρ=v ，所以220cos n a g ρα==v v1-11．在生物物理实验中用来分离不同种类的分子的超级离心机的转速为313.1410rad s -⨯⋅.在这种离心机的转子内，离轴10cm 远的一个大分子的向心加速度是重力加速度的几倍分析 根据定义可得向心加速度的大小2n a r ω=.解 所求倍数2222425244(610)0.1=410609.8rn r g g ωππ⨯⨯==⨯⨯1-12. 一质点在半径为0.10m 的圆周上运动，其角位置变化关系为324(rad)t θ=+.试求：(1) 在t =2s 时，质点的法向加速度和切向加速度大小各为多少； (2) 当切向加速度大小恰等于总加速度大小的一半时，θ值为多少 (3) 在什么时刻，切向加速度和法向加速度恰好大小相等分析 本题为物体作圆周运动的角坐标表示下的第一类运动学问题，求导可得到角速度和角加速度，再由角量与线量的关系求得切向加速度t a 和法向加速度n a .解图1-10解 (1) 角速度和角加速度分别为2d 12d t t θω== d 24d t tωβ==法向加速度22222n 0.1(12) 2.3010(m s )a r t ω-==⨯=⨯⋅切向加速度2t d 2.4 4.8(m s )d a r t tβ-====⋅v (2) 由 t /2a a =，2222t n t 4a a a a =+= 得22t n3a a = 22243(24)(12)r t r t =33t = 332424 3.15(rad)t θ=+=+⨯= (3) 由 n t a a =，即22(12)24r t rt =，解得 0.55s t =1-13．离水面高度为h 的岸上有人用绳索拉船靠岸，人以恒定速率0v 拉绳子，求当船离岸的距离为s 时，船的速度和加速度的大小.分析：收绳子速度和船速是两个不同的概念.小船速度的方向为水平方向，由沿绳的分量与垂直绳的分量合成，沿绳方向的收绳的速率恒为0v .可以由0v 求出船速v 和垂直绳的分量1v .再根据21n a ρ=v 关系，以及n a 与a关系来求解a .解： 如解图1-13，小船速度沿绳的分量20=v v ，船速2sec θ=v v当船离岸的距离为s 时，船速22s h s+=v v 解图1-13船速垂直绳的分量012tan hsθ==v v v 则船的法向加速度2211n 2222cos a a as hs hθρ====++v解得2203h a s =v1-14. A 船以130km h -⋅的速度向东航行，B 船以145km h -⋅的速度向正北航行，求A 船上的人观察到的B 船的速度和航向.分析：关于相对运动，必须明确研究对象和参考系.同时要明确速度是相对哪个参照系而言.画出速度矢量关系图求解. 解：如解图1-14所示11A B 30km h ,45km h i j --=⋅=⋅v vB 船相对于A 船的速度1BA B A 4530(km h )j i -=-=-⋅v v v则速度大小221BA B A 54.1(km h )-=+=⋅v v v方向BAarctan56.3θ==︒v v ，既西偏北56.3︒1-15. 一个人骑车以118km h -⋅的速率自东向西行进时，看见雨滴垂直落下，当他的速率增加至136km h -⋅时，看见雨滴与他前进的方向成120°角下落，求雨滴对地的速度.解图1-14分析：这是一个相对运动的问题，雨对地的速度不变，画出速度矢量图，就可根据几何关系求解.解：如解图1-15所示，r v 为雨对地的速度， 12,p p v v 分别为第一次，第二次人对地的速度，12,rp rp v v 分别为第一次，第二次雨对人的速度，120θ=︒由三角形全等的知识，可知18012060αβ==︒-︒=︒三角形ABC 为正三角形，则2136km h r p -==⋅v v ，方向竖直向下偏西30︒.1-16如题图1-16所示，一汽车在雨中以速率1v 沿直线行驶，下落雨滴的速度方向偏于竖直方向向车后方θ角，速率为2v ，若车后有一长方形物体，问车速为多大时，此物体刚好不会被雨水淋湿分析：相对运动问题，画矢量关系图，由几何关系求解.解：如解图1-16（a ），车中物体与车蓬之间的夹角 arctan l h α=若θ＞α，无论车速多大，物体均不会被雨水淋湿若θ＜α，如解图1-16（b ）则有||||||BC AC AB ==-v 车=sin sin cos tan sin αθθαθ-=-v v v v 雨雨雨雨对车又2=v v 雨则2cos (sin )l h θθ=-v v 车题图1-16 解图1-16 解图1-151-17 人能在静水中以11.10m s -⋅的速度划船前进.今欲横渡一宽为m 10.0013⨯、水流速度10.55m s -⋅的大河.他若要从出发点横渡该河而到达正对岸的一点，那么应如何确定划行方向到达正对岸需多少时间分析 船到达对岸所需时间由船相对于岸的速度v 决定，而v 由水流速度u 和船在静水中划行速度'v 确定.画出矢量图由几何关系求解.解 根据解图1-17，有'v =u+v ，解得 0.551sin 1.102u α==='v 030α= 即应沿与正对岸方向向上游偏300方向划行.船到达正对岸所需时间为 31.0510s cos d d t α===⨯'v v 1-18．一升降机以2g 的加速度从静止开始上升，在末时有一小钉从顶板下落，若升降机顶板到底板的距离h=2.0m ，求钉子从顶板落到底板的时间t , 它与参考系的选取有关吗分析：选地面为参考系，分别列出螺钉与底板的运动方程，当螺丝落到地板上时，两物件的位置坐标相同，由此可求解.解：如解图1-18建立坐标系，y 轴的原点取在钉子开始脱落时升降机的底板处，此时，升降机、钉子速度为0v ,钉子脱落后对地的运动方程为21012y h t gt =+-v 升降机底板对地的运动方程为220122y t gt =+⨯v 且钉子落到底板时，有12=y y ，即2012h t gt +-=v 20t gt +v αuv 'v 解图1-17解图1-18解出t0.37s t与参考系的选取无关.。

新编基础物理学》下册习题解答和分析题9-2解图《新编基础物理学》下册习题解答和分析第九章习题解答9-1 两个小球都带正电，总共带有电荷55.010C -⨯,如果当两小球相距2.0m 时，任一球受另一球的斥力为1.0N.试求总电荷在两球上是如何分配的？ 分析：运用库仑定律求解。

解：如图所示，设两小球分别带电q 1，q 2则有q 1+q 2=5.0×10-5C ① 由题意，由库仑定律得：912122091014π4q q q q F r ε⨯⨯⨯=== ②由①②联立得：5152 1.210C3.810Cq q --⎧=⨯⎪⎨=⨯⎪⎩ 9-2 两根6.0×10-2m 长的丝线由一点挂下，每根丝线的下端都系着一个质量为0.5×10-3kg 的小球.当这两个小球都带有等量的正电荷时，每根丝线都平衡在与沿垂线成60°角的位置上。

求每一个小球的电量。

分析：对小球进行受力分析，运用库仑定律及小球平衡时所受力的相互关系求解。

解：设两小球带电q 1=q 2=q ，小球受力如图所示220cos304πq F T R ε==︒ ①sin30mg T =︒②联立①②得：2o 024tan30mg R qπε= ③223sin 606103310(m)r l --=︒=⨯⨯=⨯ 其中2R r =代入③式，即： q =1.01×10-7C 9-3 电场中某一点的场强定义为0F E q =，若该点没有试验电荷，那么该点是否存在场强？为什么？答：若该点没有试验电荷，该点的场强不变.因为场强是描述电场性质的物理量，仅与场源电荷的分布及空间位置有关，题9-1解图与试验电荷无关，从库仑定律知道，试验电荷q 0所受力F与q 0成正比，故0F E q =是与q 0无关的。

9-4 直角三角形ABC 如题图9-4所示，AB 为斜边，A 点上有一点荷91 1.810C q -=⨯，B 点上有一点电荷92 4.810C q -=-⨯，已知BC =0.04m ，AC =0.03m ，求C 点电场强度E的大小和方向(cos37°≈0.8, sin37°≈0.6). 分析：运用点电荷场强公式及场强叠加原理求解。

新编物理学答案【篇一：新编基础物理学上册7-8单元课后答案】瓶的容积为32l,瓶内充满氧气时的压强为130atm。

若每小时用的氧气在1atm下体积为400l。

设使用过程温度保持不变，当瓶内压强降到10atm时，使用了几个小时? 分析氧气的使用过程中，氧气瓶的容积不变，压强减小。

因此可由气体状态方程得到使用前后的氧气质量。

进而将总的消耗量和每小时的消耗量比较求解。

解已知p1?130atm,p2?10atm,p3?1atm; v1?v2?v?32l,v3?400l。

质量分别为m1，m2，m3,由题意可得:m11 rt ○mm2 pv?2rt ○2mm2mpv?1所以一瓶氧气能用小时数为:n??130?10??32?9.6小时 m1?m2pv?pv2?1?m3pv1.0?400337-2 一氦氖气体激光管，工作时管内温度为 27?c。

压强为2.4mmhg，氦气与氖气得压强比是7:1.求管内氦气和氖气的分数密度.分析先求得氦气和氖气各自得压强，再根据公式p?nkt求解氦气和氖气的分数密度。

解:依题意, n?n氦?n氖， p?p氦?p氖?所以p?氦2.1?1.013?105pa,7602.4?1.013?105pa；p氦:p氖?7:1 7600.3p氖??1.013?105pa,760根据 p?nkt 所以 n氦? n氖?p氦ktp氖kt??1.013?105??1.38?10?23?300?6.76?1022m?39.66?1021m?37-3 氢分子的质量为3.3?10?24克。

如果每秒有1023个氢分子沿着与墙面的法线成45?角的方向以105厘米/秒的速率撞击在面积为2.0cm2的墙面上,如果撞击是完全弹性的,求这些氢分子作用在墙面上的压强.分析压强即作用在单位面积上的平均作用力，而平均作用力由动量定理求得。

解:单位时间内作用在墙面上的平均作用力为:f?2mvcos45?np?f2mvcos45?n??ss2?3.3?10?27?105?10?22?10?41023?2330pa7-4 一个能量为1012ev的宇宙射线粒子,射入一氖气管中,氖管中含有氦气0.10mol,如果宇宙射线粒子的能量全部被氖气分子所吸收而变为热运动能量,问氖气的温度升高了多少? 分析对确定的理想气体，其分子能量是温度的单值函数，因此能量的变化对应着温度的变化。