2.2传递函数
- 格式:ppt
- 大小:635.00 KB
- 文档页数:29




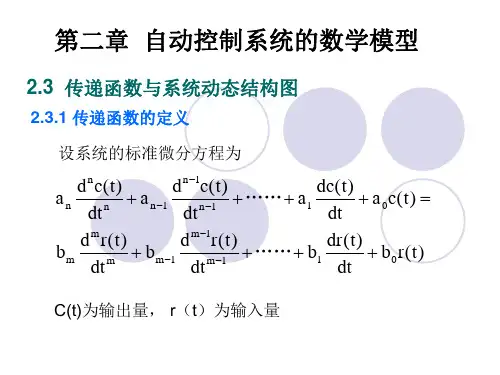


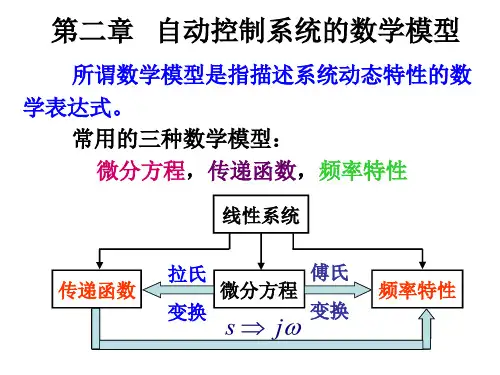


线性微分方程可以归纳其一般的表达式为:1011110111()()()...........()()()()...........()n n n n n n m m m m m m d c t d c t d c t a a a a c t dt dt dtd r t d r t d r t b b b b r t dt dt dt------++++=++++ (7.1)式子中,()c t 是输出量,()r t 是输入量。
0a ,1a ,1n a -…….. n a 和0b ,1b ,…….. 1m b -,m b 都是由系统结构决定的常数。
微分方程建立以后,便可以由此为基础分析控制系统的性能。
最直接的办法就是求解微分方程得到系统的输出响应,但是微分方程特别是高阶微分方程的求解以及参数性能分析是十分困难的,可以利用拉普拉斯变换来简化对微分方程的求解,并利用拉氏变换将微分方程这种时间域中的数学模型转化成复数s 域内的数学模型——传递函数。
传递函数不仅可以表征系统的动态特征,而且还可以用来研究系统的结构或参数变化对系统的影响。
在后面的章节中将要介绍的频率法和轨迹法,都是以传递函数为基础建立起来的,传递函数是经典控制理论中最主要和最基本的概念。
7.1传递函数的定义一般线性定常系统的微分方程课用式7.1表示,对于实际的控制系统,n 不小于m ,即n ≥m 。
设r(t)以及其各阶导数在t=0时刻的值均为0,则对式(7.1)中的各项分别求拉氏变换,可得: 10111011(......)()(..........)()n n n n m m m m a s a s a s a c s b s b s b s b r s ----++++=+++(7.2) 式子中,C(s)=L[c(t)],R(S)=L[R(t)]。
由式(2.1)可得: 10111011..........()()()......m m m m n n n n b s b s b s b C s G s R s a s a s a s a ----+++==++++ (7.3)2.2 传递函数的性质1)传递函数是复变量s 的有理真分式,具有复变函数的所有性质,只适用于线性定常系统,其分母多项式中s 的最高幂称为系统的阶次,一般分母多项式中s 的最高次方总大于或等于分钟多项式中的s 的最高次方。

RLC互连线和传输线模型的传递函数递推方法及其模型简化1. RLC互连线模型在电路中,当信号传输的距离较长或频率较高时,信号的传输线上的电感、电容和电阻等元件的影响就会变得非常重要。
为了更准确地描述信号在互连线上的传输特性,我们可以使用RLC互连线模型。
1.1 RLC互连线模型的基本结构RLC互连线模型由电感L、电阻R和电容C构成,如下图所示:+------- L --------+-------- R -------+| | |Vin --+ | +-- Vout| | |+------- C --------+-------- R -------+其中,Vin为输入电压,Vout为输出电压。
1.2 RLC互连线模型的传递函数传递函数是描述输入信号和输出信号之间关系的函数。
对于RLC互连线模型,其传递函数可以通过分析电路的响应来得到。
设输入电压Vin的函数表示为Vin(t),输出电压Vout的函数表示为Vout(t),则传递函数H(s)定义为:H(s) = Vout(s) / Vin(s)其中,s为复频域变量。
1.3 RLC互连线模型的传递函数递推方法RLC互连线模型的传递函数递推方法是一种通过递推关系来计算传递函数的方法。
具体步骤如下:1.假设输入电压Vin为单位冲激函数δ(t),即Vin(t) = δ(t)。
2.根据单位冲激函数的性质,可以得到输出电压Vout的函数表示为Vout(t)= h(t),其中h(t)为单位冲激响应函数。
3.对单位冲激响应函数h(t)进行拉普拉斯变换,得到H(s) = H(0) / (s + p),其中H(0)为初始条件,p为极点。
4.根据电路的物理特性和边界条件,确定初始条件H(0)和极点p的值。
5.根据递推关系,计算传递函数H(s)的值。
1.4 RLC互连线模型的模型简化在实际应用中,RLC互连线模型可能会过于复杂,不便于分析和计算。
为了简化模型,我们可以采用特定函数来近似描述传递函数。