数字图像处理实验2冈萨雷斯.
- 格式:doc
- 大小:266.00 KB
- 文档页数:7

数字图像处理冈萨雷斯第二版答案数字图像处理冈萨雷斯第二版答案【篇一:数字图像处理第三版 (冈萨雷斯,自己整理的2)】特数。
通常的传输是以一个开始比特,一个字节(8 比特)的信息和一个停止比特组成的包完成的。
基于这个概念回答以下问题:(b) 以750k 波特 [这是典型的电话dsl(数字用户线)连接的速度]传输要用多少时间?2.两个图像子集s1和s2图下图所示。
对于v={1},确定这两个子集是(a)4-邻接,(b)8-邻接,(c)m-邻接。
a) s1 和s2 不是4 连接,因为q 不在n4(p)集中。
(b) s1 和s2 是8 连接,因为q 在n8(p)集中。
(c) s1 和s2 是m 连接,因为q 在集合nd(p)中,且n4(p)∩ n4(q)没有v 值的像素3. 考虑如下所示的图像分割(a) 令v={0,1}并计算p 和q 间的4,8,m 通路的最短长度。
如果在这两点间不存在特殊通路,试解释原因。
(b) 对于v={1,2}重复上题。
解:(a) 当v={0,1}时,p 和q 之间不存在4 邻接路径,因为不同时存在从p 到q 像素的4 毗邻像素和具备v 的值,如图(a)p 不能到达q。
8 邻接最短路径如图(b),最短长度为4。
m邻接路径如图(b)虚线箭头所示,最短长度为5。
这两种最短长度路径在此例中均具有唯一性。
(b) 当v={1, 2}时,最短的4 邻接通路的一种情况如图(c)所示,其长度为6,另一种情况,其长度也为6;8 邻接通路的一种情况如图(d)实线箭头所示,其最短长度为4;m 邻接通路的一种情况如图(d)虚线箭头所示,其最短长度为6.或解: (1) 在v={0,1}时,p和q之间通路的d4距离为∞,d8距离为4,dm距离为5。
(2) 在v={1,2}时,p和q之间通路的d4距离为6,d8距离为4,dm距离为6。
4为什么一般情况下对离散图像的直方图均衡化并不能产生完全平坦的直方图?【因为同一个灰度值的各个象素没有理由变换到不同灰度级,所以数字图像的直方图均衡化的结果一般不能得到完全均匀分布的直方图,只是近似均匀的直方图。

For personal use only in study and research; not for commercial use 第二章2.1(第二版是0.2和1.5*1.5的矩形,第三版是0.3和1.5圆形)对应点的视网膜图像的直径x 可通过如下图题2.1所示的相似三角形几何关系得到,即()()01702302.x .d =解得x=0.06d 。
根据2.1 节内容,我们知道:如果把中央凹处想象为一个有337000 个成像单元的圆形传感器阵列,它转换成一个大小25327.⨯π成像单元的阵列。
假设成像单元之间的间距相等,这表明在总长为1.5 mm (直径) 的一条线上有655个成像单元和654个成像单元间隔。
则每个成像单元和成像单元间隔的大小为s=[(1.5 mm)/1309]=1.1×10-6 m 。
如果在中央凹处的成像点的大小是小于一个可分辨的成像单元,在我们可以认为改点对于眼睛来说不可见。
换句话说, 眼睛不能检测到以下直径的点:m .d .x 61011060-⨯<=,即m .d 610318-⨯<2.2 当我们在白天进入一家黑暗剧场时,在能看清并找到空座时要用一段时间适应。
2.1节描述的视觉过程在这种情况下起什么作用?亮度适应。
2.3 虽然图2.10中未显示,但交流电的却是电磁波谱的一部分。
美国的商用交流电频率是77HZ 。
问这一波谱分量的波长是多少?光速c=300000km/s ,频率为77Hz 。
因此λ=c/v=2.998 * 108(m/s)/77(1/s) = 3.894*106m = 3894 Km. 2.5根据图2.3得:设摄像机能看到物体的长度为x (mm),则有:500/x=35/14; 解得:x=200,所以相机的分辨率为:2048/200=10;所以能解析的线对为:10/2=5线对/mm. 2.7 假设中心在(x0,y0)的平坦区域被一个强度分布为:])0()0[(22),(y y x x Ke y x i -+--= 的光源照射。

数字图像处理(冈萨雷斯版,第二版)课后习题及解答(部分)Ch 22.1使用2.1节提供的背景信息,并采用纯几何方法,如果纸上的打印点离眼睛0.2m 远,估计眼睛能辨别的最小打印点的直径。
为了简明起见,假定当在黄斑处的像点变得远比视网膜区域的接收器(锥状体)直径小的时候,视觉系统已经不能检测到该点。
进一步假定黄斑可用1.5mm × 1.5mm 的方阵模型化,并且杆状体和锥状体间的空间在该阵列上的均匀分布。
解:对应点的视网膜图像的直径x 可通过如下图题2.1所示的相似三角形几何关系得到,即()()220.20.014d x = 解得x =0.07d 。
根据2.1节内容,我们知道:如果把黄斑想象为一个有337000个成像单元的正方形传感器阵列,它转换成一个大小580×580成像单元的阵列。
假设成像单元之间的间距相等,这表明在总长为1.5 mm 的一条线上有580个成像单元和579个成像单元间隔。
则每个成像单元和成像单元间隔的大小为s =[(1.5 mm)/1159]=1.3×10-6 m 。
如果在黄斑上的成像点的大小是小于一个可分辨的成像单元,在我们可以认为改点对于眼睛来说不可见。
换句话说,眼睛不能检测到以下直径的点:x =0.07d<1.3×10-6m ,即d <18.6×10-6 m 。
下图附带解释:因为眼睛对近处的物体聚焦时,肌肉会使晶状体变得较厚,折射能力也相对提高,此时物体离眼睛距离0.2 m ,相对较近。
而当晶状体的折射能力由最小变到最大时,晶状体的聚焦中心与视网膜的距离由17 mm 缩小到14 mm ,所以此图中选取14mm(原书图2.3选取的是17 mm)。
图 题2.12.2 当在白天进入一个黑暗的剧场时,在能看清并找到空座位时要用一段时间适应,2.1节(视觉感知要素)描述的视觉过程在这种情况下起什么作用?解:根据人眼的亮度适应性,1)由于户外与剧场亮度差异很大,因此当人进入一个黑暗的剧场时,无法适应如此大的亮度差异,在剧场中什么也看不见;2)人眼不断调节亮度适应范围,逐渐的将视觉亮度中心调整到剧场的亮度范围,因此又可以看见、分清场景中的物体了。

1. 课程设计目的1、提高分析问题、解决问题的能力,进一步巩固数字图像处理系统中的基本原理与方法。
2、熟悉掌握一门计算机语言,可以进行数字图像的应用处理的开发设计。
2.课程设计内容及实现2.1、网页安全色(Web-Safe Colors)为了完成这项工作,必须找到一个合适的程序,这个程序可以把指定的JPG图像生成RGB元素的图像。
例如,MATLAB的图像处理工具箱可以实现这一点,但你也可以使用图像编辑程序像Adobe的Photo-Shop或Corel的Photo-Paint。
为了实现把图像转换为RGB 这一目标,也可以手动修改。
(a)编写计算机程序,把任意的RGB彩色图像转换到Web安全的RGB图像(Web安全颜色定义见图6.10)。
(b)下载图像图6.8,转换为网络安全色的RGB彩色图像。
图6.8是JPG格式,所以结果返回也为JPG(请看本项目的开始注释)。
解释你的结果和图6.8之间的差异。
2.1.1程序清单:I=imread('Fig6.08.jpg');subplot(121);imshow(I);title('原图');I1=fix((I/51)*51);subplot(122);imshow(I1);title('web-safe colors');2.1.2运行结果如图1图1 网页安全色结果分析:结果图出现明显的方格,每个方格就是一个网页安全色,方格内的颜色一致。
原图则是普通的RGB,假使在原图的相同区域划分出和结果图相对应的方格,则此方格里的颜色是一个渐变的颜色,并非同一种颜色。
2.2、伪彩色图像处理(Pseudo-Color Image Processing )(a)实现图6.23的特性,你可以为输入图像指定两个范围的灰度值,然后你的程序将输出的RGB图像,它的像素有一个指定的颜色,对应于输入图像的一个范围的灰度级,RGB 图像中剩余的像素具有和输入图像相同的灰度。
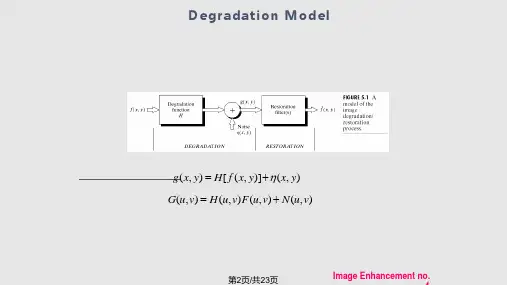



《数字图像处理》实验指导书实验一、空域图像处理一、实验目的1熟悉CCS集成开发环境的操作和基本功能;2熟悉MATLAB基本图像操作;3结合实例学习如何在程序中增加图像处理算法;4理解和掌握图像的线性变换和直方图均衡化的原理和应用;5了解平滑处理的算法和用途,学习使用均值滤波、中值滤波和拉普拉斯锐化进行图像增强处理的程序设计方法;6 了解噪声模型及对图像添加噪声的基本方法。
二、实验原理1 灰度线性变换就是将图像中所有点的灰度按照线性灰度变换函数进行变换。
2 直方图均衡化通过点运算将输入图像转换为在每一级上都有相等像素点数的输出图像。
按照图像概率密度函数PDF的定义:通过转换公式获得:3 均值(中值)滤波是指在图像上,对待处理的像素给定一个模板,该模板包括了其周围的临近像素。
将模板中的全体像素的均值(中值)来代替原来像素值的方法。
4 拉普拉斯算子如下:拉普拉斯算子首先将自身与周围的8个像素相减,表示自身与周围像素的差异,再将这个差异加上自身作为新像素的灰度。
三、实验步骤1 启动MATLAB程序,对图像文件分别进行灰度线性变换、直方图均衡化、均值滤波、中值滤波和拉普拉斯锐化操作;添加噪声,重复上述过程观察处理结果。
2 记录和整理实验报告四、实验仪器1计算机;2 MATLAB程序;3记录用的笔、纸。
五、实验报告内容1叙述实验过程;2提交实验的原始图像和结果图像。
六、思考题1.设定不同的斜率值和截距,显示效果会怎样?2.直方图均衡化是什么意思?它的主要用途是什么?3. 均值(中值)滤波的模板大小对处理效果有什么影响?基本函数:图像读入:imread图像显示:imshow计算直方图:imhist直方图均衡化:histeq添加噪声:imnoise滤波器定义:fspecial中值滤波:medfilt2实验二、图像的傅立叶变换一、实验目的1了解图像变换的意义和手段;2熟悉傅里叶变换的基本性质;3熟练掌握FFT方法及应用;4通过实验了解二维频谱的分布特点;5通过本实验掌握利用MATLAB编程实现数字图像的傅立叶变换及滤波锐化和复原处理;6 了解理想、巴特沃兹、高斯等不同滤波器的结构及滤波效果。


1. 数字数据传输通常用波特率度量,其定义为每秒钟传输的比特数。
通常的传输是以一个开始比特,一个字节(8 比特)的信息和一个停止比特组成的包完成的。
基于这个概念回答以下问题:(a) 用56K 波特的调制解调器传输一幅1024×1024、256 级灰度的图像需要用几分钟?(b) 以750K 波特[这是典型的电话DSL(数字用户线)连接的速度]传输要用多少时间?解:(a)T=M/56000=(1024×1024)×(8+2)/56000=187.25s=3.1min(b) T=M/56000=(1024×1024)×(8+2)/750000=14s2.两个图像子集S1和S2图下图所示。
对于V={1},确定这两个子集是(a)4-邻接,(b)8-邻接,(c)m-邻接。
a) S1 和S2 不是4 连接,因为q 不在N4(p)集中。
(b) S1 和S2 是8 连接,因为q 在N8(p)集中。
(c) S1 和S2 是m 连接,因为q 在集合N D(p)中,且N4(p)∩ N4(q)没有V 值的像素3. 考虑如下所示的图像分割(a) 令V={0,1}并计算p 和q 间的4,8,m 通路的最短长度。
如果在这两点间不存在特殊通路,试解释原因。
(b) 对于V={1,2}重复上题。
解:(a) 当V={0,1}时,p 和q 之间不存在4 邻接路径,因为不同时存在从p 到q 像素的4 毗邻像素和具备V 的值,如图(a)p 不能到达q。
8 邻接最短路径如图(b),最短长度为4。
m邻接路径如图(b)虚线箭头所示,最短长度为5。
这两种最短长度路径在此例中均具有唯一性。
(b) 当V={1, 2}时,最短的4 邻接通路的一种情况如图(c)所示,其长度为6,另一种情况,其长度也为6;8 邻接通路的一种情况如图(d)实线箭头所示,其最短长度为4;m 邻接通路的一种情况如图(d)虚线箭头所示,其最短长度为6.或解: (1) 在V={0,1}时,p和q之间通路的D4距离为∞,D8距离为4,Dm距离为5。
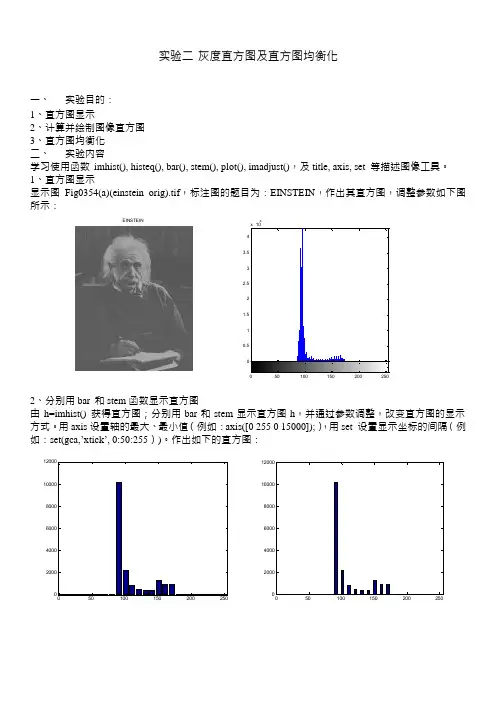
实验二 灰度直方图及直方图均衡化一、实验目的:1、直方图显示2、计算并绘制图像直方图3、直方图均衡化 二、 实验内容学习使用函数 imhist(), histeq(), bar(), stem(), plot(), imadjust(),及 title, axis, set 等描述图像工具。
1、直方图显示显示图 Fig0354(a)(einstein_orig).tif ,标注图的题目为:EINSTEIN ,作出其直方图,调整参数如下图 所示:EINSTEIN42、分别用 bar 和 stem 函数显示直方图由 h=imhist() 获得直方图;分别用 bar 和 stem 显示直方图 h ,并通过参数调整,改变直方图的显示 方式。
用 axis 设置轴的最大、最小值(例如:axis([0 255 0 15000]);),用 set 设置显示坐标的间隔(例 如:set(gca,’xtick ’, 0:50:255))。
作出如下的直方图:12000100008000600040002000501001502002503、用 plot 函数显示直方图 要求同 2.120001000080006000400020000 050 100 150 200 250 3004、用 imadjust() 函 数 调 整 图 像 对 比 度 , 并 用 imhist() 查 看 调 整 前 后 直 方 图 的 变 化 。
43 . 2 . 1 . 0 . 05、用 histeq() 进行直方图均衡化,并用 imhist() 查看均衡化前后直方图的变化。
43.5 3 2.52 1.5 1 0.50 4三、 实验要求将本实验的 10 个图用 MATLAB 显示到屏幕上。
程序:i=imread('Fig0354(a)(einstein_orig).tif'); imshow(i);title('EINSTEIN');figure; imhist(i);title('直方图');axis([0 255 0 4.5*10^4])h=imhist(i);h1=h(1:10:256); figure;x=1:10:256; bar(x,h1); title('bar');axis([0 255 0 15000]); set(gca,'xtick', 0:50:255);figure;bar(x,h1,0.5); title('bar2');figure;stem(x,h1); title('stem');axis([0 255 0 15000]);figure; plot(x,h1); title('plot');axis([0 255 0 15000]);i2=imadjust(i,[0.25 0.75 ],[0,1]); figure;imshow(i2);title('调整对比度');figure;imhist(i2);axis([0 255 0 4.5*10^4]);title('imadjust后直方图');i3=histeq(i,256);figure;imshow(i3);title('直方图均衡化');figure;imhist(i3);axis([0 255 0 4.5*10^4]);title('直方图均衡化后的直方图')。
实验二灰度直方图及直方图均衡化
一、
实验目的:
1、直方图显示
2、计算并绘制图像直方图
3、直方图均衡化二、实验内容
学习使用函数 imhist(, histeq(, bar(, stem(, plot(, imadjust(,及 title, axis, set 等描述图像工具。
1、直方图显示
显示图 Fig0354(a(einstein_orig.tif,标注图的题目为:EINSTEIN ,作出其直方图,调整参数如下图所示:
EINSTEIN
4
2、分别用 bar 和 stem 函数显示直方图
由 h=imhist( 获得直方图;分别用 bar 和 stem 显示直方图 h ,并通过参数调整,改变直方图的显示方式。
用 axis 设置轴的最大、最小值(例如:axis([0 255 0 15000];),用 set 设置显示坐标的间隔(例如:set(gca,’xtick ’, 0:50:255)。
作出如下的直方图:
00
50
100
150
200
250
3、用 plot 函数显示直方图要求同 2.
12000
1000080006000400020000 0
50 100 150 200 250 300
4、用 imadjust( 函数调整图像对比度,并用 imhist( 查看调整前后直方图的变化。
3 . 2 . 1 . 0 . 4
5、用 histeq( 进行直方图均衡化,并用 imhist( 查看均衡化前后直方图的变化。
4
三、实验要求
将本实验的 10 个图用 MATLAB 显示到屏幕上。
程序:
i=imread('Fig0354(a(einstein_orig.tif'; imshow(i; title('EINSTEIN';
figure; imhist(i;
title('直方图';
axis([0 255 0 4.5*10^4]
h=imhist(i;
h1=h(1:10:256; figure;
x=1:10:256; bar(x,h1; title('bar';
axis([0 255 0 15000]; set(gca,'xtick', 0:50:255; figure;
bar(x,h1,0.5; title('bar2';
figure;
stem(x,h1; title('stem';
axis([0 255 0 15000];
figure; plot(x,h1; title('plot';
axis([0 255 0 15000];
i2=imadjust(i,[0.25 0.75 ],[0,1]; figure;
imshow(i2;
title('调整对比度';
figure; imhist(i2;
axis([0 255 0 4.5*10^4]; title('imadjust后直方图'; i3=histeq(i,256; figure;
imshow(i3;
title('直方图均衡化';
figure; imhist(i3;
axis([0 255 0 4.5*10^4];
title('直方图均衡化后的直方图'。