按时间抽取的基2FFT算法分析

常用FFT 算法总结一、DFT 及IDFT 的定义对于N 点有限长序列)(n x ，其DFT 及IDFT 定义如下： DFT ：∑-==10)()(N n nk N W n x k XIDFT ：∑-=-=1)(1)(N k nk NWk X Nn x其中，Np j p NeW/2π-=称为旋转因子，p 称为旋转因子的指数。

二、基2-FFT 算法 设序列)(n x 的长度N 满足MN2=，M 为自然数。

1、时间域抽取FFT （DIT-FFT ） （1）算法原理按n 的奇偶把)(n x 分解为两个N/2点的子序列：)12()()2()(21+==r x r x r x r x则)(n x 的DFT 为)()()12()2()(2112/0)12(12/02k X W k X Wr x Wr x k X kN N r k r NN r rk N+=++=∑∑-=+-=其中)(1k X 和)(2k X 分别为)(1r x 和)(2r x 的N/2点DFT 。

利用)(1k X 和)(2k X 的周期性，)(k X 可以表示为⎪⎩⎪⎨⎧-=++=)()()2()()()(2121k X W k X N k X k X W k X k X kN k N 上式表明一个N 点的DFT 可以用两个N/2点的DFT 来表示。

（2）运算量 当MN2=时，共有M 级蝶形，每级N/2个蝶形，每个蝶形有1次复数乘法2次复数加法。

复数乘法：NN M N mF2log22==复数加法：NN NM a F2log==NN NN NFFT m DFT m F F 222log2log 2)()(==（3）蝶形运算⎪⎩⎪⎨⎧-=+=----)()()()()()(1111j X W k X j X j X W k X k X m pN m m m pN m m m表示第m 级迭代，k 和j 表示数据所在的行数，12-+=m k j ，m M k p -⋅=2。

按时间抽取的基2FFT算法分析基2FFT算法是一种快速傅里叶变换算法，它通过将傅里叶变换的计算复杂度从O(n^2)降低到O(nlogn)，大大提高了傅里叶变换的效率。

基2FFT算法的核心思想是将一个长度为n的序列分成长度为n/2的两个子序列，并分别做傅里叶变换。

然后将两个子序列的傅里叶变换结果合并起来，得到原始序列的傅里叶变换结果。

具体来说，基2FFT算法的步骤如下：1.如果输入序列长度为1，则返回输入序列作为傅里叶变换结果。

2.将输入序列按奇偶位置分为两个子序列。

3.对两个子序列分别递归地应用基2FFT算法，得到它们的傅里叶变换结果。

4.根据蝶形算法，将子序列的傅里叶变换结果合并起来，得到原始序列的傅里叶变换结果。

基2FFT算法通过不断将序列分成两半的方式，将傅里叶变换的计算复杂度从O(n^2)降低到O(nlogn)。

在每一层递归中，需要进行O(n)次计算，而递归的层数为logn，因此总的时间复杂度为O(nlogn)。

基2FFT算法的关键之一是蝶形算法。

蝶形算法是一种合并子序列傅里叶变换结果的方法。

在每一层递归中，对于每个位置k，需要计算一个长度为n的序列上的k点DFT。

根据蝶形算法，可以将这个计算分成两个部分：计算序列中偶数位置上的点DFT和计算序列中奇数位置上的点DFT，并通过一些乘法和加法操作合并起来。

这样做可以大大减少计算量，提高计算效率。

基2FFT算法还可以通过多线程或并行处理来进一步提高效率。

由于基2FFT算法具有递归结构，可以将不同的递归层分配给不同的线程或处理器来并行进行计算，从而加快计算速度。

基2FFT算法在数字信号处理、图像处理、通信系统和科学计算等领域有着广泛的应用。

它的高效性和快速运算速度使得它成为处理大规模数据的重要工具。

综上所述，基2FFT算法通过将傅里叶变换的计算复杂度从O(n^2)降低到O(nlogn)，大大提高了傅里叶变换的效率。

它采用递归分治的思想，通过分解和合并操作来实现傅里叶变换的计算。

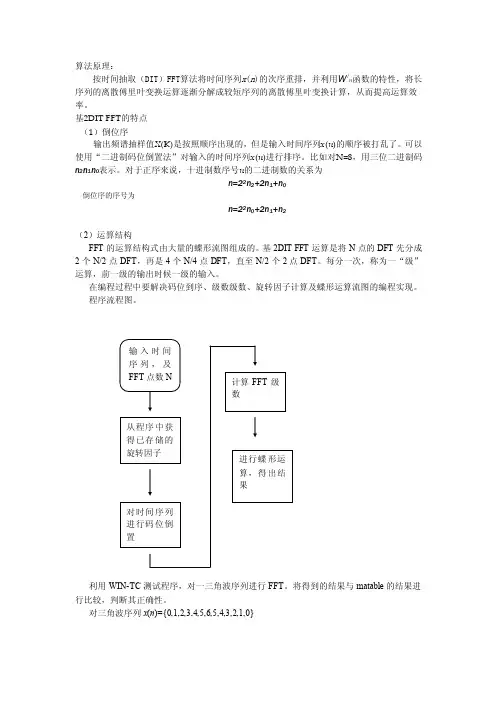
算法原理：按时间抽取（DIT）FFT算法将时间序列x(n)的次序重排，并利用W i n函数的特性，将长序列的离散傅里叶变换运算逐渐分解成较短序列的离散傅里叶变换计算，从而提高运算效率。

基2DIT FFT的特点（1）倒位序输出频谱抽样值X(K)是按照顺序出现的，但是输入时间序列x(n)的顺序被打乱了。

可以使用“二进制码位倒置法”对输入的时间序列x(n)进行排序。

比如对N=8，用三位二进制码n2n1n0表示。

对于正序来说，十进制数序号n的二进制数的关系为n=22n2+2n1+n0倒位序的序号为n=22n0+2n1+n2（2）运算结构FFT的运算结构式由大量的蝶形流图组成的。

基2DIT FFT运算是将N点的DFT先分成2个N/2点DFT，再是4个N/4点DFT，直至N/2个2点DFT。

每分一次，称为一“级”运算，前一级的输出时候一级的输入。

在编程过程中要解决码位到序、级数级数、旋转因子计算及蝶形运算流图的编程实现。

程序流程图。

利用WIN-TC测试程序，对一三角波序列进行FFT。

将得到的结果与matable的结果进行比较，判断其正确性。

对三角波序列x(n)={0,1,2,3,4,5,6,5,4,3,2,1,0}在WIN-TC进行128点FFT，得到前6个结果Matable仿真的前6个结果是XKN2 =Columns 1 through 636.0000 34.2084 -10.3770i 29.1007 -19.4445i 21.4292 -26.1115i 12.2946 -29.6817i 2.9501 -29.9525i前半段波形对比显示WIN-TC结果能保证小数点后2位的精度。

对方波序列x(n),长度为64，前32为1，幅值为1的序列在WIN-TC进行128点FFT，得到前6个结果Matable仿真的前6个结果是Columns 1 through 632.0000 20.8677 -19.8677i 1.0000 -20.3555i -6.2783 - 7.2783i 04.5539 - 3.5539i仿真波形对比显示WIN-TC结果能保证小数点后2位的精度。

FFT 算法程序及分析摘 要：《FFT 的算法程序分析》主要分析了按时间抽取（DIT)的快速傅立叶变换的基2FFT 算法，通过对基2FFT 算法的原理的分析及与DFT 算法运算量的比较，进一步推导出了基rFFT 算法，重点是基rFFT 算法的推导。

在具体的实例中，我们重点分析了FFT 过程中幅值大小与FFT 选用点数N 的关系,验证FFT 变换的可靠性,考察在FFT 中数据样本的长度与DFT 的点数对频谱图的影响。

关键字： 基2FFT 算法,基rFFT 算法，样本长度,选用点数要求：● 学习书上第六节的内容，自己编程实现FFT 算法 . ● 给出典型信号的时域和频域图，并加以分析。

● 可尝试实现分段卷积程序。

● 论文内容含原程序、运行结果，理论分析和典型信号时域图。

一．快速傅立叶变换(FFT ）简介离散傅立叶变换（DFT ）是信号分析与处理中的一种重要的变换。

因直接计算DFT 的计算量与变换区间长度N 的平方成正比，当N 较大时，计算量太大。

所以在快速傅立叶变换(FFT ）出现以前，直接用DFT 算法进行频谱分析和信号的实时处理是不切实际的。

1965年,库利（J.W.Cooley ）和图基(J.W.Tukey ）在《计算数学》杂志上发表了“机器计算傅立叶级数的一种算法”的文章，这是一篇关于计算DFT 的一种快速有效的计算方法的文章。

它的思路建立在对DFT 运算内在规律的认识之上。

这篇文章的发表使DFT 的计算量大大减少,并导致了许多计算方法的发现。

这些算法统称为快速傅立叶变换（Fast Fourier Transform),简称FFT.1984年,法国的杜哈梅尔（P.Dohamel ）和霍尔曼（H.Hollmann ）提出的分裂基快速算法，使运算效率进一步提高。

快速傅立叶变换（FFT ）不是一种新的变换,而是离散傅立叶变换（DFT ）的一种快速算法。

FFT 分成两大类,即按时间抽取（decimation —in —time,缩写为DIT ）法和按频率抽取（decimation —in —frequency ，缩写为DIF)法。

第四章 快速傅里叶变换有限长序列可以通过离散傅里叶变换(DFT)将其频域也离散化成有限长序列.但其计算量太大,很难实时地处理问题,因此引出了快速傅里叶变换(FFT). 1965年，Cooley 和Tukey 提出了计算离散傅里叶变换（DFT ）的快速算法，将DFT 的运算量减少了几个数量级。

从此，对快速傅里叶变换（FFT ）算法的研究便不断深入，数字信号处理这门新兴学科也随FFT 的出现和发展而迅速发展。

根据对序列分解与选取方法的不同而产生了FFT 的多种算法，基本算法是基２DIT 和基２DIF 。

FFT 在离散傅里叶反变换、线性卷积和线性相关等方面也有重要应用。

快速傅里叶变换（FFT ）是计算离散傅里叶变换（DFT ）的快速算法。

DFT 的定义式为)(k X =)()(10k R W n x N N n knN∑-= 在所有复指数值knN W 的值全部已算好的情况下，要计算一个)(k X 需要N 次复数乘法和N －1次复数加法。

算出全部N 点)(k X 共需2N 次复数乘法和)1(-N N 次复数加法。

即计算量是与2N 成正比的。

FFT 的基本思想：将大点数的DFT 分解为若干个小点数DFT 的组合，从而减少运算量。

N W 因子具有以下两个特性，可使DFT 运算量尽量分解为小点数的DFT运算：（1） 周期性：kN n N kn N nN k N W W W )()(++== （2） 对称性：k N N k NW W -=+)2/(利用这两个性质，可以使DFT 运算中有些项合并，以减少乘法次数。

例子：求当N ＝4时，X(2)的值)()]3()1([)]2()0([)()]3()1([)]2()0([)3()2()1()0()()2(04240464442404324对称性－＝周期性W x x x x W x x W x x W x W x W x W x W n x X n n +++++=+++==∑=通过合并，使乘法次数由4次减少到1次，运算量减少。

按时间抽取的FFT算法讲义1. 引言FFT（快速傅里叶变换）算法是一种高效的计算离散傅里叶变换（DFT）的方法，被广泛应用于信号处理、图像处理和科学计算等领域。

在本讲义中，我们将按照时间的顺序介绍FFT 算法的基本原理和步骤。

2. DFT的定义离散傅里叶变换（DFT）将离散时间域的信号转换为频域的复数信号，其定义为：X(k) = Σ[x(n) * exp(-j*2πnk/N)]其中，X(k) 表示频域的复数信号，x(n) 是输入的离散时间域信号，N 是信号的样本点数，k 是频率索引（0 ≤ k < N）。

3. DFT的计算DFT的直接计算方法是通过遍历所有频率索引 k，并计算上述公式。

但这种方法的时间复杂度为 O(N^2)，当样本点数较大时计算开销较大。

4. 快速傅里叶变换的思想FFT算法的核心思想是将 DFT 的计算过程分解为多个规模较小的 DFT 计算，以降低计算的复杂度。

具体而言，FFT算法利用了信号的周期性质，将输入信号划分为奇数索引和偶数索引的两个子序列，分别进行 DFT 的计算。

5. 雷德算法（Radix-2）雷德算法是FFT算法的一种常用实现方式，其基本思路是将DFT 计算递归地分解为规模为 M/2 的子问题，并利用旋转因子求解。

6. FFT算法的步骤（1）输入信号 x(n) 的样本点数为 N，其中 N 必须为2的幂次，否则需要进行零填充。

（2）将输入信号分解为奇数索引和偶数索引的两个子序列。

（3）对两个子序列分别进行 FFT 的计算。

（4）通过旋转因子和蝶形结构计算两个子序列的 DFT。

（5）将两个子序列的 DFT 结果合并得到整个信号的 DFT。

7. FFT算法的优势相较于直接计算DFT，FFT算法具有以下优势：- 时间复杂度为 O(NlogN)，较直接计算的 O(N^2) 更高效。

- 适用于样本点数为2的幂次的信号。

- 算法实现简单易懂，且可以通过并行计算进一步提高效率。