下载文档原格式
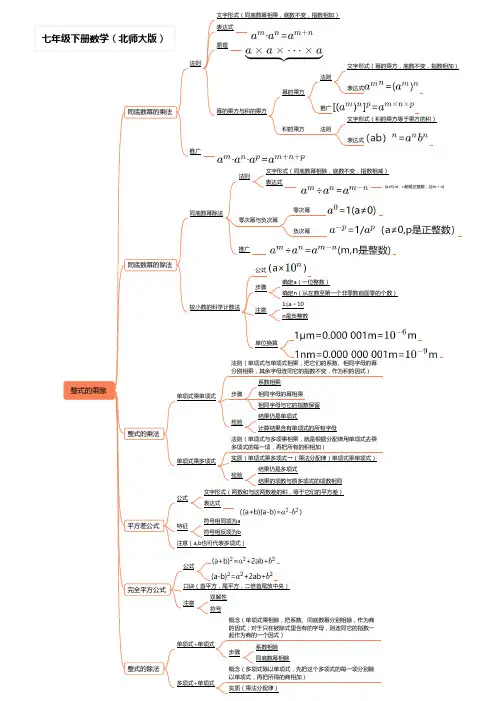
法则表达式推广文字形式（积的乘方等于乘方的积）表达式法则文字形式（同底数幂相除，底数不变，指数相减）表达式零次幂公式确定a（一位整数）确定n（从左数至第一个非零数前面零的个数）法则（单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式）符号相同项为a口诀（首平方，尾平方，二倍首尾放中央）双解性相交线与平行线两条直线的位置关系位置关系相交平行注意：同一平面内，不相交的两条直线平行定义（两条直线相交成四个角，如果有一个角是直角，那么称这两条直线互相垂直）垂直交点叫做垂足，一条直线称作另一条直线的垂线公理平面内，过一点有且只有一条直线与已知直线垂直角对顶角直线外一点与直线上各点连接的所有线段中，垂线段最短定义（∠1与∠2有公共顶点O，它们的两边互为反向延长线）定理对顶角相等补角余角公理证明（同角的补角相等）定义（两角之和180°）证明（∵∠1+∠2=180°∴∠1与∠2互为补角）定义（两角之和90°）证明（∵∠1+∠2=90°∴∠1与∠2互为余角同角或等角的补角相等同角或等角的余角相等探索直线平行的条件同位角在第三条直线同旁特点两条直线的同侧形状（“F”型）平行条件两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行简称（同位角相等，两直线平行）证明∵∠1=∠2公理∴l1∥l2（同位角相等，两直线平行）过直线外一点有且只有一条直线与已知直线平行平行于同一条直线的两直线平行（平行的传递性）内错角在第三条直线两侧特点两条直线的两侧形状（“Z”型）平行条件两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行证明简称（内错角相等，两直线平行）∵∠1=∠2∴l1∥l2（内错角相等，两直线平行）同旁内角在第三条直线同旁特点两条直线内部形状（“C”型）平行条件两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行证明简称（同旁内角互补，两直线平行）∵∠1+∠2=180°∴l1∥l2（同旁内角互补相等，两直线平行）平行线的性质两条直线被第三条直线所截，如果这两条直线平行那么同位角相等两条直线被第三条直线所截，如果这两条直线平行那么内错角相等两条直线被第三条直线所截，如果这两条直线平行，那么同旁内角互补用尺规作图概念（在变化过程中，数值发生改变的量）定义（由不在同一条直线上的三条线段首尾顺次相接所组成实质（八字对顶全等）轴对称图形（如果一个平面图行沿一条直线折叠后，直线两。
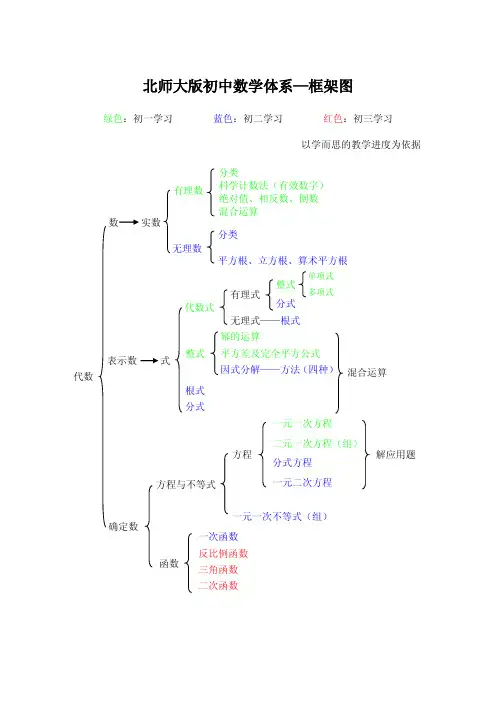
北师大版初中数学体系—框架图绿色：初一学习蓝色：初二学习红色：初三学习以学而思的教学进度为依据分类科学计数法（有效数字）绝对值、相反数、倒数混合运算幂的运算平方差及完全平方公式因式分解——方法（四种）分类平方根、立方根、算术平方根整式根式分式式实数有理数混合运算代数数表示数一元一次方程二元一次方程（组）分式方程一元二次方程解应用题方程一元一次不等式（组）方程与不等式一次函数反比例函数三角函数二次函数确定数函数代数式有理式无理式——根式整式分式单项式多项式无理数线——平行、相交、垂直角三角形四边形多边形——内/外角和平面直角坐标系轴对称图形/中心对称图形三视图，投影——平行投影、中心投影性质全等相似矩形正方形性质菱形圆各种判定图形变换等腰三角形等边三角形直角三角形——勾股定理轴对称——将军饮马，一次函数的对称，折叠平移——线、图（三角形等）旋转——三要素，图（三角形等），半角模型点与圆的位置关系线与圆的位置关系圆与圆的位置关系平行四边形梯形性质、概念（圆心角、圆周角等）垂径、切线长、切割线、弦切角、相交线定理扇形的面积（圆锥的侧面积）弧长性质特殊的平行四边形圆相关位置关系确定图变换图等腰梯形性质直角梯形图（图形及性质）几何性质、辅助线特殊梯形特殊三角形用“数、表示数、确定数”以及“图、确定图、变换图”这十四个字来概括初中代数与几何的方法是深圳学而思张明颂校长提出的。
统计与概率平均数、中位数、众数方差、标准差、极差频数、频率(频数分布直方图，频数分布表)统计图统计概率扇形统计图条形统计图折线统计图概念应用比例法列表法树状图确定事件不确定事件——等可能事件必然事件不可能事件常用判定特殊的线特殊三角形特殊四边形平行线角平分线垂直平分线切线等腰三角形等边三角形直角三角形三角形全等三角形相似平行四边形梯形矩形正方形菱形等腰梯形直角梯形。
