超静定问题
- 格式：ppt
- 大小：1.38 MB
- 文档页数：8
下载文档原格式
合集下载
材料力学-简单的超静定问题
2021/6/16
4
2021/6/16
5
2021/6/16
6
§6-2 拉压超静定问题
拉压变形时的胡克定律 l FN l EA
综合考虑变形的协调条件、虎克定律和静力 学平衡条件求解拉压超静定问题。
2021/6/16
7
例 已知1、2杆抗拉刚度为E1A1, 3杆抗拉刚度为E3A3， F的大小已知，求各杆内力。
13
2
l
A
A*
l3
FN 3l E3 A3
9
4、联解方程
FN1
2 cos
F
E 3 A3
E 1 A1 c o s 2
FN 3
1
2
F E 1 A1
cos3
E 3 A3
2021/6/16
10
装配应力的计算：超静定结构中由于加工误 差， 装配产生的应力。
平衡方程：
FN1 FN2
F N 3(F N 1F N 2)cos
超静定问题：若未知力的个数多于独立的平
衡方程的个数，仅用静力平衡方程便无法确定
全部未知力，这类问题为超静定问题。相应结
构称为超静定结构。
2021/6/16
2
超静定次数：未知力个数与独立平衡方程数之 差，也等于多余约束数。
多余约束：在结构上加上的一个或几个约束， 对于维持平衡来说是不必要的约束称多余约束。 对应的约束力称多余约束反力。
由于超静定结构能有效降低结构的内力及变 形，在工程上应用非常广泛。
2021/6/16
3
基本静定系：解除多余约束代之于未知力后的 结构。
●超静定问题的解法：综合考虑变形的几何相 容条件、物理关系和静力学平衡条件。
材料力学(I)第六章(配孙训方版)
4. 将补充方程与平衡方程联立求解得：
FN1 FN2
eEA l
1
1 2
EA
，
E3 A3
FN3
eE3 A3 l
1
1 E3 A3
2EA
所得结果为正，说明原先假定杆1,2的装配内力为拉
力和杆3的装配内力为压力是正确的。
载Me和“多余”未知力偶矩MB，如图b；它应满足的位移 相容条件为
BMe
BM B
注：这里指的是两个扭转角的绝对值相等。
33
材料力学Ⅰ电子教案
第六章 简单的超静定问题
3. 根据位移相容条件利用物理关系得补充方程：
Mea M Bl GI p GI p
由此求得“多余”未知力，亦即约束力偶矩MB为
材料力学Ⅰ电子教案
第六章 简单的超静定问题
在基本静定系上加
B
C
D
上原有荷载及“多
1
2
余”未知力
FN3
并使“多余”约束
A
A
处满足变形(位移)
ΔA'
相容条件
A'
ΔA
A
F
FN3
相当系统 (equivalent system)
6
材料力学Ⅰ电子教案
第六章 简单的超静定问题
B 1
C 2
FN3
第六章 简单的超静定问题
求算FN3需利用位移(变形)相容条件 (图a)
AA AA e
列出补充方程
FN3l3 E3 A3
FN3l1
2 E1 A1cos2
6-简单超静定问题
4、补充方程
FN 1l FN 3l cos EA cos EA FN 1 FN 3 cos 2
5、求解方程组得
FN 1 FN 2
F cos 2 1 2 cos 3
FN 3
F 1 2 cos 3
目 录
二、装配应力
构件的加工误差是难以避免的。对静定结构，加工误 差只是引起结构几何形状的微小变化，而不会在构件内引 起应力。但对静不定结构，加工误差就要在构件内引起应 力。这种由于装配而引起的应力称为装配应力。 装配应力是结构构件在载荷作用之前已具有的应力， 因而是一种初应力。
超静定结构中才有温度应力。
目 录
解题思路： 平衡方程:RA = RB 变形几何关系: 物理关系:
(t 时)
lT lF
lT l t
RB L
RB l lF EA
EA Lt
补充方程:
联立求解: RA RB EAt
EAt t Et A
目 录
一静定问题及超静定问题三基本静定系或相当系统是一个静定结构该结构上作用有荷载和多余约束力61超静定问题及其解法61超静定问题及其解法二多余约束及多余约束力在静定结构的基础上增加的约束
第六章
简单的超静定问题
§6–1 概述
§6–2 §6–3 §6–4 拉压超静定问题 扭转超静定问题 简单超静定梁
目的与要求：
M
max
WZ
32 M
d
max 3
76.4MPa
目 录
例题
结构如图示,设梁AB和CD的弯曲刚度EIz相同. 拉杆BC的拉压刚度EA为已知,求拉杆BC的轴力.
a
C
将杆CB移除，则AB,CD均为静定结构， 杆CB的未知轴力FN作用在AB,CD梁上。为1 D 次超静定。
FN 1l FN 3l cos EA cos EA FN 1 FN 3 cos 2
5、求解方程组得
FN 1 FN 2
F cos 2 1 2 cos 3
FN 3
F 1 2 cos 3
目 录
二、装配应力
构件的加工误差是难以避免的。对静定结构，加工误 差只是引起结构几何形状的微小变化，而不会在构件内引 起应力。但对静不定结构，加工误差就要在构件内引起应 力。这种由于装配而引起的应力称为装配应力。 装配应力是结构构件在载荷作用之前已具有的应力， 因而是一种初应力。
超静定结构中才有温度应力。
目 录
解题思路： 平衡方程:RA = RB 变形几何关系: 物理关系:
(t 时)
lT lF
lT l t
RB L
RB l lF EA
EA Lt
补充方程:
联立求解: RA RB EAt
EAt t Et A
目 录
一静定问题及超静定问题三基本静定系或相当系统是一个静定结构该结构上作用有荷载和多余约束力61超静定问题及其解法61超静定问题及其解法二多余约束及多余约束力在静定结构的基础上增加的约束
第六章
简单的超静定问题
§6–1 概述
§6–2 §6–3 §6–4 拉压超静定问题 扭转超静定问题 简单超静定梁
目的与要求：
M
max
WZ
32 M
d
max 3
76.4MPa
目 录
例题
结构如图示,设梁AB和CD的弯曲刚度EIz相同. 拉杆BC的拉压刚度EA为已知,求拉杆BC的轴力.
a
C
将杆CB移除，则AB,CD均为静定结构， 杆CB的未知轴力FN作用在AB,CD梁上。为1 D 次超静定。
超静定问题
2.4m
l ＞
B端必接触
C
40kN 1.2m
静力平衡方程
RA RB 100kN
B
变形协调条件为 l
RB
RA
A
60kN 2.4m 1.2m
轴 力 图
15kN
85kN
⊕ 25kN
C
40kN 1.2m
B
RA 103 1.2 ( RA 60) 103 2.4 RB 103 1.2 l 9 6 9 6 9 6 210 10 600 10 210 10 600 10 210 10 300 10
3
FC
A
FC
C
L
2
L
B
2
P
例题 6.10
当系统的温度升高时,下列结构中的____不会 A 产生温度应力.
A
B
C
D
例题 6.11
图示静不定梁承受集中力F和集中力偶Me作用, 梁的两端铰支,中间截面C处有弹簧支座.在下列 关于该梁的多余约束力与变形协调条件的讨论 中,___是错误的. C
RB
RA 85kN
RB 15kN
三、扭转超静定问题 扭转变形计算公式
Tl GI p
T ( x) dx GI p l
例3.两端固定的圆截面等直杆AB，在截面
C受外力偶矩m作用，求杆两端的支座反力
偶矩。
m
A C B
a
b
解：
A
m
ɑ
mA
C
B
b
m
静力平衡方程为： m A mB m 变形协调条件为：
5 ql 8
B
L
q
l ＞
B端必接触
C
40kN 1.2m
静力平衡方程
RA RB 100kN
B
变形协调条件为 l
RB
RA
A
60kN 2.4m 1.2m
轴 力 图
15kN
85kN
⊕ 25kN
C
40kN 1.2m
B
RA 103 1.2 ( RA 60) 103 2.4 RB 103 1.2 l 9 6 9 6 9 6 210 10 600 10 210 10 600 10 210 10 300 10
3
FC
A
FC
C
L
2
L
B
2
P
例题 6.10
当系统的温度升高时,下列结构中的____不会 A 产生温度应力.
A
B
C
D
例题 6.11
图示静不定梁承受集中力F和集中力偶Me作用, 梁的两端铰支,中间截面C处有弹簧支座.在下列 关于该梁的多余约束力与变形协调条件的讨论 中,___是错误的. C
RB
RA 85kN
RB 15kN
三、扭转超静定问题 扭转变形计算公式
Tl GI p
T ( x) dx GI p l
例3.两端固定的圆截面等直杆AB，在截面
C受外力偶矩m作用，求杆两端的支座反力
偶矩。
m
A C B
a
b
解：
A
m
ɑ
mA
C
B
b
m
静力平衡方程为： m A mB m 变形协调条件为：
5 ql 8
B
L
q
静定超静定判断及计算
目的和意义
目的
理解静定与超静定的概念，掌握判断方法，能够进行相应的计算。
意义
在实际工程中，正确判断结构和系统的静定或超静定状态对于确保结构安全、节约材料和降低成本具有重要意义。
02
静定与超静定的基本概念
静定结构的定义
静定结构
在任何外界影响下，其平衡位置都是稳定的 ，且在受到微小扰动后能自动恢复到原来的 平衡状态。
内力计算的方法
静定结构的内力计算通常采用截面法或节点法进行。截面法是通过 截取结构的一部分进行分析，节点法则是对结构的节点进行受力分 析。
内力的表示方法
内力可以用实线和虚线表示，实线表示实际受力方向，虚线表示实际 受力反方向。
静定结构的位移计算
1
位移计算的意义
在结构分析中，位移是一个重要的参数 。通过计算位移，可以了解结构的变形 情况，从而评估结构的稳定性和安全性 。
本文的研究成果已被广泛应用于建筑、机械、航空航天等工程领 域，解决了众多实际工程问题，取得了显著的经济和社会效益。
对未来研究的展望
深入研究复杂结构体系
随着科技的发展，复杂结构体系在工程中越来越常见，未 来研究可进一步探讨复杂结构体系的静定与超静定问题， 提高工程结构的稳定性和安全性。
引入先进计算技术
计算公式
自由度数 = 刚片数 - 约束数。
判断标准
若自由度数等于0，则结构为静定；若自由度数不等于0，则结 构为超静定。
几何法判断
定义
几何法判断是指通过分析结构的几何形状来判断结构是否为静定或超静定的一种方法。
判断标准
若结构的几何形状满足静定结构的条件（即所有刚片都是相互平行的），则结构为静定；否则为超静 定。
01
超静定问题——精选推荐
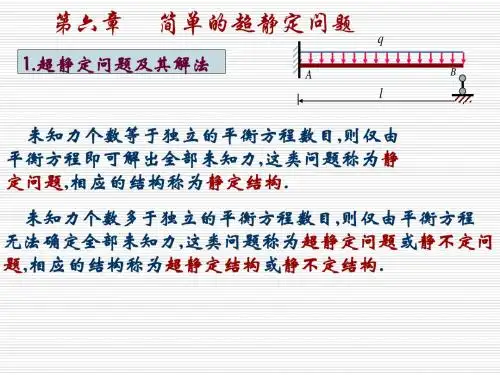
西南交通大学应用力学与工程系材料力学教研室第八章简单的超静定问题§8-1 概述静定结构: 仅靠静力平衡方程就可以求出结构的全部未知的约束反力或内力FAB2A F1BααC平面任意力系：3个平衡方程平面共点力系：2个平衡方程独立平衡方程数：超静定结构(静不定结构): 仅凭静力学平衡方程不能求解全部未知内力或反力的结构。
超静定结构的未知力的数目多于独立的平衡方程的数目；两者的差值称为超静定的次数。
BD C A 132FααF F CF B F A BC ABCADA FααF N1y xF N3F N2BD C A 132FααF F CF B F A BC AA FααF N1y xF N3F N2•习惯上把维持物体平衡并非必需的约束称为多余约束，相应的约束反力称为多余未知力。
•超静定的次数就等于多余约束或多余未知力的数目。
•注意：从提高结构的强度和刚度的角度来说，多余约束往往是必需的，并不是多余的。
超静定的求解：根据静力学平衡条件确定结构的超静定次数，列出独立的平衡方程；然后根据几何、物理关系列出需要的补充方程；则可求解超静定问题。
F F CF B F A BC A•补充方程的数目=多余未知力的数目=多余约束数。
•根据变形几何相容条件，建立变形几何相容方程，结合物理关系（胡克定律），则可列出需要的力的补充方程。
•补充方程的获得，体现了超静定问题的求解技巧与关键。
此处我们将以轴向拉压、扭转、弯曲的超静定问题进行说明。
BD C A 132FααF F CF B F A BC AA FααF N1yxF N3F N2§8.2 拉压超静定问题1拉压超静定问题解法例两端固定的等直杆AB ，在C 处承受轴向力F 如图，杆的拉压刚度为EA ，求杆的支反力.解：一次超静定问题=−+F F F B A F BA F AB ablFC (1) 由节点A 的平衡条件列出杆轴线方向的平衡方程（2）变形：补充方程(变形协调条件)可选取固定端B 为多余约束，予以解除，在该处的施加对应的约束反力F B ，得到一个作用有原荷载和多余未知力的静定结构--称为原超静定结构的基本静定系或相当系统注意原超静定结构的 B 端约束情况，相当系统要保持和原结构相等，则相当系统在B 点的位移为零。
超静定问题及其解法
核心问题：静力平衡方程不够？一 寻求补充方程
•确定超静定次数，列出静力平衡方程;
•根据变形协调条件列出变形相容方程； •将物理关系代入变形相容方程得补充方 程； •联立补充方程与静力平衡方程求 解; •求解杆件的内力，应力与变形等。
♦超静定问题及其解法 _
♦超静定问题及1
多余约束
♦超静定问题及其解法
(2).与多余约束相对应的反力称为多余未知力，多 余未知力的数目称为结构的超静定次数。
—次超静定
♦超静定问题及其解法
—次超静定
♦超静定问题及其解法
q
M
二次超静定
♦超静定问题及其解法 _
多次超静定
♦超静定问题及其解法
二.超静定问题的一般解法
超静定问题及其解法
♦超静定问题及其解法
—、= 本概念
1.静定问题：结构的约束反力或构件内力通过静力 学平衡方程可以确定的问题。
拉压静定问题
♦超静定问题及其解法
扭转静定问题
弯曲静定问题
.超静定问题及其解法 ，
2.超静定问题：单凭静力平衡方程不能完全确定结 构约束反力或构件内力的问题。
拉压超静定问题
♦超静定问题及其解法
扭转超静定问题 弯曲超静定问题
♦超静定问题及其解法
超静定问题的工程实例
大型空间 桁架结构
♦超静定问题及其解法 _
大型桥梁结构
♦超静定问题及其解法 _
大型塔吊结构
♦超静定问题及其解法 _
大型铣床
♦超静定问题及其解法
3.多余约束与超静定次数 (1).在超静定结构中，超过维持静力学平衡所必须 的约束称为多余约束。
•确定超静定次数，列出静力平衡方程;
•根据变形协调条件列出变形相容方程； •将物理关系代入变形相容方程得补充方 程； •联立补充方程与静力平衡方程求 解; •求解杆件的内力，应力与变形等。
♦超静定问题及其解法 _
♦超静定问题及1
多余约束
♦超静定问题及其解法
(2).与多余约束相对应的反力称为多余未知力，多 余未知力的数目称为结构的超静定次数。
—次超静定
♦超静定问题及其解法
—次超静定
♦超静定问题及其解法
q
M
二次超静定
♦超静定问题及其解法 _
多次超静定
♦超静定问题及其解法
二.超静定问题的一般解法
超静定问题及其解法
♦超静定问题及其解法
—、= 本概念
1.静定问题：结构的约束反力或构件内力通过静力 学平衡方程可以确定的问题。
拉压静定问题
♦超静定问题及其解法
扭转静定问题
弯曲静定问题
.超静定问题及其解法 ，
2.超静定问题：单凭静力平衡方程不能完全确定结 构约束反力或构件内力的问题。
拉压超静定问题
♦超静定问题及其解法
扭转超静定问题 弯曲超静定问题
♦超静定问题及其解法
超静定问题的工程实例
大型空间 桁架结构
♦超静定问题及其解法 _
大型桥梁结构
♦超静定问题及其解法 _
大型塔吊结构
♦超静定问题及其解法 _
大型铣床
♦超静定问题及其解法
3.多余约束与超静定次数 (1).在超静定结构中，超过维持静力学平衡所必须 的约束称为多余约束。
材料力学(I)第六章
N2 y N1 N2 N3
(2) 几何方程
L2
( L3 ) cos L1
材料力学(Ⅰ)电子教案
简单的超静定问题
15
(3)、物理方程及补充方程：
FN 1L1 FN 3 L3 ( ) cos E1 A1 E3 A3
(4) 、解平衡方程和补充方程，得:
FN1 FN 2
E1 A1 cos2 L3 1 2 cos3 E1 A1 / E3 A3
FN 1L FN 3 L 得: cos E1 A1 cos E3 A3
5）联立①、④求解：
FN ! F
④
E 3 A3 2 co s E1 A1 co s2
FN 3
F E1 A1 1 2 co s3 E A
材料力学(Ⅰ)电子教案
简单的超静定问题
[例2-19]刚性梁AD由1、2、3杆悬挂，已知三杆材料 相同，许用应力为[σ ]，材料的弹性模量为 E，杆长 均为l，横截面面积均为A，试求各杆内力。
5
1.比较变形法 把超静定问题转化为静定问题解，但 必须满足原结构的变形约束条件。
[例2-16] 杆上段为铜,下段为钢杆，
E1 A1
A
1
上段长 1 , 截面积A1 , 弹性模量E1 下段长 2 , 截面积A2 , 弹性模量E2
杆的两端为固支,求两段的轴力。
C
E 2 A2
F
FB
B
2
（1）选取基本静定结构（静定基如图），B 解： 端解除多余约束，代之以约束反力RB
2E1 A1 cos3 FN 3 3 L3 1 2 cos E1 A1 / E3 A3
例2-22
材料力学(Ⅰ)电子教案
(2) 几何方程
L2
( L3 ) cos L1
材料力学(Ⅰ)电子教案
简单的超静定问题
15
(3)、物理方程及补充方程：
FN 1L1 FN 3 L3 ( ) cos E1 A1 E3 A3
(4) 、解平衡方程和补充方程，得:
FN1 FN 2
E1 A1 cos2 L3 1 2 cos3 E1 A1 / E3 A3
FN 1L FN 3 L 得: cos E1 A1 cos E3 A3
5）联立①、④求解：
FN ! F
④
E 3 A3 2 co s E1 A1 co s2
FN 3
F E1 A1 1 2 co s3 E A
材料力学(Ⅰ)电子教案
简单的超静定问题
[例2-19]刚性梁AD由1、2、3杆悬挂，已知三杆材料 相同，许用应力为[σ ]，材料的弹性模量为 E，杆长 均为l，横截面面积均为A，试求各杆内力。
5
1.比较变形法 把超静定问题转化为静定问题解，但 必须满足原结构的变形约束条件。
[例2-16] 杆上段为铜,下段为钢杆，
E1 A1
A
1
上段长 1 , 截面积A1 , 弹性模量E1 下段长 2 , 截面积A2 , 弹性模量E2
杆的两端为固支,求两段的轴力。
C
E 2 A2
F
FB
B
2
（1）选取基本静定结构（静定基如图），B 解： 端解除多余约束，代之以约束反力RB
2E1 A1 cos3 FN 3 3 L3 1 2 cos E1 A1 / E3 A3
例2-22
材料力学(Ⅰ)电子教案
材料力学
5 Pa RD a RD a 6 EI 3EI 3EI
如何得到？
A D
P
B
自行完成
C D
RD
例题 6
图示结构AB梁的抗弯刚度为EI，CD杆的抗拉刚度为EA，
已知P、L、a。求CD杆所受的拉力。
D
a
A
C
L
2
L
B
2
P
解：变形协调条件为 wC lCD
D
a
C
FC
A
( P FC ) L wC 48EI FC L lCD EA
温度应力：
FB E t A
6 1 12 . 5 10 碳素钢线胀系数为 C0
温度应力：超静定结构中，由于温度变化，使构
件膨胀或收缩而产生的附加应力。
不容忽视！！！
路、桥、建筑物中的伸缩缝 高温管道间隔一定距离弯一个伸缩节
例题 11
图示阶梯形杆上端固定，下端与支座距离=1mm， 材料的弹性模量E=210GPa，上下两段杆的横截 面面积分别为600平方毫米和300平方毫米。试 作杆的轴力图。
C
A
FA
B
L2
FC
FA FB FC qL 0
L2
M
A
0
FB
变形协调方程
L qL2 FC FB L 0 2 2
3 FB qL 16
FA 3 qL 16
C q C FC 0
7.5kNm
5qL4 FC L3 5 0 FC qL 8 384 EI Z 48EI Z
由于超静定结构能有效降低结构的内力及变形，在 工程上（如桥梁等）应用非常广泛。
●超静定问题的解法：
静定和超静定
FDy 2F
对ADB杆受力图
MA 0
FBx 2a FDx a 0
得
FBx F
解：先整后零
F 0 F 0
y x
M
A
0
再研究DC杆 可将 FDy 求解出来 最后研究BC杆 可将 F 求解出来
Dx
§3-4
平面简单桁架的内力计算
桁架：一种由杆件彼此在两端用铰链连接而成的结构， 它在受力后几何形状不变。 节点：桁架中杆件的铰链接头。
解: 取大轮，塔轮及重物C,画受力图.
M
由
B
0
Pr F R 0
Pr F 10 P t 1 R
Fr tan 200 Ft
Fr Ft tan 200 3.64 P 1
F
x
yLeabharlann 0 FBx Fr 0
0 FBy P P2 F 0
FBx 3.64P 1
M
C
0
FDB cos 45 2l FK l FEx 2l 0
0
FDB
3 2 P 8
(拉)
习题
已知: P2=2P1， P=20P1 ，r, R=2r, 20 ;
求:物C 匀速上升时，作用于小轮上的力偶矩M； 轴承A，B处的约束力.
齿轮传动机构，大轮上固定一塔轮，大轮和塔轮共重P2,压力 角又叫啮合角，啮合力与节圆切线的夹角
静定物系的平衡问题解题步骤：
1.分析系统由几个物体组成； 2.按照便于求解的原则，适当选取整个或者 个体为研究对象进行受力分析并画出受力 图，一般先取整体，整体行不通再拆； 3.列出平衡方程并解出未知量。
选取研究对象和列平衡方程时，尽量使方 程中只含一个未知量，避免求解联立方程。
第七章超静定结构
3
MA MA FA y FA y
A A 2a 2a (a) (a) A A
B B a a
F F
C C
例7-8 求梁的支反力，梁 的抗弯刚度为EI。
解 (1）判定超静定次数
(b) (b)
B B F F FBy FBy B B B
C C
(2）解除多余约束，建立相 当系统 (3）进行变形比较，列出变 形协调条件
各杆的内力按其刚度分配；
温度变化，制造不准确等都可能使杆内产
生初应力。
§ 7-3 扭转超静定问题
定义 当杆端的支反力偶矩或横截面上的扭矩 仅由平衡方程不能完全确定，这类问题称为扭 转超静定问题。 扭转超静定问题的解法 根据变形协调条件建立变形几何方程，将扭 转角与扭矩间的物理关系代入变形几何方程得 到补充方程，再与静力平衡方程联立求解，可 得全部未知力偶。
二.超静定问题的求解方法 解除多余约束，建立相当系统——比较变形 (比较相当系统与原超静定结构在多余约束处的 变形)，列变形协调条件,得变形几何方程,将变形 与力(力偶)之间的物理关系带入变形几何方程得 到补充方程，再与静力平衡方程联立求解，可得 到全部未知量。强度、刚度的计算与静定问题相 同.
§7-2 拉压超静定问题
+Leabharlann RC l 3 5ql 4 0 补充方程 24 EI 6 EI
5 RC ql 4
（5）列静平衡方程得:
3 RA RB ql 8
求出约束反力后,就象静定问题那样计算应 力和变形,进而可以进行强度、刚度的计算. 静定基的选择可根据方便来选取，同一问 题可以有不同的选择。例如,该问题也可选 下列静定基
A B C
[M 0 ] 5.24
第九章-超静定
对于一个平衡物体，若独立平衡方程数目与未知数的数目恰 好相等，则全部未知数可由平衡方程求出，这样的问题称为静 定问题。（图a） 但工程上有时为了增加结构的刚度或坚固性，常设置多余的 约束， 未知数的数目多于独立方程的数目，未知数不能由平 衡方程全部求出，这样的问题称为静不定问题或超静定问题。 （图b）
（3）本构方程
LT 2aT ;
FN 1a FN 2 a LN EA1 EA2
由变形和本构方程消除位移未知量
FN 1 FN 2 2T EA1 EA2
（4）联立求解得
FN 1 FN 2 33.3kN
（5）温度应力
FN 1 1 66.7MPa A1
FN 2 2 33.3MPa A2
A
2
1
A P
2
1、问题的提出
两杆桁架变成 三杆桁架，缺一个 方程，无法求解
P
F
x
FN 1 sin FN 2 sin 0
F
y
FN 1 cos FN 2 cos FN 3 P 0
三杆桁架是单靠静力方程求解不了的，称为 静不定（ Static indeterminate ）——静力不能确定 超静定问题（Hyperstatic ）——超出了静力范围 其实我们在拉压杆应力遇到过这类问题 拉压杆截面上有无穷个应力，单凭静力平衡方程 不能求解 —— 超静定问题： 补充变形协调方程 建立本构（或物理）方程予以沟通 结合平衡方程联立求解
q
1
2
3
如何求解？
1. 静力不定 2. 变形方程补充--------几何相容条件（不允许 一部分脱离另一部分，也不允许一部分嵌入 另一部分） 3. 物理方程在静力平衡与变形协调之间架桥
超静定问题的解题步骤_概述说明以及解释
超静定问题的解题步骤概述说明以及解释1. 引言1.1 概述目前，超静定问题在工程设计和科学研究中扮演着至关重要的角色。
超静定问题是指那些具有多余约束条件的力学系统，在这种情况下，物体的运动过程不止一个可能的解。
解决超静定问题需要使用特定的数学工具和分析方法。
本文将介绍解题步骤，为读者提供一个清晰而简洁的指南。
1.2 文章结构本文分为五个主要部分。
在引言部分，我们将概述文章内容，并简要介绍超静定问题及其重要性。
第二部分将对超静定问题进行详细讨论，包括定义、背景知识以及实际应用场景。
接下来，第三部分将总结解题步骤，并概括每个步骤所需考虑的关键点。
第四部分则会更加详细地解释每个步骤，并提供具体操作步骤和示例。
最后，在结论与总结部分，我们将总结解题步骤，并讨论可能遇到的困难与挑战，以及其他相关问题和研究方向。
1.3 目的本文旨在帮助读者全面了解超静定问题和解题步骤。
通过详细讲解每个步骤的要点和操作方法，读者将能够更加轻松地解决超静定问题，并理解其在实际工程和科学领域的应用。
我们希望本文能成为读者解题过程中的有价值的参考资料，提供清晰而系统化的指导。
2. 超静定问题简介:2.1 定义和背景知识:超静定问题是指在静力学中，物体受到的约束超过了必要的约束数量。
这意味着通过仅使用平衡方程无法求解未知变量的值。
超静定问题在工程、建筑和力学领域中经常出现，并需要特殊的解题方法来找到合适的解决方案。
2.2 超静定问题的重要性:理解和解决超静定问题对于设计和分析结构非常重要。
一些实际应用场景中，超静定结构可以提供更高的刚度、稳定性和可持续性。
因此，研究人员和工程师需要掌握解决超静定问题的技巧。
2.3 实际应用场景:超静定问题广泛应用于建筑、土木工程、桥梁设计以及机械工程等领域。
例如，在建筑设计中，支撑柱或梁受到多个支点约束时可能会出现超静定问题。
在机械工程中，一些连接件或装配件也可能涉及到超静定问题。
了解超静定问题的定义、背景知识以及其在实际应用中的重要性对于理解本文后续将介绍的解题步骤至关重要。
TM.3-3物体系的平衡.静定和超静定问题
四、例题
理论力学 3-3 物体系的平衡. 静定和超静定问题
例3-5 图3-13a所示为曲轴冲床简图，
由轮Ⅰ、连杆AB和冲头B 组成。 OA=R，AB=l。 忽略摩擦和自重， 当 OA 在水平位置、冲压力为 F 时系统处于平衡状态。
理论力学 3-3 物体系的平衡. 静定和超静定问题
求： （1）作用在轮Ⅰ上的力偶之矩 M的大小； （2）轴承O处的约束力； （3）连杆AB受的力； （4）冲头给导轨的侧压力。
，
(c)
，
(d)
，
(e)
M 理F 论R力学 3-3 物体系的平衡. 静定和超静定问题
（3）由式（c）得 由式（d）得
理论力学 3-3 物体系的平衡. 静定和超静定问题
由式（e）得
负号说明，力FOx，Foy 的方向与图示 假设的方向相反。此题也可先取整个 系统为研究对象，再取冲头或轮Ⅰ为 研究对象，列平衡方程求解。
如图3-14b所示，有
理论力学 3-3 物体系的平衡. 静定和超静定问题 图3-14 b
理论力学 3-3 物体系的平衡. 静定和超静定问题
(d)
理论力学 3-3 物体系的平衡. 静定和超静定问题
由式 (d) 得 代入式 (a)，(b)，(c) 得
理论力学 3-3 物体系的平衡. 静定和超静定问题
理论力学 3-3 物体系的平衡. 静定和超静定问题
1．物体系的平衡
工程中，如组合构架、三铰拱等结构， 都是由几个物体组成的系统。当物体系平 衡时，组成该系统的每一个物体都处于平 衡状态，因此对于每一个受平面任意力系 作用的物体，可写出三个平衡方程。如物 体系由 n 个物体组成，则共有3n个独立方 程。
轮Ⅰ上力偶的矩 M ； （2）光滑轴承 A，B 的约束力。
理论力学 3-3 物体系的平衡. 静定和超静定问题
例3-5 图3-13a所示为曲轴冲床简图，
由轮Ⅰ、连杆AB和冲头B 组成。 OA=R，AB=l。 忽略摩擦和自重， 当 OA 在水平位置、冲压力为 F 时系统处于平衡状态。
理论力学 3-3 物体系的平衡. 静定和超静定问题
求： （1）作用在轮Ⅰ上的力偶之矩 M的大小； （2）轴承O处的约束力； （3）连杆AB受的力； （4）冲头给导轨的侧压力。
，
(c)
，
(d)
，
(e)
M 理F 论R力学 3-3 物体系的平衡. 静定和超静定问题
（3）由式（c）得 由式（d）得
理论力学 3-3 物体系的平衡. 静定和超静定问题
由式（e）得
负号说明，力FOx，Foy 的方向与图示 假设的方向相反。此题也可先取整个 系统为研究对象，再取冲头或轮Ⅰ为 研究对象，列平衡方程求解。
如图3-14b所示，有
理论力学 3-3 物体系的平衡. 静定和超静定问题 图3-14 b
理论力学 3-3 物体系的平衡. 静定和超静定问题
(d)
理论力学 3-3 物体系的平衡. 静定和超静定问题
由式 (d) 得 代入式 (a)，(b)，(c) 得
理论力学 3-3 物体系的平衡. 静定和超静定问题
理论力学 3-3 物体系的平衡. 静定和超静定问题
1．物体系的平衡
工程中，如组合构架、三铰拱等结构， 都是由几个物体组成的系统。当物体系平 衡时，组成该系统的每一个物体都处于平 衡状态，因此对于每一个受平面任意力系 作用的物体，可写出三个平衡方程。如物 体系由 n 个物体组成，则共有3n个独立方 程。
轮Ⅰ上力偶的矩 M ； （2）光滑轴承 A，B 的约束力。
材料力学第五版课件 主编 刘鸿文 第六章 简单的超静定问题
例题： 试判断下图结构是静定的还是超静定的？若是超静定， 则为几次超静定？
B
DE
A
C
FP
(a)静定。 未知内力数：3 平衡方程数：3
B
D
A
C
F
P
(b)超静定。 未知力数：5 平衡方程数：3 静不定次数=2
(c)静不定。
未知内力数：3
平衡方程数：2
FP
静不定次数=1
静不定问题的解法： （1）建立静力平衡方程； （2）由变形协调条件建立变形协调方程； （3）应用物理关系，代入变形协调方程，得到补充方程；
基本静定基的选取：
(1)解除B支座的约束,以约束反力
代替，即选择一端固定一端自由
的悬臂梁作为基本静定基。
(2)解除A端阻止转动的约束，以 约束反力代替，即选择两端简支 的梁作为基本静定基。
基本静定基选取可遵循的原则：
(1) 基本静定基必须能维持静力平衡，且为几何不变系统； (2) 基本静定基要便于计算，即要有利于建立变形协调条
E3 A3
F FN3 = 1+ 2E1 A1 cos3 a
E3 A3
(拉力) (拉力)
温度应力和装配应力
一、温度应力
在超静定结构中，由于温度变化引起的变形受到约束的限制， 因此在杆内将产生内力和应力，称为温度应力和热应力。
杆件的变形 ——
由温度变化引起的变形 温度内力引起的弹性变形
例：阶梯钢杆的上下两端在T1=5℃时被固 定,上下两段的面积为
=-
[13EI
32(1+
24
I Al
2
)
]
M
M
A
C
B D
l
材料力学--简单的超静定问题
故为一次超静定问题。
Mx 0， M A Me MB 0
2. 变形几何方程为：
AB 0
24
MA
MB
(a)
3. 根据位移相容条件利用物理关系得补充方程：
AB
M Bb GI p
(M B Me )a GI p
0
MB
Mea l
另一约束力偶矩MA可由平衡方程求得为
MA
A
A
2EA a
C
C
RA 解: 放 松B端，加支反力RA、RB
则，RA RB F 0 (1) 变形协调条件 : l总 0
F 2a
B EA
F
lAC
lCB
F RB a
2EA
RB 2a
EA
0
(2)
B
由（1）、（2）式得
RB
RB
F 5
,
RA
4F 5
14
B
D
C (2) 几何方程
1
3
aa
2
AA1 0
A
A0
l1 ( l3 ) cosa
(3) 物理方程及补充方程：
FN1l1 ( FN3l3 ) cosa
E1 A1
E3 A3
l3 A1
(4) 解平衡方程和补充方程，得:
FN1
FN2
l3
1
E1A1 cos2 a 2 cos3 a E1A1 /
(a)
26
Tb Ta
(b)
解: 1. 设铜杆和钢管的横截面上内力矩分别
Mx 0， M A Me MB 0
2. 变形几何方程为：
AB 0
24
MA
MB
(a)
3. 根据位移相容条件利用物理关系得补充方程：
AB
M Bb GI p
(M B Me )a GI p
0
MB
Mea l
另一约束力偶矩MA可由平衡方程求得为
MA
A
A
2EA a
C
C
RA 解: 放 松B端，加支反力RA、RB
则，RA RB F 0 (1) 变形协调条件 : l总 0
F 2a
B EA
F
lAC
lCB
F RB a
2EA
RB 2a
EA
0
(2)
B
由（1）、（2）式得
RB
RB
F 5
,
RA
4F 5
14
B
D
C (2) 几何方程
1
3
aa
2
AA1 0
A
A0
l1 ( l3 ) cosa
(3) 物理方程及补充方程：
FN1l1 ( FN3l3 ) cosa
E1 A1
E3 A3
l3 A1
(4) 解平衡方程和补充方程，得:
FN1
FN2
l3
1
E1A1 cos2 a 2 cos3 a E1A1 /
(a)
26
Tb Ta
(b)
解: 1. 设铜杆和钢管的横截面上内力矩分别
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三、扭转超静定问题 扭转变形计算公式
Tl
GI p
T ( x)dx
l GI p
例3.两端固定的圆截面等直杆AB，在截面 C受外力偶矩m作用，求杆两端的支座反力 偶矩。
m
A
C
a
B
b
解：
A
m
C
ɑ
m
B
b
mA
mB
静力平衡方程为： mA mB m
变形协调条件为： AB AC CB 0
即： mA a mB b 0 GIp GIp
例题 6.1
有载荷F,垂直杆1,2的抗拉压刚度分别为E1A1,E2A2,若横 梁AB的自重不计,求两杆中的内力.
MA 0
1
A
C
2
L1
FN1a FN22a F2a 0
B
变形协调方程
a
a
F
FN1
FN 2
A
B
C L1
L2
a
a
F
2L1 L2
2 FN1L FN 2L E1 A1 E2 A2
FN1
1
2F 4E2 A2
第六章 简单的超静定问题 q
1.超静定问题及其解法
A
B
l
未知力个数等于独立的平衡方程数目,则仅由 平衡方程即可解出全部未知力,这类问题称为静 定问题,相应的结构称为静定结构.
未知力个数多于独立的平衡方程数目,则仅由平衡方程 无法确定全部未知力,这类问题称为超静定问题或静不定问 题,相应的结构称为超静定结构或静不定结构.
E1 A1
FN 2
4
4F E1 A1
E2 A2
L
1.8L LDB
例题 6.2 图示刚性梁AB受均布载荷作用，梁在A端铰支，在B点和 C点由两根钢杆BD和CE支承。已知钢杆的横截面面积
ADB=200mm2，ACE=400mm2，其许用应力[σ]=170MPa，
试校列核静力钢平杆衡的方强程度。MA 0
超静定次数：未知力个数与平衡
方程数之差，也等于多余约束数
由于超静定结构能有效降低 结构的内力及变形，在工程上 （如桥梁等）应用非常广泛。
多余约束：在静定结构
上加上的一个或几个约束， 对于维持平衡来说是不必 要的约束（对于特定地工 程要求是必要的）称为多 余约束。对应的约束力称 多余约束反力。
RA A
=1mm，材料的弹性模量E=210GPa，上下两段杆的横 截面面积分别为600平方毫米和300平方毫米。试作杆的
轴力图。
RA
解: 若B端不接触，则杆件总变形为
A
60kN
1.2m
l
40
103 2.4 210 109
100103 1.2 600106
m
1.71mm
2.4m
l ＞ B端必接触
C
静力平衡方程 RA RB 100kN
mb mA l
mB
m l
a
四、简单超静定梁
用“多余未知力”代替“多余”约束， 就得到一个形式上的静定梁，该梁称为原 静不定梁的相当系统,亦称基本静定系。
综合考虑变形的几何方程、力和变形关 系可求解多余未知力。
E1 A1
C
E2 A2
1
P 2
B RB
●超静定问题的解法：综合考虑变形的几何相 容条件、物理关系和静力学平衡条件。
解超静定问题必须找出求解所有未知约束反 力所缺少的补充方程。
关键：变形协调条件（几何相容条件）
拉（压）杆超静定问题的解法
解超静定问题必须找出求解所有未 知约束反力所缺少的补充方程。结构 变形后各部分间必须象原来一样完整、 连续、满足约束条件----即满足变形 相容条件（变形协调条件）。
由对称性知:
l1 l2
l1 l3 cos
3、物理关系
l1
FN 1l
E1A1 cos
13
2
l
A
A*Βιβλιοθήκη l3FN 3l E3 A3
4、联解方程
F
FN 1
2 cos
E3 A3
E1 A1 cos2
FN 3
1 2
F E1 A1
cos3
E3 A3
2.拉压超静定问题 一铰接结构如图示,在水平刚性横梁的B端作用
FNBD ADB
31261.2M1P0a3 N
200 mm 2
D
30kN / m
FBD B
A
C
B FBD
1m
CE
FNCE ACE
39846.04M0Pm1am0 32N
2m
E LCE
装配应力：超静定结构中由于加工误差， 装 配产生的应力。
平衡方程：
FN1 FN 2
13
2
l
FN 3 (FN1 FN 2 )cos
FNCE 135 kN 3FNBD
变形协调方程 FLNDCBE31mLCE30kN / m 230m0FN1B1D0.5F6m1Nm.B8D2lFNEB65DF4N3C0mE0310F0NC6Em2l E
D
30kN / m
B
A
C
1m
2m
E
FNBD 32.2kN
FNCE 38.4kN
BD
a
B 物理关系
F1
变形协调条件
l1 a
l2 2a
F2
l1
F1 l EA
F1
4 5
l
EA
（拉力）
l2
F2 l EA
F2
2 5
l
EA
（压力）
温度应力的计算：
温度由
A
l
t1 t2 , t t2 t1
平衡方程
FA FB 0
FA
A l
变形相容条件
lt lF 物理方程 lt l t
40kN
1.2m
B
变形协调条件为 l
RB
RA
A
轴
1.2m
力
60kN
2.4m
图
85kN
⊕ 25kN
C
40kN
1.2m
B
15kN
RB
l
RA 103 1.2 210109 600106
(RA 60)103 2.4 210109 600106
RB 103 1.2 210109 300106
RA 85kN RB 15kN
关键：变形协调条件
注意：力与变形一致
例1.已知:1、2杆抗拉刚度为E1A1, 3杆抗拉刚度
为E3A3,F，求各杆内力。
解: 1、分析A结点 一次超静定问题。
13
2
l
Fx 0,
FN1 FN 2
FN1 FN3 FN2
A F
A
F
Fy 0, (FN1 FN 2 )cos FN 3 F
2、考虑变形几何相容条件
A
变形协调条件：
l3
l1 cos
FN1
F N3 F N2
A
l3
l1 l2
A
练习：图示AB为刚性梁，1、2两杆的抗拉（压）刚度
均为EA，制造时1杆比原长L短，将1杆装到横梁后，求
两杆内力。
解: 装配后1杆伸长，
1
2
2杆缩短。
l1
l 研究AB 静力平衡方程
l2
F1 a F2 2a 0
Aa
B
FB
lt
Lt FBl
EA
FB EAt
温度应力：
FB Et
A
碳素钢线胀系数为
12.5 10 6
1 C0
温度应力：超静定结构中，由于温度变化，使构
件膨胀或收缩而产生的附加应力。
不容忽视！！！
路、桥、建筑物中的伸缩缝 高温管道间隔一定距离弯一个伸缩节
练习2：图示阶梯形杆上端固定，下端与支座距离