《数值分析》完整版讲义

第1章数值分析中的误差一、重点内容误差设精确值x* 的近似值x，差e＝x－x* 称为近似值x 的误差(绝对误差)。

误差限近似值x 的误差限 是误差e 的一个上界，即|e|＝|x－x*|≤ε。

相对误差e r是误差e 与精确值x* 的比值，。

常用计算。

相对误差限是相对误差的最大限度，，常用计算相对误差限。

绝对误差的运算：ε(x1±x2)＝ε(x1)＋ε(x2)ε(x1x2)≈|x1|ε(x2)＋|x2|ε(x1)有效数字如果近似值x 的误差限ε 是它某一个数位的半个单位，我们就说x 准确到该位。

从这一位起到前面第一个非0 数字为止的所有数字称为x 的有效数字。

关于有效数字：(1) 设精确值x* 的近似值x，x＝±0.a1a2…a n×10ma1，a2，…，a n是0～9 之中的自然数，且a1≠0，|x－x*|≤ε＝0.5×10m－l，1≤l≤n则x 有l位有效数字.(2) 设近似值x＝±0.a1a2…a n×10m有n 位有效数字，则其相对误差限(3) 设近似值x＝±0.a1a2…a n×10m的相对误差限不大于则它至少有n 位有效数字。

(4) 要求精确到10－3，取该数的近似值应保留4 位小数。

一个近似值的相对误差是与准确数字有关系的，准确数字是从一个数的第一位有效数字一直数到它的绝对误差的第一位有效数字的前一位，例如具有绝对误差e＝0.0926 的数x＝20.7426 只有三位准确数字2，0，7。

一般粗略地说，具有一位准确数字，相对于其相对误差为10% 的量级；有二位准确数字，相对于其相对误差为1% 的量级；有三位准确数字，相对于其相对误差为0.1% 的量级。

二、实例例1 设x*＝ ＝3.1415926…近似值x＝3.14＝0.314×101，即m＝1，它的误差是0.001526…，有|x－x*|＝0.001526…≤0.5×101－3即l＝3，故x＝3.14 有 3 位有效数字。

数值分析讲义第三章线性方程组的解法§3.0 引言§3.1 雅可比(Jacobi)迭代法§3.2 高斯-塞德尔(Gauss-Seidel)迭代法§3.3 超松驰迭代法§3.7 三角分解法§3.4 迭代法的收敛性§3.8 追赶法§3.5 高斯消去法§3.9 其它应用§3.6 高斯主元素消去法§3.10 误差分析§3 作业讲评3 §3.11 总结§3.0 引言重要性：解线性代数方程组的有效方法在计算数学和科学计算中具有特殊的地位和作用.如弹性力学、电路分析、热传导和振动、以及社会科学及定量分析商业经济中的各种问题.分类：线性方程组的解法可分为直接法和迭代法两种方法.(a) 直接法：对于给定的方程组，在没有舍入误差的假设下，能在预定的运算次数内求得精确解.最基本的直接法是Gauss消去法，重要的直接法全都受到Gauss消去法的启发.计算代价高.(b) 迭代法：基于一定的递推格式，产生逼近方程组精确解的近似序列.收敛性是其为迭代法的前提，此外，存在收敛速度与误差估计问题.简单实用,诱人.§3.1 雅可比Jacobi 迭代法 (AX =b )1基本思想:与解f (x )=0 的不动点迭代相类似,将AX =b 改写为X =BX +f 的形式,建立雅可比方法的迭代格式：X k +1=BX (k )+f ,其中，B 称为迭代矩阵.其计算精度可控,特别适用于求解系数为大型稀疏矩阵(sparse matrices)的方程组. 2问题:(a) 如何建立迭代格式？(b) 向量序列{X k }是否收敛以及收敛条件? 3 例题分析:考虑解方程组⎪⎩⎪⎨⎧=+--=-+-=--2.453.82102.7210321321321x x x x x x x x x (1)其准确解为X *={1, 1.2, 1.3}. 建立与式(1)相等价的形式：⎪⎩⎪⎨⎧++=++=++=84.02.01.083.02.01.072.02.01.0213312321x x x x x x x x x (2) 据此建立迭代公式：⎪⎩⎪⎨⎧++=++=++=+++84.02.01.083.02.01.072.02.01.0)(2)(1)1(3)(3)(1)1(23)(2)1(1k k k k k k kk k x x x x x x x x x (3) 取迭代初值0)0(3)0(2)0(1===x x x ,迭代结果如下表. JocabiMethodP31.cpp迭代次数 x1 x2 x30 0 0 01 0.72 0.83 0.842 0.971 1.07 1.153 1.057 1.1571 1.24824 1.08535 1.18534 1.282825 1.095098 1.195099 1.2941386 1.098338 1.198337 1.2980397 1.099442 1.199442 1.2993358 1.099811 1.199811 1.2997779 1.099936 1.199936 1.29992410 1.099979 1.199979 1.29997511 1.099993 1.199993 1.29999112 1.099998 1.199998 1.29999713 1.099999 1.199999 1.29999914 1.1 1.2 1.315 1.1 1.2 1.34Jocobi迭代公式:设方程组AX=b, 通过分离变量的过程建立Jocobi迭代公式，即),,2,1()(1),,2,1(0,11n i x a b a x n i a b x a n ij j j ij i iii ii ni i j ij =∑-==≠∑=≠== 由此我们可以得到Jacobi 迭代公式：),,2,1()(11)1(n i x a b a xn ij j k i ij i iik i=∑-=≠=+[Jacobi 迭代公式的算法] 1: 初始化. n , (a ij ), (b j ), (x 1) , M . 2: 执行k =1直到M 为止. ① 执行i =1直到n 为止.ii nij j j ij i i a x a b u /)(1∑-←≠= ;② 执行i =1直到n 为止.i i u x ← ;③输出k , (x i ).另外，我们也可以建立Jacobi 迭代公式的矩阵形式. 设方程组AX =b ,其中，A =(a ij )n 为非奇异阵，X =(x 1,x 2,…,x n )T , b =(b 1,b 2,…,b n )T将系数阵A 分解为: A =U +D +L ,U 为上三角矩阵，D 为对角矩阵，L 为下三角矩阵.于是AX =b 可改写为 (U +D +L )X =b⇔ X =D -1b -D -1(U +L )X由此可得矩阵形式的Jocobi 迭代公式： X k +1=BX (k )+f □§3.2 高斯-塞德尔Gauss-Seidel 迭代法注意到利用Jocobi 迭代公式计算)1(+k ix 时，已经计算好)(1)(2)(1,,,k i k k x x x - 的值，而Jocobi 迭代公式并不利用这些最新的近似值计算，仍用)(1)(2)(1,,,k i k k x x x - .这启发我们可以对其加以改进,即在每个分量的计算中尽量利用最新的迭代值，得到),,2,1()(1111)1()1(n i x a x a b a xn i j k jij i j k j ij i iik i=∑-∑-=+=-=++上式称为Gauss-Seidel 迭代法. 其矩阵形式是X =-(D +L )-1UX +(D +L )-1b , X k +1=BX (k )+f .迭代次数 x1 x2 x3 0 0 0 0 1 0.72 0.902 1.1644 2 1.04308 1.167188 1.282054 3 1.09313 1.195724 1.2977714 1.099126 1.199467 1.2997195 1.09989 1.199933 1.2999656 1.099986 1.199992 1.2999967 1.099998 1.199999 1.2999998 1.1 1.2 1.3§3.3 超松驰迭代法SOR 方法1基本思想:逐次超松弛迭代法(Successive Over Relaxation Method,简写为SOR)可以看作带参数ω的高斯-塞德尔迭代法，是G-S 方法的一种修正或加速.是求解大型稀疏矩阵方程组的有效方法之一. 2 SOR 算法的构造:设方程组AX =b , 其中，A =(a ij )n 为非奇异阵，X =(x 1,x 2,…,x n )T , b =(b 1,b 2,…,b n )T . 假设已算出x (k )，),,2,1()(1111)1()1(n i x a x a b a xn i j k j ij i j k j ij i iik i=∑-∑-=+=-=++ (1)相当于用高斯-塞德尔方法计算一个分量的公式. 若对某个参数ω，作)1(+k ix与)(k i x 加权的平均,即)()1()()1()()1()(1k i k ik i k ik ik ix xx xxx-+=+-=+++ωωω (2)其中，ω称为松弛因子.用(1)式代入(2)式，就得到解方程组AX =b 的逐次超松弛迭代公式：⎪⎩⎪⎨⎧=∑-∑-=∆∆+==-=++),,2,1()()(11)1()()1(n i x a x a b a x x x x n ij k j ij i j k j ij i iii i k i k i ω (3) 显然，当取ω=1时，式(3)就是高斯-塞德尔迭代公式. 3 例题分析:利用SOR 方法解方程组⎪⎩⎪⎨⎧=+---=-+-=--3322242024321321321x x x x x x x x x (1) 其准确解为X *={1, 1, 2}. 建立与式(1)相等价的形式：⎪⎪⎩⎪⎪⎨⎧++=-+=+=132315.05.05.025.05.021*******x x x x x x x x x (2) 据此建立迭代公式：⎪⎪⎩⎪⎪⎨⎧++=-+=+=+++132315.05.05.025.05.0)(2)(1)1(3)(3)(1)1(23)(2)1(1k k k k k k kk k x x x x x x x x x (3)利用SOR 算法，取迭代初值1)0(3)0(2)0(1===x x x ,ω=1.5,迭代结果如下表.逐次超松弛迭代法次数 x1 x2 x3 1 0.625000 0.062500 1.750000 2 0.390625 0.882813 1.468750 3 1.017578 0.516602 1.8085944 0.556885 0.880981 1.7104495 1.023712 0.743423 1.8681036 0.746250 0.908419 1.8387377 0.997715 0.860264 1.9138948 0.864050 0.936742 1.9086059 0.986259 0.922225 1.94552310 0.928110 0.958649 1.94749311 0.985242 0.955944 1.96619812 0.961661 0.973818 1.96952113 0.988103 0.974699 1.97928914 0.979206 0.983746 1.98217215 0.991521 0.985318 1.98741616 0.988509 0.990038 1.98951317 0.994341 0.991414 1.99239718 0.993538 0.993946 1.99380619 0.996367 0.994950 1.99542420 0.996313 0.996342 1.99633121 0.997724 0.997018 1.99725422 0.997871 0.997798 1.99782223 0.998596 0.998234 1.998355GS迭代法须迭代85次得到准确值X*={1, 1, 2};而SOR方法只须55次即得准确值.由此可见，适当地选择松弛因子ω，SOR法具有明显的加速收敛效果. □§3.4 迭代法的收敛性1. 向量和矩阵范数 (a) 向量范数R n 空间的向量范数 || · || ,对任意n R y x ∈,, 满足下列条件：00||||;0||||)1(=⇔=≥x x x (正定性)||||||||||)2(x x⋅=αα (齐次性)||||||||||||)3(y x y x+≤+ （三角不等式）常见的向量范数有： (1) 列范数：(2) 谱范数：(欧几里德范数或向量的长度,模)(3) 行范数：(4) p 范数:上述范数的几何意义是:∞||||x =max(|x 2-x 1|,|y 2-y 1|) ; 1||||x =|x 2-x 1|+|y 2-y 1| ;2122122)()(||||y y x x x -+-=.向量序列}{)(k x依坐标收敛于向量x * 的充要条件是向量序列}{)(k x 依范数收敛于向量x *,即0||||lim *)(=-∞→x x k k .(b) 矩阵范数n m R ⨯空间的向量范数 || ·|| ,对任意 n m R B A ⨯∈,, 满足下列条件：|||||||| || AB || (4)||||||||||||)3(||||||||||)2(00||||;0||||)1(B A B A B A A A A A A ≤+≤+⋅==⇔=≥αα常见的矩阵范数有：∑==∞≤≤nj ij a A ni 1||max ||||1 (行和范数)∑==≤≤ni ij a A nj 11||max ||||1 (列和范数))(||||max 2A A A T λ= (谱范数)若A 对称，则有)()(2max max A A A T λλ=.矩阵A 的谱半径记为)(||||2A A ρ=,ρ(A ) =||max1i ni λ≤≤,其中λi 为A 的特征根。

第十章 数值分析方法在生产实际中，常常要处理由实验或测量所得到的一批离散数据，数值分析中的插值与拟合方法就是要通过这些数据去确定某一类已经函数的参数，或寻求某个近似函数使之与已知数据有较高的拟合精度。

插值与拟合的方法很多，这里主要介绍线性插值方法、多项式插值方法和样条插值方法，以及最小二乘拟合方法在实际问题中的应用。

相应的理论和算法是数值分析的内容，这里不作详细介绍。

§1 数据插值方法及应用在生产实践和科学研究中，常常有这样的问题：由实验或测量得到变量间的一批离散样点，要求由此建立变量之间的函数关系或得到样点之外的数据。

与此有关的一类问题是当原始数据),(,),,(),,(1100n n y x y x y x 精度较高，要求确定一个初等函数)(x P y =（一般用多项式或分段多项式函数）通过已知各数据点（节点），即n i x P y i i ,,1,0,)( ==，或要求得函数在另外一些点（插值点）处的数值，这便是插值问题。

1、分段线性插值这是最通俗的一种方法，直观上就是将各数据点用折线连接起来。

如果b x x x a n =<<<= 10那么分段线性插值公式为n i x x x y x x x x y x x x x x P i i i i i i i i i i ,,2,1,,)(11111 =≤<--+--=-----可以证明，当分点足够细时，分段线性插值是收敛的。

其缺点是不能形成一条光滑曲线。

例1、已知欧洲一个国家的地图，为了算出它的国土面积，对地图作了如下测量：以由西向东方向为x 轴，由南向北方向为y 轴，选择方便的原点，并将从最西边界点到最东边界点在x 轴上的区间适当的分为若干段，在每个分点的y 方向测出南边界点和北边界点的y 坐标y1和y2，这样就得到下表的数据（单位：mm ）。

根据地图的比例，18 mm 相当于40 km 。

根据测量数据，利用MA TLAB 软件对上下边界进行线性多项式插值，分别求出上边界函数)(2x f ，下边界函数)(1x f ，利用求平面图形面积的数值积分方法—将该面积近似分成若干个小长方形，分别求出这些长方形的面积后相加即为该面积的近似解。

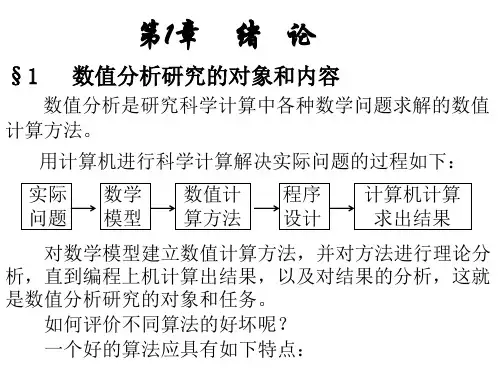
第1章 绪论数值计算方法是一门与计算机使用密切结合的实用性很强的数学课程，其特点如下: 第一，面向计算机，要根据计算机特点提供实际可行的有效算法，即算法只能包括加、减、 乘、除运算和逻辑运算，是计算机能直接处理的。

第二，有可靠的理论分析，能任意逼近并达到精度要求，对近似算法要保证收敛性和数值稳 定性，还要对误差进行分析，这些都建立在相应数学理论基础上。

第三，要有好的计算复杂性，时间复杂性好是指节省时间，空间复杂性好是指节省存储量， 这也是建立算法要研究的问题，它关系到算法能否在计算机上实现。

第四，要有数值实验，即任何一个算法除了从理论上要满足上述三点外，还要通过数值试验 证明是行之有效的。

1.1 误差的基本概念除了极个别的情况外，数值计算总是近似计算，实际计算结果与理论结果之间存在着误差。

数值分析的任务之一是将误差控制在一定的容许范围内或者至少对误差有所估计。

一、误差的来源 1、模型误差用计算机解决科学计算问题首先要建立数学模型，它是对被描述的实际问题进行抽象，简化而得到的，因而是近似的，数学模型与实际问题之间出现的这种误差称为模型误差。

这种误差可忽略不计，在数值计算方法中不予讨论。

2、观测误差在数学模型中往往还有一些根据观测得到的物理量，如温度，长度，电压等等，测量的结果不可能绝对正确，由此产生的误差称为观测误差。

观测误差在数值计算方法中也不予讨论。

3、截断误差（方法误差）在数学模型不能得到精确解时，通常要用数值方法求它的近似解，其近似解与精确解之间的误差称为截断误差或方法误差。

4、舍入误差在计算过程中，由于计算机的字长有限，采用计算机数系中和实际数据比较接近的数来表示，由此产生的误差以及计算过程又可能产生新的误差，这些误差称为舍入误差。

二、绝对误差和相对误差1、绝对误差秘绝对误差限设数x (精确值)有一个近似值为*x ，记 称e(x)为近似值*x 的绝对误差，简称误差。

当e(x)为正时，近似值*x 偏大，叫做强近似值 ；当它为负时，近似值*x 偏小，叫作弱近似值。