SAS例题及程序输出
- 格式:doc
- 大小:525.50 KB
- 文档页数:9

sas练习题(打印版)### SAS练习题(打印版)#### 一、基础数据操作1. 数据导入- 题目:使用SAS导入一个CSV文件,并列出前5个观测值。
- 答案:使用`PROC IMPORT`过程导入数据,并用`PROC PRINT`展示前5个观测。
2. 数据筛选- 题目:筛选出某列数据大于50的所有观测。
- 答案:使用`WHERE`语句进行筛选。
3. 数据分组- 题目:根据某列数据对数据集进行分组,并计算每组的均值。
- 答案:使用`PROC MEANS`过程和`BY`语句进行分组和计算。
4. 数据排序- 题目:按照某列数据的升序或降序对数据集进行排序。
- 答案:使用`PROC SORT`过程进行排序。
#### 二、描述性统计分析1. 单变量分析- 题目:计算某列数据的均值、中位数、标准差等统计量。
- 答案:使用`PROC UNIVARIATE`过程进行单变量描述性统计分析。
2. 频率分布- 题目:计算某列数据的频数和频率分布。
- 答案:使用`PROC FREQ`过程进行频率分布分析。
3. 相关性分析- 题目:计算两列数据的相关系数。
- 答案:使用`PROC CORR`过程计算相关系数。
#### 三、假设检验1. t检验- 题目:对两组独立样本的均值进行t检验。
- 答案:使用`PROC TTEST`过程进行t检验。
2. 方差分析- 题目:对多个组别数据进行方差分析。
- 答案:使用`PROC ANOVA`过程进行方差分析。
3. 卡方检验- 题目:对分类变量进行卡方检验。
- 答案:使用`PROC FREQ`过程和`CHI2TEST`选项进行卡方检验。
#### 四、回归分析1. 简单线性回归- 题目:使用一个自变量和一个因变量进行简单线性回归分析。
- 答案:使用`PROC REG`过程进行简单线性回归。
2. 多元线性回归- 题目:使用多个自变量和一个因变量进行多元线性回归分析。
- 答案:同样使用`PROC REG`过程,但包括多个自变量。

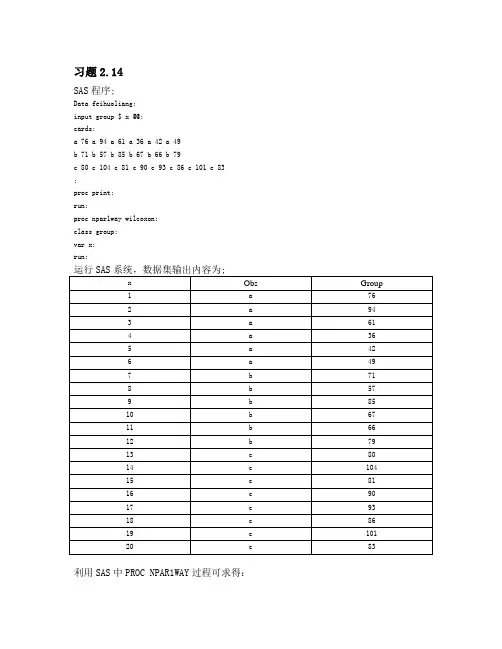
习题2.14SAS程序;Data feihuoliang; input group $ x @@; cards;a 76 a 94 a 61 a 36 a 42 a 49b 71 b 57 b 85 b 67 b 66 b 79c 80 c 104 c 81 c 90 c 93 c 86 c 101 c 83 ; proc print; run; proc npar1way wilcoxon; class group; var x; run;运行SAS系统,数据集输出内容为;x Obs Group1a762a943a614a365a426a497b718b579b8510b6711b6612b7913c8014c10415c8116c9017c9318c8619c10120c83利用SAS中PROC NPAR1WAY过程可求得:从SAS 数据分析来看,三组数据分散程度相差不大利用PROC NPAR1WAY 过程计算,检验3417.92=χ,05.00094.0=<=αP 故认为这一经验可靠.习题2.16SAS 程序:data shengchanzongzhif;input group $ x @@;cards;a 7870.28 a 4359.15 a 11660.43 a 4752.54 a 4791.48b 9251.15 b 4572.12 b 6188.9c 10366.37 c 21645.08 c 15742.51 c 6148.73 c 7614.55 c 4670.53 c 22077.36d 12495.97 d 7581.32 d 7568.89 d 26202.47 d 4828.51 d 1052.85e 3491.57 e 8637.81 e 2282 e 4006.72 e 291.01f 4523.74 f 2276.7 f 641.58 f 710.76 f 3045.26 ; proc print; run; proc npar1way wilcoxon; class group; var x; run;数据集输出内容为:Obs group x1a7870.282a4359.153a11660.434a4752.545a4791.486b9251.157b4572.128b6188.909c10366.3710c21645.0811c15742.5112c6148.7313c7614.5514c4670.5315c22077.3616d12495.9717d7581.3218d7568.8919d26202.4720d4828.5121d1052.8522e3491.5723e8637.8124e2282.0025e4006.7226e291.0127 f 4523.74 28 f 2276.70 29 f 641.58 30 f 710.76 31f3045.26利用SAS 中PROC NPAR1WAY 过程可求得:利用PROC NPAR1WAY 过程计算,检验8243.142=χ,05.00111.0=<=αP ,故各地区生产有明显的差异又有计算输出知,华北、东北、华东、中南、西南、西北的平均得分依次为;17.4,18,23.3,19.5,9.4,5.6,所以平均秩得分由大到小排序为:西北、西南、华北、东北、中南、华东。


程序:简短数据运用datalines或cards直接输入数据进行运算.运行结果:方法二:运用format读入数据;运行结果:You see here that there is a colon preceding each informat. This colon (called an informat modifier) tells SAS to use the informat supplied but to stop reading the value for this variable when a delimiter is encountered. Do not forget the colons because without them。
SAS may read past a delimiter to satisfy the width specified in the informat.Colon:冒号;delimiter:定界符(在这里定界符是空格);冒号的作用是从下一个非空的字符开始,读到下一个空格或者是informat指定的长度为止。
libname lear n ”E:/SAS1/chapter4”;data learn。
Perm;input ID : 3.Gender : 1.DOB : mmddyy10.Height Weight;label DOB="Date of Birth”Height=”Height in inches”Weight=”Weight in pounds";format DOB date9。
;datalines;001 M 10/21/1946 68 150002 F 5/26/1950 63 122003 M 5/11/1981 72 175004 M 7/4/1983 70 128005 F 12/25/2005 30 40;run;title ”Listing of Information";proc print data=learn.Perm;run;如果吧ID和GENDER的两个冒号去掉,那SAS读记录的时候,1. ID只会读取informat中指定的长度,即前三个字符 (如果每行数据前没有空格,那ID的值是正常的);2. GENDER会是接下来的一个字符,而不会跳过空格,所以GENDER不会读到F和M这两个值。

表3.4给出15名两周岁婴儿的身高(X 1),胸围(X 2)和上半臂围(X 3)的测量数据。
假设男婴的测量数据()()1,,6X αα= 为来自总体()13,N μ∑()的随机样本;女婴的测量数据()()1,,9Y αα= 为来自总体()3,N μ∑(2)的随机样本,试利用表3.4中的数据检验(1)(2)0:(0.05)H μμα==。
解:检验假设(1)(2)(1)(2)01::H H μμμμ=≠,。
取检验统计量为2+1(3,6,9)(2)n m p F T p n m n m --====+-,由样本值计算得:=(82,60.2,14.5)=(7658.47613.5)X Y '',,,, 1215840.2 2.5=40.215.86 6.552.5 6.559.519645.134.5=45.115.7611.6534.511.6514.5A A ⎛⎫ ⎪ ⎪ ⎪⎝⎭⎛⎫ ⎪ ⎪ ⎪⎝⎭,, 进一步计算得: 2112(2)()'()()=1.4754793D n m X Y A A X Y -=+--+-, 22 5.3117256,nm T D n m==+ 21 1.498179(2)n m p F T n m p+--==+-。
对给定显著性水平=0.05α,利用软件SAS9.3进行检验时,首先计算p 值:p =P {F ≥1.498179}=0.2692616。
因为p值=0.2692616>0.05,故接收H,即认为男婴和女婴的测量数据无显著性差异。
在这种情况下,可能犯第二类错误,且犯第二类错误的概率为。
=0.0268093SAS程序及结果如下:proc iml;n=6;m=9; p=3;x={ 7860.616.5 ,7658.112.5 ,9263.214.5 ,815914 ,8160.815.5 ,8459.514} ;print x;ln={[6] 1} ;x0=(ln*x)/n; print x0;mx=i(n)-j(n,n,1)/n;a1=x`*mx*x; print a1;y={ 8058.414 ,7559.215 ,7860.315 ,7557.413 ,7959.514 ,7858.114.5 ,755812.5 ,6455.511 ,8059.212.5} ;print y; lm={[9] 1} ;y0=(lm*y)/m; print y0;my=i(m)-j(m,m,1)/m;a2=y`*my*y; print a2;a=a1+a2; xy=x0-y0;ai=inv(a); print a ai;dd=xy*ai*xy`; d2=(m+n-2)*dd; t2=n*m*d2/(n+m) ;f=(n+m-1-p)*t2/((n+m-2)*p); fa=finv(0.95,p,m+n-p-1);beta=probf(f,p,m+n-p-1,t2); print d2 t2 f beta;pp=1-probf(f,p,m+n-p-1);print pp; quit;。

判别分析例题某医院眼科研究糖尿病患者的视网膜病变情况, 视网膜病变分轻、中、重三型。
研究者用年龄(age)、患糖尿病年数(time)、血糖水平(glucose)、视力(vision)、视网膜电图中的a波峰时(at)、a波振幅(av)、b波峰时(bt)、b波振幅(bv)、qp波峰时(qpt)及qp波振幅(qpv)等指标建立判别视网膜病变的分类函数, 以判断糖尿病患者的视网膜病变属于轻、中、重中哪一型。
为此观察131例糖尿病患者,要求其患眼无其他明显眼前段疾患, 眼底无明显其他视网膜疾病和视神经、葡萄膜等疾患,测定了他们的以上各指标值,并根据统一标准诊断其疾患类型,记分类指标名为group。
见表1 (表中仅列出前5例)。
试以此为训练样本, 仅取age,vision,at,bt和qpv 等指标, 求分类函数, 并根据王××的信息: 38岁, 视力1.0, 视网膜图at=14.25, bv=383.39, qpv=43.18判断其视网膜病变属于哪一型。
表1 131例糖尿病患者各指标实测记录(前5例)──────────────────────────────────例号年龄患病血糖视力a波a波b波b波qp波pq波视网膜年数峰时振幅峰时振幅峰时振幅病变程度──────────────────────────────────1 49 2.00 191 1.5 12.25 235.40 52.50 417.57 78.5 27.43 A12 49 2.00 191 1.2 13.50 225.15 52.00 391.20 78.5 46.69 A13 63 4.00 200 1.0 14.25 318.92 53.25 616.35 77.5 35.38 A14 63 4.00 200 0.6 14.00 361.90 55.00 723.30 77.0 47.01 A15 54 10.00 137 0.6 13.75 269.59 55.50 451.27 78.0 33.70 A2──────────────────────────────────解假定样本系从总体中随机抽取,则样本中三种疾患类型的样本量可近似地反映先验概率, 利用SAS的Discrim过程可得分类函数Y1=-181.447+0.473(age)+60.369(vision)+17.708(at)+0.048(bv)+0.364(qpv)Y2=-165.830+0.472(age)+49.782(vision)+17.658(at)+0.034(bv)+0.325(qpv)Y3=-189.228+0.178(age)+43.974(vision)+20.447(at)+0.040(bv)+0.265(qpv)以王××的观察值代入分类函数, 得Y1=-181.447+0.473×38+60.369×1.0+17.708×14.25+0.048×383.39+0.364×43.18 =183.36同样可算得:Y2=180.58, Y3=179.66其中最大者为Y1, 故判断为轻度病变。

实用标准文档地质勘探中,在A,B,C三个地区采集了一些岩石,测量其部分化学成分,其数据见表3.5。
假定这三个地区掩饰的成分遵从N3(°, i (i 123)( 0.05)H o: 1 3 ;H1 : 1, 2, 3 不全等,(1) 检验不全H= 3 ;H 1 : 1, 2 , 3 不全等;0: 1 2(2) 检验H0:⑴⑵ (1) ⑵;H 1 : ;(3) 检验H。
:⑴⑵⑶⑴(j);H1:存在1 J,使。
表3.5岩石部分化学成分数据SiO2 FeO K2O47.22 5.06 0.1047.45 4.35 0.15A地区47.52 6.85 0.1247.86 4.19 0.1747.31 7.57 0.1854.33 6.22 0.12B地区56.17 3.31 0.1554.40 2.43 0.2252.62 5.92 0.1243.12 10.33 0.05C地区42.05 9.67 0.0842.50 9.62 0.0240.77 9.68 0.04解:(1)检验假设在H0成立时,取近似检验统计量为2(f)统计量:=1 d M 2 1 d l n 4*。
由样本值计算三个总体的样本协方差阵:S 士A ±n1(x(⑴)X⑴)(X(⑴)X⑴)n 1 n 1 1 10.243081= 0.64264 9.28552 ,40.01406 0.02052 0.004526.3046 1二- 4.7567 10.672230.0557 0.2388 0.0066751 1 n1S 3 亠人亠(x ((3))X ⑶)(x (⑶)X (3)) n 3 1n 3112.97141二-0.6337 0.3421 。
40.0001 0.00295 0.001875进一步计算可得M 24.52397, d 0.433333, f 12,(1 d)M =13.896916。
对给定显著性水平 =0.05,利用软件SAS9.3进行检验时,首先计算p 值:p=P{ E > 13.896916}=0.3073394。

1.随机取组随机取组 有无重复试验的两种有无重复试验的两种 本题是无重复本题是无重复 DATA PGM15G; DO A=1 TO 4; /*A 为窝别*/ DO B=1 TO 3; ; /*B /*B 为雌激素剂量*/ INPUT X @@; X @@; /*X /*X 为子宫重量*/OUTPUT ;END ;END ;CARDS ;106 116 145 42 68 115 70 111 133 42 63 87 ; RUN ;ods html ; /*将结果输出成网页格式,SAS9.0以后版本可用*/ PROC GLM DATA =PGM15G; CLASS A B;MODEL X=A B / X=A B / SS3SS3;MEANS A B; /*给出因素A 、B 各水平下的均值和标准差*/MEANS B / B / SNK SNK ; /*对因素B (即剂量)各水平下的均值进行两两比较*/ RUN ;ODS HTML CLOSE ;2. 2*3析因设计析因设计 两因素两因素 完全随机完全随机 统计方法统计方法 2*3析因设计析因设计 tiff =f 的开方的开方DATA aaa; DO zs=125,200;DO repeat=1 TO 2; ; /*/*每种试验条件下有2次独立重复试验*/ do js=0.015,0.030,0.045; INPUT cl @@; OUTPUT ;END ;END ;END ; CARDS ;2.70 2.45 2.60 2.78 2.49 2.72 2.83 2.85 2.86 2.86 2.80 2.87 ; run ;PROC GLM ;CLASS zs js; MODEL cl=zs js zs*js / cl=zs js zs*js / SS3SS3; MEANS zs*js;LSMEANS zs*js / TDIFF PDIFF ; ; /*/*对 zs 和js 各水平组合而成的试验条件进行均数进行两两比较*/ RUN ;ODS HTML CLOSE ;练习一:2*2横断面研究列链表横断面研究列链表 方法:卡方方法:卡方 矫正卡方矫正卡方 FISHERDATA PGM19A;DO A=1 TO 2; DO B=1 TO 2;INPUT F @@;OUTPUT ;END ;END ;CARDS ; 2 26 8 21 ;run ;PROC FREQ ; WEIGHT F;TABLES A*B / A*B / CHISQ CHISQ ;RUN ;样本大小 = 57练习二:对裂列连表练习二:对裂列连表 结果变量结果变量 换和不换换和不换 三部曲三部曲 1横断面研究横断面研究 P 《0.05 RDATA PGM19B; DO A=1 TO 2; DO B=1 TO 2;INPUT F @@;OUTPUT ;END ;END ;CARDS ; 40 3414 1 19252 ; run ; ods html ;PROC FREQ ; WEIGHT F;TABLES A*B / A*B / CHISQCHISQ cmh ; RUN ;ods html close ;样本大小 = 57练习三:病例对照2*2 病例组中病例组中 有何没有那个基因有何没有那个基因 是正常的3.8倍,倍, 则有可能导致痴呆则有可能导致痴呆 要做前瞻性研究要做前瞻性研究 用对裂用对裂DATA PGM20;DO A=1 TO 2; DO B=1 TO 2;INPUT F @@;OUTPUT ;END ;END ;CARDS ; 240 60 360 340 ;run ; ods html ; PROC FREQ ; WEIGHT F;TABLES A*B / A*B / CHISQ CHISQcmh ; RUN ; ods html close ;总样本大小 = 1000 练习四:配对设计配对设计 隐含金标准2*2 MC 卡方卡方 检验检验 34和0在总体上在总体上((B+C 《40 用矫正卡方) 是否相等是否相等 则可得甲培养基优于乙培养基则可得甲培养基优于乙培养基 一般都用矫正一般都用矫正 因卡方为近似计算因卡方为近似计算DATA PGM19F; INPUT b c;chi=(ABS(b-c)-1)**2/(b+c);p=1-PROBCHI(chi,1);求概率 1减掉从左侧积分到卡方的值减掉从左侧积分到卡方的值 chi=ROUND(chi, 0.001);IF p>0.0001 THEN p=ROUND(p,0.0001);FILEPRINT ; PUT (打印在输出床口) #2 @10'Chisq' @30 'P value'(#表示行) #4 @10 chi @30 p; CARDS ; 34 0 ;run;ods html close;练习五:双向有序R*C列连表列连表用KPA data aaa;do a=1 to 3;do b=1 to 3;input f @@;output;end;end;cards ;58 2 31 42 78 9 17;run;ods html;*简单kappa检验;proc freq data=aaa;weight f;(频数)(频数)tables a*b;test kappa;run ;*加权kappa检验;proc freq;weight f;tables a*b;test wtkap;run ;ods html close;SAS 系统FREQ 过程频数 百分比 行百分比列百分比a *b 表a b 合计1 2 31 5839.4621.3632.046342.8692.06 86.57 3.173.774.7611.112 10.682.001.49 4228.5784.0079.2574.7614.0025.935034.013 85.4423.5311.94 96.1226.4716.981711.5650.0062.963423.13合计 6745.58 5336.052718.37147100.00a *b 表的统计量对称性检验统计量 (S) 2.8561自由度 3Pr > S 0.4144对称性检验指 总体上主对角线的上三角数相加是否与下三角三个数相加 对称性检验与KPA 检验是否一致 是否一个可以代替另一个检验 Pe理论观察一致率 独立假设性基础上计算的 相互独立简单 Kappa 系数Kappa 0.6809渐近标准误差 0.050095% 置信下限 0.583095% 置信上限 0.7788H0 检验: Kappa = 0总体的H0 下的渐近标准误差 0.0597Z 11.4112H0 检验: Kappa = 0单侧 Pr> Z <.0001双侧 Pr>|Z| <.0001总体的KPA是否为0 KPA大于0两种方法的一致性有统计学意义 小于0 不一致性有统计学意义加权的 Kappa 系数加权的 Kappa 0.6614渐近标准误差 0.056095% 置信下限 0.551695% 置信上限 0.7711置信区间不包括0 拒绝H0 按此计算结果可以用一种取代另一种方法 但要看专业要求达到多少才可以 观测一致率达到多少才可以代替样本大小 = 147FREQ 过程频数 百分比 行百分比列百分比a *b 表a b 合计1 2 31 5839.4692.0686.5721.363.173.7732.044.7611.116342.862 10.682.001.494228.5784.0079.2574.7614.0025.935034.013 85.4423.5311.9496.1226.4716.981711.5650.0062.963423.13合计 6745.58 5336.052718.37147100.00a *b 表的统计量对称性检验统计量 (S) 2.8561自由度 3Pr > S 0.4144简单 Kappa 系数Kappa 0.6809渐近标准误差 0.050095% 置信下限 0.583095% 置信上限 0.7788加权的 Kappa 系数加权的 Kappa 0.6614渐近标准误差 0.056095% 置信下限 0.551695% 置信上限 0.7711H0 检验: 加权的 Kappa = 0H0 下的渐近标准误差 0.0646Z 10.2406单侧 Pr> Z <.0001双侧 Pr>|Z| <.0001对加权的KPA 检验 与简单的(利用对角线上的数据分析)加权还要利用对角线以外的数据分析 样本大小 = 147练习六:双向无序R*C 列连表列连表 用卡方理论频数小于5没有超过五分之一,没有超过五分之一,一般用卡方一般用卡方一般用卡方 实在不行用FISHER 检验检验 超过用KPA 两种血型都是按小中大排列两种血型都是按小中大排列 相互不影响相互不影响 独立的独立的 接受H0 不一致不一致行与列变量相互不影响行与列变量相互不影响 DATA PGM20A; DO A=1 TO 4; DO B=1 TO 3;INPUT F @@;OUTPUT ;END ;END ;CARDS ;431 490 902 388 410 800 495 587 950 137 179 325 ; run ; ods html ; PROC FREQ ; WEIGHT F;TABLES A*B / A*B / CHISQCHISQ ;*exact; RUN ;ods html close ;样本大小 = 6094练习七:单向有序R*C 秩和检验秩和检验*方法1;(单因素非参数 HO 三个药物疗效相同 H1不完全相等)不完全相等) DATA PGM20C; DO A=1 TO 4; DO B=1 TO 3; INPUT F @@;OUTPUT ;END ;END ;CARDS ; 15 4 1 49 9 15 31 50 45 5 22 24 ; run ; ods html ;PROC NPAR1WAY WILCOXON ; FREQ FREQ F;CLASS B; VAR A; RUN ;*方法2;(FIQ CHIM ) proc freq data =PGM20C; weight f;tables b*a/ b*a/cmh cmhscores =rank; run ; ods html close ;总样本大小 = 270练习八:练习八: 双向有序双向有序 属性不同属性不同 R*C 4种目的4种方法种方法SPEARMAN 秩相关分析 DATA PGM20E; DO A=1 TO 3; DO B=1 TO 3;INPUT F @@;OUTPUT ;END ;END ;CARDS ; 215 131 148 67 101 128 44 63 132;run ; ods html ; PROC CORR SPEARMAN ;VAR A B; FREQ F; RUN ;ods html close ;统计分析与SAS 实现第1次上机实习题一、定量资料上机实习题要求:要求:(1) 先判断定量资料所对应的实验设计类型;(2) 假定资料满足参数检验的前提条件,请选用相应设计的定量资料的方差分析,并用SAS 软件实现统计计算;(3) 摘录主要计算结果并合理解释,给出统计学结论和专业结论。

应用数理统计报告所在院系计算机与信息工程学院学科专业农业信息化研究生姓名宋玲指导老师:薛河儒2013年12月21日用线性回归分析方法分析林木生物量的影响因素1.题目在林木生物量生产率研究中,为了了解林地施肥量(x1,kg)、灌水量(x2,10)与生物量(Y,kg)的关系,在同一林区共进行了20次试验,观察值见下表,试建立Y关于x1,x2的线性回归方程。
1.程序DATA ct;INPUT x1 x2 y @@; XSQ=x1*x2; CARDS;54 29 5061 39 5152 26 5270 48 5463 42 5379 64 6068 45 5965 30 6579 51 6776 44 7071 36 7082 50 7375 39 7492 60 7896 62 8292 61 8091 50 8785 47 84 106 72 8890 52 92;PROC REG;MODEL y=x1 x2/P CLI; MODEL y=x1 x2 xsq/P CLI; Run;3.输出结果4.分析结果(1)回归模型是否显著,显著水平是多少?复相关系数是多少?答:回归方程显著,显著水平是<0.0001。
复相关系数是0.9659。
(2)回归系数的估计值是多少?显著性如何?答:Intercept -4.94048 0.1711X1 1.53952 <0.0001X2 -0.94385 <0.0001X1与X2的系数对于表达式极显著,intercept对应的系数对表达式在0.01下不显著(3)写出回归方程的表达式。
y=1.53952x1-0.94385x2 - 4.94048(4)利用残差(实测值与预测值之差)、95%置信取间的上下限讨论预测预报效果及预报的稳定性。
答:根据上面结果可知残差和95%置信区间的上下限的差异很大,最大的达到7.4640.最小的达到0.2868.幅度比较大。

已知某研究对象分为三类,每个样品考察4项指标,各类的观测样品数分别为7,4,6;类外还有3个待判样品(所有观测数据见表2)。
假定样本均来自正态总体。
表2 判别分类的数据(1)试用马氏距离判别法进行判别分析,并对3个待判样品进行判别归类。
(2)使用其他的判别法进行判别分析,并对3个待判样品进行判别归类,然后比较之。
问题求解1判别分析及判别归类使用SAS软件中的DISCRIM过程进行判别归类,SAS程序及结果如下。
data d510;input x1-x4 group @@;cards;6 -11.5 19 90 1-11 -18.5 25 -36 390.2 -17 17 3 2-4 -15 13 54 10 -14 20 35 20.5 -11.5 19 37 3-10 -19 21 -42 30 -23 5 -35 120 -22 8 -20 3-100 -21.4 7 -15 1-100 -21.5 15 -40 213 -17.2 18 2 2-5 -18.5 15 18 110 -18 14 50 1-8 -14 16 56 10.6 -13 26 21 3-40 -20 22 -50 3-8 -14 16 56 .92.2 -17 18 3 .-14 -18.5 25 -36 .;proc print;run;proc discrim data=d510 simple pcov wsscp psscp wcovdistance list;class group;var x1-x4;run;从结果来看,样本2、3类之间的马氏距离为d 212=1.34,检验(2)(3)0:H μμ= 的F 统计量为0.63177,相应的p =0.651>0.10,故在显著性水平=0.10α时量总体2、3类的均值向量没有显著差异,即认为对讨论样本分为2、3类的判别问题是没有太大意义的。
此外,判别结果中两个样本被判错归类:1类中8号样本应属于2类,2类中9号样本应属于1类;且待判得三个样本分别属于1,2,3类。
一、数据集整理与SAS基本编程1、试用产生标准正态分布函数的随机函数normal(seed)产生均值为170,方差为64的正态随机数100个,并计算其常规统计量(均值、标准差、变异系数、偏度和峰度)。
data date1;mu=170;sigma=8;do i=1to100;y=mu+sigma*RANNOR(0);output ;end;run;proc means data=data1 mean std cv stderr skewness;var y;output out=result;run;2、设已知数据集class中有5个变量:name, sex, age, height 和weight,请编写程序新建数据集class1,其中class1只包含name, sex, age三个变量,且把name重命名为id。
data class;input name$ sex$ age heigh weigh;cards;小明男 15 160 50;run;data class1;set class;keep name sex age; rename name=id ; run ;proc print data =class1; run ;3、SAS 的逻辑库可分为永久库和临时库两种,请编写一段程序直接建立永久库sasuser 中的下例数据集,并按降序排序。
数据名tong :20 13 20 16 23 19 19 16data Sasuser.tong; input x@@; cards ;20 13 20 16 23 19 19 16 ; run ;proc sort data =Sasuser.tong; by descending x ; run ;proc print data =Sasuser.tong; run ;4、设已知数据集data1和数据集data2number province 1 Hebei 3 Zhejiang 5Gansu请编写程序串接data1和data2,且分组变量为number 。
02.输出数据报表利用SAS数据集,可以用PROC PRINT过程步根据需要输出各种满足一定条件的报表。
一、直接输出语法:proc print data = 数据集;run;注:此时(不加任何参数),默认(1)输出数据集中的所有观测值和变量;(2)报表最左侧增加一列观测值计数列“[Obs]列”;(3)报表中变量出现的顺序与数据集中位置相同。
(4)若要双倍行距输出报表,可以在数据集后面加上可选参数:“double”.例1输出路径'D:\我的文档\My SAS Files\9.3'下的SAS数据集therapy.代码:libname patients 'D:\我的文档\My SAS Files\9.3';proc print data=patients.therapy; /* 注意数据集前加上 data = 否则报错 */运行结果(部分):二、选择变量和输出顺序语法:proc print data = 数据集;var 变量1 变量2 …;run;注:(1)若不输出观测值计数列[Obs],需加上参数noobs;(2)若要指定某列或某几列代替“[Obs]列”,可用id 变量1 变量2 …注意:若一个变量既是var变量又是id变量,将输出两次。
例2(1)输出原始数据集sasuser.admit(2)只输出变量age height weight fee代码:run;proc print data=sasuser.admit;var Age Height Weight Fee;id ID Name;run;运行结果(部分):三、选择部分观测值语法:proc print data = 数据集;where 条件语句run;表示选择满足某条件的观测值。
注意,where语句可以指定数据集中任何变量,而不受var语句的限制。
条件语句可以由各种SAS算符和括号组合而成,为此下面介绍一点SAS中的比较、逻辑算符:例3输出数据集Sasuser.admit中满足条件Age>30并且Height>65的观测值,只输出变量Age Height Weight Fee.代码:var Age Height Weight Fee;where Age>30 and Height>65;run;运行结果(部分):四、对数据进行排序语法:proc sort data=数据集out=新数据集;by <descending > 变量1 变量2 …;run;注:(1)省略“out=新数据集”,原数据集将被排好序的数据集替换;(2)“<descending >”为可选参数(递减排序),只对紧随其后变量起作用;默认是递增排序;(3)先按变量1排序,变量1相同,再按变量2排序…(4)缺省值,当成最小的值。
设在某地区抽取了14块岩石标本,其中7块含矿,7块不含矿。
对每块岩石测定了Cu,Ag,Bi三种化学成分的含量,得到的数据如表1。
表1 岩石化学成分的含量数据(1)假定两类样本服从正态分布,使用广义平方距离判别法进行判别归类(先验概率取为相等,并假定两类样本的协方差阵相等);(2)今得一块标本,并测得其Cu,Ag,Bi的含量分别为2.95,2.15和1.54,试判断该标本是含矿还是不含矿?问题求解1 使用广义平方距离判别法对样本进行判别归类用SAS软件中的DISCRIM过程进行判别归类。
SAS程序及结果如下。
data d59;input group x1-x3@@;cards;1 2.58 0.9 0.951 2.9 1.23 11 3.55 1.15 11 2.35 1.15 0.791 3.54 1.85 0.791 2.7 2.23 1.31 2.7 1.7 0.482 2.25 1.98 1.062 2.16 1.8 1.062 2.33 1.74 1.12 1.96 1.48 1.042 1.94 1.4 12 3 1.3 12 2.78 1.7 1.48;proc print data=d59;run;proc discrim data=d59 pool=yes distance list; class group;var x1-x3;run;由输出结果可知,两总体间的广义平方距离为D 2=3.19774。
还可知两个三元总体均值相等的检验结果:D =3.19774,F =3.10891,p =0.0756<0.10,故在显著性水平=0.10α时量总体的均值向量有显著差异,即认为讨论这两个三元总体的判别问题是有意义的。
线性判别函数为:1231.110513.78958.212011.3311,28.737510.31398.990416.8578.Y Cu Ag Bi Y Cu Ag Bi =-+++=-+++判别结果为含矿的6号样本错判为不含矿;不含矿的13号样本错判为含矿。
地质勘探中,在A,B,C 三个地区采集了一些岩石,测量其部分化学成分,其数据见表3.5。
假定这三个地区掩饰的成分遵从()3,(1,2,3)(0.05)i i N i μα∑==()。
(1)检验不全01231123:=:,,H H ∑=∑∑∑∑∑;不全等; (2)检验(1)(2)(1)(2)01::H H μμμμ=≠;;(3)检验(1)(2)(3)()()01::,i j H H i j μμμμμ==≠≠;存在使。
表3.5 岩石部分化学成分数据解: (1)检验假设01231123:=:,,H H ∑=∑∑∑∑∑;不全等,在H 0成立时,取近似检验统计量为2()f χ 统计量:()()*4=121ln d M d ξλ-=--。
由样本值计算三个总体的样本协方差阵:1(1)(1)(1)(1)11()()11111110.243081=0.642649.2855240.014060.020520.00452n S A X X X X n n ααα='==----⎛⎫ ⎪- ⎪ ⎪⎝⎭∑()(),1(2)(2)(2)(2)23()()12211116.30461= 4.756710.672230.05570.23880.006675n S A X X X X n n ααα='==----⎛⎫ ⎪- ⎪ ⎪-⎝⎭∑()(), 1(3)(3)(3)(3)33()()13311112.97141=0.63370.342140.00010.002950.001875n S A X X X Xn n ααα='==----⎛⎫ ⎪ ⎪ ⎪-⎝⎭∑()()。
进一步计算可得12310.0018318,0.0000942,0.0011851,0.0000417,10S A S S S ===== 24.52397,0.433333,12,M d f ===(1)=13.896916d M ξ=-。
对给定显著性水平=0.05α,利用软件SAS9.3进行检验时,首先计算p 值:p =P {ξ≥13.896916}=0.3073394。
因为p 值=0.3073394>0.05,故接收0H ,即认为方差阵之间无显著性差异。
proc iml ; n1=5;n2=4;n3=4; n=n1+n2+n3;k=3;p=3; x1={47.22 5.06 0.1, 47.45 4.35 0.15,47.526.850.12,47.864.190.17,47.317.570.18};x2={54.33 6.220.12,56.173.310.15,54.42.430.22,52.625.920.12};x3={43.1210.330.05,42.059.670.08,42.59.620.02,40.779.680.04};xx=x1//x2//x3; /*三组样本纵向拼接*/mm1=i(5)-j(5,5,1)/n1;mm2=i(4)-j(4,4,1)/n2;mm=i(n)-j(n,n,1)/n;a1=x1`*mm1*x1;print a1;a2=x2`*mm2*x2;print a2;a3=x3`*mm2*x3;print a3;tt=xx`*mm*xx;print tt;/*总离差阵*/a=a1+a2+a3;print a;/*组离差阵*/da=det(a/(n-k));/*合并样本协差阵*/da1=det(a1/(n1-1));/*每个总体的样本协差阵阵*/da2=det(a2/(n2-1));da3=det(a3/(n3-1));m=(n-k)*log(da)-(4*log(da1)+3*log(da2)+3*log(da3)); dd=(2*p*p+3*p-1)*(k+1)/(6*(p+1)*(n-k));df=p*(p+1)*(k-1)/2; /*卡方分布自由度*/kc=(1-dd)*m; /*统计量值*/print da da1 da2 da3 m dd df;p0=1-probchi(kc,df); /*显著性概率*/print kc p0;quit;(2) 提出假设(1)(2)(1)(2)01::H H μμμμ=≠,。
取检验统计量为2+1(3,6,9)(2)n m p F Tp n m n m --====+-,由样本值计算得:1=(47.472.5.604,0.144)=(54.38,4.47,0.1525)X X ''()(2),,120.24308=0.642649.285520.014060.020520.004526.3046= 4.756710.67220.05570.23880.006675A A ⎛⎫⎪- ⎪ ⎪⎝⎭⎛⎫⎪- ⎪ ⎪-⎝⎭,,进一步计算得:211112(2)()'()()=60.666995D n m X X A A X X -=+--+-()(2)()(2),22134.81554,nm T D n m==+ 2132.098939(2)n m p F T n m p+--==+-。
对给定显著性水平=0.05α,利用软件SAS9.3进行检验时,首先计算p 值:p =P {F ≥32.098939}=0.0010831。
因为p 值=0.0010831<0.05,故否定0H ,即认为A ,B 两地岩石化学成分数据存在显著性差异。
在这种情况下,可能犯第一类错误,且犯第一类错误的概率为0.05。
SAS 程序及结果如下:proc iml ; n=5;m=4; p=3; x={ 47.22 5.06 0.1, 47.45 4.35 0.15, 47.52 6.85 0.12, 47.86 4.19 0.17, 47.31 7.57 0.18 } ;ln={[5] 1} ;x0=(ln*x)`/n; print x0; mx=i(n)-j(n,n,1)/n; a1=x`*mx*x; print a1; y={ 54.33 6.22 0.12, 56.17 3.31 0.15, 54.4 2.430.22,52.62 5.92 0.12} ;lm={[4] 1} ;y0=(lm*y)`/m; print y0; my=i(m)-j(m,m,1)/m; a2=y`*my*y; print a2; a=a1+a2; xy=x0-y0; ai=inv(a); print a ai; dd=xy*ai*xy`; d2=(m+n-2)*dd; t2=n*m*d2/(n+m) ;f=(n+m-1-p)*t2/((n+m-2)*p); fa=finv(0.95,p,m+n-p-1); beta=probf(f,p,m+n-p-1,t2); print d2 t2 f beta; pp=1-probf(f,p,m+n-p-1); print pp; quit ;(3) 检验假设(1)(2)(3)()()01::,i j H H i j μμμμμ==≠≠;存在使;因似然比统计量~(,,1)p n k k ΛΛ-- ,本题中k-1=2,可以利用Λ统计量与F 统计量的关系,去检验统计量为F 统计量:3,3,13),F k p n p Λ====Λ由样本值计算得:47.947696.5538460.11692=)3(,X ',,及(1)(2)(3)47.47254.3842.115.604 4.479.8250.1440.15250.047,,5X X X ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦, 3(1)()(1)()123()()113(1)(1)()()11()()9.51908= 4.7656420.299820.069660.215330.01307=()()312.46343132.506284.9823082.5417077 1.5488460.0410769ttn t t t n t A A A A X X X XT X X X X αααααα===='=++=--⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦'--⎡=--⎣∑∑∑∑⎤⎢⎥⎢⎥⎢⎥⎦,进一步计算得:1.8318441=0.0160379114.21942A T Λ==,22134.81554,nm T D n m==+810.12664118.39023430.126641f -===。
对给定显著性水平=0.05α,利用软件SAS9.3进行检验时,首先计算p 值:p =P {F ≥18.390234}=2.3451×10-6。
因为p 值=2.3451×10-6<0.05,故否定0H ,即认为A ,B ,C 三地岩石化学成分数据存在显著性差异。
在这种情况下,可能犯第一类错误,且犯第一类错误的概率为0.05。
proc iml ; n1=5;n2=4;n3=4; n=n1+n2+n3;k=3;p=3; x1={47.22 5.06 0.1, 47.45 4.35 0.15, 47.52 6.85 0.12, 47.86 4.19 0.17,47.317.570.18};x2={54.33 6.220.12,56.173.310.15,54.42.430.22,52.625.920.12};x3={43.1210.330.05,42.059.670.08,42.59.620.02,40.779.680.04};xx=x1//x2//x3; /*三组样本纵向拼接*/ln={[5]1};lnn{[4]1};lnnn={[13]1};x10=(ln*x1)`/n1;x20=(lnn*x2)`/n2;x30=(lnn*x3)`/n3;xx0=(lnnn*x1)`/n1;mm1=i(5)-j(5,5,1)/n1;mm2=i(4)-j(4,4,1)/n2;mm=i(n)-j(n,n,1)/n;a1=x1`*mm1*x1;a2=x2`*mm2*x2;a3=x3`*mm2*x3;tt=xx`*mm*xx;print tt;/*总离差阵*/a=a1+a2+a3; print a;/*组离差阵*/da=det(a);/*合并样本协差阵*/dt=det(tt);a0=da/dt;print da dt a0;b=sqrt(a0); print b;f=(n-k-p+1)*(1-b)/(b*p);df1=2*p;df2=2*(n-k-p+1);p0=1-probf(f,df1,df2); /*显著性概率*/print f p0;f1=(tt[1,1]-a[1,1])*(n-k)/((k-1)*a[1,1]); p1=1-probf(f1,k-1,n-k);fa=finv(0.95,k-1,n-k);print fa f1 p1;quit;。