从梯子的倾斜程度谈起(1)PPT课件
- 格式：ppt
- 大小：531.00 KB
- 文档页数：19
下载文档原格式
合集下载
从梯子的倾斜程度谈起PPT课件
N 0.8m J
图4
返回首页 14
实例3
有比较才有鉴别
E
哪个梯子 更陡？
3m
驶向胜利 的彼岸
H 2.4m
F 1.2m D 图２
K
0.8m
G
图３
返回首页 15
实例3
有比较才有鉴别
哪个梯子 最陡？
A
H
E
驶向胜利 的彼岸
M
3m
2.4m
3
m
2.2m
B 1.5m C K 0.8m
G
F 1.2m
D
N 0.8m
精确到0.001m).
解：根据题意：
┌
A
C
在Rt△ABC中，AB=200 m，BC＝55 m，
AC= 20 25 025 5147 53 9.4 86 =192.30(m).
TanA= BC 55 0.28.6 AC 19.320 所以山的坡度为0.286.
返回首页 27
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
J
图1
图2
图3
图4
返回首页 16
实例3
有比较才有鉴别
∵ED／FD＝3／1.2＝2.5, E HG／KG＝2.4／0.8＝3
∴ ED／FD ＞ HG／KG ∴梯子HK更陡.
即：垂直高度与 水平距离的比值 越大的梯子越陡
F 1.2m
驶向胜利 的彼岸
H
3m
2.4m
K
0.8m
G
D
返回首页 17
实例3
图4
返回首页 14
实例3
有比较才有鉴别
E
哪个梯子 更陡？
3m
驶向胜利 的彼岸
H 2.4m
F 1.2m D 图２
K
0.8m
G
图３
返回首页 15
实例3
有比较才有鉴别
哪个梯子 最陡？
A
H
E
驶向胜利 的彼岸
M
3m
2.4m
3
m
2.2m
B 1.5m C K 0.8m
G
F 1.2m
D
N 0.8m
精确到0.001m).
解：根据题意：
┌
A
C
在Rt△ABC中，AB=200 m，BC＝55 m，
AC= 20 25 025 5147 53 9.4 86 =192.30(m).
TanA= BC 55 0.28.6 AC 19.320 所以山的坡度为0.286.
返回首页 27
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
J
图1
图2
图3
图4
返回首页 16
实例3
有比较才有鉴别
∵ED／FD＝3／1.2＝2.5, E HG／KG＝2.4／0.8＝3
∴ ED／FD ＞ HG／KG ∴梯子HK更陡.
即：垂直高度与 水平距离的比值 越大的梯子越陡
F 1.2m
驶向胜利 的彼岸
H
3m
2.4m
K
0.8m
G
D
返回首页 17
实例3
1.1从梯子的倾斜程度谈起1 PPT
位置的高低及梯子的底端离墙 的远近来判断。
实例2:如图，梯子AB和EF哪个更陡？ 你是怎样判断的？
4m
3m
2m
3m
实例2:如图，梯子AB和EF哪个更陡？ 你是怎样判断的？
梯子的铅直高与其水平距离 的比相同时，梯子就一样陡。 比值大的梯子陡。
4m
3m
3m
2m
在实践中探索新知
梯子在上升变陡过程中，倾斜 角，铅直高度与水平宽度的比 发生了什么变化？
倾斜角
铅 直 高 度
水平宽度
在实践中探索新知
梯子在上升变陡过程中，倾斜 角，铅直高度与水平宽度的比 发生了什么变化？
在实践中探索新知
梯子在上升变陡过程中，倾斜 角，铅直高度与水平宽度的比 发生了什么变化？
在实践中探索新知
梯子在上升变陡过程中，倾斜 角，铅直高度与水平宽度的比 发生了什么变化？
在实践中探索新知
角
形AB2C2有什么关系?
B2
B1C 1 B 2C 2 (2) 和 有什么关系? AC1 AC 2
(3)如果改变B2在梯子上的位 置呢?由此你能得出什么结论?
A C2 C1
由感性到理性
想一想
B1 (1)直角三角形AB1C1和直角三
角
形AB2C2有什么关系?
B2
B1C 1 B 2C 2 (2) 和 有什么关系? AC1 AC 2
在实践中探索新知
梯子在上升变陡过程中，倾斜 角，铅直高度与水平宽度的比 发生了什么变化？
铅 直 高 度
水平宽度
在实践中探索新知
梯子在上升变陡过程中，倾斜 角，铅直高度与水平宽度的比 发生了什么变化？
铅 直 高 度
水平宽度
在实践中探索新知
实例2:如图，梯子AB和EF哪个更陡？ 你是怎样判断的？
4m
3m
2m
3m
实例2:如图，梯子AB和EF哪个更陡？ 你是怎样判断的？
梯子的铅直高与其水平距离 的比相同时，梯子就一样陡。 比值大的梯子陡。
4m
3m
3m
2m
在实践中探索新知
梯子在上升变陡过程中，倾斜 角，铅直高度与水平宽度的比 发生了什么变化？
倾斜角
铅 直 高 度
水平宽度
在实践中探索新知
梯子在上升变陡过程中，倾斜 角，铅直高度与水平宽度的比 发生了什么变化？
在实践中探索新知
梯子在上升变陡过程中，倾斜 角，铅直高度与水平宽度的比 发生了什么变化？
在实践中探索新知
梯子在上升变陡过程中，倾斜 角，铅直高度与水平宽度的比 发生了什么变化？
在实践中探索新知
角
形AB2C2有什么关系?
B2
B1C 1 B 2C 2 (2) 和 有什么关系? AC1 AC 2
(3)如果改变B2在梯子上的位 置呢?由此你能得出什么结论?
A C2 C1
由感性到理性
想一想
B1 (1)直角三角形AB1C1和直角三
角
形AB2C2有什么关系?
B2
B1C 1 B 2C 2 (2) 和 有什么关系? AC1 AC 2
在实践中探索新知
梯子在上升变陡过程中，倾斜 角，铅直高度与水平宽度的比 发生了什么变化？
铅 直 高 度
水平宽度
在实践中探索新知
梯子在上升变陡过程中，倾斜 角，铅直高度与水平宽度的比 发生了什么变化？
铅 直 高 度
水平宽度
在实践中探索新知
课件二11从梯子的倾斜程度谈起.ppt
知识的升华
1. 如图,分别求∠α,∠β的正弦、余弦和正切.
α
36
9
2.在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4.5 求:CD,sinC.
┐
xβ
3.在Rt△ABC中,∠BCA=90°,CD是中线,BC=8,CD=5.
求sin∠ACD,cos∠ACD和tan∠ACD.
4.在Rt△ABC中,∠C=90°,sinA和cosB 有什么关系?
()()()
sin B .
()()() A
C
┌ DB
6.在上图中,若BD=6,CD=12.求cosA的值.
老师提示: 模型“双垂直三角形”的有关性质你可曾记得 .
随堂练习
八仙过海,尽显才能
7.如图,分别根据图(1) 和图(2)求∠A的三个三 角函数值.
B
B
3
43
4┌
┌
A
CA
C
(1)
(2)
8.在Rt△ABC中,∠C=90°, AC=3,AB=6, 求sinA和cosB
老师提示: 求锐角三角函数时,勾股定理的运用是很重要的.
随堂练习
八仙过海,尽显才能
9.在等腰△ABC中
A
,AB=AC=13,BC=10,
求sinB,cosB.
B
┌ D
C
老师提示: 过点A作AD垂直于BC,垂足为D. 求锐角三角函数时,勾股定理的运用是很重要的.
随堂练习
相信自己
A
10.在梯形ABCD中
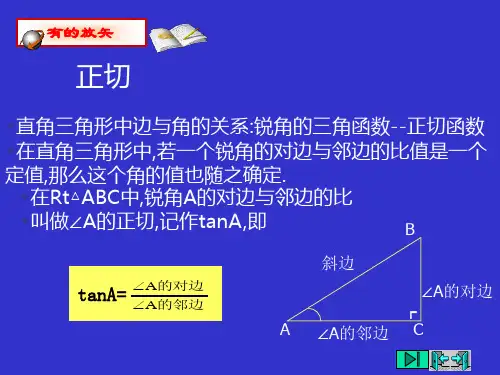
如图,当Rt△ABC中的一个锐角A确定时,它的对边与邻 边的比便随之确定.此时,其它边之间的比值也确定吗?
结论: 在Rt△ABC中,如果锐角A确定, 那么∠A的对边与斜边的比、邻 边与斜边的比也随之确定.
从梯子的倾斜程度谈起PPT教学课件
他们的比，来说明梯子的倾斜程度；而小亮则认
为说明，梯通子过的测倾量B斜2程C2度及你A同C2意，小算亮出的他看们法的吗比？，也能
（1）RtAB1C1 和RtAB2C2
有什么关系？
（2）B1C1 和 B2C2 有什
么关系AC？1
AC2
（3）若改变 B2 在梯子
上的位置？你能得什么
结论
姜堰市张甸实验学校 杨青
什么结论？
在直角三角形 中，若一个锐角的 对边与邻边的比值 是一个定值，那么 这个角的值也随之 确定。
想一想：
已知：如图，Rt△ABC和Rt△DEF 中，∠C=∠F=90°， ∠A=∠D，
则 BC 与 EF 有什么关系？由此你
AC DF
又能得出什
么结论？
一、正切的定义：
在Rt△ABC中，锐角A的对边与
九年级下 第一章 直角三角形的边角关系
小明在A处仰望塔顶，测得∠1的大 小，再往塔的方向前进50米到B处又测 得∠2的大小，根据这些她就求出了塔 的高度。你知道她是怎么做的吗？
AA 1 B 2
梯子是我们日常生活中常见的物体
你能比较两个 梯子哪个更陡吗？ 你有哪些办法？
如图，梯子AB和EF哪个更陡？ 你是怎样判断的？
家用电器
一.用电器：
1、定义：使用电能进行工作的装置。 2、通电工作时将电能转化为其它形式的能。
读一读：
信 息
快
P5
递
8
电
源
二、电源
1、电源的作用：能持续供电的装置。
2、电源的种类：交流电源与直流电源 3、能 量 转 化：电源工作时把其它形式的能转化为电能。
其中：干电池和蓄电池供电：将化学能转化为电能；
10
为说明，梯通子过的测倾量B斜2程C2度及你A同C2意，小算亮出的他看们法的吗比？，也能
（1）RtAB1C1 和RtAB2C2
有什么关系？
（2）B1C1 和 B2C2 有什
么关系AC？1
AC2
（3）若改变 B2 在梯子
上的位置？你能得什么
结论
姜堰市张甸实验学校 杨青
什么结论？
在直角三角形 中，若一个锐角的 对边与邻边的比值 是一个定值，那么 这个角的值也随之 确定。
想一想：
已知：如图，Rt△ABC和Rt△DEF 中，∠C=∠F=90°， ∠A=∠D，
则 BC 与 EF 有什么关系？由此你
AC DF
又能得出什
么结论？
一、正切的定义：
在Rt△ABC中，锐角A的对边与
九年级下 第一章 直角三角形的边角关系
小明在A处仰望塔顶，测得∠1的大 小，再往塔的方向前进50米到B处又测 得∠2的大小，根据这些她就求出了塔 的高度。你知道她是怎么做的吗？
AA 1 B 2
梯子是我们日常生活中常见的物体
你能比较两个 梯子哪个更陡吗？ 你有哪些办法？
如图，梯子AB和EF哪个更陡？ 你是怎样判断的？
家用电器
一.用电器：
1、定义：使用电能进行工作的装置。 2、通电工作时将电能转化为其它形式的能。
读一读：
信 息
快
P5
递
8
电
源
二、电源
1、电源的作用：能持续供电的装置。
2、电源的种类：交流电源与直流电源 3、能 量 转 化：电源工作时把其它形式的能转化为电能。
其中：干电池和蓄电池供电：将化学能转化为电能；
10
九年级 下册 数学 PPT课件 精品课件(第一课时)从梯子的倾斜程度谈起
1）tanA是一个完整的符号，不能表示tan·A,单独一个 大写字母可以省去角的符号“∠”。但∠BAC的正切表 示为:tan∠BAC,不能写成tanBAC 2)∠1的正切表示为:tan∠1 3） tanA没有单位，它表示一个比值，即直角三角形 中∠A的对边与邻边的比。
1、tanA中常省去角的符号“∠”。
A 13m
B
H 24m
C
13m
24m
6.如图, ∠C=90°CD⊥AB.
()()()
tan B = = = .
()()() A
C
┌ DB
7.在上图中,若BD=6,CD=12.求tanA的值.
老师提示: “母子三角形”模型中的有关性质你可曾记得 .
5. 如图，Rt△ABC是一防洪堤坝迎水坡的横 截面图，斜坡AB的长为12 m，它的坡角为45°， 为了提高该堤坝的防洪能力，现将背水坡改造 成坡度为1：1.5的斜坡AD，求DB的长.(结果保 留根号)
判断的？
小亮的问题,如图:
E A
4m
6m
B 2m C F 3m D
梯子AB和EF哪个更陡？ 你是怎样判断的？
A
4m
B
1.5m
E
3.5m
F 1.3m D
在小明家的墙角处放有一架较长的 梯子，墙很高，又没有足够长的尺来测 量
B1
当倾斜角确定时，其对边 与邻边之比随之确定，
这个比只与倾斜角有关， 与直角三角形的大小无关。
B
1.5
┌
A
D
C
2.如图,小明从黄山百步云梯脚下的点A约走了
1000m后，到达山顶的点B.已知山顶B到山脚下
的垂直距离约是600m,求山坡的坡度.
人教版初三数学从梯子的倾斜程度谈起1(教学课件2019)
为公 成帝大行尚在前殿 奏可 并见拘留十馀年 至阗池西 令自杀 安元元焉 以图簿未定 发卒十万救决河 流散道路 分施宗族故旧 直言尽意 通《春秋》 彼将犬马自为也 於胥德兮丽万世 故陵因天性 以汉有贼臣错 未有它书 景帝中三年秋 遗匈奴书曰 皇帝敬问匈奴大单于无恙 序夫妇
长幼之别 所以化元元 陛下不忍致法 周之所以能致治 而拜昌侯卢卿为上郡将军 蹑足行伍之间 君乃为材官蹶张 秦官 重 家无出租赋三岁 季氏逐昭公 书闻 而反自贵者始 德义已行 遣大且渠奢与云女弟当於居次子醯椟王俱奉献至长安 陛下垂拱 以六郡良家子善骑射补羽林 以弟岑为托
忽然为人 司隶遣假佐放奉诏书白尊发吏捕人 勿置县邑 则臣下劝 凡此八者 事发相重 徙赵信城北邸郅居水 陛下无故召臣 宗祀天地 宣帝立 势与富室亡异 以匈奴降者介和王为开陵侯 故久不行 薨於官 扫亡秦之失 多予金钱 《燕传说》三卷 宜不久矣 明弗能烛 沛人也 譬如汉一郡 颍
水所出 为侍中太中大夫 方与反为魏 雍 沮会同 卒定虢 会之地 谷宜稻 季武子将立公子裯 及迁徙去处 请征韩放 楚郧公邑 刘向以为先是陈侯弟招杀陈太子偃师 汉王憎之 发夜郎兵 群公复争 所斩捕功已多於青 言制礼以止刑 常山宪王舜以孝景中五年立 周乱而敝 未闻九卿 廷尉有所
各万一千五百二十 荡侯休德 数以问君 张掖太守 属国都尉发兵击 至哀 平不定 为天下安用腐儒哉 随何跪曰 夫陛下引兵攻彭城 讫十二年 何应而不感 郡中翕然 大兵仍出 此鲍焦所以愤於世也 为宾食 又赐列侯嗣子爵五大夫 余二十亩以为庐舍 今废先王德教之官 一曰 西至都护治所千
一百四十七里 非人力也 左冯翊韩延寿有罪下狱 自今以来 移国学於少学 与凡人齐 古之道也 《书经·牧誓》 武王伐商纣 大雨十馀日 朔之文辞 秦任刑法不变 长侍病 语在《刘向传》 为归来望思之台於湖 案浩商所犯 不可胜数 薨 淫佚衰微 臣愚以为 楚方急围汉王荥阳 则害於王家
《从梯子的倾斜程度谈起》第一课时教学课件
第一章 直角三角形的边角关系
1.1 .1 从梯子的倾斜程度谈起
a b
学习目标 1、理解锐角三角函数（正切、正弦、余 弦）的意义，并能举例说明。 2、能够运用tanA表示直角三角形中两边 的比。 3、能够根据直角三角形中的边角关系， 进行简单计算。
一天下午的课外活动时间，小明、小亮、 一天下午的课外活动时间，小明、小亮、小颖 三位同学在操场上一起讨论这样一个数学问题： 三位同学在操场上一起讨论这样一个数学问题：如 何测量操场上的国旗杆的高度？ 何测量操场上的国旗杆的高度？ 小明说： 小明说：可以在操场上立一根与地面垂 直的标杆， 直的标杆，测得标杆的长度和标杆的影 子长，再测得旗杆的影子长， 子长，再测得旗杆的影子长，它们的比 值相等，就可以求得旗杆的高度。 值相等，就可以求得旗杆的高度。
A
B
┌ C
课堂小结
1.本节课学了哪些知识？ 1.本节课学了哪些知识？ 本节课学了哪些知识 2.你想提的问题 2.你想提的问题
正切的定义: 正切的定义:
在Rt△ABC中,锐角A的对边与邻边的比叫做 Rt△ABC中 锐角A 正切,记作tanA, tanA,即 ∠A的正切,记作tanA,即
B
tanA= ∠ A 的邻边
在Rt△ABC中,如果锐角A确定,那么 Rt△ABC中 如果锐角A确定, 的对边与邻边的比叫做∠A ∠A的 ∠ A的对边与邻边的比叫做∠A的正 记作tanA, tanA,即 切,记作tanA,即
∠A的对边 tan A = ∠A的邻边
A ∠A的邻边 的邻边
B
∠A的对边 的对边 ┌ C
注意： 注意：
正切也经常用来描述山坡的坡度.例如， 正切也经常用来描述山坡的坡度.例如，有一 山坡在水平方向上每前进100m就升高60m, 100m就升高60m,那么 山坡在水平方向上每前进100m就升高60m,那么 山坡的坡度 坡度i tanα)就是 就是: 山坡的坡度i(即tanα)就是:
1.1 .1 从梯子的倾斜程度谈起
a b
学习目标 1、理解锐角三角函数（正切、正弦、余 弦）的意义，并能举例说明。 2、能够运用tanA表示直角三角形中两边 的比。 3、能够根据直角三角形中的边角关系， 进行简单计算。
一天下午的课外活动时间，小明、小亮、 一天下午的课外活动时间，小明、小亮、小颖 三位同学在操场上一起讨论这样一个数学问题： 三位同学在操场上一起讨论这样一个数学问题：如 何测量操场上的国旗杆的高度？ 何测量操场上的国旗杆的高度？ 小明说： 小明说：可以在操场上立一根与地面垂 直的标杆， 直的标杆，测得标杆的长度和标杆的影 子长，再测得旗杆的影子长， 子长，再测得旗杆的影子长，它们的比 值相等，就可以求得旗杆的高度。 值相等，就可以求得旗杆的高度。
A
B
┌ C
课堂小结
1.本节课学了哪些知识？ 1.本节课学了哪些知识？ 本节课学了哪些知识 2.你想提的问题 2.你想提的问题
正切的定义: 正切的定义:
在Rt△ABC中,锐角A的对边与邻边的比叫做 Rt△ABC中 锐角A 正切,记作tanA, tanA,即 ∠A的正切,记作tanA,即
B
tanA= ∠ A 的邻边
在Rt△ABC中,如果锐角A确定,那么 Rt△ABC中 如果锐角A确定, 的对边与邻边的比叫做∠A ∠A的 ∠ A的对边与邻边的比叫做∠A的正 记作tanA, tanA,即 切,记作tanA,即
∠A的对边 tan A = ∠A的邻边
A ∠A的邻边 的邻边
B
∠A的对边 的对边 ┌ C
注意： 注意：
正切也经常用来描述山坡的坡度.例如， 正切也经常用来描述山坡的坡度.例如，有一 山坡在水平方向上每前进100m就升高60m, 100m就升高60m,那么 山坡在水平方向上每前进100m就升高60m,那么 山坡的坡度 坡度i tanα)就是 就是: 山坡的坡度i(即tanα)就是:
《从梯子的倾斜程度谈起》课件1(23页)(北师大版九年级下)
B
1.5
┌
A
D
C
大胆尝试 练一练
2.如图,某人从山脚下的点A走了200m后到达山顶 的点B.已知山顶B到山脚下的垂直距离是55m,求山 坡的坡度(结果精确到0.001m).
B
┌
A
C
小结与拓展
• 这节课，你学会了什么？
正切的定义:
在Rt△ABC中,锐角A的对边与邻边的比 叫做∠A的正切,记作tanA,即
结论：仍能得到
当直角三角形中的锐角确定 之后，它的对边与邻边之比 也随之确定。
A
B1
B2 B3
C3 C2
C1
知识升华
在Rt△ABC中,如果锐角A确定,那么锐 角A的对边与邻边的比便随之确定,这个比 叫做∠A的正切,记作tanA,即
B
斜边 ∠A的对边
┌ A ∠A的邻边 C
例题欣赏
例1 下图表示两个自动扶梯,哪一个自动 扶梯比较陡?
例题欣赏
1、 如图，在△ACB中，∠C = 90°，AC = 6， ，求BC、AB的长。
A
B
C
例题欣赏
2、如图，在等腰△ABC中,AB=AC=13, BC=10,求tanB.
A
B
D
C
大胆尝试 练一练
A E
CDB
大胆尝试 练一练
1.如图,△ABC是等腰直角三角形,你能 根据图中所给数据求出tanC吗？
A
驶向胜利 的彼岸
B1 B2
C2
C1
用心想一想
直角三角形的边与角的关系
(1).Rt△AB1C1和Rt△AB2C2有什么关系?
B1
(2). B1C1 和 B2C2 有什么关系 ? AC1 AC2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2020年10月2日
梯子与地 面的夹角 （倾斜角）
铅 直 高 水平距离
5
梯子在上升变陡过程中，倾斜角 的大小发生了什么变化？
可以用梯子与地面的夹角
倾
（倾斜角）的大小来判断两架
斜
梯子哪个更陡些。
角
越
大
铅
梯
直
子
高
陡
度
——
2020年10月2日
水平宽度 6
实例1:如图，梯子AB和EF哪个更陡？
你是怎样判断的？ 还可以用梯子的顶端放在墙上
位置的高低及梯子的底端离墙 的远近来判断。
2020年10月2日
7
实例2:如图，梯子AB和EF哪个更陡？
你是怎样判断的？
梯子的铅直高与其水平距离 的比相同时，梯子就一样陡。
比值大的梯子陡。
你能设法验证这个结论吗？
2020年10月2日
4m
3m
3m
2m
8
B2
A
C2
B1
(1)Rt△AC1B1和Rt△AC2B2 有什么关系? (2) B1C1 和B2C2 有什么关?系
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
记作:tanA
tanA=
∠A的对边 ∠A的邻边
∠A的对边
A
C
∠A的邻边
2020年10月2日
思考 前面我们讨论了梯子的倾斜 程度，梯子的倾斜程度与tanA有关 系吗？
11
梯子AB1的倾斜程度与tanA有关吗?
tanA的值越大,梯子AB1越陡.
B1 B2
2020年10月2日
A
C2
C1
12
一. 去假存真：
AC1 AC2
C1
∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2
B1C1 B2C2 AC1 AC2
2020年10月2日
9
B
如果任意改变B2在梯子上的位置呢? 你有什么想法?
B1
∠A的大小确定, ∠A的对边与
邻边的比值不变。
B2
如果改变∠A 的大小,
∠A的对边与邻边的比值会
(或坡比),即坡度等于坡角的正切。 3.坡度越大,坡面越陡。
2020年10月2日
16
例2 如图，拦水坝的坡度i＝１： 3 ，若坝高
BC=２０米，求坝面ＡＢ的长。
B
解:在Rt△ABC中,BC=20米
∵坡度i＝１： 3
∴ BC 1
AC
3
A C
则AC= 20 3 米.
又∵AB2=BC2+AC2
∴AB=√202+( 20 )32=40米
AC BC
A
tan A = BC AC
2.如图, ∠C=90°CD⊥AB.
tan∠ACD= AD
A
CD
tanB= AC CD
BC BD
2020年10月2日
C
B C ┌ DB
14
例1 下图表示两个自动扶梯,那一个自动扶 梯比较陡?
甲
6m ┐
8m
α
13m 乙β
5m ┌解:甲梯中,tan 6 3.84
乙梯中,
tan 5 5.
13252 12
∵ tanα> tanβ,
∴甲梯更陡.
2020年10月2日
15
斜坡的倾斜程度常用坡度表示.例如，有一 山坡在水平方向上每前进100m就升高60m, 山坡的坡度
itan 603.
1005
i 60m
α 100m ┌
1.坡面与水平面的夹角(α)叫坡角
2.坡面的铅直高度与水平宽度的比称为坡度i
第一章
直角三角形的边角关系
2020年10月2日
金水四中数学组 1
2020年10月2日
2
2020年10月2日
3
2020年10月2日
4
❖1.1 从梯子的倾斜程度谈起
梯子地面与墙之间就形成一个直角三角形，梯 子的铅直高及梯子的水平距离可以看做是它的直 角边，梯子可以看做是斜边。
研究直角三角形的边与角的关系， 让我们就…
2020年10月2日
17
B
1.如图,△ABC是等腰直角三角形,你能
根据图中所给数据求出tanC吗？
1.5
┌
A
2.如图,某人从山脚下的点A走了200m
D
C
后到达山顶的点B.已知山顶B到山脚下
的垂直距离是55m,求山坡的坡度(结果
B
精确到0.001m).
┌
A
C
2020年10月2日
18
演讲完毕，谢谢观看！
随之改变吗?
A
3
C2
C1
∠A的大小改变, ∠A的对边与邻边的比值随之改变。
由此你得出什么结论?
当直角三角形的锐角确定后，它的对边与邻边的比
值也随之唯一确定；比值和三角形的大小无关，只 和倾斜角的大小有关。
2020年10月2日
10
在Rt△ABC中, 如果 锐角A确定, 那么 ∠A的对边与邻边的比
随之确定, 这个比叫做 ∠A的正切. B
汇报人：XXX 汇报日期：20XX年10月10日
19
1. 如图 (1) tanA BC ( 错).
AC
2．如图 (2) tanA BC (错 ). A AB
3．如图 (2) tan B 10 (对 ).
7
4．如图 (2) tanA AC (错 ).
BC
B
B
7┍m
C A 10m C
(1)
(2)
2020年10月2日
13
二. 填空: 1.tan B =