傅里叶变换的时移特性和频移特性
- 格式:ppt
- 大小:892.00 KB
- 文档页数:15



离散傅里叶变换时移-概述说明以及解释1.引言1.1 概述离散傅里叶变换(Discrete Fourier Transform,简称DFT)是一种将一个离散信号(或称时域信号)转换为频域表示的数学工具。
在现代信号处理和通信领域中,DFT被广泛应用于信号分析、滤波、频谱估计等领域。
DFT的概念源于傅里叶分析,它是将一个连续时间函数表示为一组基函数乘以一系列复数系数的线性组合。
而离散傅里叶变换则是将这一思想应用于离散信号,将离散时间序列转换为离散频率表示。
通过使用离散傅里叶变换,我们可以将一个时域上的离散信号转换为频域上的频谱表示,从而可以更加直观地观察信号的频率成分和能量分布。
离散傅里叶变换的时移性质是指当输入信号在时域上发生时移时,其在频域上的表示也随之发生相应的时移。
这一性质使得我们可以通过时移操作对信号进行处理和分析。
具体来说,如果我们对一个信号进行时移操作,即将信号中的每个样本向前或向后平移若干个位置,那么该信号在频域上的表示也会相应地发生同样的平移。
在本文中,我们将着重讨论离散傅里叶变换时移的原理和性质。
我们将介绍离散傅里叶变换的基本概念和原理,包括如何进行DFT变换、如何计算DFT系数以及DFT的逆变换等。
然后,我们将详细解释离散傅里叶变换的时移性质,包括时域上的时移操作如何在频域上体现以及时域和频域之间的变换关系等。
通过对离散傅里叶变换时移性质的研究,我们可以更好地理解信号在时域和频域之间的关系,以及对信号进行时移操作的影响。
同时,我们还将探讨离散傅里叶变换时移的应用,包括在信号处理、通信系统和图像处理等领域中的具体应用案例。
通过这些应用案例,我们将展示离散傅里叶变换时移的重要性以及它在实际问题中的实用价值。
1.2 文章结构文章结构部分的内容:本文主要分为三个部分:引言、正文和结论。
在引言部分,首先概述了离散傅里叶变换时移的主题,介绍了离散傅里叶变换的基本概念和原理。
接着,详细说明了本文的结构,即按照离散傅里叶变换时移的相关性质展开论述。





傅里叶变换的性质实质就是信号的时域运算关系在傅里叶变换域中的体现,也是求解信号傅里叶变换的基本手段.之迟辟智美创作傅里叶变换具有唯一性.傅氏变换的性质揭示了信号的时域特性和频域特性之间简直定的内在联系.讨论傅里叶变换的性质,目的在于:1. 了解特性的内在联系2. 用性质求3. 了解在通信系统领域中的实用这些性质在内容和形式上具有某种水平的对称性.1.性质2.意义例3-7-1例3-7-2例3-7-3§3.7.2 线性1.性质2.说明这个性质虽然简单,但实际上是应用最多的.例3-7-4§3.7.3 奇偶虚实性奇偶虚实性实际上在§3.4的“傅里叶变换的特殊形式”中已经介绍过. 1.证明:由界说可以获得,则证明:设f(t)是实函数(为虚函数或复函数情况相似,略)显然§3.7.4 标准变换性质1. 性质:2. 证明:综合上述两种情况3.意义(1) 0<a<1 时域扩展,频带压缩.脉冲继续时间增加a倍,信号变动减缓,信号在频域的频带压缩a倍.因此高频分量减少,幅度上升a倍.(2) a>1 时域压缩,频域扩展a倍.继续时间短,变动加快.信号在频域高频分量增加,频带展宽,各分量的幅度下降a倍.此例说明:信号的继续时间与信号占有频带成反比,有时为加速信号的传递,要将信号继续时间压缩,则要以展开频带为价格.§3.7.5 时移特性性质幅度频谱无变动,只影响相位频谱,例3-7-8求下图所示函数的傅里叶变换.解:由对称关系求,又因为得幅频、相频特性分别如下图所示.幅度频谱无变动,只影响相位频谱§3.7.6 时移+标准变换1. 性质:2. 证明:(仿的证明过程)那时,设,则例3-7-9方法一:先标度变换,再时延方法二:先时延再标度变换两种方法结果相同.§3.7.7 频移特性1.性质2.证明3.说明4.应用通信中调制与解调,频分复用§3.7.8 频移特性1.性质2.证明3.说明4.应用通信中调制与解调,频分复用§3.7.9 时域微分性质1.性质2. 证明即3. 特别注意如果f(t)中有确定的直流分量,应先取出直流分量独自求傅里变换,余下部份再用微分性质.§3.7.10 频域微分性质性质:则或例3-7-6解:例3-7-7解:……1. 性质2. 证明其中:(1)变上限积分用带时移的单元阶跃的无限积分暗示,成为(2)交换积分顺序,即先求时移的单元阶跃的信号的傅里叶变换(3)(5).例题——时域积分性质1. 求单元阶跃函数的傅里叶变换.解:则2. 求门函数积分的频谱函数.解:。

一、 信号及其描述1、周期信号频谱的特点:①离散性——周期信号的频谱是离散的;②谐波性——每条谱线只出现在基波频率的整数倍上,基波频率是诸分量频率的公约数;③收敛性——谐波分量的幅值按各自不同的规律收敛。
2、傅里叶变换的性质:奇偶虚实性、对称性、线性叠加性、时间尺度改变特性、时移和频移特性、卷积特性、积分和微分特性。
3、非周期信号频谱的特点:①非周期信号可分解成许多不同频率的正弦、余弦分量之和,包含了从零到无穷大的所有频率分量;②非周期信号的频谱是连续的;③非周期信号的频谱由频谱密度函数来描述,表示单位频宽上的幅值和相位;④非周期信号频域描述的数学基础是傅里叶变换。
二、测试装置的基本特性1、测量装置的静态特性是在静态测量情况下描述实际测量装置与理想时不变线性系统的接近程度。
线性度——测量装置输入、输出之间的关系与理想比例关系的偏离程度。
灵敏度——单位输入变化所引起的输出变化。
回程误差——描述测量装置同输入变化方向有关的输出特性,在整个测量范围内,最大的差值称为回程误差。
分辨力——能引起输出量发生变化的最小输入量。
零点漂移——测量装置的输出零点偏离原始零点的距离,它是可以随时间缓慢变化的量。
灵敏度漂移——由于材料性质的变化所引起的输入与输出关系的变化。
2、传递函数的特点:①()s H 与输入()t x 及系统的初始状态无关,它只表达系统的传输特性;②()s H 是对物理系统的微分描述,只反映系统传输特性而不拘泥于系统的物理结构;③对于实际的物理系统,输入()t x 和输出()t y 都具备各自的量纲;④()s H 中的分母取决于系统的结构。
3、一阶测试系统和二阶测试系统主要涉及哪些动态特性参数,动态特性参数的取值对系统性能有何影响?一般采用怎样的取值原则? 答:测试系统的动态性能指标:一阶系统的参数是时间常数τ;二阶系统的参数是固有频率n ω和阻尼比ξ。
对系统的影响:一阶系统的时间常数τ值越小,系统的工作频率范围越大,响应速度越快。

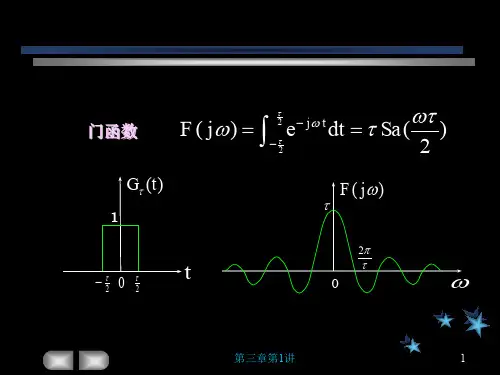
1、门函数F(w)=2w w sin=Sa() w
222、指数函数(单边)f(t)=e-atu(t) F(w)=1,实际上是一个低通滤波器a+jw
3、单位冲激函数F(w)=1,频带无限宽,是一个均匀谱
4、常数1 常数1是一个直流信号,所以它的频谱当然只有在w=0的时候才有值,体现为(w)。
F(w)=2(w) 可以由傅里叶变换的对称性得到
5、正弦函数F(ejw0t)=2(w-w0),相当于是直流信号的移位。
F(sinw0t)=F((ejw0t-e-jw0t)/2)=((w-w0)-(w+w0))
F(sinw0t)=F((e
6、单位冲击序列jw0t-e-jw0t)/2j)=j((w-w0)-(w+w0)) T(t)=(t-Tn) -这是一个周期函数,每隔T出现一个冲击,周期函数的傅里叶变换是离散的F(T(t))=w0(w-nw0)=w0
w0(w) n=-单位冲击序列的傅里叶变换仍然是周期序列,周期是w0=2T
1、线性性傅里叶变换是积分运算,而积分运算是加法。
2、时移特性信号在时域的时移,相当于信号在频域的各频率分量相移,即
3、频移特性(调制定理)f(t-t0)--e-jwt0F(w) 傅里叶变换公式。
傅里叶变换的性质Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】傅里叶变换的性质本质就是信号的时域运算关系在傅里叶变换域中的体现,也是求解信号傅里叶变换的基本手段。
傅里叶变换具有唯一性。
傅氏变换的性质揭示了信号的时域特性和频域特性之间的确定的内在联系。
讨论傅里叶变换的性质,目的在于:1. 了解特性的内在联系2. 用性质求3. 了解在通信系统领域中的实用这些性质在内容和形式上具有某种程度的对称性。
§对称性质1.性质2.意义例3-7-1例3-7-2例3-7-3§ 线性1.性质§ 奇偶虚实性奇偶虚实性实际上在§的“傅里叶变换的特殊形式”中已经介绍过。
1.证明:由定义可以得到2.若,则证明:设f(t)是实函数(为虚函数或复函数情况相似,略)显然§ 尺度变换性质1. 性质:2. 证明:综合上述两种情况3.意义(1) 0<a<1 时域扩展,频带压缩。
脉冲持续时间增加a倍,信号变化减缓,信号在频域的频带压缩a倍。
因此高频分量减少,幅度上升a倍。
(2) a>1 时域压缩,频域扩展a倍。
持续时间短,变化加快。
信号在频域高频分量增加,频带展宽,各分量的幅度下降a倍。
此例说明:信号的持续时间与信号占有频带成反比,有时为加速信号的传递,要将信号持续时间压缩,则要以展开频带为代价。
§ 时移特性幅度频谱无变化,只影响相位频谱,例3-7-8求下图所示函数的傅里叶变换。
解:由对称关系求,又因为得幅频、相频特性分别如下图所示。
幅度频谱无变化,只影响相位频谱§ 时移+尺度变换1. 性质:2. 证明: (仿的证明过程)当时,设,则例3-7-9方法一:先标度变换,再时延方法二:先时延再标度变换两种方法结果相同。
§ 频移特性1.性质2.证明4.应用通信中调制与解调,频分复用§ 频移特性1.性质2.证明4.应用通信中调制与解调,频分复用§ 时域微分性质1.性质即3. 特别注意如果f(t)中有确定的直流分量,应先取出直流分量单独求傅里变换,余下部分再用微分性质。