1.4 穆斯堡尔效应
- 格式:docx
- 大小:532.69 KB
- 文档页数:12

穆斯堡尔参量
穆斯堡尔参量(Mössbauer parameter),也称为穆斯堡尔效应参量(Mössbauer effect parameter),是描述穆斯堡尔效应的一个重要参数。
穆斯堡尔效应是一种通过核能级的共振吸收和放射特定的γ射线的现象。
穆斯堡尔参量包括两个主要部分:同位素位移(isomer shift)和四极分裂(quadrupole splitting)。
- 同位素位移指的是在穆斯堡尔效应中核能级吸收峰的位置相对于标准参考物质的偏移量。
同位素位移可以提供关于样品中的电荷分布和化学环境的信息。
- 四极分裂是由于核电子周围的电场分布导致的。
它描述了核能级的磁性分裂,可以提供有关样品中的晶体结构和电荷分布的信息。
穆斯堡尔参量可以通过穆斯堡尔光谱实验来测量,利用这些参量可以得到关于样品的结构、化学环境和电子状态等信息。
穆斯堡尔参量在材料科学、物理学、化学以及地球科学等领域中得到广泛应用。


穆斯堡尔当一种原子核发射的电磁辐射(g辐射)作用于同一种原子核上时,一般不会发生共振吸收,这是因为原子核要受到反冲,g辐射的能量和频率将会减少在穆思堡尔效应被发现以前,一般采用补偿反冲能量损失的办法来研究g辐射的共振吸收,但是,这样观察到的共振谱线的宽度远大于核谱线的自然宽度,共振吸收的信号太弱,本底太强,使得核谱线共振吸收技术的应用受到很大限制。
1958年,穆思堡尔在研究铱低温g辐射共振吸收实验时发现:如果发射或吸收g辐射的原子核束缚在晶体的晶格中,便可以消除原子核反冲及其对波长的影响。
这种无反冲的g辐射共振吸收效应就被称为穆思堡尔效应。
1960年,人们利用穆思堡尔效应成功地验证了爱因斯坦在相对论中预言的引力红移。
现在,穆思堡尔效应应用十分广泛,除了是研究固态物理微观结构的一种有力工具外,它的应用几乎遍及物理学的各个部门,甚至在化学、分子生物学、地质学和医学等方面也都起着广泛和重要的作用。
穆斯堡尔谱学给出的信息:穆斯堡尔谱学主要论述的是具有一定体积的原子核与其周围环境电或磁的相互作用。
这种相互作用的一方是原子核,它具有电荷、电四极距和磁偶极距,相互作用的另一方面是环境在核处形成的电荷分布、电场梯度和磁场。
所谓环境通常是指原子核的核外电子、近邻原子的电荷和磁距。
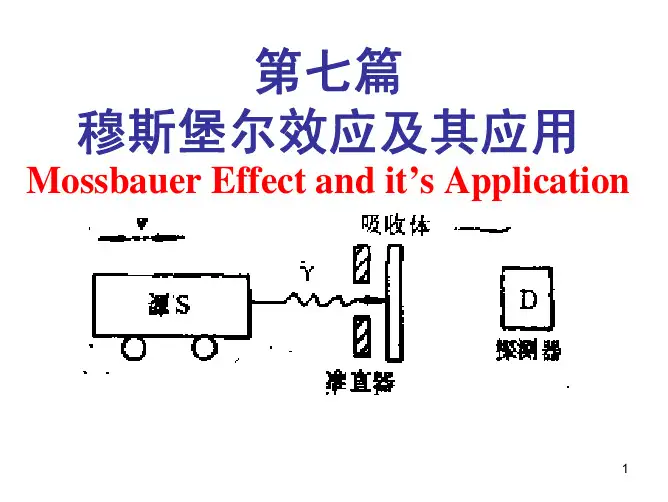
穆斯堡尔仪器的基本构成和原理。
穆斯堡尔效应是一种无反冲的γ射线的共振吸收或共振散射效应。
当穆斯堡尔放射源在振子中获得多普勒速度补偿时,它就有可能和吸收体(样品)产生共振吸收。
在共振吸收时,探测器探测到的γ射线强度明显下降,从而可得到样品的共振吸收谱线。
如典型的α-Fe样品谱线共有六个峰,对应于不同的速度值,即不同的补偿能量值。
通用接口送出步进信号给函数产生器。
函数产生器将此序列脉冲分频,获得对称的方波信号,经积分后得到三角波信号,并作为基准信号被送入功率放大器。
同时,对应于三角波的谷点输出正同步信号给通用接口。
振动子处拾波线圈感应的信号也加入到功率放大器,功率放大器放大基准信号和感应信号的差值,将其送入到振动子的驱动线圈上。


指一种原子核无反冲的γ射线共振散射或吸收的现象。
德国物理学家R.L.穆斯堡尔于 1957年~1958年间在观察19 1Ir(129keV)的γ射线共振本底时首先发现这种现象,并在理论上作了解释。
一个自由原子核发射或吸收γ光子时,原子核要受到反冲,反冲能量损失,发射谱或吸收谱便产生偏差,对大部分核辐射,难以实现共振吸收。
若原子核被束缚在晶体点阵上,晶体质量远大于一个原子核的质量,发射或吸收γ光子时,整个晶体反冲,反冲能量将显著减小,容易观察到共振吸收现象。
这就是所谓无反冲γ共振吸收。
但实际上点阵振动状态是量子化的,在反冲能量小于点阵振动的能级间隔时,它将被整个晶体吸收。
所以穆斯堡尔效应又称零声子发射和吸收。
迄今为止,已经观察到的穆斯堡尔效应有40多种元素,80多种核素,100多条穆斯堡尔跃迁线。
这些核素称为穆斯堡尔核。
其中最常用的是57Fe(14.4keV)和119Sn(23.8keV),括号内为γ光子的能量。
无反冲γ射线最主要特点是谱线的宽度接近于核能级宽度,这表明它具有极高的γ射线能量分辨率,因此能观察到原子核能级的超精细结构。
在共振实验中,由于源同吸收体的化学环境的差异,原子核外s电子电荷密度发生变化,它与原子核电荷的相互作用使跃迁能量相应变化,其差值表现为能量位移。
称为同质异能位移或化学位移。
自旋大于 1/2的核,电荷分布非球形对称,核具有电四极矩,它与核所处的电场梯度发生相互作用,核能级便产生四级分裂。
自旋大于零的核,具有核磁矩,它与核所处的内磁场相互作用,核能级就产生分裂。
在穆斯堡尔谱中可以清楚地分辨这些超精细相互作用引起的位移和分裂。
若已知核周围环境的电磁结构,则可以研究核的特性;反之,若核的性质已知,由测量结果可以推得核周围环境的电磁结构,即利用穆斯堡尔核,能探测物质的微观结构。
利用多普勒速度扫描可以实现共振吸收测量,这种装置称为穆斯堡尔谱仪。
由该仪器能获得穆斯堡尔谱——透过吸收体的γ射线光子数对多普勒速度的函数。

穆斯堡尔效应及其应用摘要:穆斯堡尔效应是现代核物理技术的核心理论,也是解决空间测距精确程度的重要方法。
本文具体而清晰地阐述了穆斯堡尔效应及应用形式,也对相应的科学领域进行了针对性的概述。
关键词:穆斯堡尔效应γ光子发射谱吸收谱一.引言在1958年由德国青年物理学家穆斯堡尔首次发现由γ射线所发出的一种共振荧光现象,后来人们把这一种现象称为无反冲γ射线共振吸收效应又称穆斯堡尔效应。
这一效应发现之后马上引起了物理学界以及与物理学相关的科学界的重视,很快成为跨学科多门类的新兴技术,渗透到了物理学中的核物理、点阵动力学、超导物理、磁学;化学中的化学键、化合物的结构、催化;以及地质学、生物学、医学、工学、人文科学甚至到考古学、美术学都有广泛的应用。
换句话说,只要是与物质结构微观结构有关的研究学科,都有穆斯堡尔效应的踪迹。
因此,穆斯堡尔效应的应用探究直到现在仍然是一个十分重要的研究领域。
穆斯堡尔在完成他的硕士论文时首次观察了191Os经过β衰变成191Ir 以及187Re、177Hf、188Er等原子核无反冲γ共振吸收现象。
本文阐述穆斯堡尔效应之后,对穆斯堡尔效应的具体应用分几个方面进行阐述,现代很多技术都与穆斯堡尔效应有关,这一结果是十分令人满意的。
二.穆斯堡尔效应的理论诠释一个处于静止状态的自由原子核,根据动量守恒定律,释放一个γ光子时,将受到一个反冲动量,反冲动量为:P=mv=h c ν (1) 所以:R E =12m 2v =22m p =222m E c (2) 式中:m 为原子核的质量 E 为释放γ光子的能量 c 为真空的光速 这个动量应该由原子核的跃迁所释放的能量021E E E =-来提供,所以发射γ光子所需要的能量为:·¢E =h ν=0R E E -=2202m E E c- (3) 我们使发射谱线的中心发生偏移,使谱线不在0E 处,而在0R E E -处。
如果一个原子核发射的γ射线的有一个反冲,发出的γ射线相应的能量就会减少一部分:10R E E E -=另外一个吸收的原子核也具有一个反冲能量,所以,要产生共振荧光现象就应该提供相应的能量:20R E E E -=这样会导致发射谱和吸收谱产生相差为2R E 的距离,如图1;图1;原子核吸收γ光子的过程,同时也会获得光子所发射的反冲能量222R m E E c =,这种反冲动量一定是入射光子提供的,则:22Îü002R m E E E E E c=+=+ (4) 经过这样的操作,会使发射谱和吸收谱相距2R E 的距离,如图一;例如对于57Fe 来说,第一激发态释放14.4kev 的γ光子能量。


穆斯堡尔谱原理
穆斯堡尔谱是利用穆斯堡尔效应进行的,穆斯堡尔效应是指当束缚在
晶体中的原子或离子受到高频谱线激发时,发出的谱线具有特殊的性质。
材料中的杂质在晶格内的运动会导致探测到的谱线发生频移,从而可以研
究杂质的振动、扩散、晶格位移等现象。
1.穆斯堡尔效应:当束缚在晶体中的原子或离子受到高频谱线激发时,其发出的谱线具有特殊的性质,包括能量、强度和频率等方面。
2.相对运动效应:杂质在晶体内的运动会导致探测到的谱线发生频移。
例如,晶体中的杂质原子因热运动而发生振动或扩散,导致谱线的频率发
生变化。
3.多晶样品效应:多晶样品中的不同晶粒方向相对于探测器的效应不同,可以通过分析谱线的形状和位置来研究晶格的位向。
穆斯堡尔谱原理的应用范围广泛。
在材料科学中,它可以用来研究晶
格缺陷、杂质扩散、相变、晶格位移等现象。
在物理化学中,穆斯堡尔谱
可以用来研究化学反应、催化剂的活性中心等。
在固态物理学中,它可以
用来研究磁性体的磁性行为、超导现象等。
总结起来,穆斯堡尔谱原理是一种重要的实验方法,通过研究杂质在
晶体中的运动特性,可以深入了解晶格的结构和性质,为材料科学、物理
化学和固态物理学等领域的研究提供了重要的实验手段。

穆斯堡尔效应
穆斯堡尔效应(Moussoural Effect)是一种心理投射的观点,它是以俄国心理学家雅克·梅斯堡(JacovMossel)为代表的俄国末代心理学家们所提出的。
根据梅斯堡在19世纪30年代所研究的结果,他提出人们会借助字面意义上的蜂窝来映射自身的情绪反应到其它事物上,然后再进行咨询活动,有助于推断问题的解决方案。
另一方面,穆斯堡尔效应是一种可靠的机制,它可以有效的理解其它人的情绪反应和行为,并进行行动。
通过此种机制,人可以把每一种情绪反映到自身之上,以便更加理解和深入了解其它的想法和生活方式。
根据穆斯堡尔的研究以及其他有关研究,有一些心理技巧可以帮助人们更好的推断其他人的情绪反应和行为,从而有助于更加有效的沟通。
比如,通过反思,一个人可以更加清楚和有效的认识某人的情绪反应,以及如何更好地理解其中的机理。
2005年,穆斯堡效应的研究成果被发表到学术论文中,表明它可以帮助人们理解其它人的情绪反应,并且有助于有效的沟通和决策。
此外,穆斯堡尔效应可以应用于娱乐、消费产品设计等极具挑战性的方面,这可以帮助人们更好地理解消费者的情绪与行为。
此外,还可以应用于销售行业,帮助企业了解消费者的需求,从而使其能够有效的满足客户的需求。

穆斯堡尔效应薛定谔穆斯堡尔效应(Mössbauer effect)1. 引言穆斯堡尔效应是由德国物理学家鲁道夫·穆斯堡尔于1957年首次观察到的一种特殊的原子核辐射现象。
这一效应的发现对于研究固体材料的原子核物理性质以及应用于其他领域具有重要意义。
2. 穆斯堡尔效应原理穆斯堡尔效应是基于薛定谔方程的量子机械原理的一种现象。
当原子核处于某种能级时,它可以通过发射或吸收一个能量为∆E的光子而跃迁至另一个能级。
根据薛定谔方程,这一能级差必须等于光子的能量,即∆E = hν,其中h为普朗克常数,ν为光子的频率。
然而,如果固定了带电粒子的位置,其速度和动能将模糊不清,因此无法确定光子的精确能量。
薛定谔方程给出了光子能量的概率分布,从而允许我们计算这种不确定性,即能级差的模糊度。
3. 穆斯堡尔效应的观察穆斯堡尔利用铁-57同位素进行了实验观察穆斯堡尔效应。
他将这种同位素封装在一个晶体中,并通过其他能量较高的射线使之跃迁至较高的能级。
然后,他用一个探测器收集通过样品的γ射线,并测量其能量分布。
穆斯堡尔发现,不同晶体的能谱分布存在微小的偏移,这一现象即为穆斯堡尔效应。
4. 理论解释穆斯堡尔效应的理论解释由薛定谔提出。
薛定谔认为,穆斯堡尔效应是由于原子核在固体晶格中的位置不同而引起的。
当核处于不同的位置时,它们会受到不同的相对动能的影响,从而导致能级差的变化。
这种位置效应使得不同位置的核会发出略微不同能量的γ射线,从而观察到能谱的偏移。
5. 应用领域穆斯堡尔效应在材料科学和物理学的研究中有广泛的应用。
利用穆斯堡尔效应可以对固体材料中的原子核性质进行精确的测量。
例如,通过测量铁原子的穆斯堡尔效应可以研究铁磁材料的性质。
此外,穆斯堡尔谱还可用于研究化学反应、材料表面的吸附过程以及催化剂的性质。
结论穆斯堡尔效应是量子物理的重要现象之一,它通过观察原子核能谱的变化揭示出原子核在晶体中的位置效应。
穆斯堡尔效应在材料科学和物理学的研究中有广泛的应用,并对其他领域的发展产生了重要的影响。
穆斯堡尔效应用于测量同位素移动和化学反应中核反应的方法核反应是指原子核发生变化的过程,可以通过测量同位素移动和化学反应来研究。
穆斯堡尔效应是一种利用核反应特性来测量同位素移动和核反应速率的方法,在科学研究和工业应用中具有重要的意义。
一、穆斯堡尔效应的基本原理穆斯堡尔效应是由德国物理学家罗伯特·J·穆斯堡尔于1957年首次发现的,他因此获得了1961年度的诺贝尔物理学奖。
穆斯堡尔效应利用同位素的特性,通过测量核反应特征来研究同位素移动和核反应速率。
穆斯堡尔效应的基本原理是利用原子核在核反应过程中释放或吸收光子时所产生的相对位移,通过测量光子的能谱来推测核反应的发生和核反应速率。
具体而言,当同位素所处的环境发生变化时,核反应发生的速率也会随之改变,从而导致光子能谱的变化,通过分析这种变化可以推断出同位素移动和核反应速率的情况。
二、测量同位素移动的方法1. 源移动法源移动法是一种常用的测量同位素移动的方法。
该方法通过将探测器固定在一个位置,利用原子核反应时所产生的峰值能量来推断同位素在环境中的移动情况。
源移动法需要通过对比同位素在不同环境下的能谱峰值的位置和强度来分辨同位素的移动情况。
2. 时间差法时间差法是另一种测量同位素移动的方法。
该方法通过利用同位素移动时所产生的能谱的时间差来推断同位素的移动速率。
时间差法需要测量两个能谱之间的时间差,并将其与同位素的移动速率进行对比,以确定同位素的移动情况。
三、测量化学反应中核反应速率的方法1. 自吸收法自吸收法是一种常用于测量化学反应中核反应速率的方法。
该方法通过测量核反应产生的光子在样品中的吸收比例来推断核反应的速率。
自吸收法需要测量样品中核反应所产生的光子的能量,并通过其吸收比例来推算核反应的发生情况。
2. 形变法形变法是另一种测量化学反应中核反应速率的方法。
该方法通过分析核反应产生的光子在样品中所产生的形变来推测核反应的速率。
形变法需要测量光子在样品中的形变情况,并通过对比样品前后的形变程度来确定核反应的发生情况。
穆斯堡尔效应穆斯堡尔效应,也称为穆斯堡尔预言效应,是一种心理学现象,指的是一个预言会对动摇相信这个预言的人们的行为产生影响。
它是命名以犹太神经病学家阿道夫穆斯布尔(Adolf Mueller)的名字而命名,他提出了这一概念,尽管它在普通心理学实验中已经受到证实。
穆斯堡尔效应受到众多研究和研究的关注,并在神经心理学有重要的观点,其研究表明,它可以影响个体的行为和心理状态。
本文将介绍穆斯堡尔效应如何联系神经心理学和普通心理学,以及穆斯堡尔效应如何影响行为。
穆斯堡尔效应是一个与神经心理学有关的重要现象,表现为一个预言对信仰这个预言的个体的行为产生影响。
它的研究表明,预言可以通过改变个体的自我观念和对环境的解释,从而改变行为。
穆斯堡尔效应是一种思维模式,即认知结构的改变,这一点也得到了神经心理学的认可。
神经心理学的研究显示,当一个预言改变了一个人的自我观念和行为期望时,这个预言就会对这个人的行为产生影响。
因此,我们可以推断,当某人对一个预言有兴趣,那么他会受到这个预言的影响,这就是穆斯堡尔效应。
穆斯堡尔效应不仅仅是一个在神经心理学中有重要意义的现象,也是一个在普通心理学中有重要意义的现象。
在普通心理学的实验中,研究人员发现,通过说服某人去信仰一个预言,这个人就会改变他的行为。
这里的信仰就是穆斯堡尔效应的关键,也就是说,当一个人被说服并相信一个预言时,他的行为就会改变。
这种影响力也可以在普通心理学中找到,比如自我满足假设,它指出,一个人会根据他的行为期望或偏好来做出选择或付出极大的努力,以符合这些活动期望。
因此,穆斯堡尔效应可以被视为一个结合了神经心理学和普通心理学的重要观点。
穆斯堡尔效应可以改变一个人的行为,这一点也得到了神经心理学家和普通心理学家的认可。
通过认知结构的改变,某个预言可以影响一个人的行为,而且影响可以持续很长时间,取决于这个人如何使用这些信息。
如果一个人相信一个预言,这个预言就会对他的行为产生影响,但他也可能仍然相信这个预言,即使他的行为没有改变。
实验1.4 穆斯堡尔谱一、引言1957年,德国的穆斯堡尔(R. L. Mössbauer)意外发现(论文在1958年发表),嵌入固体晶格中的放射性原子核在发射γ射线时有一定的几率是无反冲的;发射的γ光子具有全部核跃迁能量。
同样,嵌入固体晶格中处于基态的核在吸收γ射线时也有一定的几率是无反冲的。
原子核无反冲发射γ射线和无反冲共振吸收γ射线的现象被命名为Mössbauer效应。
无反冲的几率常被称为无反冲分数f。
Mössbauer效应的一大特点是可以得到很窄的共振吸收(或发射)谱线。
如对于常用的Fe的14.4keV的γ射线,其自然宽度Γn为4.7×10-9eV,理想的Mössbauer共振线宽Γ略大于2Γn,约10-8eV量级,其相对的能量分辨率Γ/Eγ~6×10-13。
而对于67Zn的93keV的γ射线,其Γ/Eγ~1×10-15,有很高的能量分辨率。
用67 Zn的Mössbauer效应可以在实验桌上做广义相对论引力红移实验。
还有人发现,对109Ag的88 keV的γ射线,其相对的能量分辨率可达10-22数量级。
由于Mössbauer效应有极高的能量分辨率,以及γ射线可以方便地将物质内部信息携带出来等优点,Mössbauer效应一经发现,很快就在物理学、化学、磁学、地质学、生物医学、物理冶金学、材料科学、表面科学、考古学等许多领域得到广泛应用。
R. L. Mössbauer于1961年获得了诺贝尔物理奖。
二、实验目的1. 了解穆斯堡尔效应、穆斯堡尔谱学和穆斯堡尔谱仪的基本原理。
2. 掌握穆斯堡尔谱和穆斯堡尔谱基本参数的测定方法。
三、实验原理1. 穆斯堡尔效应设原子核A衰变到原子核B的激发态B* ,然后从激发态B*退激到基态B,发射出γ光子(图1),当这个光子遇到一个图1 γ光子的发射和吸收同样的原子核B 时,就应被共振吸收。
本科生实验报告实验课程核分析基础学院名称核技术与自动化工程学院专业名称核工程与核技术学生姓名学生学号指导教师马英杰实验地点6C802实验成绩二〇一五年十一月二〇一五年十二月穆斯堡尔效应【实验目的】1、了解穆斯堡尔效应的基本原理2、了解穆斯堡尔谱仪的结构和基本的实验方法【实验器材】穆斯堡尔谱仪 通用示波器57Co 放射源α-Fe 薄膜样品【实验原理】穆斯堡尔效应是一种原子核无反冲的γ射线共振吸收或共振散射现象。
由于核激发态有一定寿命,相应的跃迁谱线宽度很窄,而核发射的γ射线能量较大,造成核的反冲,所以即使考虑到热运动的多普勒展宽造成的发射谱线与吸收谱线的重叠,一般也无法观察到核共振吸收现象。
穆斯堡尔考虑把靶原子核镶嵌在晶格中,发射γ射线时带着整个晶体一起反冲,这样的反冲很小,有很大的概率观察到核共振吸收现象,这就是穆斯堡尔效应.一、γ射线共振吸收 1、谱线的自然线宽核的激发态存在有限长的寿命τ,回到基态时发出的γ射线存在一定的线宽,谱线强度与光子频率ω之间有关,为:2021()1()4I ωωωτ∝-+即洛仑兹线性。
将E=hω/2π代入,22021()()4I E E E τ∝-+则当0/2E E τ-=±时I (E)强度下降为最大值的一半,这时曲线宽度为/τ,称为谱线的自然线宽Γ。
2、自由原子核的反冲由能量、动量守恒定律可知核反冲能量E R 为:222202212222R R p E E E Mu M Mc Mcγγ===≈ 即M 越大,反冲能量E R 越小。
如以57Fe 为例,E 0=14.4keV ,则有E R ≈2×10-3eV 比自然线宽大得多。
故对57Fe ,当谱线不存在其他展宽,发射与吸收谱线之间不存在任何重叠,所以不可能观察到γ射线的共振吸收现象。
3、多普勒展宽由相对论性的多普勒效应2210T D eV -==⨯室温下的多普勒效应不是观察到的57Fe 发射γ射线的共振吸收.二、穆斯堡尔谱线的强度和宽度原子发射γ射线时,反冲能量一般不足以激发声子,则发射前后晶格处于相同的状态,这种无声子跃迁过程的概率称为无反冲分数f 。
穆斯堡尔效应引⼒红移穆斯堡尔效应在验证引⼒红移中的应⽤1.引⼒红移引⼒红移是指⼀个处于重⼒场中的源发射的电磁波会出现频率减少(即能量减少)的现象,这是⼴义相对论的⼀个结论[i](蓝⾊星球上接受的从黄⾊星球发出的电磁波)红移常常⽤⽆量纲的⼀个量来表征:光⼦重⼒红移可以靠⼴义相对论的史⽡西度规[ii]求出(即场⽅程⼀边是能量-动量张量,代表物质或者能量的分部情况,⼀边是度规,描述了空间每⼀点的弯曲情况,史⽡西解是⽆旋转⽆电荷的解,即史⽡西度规,描述了⽆旋⽆荷的引⼒源周围空间弯曲的情况,直接推出的结果就有引⼒红移[iii],即光⼦能量减少;当然从另⼀个⾓度来看,根据弱等效原理,不均匀的引⼒场中应有与加速度运动物体产⽣相同的效果,引⼒场应当引起与多普勒红移等效的红移,但其本质并不是多普勒红移,⽽是由于度规变化)其中r趋于⽆穷代表空间是平直的(即闵可夫斯基空间),rs为史⽡西半径,R是观察者离发射源的距离,在⽜顿经典极限下,当R远⼤于rs,展开后略去⾼阶项,上式化作代⼊并利⽤频率-波长关系可得2.穆斯堡尔效应2.1核反冲对gama共振吸收的影响由于在gama共振吸收中,放出gama射线的原⼦核有个反冲,使得放出的光⼦能量要减少⼀部分,⽽吸收的核也有⼀个反冲,因此要发⽣共振吸收就必须提供能量这样,发射谱线和吸收谱线就错开了2ER ,例如对实验中⽤到的57Fe的14.4KeV的gama射线(I=1.5到I=0.5)⽽⾔,由动量守恒⽐能级宽度(即图中ED )⼤得多,所以不会发⽣共振吸收2.2穆斯堡尔的⼯作穆斯堡尔为了消除反冲的影响,将发射的原⼦核和吸收的原⼦核置于固体晶格中,这样原⼦核在吸收或者发射的时候,受到反冲的是整个晶格,从⽽ER趋近于0,这样就近似于⽆反冲过程,能够满⾜共振条件。
2.3穆斯堡尔谱如果发射源和吸收体之间有⼀定相对速度,引起的多普勒红移造成的能量差异是根据:通过调制速度就可以调制发射的gama射线的能量,继⽽印象吸收率,吸收率随相对速度变化的曲线即为穆斯堡尔谱(如57Fe的穆斯堡尔谱,六条吸收线代表了精细结构,但在验证引⼒红移中⽤不到精细结构)3.验证引⼒红移3.1测量原理在上⾯的推导中我们可以看到,由于引⼒场的不均匀分布,地球表⾯附近,即R约等于h (也满⾜⽜顿经典极限,计算可得地球的史⽡西半径⼤概在10^-3⽶数量级),在地⾯的接受到的光⼦和在⾼度H的发射出的光⼦能量差为也就是说如果发射源和吸收体之间处于引⼒场中不同的位置,除了多普勒红移,还有有⼀个额外的不随相对速度变化的由引⼒场不均匀分布引起的红移,即引⼒红移表现在穆斯堡尔谱上就是中⼼偏移了⼀个位移量。
实验1.4 穆斯堡尔谱一、引言1957年,德国的穆斯堡尔(R. L. Mössbauer)意外发现(论文在1958年发表),嵌入固体晶格中的放射性原子核在发射γ射线时有一定的几率是无反冲的;发射的γ光子具有全部核跃迁能量。
同样,嵌入固体晶格中处于基态的核在吸收γ射线时也有一定的几率是无反冲的。
原子核无反冲发射γ射线和无反冲共振吸收γ射线的现象被命名为Mössbauer效应。
无反冲的几率常被称为无反冲分数f。
Mössbauer效应的一大特点是可以得到很窄的共振吸收(或发射)谱线。
如对于常用的Fe的14.4keV的γ射线,其自然宽度Γn为4.7×10-9eV,理想的Mössbauer共振线宽Γ略大于2Γn,约10-8eV量级,其相对的能量分辨率Γ/Eγ~6×10-13。
而对于67Zn的93keV的γ射线,其Γ/Eγ~1×10-15,有很高的能量分辨率。
用67 Zn的Mössbauer效应可以在实验桌上做广义相对论引力红移实验。
还有人发现,对109Ag的88 keV的γ射线,其相对的能量分辨率可达10-22数量级。
由于Mössbauer效应有极高的能量分辨率,以及γ射线可以方便地将物质内部信息携带出来等优点,Mössbauer效应一经发现,很快就在物理学、化学、磁学、地质学、生物医学、物理冶金学、材料科学、表面科学、考古学等许多领域得到广泛应用。
R. L. Mössbauer于1961年获得了诺贝尔物理奖。
二、实验目的1. 了解穆斯堡尔效应、穆斯堡尔谱学和穆斯堡尔谱仪的基本原理。
2. 掌握穆斯堡尔谱和穆斯堡尔谱基本参数的测定方法。
三、实验原理1. 穆斯堡尔效应设原子核A衰变到原子核B的激发态B* ,然后从激发态B*退激到基态B,发射出γ光子(图1),当这个光子遇到一个图1 γ光子的发射和吸收同样的原子核B 时,就应被共振吸收。
但对于自由原子核要实现上述共振吸收是很困难的,因为在发射和吸收γ光子的过程中,由于原子核反冲而损失一部分能量E R ,由能量—动量守恒关系可推知()eV 1037.5222042202A E mcE m P E n R -⨯=≈=图2 自由原子核发射光子时的反冲 图3 自由原子核的发射谱和吸收谱式中P n 为原子核反冲动量,m 为原子核质量,A 为原子量,E 0为以keV 为单位的γ跃迁能量(图2)。
对于57Fe 的14.4 keV 能级,E R =1.95×10-3eV 。
反冲效应使γ光子能量变小,γ光子的发射谱向低能方向移动E R ,而吸收谱向高能量方向移动E R (图3)。
这样发射谱和吸收谱就相差2E R ≈106Γn 。
所以对气体中的自由原子核是无法实现无反冲共振吸收的。
1957年底德国青年物理学家穆斯堡尔提出实现γ射线共振吸收的关键在于寻求消除反冲能量的方法。
如果把发射核与吸收核嵌入固体晶格中,使它们牢固地受晶格的束缚,当穆斯堡尔原子核的反冲能量E R 小于它在固体中的结合能(1~10eV )时,就有一定的无反冲几率。
我们知道,嵌有Mössbauer 原子核的晶体,发射一个动量ħq 为或吸收一个动量为-ħq 的γ光子的几率是:()()()∑-+Ω⋅Ωiff i i E E i f W q P δ2i exp ,x q其中W i 是各简并初态几率,x 是发射或吸收γ光子的原子核坐标。
δ函数保证了能量守恒关系γω ±+=+f f i i E E E E (并令γω f i E E -=Ω,上标表示核能级,下标表示晶体状态,+ħωγ表示发射γ光子,-ħωγ表示吸收γ光子),且有:()()()⎰∞+∞--⎥⎦⎤⎢⎣⎡-=-+t t Ωi t E E i E E Ωi f f i d ex p ex p 21 πδ 将上式代入前式,引入海森堡表象及声子产生、湮没概念,经仔细计算得:()()()[]∏∑∑⎪⎭⎫⎝⎛⎥⎦⎤⎢⎣⎡-=σσσσσσσσσϕϕσk k k m k k k k k k Y I Y m Y ΩP k csch exp cth exp ,q其中m 是k ,σ模的声子数,()T k Y B k 2k σσω =,()()σσσωϕk k q NM e q k ,cos 222=,ωσ(k )是k ,σ模声子角频率,k 为格波矢,σ为偏振,e k σ为波基矢,k B 为玻尔兹曼常数,T 为温度,M 为原子质量,N 为原子数。
I mk σ是虚宗量Bessel 函数的母函数。
γ射线无反冲发射或吸收,就是发射或吸收的γ光子能量E ,严格等于原子核初、终态能量差,即E γ=E f -E i 。
相应发射或吸收γ光子前后,晶体能量亦不变。
()0==-∑σσσωk k i f m E E k 的几率就是无反冲几率,常称为无反冲分数f ,()()()∏∑∑∑⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-==σσσσσσσσσϕωδϕσσk k k m m k k k k k Y I m Y P f k k csch cth exp 0,k q图4 穆斯堡尔元素周期表满足ħΩ=0有三种情况:(1)无声子产生和湮灭,即“零声子”过程;(2)几个简并态间的声子产生和湮灭;(3)多声子交换,但初、终态能量不变。
而由各过程的几率计算知,(2)(3)两种情况对f 贡献较小,若只考虑“零声子”过程()[]Y f k k k 2exp cth exp x q ⋅-=⎪⎭⎫ ⎝⎛-≈∑σσσϕ如采用Debye 模型,前式简化成为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛+-=⎰T x D D B RD x e x T kE f θθθ02d 1416exp当T <<θD 时,⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫⎝⎛+-=22232123exp D D B R T k E f θπθ; 当T >>θD 时,⎥⎦⎤⎢⎣⎡-=D D B R T k E f θθ6exp 。
其中θD =ħωD /k B 是Debye 温度。
由上述分析显见,无反冲分数与发射或吸收γ光子的原子核植入的基体性质,γ射线能量和温度均有关系。
特别要指出的是,γ射线无反冲发射或无反冲吸收只发生于相互作用较强的多体系统,其发生几率小于1(室温下一般都小于0.8),是一种多体效应,不能简单地理解为前)式中的M →∞,E R →0的结果。
目前已发现40多种元素的90多个同位素可以观察到穆斯堡尔效应。
图4是已观察到Mössbauer 效应的元素周期表。
绝大多数同位素必须在低温下(液氮甚至液氦温度下)才能观察到穆斯堡尔效应。
在室温下,只有57Fe 、119Sn 、15l Eu 等少数同位素能观察到穆斯堡尔效应。
因此57Fe 、119Sn 、15l Eu 是实验中常用的穆斯堡尔同位素。
2. 穆斯堡尔谱学穆斯堡尔谱学是利用Mössbauer 效应,通过探测原子核(穆斯堡尔核)与核外环境的超精细相互作用,对物质微结构进行分析研究的学科。
一般情况下,我们可以把原子核看作电荷电流分布的小区域,这个小区域与核外的电子和其他原子核产生的静电磁场(有时也有外加场)相互作用。
这种作用使核能级发生微小变动,简并部分或全部解除,形成核能级的超精细结构,一般而言,这种作用引起的能级分裂,比原子能级的精细结构要小三个数量级,因而称为超精细相互作用。
大多数情况下,可把超精细相互作用作微扰处理。
用多极展开的方法,微扰哈密顿可写为:()()+++=)2(10e M e H H H H其中第一项为电单极相互作用,第二项为磁偶极相互作用,第三项为电四极相互作用。
更高次的相互作用非常微弱,从穆斯堡尔谱学的技术角度一般不再考虑。
由于核力的时间反演不变性,原子核只有偶次项电多极(2l )矩,原子核无电偶极矩,因此无电偶极相互作用。
(1)电单极作用与同质异能移(Isomer shift 简称I.S.)电单极相互作用是分布在核体积内的核电荷与核外电磁场的库仑作用。
核电荷分布体积越大,体系能量越高。
设核电荷分布在半径为R 的球内,则其静电势为()⎪⎪⎩⎪⎪⎨⎧≥≤⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=R r rZeR r R r R Ze r U ,,22322 核外电子电荷分布密度为()20Ψe -。
相对于点核、半径为R 的核由于电单极相互作用引起的能级移动为:图5 同质异能移 图6 自旋与磁场方位原子核基态的核半径为R g 与激发态的核半径R e 不一样,因此引起的γ跃迁能量变化为:()[]2222052g e R R ΨZe E -=∆π而发现γ射线的原子核所处的核外环境与吸收射线原子核所处的核外环境通常不一样。
即对于放射源S 和吸收体A 而言,原子核处的Ψ(0)不同。
因此实验上测到的由于单电极相互作用引起的净能量变化(称为同质异能移δ)为:()()[][]222220052g e S A R R ΨΨZe --=πδ 可正可负,图5是同质异能移的示意图。
(2)磁偶极相互作用自旋大于零(I >0)的核具有磁偶极矩μ=g N μN I ,(g N 为核朗德因子),它与原子核处的磁场H 的相互作用哈密顿为:()()ϕϕϕμcos ˆsin sin ˆcos sin ˆ1z y x N N I a I a I H g m +--=⋅-=H μH对I =1/2的核能级,()⎪⎪⎭⎫⎝⎛---=-ϕϕϕϕμcos sin sin cos 21121iaia N e e H g m H 对I =3/2的核能级,()⎪⎪⎪⎪⎪⎭⎫⎝⎛------=----ϕϕϕϕϕϕϕϕϕϕμcos 3sin 300sin 3cos sin 200sin 2cos sin 300sin 3cos 321123iaia iaiaia iaN e e e e e e H g m H ()[]()[]()[]()22202222022052d 40223d 40ΨR Ze r r Ψe r Ze R r R Ze rr Ψe U r U E pr πππ=-⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=--=∆⎰⎰∞∞图7 磁超精细分裂和室温α-Fe 穆斯堡尔谱(57Co/Rh 源)由微扰方程H (m 1)|E >=E m 1|E >可解得: 对21=I 核能级,H g E N m μ21121±=; 对23=I 核能级,H g H g H g H g E N NN N m μμμμ23232323123,212123--=,,。
图7是能级分裂示意图与相应的α-Fe 穆斯堡尔谱(g 1/2=-0.0906,g 3/2=+0.1547)。