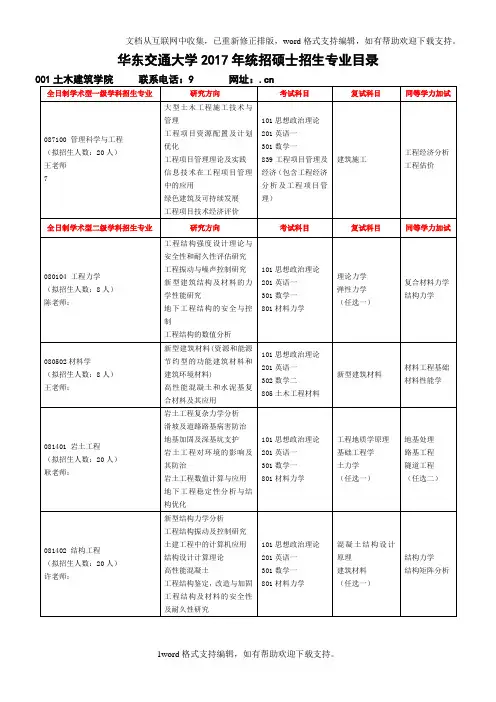
数值分析-华东交通大学研究生院

第五章函数插值§1 插值问题与插值多项式§2 Lagrange插值法§3 Newton插值法§4 等距节点插值§5 Hermite插值§6 分段低次插值§7 三次样条插值欧阳洁1问题提出仅有采样值，但需要知道非采样点处的函数值。

解决上述问题的一种思路：对用数据表给出的未知函数，建立一个便于计算的近似函数作为表达式。

函数插值法是建立近似函数表达式的一种基本方法。

欧阳洁2§1 插值问题与插值多项式一插值问题二插值多项式欧阳洁3欧阳洁4一插值问题ni x f x i i ,,1,0),()(L ==ϕ已知定义于区间[a,b ]上的实值函数f (x )在n+1 个互异节点处的函数值。

若函数集合Φ中的函数ϕ(x )满足{}n i i x f 0)(={}],[0b a x n i i ⊂={}n i i x 0=则称ϕ(x )为f (x )在函数集合Φ中关于节点的一个插值函数，称f (x )为被插值函数,[a,b ]为插值区间。

{}ni i x 0=称为插值节点。

n i x f x i i ,,1,0),()(L ==ϕ称为插值条件。

如何求插值函数ϕ(x )称为插值问题。

欧阳洁71 代数插值多项式的存在唯一性分析：对于多项式插值问题，插值条件等价于确定多项式的系数，使得满足如下的线性方程组：⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡)()()()(111210************n n n n n n n n x f x f x f x f a a a a x x x x x x x x x M M L L L L L L L L 当节点互异, 系数矩阵非奇异, 故满足插值条件的不超过n 次的插值多项式是存在惟一的。

{}n i i x 0=二插值多项式定理满足插值条件的不超过n 次的插值多项式存在惟一。

第一章测试1.解对数据的微小变化高度敏感是病态的 ( )A:错B:对答案:B2.为使π*的相对误差限小于0.001%, 至少应取的有效数字为（）。

A:5B:4C:7D:6答案:D3.按四舍五入原则得到的近似数4.25，则这个近似数的相对误差是（）。

A:0.012%B:0.5%C:0.12%D:0.05%答案:C4.测得某场地长l的值为l* =100m,宽d值为d*的=80m,已知，则面积s=ld的绝对误差限位（）。

A:0.325%B:28(m2)C:26(m2)D:27(m2)答案:C5. 3.1421是π的近似值，3.1421的有效数字是（）。

A:3B:2C:4D:5答案:A第二章测试1.下列说法正确的是( ）A:不动点迭代总是线性收敛的B:斯特芬森迭代可以看成不动点迭代C:牛顿法有可能不收敛D:非线性方程的解通常不唯一答案:BCD2.不动点迭代局部收敛的条件是（）。

A:B:C:D:答案:CD3.对f(x)=0的m重根的迭代格式的收敛阶是 ( ）A:1.840B:2C:1D:3答案:B4.的等价方程形成的不动点迭代的收敛阶是（）A:1.618B:2C:1.840D:1答案:D5.方程的牛顿迭代格式为（）A:B:C:D:答案:D第三章测试1.解线性方程组通常有直接法和迭代法。

A:对B:错答案:A2.若方程组的系数矩阵严格主对角占优，下列哪个说法正确 ( )A:谱半径大于1.B:雅可比迭代法一定收敛；C:高斯消元法不需要换行可以顺利进行；D:高斯-赛德尔方法一定收敛；答案:ABCD3.用松弛法解系数矩阵是对称正定矩阵的线性方程组时，松弛因子是下列哪个值时该方法一定是收敛的( )A:1.5B:2.0C:0.5D:1.0答案:ACD4.下面那个初等方阵是初等方阵E((k),j)的逆矩阵是( )A: E(i,j)；B:E(i(-k),j)；C:E(i(1/k)).D:E(i(k))；答案:B5.用列主元高斯消去法解方程组第一步所选的主元是( )A:1B:2C:5D:3答案:B第四章测试1.A:B:C:D:答案:C2.A:x-1,xB:1-x,-xC:1-x,xD:x-1,-x答案:A3.A:1B:2C:3D:0答案:D4.A:B:C:D:答案:B5.A:1,2B:0,1C:3,0D:2,0答案:C第五章测试1.常用的正交多项式族有( )A:勒让德多项式；B:切比雪夫多项式；C:埃尔米特多项式.D:拉盖尔多项式；答案:ABCD2.最小二乘法可以解超定方程A:错B:对答案:B3.选用不同的权函数和求解区间，通过施密特正交化过程，由完全多项式基函数得到的正交多项式是不同的A:对B:错答案:A4.正交多项式作最小二乘法时，得到的法方程的矩阵是( )A:对称矩阵；B:正定矩阵；C:可逆矩阵.D:对角矩阵；答案:ABCD5.正交多项式和非正交多项式的格拉姆矩阵的性质完全相同A:对B:错答案:B第六章测试1.A:0.43093403B:0.43096407C:0.43096441D:0.4267767答案:A2.龙贝格求积算法公式是A:B:C:D:答案:C3.A:b-aB:0.5(b-a)C:3(b-a)D:2(b-a)答案:A4.A:2n+1B:n+2C:n答案:C5.A:74B:75C:72D:76答案:B第七章测试1.欧拉法的绝对稳定区间为A:B:C:D:答案:B2.下面哪句话是正确的A:梯形公式的优点是稳定性好，计算简单。

研究生创新计划项目科研工作量分配表
根据《华东交通大学科研工作业绩量化及教师套档办法(修改)》（华交科[2010]146号）等有关文件规定，通过立项的省级研究生教改项目、优质课程、教学成果奖等（统称为研究生创新计划项目）可以计算科研工作量。

其计算方法如下：
1、省级研究生教改项目过程工作量：
总工作量＝100＋立项经费（万元）×200（学时）
2、省级研究生教改项目结题（鉴定）工作量：150学时
3、通过立项的省级研究生优质课程按获得省部级三等奖计算，计200学时科研工作量。

4、省级研究生教学成果奖：
一等奖计600学时科研工作量；
二等奖计200学时科研工作量。

以上科研工作量由项目负责人进行分配，由研究生处负责审核。

填表日期：年月日。