建筑力学课件-力在轴上的投影

可编辑ppt
59
2.力矩
一个力作用在具有固定的物体上，若力的作用线不通过
固定轴时，物体就会产生转动效果。
如图所示，力F使扳手
绕螺母中心O转动的效应， 既与力F的大小有关，又与
F d
该力F的作用线到螺母中心
O的垂直距离d有关。可用两
.
者的乘积来量度力F对扳手 O
的转动效应。
M
转动中心O称为力矩中心，简称矩心。矩心到力
足分别为a′和b′，线段a′b′称为力F在
坐标轴y上的投影，用Y表示。 可编辑ppt
B F
A
a FXx b x
53
1. 力在坐标轴上的投影 X=±Fcosα Y=±Fsinα
F X2Y2
tan Y
X
y
B b’
YFy
F
A
a’
O a FXx b x
力与x轴的夹角为α, α为锐角
可编辑ppt
54
投影正、负号的规定: 当从力的始端的投影a到终端的投影b的方向与坐标
F
=
= B
F1
F F2
B
F1
A
A
A
可编辑ppt
18
力的平行四边形法则
作用在物体上同一点的两个力，可以合成为仍作用于该 点的一个合力，合力的大小和方向由以原来的两个力为邻 边所构成的平行四边形的对角线矢量来表示。
力的平行四边形法则
力的三角形法则
可编辑ppt
19
三力平衡汇交定理
一刚体受共面不平行的三力作用而平衡时，此三力的作
(c)
FA(RA)
(e)
可编辑ppt
34
可编辑ppt
35
可编辑ppt

？
l
3 o
θ
2
C
1
G
解: MO(F) = Fd
位置1: MO(F) = Gd = 0 位置2: MO(F) = －G －Glsinθ
Gd=lsinθ 位置3: MO(F) = －Gl
陕西铁路工程职业技术学院结构教研室
LOGO
三、力偶及力偶矩
由大小相等、方向相反、不共线的两个力组d成 F′
的力系称为力偶。(F,F’) 力偶对物体的效应：只产生转动效应，而无F移动效应。
M=±F.d
陕西铁路工程职业技术学院结构教研室
d F′
d F′
F
F
❖ ⑴力偶没有合力。一个力偶不能用一个力代替，也不能与一个 力平衡。力偶在任一轴上的投影为零。
平面汇交力系的合力在某轴上的投影等于力系 中各分力在同一轴上投影的代数和。即：
Rx = X1 + X2 + ···Xn= ∑ X Ry = Y1 + Y2 + ···Yn = ∑ Y
R = √ (∑X )2 + (∑ Y ) 2
∑Y Tanα= ∑ X
陕西铁路工程职业技术学院结构教研室
合力投影定理应用
1.6 力矩和力偶
陕西铁路工程职业技术学院结构教研室
一、力矩
❖ 定义：力与力臂的乘积冠以正、负号定义为力F对O点的力 矩。
表达式：Mo(F) = ±F·d
F1 F2
O — 转动的中心。称为力矩中
O
心，简称矩心
d — 转动中心到力作用线之 间的距离称为力臂(注意单位)
正负号规定：若力使物体绕矩心作逆时针 转向转动力矩取正号,反之取负号。
1.5 力的投影
一、力在平面直角坐标轴上的投影

§3–2物体的受力分析及受力图
取AB梁，其受力图如图 (c)
杆的受力图能否画为 图（d）所示？
若这样画，梁AB的受力 图又如何改动?
§3–2物体的受力分析及受力图
例1-4
不计三铰拱桥的自重与摩擦，画 出左、右拱AC,CB的受力图与 系统整体受力图。
解： 右拱CB为二力构件，其受力 图如图（b）所示
于同一点的一个力，即合力。合力的矢由原两
力的矢为邻边而作出的力平行四边形的对角矢
来表示。
F2
R
即，合力为原两力的矢量和。
矢量表达式：R= F1+F2
A
F1
§2–2 静力学公理
推论 (三力汇交定理)
当刚体在三个力作用下平衡时，设其中两力的
作用线相交于某点，则第三力的作用线必定也通过
这个点。
证明：
F1
A1 A A2
F2
=
R1 F1
A
F2
A3
A3
F3
F3
§2–2 静力学公理
公理四 (作用和反作用公理) 任何两个物体间的相互作用的力，总是大小相
等，作用线相同，但指向相反，并同时分别作用于 这两个物体上。
§2-3 力矩与力偶
一、力矩的定义——力F 的大小乘以该力作用线到某点O 间距离d，并加上适当正负号，称为力F 对O 点的矩。
作用于刚体上某点力F，可以平行移动到刚体上任意一点 ，但须同时附加一个力偶，此附加力偶的矩等于原力F
对新作用点的矩。
证明： F
F
F
F
Od A
= Od A
=
mO A
F
F F F
m Fd m0 F
§3– 2

(b)
a Fx b
(a)
x
通常，对于直线段ab，若由a到b的指向与x轴的正向一致， 则投影Fx 取正号, 如图（a）所示；若由a到b的指向与x轴的正
向相反，则投影Fx 取负号, 如图（b ）所示。
F A
B θ x
B
F θ A b Fx a
(b)
a Fx b
(a)
x
若力F 和x轴正向之间的夹角为θ，则有
y
F3
x 60 o 69.5
o
F2
o 45
o
由力在坐标轴上的投影和合力
投影定理，采用解析法求解此 力系的合力，可得合力在坐标 轴上的投影
F4 F1
(a)
FR
FRx =
å
Fxi
= - F2 + F3 cos 600 + F4 cos 450 = - 1 + 1.5 ?cos 600 = 1.164kN 2 ?cos 450
பைடு நூலகம்
j
F1
i
Fn
x
o
FR = F1 + F2 + L + Fn =
å
Fi
（3-6）
证明：在各力作用线所在平面内建立直角坐标系Oxy，并沿x、
y方向取单位矢量i、j，如图所示。将（3-6）式右端各分力写 为解析表达式为
Fi = Fix i +Fiy j
(i =1,2,L , n) （3-7）
j
F2 F1
2 2 F R F Rx F Ry
F x F y
2
2
cos( F R, i ) F Rx FR F Ry cos( F R, j ) FR

FA 22.4 kN FC 28.3 kN
一、平面汇交力系的合成
桁架： 由若干直杆彼此在两端铰接而成的一种结构。
桁架中各杆的铰接点称为节点。
一、平面汇交力系的合成
工程实例：
一、平面汇交力系的合成
一、力在坐标轴上的投影 力 投影
X=Fx=Fcos Y=Fy=Fsin=F cos 投影 力 注：力在坐标 2 2 F Fx Fy 轴上的投影为 代数量，即标 X Fx cos Y F y 量，其值可正、 cos F F F F 可负、可为零。
一、平面交汇力系的合成
步骤）：1、据力在刚体上的可传性
原来的平面汇交力系就转 化为平面共点力系；2、据平行四边形法则求合力R。
F1 O
F2
F1 F2 O F3
F3 Fn
合力为各力的矢量和，即
Fn
R Fi
R
一、平面交汇力系的合成
F1
平面汇交 力系的合成：力的多边形法则
F2
A
F3
F3
合力：
FR
夹角：
2 2 FRx FRy 171.3N F arctan Rx 40.99o FRy
§1.2 平面汇交力系的平衡
从前述可知：平面汇交力系平衡的必要与充分条件 是该力系的合力为零。
Rx X 0 Ry Y 0
R 0 Rx Ry 0
45
D
所受的力。
§1.2 平面汇交力系的平衡
例题
解：
取AB为研究对象，其受力图为：
F E FA A
A
C

FC
C
F
45
45
B
B D

性质1：力偶无合力，本身又不平衡，是一个基本力学量。 力偶只能和力偶平衡，而不能和一个力平衡。 性质2：力偶中两个力在任意坐标轴上投影之代数和为零。 性质3：力偶中两力对任一点取矩之和恒等于力偶矩，而与 矩心的位置无关。
性质4：力偶可以在其作用面内任意移动或转动,而不影响它
对刚体的作用效应。
17
性质5：只要保持力偶矩大小和转向不变，可以任意改变力 偶中力的大小和相应力偶臂的长短，而不改变它对 刚体的作用效应。
FRy F1 y F2 y F3 y F4 y Fy
x
o
FRx F1x F2x
F4x F3x
FRx Fx
FRy Fy
合力投影定理：合力在任一轴上的投影，等于各分力在同一
轴上投影的代数和。
6
作业
P20 例2-1
为什么在离转动 轴不远的地方推门 , 用比较大的力才能把 门推开？ 为什么在离转动 轴较远的地方推门 , 用比较小的力就能把 门推开？
用 （F，F'）表示
F
d
F'
力偶的作 用面
力偶系：作用在刚体上的一群力偶。 力偶的作用效应：使刚体转动（由两个力共同作用引起）。 力的作用效应： 移动效应--取决于力的大小、方向；
转动效应--取决于力偶矩的大小、方向。
15
2、力偶矩
F
力偶臂 力偶的作 用面
d F' 力偶矩：m=±Fd
+ —
16
3、力偶的性质
利用合力矩定理：
求M O (F )
M O (Fx )+M O (Fy )=Fx b + Fy L a =F (Lsina +bcosa +asina )=M O (F )

Fx=Fcosa Fy=Fcosb =Fsina
bF a
Fx Fx
B
Fy
j O i
Fy A
F Fx2 F y2
x cos(F, i )= Fx /F cos(F, j )= Fy /F Fx= Fx i Fy = Fy j 力的解析表达式
二、力沿坐标轴分解
F=Fx+Fy = Fx i+y j
第二章 平面力系
平面力系：各力的作用线都在同一平面内的力系。
方法：
(1)几何法——用平行四边形法则对各力两两合成。
(2) 解析法——力系向一点简化 (理论根据：力的平移定理)。 本章介绍平面力系的简化和平衡问题，包括有摩擦的平衡问 题。
第一节 力在轴上的投影与力的分解 一、力在直角坐标轴上的投影
y 力在某轴上的投影，等于该力 的大小乘以力与投影轴正向间 夹角的余弦(代数量) 。
注意:力的投影与分力的区别(图示)
三、合力投影定理
y
Fn
y
FR x F2 O
合力
FR= SF
Fi F3
向x、y轴投影 FRx= SFx FRy= SFy x
2 2 F FR x FR y
F1
O
平面汇交力系
cos(FR, i )= FRx /FR cos(FR, j )= FRy /FR
平面汇交力系可合成为通过汇交点的合力，合力矢等于各分 力的矢量和。 合力投影定理：合力在某一轴上的投影，等于各分力在同一 轴上投影的代数和。

2 2 F F F 88 . 02 N R Rx Ry
F cos Rx 0 .112 F R
cos
F Ry F R
0.994
C
F3
F2
B
D
F4
E
F1
A
FR
a b c e d x
ae ab bc cd de
合力投影定理
n
F F F F F F Rx 1 x 2 x ix nx ix
i 1
[例3—1] 在图所示的平面汇交力系中，各力的大小 分别为F1＝30N,F2＝100N,F3＝20 N，方向给定 如图，o点为力系的汇交点。求该力系的合力。
y F
Fy
Fy
Fx

x
O
Fx
• 当x, y两轴不相互垂直时，则沿两轴的分力F’x和
•
F’y，在数值上不等于力F在此两轴上的投影Fx和Fy 力F在轴上的投影是代数量，而力F沿轴方向的分量 是矢量
y
Fy
Fy
'
F

F x'
x
O
Fx
合力投影定理
• 力系的合力在任一轴上的投影，等于力系中各
力在同一轴上投影的代数和。
F F cos x
F A

b
B
B
F

A x
a
x
b
a
Fx
Fx
• 力在轴上的投影是代数量。当力矢量与轴的正向
夹角α 为锐角时，此代数值取正，反之为负。
F A
பைடு நூலகம்

b
B
B
F

A x

第1章
1.1.2
建筑力学基础
力的三要素：
力的大小 、力的方向 、力的作用点 。
1.1.3 力的图示法
力具有大小和方向， 所以说力是矢量(vector )。 可以用一带箭头的直 线段将力的三要素 表示出来，
如图1.1所示。
第1章
建筑力学基础
力的定义
力是物体间相互间的机械作用。
力的效应
使物体的机械运动状态发生改变，叫做力 的运动效应或外效应。使物体的形状发生改变， 叫做力的变形效应或内效应。 力的三要素 力的大小、方向、作用点称为力的三要素。
讨论力的转动效应时， 主要关心力矩的大小与转 动方向，而这些与力的大 小、转动中心（矩心）的 位置、动中心到力作用线 的垂直距离（力臂）有关。
力矩与力偶
力的转动效应——力矩 M 可由下式计算：
M = ± FP ·d
式中：FP 是力的数值大小，d 是 力臂，逆时针转取正号，常用单 位是 KN-m 。力矩用带箭头的弧 线段表示。 集中力引起的力矩直接套用公式进行计算； 对于均布线荷载引起的力矩，先计算其合力， 再套用公式进行计算。
如图1.18(c)所示，可以用FRA和一未知方向角α表示，也可
以用一个水平力FXA和垂直力FYA表示。
第1章
建筑力学基础
2．可动铰支座
图l.20(a)是可动铰支座的示意图。构件与支 座用销钉连接，而支座可沿支承面移动，这种约 束，只能约束构件沿垂直于支承面方向的移动， 而不能阻止构件绕销钉的转动和沿支承面方向的 移动。所以，它的约束反力的作用点就是约束与 被约束物体的接触点、约束反力通过销钉的中心， 垂直于支承面，方向可能指向构件，也可能背离 构件，视主动力情况而定。这种支座的简图如 1.20(b)所示，约束反力如图1.20(c)所示。

一、力在坐标轴上的投影
•
力F在平面直角坐标轴上的 y A (起点） F 投影定义为：过力F两端向坐标 X / / α 轴引垂线得垂足a,b 和a ,b 。线段 F FY FY / / ab和a b 冠以相应的正号或负号， a′ （终点） b′ B 称为力F在x轴上的投影和力F在y 轴上的投影，用Fx,Fy表示。投影 o a FX b x 的符号规定为：由起点a到终点b / / 连线（或a 由b 到）的指向与坐标 轴正向相同时为正，反之为负。
2.2 平面汇交力系的合成
重 点 难 点
平面汇交力系合成的解析 法
一、平面汇交力系的合成
平面汇交力系是简单力系，是研究复杂力系的基础。平面汇 交力系的合成有两种方法。 1、几何法—用力的三角形法则或力的多边形法制求合力的方 法，是一种定性的粗略的计算方法 （1）两个汇交力的合成
2. 多个共点力的合成
合力：
R
F2 F1
a
b
c x
R Rx 2 Ry
tan Ry Rx
2
X Y
2
2
合力的投影 y

Y X
Rx

Ry
R
x
表示合力R与 x轴所夹的锐角， 合力的指向由∑X、∑Y的符号判定。
【例2-2】 试分别求出图2-6中各力的合力在x轴和y轴上投 影。已知
F1 20N
第二章 力的投影与平面汇交力系
平面汇交力系的合成与平衡
教学目标：
1、掌握力的投影计算、合力投影定理； 2、掌握平面汇交力系合成的几何法 3、牢固掌握平面汇交力系合成的解析法 4、牢固掌握平面汇交力系的平衡条件、 平衡方程 5、会用平衡方程解决力学问题
2.1

再以B（或C）管为研究对象，画出其受力图。 选图示坐标系，列平衡方程
∑Fx＝0，
得
F4－F1′cos60°=0
3 1 G 0.577kN 3 2
F4 F1cos60
考虑到管子每边在两端都各有一立柱，所以每根立柱所受 力的大小为
1 1 F F4 F4 0.289 kN 2 2
取投影轴x、y如图所示， 其中x轴沿CB方向， y轴垂直于FBC，列平衡方程
∑Fy=0， FABcos60°－FBDcos75°－Gcos30°=0 FAB=（FBDcos75°＋Gcos30°）/ cos60° =G（cos75°＋cos30°）/ cos60° =45.0kN(压力)
FAB =45.0kN(压力)
, ,
F4
e d Fx4 e, e,,
,
FRx Fxi
a
c
,
Fx3
a,,
FRx
合力在某个轴上的投影等于各个分力在同一 个坐标轴轴上投影的代数和.
2.3 汇交力系合成与平衡的解析法
2．3．1合成的解析法
1． 空间汇交力系
设空间汇交力系（F1，F2，…，Fn），其合
力为FR 。
FR Fi
O
y
A
θ B1 x
a
Fxy
b
其大小为： Fxy＝Fcosθ
2.2.3 力在直角坐标轴上的投影
1．直接投影法：
已知力F 和各坐标轴
正向间夹角为α，β，γ
γ α β
（称为F的三个方向角）
则：力F在空间直角坐标轴上的投影为：
Fx Fcos Fy Fcos Fz Fcos
这称为直接投影法。
D

2．力在轴上的投影、合力投影定理 力在轴上的投影、
• 力F在某轴x上的投影，等于力F的大小乘以力与该 在某轴x上的投影，等于力F
轴正向夹角α的余弦记为Fx， 轴正向夹角α的余弦记为Fx，即 Fx
Fx = F cos α
F A B
α
B
F
α
A
a
x b b a
x
FxΒιβλιοθήκη Fx• 力在轴上的投影是代数量。当力矢量与轴的正向 力在轴上的投影是代数量。
y
Fy
F
' y
F
α
Fx'
x
O
Fx
合力投影定理
• 力系的合力在任一轴上的投影，等于力系中各 力系的合力在任一轴上的投影，
力在同一轴上投影的代数和。 力在同一轴上投影的代数和。
C
F3
F4
E
F2
B
D
F1
A
FR
a b c e d x
ae = ab + bc + cd − de
合力投影定理
FRx = F1x + F2 x + L + Fix + L + Fnx = ∑ Fix
夹角α为锐角时，此代数值取正，反之为负。 夹角α为锐角时，此代数值取正，反之为负。
F A
B
α
B
F
α
A
a
x b b a
x
Fx
Fx
• 当力F沿正交的x轴和y轴分解为两个分力Fx和Fy时， 当力F沿正交的x轴和y轴分解为两个分力Fx和Fy时 Fx
它们的大小恰好等于力F在这两个轴上的投影Fx和 它们的大小恰好等于力F在这两个轴上的投影Fx和 Fx Fy的绝对值 的绝对值。 Fy的绝对值。

空间力系 的平衡条 件从简化 结果推出
三、空间一般力系平衡的方程（基本形式） ：
空间力偶系： ∑mX (F) =0 ∑mY (F) =0 ∑mZ (F) =0 空间平行力系： ∑FZ =0 ∑mX (F) =0 ∑mY (F) =0
b、先求出力 F 沿三个直角坐标轴的分力 Fx,Fy,Fz，然后根据力对轴之 矩的定义和合力矩定理进行计算
mx(F) =mx(Fz)+mx(Fy) = yFz-zFy my(F) =my(Fx)+my(Fz) = zFx – xFz mz(F) =mz(Fy)+mz(Fx) = xFy – yFx
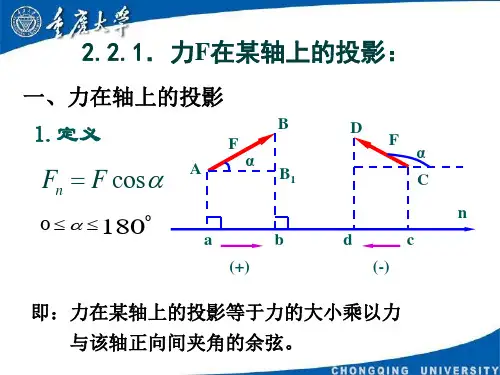
力在空间
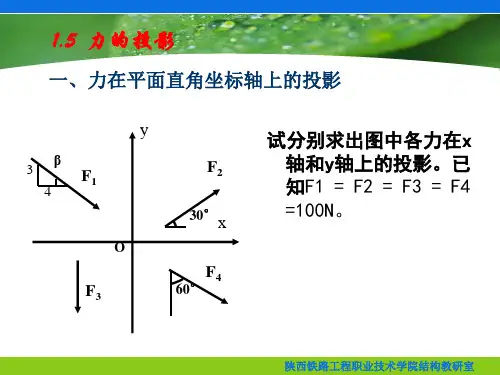
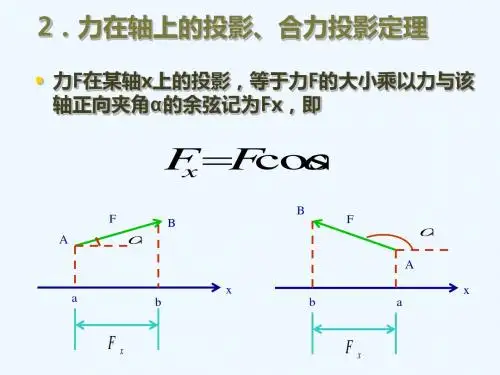
§1 力在空间直角坐标轴上的投影 研究空间力系应先掌握力在空间直角坐标轴上投影的计算，一般有直 接投影和二次投影两种方法。 一、直接投影法 已知一力 F 在空间直角坐标轴 x，y，z 的正向之间的夹角分别为α, β,γ则 F 在 x,y,z 轴上的投影记作:Fx,Fy,Fz.故有 Fx =±F cosα Fy =±Fcosβ Fz =±Fcosγ 上式中的 cosα,cosβ,cosγ为力 F 对 x,y,z 轴的方向余弦，故力在轴上 直接投影法公式
黄 河 水 利 职业技术学院
授 课 日 期 授 课 班 级 课题与主要 内
．． ．． ．． ．． ．． ．． ．． ．． ．． ．． ．． ． 装 ． ．． ．． ．． ．． ．． ．． 订 ． ．． ．． ．． ．． ． 线 ．． ．． ．． ．． ．． ．． ．． ．． ．． ．． ．．
课时授课计划
§2 力对轴之矩 1、定义： 力对轴之矩是力使物体绕轴转动效果的度量。 2、力对轴之矩的求解 （1）F 作用平面与轴垂直 力对 z 轴之矩，就是力对 O 点之矩，因此有 mz(F) = mo(F) =±Fd 符号规定：从轴的正向看,使物体绕轴逆时针方向 转为正，反之为负。 （2）F 作用平面与轴垂直并与轴正交 mz(F) = 0 （3）F 作用面与轴共面（F 与 z 轴平行） mz(F)=0