正方形专题复习之六大常考模型【精品】

正方形【命题趋势】在中考中.正方形主要在选择题.填空题.解答题考查为主.并结合相似.锐角三角函数结合考查.；其中正方形常考4种模型是中考中的重难点。

【中考考查重点】一、正方形的性质及判定二、正方形常考模型考点：正方形性质及判定一、正方形的概念和性质1.概念：有一组邻边相等.并且有一个角是直角的平行四边形是正方形.2.性质：（1）具有平行四边形、矩形、菱形的一切性质（2）正方形的四个角都是直角.四条边都相等（3）正方形的两条对角线相等.并且互相垂直平分.每一条对角线平分一组对角（4）正方形是轴对称图形.有4条对称轴（5）正方形的一条对角线把正方形分成两个全等的等腰直角三角形.两条对角线把正方形分成四个全等的小等腰直角三角形（6）正方形的一条对角线上的一点到另一条对角线的两端点的距离相等。

二、正方形的判定判定方法：（1）有一个角是直角的菱形是正方形；（2）对角线相等的菱形是正方形；（3）对角线互相垂直的矩形是正方形。

注意：判定一个四边形为正方形的一般顺序如下：先证明它是平行四边形.再证明它是菱形（或矩形）.最后证明它是矩形（或菱形）。

1.（2020秋•法库县期末）平行四边形、矩形、菱形、正方形共有的性质是（）A．对角线互相平分B．对角线相等C．对角线互相垂直D．对角线互相垂直平分【答案】A【解答】解：A、平行四边形、矩形、菱形、正方形的对角线都互相平分.故本选项正确；B、只有矩形.正方形的对角线相等.故本选项错误；C、只有菱形.正方形的对角线互相垂直.故本选项错误；D、只有菱形.正方形的对角线互相垂直平分.故本选项错误．故选：A．2.（2020秋•武功县期末）如图.在正方形ABCD中.AB＝2.P是AD边上的动点.PE⊥AC于点E.PF⊥BD于点F.则PE+PF的值为（）A．4B．2C．D．2【答案】C【解答】解：在正方形ABCD中.OA⊥OB.∠OAD＝45°.∵PE⊥AC.PF⊥BD.∴四边形OEPF为矩形.△AEP是等腰直角三角形.∴PF＝OE.PE＝AE.∴PE+PF＝AE+OE＝OA.∵正方形ABCD的边长为2.∴OA＝AC＝＝．故选：C．3.（2010秋•金口河区期末）如图.在正方形ABCD中.E是DC上一点.F为BC延长线上一点.∠BEC＝70°.且△BCE≌△DCF．连接EF.则∠EFD的度数是（）A．10°B．15°C．20°D．25°【答案】D【解答】解：∵四边形ABCD是正方形.∴∠BCE＝∠DCF＝90°；由旋转的性质知：CE＝CF.∠BEC＝∠DFC＝70°；则△ECF是等腰直角三角形.得∠EFC＝45°.∴∠EFD＝∠DFC﹣∠EFC＝25°．故选：D．4.（2020春•沙坪坝区期末）如图.正方形ABCD中.AB＝.点E是对角线AC上一点.EF⊥AB于点F.连接DE.当∠ADE＝22.5°时.EF的长是（）A．1B．2﹣2C．﹣1D．【答案】C【解答】解：∵四边形ABCD是正方形.∴AB＝CD＝BC＝.∠B＝∠ADC＝90°.∠BAC＝∠CAD＝45°.∴AC＝AB＝2.∵∠ADE＝22.5°.∴∠CDE＝90°﹣22.5°＝67.5°.∵∠CED＝∠CAD+∠ADE＝45°+22.5°＝67.5°.∴∠CDE＝∠CED.∴CD＝CE＝.∴AE＝2﹣.∵EF⊥AB.∴∠AFE＝90°.∴△AFE是等腰直角三角形.∴EF＝＝﹣1.故选：C．5.（2021•罗湖区校级模拟）如图.在平面直角坐标系xOy中.正方形ABCD的顶点D在y轴上且A（﹣3.0）.B（2.b）.则正方形ABCD的面积是（）A．20B．16C．34D．25【答案】C【解答】解：作BM⊥x轴于M．∵四边形ABCD是正方形.∴AD＝AB.∠DAB＝90°.∴∠DAO+∠BAM＝90°.∠BAM+∠ABM＝90°.∴∠DAO＝∠ABM.∵∠AOD＝∠AMB＝90°.∴在△DAO和△ABM中.∴△DAO≌△ABM（AAS）.∴OA＝BM.AM＝OD.∵A（﹣3.0）.B（2.b）.∴OA＝3.OM＝2.∴OD＝AM＝5.∴AD＝＝.∴正方形ABCD的面积＝34.故选：C．6.（2020春•老城区校级月考）如图.点P是正方形ABCD的对角线BD上一点.PE⊥BC于点E.PF⊥CD于点F.连接EF给出下列四个结论：①AP＝EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE＝∠BAP．其中正确结论个数是（）A．1B．2C．3D．4【答案】C【解答】解：如图.连接PC.延长AP交EF于H.延长FP交AB于G.在正方形ABCD中.∠ABP＝∠CBP＝45°.AB＝CB.∵在△ABP和△CBP中..∴△ABP≌△CBP（SAS）.∴AP＝PC.∠BAP＝∠BCP.又∵PE⊥BC.PF⊥CD.∴四边形PECF是矩形.∴PC＝EF.∠BCP＝∠PFE.∴AP＝EF.∠PFE＝∠BAP.故①④正确；只有点P为BD的中点或PD＝AD时.△APD是等腰三角形.故③错误；∵PF∥BC.∴∠AGF＝∠ABC＝90°.∵∠BAP＝∠PFE.∠APG＝∠FPH.∴∠AGP＝∠AHF＝90°.∴AP⊥EF.故②正确.故选：C．7.（2021秋•南海区月考）如图.点B在MN上.过AB的中点O作MN的平行线.分别交∠ABM的平分线和∠ABN的平分线于点C、D．（1）试判断四边形ACBD的形状.并证明你的结论．（2）当△CBD满足什么条件时.四边形ACBD是正方形？并给出证明．【答案】（1）四边形ACBD是矩形（2）△CBD满足CB＝BD时.四边形ACBD是正方形【解答】解：（1）四边形ACBD是矩形.证明：∵CD平行MN.∴∠OCB＝∠CBM.∵BC平分∠ABM.∴∠OBC＝∠CBM.∴∠OCB＝∠OBC.∴OC＝OB.同理可证：OB＝OD.∴OA＝OB＝OC＝OD.∵CD＝OC+OD.AB＝OA+OB.∴AB＝CD.∴四边形ACBD是矩形；（2）△CBD满足CB＝BD时.四边形ACBD是正方形.证明：由（1）得四边形ACBD是矩形.∵CB＝BD.∴四边形ACBD是正方形．1．（2021秋•武侯区期末）下列说法中.是正方形具有而矩形不具有的性质是（）A．两组对边分别平行B．对角线互相垂直C．四个角都为直角D．对角线互相平分【答案】B【解答】解：因为正方形的对角相等.对角线相等、垂直、且互相平分.矩形的对角相等.对角线相等.互相平分.所以正方形具有而矩形不具有的性质是对角线互相垂直．故选：B．2．（2017春•柳州期末）边长为4的正方形ABCD中.P是边AD上的动点.PE⊥AC于点E.PF⊥BD于点F.则PE+PF的值为（）A．2B．4C．2D．6【答案】A【解答】解：如图.∵四边形ABCD为正方形.∴∠CAD＝∠BDA＝45°.∵PE⊥AC于点E.PF⊥BD于点F.∴△APE和△PDF为等腰直角三角形.∴PE＝AP.PF＝PD.∴PE+PF＝（AP+PD）＝×4＝2．故选：A．3．（2021秋•普宁市期末）下列说法中正确的是（）A．矩形的对角线平分每组对角B．菱形的对角线相等且互相垂直C．有一组邻边相等的矩形是正方形D．对角线互相垂直的四边形是菱形【答案】C【解答】解：A、矩形的对角线平分每组对角.说法错误.故本选项不符合题意；B、菱形的对角线互相垂直.故本选项不符合题意；C、有一组邻边相等的矩形是正方形.正确.故本选项符合题意；D、对角线互相垂直的四边形不一定是菱形.故本选项不符合题意．故选：C．4．（2020•眉山）下列说法正确的是（）A．一组对边平行另一组对边相等的四边形是平行四边形B．对角线互相垂直平分的四边形是菱形C．对角线相等的四边形是矩形D．对角线互相垂直且相等的四边形是正方形【答案】B【解答】解：A、一组对边平行另一组对边相等的四边形可以是等腰梯形.可以是平行四边形.故选项A不合题意；B、对角线互相垂直平分的四边形是菱形.故选项B符合题意；C、对角线相等的平行四边形是矩形.故选项C不合题意；D、对角线互相垂直平分且相等的四边形是正方形.故选项D不合题意；故选：B．5．（2021秋•海州区期末）如图.在正方形ABCD中.点E在对角线AC上.EF⊥AB于点F.EG⊥BC于点G.连接DE.若AB＝10.AE＝3.则ED的长度为（）A．7B．2C．D．【答案】C【解答】解：如图.连接BE.∵四边形ABCD是正方形.∴∠BAC＝∠DAC＝45°.AB＝AD.∵AE＝AE.∴△ABE≌△ADE（SAS）.∴BE＝DE.∵EF⊥AB于点F.AE＝3.∴AF＝EF＝3.∵AB＝10.∴BF＝7.∴BE＝＝.∴ED＝．故选：C．6．（2021秋•铁锋区期末）如图.已知在正方形ABCD中.AB＝BC＝CD＝AD＝10厘米.∠A＝∠B＝∠C＝∠D＝90°.点E在边AB上.且AE＝4厘米.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动.同时.点Q在线段CD上由C点向D点运动.设运动时间为t秒．当△BPE与△CQP全等时.t的值为（）A．2B．2或1.5C．2.5D．2.5或2【答案】D【解答】解：当点Q的运动速度与点P的运动速度都是2厘米/秒.若△BPE≌△CQP.则BP＝CQ.BE＝CP.∵AB＝BC＝10厘米.AE＝4厘米.∴BE＝CP＝6厘米.∴BP＝10﹣6＝4厘米.∴运动时间＝4÷2＝2（秒）；当点Q的运动速度与点P的运动速度不相等.∴BP≠CQ.∵∠B＝∠C＝90°.∴要使△BPE与△OQP全等.只要BP＝PC＝5厘米.CQ＝BE＝6厘米.即可．∴点P.Q运动的时间t＝＝（秒）.故选：D．7．（2021春•海淀区校级期末）如图.点E是正方形ABCD对角线AC上一点.EF⊥AB.EG ⊥BC.垂足分别为F.G.若正方形ABCD的周长是40cm．（1）求证：四边形BFEG是矩形；（2）求四边形EFBG的周长；（3）当AF的长为多少时.四边形BFEG是正方形？【答案】（1）略（2）20cm （3）AF＝5cm【解答】解：（1）证明：∵四边形ABCD为正方形.∴AB⊥BC.∠B＝90°．∵EF⊥AB.EG⊥BC.∴∠BFE＝90°.∠BGE＝90°．又∵∠B＝90°.∴四边形BFEG是矩形；（2）∵正方形ABCD的周长是40cm.∴AB＝40÷4＝10cm．∵四边形ABCD为正方形.∴△AEF为等腰直角三角形.∴AF＝EF.∴四边形EFBG的周长C＝2（EF+BF）＝2（AF+BF）＝20cm．（3）若要四边形BFEG是正方形.只需EF＝BF.∵AF＝EF.AB＝10cm.∴当AF＝5cm时.四边形BFEG是正方形．1．（2021•玉林）一个四边形顺次添加下列条件中的三个条件便得到正方形：a．两组对边分别相等b．一组对边平行且相等c．一组邻边相等d．一个角是直角顺次添加的条件：①a→c→d②b→d→c③a→b→c则正确的是（）A．仅①B．仅③C．①②D．②③【答案】C【解答】解：①由a得到两组对边分别相等的四边形是平行四边形.添加c即一组邻边相等的平行四边形是菱形.再添加d即一个角是直角的菱形是正方形.故①正确；②由b得到一组对边平行且相等的四边形是平行四边形.添加d即有一个角是直角的平行四边形是矩形.再添加c即一组邻边相等的矩形是正方形.故②正确；③由a得到两组对边分别相等的四边形是平行四边形.添加b得到一组对边平行且相等的平行四边形仍是平行四边形.再添加c即一组邻边相等的平行四边形是菱形.不能得到四边形是正方形.故③不正确；故选：C．2．（2019•毕节市）如图.点E在正方形ABCD的边AB上.若EB＝1.EC＝2.那么正方形ABCD的面积为（）A．B．3C．D．5【答案】B【解答】解：∵四边形ABCD是正方形.∴∠B＝90°.∴BC2＝EC2﹣EB2＝22﹣12＝3.∴正方形ABCD的面积＝BC2＝3．故选：B．3．（2021•重庆）如图.正方形ABCD的对角线AC.BD交于点O.M是边AD上一点.连接OM.过点O作ON⊥OM.交CD于点N．若四边形MOND的面积是1.则AB的长为（）A．1B．C．2D．2【答案】C【解答】解：∵四边形ABCD是正方形.∴∠MDO＝∠NCO＝45°.OD＝OC.∠DOC＝90°.∴∠DON+∠CON＝90°.∵ON⊥OM.∴∠MON＝90°.∴∠DON+∠DOM＝90°.∴∠DOM＝∠CON.在△DOM和△CON中..∴△DOM≌△CON（ASA）.∵四边形MOND的面积是1.四边形MOND的面积＝△DOM的面积+△DON的面积.∴四边形MOND的面积＝△CON的面积+△DON的面积＝△DOC的面积.∴△DOC的面积是1.∴正方形ABCD的面积是4.∴AB2＝4.∴AB＝2.故选：C．4．（2021•湖北）如图.在正方形ABCD中.AB＝4.E为对角线AC上与A.C不重合的一个动点.过点E作EF⊥AB于点F.EG⊥BC于点G.连接DE.FG.下列结论：①DE＝FG；②DE⊥FG；③∠BFG＝∠ADE；④FG的最小值为3．其中正确结论的个数有（）A．1个B．2个C．3个D．4个【答案】C【解答】解：①连接BE.交FG于点O.如图.∵EF⊥AB.EG⊥BC.∴∠EFB＝∠EGB＝90°．∵∠ABC＝90°.∴四边形EFBG为矩形．∴FG＝BE.OB＝OF＝OE＝OG．∵四边形ABCD为正方形.∴AB＝AD.∠BAC＝∠DAC＝45°．在△ABE和△ADE中..∴△ABE≌△ADE（SAS）．∴BE＝DE．∴DE＝FG．∴①正确；②延长DE.交FG于M.交FB于点H.∵△ABE≌△ADE.∴∠ABE＝∠ADE．由①知：OB＝OF.∴∠OFB＝∠ABE．∴∠OFB＝∠ADE．∵∠BAD＝90°.∴∠ADE+∠AHD＝90°．∴∠OFB+∠AHD＝90°．即：∠FMH＝90°.∴DE⊥FG．∴②正确；③由②知：∠OFB＝∠ADE．即：∠BFG＝∠ADE．∴③正确；④∵点E为AC上一动点.∴根据垂线段最短.当DE⊥AC时.DE最小．∵AD＝CD＝4.∠ADC＝90°.∴AC＝．∴DE＝AC＝2．由①知：FG＝DE.∴FG的最小值为2.∴④错误．综上.正确的结论为：①②③．故选：C．5．（2020•陕西）如图.在矩形ABCD中.AB＝4.BC＝8.延长BA至E.使AE＝AB.以AE为边向右侧作正方形AEFG.O为正方形AEFG的中心.若过点O的一条直线平分该组合图形的面积.并分别交EF、BC于点M、N.则线段MN的长为．【答案】4【解答】解：如图.连接AC.BD交于点H.过点O和点H的直线MN平分该组合图形的面积.交AD于S.取AE中点P.取AB中点Q.连接OP.HQ.过点O作OT⊥QH于T.∵四边形ABCD是矩形.∴AH＝HC.又∵Q是AB中点.∴QH＝BC＝4.QH∥BC.AQ＝BQ＝2.同理可求PO＝AG＝2.PO∥AG.EP＝AP＝2.∴PO∥AD∥BC∥EF∥QH.EP＝AP＝AQ＝BQ.∴MO＝OS＝SH＝NH.∠OPQ＝∠PQH＝90°.∵OT⊥QH.∴四边形POTQ是矩形.∴PO＝QT＝2.OT＝PQ＝4.∴TH＝2.∴OH＝＝＝2.∴MN＝2OH＝4.故答案为：4．6．（2021•邵阳）如图.在正方形ABCD中.对角线AC.BD相交于点O.点E.F是对角线AC上的两点.且AE＝CF．连接DE.DF.BE.BF．（1）证明：△ADE≌△CBF．（2）若AB＝4.AE＝2.求四边形BEDF的周长．【答案】（1）略（2）8【解答】（1）证明：由正方形对角线平分每一组对角可知：∠DAE＝∠BCF＝45°.在△ADE和△CBF中..∴△ADE≌△CBF（SAS）．（2）解：∵AB＝AD＝.∴BD＝＝＝8.由正方形对角线相等且互相垂直平分可得：AC＝BD＝8.DO＝BO＝4.OA＝OC＝4.又AE＝CF＝2.∴OA﹣AE＝OC﹣CF.即OE＝OF＝4﹣2＝2.故四边形BEDF为菱形．∵∠DOE＝90°.∴DE＝＝＝2．∴4DE＝.故四边形BEDF的周长为8．1．（2021•云岩区模拟）数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具.此时测得∠D＝60°.对角线AC长为16cm.改变教具的形状成为图2所示的正方形.则正方形的边长为（）A．8cm B．4cm C．16cm D．16cm【答案】C【解答】解：如图1.图2中.连接AC．图1中.∵四边形ABCD是菱形.∴AD＝DC.∵∠D＝60°.∴△ADC是等边三角形.∴AD＝DC＝AC＝16cm.∴正方形ABCD的边长为16cm.故选：C．2．（2021•石家庄一模）将图1中两个三角形按图2所示的方式摆放.其中四边形ABCD 为矩形.连接PQ.MN.甲、乙两人有如下结论：甲：若四边形ABCD为正方形.则四边形PQMN必是正方形；乙：若四边形PQMN为正方形.则四边形ABCD必是正方形．下列判断正确的是（）A．甲正确.乙不正确B．甲不正确.乙正确C．甲、乙都不正确D．甲、乙都正确【答案】B【解答】解：若ABCD是正方形.可设AB＝BC＝CD＝AD＝x.∴AQ＝4﹣x.AP＝3+x.∴PQ2＝AQ2+AP2.即PQ＝＝＝.x取值不同则PQ的长度不同.∴甲不正确.若四边形PQMN为正方形.则PQ＝PN＝MN＝MQ＝5.且∠QMD+∠MQD＝∠QAP＝∠AQP+∠QP A＝90°.在△QMD和△PQA中..∴△QMD≌△PQA（ASA）.∴QD＝AP.同理QD＝AP＝MC＝BN.又∵BP＝MD＝AQ.∴QD﹣AD＝P A﹣AB.∴AB＝AD.同理AB＝CD＝AD＝BC.即四边形ABCD为菱形.∵∠DAB＝180°﹣∠QAP＝90°.则四边形ABCD为正方形.∴乙正确.故选：B．3．（2021•临沂模拟）如图.AD是△ABC的角平分线.DE.DF分别是△ABD和△ACD的高.得到下列四个结论：①OA＝OD；②AD⊥EF；③当∠A＝90°时.四边形AEDF是正方形；④AE+DF＝AF+DE．其中正确的是（）A．②③B．②④C．①③④D．②③④【答案】D【解答】解：如果OA＝OD.则四边形AEDF是矩形.没有说∠A＝90°.不符合题意.故①错误；∵AD是△ABC的角平分线.∴∠EAD＝∠F AD.在△AED和△AFD中..∴△AED≌△AFD（AAS）.∴AE＝AF.DE＝DF.∴AE+DF＝AF+DE.故④正确；∵在△AEO和△AFO中..∴△AEO≌△AFO（SAS）.∴EO＝FO.又∵AE＝AF.∴AO是EF的中垂线.∴AD⊥EF.故②正确；∵当∠A＝90°时.四边形AEDF的四个角都是直角.∴四边形AEDF是矩形.又∵DE＝DF.∴四边形AEDF是正方形.故③正确．综上可得：正确的是：②③④.故选：D．4．（2020•宁津县一模）下列说法正确的是（）A．对角线相等且相互平分的四边形是矩形B．对角线相等且相互垂直的四边形是菱形C．四条边相等的四边形是正方形D．对角线相互垂直的四边形是平行四边形【答案】A【解答】解：A、对角线相等且相互平分的四边形是矩形.故该选项正确；B、对角线相等且相互垂直的四边形不一定是菱形.故该选项错误；C、四条边相等的四边形是菱形.不是正方形.故该选项错误；D、对角线相互垂直的四边形不是平行四边形.故该选项错误.故选：A．5．（2021•南浔区模拟）如图.E.F是正方形ABCD的边BC上两个动点.BE＝CF．连接AE.BD交于点G.连接CG.DF交于点M．若正方形的边长为1.则线段BM的最小值是（）A．B．C．D．【答案】D【解答】解：如图.在正方形ABCD中.AB＝AD＝CB.∠EBA＝∠FCD.∠ABG＝∠CBG.在△ABE和△DCF中..∴△ABE≌△DCF（SAS）.∴∠BAE＝∠CDF.在△ABG和△CBG中..∴△ABG≌△CBG（SAS）.∴∠BAG＝∠BCG.∴∠CDF＝∠BCG.∵∠DCM+∠BCG＝∠FCD＝90°.∴∠CDF+∠DCM＝90°.∴∠DMC＝180°﹣90°＝90°.取CD的中点O.连接OB、OF.则OF＝CO＝CD＝.在Rt△BOC中.OB＝＝＝.根据三角形的三边关系.OM+BM＞OB.∴当O、M、B三点共线时.BM的长度最小.∴BM的最小值＝OB﹣OF＝＝．故选：D．6.（2021•平凉模拟）如图.在矩形ABCD中.M、N分别是边AD、BC的中点.E、F分别是线段BM、CM的中点．（1）求证：BM＝CM．（2）当AB：AD的值为多少时.四边形MENF是正方形？请说明理由．【答案】（1）略（2）当AB：AD＝1：2时.四边形MENF是正方形【解答】（1）证明：∵四边形ABCD是矩形.∴AB＝DC.∠A＝∠D＝90°.∵M为AD中点.∴AM＝DM.在△ABM和△DCM中..∴△ABM≌△DCM（SAS）.∴BM＝CM；（2）解：当AB：AD＝1：2时.四边形MENF是正方形.理由如下：∵N、E、F分别是BC、BM、CM的中点.∴NE∥CM.NE＝CM.∵MF＝CM.∴NE＝FM.∵NE∥FM.∴四边形MENF是平行四边形.由（1）知△ABM≌△DCM.∴BM＝CM.∵E、F分别是BM、CM的中点.∴ME＝MF.∴平行四边形MENF是菱形；∵M为AD中点.∴AD＝2AM.∵AB：AD＝1：2.∴AD＝2AB.∴AM＝AB.∵∠A＝90°.∴∠ABM＝∠AMB＝45°.同理∠DMC＝45°.∴∠EMF＝180°﹣45°﹣45°＝90°.∵四边形MENF是菱形.∴菱形MENF是正方形．7．（2021•沂水县二模）如图.四边形ABCD是正方形.△ABE是等边三角形.M为对角线BD（不含B点）上的点．（1）当点M是CE与BD的交点时.如图1.求∠DMC的度数；（2）若点M是BD上任意一点时.将BM绕点B逆时针旋转60°得到BN.连接EN.CM.求证：EN＝CM；（3）当点M在何处时.BM+2CM的值最小.说明理由．【答案】（1）60°（2）略（3）当M点位于BD.CE交点时.BM+2CM的值最小【解答】（1）解：∵△AEB是等边三角形.∴EB＝AB＝AE.∠EBA＝60°.∵四边形ABCD是正方形.∴AB＝BC.∠ABC＝90°.∴EB＝CB.∠EBC＝∠EBA+∠ABC＝60°+90°＝150°.∴∠BCE＝（180°﹣∠EBC）＝×（180°﹣150°）＝15°.∵BD是正方形ABCD的对角线.∴∠DBC＝45°.∵∠DMC是△BMC的外角.∴∠DMC＝∠DBC+∠BCE＝45°+15°＝60°；（2）证明：由旋转可知.BM＝BN.∠MBN＝60°.∵∠MBA＝45°.∴∠ABN＝∠MBN﹣∠MBA＝15°.∵∠ABE＝60°.∴∠NBE＝∠ABE﹣∠ABN＝45°.在△BMC和△BNE中..∴△BMC≌△BNE（SAS）.∴CM＝EN；（3）当M点位于BD.CE交点时.BM+2CM的值最小.理由如下：在△ADM和△CDM中..∴△ADM≌△CDM（SAS）.∴AM＝CM.将BM绕点B旋转60°.得到BN.∵∠EBN+∠NBA＝60°.∠NBA+∠ABM＝60°.∴∠EBN＝∠ABM.在△ENB和△AMB中..∴△ENB≌△AMB（SAS）.∴AM＝EN.∵BM＝BN.∠NBM＝60°.∴△BMN是等边三角形.∴BM＝NM.∴BM+2CM＝BM+AM+CM＝MN+EN+CM＝EN+MN+CM.即E.N.M.C四点共线时.有最小值．8．（2022•南昌模拟）已知正方形ABCD与正方形AEFG.正方形AEFG绕点A旋转一周．（1）如图1.连接BG、CF.①求的值；②求∠BHC的度数．（2）当正方形AEFG旋转至图2位置时.连接CF、BE.分别取CF、BE的中点M、N.连接MN.猜想MN与BE的数量关系与位置关系.并说明理由．【答案】（1）①＝②45°（2）BE＝2MN.MN⊥BE【解答】解：（1）①如图1.连接AF.AC.∵四边形ABCD和四边形AEFG都是正方形.∴AC＝AB.AF＝AG.∠CAB＝∠GAF＝45°.∠BAD＝90°.∴∠CAF＝∠BAG..∴△CAF∽△BAG.∴＝；②∵AC是正方形BCD的对角线.∴∠ABC＝90°.∠ACB＝45°.在△BCH中.∠BHC＝180°﹣（∠HBC+∠HCB）＝180°﹣（∠HBC+∠ACB+∠ACF）＝180°﹣（∠HBC+∠ACB+∠ABG）＝180°﹣（∠ABC+∠ACB）＝45°；（2）BE＝2MN.MN⊥BE.理由如下：如图2.连接ME.过点C作CQ∥EF.交直线ME于Q.连接BH.设CF与AD 交点为P.CF与AG交点为R.∵CQ∥EF.∴∠FCQ＝∠CFE.∵点M是CF的中点.∴CM＝MF.又∵∠CMQ＝∠FME.∴△CMQ≌△FME（ASA）.∴CQ＝EF.ME＝QM.∴AE＝CQ.∵CQ∥EF.AG∥EF.∴CQ∥AG.∴∠QCF＝∠CRA.∵AD∥BC.∴∠BCF＝∠APR.∴∠BCQ＝∠BCF+∠QCF＝∠APR+∠ARC.∵∠DAG+∠APR+∠ARC＝180°.∠BAE+∠DAG＝180°.∴∠BAE＝∠BCQ.又∵BC＝AB.CQ＝AE.∴△BCQ≌△BAE（SAS）.∴BQ＝BE.∠CBQ＝∠ABE.∴∠QBE＝∠CBA＝90°.∵MQ＝ME.点N是BE中点.∴BQ＝2MN.MN∥BQ.∴BE＝2MN.MN⊥BE．。

最全：初中数学几何模型几何是初中数学中非常重要的内容，一般会在压轴题中进行考察，而掌握几何模型能够为考试节省不少时间，小编整理了常用的各大模型，一定要认真掌握哦~全等变换平移：平行等线段（平行四边形）对称：角平分线或垂直或半角旋转：相邻等线段绕公共顶点旋转对称全等模型说明：以角平分线为轴在角两边进行截长补短或者作边的垂线，形成对称全等。

两边进行边或者角的等量代换，产生联系。

垂直也可以做为轴进行对称全等。

对称半角模型说明：上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称（翻折），翻折成正方形或者等腰直角三角形、等边三角形、对称全等。

旋转全等模型半角：有一个角含1/2角及相邻线段自旋转：有一对相邻等线段，需要构造旋转全等共旋转：有两对相邻等线段，直接寻找旋转全等中点旋转：倍长中点相关线段转换成旋转全等问题旋转半角模型说明：旋转半角的特征是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一起，成对称全等。

自旋转模型构造方法：遇60度旋60度，造等边三角形；遇90度旋90度，造等腰直角遇等腰旋顶点，造旋转全等；遇中点旋180度，造中心对称共旋转模型说明：旋转中所成的全等三角形，第三边所成的角是一个经常考察的内容。

通过“8”字模型可以证明。

模型变形说明：模型变形主要是两个正多边形或者等腰三角形的夹角的变化，另外是等腰直角三角形与正方形的混用。

当遇到复杂图形找不到旋转全等时，先找两个正多边形或者等腰三角形的公共顶点，围绕公共顶点找到两组相邻等线段，分组组成三角形证全等。

中点旋转：说明：两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点，证明另外两个顶点与中点所成图形为等腰直角三角形。

证明方法是倍长所要证等腰直角三角形的一直角边，转化成要证明的等腰直角三角形和已知的等腰直角三角形（或者正方形）公旋转顶点，通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。

模型正方形模型·全归纳来源：周老师的初中理科课堂（ID：zhou_studyclub）这次要归纳的是和正方形相关的几何模型，内容基本涵盖了中考中考查频率较高的各种类型，既有比较基础的，也有提升和拓展，更有我的独家解题心得。

我愿意毫无保留地分享这些经验，希望能帮助到学有所需的同学！首先，我们概览一下正方形模型总图：咱们再放大了看清楚：乍一看是不是觉得线条纷杂？因为正方形当中的特殊点、特殊线相互之间都是有关联的，所以我可以把所有相关模型组合在一起。

接下来我会把这些元素拆开细讲，如果同学们看过之后全都理解掌握了，也可以试着画一画，我觉得如果能把这张图画好，正方形就被你看透，毫无秘密了。

分解一：这是各种模型中最常考的，几乎没有秘密，每个人都必须熟练掌握。

在我的教学体系中，它被归为“半角模型”中的一种常考特例，所以只要采用解决“半角模型”的通用方法——旋转+二次全等，就可以轻松解题。

（“半角模型”也是非常有用的，建议掌握。

）分解二：“轨迹”是一种重要的数学思想方法，其影响贯穿整个初高中阶段，现在就习惯和掌握这种思维模式，对高中阶段的解析几何学习是非常有益的。

对“轨迹”的考查在中考中一般都是以难题、压轴题出现，单是“轨迹”这个专题我就会给学生讲好几个课时。

很多同学在初三下的最后阶段，才开始接触到真正的压轴题，很多高阶的内容是来不及掌握的，所以我都是很早就开始给学生灌输这些思想和观点。

我建议学有余力的同学，一定要好好领悟下“轨迹”思想。

分解三：因为很多分析都已经写在图上了，我就不再赘述。

请需要学习的同学仔细看图上的批注，特别是方法总结。

这个模型还有几种引申的考法：请同学注意上图中打星的句子，这可不是句无关痛痒的废话，请好好理解下，如果你真的懂我的意思了，解这类几何题绝对没问题。

分解四：这部分涉及到圆和相似三角形，是九年级数学的内容。

首先看一下是不是和“分解二”的模型很类似，其实这两个是互逆的过程，不过“分解四”的证明难度略高些。

一、中点模型1．倍长中线条件：AD 为△ABC 的中线辅助线：延长AD 到点E ，使得AD =DE结论：△ADC ≌△EDB ，AC ∥BE2．连中点构造中位线条件：点D 、E 为AB 、AC 的中点辅助线：连接DE 结论：12DE BC DE BC =，∥3．倍长一边构造中位线条件：点D 为AB 的中点辅助线：延长AC 到点E ，使得AC =CE ，连接BE 结论：12DC BE DC BE =，∥4．构造三线合一条件：AB =AC辅助线：取BC 的中点D ，连接AD结论：AD ⊥BC ，∠BAD =∠CADB5．构造斜边中线条件：∠ABC =90°辅助线：取AC 的中点D ，连接BD 结论：12BD AC AD CD ===二、角平分线模型6．往角两边作垂线条件：AD 平分∠BAC辅助线：过点D 作AB 、AC 的垂线，垂足分别为E 、F结论：△ADE ≌△ADF7．在角的两边截取等长线段条件：AD 平分∠BAC辅助线：在AB 、AC 上取点E 、F ，满足AE =AF ，连接DE 、DF 结论：△ADE ≌△ADF8．过角平分线上一点作垂线条件：AD 平分∠BAC辅助线：过点D 作EF ⊥AD ，交AB 、AC 于点E 、FD CBB CCC结论：△ADE ≌△ADF三、双角平分线模型9．内内模型条件：BD 、CD 平分∠ABC 、∠ACB 结论：1902D A ∠=︒+∠10．内外模型条件：BD 、CD 平分∠ABC 、∠ACE 结论：12D A ∠=∠11．外外模型条件：BD 、CD 平分∠CBE 、∠BCF 结论：1902D A ∠=︒-∠四、平行线模型12．猪蹄模型CA BCC ED条件：AB ∥CD辅助线：过点E 作EF ∥AB结论：∠B +∠D =∠BED13．铅笔头模型条件：AB ∥CD辅助线：过点E 作EF ∥AB结论：∠B +∠D +∠BED =360°14．鸟头模型条件：AB ∥CD辅助线：过点E 作EF ∥AB结论：∠D +∠BED =∠B15．平行线+角平分线模型条件：AB ∥CD ，CE 平分∠ACD结论：AC =AE五、等积模型16．等底等高条件：AD ∥BCFAFBC结论：ABC DBC S S =，ADB ADC S S =17．等高模型条件：B 、C 、D 共线结论：::ABD ADC S S BD CD =18．等底模型条件：AE 、DE 为△ABC 、△DBC 边BC 上的高结论：::ABC DBC S S AE DE =六、对称半角模型19．对称半角模型-含45°角的三角形条件：∠BAC =45°，AD ⊥BC辅助线：作点D 关于AB 的对称点E ，关于AC 的对称点F ， 连接AE 、AF 、BE 、CF 、EF结论：△AEF 是等腰直角三角形20．对称半角模型-含30°角的三角形B CB C DED条件：∠BAC =30°，AD ⊥BC辅助线：作点D 关于AB 的对称点E ，关于AC 的对称点F ， 连接AE 、AF 、BE 、CF 、EF结论：△AEF 是等边三角形七、旋转半角模型21．旋转半角模型-等腰直角三角形条件：AB =AC ，∠BAC =90°，∠MAN =45°辅助线：将△ABM 绕点A 逆时针旋转90°，得到△ACM ＇ 结论：ANM ANM '≌，222BM CN MN +=22．旋转半角模型-等边三角形条件：△ABC 是等边三角形，BD =CD ，∠BDC =120°， ∠MDN =60°辅助线：将△BDM 绕点D 顺时针旋转120°，得到△DCM ＇ 结论：NDM NDM '≌，BM CN MN +=23．旋转半角模型-正方形条件：正方形ABCD ，∠MAN =45°，FEAM'M CAB辅助线：将△ABM 绕点A 逆时针旋转90°，得到△ADM ＇ 结论：NAM NAM '≌，BM DN MN +=八、自旋转模型24．自旋转模型-等边三角形条件：△ABC 是等边三角形，点P 为其内任意一点辅助线：将△BAP 绕点B 顺时针旋转60°，得到△BCP ＇ 结论：△BPP ＇是等边三角形25．自旋转模型-等腰直角三角形条件：△ABC 中，∠BAC =90°，AB =AC ，点P 为△ABC 内任 意一点辅助线：将△BAP 绕点A 逆时针旋转90°，得到△ACP ＇ 结论：△APP ＇是等腰直角三角形26．自旋转模型-等腰三角形条件：△ABC 中，AB =AC ，点P 为△ABC 内任意一点，∠BAC =α 辅助线：将△BAP 绕点A 逆时针旋转α，得到△ACP ＇ 结论：△APP ＇是等腰三角形M'DNCBAB九、手拉手模型29．手拉手模型-等边三角形条件：△ABC和△CDE都是等边三角形结论：△ACE≌△BCD27．手拉手模型-等腰直角三角形条件：△ABC和△CDE都是等腰直角三角形结论：△ACE≌△BCD，AE⊥BDEE28．手拉手模型-等腰三角形条件：△ABC 和△CDE 都是等腰三角形，CA =CB ， CD =CE ，且∠ACB =∠DCE结论：△ACE ≌△BCD30．手拉手模型-正方形条件：四边形ABCD 和AEFH 都是正方形结论：△ABE ≌△ADH ，BE ⊥DH十、最短路程模型31．直线同侧两线段之和最小（将军饮马）条件：点A 、B 在直线l 同侧，点P 为l 上一点辅助线：作点A 关于直线l 的对称点A ＇，连接A ＇B 结论：点P 为A ＇B 和l 交点时，AP +BP 最小C32．直线异侧两线段之差最小条件：点A 、B 在直线l 异侧，点P 为l 上一点辅助线：作线段AB 的垂直平分线m结论：点P 为m 和l 交点时，|AP -BP |最小33．直线同侧两线段之差最小条件：点A 、B 在直线l 同侧，点P 为l 上一点辅助线：作线段AB 的垂直平分线m结论：点P 为m 和l 交点时，|AP -BP |最小34．过桥模型（将军饮马）条件：A 、B 为定点，l 1∥l 2，MN 为定长线段且MN ⊥l 1 辅助线：将点A 向上平移MN 的长度得到A ＇，连接A ＇B 结论：点N 为A ＇B 与l 1交点时，AM +MN +BN 最小35．四边形周长最小（将军饮马）条件：A 、B 为定点，M 、N 为角两边上的动点辅助线：作点A 、B 关于角两边的对称点A ＇、B ＇，连接 lAlAll 1l 2A＇B＇结论：M、N为A＇B＇与角两边交点时，四边形ABMN的周长最小B'36．三角形周长最小（将军饮马）条件：A为定点，B、C为角两边上的动点辅助线：作点A关于角两边的对称点A＇、A＂，连接A＇A＂结论：B、C为A＇A＂与角两边交点时，△ABC的周长最小37．旋转类最短路程模型条件：线段OA=a，OB=b（a＞b），OB绕点O在平面内旋转结论：点B与点N重合时，AB最小；点B与点M重合时，AB最大十一、基本相似模型38．A字型条件：BC∥DE结论：△ABC∽△ADE条件：∠ABC =∠ADE结论：△ABC ∽△ADE39．8字型条件：AB ∥CD结论：△AOB ∽△DOC条件：∠BAO =∠DCO结论：△AOB ∽△COD40．母子型条件：△ABC 中，∠ACB =90°，CD ⊥AB结论：△ABC ∽△ACD ∽△CBD41．一线三等角模型条件：∠B =∠D =∠ACE结论：△ABC ∽△CDECBCC A42．手拉手相似模型条件：△ABC ∽△ADE结论：△ACE ∽△ABD十二、对角互补模型43．对角互补模型-90°全等型条件：∠AOB =∠DCE =90°，OC 平分∠AOB辅助线：过点C 作CM ⊥AO ，CN ⊥BO ，垂足分别为M 、N 结论：△CDM ≌△CEN ，CD =CE ，OD +OEOC ，212OECD S OC 四边形CB ACE AB D CDD44．对角互补模型-120°全等型条件：∠AOB =120°，∠DCE =60°，OC 平分∠AOB辅助线：过点C 作CM ⊥AO ，CN ⊥BO ，垂足分别为M 、N 结论：△CDM ≌△CEN ，CD =CE ，OD +OE =OC ，24OECD S =四边形45．对角互补模型-任意角全等型条件：∠AOB =2α，∠DCE =180°-2α，OC 平分∠AOB辅助线：过点C 作CM ⊥AO ，CN ⊥BO ，垂足分别为M 、N 结论：△CDM ≌△CEN ，CD =CE ，2cos OD OE OC α+=⋅， 2sin cos OEC OCD S S OC αα+=⋅46．邻边相等的对角互补模型条件：四边形ABCD 中，AB =AD ，∠ABC +∠ADC =180°D BAN E OB辅助线：延长CD 到E ，使得DE =BC ，连接AE结论：△ABC ≌△ADE ，CA 平分∠BCD十三、隐圆模型47．动点定长模型条件：AB =AC =AP ，点P 为动点结论：点B 、C 、P 三点共圆，点A 为圆心，AB 为半径48．直角圆周角模型条件：点C 为动点，∠ACB =90°结论：点A 、B 、C 三点共圆，线段AB 的中点为圆心，线段 AB 为直径49．定弦定长模型条件：点P 为动点，固定线段AB 所对的动角∠APB 为定值 结论：点A 、B 、P 三点共圆，线段AB 和BP 的中垂线的交点 为圆心BA50．四点共圆模型①条件：点A 、C 为动点，∠BAD +∠BCD =180°结论：点A 、B 、C 、D 四点共圆，线段AB 和BC 的中垂线的 交点为圆心当∠BAD =∠BCD =90°，BD 为直径51．四点共圆模型②条件：线段AB 为固定长度，点D 为动点，∠C =∠D结论：点A 、B 、C 、D 四点共圆，线段AB 和BC 的中垂线的 交点为圆心CCA当∠C=∠D=90°，AB为直径。

一、弦图相关模型1．勾股弦图2．弦图变形一3．弦图变形二4．弦图变形二的拓展正方形有关的模型在正方形中，，，，．【结论】①利用或推出≌≌≌，从而推出四边形为正方形．②．【方法】遇到直线上出现两个直角的题型可以考虑构造一线三垂直模型进行证明计算．在正方形中，．【结论】利用推出≌≌≌，从而推出四边形为正方形．【方法】遇到直线上出现两个直角的题型可以考虑构造一线三垂直模型进行证明计算．在正方形中，．【结论】利用推出≌≌≌，从而推出，，四边形为正方形．【注意】本模型与“L”模型有区别，如果“L”模型无法解题，可以考虑构造本模型进行证明计算．①已知在正方形中，，则．爱智康 2018/6/12ABCD AE ⊥BF BF ⊥CG CG ⊥DH DH ⊥AE AAS ASA △AEB △BF C △CGD △DHA EF GH AE −CF =EF ABCD AE =BF =CG =DH SAS △AEH △BF E △CGF △DHG EF GH ABCD AH =BE =CF =DG SAS △DAH △ABE △BCF △CDG DH =AE =BF =CG AE ⊥BF MNP Q ABCD AE =MN AE ⊥MN二、绕顶点旋转的基本模型三、手拉手旋转模型1．直角的手拉手模型②反之，已知在正方形中，，则．【辅助线】过点作，证明≌，或过点作，再证明≌即可．（）如图，正方形，将绕点顺时针旋转得到，则为等腰直角三角形，．【注意】辅助线为延长至点，使，再证明≌．（）如图，正方形，将绕点顺时针旋转得到，为等腰直角三角形．已知：如图，四边形、都是正方形，连接、，与交于点．爱智康 2018/06/12ABCD AE ⊥MB AE =MN B BF //MN △ABE △BCF M MH ⊥CD △ABE △MHN 1ABCD △ADE A 90∘△ABF △EAF =S 边形AFCE S 正 形ABCD CB F BF =DE △BAF △DAE 2ABCD △ABE B 90∘△CBF △EBF ABCD AEF G BE DG BE DG P2．形外形【结论】①≌；②，；③平分．【变形一】绕点旋转，以上结论均成立．【变形二】将正方形变成等腰直角三角形，以上结论均成立．（）以的、边向外分别作正方形、，则．【辅助线】延长至点，出现“等线段，共顶角，顶角等”，因此手拉手全等，≌，再根据和等底同高，从而面积相等．爱智康218/6/12△BAE△DAGBE=DG BE⊥DGAP∠BP GA AEF G1△ABC AB AC ABDE ACF G=S△ABC S△AEGBA H△AEG△AHC△ABC △AHC（）以的、边向外分别作正方形、，点为中点，则，．【辅助线】利用倍长中线法解题：①倍长中线得到≌，从而得到，，，②利用推出≌，从而得到，，．【变形】若条件变成点为中点，则，．（）以的、边向外分别作正方形、，，反向延长线交于，则点为中点，．【辅助线】利用一线三垂直解题：①过点作于，过点作的延长线于点，②易证≌，≌，从而得到，③利用推出≌，从而得到点为中点，，④根据，，，可推出．2△ABC AB AC ABDE ACF G P EG BC =2AP AM ⊥BC △AP E △HP G AE //HG ∠EAG +∠AGH =180∘∠AGH =∠CAB SAS △AGH △CAB BC =2AP ∠GAH =∠ACB AM ⊥EG Q BC EG =2AQ AN ⊥EG 3△ABC AB AC ABDE ACF G AM ⊥BC AM EGP P EG BC =2AP E EK ⊥MP K G GL ⊥MP L △AMB △EKA △AMC GLA AM =EK =GL AAS △P EK △P GL P EG P K =P L BM =AK CM =AL P K =P L BC =2AP四、对角互补模型（垂直）1．对角互补模型（垂直）2．对角互补模型的变形（垂直）【变形】若条件变成，反向延长线交于，则点为中点，．如图，正方形，对角线、交于点，，与正方形的两边分别交于点、．【结论】①≌，≌．②，．③．【辅助线】①过点作，根据等腰三角形的判定得，再利用或推出≌．②过点作，，根据角平分线的性质得，再利用或推出≌．如图，正方形，对角线、交于点，，旋转与正方形的两边延长线分别交于、．AN⊥EG AN BC Q Q BC EG=2AQABCD AC BD O∠EOF=90∘E F△BOE△COF△AOE△BOFOE=OF EF=OE2√=S 边形OEBF14S正 形ABCDO OD⊥OB OB=OD ASA AAS△OBE△ODFO OG⊥AB OH⊥BC OG=OH ASA AAS△OGE△OHF ABCD AC BD O∠EOF=90∘∠EOF E F五、角含半角模型（直角）1．正方形中的角含半角模型（直角）2．正方形中的角含半角模型的变形（直角）【结论】①≌，≌．②，．③图一：；图二：．．【辅助线】①过点作，根据等腰三角形的判定得，再利用或推出≌．②过点作，，根据角平分线的性质得，再利用或推出≌．如图，正方形，点在边上，点在边上，．【辅助线】延长至点，使，连接．【结论】①利用推出≌，，．②利用推出≌，．③，进而推出的周长等于正方形周长的一半．④平分，平分．如图，正方形，，旋转与的延长线交于点，与的延长线交于点．△BOE △COF △AOE △BOF OE =OF EF =OE 2√−=S △OBF S △OBE 14S 正 形ABCD −=S △OCE S △OCF 14S 正 形ABCD O OD ⊥OB OB =OD ASA AAS △OBE △ODF O OG ⊥AB OH ⊥BC OG =OH ASA AAS △OGE △OHF ABCD E CD F BC ∠EOF =45∘BC G BG =DE AG SAS △ABG △ADE AG =AE ∠F AG =∠F AE SAS △F AG △F AE F G =EF EF =BF +DE △CEF AF ∠BF E AE ∠DEF ABCD ∠EOF =45∘∠EOF DC E CB F3．等腰直角三角形中的角含半角模型（直角）4．等腰直角三角形中的角含半角模型的变形（直角）【辅助线】在截取，连接．【结论】①利用推出≌，，．②利用推出≌，．③．④平分．如图，等腰直角，，，．【辅助线】过点作，并截取，连接，．【结论】①利用推出≌，，．②利用推出≌，．③．【模型的演变】如图，等腰直角，，，．【辅助线】过点作，并截取，连接，．CD DG =BF AG SAS △ABF △ADG AG =AE ∠EAG =∠EAF SAS △EAG △EAF EG =EF EF =DE −BF AE ∠DEF △ABD AB =AD ∠BAD =90∘∠MAN =45∘B BH ⊥BD BH =DN AH MH SAS △ABH △ADN AH =AN ∠BAH =∠DAN SAS △MAH △MAN MH =MN =+MN 2BM 2DN 2△ABD AB =AD ∠BAD =90∘∠MAN =45∘D DH ⊥BD DH =BM AH NH5．【归纳】角含半角模型（直角）【结论】①利用推出≌，，．②利用推出≌，．③．【模型的演变】如图，已知正方形中，，连接与、分别交于、．【结论】①．②的周长等于正方形边长的倍．③平分，平分．④点到的距离等于正方形边长．⑤．爱智康 2018/06/12SAS △ADH △ABM AH =AM ∠DAH =∠BAM SAS △NAH △NAM NH =MN =+MN 2BM 2DN 2ABCD ∠EAF =45∘BD AE AF N M EF =BF +DE △CEF 2AE ∠DEF AF ∠BF E A EF =+MN 2BM 2DN 2。

专题06正方形的几何模型（三垂直模型）（基础篇）1．B【分析】过点P 作PM OE ⊥，PN OF ⊥，证明△△OME PNF ≅，再根据面积计算即可；解：如图所示，过点P 作PM OE ⊥，PN OF ⊥，∵点P 的坐标为(4,4)，∴PM=PN ，∵PE PF ⊥，∴MPE EPN FPN EPN ∠+∠=∠+∠，∴∠=∠MPE NPF ，又∵PME PNF ∠=∠，∴()△△OME PNF ASA ≅，∴四边形四边形△正方形4416OEPF ONPE PME ONPM S S S S =+==⨯=．故答案选B ．2．C【分析】易证△AEC ≌△FBA ，得AB=EC ，即可求得．解：∵四边形AFDC 是正方形∴AC=AF ，∠FAC=90°∴∠CAE+∠FAB=90°又∵∠CAE+∠ACE=90°∴∠ACE=∠FAB又∵∠CEA=∠FBA=90°∴△AEC ≌△FBA∴AB=EC=4∴图中阴影部分的面积=144=82⨯⨯故选C【点拨】本题考查全等三角形的判定，掌握全等三角形的判定条件是解题的关键．3．45°【分析】作AE ⊥BC 于E ，AF ⊥CD 延长线于点F ，易证四边形AECF 为矩形，可得∠FAE ＝90°，再根据∠DAB ＝90°，可得∠DAF ＝∠BAE ，即可证明△BAE ≌△DAF ，可得AE ＝AF ，即可判定矩形AECF 为正方形，即可解题．解：作AE⊥BC于E，AF⊥CD延长线于点F，∵∠AEC＝∠AFC＝∠BCD＝90°，∴四边形AECF为矩形，∴∠FAE＝90°，即∠DAF＋∠DAE＝90°，∵∠DAE＋∠BAE＝90°，∴∠DAF＝∠BAE，在△BAE和△DAF中，∠AEB＝∠F，∠BAE＝∠DAF，AB＝AD，∴△BAE≌△DAF（AAS），∴AE＝AF，∴矩形AECF为正方形，∴∠ACB＝45°；故答案为：45°．【点拨】本题考查了全等三角形的判定与性质、矩形的判定与性质、正方形的判定与性质等知识；熟练掌握正方形的判定与性质，证明三角形全等是解题的关键．4．125或52【分析】分两种情况进行讨论，点F在AD上或点F在AB上，依据全等三角形的性质以及矩形的性质，即可得到CM的长．解：分两种情况：①如图1所示，当点F在AD上时，由CF=BE，CD=BC，∠BCE=∠CDF=90°可得，Rt△BCE≌Rt△CDF（HL），∴∠DCF=∠CBE，又∵∠BCF+∠DCF=90°，∴∠BCF+∠CBE=90°，∴∠BMC=90°，即CF⊥BE，∵BC=4，CE=3，∠BCE=90°，∴BE=5，∴CM=125 BC CEBE⨯=；②如图2所示，当点F在AB上时，同理可得，Rt△BCF≌Rt△CBE（HL），∴BF=CE，又∵BF∥CE，∴四边形BCEF是平行四边形，又∵∠BCE=90°，∴四边形BCEF是矩形，∴CM=12BE=12×5=52．故答案为：125或52．【点拨】本题考查了正方形的性质，全等三角形的判定与性质以及勾股定理的运用，全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．55【分析】过C点作CH⊥BF于H点，过B点作BK⊥CM于K，过D作DQ⊥MF交MF延长线于Q，只要证明△AGB≌△BHC，△BKC≌△CQD即可解决问题．解：如图，过C点作CH⊥BF于H点，过B点作BK⊥CM于K，过D作DQ⊥MF交MF延长线于Q．∵∠CFB＝45°∴CH＝HF，∵∠ABG+∠BAG＝90°，∠FBE+∠ABG＝90°，∴∠BAG＝∠FBE，∵AG⊥BF，CH⊥BF，∴∠AGB＝∠BHC＝90°，在△AGB和△BHC中，∵∠AGB＝∠BHC，∠BAG＝∠HBC，AB＝BC，∴△AGB≌△BHC（AAS），∴AG＝BH，BG＝CH，∵BH＝BG+GH，∴BH＝HF+GH＝FG，∴AG＝FG；∵CH⊥GF，∴CH∥GM，∵C为FM的中点，∴CH＝12 GM，∴BG＝12 GM，∵BM＝5，∴BG GM＝∴AG＝AB＝5，∴HF∴CF，∴CM，∵CK＝12CM＝12CF＝102，∴BK＝2，∵在△BKC和△CQD中，∵∠CBK＝∠DCQ，∠BKC＝∠CQD＝90°，BC＝CD，∴△BKC≌△CQD（AAS），∴CQ＝BK＝2，DQ＝CK＝102，∴QF＝CQ﹣CF＝2∴DQ ＝QF ＝2，∴DF ＝102【点拨】此题考查的是全等三角形的判定及性质、等腰三角形的判定及性质和正方形的性质，掌握全等三角形的判定及性质、等腰三角形的判定及性质和正方形的性质是解题关键．6．（4，1）．【分析】过点D 作DE ⊥y 轴于E ，由“AAS ”可证△ABO ≌△DAE ，可得AE ＝OB ，DE ＝OA ，即可求解．解：如图，过点D 作DE ⊥y 轴于E ，∵∠BAO +∠DAE ＝∠ADE +＝90°，∴∠BAO ＝∠ADE ，在△ABO 和△DAE 中，90BAO ADE AOB DEA AB AD ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩，∴△ABO ≌△DAE （AAS ），∴AE ＝OB ，DE ＝OA ，∵A （0，4），B （﹣3，0），∴OA ＝4，OB ＝3，∴OE ＝4﹣3＝1，∴点D 的坐标为（4，1）．【点拨】本题考查了正方形的性质，坐标与图形性质，全等三角形的判定和性质，熟记各性质并作辅助线构造出全等三角形是解题的关键．7．17【分析】过E 作EF ⊥AC ，垂足为F ，由ABDE 为正方形，利用正方形的性质得到一对角为直角，AE ＝AB ，利用同角的余角相等得到一对角相等，再由一对直角相等，利用AAS 得到△AEF ≌△BAC ，利用全等三角形的对应边相等得到EF ＝AC ＝8，AF ＝BC ＝7，由FA ＋AC 求出FC 的长，在直角三角形CEF 中，利用勾股定理即可求出EC 的长．解：过E 作EF ⊥AC ，交CA 的延长线于F，∵四边形ABDE 为正方形，∴∠BAE ＝90°，AE ＝AB ，∵∠EAF ＋∠AEF ＝90°，∠EAF ＋∠BAC ＝90°，∴∠AEF ＝∠BAC ，在△AEF 和△BAC 中，90F ACB AEF BAC AE AB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△BAC （AAS ），∴EF ＝AC ＝8，AF ＝BC ＝7，在Rt △ECF 中，EF ＝8，FC ＝FA ＋AC ＝8＋7＝15，根据勾股定理得：CE＝17．故答案为：17．【点拨】此题考查了勾股定理，正方形的性质，以及全等三角形的判定与性质，熟练掌握勾股定理是解本题的关键．8．()【分析】如图作AF ⊥x 轴于F ，CE ⊥x 轴于E ，先证明△COE ≌△OAF ，推出CE ＝OF ，OE ＝AF ，由此即可解决问题．解：如图作AF ⊥x 轴于F ，CE ⊥x 轴于E．∵四边形ABCO 是正方形，∴OA ＝OC ，∠AOC ＝90°，∵∠COE +∠AOF ＝90°，∠AOF +∠OAF ＝90°，∴∠COE ＝∠OAF ，在△COE 和△OAF 中，CEO AFO COE OAF OC OA ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△COE ≌△OAF ，∴CE ＝OF ，OE ＝AF ，∵A （1∴CE ＝OF ＝1，OE ＝AF∴点C坐标()，故答案为：()．【点拨】本题考查全等三角形的判定与性质，作出辅助线构造全等三角形是解题的关键．9．()3,1-【分析】过点A 作AD y ⊥轴于D ，过点C 作CE x ⊥轴，过点B 作BF CE ⊥交CE 的延长线于F ．先证明AOD COE BCF ∆∆∆≌≌，得到1AD CE BF ===，2OD OE CF ===，根据点的坐标定义即可求解．解：如图，过点A 作AD y ⊥轴于D ，过点C 作CE x ⊥轴，过点B 作BF CE ⊥交CE 的延长线于F ．()2,1C --，2OE ∴=，1CE =．四边形OABC 是正方形，OA OC BC ∴==．易求AOD COE BCF ∠=∠=∠．又90ODA OEC F ∠=∠=∠=︒∴AOD COE BCF ∆∆∆≌≌，1AD CE BF ∴===，2OD OE CF ===，∴点A 的坐标为()1,2-，211EF =-=，点B 到y 轴的距离为123+=，∴点B 的坐标为()3,1-．故答案为：()3,1-【点拨】本题考查了平面直角坐标系点的坐标，全等三角形的判定与性质，根据题意，添加辅助线构造全等三角形是解题关键．10．2【分析】根据题意，利用勾股定理可以求得DF 的长，然后根据正方形的性质可以得到△DBF 的形状，再根据直角三角形斜边上的中线等于斜边的一半，即可得到BH 的长．解：延长DC 交FE 于点M ，连接BD 、BF ，∵正方形ABCD ，BEFG 的边长分别为2，3，∴DM ＝5，MF ＝1，∠DMF ＝90°，∴DF ，∵BD 、BF 分别是正方形ABCD ，BEFG 的对角线，∴∠DBC =∠GBF =90︒，∴∠DBF ＝90°，∴△DBF 是直角三角形，∵点H 为DF 的中点，∴BH ＝12DF ＝2，．【点拨】本题考查了正方形的性质、直角三角形斜边上的中线与斜边的关系、勾股定理，解答本题的关键是明确题意，利用数形结合的思想解答．11．25【分析】画出l 1到l 2，l 2到l 3的距离，分别交l 2，l 3于E ，F ，通过证明△ABE ≌△BCF ，得出BF=AE ，再由勾股定理即可得出结论．解：过点A 作AE ⊥l 2，过点C 作CF ⊥l 2，∴∠CBF +∠BCF =90°，四边形ABCD 是正方形，∴AB =BC =CD =AD ，∴∠DAB =∠ABC =∠BCD =∠CDA =90°，∴∠ABE +∠CBF =90°，∴∠ABE =∠BCF ，在△ABE 和△BCF 中，AEB BFC ABE BCF AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△BCF （AAS ）∴BF =AE ，∵l 1∥l 2∥l 3，且l 1、l 2之间的距离是3，l 2、l 3之间的距离是4，∴BF=AE=3，CF=4,∵BF 2+CF 2=BC 2，∴BC 2=42+32=25．故答案为：25．【点拨】本题主要考查了正方形的性质，勾股定理，全等三角形的判定与性质以及正方形面积的求解方法．证得△ABE ≌△BCF 是解题的关键．12．5【分析】过D 点作直线EF 与平行线垂直，与l 1交于点E ，与l 4交于点F ．易证△ADE ≌△DCF ，得CF ＝1，DF ＝2．根据勾股定理可求CD 2得正方形的面积．解：过D 点作EF ⊥l 2，交l 1于E 点，交l 4于F点．∵l 1∥l 2∥l 3∥l 4，EF ⊥l 2，∴EF ⊥l 1，EF ⊥l 4，即∠AED ＝∠DFC ＝90°．∵四边形ABCD 为正方形，∴∠ADC ＝90°．∴∠ADE ＋∠CDF ＝90°．又∵∠ADE ＋∠DAE ＝90°，∴∠CDF ＝∠DAE ．在△ADE 和△DCF 中DEA CFD EAD CDF AD DC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△DCF （AAS ），∴CF ＝DE ＝1．∵DF ＝2，∴CD 2＝12＋22＝5，即正方形ABCD 的面积为5．故答案为：5．【点拨】此题主要考查了正方形的性质和面积计算，根据平行线之间的距离构造全等的直角三角形是关键．13．13【分析】本题是典型的一线三角模型，根据正方形的性质、直角三角形两个锐角互余以及等量代换可以证得△AFB ≌△AED ；然后由全等三角形的对应边相等推知AF ＝DE 、BF ＝AE ，所以EF ＝AF +AE ＝13．解：∵ABCD 是正方形（已知）∴AB ＝AD ，∠ABC ＝∠BAD ＝90°又∵∠FAB+∠FBA ＝∠FAB+∠EAD ＝90°∴∠FBA ＝∠EAD （等量代换）∵BF ⊥a 于点F ，DE ⊥a 于点E∴在Rt △AFB 和Rt △AED 中∵90AFB DEA FBA EAD AB DA ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△AFB ≌△DEA （AAS ）∴AF ＝DE ＝8，BF ＝AE ＝5（全等三角形的对应边相等）∴EF ＝AF+AE ＝DE+BF ＝8+5＝13故答案为：13【点拨】本题考查了正方形的性质、直角三角形的性质、全等三角形的判定和性质及熟悉一线三角模型是解本题的关键．14．（1）见分析；（2）AE【分析】（1）由旋转的性质可得AE=AF ，∠EAF=90°，可得结论；（2）由题意可得四边形AECF 的面积等于正方形ABCD 的面积等于25，可求正方形的边长，由勾股定理可求解．解：（1）∵把△ADE 绕点A 顺时针旋转90°到△ABF 的位置，∴△ADE ≌△ABF ，∠EAF=90°，∴AE=AF ，∴△AEF 是等腰直角三角形；（2）∵△ADE绕点A顺时针旋转90°到△ABF的位置．∴四边形AECF的面积等于正方形ABCD的面积等于25，∴AD=DC=5，∵DE=2，∴Rt△ADE中，==【点拨】本题主要考查了旋转的性质以及正方形的性质，等腰直角三角形的判定，勾股定理，正确利用旋转的性质得出对应边关系是解题关键．15．(1)证明见分析；(2)2OC=【分析】（1）由题意易得AD＝AF，∠DAF＝90°，则有∠DAB＝∠FAC，进而可证AB＝AC，然后问题可证；（2）由（1）可得△ABD≌△ACF，则有∠ABD＝∠ACF，进而可得∠ACF＝135°，然后根据正方形的性质可求解．解：(1)证明：∵四边形ADEF为正方形，∴AD＝AF，∠DAF＝90°，又∵∠BAC＝90°，∴∠DAB＝∠FAC，∵∠ABC＝45°，∠BAC＝90°，∴∠ACB＝45°，∴∠ABC＝∠ACB，∴AB＝AC，∴△ABD≌△ACF(SAS)；(2)解：由(1)知△ABD≌△∴∠ABD＝∠ACF，∵∠ABC＝45°，∴∠ABD＝135°，∴∠ACF＝135°，由(1)知∠ACB＝45°，∴∠DCF＝90°，∵正方形ADEF边长为∴DF＝4，∴OC＝12DF＝12×4＝2．【点拨】本题主要考查正方形的性质及等腰直角三角形的性质，熟练掌握正方形的性质及等腰直角三角形的性质是解题的关键．16．（1）见分析；（2）见分析；（3【分析】（1）由正方形的性质可得AB＝AD，∠ABC＝∠BAD＝90°，根据DE⊥AG，利用直角三角形两锐角互余的关系可得∠BAF＝∠ADE，利用AAS即可证明△ADE≌△BAF；（2）根据全等三角形的性质可得DE=AF，BF=AE，根据线段的和差关系即可得结论；（3）利用勾股定理可求出AG 的长，利用面积法可求出BF 的长，进而利用勾股定理可求出AF 的长，根据BF=AE ，EF=AF-AE 即可得答案．解：（1）∵四边形ABCD 是正方形，∴AB ＝AD ，∠ABC ＝∠BAD ＝90°，∵DE ⊥AG ，∴∠AED ＝∠DEF ＝90°，∵BF ∥DE ，∴∠AFB ＝∠DEF ＝∠AED ＝90°，∴∠BAF ＋∠DAE ＝∠ADE ＋∠DAE ＝90°．∴∠BAF ＝∠ADE ．在△ABF 和△DAE 中，AFB DEA BAF ADE AB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADE ≌△BAF ．（2）∵△DAE ≌△ABF ，∴AE ＝BF ，DE ＝AF∵AF －AE ＝EF ，∴DE －BF ＝EF ．（3）∵∠ABC ＝90°，∴AG 2＝AB 2＋BG 2＝12＋22＝5，∴AG =．∵S △ABG ＝1122AB BG AG BF ⋅=⋅，∴AB BG BF AG ⋅=在Rt △ABF 中，AF 2＝AB 2－BF 2＝22－2＝165，∴∵AE=BF ，EF=AF-AE ，∴EF AF BF =-=【点拨】本题主要考查了正方形的性质、全等三角形的判定与性质以及勾股定理等知识，解答本题的关键是根据AAS 证明△ABF ≌△DAE ，此题难度一般．17．见分析.【分析】首先证明△AED ≌△DFC ，则能得出DE=FC ，AE=DF ，进而得出结论．解：证明：∵四边形ABCD 是正方形，∴AD=DC ，∠ADC=90°．又∵AE ⊥DG ，CF ∥AE ，∴∠AED=∠DFC=90°，∴∠EAD+∠ADE=∠FDC+∠ADE=90°，∴∠EAD=∠FDC ，在△AED 和△DFC 中，AED DFC EAD FDC AD DC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AED ≌△DFC （AAS ）．∴AE=DF ，ED=FC ．∵DF=DE+EF ，∴AE=FC+EF ．【点拨】本题考查了正方形的性质，三角形全等的判定和性质，熟练掌握正方形的性质以及三角形全等的判定方法是解题的关键．18．（1）见分析；（2）见分析【分析】（1）利用正方形的性质及SAS 定理证△AOE ≌△DOF ，得出AE=DF 即可；（2）由△AOE ≌△DOF 得出∠OEA=∠OFD ，证出∠OAE+∠OFD=90°，得出∠AMF=90°，即可得出结论．解：（1）四边形ABCD 是正方形，OA CO OD ∴==，AC BD ⊥，90AOE DOF ∴∠=∠=︒，又DE CF =，OD DE OC CF ∴-=-，即OE OF =，在AOE ∆和DOF ∆中，OA OD AOE DOF OE OF =⎧⎪∠=∠⎨⎪=⎩，()AOE DOF SAS ∴∆≅∆，AE DF ∴=；（2）由（1）得：AOE DOF ∆≅∆，OEA OFD ∴∠=∠，90OAE AEO ∠+∠=︒，90OAE OFD ∴∠+∠=︒，90AMF ∴∠=︒，AM DF ∴⊥．【点拨】此题考查了正方形的性质、全等三角形的判定与性质以及直角三角形的性质等知识；解答本题的关键是通过全等的证明和利用等角代换解题，属于中考常考题型．19．10【分析】作AF ∥x 轴，DF ∥y ，CG ⊥DF ．通过证明△AFD ≌△EOA ，△CDG ≌△DAF ，可证DG ＝AF ＝EO＝2，GC ＝DF ＝AO ＝4，从而求出点C 与点E 的坐标，然后根据勾股定理求解即可.解：正方形ABCD 的中心如图：作AF ∥x 轴，DF ∥y ，CG ⊥DF ．∵DF ∥y ，∴∠ADF=∠EAO ，∵AD ＝AE ，∠F=∠AOE ，∴△AFD ≌△EOA ，∵∠DGC=∠AFD,∠DCG=∠ADF,CD ＝AD ，∴△CDG ≌△DAF,∴DG ＝AF ＝EO ＝2，GC ＝DF ＝AO ＝4,∴C 为(2+4，4+(4-2))，即(6，6),E 为(-2，0)，C 为(6，6)10CE ===.【点拨】本题考查了正方形的性质，全等三角形的判定与性质，图形与坐标及勾股定理，正确作出辅助线是解答本题的关键.20．()2,3B ；()3,1C 【分析】过B 作BE ⊥y 轴，过C 作CF ⊥x 轴，垂足分别为E 、F ，可证明△ABE ≌△DAO ≌△CDF ，可求得OE 、BE 、CF 、OF 的长，可求得B 、C 的坐标．解：如图，过B 作BE ⊥y 轴，过C 作CF ⊥x 轴，垂足分别为E 、F ，∵四边形ABCD 为正方形，∴∠A =∠D =90°，AB =CD ，∴∠BAE +∠DAO =∠DAO +∠ADO =90°，∴∠BAE =∠ADO ，在△ABE 和△DAO 中，BEA AOD BAE ADO AB AD ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，，∴△ABE ≌△DAO （AAS ），同理可得△DAO ≌△CDF ，∵A （0，2），D （1，0），∴BE =DF =OA =2，AE =CF =OD =1，∴OE =OA +AE =2+1=3，OF =OD +DF =1+2=3，∴B 点坐标为（2，3），C 点坐标为（3，2）．【点拨】本题主要考查正方形的性质及全等三角形的判定和性质，利用正方形的四边相等找到条件通过证明三角形全等求得BE 、AE 、CF 、OF 的长是解题的关键．21．（1）见分析；（2）在P 点运动的过程中，PF 的长度不发生变化．PF3）PC PA =．理由见分析．【分析】（1）做辅助线，构建全等三角形，根据ASA 证明△△BMP PNE ≅即可求解．（2）如图，连接OB ，通过证明△△OBP FPE ≅，得到PF=OB ，则PF（3）根据△AMP 和△PCN是等腰直角三角形，得PA，PC =，整理可得结论．解：（1）证明：如图①，过点P 作MN ∥AD ，交AB 于点M ，交CD 于点N．∵PB ⊥PE ，∴∠BPE ＝90°，∴∠MPB +∠EPN ＝90°．∵四边形ABCD 是正方形，∴∠BAD ＝∠D ＝90°．∵AD ∥MN ，∴∠BMP ＝∠BAD ＝∠PNE ＝∠D ＝90，∵∠MPB +∠MBP ＝90°，∴∠EPN ＝∠MBP ．在Rt △PNC 中，∠PCN ＝45°，∴△PNC 是等腰直角三角形，∴PN ＝CN ，∴BM ＝CN ＝PN ，∴△BMP ≌△PNE （ASA ），∴PB ＝PE ．（2）解：在P 点运动的过程中，PF 的长度不发生变化．理由：如图2，连接OB ．∵点O 是正方形ABCD 对角线AC 的中点，∴OB ⊥AC ，∴∠AOB ＝90°，∴∠AOB ＝∠EFP ＝90°，∴∠OBP +∠BPO ＝90°．∴∠BPE ＝90°，∴∠BPO +∠OPE ＝90°，∴∠OBP ＝∠OPE ．由（1）得PB ＝PE ，∴△OBP ≌△FPE （AAS ），∴PF ＝OB ．∵AB ＝2，△ABO 是等腰直角三角形，∴OB =∴PF（3）解：PC PA =．理由：如图1，∵∠BAC ＝45°，∴△AMP 是等腰直角三角形，∴PA =．由（1）知PM ＝NE ，∴PA =．∵△PCN 是等腰直角三角形，∴)PC NE EC PA ==+=+=+．【点拨】本题主要考查了四边形综合应用，通过对三角形全等的证明找出边之间的关系，准确分析代换求解是解题的关键．22．（1）见分析；（2）；（3）∠EFC ＝130°或40°【分析】（1）作EP ⊥CD 于P ，EQ ⊥BC 于Q ，证明Rt △EQF ≌Rt △EPD ，得到EF ＝ED ，根据正方形的判定定理证明即可；（2）通过计算发现E 是AC 中点，点F 与C 重合，△CDG 是等腰直角三角形，由此即可解决问题；（3）分两种情形：①如图3，当DE 与AD 的夹角为40°时，求得∠DEC ＝45°＋40°＝85°，得到∠CEF ＝5°，根据角的和差得到∠EFC ＝130°，②如图4，当DE 与DC 的夹角为40°时，根据三角形的内角和定理即可得到结论．解：（1）证明：如图1，作EP ⊥CD 于P ，EQ ⊥BC 于Q，∵∠DCA ＝∠BCA ，∴EQ ＝EP ，∵∠QEF ＋∠FEC ＝45°，∠PED ＋∠FEC ＝45°，∴∠QEF ＝∠PED ，在△EQF 和△EPD 中，QEF PED EQ EP EOF EPD ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△EQF ≌△EPD （ASA ），∴EF ＝ED ，∴矩形DEFG 是正方形；（2）如图2中，在Rt △ABC 中，AC＝∵CE ＝∴AE ＝CE ，∴点F 与C 重合，此时△DCG 是等腰直角三角形，∴四边形DECG是正方形，∴CG＝CE＝；（3）①如图3，当DE与AD的夹角为40°时，∠DEC＝45°＋40°＝85°，∵∠DEF＝90°，∴∠CEF＝5°，∵∠ECF＝45°，∴∠EFC＝130°，②如图4，当DE与DC的夹角为40°时，∵∠DEF＝∠DCF＝90°，∴∠EFC＝∠EDC＝40°，综上所述，∠EFC＝130°或40°．【点拨】此题考查了正方形的判定以及性质，涉及了全等三角形的证明、等腰直角三角形等性质，熟练掌握相关基本性质是解题的关键．23．（1）AE=AF，理由见分析；（2）CE=MF，理由见分析；（3）如图所示，见分析．【分析】（1）根据两角互余的关系先求出∠BAF=∠DAE，再由ASA定理可求出△ABF≌△ADE，由全等三角形的性质即可解答；（2）根据△ABF≌△ADE及三角形外角的性质可求出∠AFM=∠AEC，根据两角互余的关系∠MAF=∠EAC，再由ASA定理求出△AMF≌△ACE，可得CE=MF；（3）画出示意图，只要求出C、D、F共线，即可求出四边形AECF是正方形；解：（1）AE=AF．理由：∵四边形ABCD是正方形，∴∠ABF=∠ADE=90°，AB=AD．∵∠BAF+∠BAE=90°，∠DAE+∠BAE=90°，∴∠BAF=∠DAE ．在△ABF 和△ADE 中BAF DAE AB AD ABF ADE ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ABF ≌△ADE （ASA ）∴AE=AF ；（2）CE=MF ．理由：∵△ABF ≌△ADE ，∴∠BAF=∠DAE ，∴∠ABF+∠FAB=∠ADE+∠DAE ，即∠AFM=∠AEC ．∵∠MAF+∠FAC=90°，∠EAC+∠FAC=90°，∴∠MAF=∠EAC ，在△AMF 和△ACE 中AFM AEC AF AE MAF EAC ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AMF ≌△ACE （ASA ），∴CE=MF ．(3)如图所示．过A 作AE ⊥BC 交BC 于E ，由于AB=AD ，所以可以把△ABE 切下，拼到△ADF 的位置，∵∠C=∠BAD=90°，∴∠B+∠ADC=180°，∴∠ADF+∠ADC=180°，∴C 、D 、F 共线，∵AE=AF ，∠AEC=∠ECF=∠AFC=90°，∴四边形AECF是正方形．【点拨】此题考查了正方形的性质、全等三角形的判定与性质、余角的性质、多边形的内角和等知识．解题的关键是利用全等三角形进行割补．24．△BCD 的面积为212a ．【分析】根据问题情景的解题思路，如下图2，根据旋转的对应关系，可得△ABC ≌△BDE （AAS ），进而求出线段DE 的长，根据三角形的面积公式计算即可.解：△BCD 的面积为212a ．理由如下：过点D 作△BCD 的BC 边上的高DE ．如图2，∵边AB 绕点B 顺时针旋转90°得到线段BD ，∴BA ＝BD ，∠ABD ＝90°，∵∠ABC +∠DBE ＝90°，∠ABC +∠A ＝90°，∴∠A ＝∠DBE ，在△ABC 和△BDE 中ACB DBE A DBE AB BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△BDE （AAS ），∴DE ＝BC ＝a ，∴△BCD 的面积＝12BC •DE ＝212a．【点拨】本题主要考查了学生对新提出的问题情境的理解能力，学会和已有的知识（三角形全等）相结合是解答本题的关键.。

一、弦图相关模型1．勾股弦图2．弦图变形一3．弦图变形二4．弦图变形二的拓展正方形有关的模型在正方形中，，，，．【结论】①利用或推出≌≌≌，从而推出四边形为正方形．②．【方法】遇到直线上出现两个直角的题型可以考虑构造一线三垂直模型进行证明计算．在正方形中，．【结论】利用推出≌≌≌，从而推出四边形为正方形．【方法】遇到直线上出现两个直角的题型可以考虑构造一线三垂直模型进行证明计算．在正方形中，．【结论】利用推出≌≌≌，从而推出，，四边形为正方形．【注意】本模型与“L”模型有区别，如果“L”模型无法解题，可以考虑构造本模型进行证明计算．①已知在正方形中，，则．爱智康 2018/6/12ABCD AE ⊥BF BF ⊥CG CG ⊥DH DH ⊥AE AAS ASA △AEB △BF C △CGD △DHA EF GH AE −CF =EF ABCD AE =BF =CG =DH SAS △AEH △BF E △CGF △DHG EF GH ABCD AH =BE =CF =DG SAS △DAH △ABE △BCF △CDG DH =AE =BF =CG AE ⊥BF MNP Q ABCD AE =MN AE ⊥MN二、绕顶点旋转的基本模型三、手拉手旋转模型1．直角的手拉手模型②反之，已知在正方形中，，则．【辅助线】过点作，证明≌，或过点作，再证明≌即可．（）如图，正方形，将绕点顺时针旋转得到，则为等腰直角三角形，．【注意】辅助线为延长至点，使，再证明≌．（）如图，正方形，将绕点顺时针旋转得到，为等腰直角三角形．已知：如图，四边形、都是正方形，连接、，与交于点．爱智康 2018/06/12ABCD AE ⊥MB AE =MN B BF //MN △ABE △BCF M MH ⊥CD △ABE △MHN 1ABCD △ADE A 90∘△ABF △EAF =S 边形AFCE S 正 形ABCD CB F BF =DE △BAF △DAE 2ABCD △ABE B 90∘△CBF △EBF ABCD AEF G BE DG BE DG P2．形外形【结论】①≌；②，；③平分．【变形一】绕点旋转，以上结论均成立．【变形二】将正方形变成等腰直角三角形，以上结论均成立．（）以的、边向外分别作正方形、，则．【辅助线】延长至点，出现“等线段，共顶角，顶角等”，因此手拉手全等，≌，再根据和等底同高，从而面积相等．爱智康218/6/12△BAE△DAGBE=DG BE⊥DGAP∠BP GA AEF G1△ABC AB AC ABDE ACF G=S△ABC S△AEGBA H△AEG△AHC△ABC △AHC（）以的、边向外分别作正方形、，点为中点，则，．【辅助线】利用倍长中线法解题：①倍长中线得到≌，从而得到，，，②利用推出≌，从而得到，，．【变形】若条件变成点为中点，则，．（）以的、边向外分别作正方形、，，反向延长线交于，则点为中点，．【辅助线】利用一线三垂直解题：①过点作于，过点作的延长线于点，②易证≌，≌，从而得到，③利用推出≌，从而得到点为中点，，④根据，，，可推出．2△ABC AB AC ABDE ACF G P EG BC =2AP AM ⊥BC △AP E △HP G AE //HG ∠EAG +∠AGH =180∘∠AGH =∠CAB SAS △AGH △CAB BC =2AP ∠GAH =∠ACB AM ⊥EG Q BC EG =2AQ AN ⊥EG 3△ABC AB AC ABDE ACF G AM ⊥BC AM EGP P EG BC =2AP E EK ⊥MP K G GL ⊥MP L △AMB △EKA △AMC GLA AM =EK =GL AAS △P EK △P GL P EG P K =P L BM =AK CM =AL P K =P L BC =2AP四、对角互补模型（垂直）1．对角互补模型（垂直）2．对角互补模型的变形（垂直）【变形】若条件变成，反向延长线交于，则点为中点，．如图，正方形，对角线、交于点，，与正方形的两边分别交于点、．【结论】①≌，≌．②，．③．【辅助线】①过点作，根据等腰三角形的判定得，再利用或推出≌．②过点作，，根据角平分线的性质得，再利用或推出≌．如图，正方形，对角线、交于点，，旋转与正方形的两边延长线分别交于、．AN⊥EG AN BC Q Q BC EG=2AQABCD AC BD O∠EOF=90∘E F△BOE△COF△AOE△BOFOE=OF EF=OE2√=S 边形OEBF14S正 形ABCDO OD⊥OB OB=OD ASA AAS△OBE△ODFO OG⊥AB OH⊥BC OG=OH ASA AAS△OGE△OHF ABCD AC BD O∠EOF=90∘∠EOF E F五、角含半角模型（直角）1．正方形中的角含半角模型（直角）2．正方形中的角含半角模型的变形（直角）【结论】①≌，≌．②，．③图一：；图二：．．【辅助线】①过点作，根据等腰三角形的判定得，再利用或推出≌．②过点作，，根据角平分线的性质得，再利用或推出≌．如图，正方形，点在边上，点在边上，．【辅助线】延长至点，使，连接．【结论】①利用推出≌，，．②利用推出≌，．③，进而推出的周长等于正方形周长的一半．④平分，平分．如图，正方形，，旋转与的延长线交于点，与的延长线交于点．△BOE △COF △AOE △BOF OE =OF EF =OE 2√−=S △OBF S △OBE 14S 正 形ABCD −=S △OCE S △OCF 14S 正 形ABCD O OD ⊥OB OB =OD ASA AAS △OBE △ODF O OG ⊥AB OH ⊥BC OG =OH ASA AAS △OGE △OHF ABCD E CD F BC ∠EOF =45∘BC G BG =DE AG SAS △ABG △ADE AG =AE ∠F AG =∠F AE SAS △F AG △F AE F G =EF EF =BF +DE △CEF AF ∠BF E AE ∠DEF ABCD ∠EOF =45∘∠EOF DC E CB F3．等腰直角三角形中的角含半角模型（直角）4．等腰直角三角形中的角含半角模型的变形（直角）【辅助线】在截取，连接．【结论】①利用推出≌，，．②利用推出≌，．③．④平分．如图，等腰直角，，，．【辅助线】过点作，并截取，连接，．【结论】①利用推出≌，，．②利用推出≌，．③．【模型的演变】如图，等腰直角，，，．【辅助线】过点作，并截取，连接，．CD DG =BF AG SAS △ABF △ADG AG =AE ∠EAG =∠EAF SAS △EAG △EAF EG =EF EF =DE −BF AE ∠DEF △ABD AB =AD ∠BAD =90∘∠MAN =45∘B BH ⊥BD BH =DN AH MH SAS △ABH △ADN AH =AN ∠BAH =∠DAN SAS △MAH △MAN MH =MN =+MN 2BM 2DN 2△ABD AB =AD ∠BAD =90∘∠MAN =45∘D DH ⊥BD DH =BM AH NH5．【归纳】角含半角模型（直角）【结论】①利用推出≌，，．②利用推出≌，．③．【模型的演变】如图，已知正方形中，，连接与、分别交于、．【结论】①．②的周长等于正方形边长的倍．③平分，平分．④点到的距离等于正方形边长．⑤．爱智康 2018/06/12SAS △ADH △ABM AH =AM ∠DAH =∠BAM SAS △NAH △NAM NH =MN =+MN 2BM 2DN 2ABCD ∠EAF =45∘BD AE AF N M EF =BF +DE △CEF 2AE ∠DEF AF ∠BF E A EF =+MN 2BM 2DN 2。

【模型研究】正方形之对称与旋转，半角与三垂直模型（推荐）当我们学习完了全等、勾股、相似，平移、对称、旋转，如果还想再加点料的话，不妨看看正方形．正方形是一种既简单又复杂的图形，其图形本身很基本、简单，因而在此基础上可以作很多复杂的变形与构造，我们所知的几何内容，一个都不缺．本专题以近两年中考题为例，简单了解关于正方形在中考题中的应用．本文将介绍三个方面的内容：（1）正方形与对称；（2）正方形与旋转；（3）反相似手拉手．01正方形与对称正方形既是轴对称图形，也是中心对称图形，关于对称可以考察对称的基本性质，也可以有关于构造对称，而涉及到计算的，无非就是勾股或者三角函数．且看相关例子：图形的基本性质求线段长度——勾股定理对称性质——对称点连线被对称轴垂直且平分对称性质——对称点连线被对称轴垂直且平分构造对称——将军饮马问题构造对称——不一样的将军饮马02正方形与旋转关于旋转，关注点在于①绕哪个点旋转；②是否是特殊角度．对于正方形，可绕其中一顶点旋转，可绕对角线交点旋转，大致如下：（1）绕顶点旋转的手拉手模型（2）绕O点的等腰直角共点旋转看几个关于旋转的简单例子：旧题重看——正方形手拉手模型共点旋转——以对角线交点为旋转点旋转——旋转点在对角线上的旋转若已知旋转，寻找其中的全等或相似即可，而构造旋转，往往更考验对图形构造及旋转的理解．关于正方形的共点旋转，有如下结论：在正方形ABCD中，点P是正方形内一点，若满足∠APD=135°，则有2PA²+PD²=PB²．反之，若2PA²+PD²=PB²，则∠APD=135°．（在旋转章节中有过介绍）2018烟台中考——旋转的构造关于正方形的旋转大题也有很多，举一例：探究正方形的旋转03反相似手拉手模型在上一个例题中不难得出这样一个图形：若连接两个正方形的对角线，则会有一组旋转型相似，这里其实利用的是等腰直角三角形直角边与斜边的比例关系，可将图形简化如下：连接起对角线，转化成等腰直角三角形，则还另有结论．如图，正方形ABCD与正方形CEFG共顶点C，连接CA、CF，取AF中点M．连接ME、MD，则有：MD=ME，ME⊥ME．连接MB、MG，则有：MB=MG，MB⊥MG．在说这个证明之前，我们要说说一个模型：反相似手拉手模型（苏州学而思徐杰老师取名）手拉手模型：四线共点、两两相等、夹角相等，即可构成一组旋转型全等，称之为手拉手模型．如图，AB=AC，AD=AE，∠BAC=∠DAE，即可得：△ABD≌△ACE．手拉手相似：改变全等的条件，即线段由相等变为成比例，AB:AC=AD:AE，∠BAC=∠DAE，即可构成手拉手相似．可将条件化为：当△ABC和△ADE为直角三角形，且∠BAC=∠DAE，可得△ABE∽△ACE．反相似手拉手：将其中一个三角形“反”过来，故称反相似手拉手．特别地，△ABC和△ADE是等腰直角三角形，则有FC=FE，FC⊥FE．模型证明在△ABC中，分别以AB、AC为斜边分别向外侧作等腰直角△ABD 和等腰直角△ACE，∠ADB=∠AEC=90°，F为BC边中点，连接DF、EF，求证：DF=EF，DF⊥EF．法1：构造中位线与斜边中线法2：还原手拉手法3：倍长中线法4：构造三垂直模型中考题中的反相似手拉手：动态探究——运动中的反相似手拉手方法提炼——静止的反相似手拉手观察在旋转专题中关于“半角模型”与“三垂直模型”知识点已经有所介绍，学习模型，大概有这样的不同阶段：1、认识模型——了解模型的基本条件及基本结论；2、理解模型——理解模型的构造，灵活变换条件与结论，以及条件的弱化和结论的拓展；3、构造模型——结合已知条件与相关模型，添加辅助线构造模型解决问题．以几个题目来练习回顾下关于“半角模型”与“三垂直模型”：04模型练习半角模型的基本结论半角模型中的计算三垂直得线段关系构造三垂直求面积最值三垂直模型在综合题中的应用等腰直角——构造三垂直与勾股定理结合05例题变式—当半角遇到三垂直从以上例子不难发现，半角模型常见为题型，我们需要了解的是给定什么样的条件会有半角模型，如下图，条件可以是：配置一：已知∠EAG=45°，则为半角模型；配置二：已知AE平分∠BEG或AE平分∠BAF（AG同理），则为半角模型；配置三：已知EG=BE+DG，则为半角模型．（可构造半角EAH，证H、G重合）．至于三垂直模型，则更多以一种方法运用，其作用一方面在于得到不同线段之间的数量关系，另外也可“化斜为直”，便于计算．那在什么条件下考虑构造三垂直呢？配置一：当存在等腰直角时，可考虑构造三垂直；配置二：当存在45°时，先由45°构造等腰直角，再构造三垂直．当半角模型的配置一遇到三垂直的配置二，不妨先来看个例子：典型例子：当半角遇到三垂直本题难度并不大，但巧妙地将半角与三垂直结合在一张图中，条件与结论的巧妙组合，并且还可以有更多变形．在本题图中，除了正方形条件外，其实还存在另外三个条件与结论：（1）∠DEH=90°；（2）∠EDH=45°；（3）∠CBH=45°．其中任意两个组合均可得到第三个，本题是由（1）、（2）结合得到（3）．所以，还可以：变式一：由（1）、（3）→（2）变式二：由（2）、（3）→（1）继续看一些练习：模型结论的探究模型的另类反推【写在最后】对于不同的知识点，其定位是不同的，模型亦然，认识模型、理解模型、运用模型，再去看题目的时候，可以发现所谓的变式就是条件与结论的不同组合，从条件出发选择恰当的方法，当条件各司其职时，离正确答案也就很接近了~来源：有一点数学。

模型一：等高模型定义：三角形面积的大小，三角形面积的大小，取决于三角形底和高的乘积。

取决于三角形底和高的乘积。

取决于三角形底和高的乘积。

如果固定三角形的如果固定三角形的底（或高）不变，另一者变大（小）n 倍，三角形的面积也就变大（小）n 倍。

六种基本类型：两个三角形高相等，两个三角形高相等，面积比等于底之比；面积比等于底之比；面积比等于底之比；两个三角形底相等，两个三角形底相等，两个三角形底相等，面积比等于高之比面积比等于高之比公式：DC BD S S ADC ABD ；FCED S S ABC ABD 其中，BC=EF 且两三角形的高相等公式：1 DEFABC S S 夹在一组平行线之间的等积变形公式：1 ABD ABC BCD ACDS S S S等底等高的两个平行四边形面积相等（长方形和正方形可看作特殊的平行四边形）公式：1 CDEFABCD S S三角形面积等于与它等底等高的平行四边形面积的一半公式：ABCDEDC S S 21两个平行四边形高相等，面积比等于他们底的比公式：EFAB S S DEFG ABCD 例题：长方形ABCD 的面积为36cm 2，E 、F 、G 为各边中点，H 为AD 边上任意一点，问阴影部分面积是多少？5.135.41818543681211836212136212121 BEF BEF BEF DGH BFH BEH CDH BCH ABH DGH BFH BEH CDH BCH ABH ABCD CDH DGH BCH BFH ABH BEH CGHDGH CFH BFH BEHAEH S S BF BE S S S S S S S S S S S S S S S S S S S S S S S S S S S S EBAE HCBH 阴影阴影，，，，同理，、如图，连接模型二：相似模型定义：形状相同，大小不相同的两个三角形，一切对应线段的长度成比例的模型。

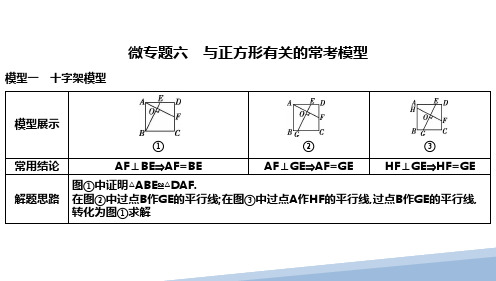
【同步讲练】与正方形有关的四个常考模型模型1 正方形中相交垂线段问题——教材P21例1的变式与应用【教材母题变式】(教材北师9上P21例1变式)如图，在正方形ABCD 中，E ，F 分别在BC ，CD 上，BE ＝CF.AE 与BF 之间有怎样的关系？请说明理由.解：AE ＝BF 且AE⊥BF.理由：∵四边形ABCD 是正方形，∴AB ＝BC ，∠ABE ＝∠C.又∵BE ＝CF ，∴△ABE ≌△BCF(SAS).∴∠BAE ＝∠CBF ，AE ＝BF.又∵∠BAE ＋∠AEB ＝90°，∴∠CBF ＋∠AEB ＝90°.∴∠BOE ＝90°.∴AE ⊥BF.【变式】 如图，在正方形ABCD 中，点E ，F 分别在边BC ，CD 上，AE ，BF 交于点O ，∠AOF ＝90°.求证：BE ＝CF.证明：∵四边形ABCD 是正方形，∴AB ＝BC ，∠ABE ＝∠BCF ＝90°.∵∠AOB ＝180°－∠AOF ＝90°，∴∠BAE ＋∠OBA ＝90°.又∵∠ABE ＝∠CBF ＋∠OBA ＝90°，∴∠BAE ＝∠CBF.在△ABE 和△BCF 中，⎩⎨⎧∠ABE ＝∠BCF ，AB ＝BC ，∠BAE ＝∠CBF ，∴△ABE ≌△BCF(ASA).∴BE ＝CF.正方形内，分别连接两组对边上任意两点，得到的两条线段(如：图1中的线段AF 与BE ，图2中的线段AF 与EG ，图3中的线段HF 与EG)满足：若垂直，则相等.模型2 正方形中过对角线交点的直角问题——教材北师9上P25习题T4的变式与应用【教材母题变式】(教材P25习题T4变式)如图，正方形ABCD 的对角线AC 和BD 相交于点O ，O 又是正方形A 1B 1C 1O 的一个顶点，OA 1交AB 于点E ，OC 1交BC 于点F.(1)求证：△AOE≌△BOF ；(2)如果两个正方形的边长都为a ，那么正方形A 1B 1C 1O 绕O 点转动，两个正方形重叠部分的面积等于多少？为什么？解：(1)证明：在正方形ABCD 中，AO ＝BO ，∠AOB ＝∠A 1OC 1＝90°，∠OAB ＝∠OBC ＝45°.∴∠AOE ＋∠EOB ＝90°，∠BOF ＋∠EOB ＝90°.∴∠AOE ＝∠BOF.在△AOE 和△BOF 中，⎩⎨⎧∠OAE ＝∠OBF ，OA ＝OB ，∠AOE ＝∠BOF ，∴△AOE ≌△BOF(ASA).(2)两个正方形重叠部分的面积等于14a 2.理由如下： ∵△AOE ≌△BOF ，∴S 四边形OEBF ＝S △EOB ＋S △BOF ＝S △EOB ＋S △AOE ＝S △AOB ＝14S 正方形ABCD ＝14a 2.【变式】 如图，在等腰Rt △ABC 中，∠C ＝90°，点O 是AB 的中点，且AC ＝1，将一块直角三角板的直角顶点放在点O 处，始终保持该直角三角板的两直角边分别与AC ，BC 相交，交点分别为D ，E ，则两个三角形重叠部分的面积为14.①△ABC 是等腰直角三角形，O 为斜边AB 的中点.连接OC ，则△DOC≌△EOB ，△ADO ≌△CEO.②在正方形ABCD 中，O 为对角线的交点，直角∠EOF 绕点O 旋转，若OE ，OF 分别与DA ，AB 延长线交于点G ，H ，则△AGO≌△BHO ，△OGH 是等腰直角三角形.(温馨提示：可尝试应用模型做一做活页卷P4T15)模型3 正方形中的“外角平分线”模型3.如图，四边形ABCD 是正方形，点E 是边BC 上任意一点，∠AEF ＝90°，且EF 交正方形外角的平分线CF 于点F.求证：AE ＝EF.证明：在AB 上截取BM ＝BE ，连接ME.∵∠B ＝90°，∴∠BME ＝∠BEM ＝45°.∴∠AME ＝∠ECF ＝135°.∵∠AEF ＝90°，∠AEB ＋∠FEC ＝90°，∠AEB ＋∠MAE ＝90°，∴∠MAE ＝∠FEC.∵AB ＝BC ，BM ＝BE ，∴AM ＝EC.在△AME 和△ECF 中，⎩⎨⎧∠MAE ＝∠CEF ，AM ＝EC ，∠AME ＝∠ECF ，∴△AME ≌△ECF(ASA).∴AE ＝EF.【变式】 在上题的前提下，若题中结论“AE ＝EF”与条件“CF 是正方形外角的平分线”互换，则命题是否还成立？请给出证明.解：命题仍然成立.证明：过点F 作FH⊥BC ，交BC 的延长线于点H ，∵∠AEF ＝90°，∴∠AEB ＋∠FEH ＝90°.∵∠ABE ＝90°，∴∠AEB ＋∠BAE ＝90°.∴∠BAE ＝∠HEF.在△ABE 和△EHF 中，⎩⎨⎧∠BAE ＝∠HEF ，∠ABE ＝∠EHF ，AE ＝EF ，∴△ABE ≌△EHF(AAS).∴BE ＝HF ，AB ＝EH ＝BC.∴BC －EC ＝EH －EC ，即BE ＝CH.∴HF ＝CH.∴∠HCF ＝∠HFC ＝45°，∠DCF ＝45°.∴CF 是正方形外角的平分线.模型4 正方形中的半角模型4.如图，在正方形ABCD 中，E 是AB 上一点，F 是AD 延长线上一点，且DF ＝BE.(1)求证：CE ＝CF ；(2)若点G 在AD 上，且∠GCE ＝45°，则GE ＝BE ＋GD 成立吗？为什么？解：(1)证明：∵四边形ABCD 是正方形，∴BC ＝CD ，∠B ＝∠CDF.又∵BE ＝DF ，∴△CBE ≌△CDF(SAS).∴CE ＝CF.(2)GE ＝BE ＋GD 成立.理由：由(1)得，△CBE ≌△CDF ，∴∠BCE ＝∠DCF.∴∠BCE ＋∠ECD ＝∠DCF ＋∠ECD ，即∠BCD ＝∠ECF ＝90°.又∵∠GCE ＝45°，∴∠GCF ＝∠GCE ＝45°.∵CE ＝CF ，∠GCE ＝∠GCF ，GC ＝GC ，∴△ECG ≌△FCG(SAS).∴GE ＝GF.∴GE ＝DF ＋GD ＝BE ＋GD.【变式】 如图，在正方形ABCD 中，点E ，F 分别为边BC ，CD 上一点，且∠EAF ＝45°，AE ，AF 分别交对角线BD 于点M ，N.求证：MN 2＝BM 2＋DN 2.解：过点A 作GA⊥AN ，使GA ＝NA ，连接GB ，GM.∵∠GAB ＋∠BAF ＝90°，∠DAN ＋∠BAF ＝90°，∴∠GAB ＝∠DAN.在△GAB 和△NAD 中，⎩⎨⎧GA ＝NA ，∠GAB ＝∠DAN ，BA ＝DA ，∴△GAB ≌△NAD(SAS).∴∠ABG ＝∠ADN ＝45°，BG ＝DN.∴∠GBM ＝90°.∵∠EAF ＝45°，∠GAN ＝90°，∴∠GAM ＝45°.在△GAM 和△NAM 中，⎩⎨⎧GA ＝NA ，∠GAM ＝∠NAM ，AM ＝AM ，∴△GAM ≌△NAM(SAS).∴GM ＝MN.在Rt△GBM中，GM2＝GB2＋BM2，∴MN2＝BM2＋DN2.(1)如图1，在正方形ABCD中，若∠EAF＝45°，则：①EF＝BE＋DF；②△CEF的周长为正方形ABCD边长的2倍；③FA平分∠DFE，EA平分∠BEF；④MN2＝BM2＋DN2.图1 图2(2)如图2，在正方形ABCD中，若∠EAF＝45°，FA平分∠DFE，则EF＝DF－BE.。

第11讲 正方形中的几个常用模型探究模型一 正方形的“十字架”模型【例题】：1．如图，有两个动点E ，F 分别从正方形ABCD 的两个顶点B ，C 同时出发，以相同速度分别沿边BC 和CD 移动，问：在E ，F 移动过程中，AE 与BF 的位置和大小有什么关系吗？并给予证明．【变式】去掉BE ＝CF 时，（1）若已知AE=BF ，则AE ⊥BF 成立吗？（2）若已知AE ⊥BF ，则AE=BF 成立吗？【针对练习】1．如图，已知正方形ABCD 的边长为5，点E 、F 分别在AD 、DC 上，AE ＝DF ＝2，BE 与AF 相交于点G ，点H 为BF 的中点，连接GH ，则GH 的长为（ ）A BCD H GEF如图，正方形ABCD 中，E 、F 在其左右两对边上，G 、H 在其上下两对边上. 若有EF ⊥GH ，则必有EF=GH. 证明方法：构造全等；逆向应用：见“十字架”想直角三角形全等A．2B．C．4D．2．如图，E、F分别是正方形ABCD的边CD，AD上的点，且CE＝DF，AE，BF相交于点O，下列结论①AE＝BF；②AE⊥BF；③AO＝OE；④S△AOB＝S四边形DEOF中，正确结论的个数为（）A．4个B．3个C．2个D．1个3．如图所示，E、F、G、H分别为正方形ABCD的边AB，BC，CD，DA上的点，且AE＝BF＝CG＝DH＝AB，则图中阴影部分的面积与正方形ABCD的面积之比为（）A．B．C．D．4．如图，正方形ABCD的边长为4，点E，F分别是CD，BC边上的动点，且CE+CF＝4，BE和AF相交于点G，在点E、F运动的过程中，当△AGB中某一个内角是另一个内角的2倍时，△BCG的面积为．5．如图，在正方形ABCD中，点E，F分别是BC，CD上的点，AE与BF相交于点G，连接AC交BF于点H．若CE＝DF，BG＝GH，AB＝2，则△CFH的面积为．6．如图，在正方形ABCD中，点E、F、G分别在CD、AD、BC上，且FG⊥BE，垂足为O．（1）求证：BE＝FG；（2）若O是BE的中点，且BC＝8，EC＝3，求AF的长．模型二正方形中的“三垂定理”模型如图，已知正方形ABCD，过点B、D两点分别向过点C的直线作垂线，垂足分别为E、F，则有△BCE≌△CDF【例题】．（1）数学课上，张老师给出了一个问题：如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF＝90°，且EF交正方形外角∠DCG的平分线CF于点F．求证：AE ＝EF．小明经过思考展示了一种正确的解题思路：取AB的中点H，连接HE，则可以证明AE＝EF．请你写出证明过程．（2）在此基础上，小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B、C外）的任意一点”，其他条件不变，那么结论“AE＝EF”仍然成立，你认为小颖的观点正确吗？如果正确，请写出证明过程；如果不正确，请说明理由；（3）如图3，如果点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE＝EF”仍然成立吗？直接写出结论，不用说明理由．【针对练习】1．如图，直线l过正方形ABCD的顶点B，点A，C到直线l的距离分别是1和2，则正方形ABCD的面积是．2．在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（0，2），点B的坐标为（﹣3，0），则点C到y轴的距离是（）A．6 B．5 C．4 D．33．如图，在△ABC中以AC，BC为边向外作正方形ACFG与正方形BCDE，连结DF，并过C点作CH⊥AB于H并交FD于M．若∠ACB＝120°，AC＝3，BC＝2，则MD的长为（）A．B．C．D．4．如图，已知四边形ABCD为正方形，AB＝，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE．交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．①求证：矩形DEFG是正方形；②探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．5．[经典问题回顾]如图，四边形ABCD是正方形，点E是边BC上一点，∠AEF＝90°，且EF交正方形外角的平分线CF于点F，求证：AE＝EF．对于本题，我们常用的思路是在AB上截取BM＝BE，构造全等三角形进行证明．小明通过深度研究，又总结出了以下三种思路：思路一：如图（1），在AB的延长线上截取BN，使BN＝BE，连接NE，利用全等三角形和特殊四边形，转化得到线段之间的数量关系，获证；思路二：如图（2），连接AC，过点E作EP⊥AC于点P，EQ⊥CF于点Q，利用全等三角形，获证；思路三：如图（3），连接AC，作EG∥AB，交AC与点G，利用全等三角形，获证．[进一步探究]小明继续对这道题目进行了改编，请完成下面改编题目的解答．四边形ABCD是正方形，点E是直线BC上一点，∠AEF＝β，EF交正方形外角平分线CF 于点F．（1）如图（4），若点E在边BC延长线上，β＝90°，线段AE与线段EF存在怎样的数量关系？并加以证明；（2）如图（5），若点E在边BC上，AE＝EF，求β的度数．模型三正方形半角模型条件：①正方形ABCD，②∠EAF=45°结论：①EF=BE+DF；(△CEF的周长=正方形ABCD周长的一半）②EA平分∠BEF③FA平分∠DAE☆：当∠EAF旋转到正方形ABCD外部时，则有：条件：①正方形ABCD；②∠EAF=45°结论：EF=DFBE【例题】．如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．（1）求证：CE＝CF．（2）在图1中，若G在AD上，且∠GCE＝45°，则GE＝BE+GD成立吗？为什么？（3）运用（1）（2）解答中所累积的经验和知识，完成下题：如图2，在直角梯形ABCG中，AG∥BC（BC＞AG），∠B＝90°，AB＝BC＝12，E是AB上一点，且∠GCE＝45°，BE＝4，求GE的长．【针对练习】1．如图，在四边形ABCD中，∠ADC＝∠B＝90°，DE⊥AB，垂足为E，且DE＝EB＝5，则四边形ABCD的面积．2．已知正方形ABCD中，M，N是边BC，CD上任意两点，∠MAN＝45°，连结MN．（1）如图①，请直接写出BM，DN，MN三条线段的数量关系：；（2）如图②，过点A作AH⊥MN于点H，求证：AB＝AH；（3）如图③，已知∠MAN＝45°，AH⊥MN于点H，且MH＝2，NH＝3，求AH的长．3．已知：正方形ABCD中，∠MAN＝45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N．（1）如图1，当∠MAN绕点A旋转到BM＝DN时，有BM+DN＝MN．当∠MAN绕点A旋转到BM≠DN时，如图2，请问图1中的结论还是否成立？如果成立，请给予证明，如果不成立，请说明理由；（2）当∠MAN绕点A旋转到如图3的位置时，线段BM，DN和MN之间有怎样的等量关系？请写出你的猜想，并证明．【其他模型练习】1．（1）如图1，边长为a的正方形ABCD对角线AC与BD相交于点O，且正方形OEFG绕点O 旋转时，OE交边AB于点H，OG交边BC于点R．则图中阴影部分（四边形BROH）的面积为；（用含a的代数式表示）（2）如图2，已知△ABC中，∠ABC＝90°，AB＝BC＝a，BD平分∠ABC，点O为BD的中点．正方形OEFG绕点O旋转时，OE交边AB于点H，OG交边BC于点R．求图中阴影部分（即四边形BROH）的面积；（3）如图3，△ABC与△OEF均为等腰直角三角形，∠ABC＝∠EOF＝90°，AB＝BC，OE ＝OF．BD是Rt△ABC斜边AC上的中线，点O为BD的中点，OE交边AB于点H，OF交边BC于点R．设两三角形重叠部分（阴影部分）的面积为S，已知EF＝3，当两三角形的空白部分（除去阴影部分）的面积差为2时，直接写出阴影部分面积S的值．2．已知四边形ABCD是正方形，点F为射线AD上一点，连接CF并以CF为对角线作正方形CEFG，连接BE，DG．（1）如图1，当点F在线段AD上时，求证：BE＝DG；（2）如图1，当点F在线段AD上时，求证：CD﹣DF＝BE；（3）如图2，当点F在线段AD的延长线上时，请直接写出线段CD，DF与BE间满足的关系式．3．【实践与探究】操作一：如图①，已知正方形纸片ABCD，将正方形纸片沿过点A的直线折叠，使点B 落在正方形ABCD内部，点B的对应点为点M，折痕为AE，再将纸片沿过点A的直线折叠，使AD与AM重合，折痕为AF，则∠EAF＝．操作二：如图②，将正方形纸片沿EF继续折叠，点C的对应点为点N．当点N恰好落在折痕AE上，则∠AEF＝度．在图②中，运用以上操作所得结论，解答下列问题：（1）设AM与NF的交点为点P，求证：AP＝EF；（2）若AB＝4，则线段EF的长为．。

专题相似正方体的几种基本模型及练习
本文将介绍几种关于相似正方体的基本模型和练方法，帮助读
者更好地理解和应用相似正方体的概念。

1. 等腰正方体
等腰正方体是指除了底面为长方形、其余五个面都是等腰三角
形的正方体。

读者可以练识别等腰正方体的特征以及计算其边长、
面积和体积。

2. 长方体与相似正方体
本节将介绍长方体与相似正方体之间的关联。

读者可以通过练，了解长方体如何变换成相似正方体以及计算相应的边长比例、面积
比例和体积比例。

3. 相似正方体的错位组合与分割
相似正方体的错位组合与分割是指通过将多个相似正方体进行组合或分割，从而产生新的立体图形的方法。

读者可以通过练，研究如何正确地组合和分割相似正方体，并计算新图形的边长、面积和体积。

4. 相似正方体的应用
相似正方体在实际生活中有许多应用。

本节将探讨相似正方体在建筑、工程和设计等领域的运用，并提供相关的练题供读者锻炼应用相似正方体概念的能力。

结论
通过学习本文介绍的几种相似正方体的基本模型和练习方法，读者可以加深对相似正方体概念的理解，并更好地应用于实际问题中。

相似正方体的应用非常广泛，对于建筑、工程和设计领域的从业人员尤为重要。