阶段性测试三

阶段性测试题三(必修一第三单元评估测试) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

考试时间90分钟，满分100分。

第Ⅰ卷(选择题共50分)一、选择题(共25小题，每小题2分，共50分)1．(2012·日照)“把新的内容装进传统的外壳，使古老的形式与时代精神相结合，这是该国国民性中最大的特点。

”近代以来该国政治体制的确立也鲜明地体现了这一特点。

该国是()A．美国B．法国C．中国D．英国[答案] D[解析]“民主政治可以在完全古老的形式中产生”说明近代民主形式与封建制度的传统相结合，英国的君主立宪制符合这一特点。

2．(2011·南通)有学者认为，1688年“光荣革命”开辟了一条英国式的发展道路，其基本含义是()A．为现代英国的发展奠定坚实基础B．以法律制约王权，实行以法治国C．以和平方式进行变革，推动社会进步D．克服王权的专制，建立议会的主权[答案] C[解析]本题考查英国政治制度的特点。

1688年光荣革命以和平方式进行，是一场不流血的宫廷政变。

它使英国上下达成共识：即抛弃革命，用和平渐进方式实行制度创新来促进国家的近代化，成为英国模式的鲜明特点，为近年史学界所强调，故答案选C。

3．(2012·马鞍山)2011年5月，英国女王伊丽莎白二世对爱尔兰进行了国事访问，成为自爱尔兰脱离英国统治以来首位访爱的英国君主。

对此理解不正确的是()A．伊丽莎白二世行使政府首脑权力B．英国重视发展与周边国家的关系C．伊丽莎白二世对外代表英国访问D．君主制度在英国持续的时间较长[答案] A[解析]英国实施君主立宪制，女王统而不治，她是名义上的国家元首，无实权。

政府掌握行政权，所以A项不正确。

4．(2012·丹东)有学者认为，“在其他民族还苦于找不到一个对付王权或皇权的独裁和专制的时候，英国就已经利用了弹劾这个工具……保护着贵族进而也保护了千千万万普通人的权利和自由。

”在英国，拥有弹劾权的机构是()A．国王B．首相C．议会D．内阁[答案] C[解析]在英国君主立宪制下，国王统而不治无实权，首相与内阁必须在大政方针上保持一致，与首相共进退，对其具有弹劾之权的应属掌握立法权的议会，所以选C项。

天一大联考2020年高中毕业班阶段性测试（三）语文一、现代文阅读（一）论述类文本阅读（本题共3小题）阅读下面的文字，完成1～3题。

中国文化轴心时代的春秋战国，儒墨同显，一致百虑，对立互补，相反相成。

墨子先学儒，后觉察儒学缺点，自创墨学。

非儒反儒，补充改造儒学，提出兼爱等人文学的重要原理。

墨子肯定孔学有“当而不可易”的真理成分。

墨家是先秦唯一堪与儒家分庭抗礼的学派。

孟子推崇墨子兼爱的人格精神魅力。

《孟子·尽心上》说：“墨子兼爱，摩顶放踵利天下，为之。

”这种损己利人、大公无私的精神，突显了墨子追求真善美理想的高贵品格。

孟子对墨子精神的赞扬，影响深远。

儒墨之学，各有所长，舍短取长，有助于把握全面真理和治国良方。

从公元前5世纪墨子推出《兼爱》等重要论文，到公元前3世纪后期墨家《墨经》六篇，历时近三百年的学理积淀，墨家学人从十多个角度，阐发“兼爱”学说的深层意蕴。

墨家“兼爱”论题的论证，强调全人类的共同本性和爱的整体性、普遍性、彻底性、穷尽性、交互性、平等性与不可分割性，强调兼爱是人类善良的理想愿望和奋斗目标。

过去、现在和未来一切人，都包含在“兼爱”的范围。

秦汉学界，儒墨对举，孔墨并提；汉后至清，墨学衰竭。

作为墨子“兼爱”理想深刻理论基础的全人类共同人性论，不符合宗法等级制的要求。

“兼爱”理想，在一个相当长的历史时期内，是无法实现的超越性善良愿望和理论假设。

儒家“爱有差等”，适应宗法等级制要求，随血缘亲疏远近，施爱厚薄不同，其人性论的理论基础和灵魂，是“亲亲尊尊”的“血统论”，是“中世纪”漫长宗法等级制社会的主流统治思想。

墨子坚决反对儒家“亲亲尊尊”的“血统论”，主张“可学而能”的共同人性论，是科学的认知理论，认为知识由后天学习得来。

《尚贤下》说：“王公大人骨肉之亲、无故富贵、面目美好者，此非可学能者也。

”只凭血统高贵，治理国家，不通过学习，获得智能，“此譬犹喑者而使为行人，聋者而使为乐师”，就像叫哑巴当外交官，聋人当乐队指挥，必然越治越乱。

电子电工专业复习阶段性测试三（五六章）1.在RLC串联电路中，容抗和感抗的数值越大，电路中的电流就越小，电流与电压的相位差就越大（×）2.串联谐振时，感抗等于容抗，此时电路中的电流最大。

（√）3.在RLC串联电路中若谐振频率为3KHz，则当电源频率为6KHz 时电路呈电感性，且电压超前于电流相位。

（√）4.串联谐振又称电压谐振，可在电路元件上产生高电压。

故在电力电路中不允许出现串联谐振。

（√）5.RLC并联电路谐振时阻抗最大。

（√）6.理想并联谐振电路对总电流产生的阻碍作用无穷大，因此总电流为零。

（∨）7.串联谐振电路不仅广泛应用于电子技术中，也广泛应用于电力系统中。

（×）8.串联谐振在L和C两端将出现过电压现象，因此也把串谐称为电压谐振。

（∨）9.并联谐振在L和C支路上出现过流现象，因此常把并谐称为电流谐振。

（∨）10.谐振状态下电源供给电路的功率全部消耗在电阻上。

（∨）=400 V 11.RLC串联谐振电路，品质因数Q=100，若U= 4V，则UL（√）12.在RLC串联谐振电路中，若电路参数R.L.C确定，则电路的谐振频率f o和品质因数Q也就确定了。

（√）Q越大，13.不管是RLC串联谐振还是并联谐振电路，其品质因数则选择性越好，但通频带则越窄。

（√）14.在R-L-C 串联电路中，U R 或U L 或U C 的数值有可能大于端电压。

（X ）15.串联谐振又称电压谐振，可在电路元件上产生高电压。

故在电力电路中不允许出现串联谐振。

（ √ ） 16 . RLC 串联电路由感性变为容性的过程中，必然经过谐振点。

（ ∨）17.由三个频率相同.振幅相同，但相位彼此相差120°的电压源可构成三相交流电源。

（ √ ）18.三相对称电动势任一瞬间的代数和为零。

(√ )19.三相负载作Y 形连接时，总有P l U U 3 关系成立。

（×） 20.三相用电器正常工作时，加在各相上的端电压等于电源线电压。

比较初等教育阶段性测试三答案一、选择题（每题2.5分，共20分）1.B、5W-H2.C、校内教师评价3.A、书法指导4.A、态度价值观5.B、对生命的敬畏之念6.B、好公民7.A、国家民主生活8.B、经济二、简答题（每题10分，共50分）1．【简答题】英国初等教育学生的学业评定中的课程作业有哪些类型？答案：（1）实践作业（2）书面作业（3）口头、听力作业（4）表演作业2．【简答题】法国初等学校科学与技术课程的教师应遵守的科学教育的三条原则是什么？答案：一是凡能在室外学习的东西，一律不再室内进行；二是凡能通过自然界可以掌握到手的东西，绝不停留在书本知识上；三是凡能研究看得见、摸得着的动态事物，绝不研究停止不动的静物。

强调教师应在大自然中进行科学教学活动。

３.【简答题】在写作教学上，联邦德国初等学校的教师往往会通过哪四个途径来指导学生编些故事？答案：在写作教学上，联邦德国初等学校的教师往往会通过四个途径来指导学生们编写故事，一是先说个笑话，让学生把笑话编写成故事；二是看图编写故事；三是提供几个词汇，让学生利用这几个词汇来编写故事；四是阅读报刊上的某一新闻或消息，让学生围绕此消息来编些故事。

４.【简答题】简述法国公民道德教育的特点。

答案：（1）注重社会性道教育。

（2）内容安排强调阶段性和现实性。

（3）多渠道、多途径实施公民教育。

５.【简答题】简述新加坡小学开设公民道德教育课程的宗旨。

答案：新加坡小学开设公民道德教育课程的宗旨是培养具有以下素质的好公民：社会利益高于个人利益；维护组成社会的家庭；提倡种族和宗教间的宽宏大量和相互体谅；培养协商解决问题的美德。

三、论述题（30分）1．谈谈世界初等学校道德教育的改革趋势。

答案：各国普遍认为，从学校教育和人的培养的历史发展来看，特别是从21世纪对人才新的要求来看，道德教育只能加强，而不能忽视。

因此，各国纷纷采取措施，加强对学校道德教育课程、内容、方法的建设，并在相互影响、相互借鉴、相互促进中，形成一种共同的改革趋向。

人力资源阶段性测试三（A）一、单项选择题1、公司若要进行全员培训，应采纳（）。

A 岗前培训B 脱产培训C 在岗培训D 轮岗培训2、在入职教育中，由新员工的直属上级执行（）的指导。

A 技术性B 共同性C 基础性D 特定性3、入职培训的（）决定了某些新员工只管有必定工作经验，但因为公司和详细工作的特色，仍须接受培训。

A 基础性B 专业性C 适应性D 非个性化4、公司不该为培训而培训，而应听从于公司的整体发展战略，为（）而培训。

A 达成公司发展目标B 提高员工工作绩效C 解决现实存在问题D 提高员工生活质量5、（）是最有益于员工之间互相沟通的学习方式。

A 自我学习B 团队学习C 讲堂学习D 任职学习6、公司员工培训需要投入大批的人力、物力和财力，它对公司目前的工作可能会造成必定影响。

特别是有些培训项目不行能获得立竿见影的成效，需经过必定的实践此后才能反应出来，这就需要公司培训坚持（）。

A 战略性原则B 长久性原则C 学致使用原则D 投资效益原则7、权衡培训成效最常用的经济指标是（）。

A 产值增添率B 投资回报率C 劳动生产率D 绩效成本率8、向受训人员认识信息一般采纳（）。

A 访谈形式、发问形式B 问卷形式、访谈形式C 问卷形式、提高形式D 问卷形式、观察形式9、用（）的方式认识培训信息更直接，更无拘束，更能认识受训人的感觉。

A 发问B 问卷C 参加D 观察10、（）是培训的直接得益者，所以向其认识培训成效信息，是最便利的渠道。

A 主管部门B 受训人员C 岗位管理者D 基层员工11、（）是指组织为了实现其战略发展目标，知足培育人材、提高员工职业素质的需要，采纳各样方法对员工进行有计划的教育、培育和训练的活动过程。

A 人力资源规划B 员工培训C 员工招聘D 绩效管理12、员工培训的功能不包含（）。

A 培育人材，造就队伍，促使组织战略目标的实现B 提高效率，保证质量，为客户供给最满意的服务C 改变员工的态度和行为，提高员工自己的素质D 完美公司的规章和制度，实现公司管理的法制化13、以下各项不属于员工培训的特色的是（）。

2022-2023学年河南省周口市太康县第一高级中学等两校高一下学期阶段性测试（三）地理试题1. 图为世界某区域人口密度及相关地理事物分布图。

据此完成下面小题。

1．图示区域人口分布的总体特点是（）A．沿海多,内陆少B．中部多,四周少C．人口重心偏向西南部D．河流中下游多2．图示区域北部人口稀少的主要自然原因是（）A．终年严寒B．台风多发C．气候干旱D．地形崎岖3．造成图示区域人口空间分布特点的决定性因素是（）A．纬度位置B．经济发展水平C．矿产资源D．河流流向2. 老年人口系数是指一个国家或地区65岁及以上老年人口数占总人口数的比重,当其大于7%时，则意味着这个国家或地区进入老龄化社会。

读我国南疆县区老年人口系数变化图,完成下面小题。

1．据图可知,南疆（）A．1990年有部分县区进人老龄化社会B．2020年全面进入老龄化社会C．历经30年,部分县区老龄化程度有所减轻D．近30年部分县区老龄化程度变化很小2．近30年来,南疆东部县区人口老龄化程度加深的主要原因有（）①人口出生率下降②城乡生育政策差异③人均寿命延长④少数民族聚集程度提高A．①②B．②④C．①③D．③④3．南疆地区人口年龄结构的变化,短期内对当地社会经济发展产生的影响是（）A．劳动力供给增多B．社会养老负担加重C．经济增长活力增强D．产业结构优化升级3. 吉布提位于非洲东北部的亚丁湾西岸,国土面积2.32万平方千米,人口约100万。

20世纪末,由于边界争端不断,埃塞俄比亚、索马里的难民大量涌入吉布提。

图示意1990-2019年吉布提人口迁往其他国家的分布。

据此完成下面小题。

1．20世纪末,埃塞俄比亚、索马里两国进入吉布提的难民（）A．属于暂时性人口流动B．跨越大洲长距离迁移C．为政治原因所引发D．群体规模较小2．1990-2019年,吉布提外迁人口的特点是（）A．2019年外迁人数是1990年的两倍B．大多数移民迁往发展中国家C．迁往埃塞俄比亚的人口数最为稳定D．法国是外迁人口的首选国家3．大量人口外迁,对吉布提可能产生的影响是（）A．促进当地社会经济发展B．加速人才外流C．加大社会治安管理难度D．提升生活水平4. 适度人口指对一国或地区发展最适宜的人口数量,其大小由区域综合承载力（综合承载力包括资源、生态和经济承载力3个子系统）决定。

天一大联考高中毕业班阶段性测试（三）数学试题一、单选题1．设集合，，则下列结论正确的是A．B．C．D．【答案】B【解析】利用一元二次不等式的解法求得集合,即可得出集合与集合的关系，从而可得出结论.【详解】，，，故选B.【点睛】集合的基本运算的关注点：（1）看元素组成，集合是由元素组成的，从研究集合中元素的构成入手是解决集合运算问题的前提；（2）有些集合是可以化简的，先化简再研究其关系并进行运算，可使问题简单明了，易于解决；（3）注意数形结合思想的应用，常用的数形结合形式有数轴、坐标系和图．2．复数的共轭复数对应的点位于A．第一象限B．第二象限C．第三象限D．第四象限【答案】C【解析】利用复数的除法运算法则：分子、分母同乘以分母的共轭复数，化简复数，再利用共轭复数的概念求出复数的共轭复数，进一步求出对应点的坐标得结果. 【详解】，的共轭复数为，对应坐标是在第三象限，故选C.【点睛】复数是高考中的必考知识，主要考查复数的概念及复数的运算．要注意对实部、虚部的理解，掌握纯虚数、共轭复数、复数的模这些重要概念，复数的运算主要考查除法运算，通过分母实数化转化为复数的乘法，运算时特别要注意多项式相乘后的化简，防止简单问题出错，造成不必要的失分. 3．函数的部分图像大致为（ ）A ．B ．C ．D ．【答案】A 【解析】利用，排除选项；利用排除选项，从而可得结果.【详解】，，排除选项；，排除选项，故选A.【点睛】函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置． (2)从函数的单调性，判断图象的变化趋势； (3)从函数的奇偶性，判断图象的对称性； (4)从函数的特征点，排除不合要求的图象.4．若非零向量,a b rr 满足3a b =r ，且()()2a b a b -⊥+r r r r ，则a r 与b r 的夹角的余弦值为( ) A ．6 B ．33C ．6-D ．3【答案】D【解析】根据()()2a b a b -⊥+r r r r 可得()()20a b a b -⋅+=r r r r ,代入3a =r 化简求解夹角余弦值即可. 【详解】设a r 与b r的夹角为θ,()()2a b a b -⊥+r r r r Q ,()()2a b a b ∴-⋅+r r r r 222cos 0ab a b θ=-+=r r r r.3a b =r r Q ,222223cos 3b a b a b bθ-∴=-=-=-r r r r r r , 故选：D. 【点睛】本题主要考查了利用数量积的公式与模长求解夹角的问题.属于中档题. 5．执行如图所示的程序框图，则输出的结果为A ．4B ．5C ．6D ．7【答案】B【解析】模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可得到输出的的值. 【详解】 第一次循环，； 第二次循环，；第三次循环，，退出循环，输出，故选B. 【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.6．已知等差数列的前项和为，，为整数，且最大，则公差A ．-2B ．-3C ．-4D ．-5【答案】B【解析】利用排除法，令，分别判断出前项和的最大值，即可得结果. 【详解】时，，或最大，故不合题意；时，，最大，故合题意；时，，最大，故不合题意；时，， 或最大，故不合题意，故选B. 【点睛】本题考查了等差数列的通项公式及其前项和公式，以及排除法的应用，属于基础题. 用特例代替题设所给的一般性条件，得出特殊结论，然后对各个选项进行检验，从而做出正确的判断，这种方法叫做特殊法. 若结果为定值，则可采用此法. 特殊法是“小题小做”的重要策略，排除法解答选择题是高中数学一种常见的解题思路和方法，这种方法即可以提高做题速度和效率，又能提高准确性.7．已知直线y=2b 与双曲线22x a -22y b=1（a ＞0，b ＞0）的斜率为正的渐近线交于点A ，曲线的左、右焦点分别为F 1、F 2，若21tan AF F 15∠=，则双曲线的离心率为（ ） A ．4或1611B ．1611C ．2D ．4【答案】D【解析】由题意表示出点A 的坐标，又21tan 15AF F ∠=求出结果 【详解】 由渐近线方程y bx a=与直线2y b =求出点A 的坐标为()2,2a b ,过A 点作AB x ⊥轴于点B ，则22,2AB b BF c a ==-由已知可得212tan 152bAF F c a∠==-22264a 60110116064016411ac c e e e e ∴-+=∴-+=∴==或当1611e =时，1611c a =则20c a -<故舍去，综上4e = 故选D 【点睛】本题考查了求双曲线的离心率问题，在求解过程中一定依据题目已知条件，将其转化为关于离心率的方程，继而求出结果，本题属于中档题 8．如图放置的边长为1的正方形沿轴顺时针滚动一周，设顶点的运动轨迹与轴所围区域为，若在平面区域内任意取一点，则所取的点恰好落在区域内部的概率为A ．B ．C ．D ．【答案】C【解析】顶点的运动轨迹，分三部分：前一部分的图象为四分之一圆周，后一部分的图象为四分之一圆周，且半径都是1,中间部分的轨迹为以为半径的四分之一圆周，分别求出与轴围成的面积，求和后利用几何概型概率公式求解即可. 【详解】正方形沿轴顺时针滚动一周，顶点的运动轨迹，分三部分：前一部分的图象为四分之一圆周，后一部分的图象为四分之一圆周，且半径都是1,此时两部分扇形所占面积为,中间部分的轨迹为以为四分之一圆周，与围成的面积为,顶点的运动轨迹与轴所围区域的面积为，平面区域的面积为，所以在平面区域内任意取一点，则所取的点恰好落在区域内部的概率为故选C.【点睛】本题主要考查“面积型”的几何概型，属于中档题. 解决几何概型问题常见类型有：长度型、角度型、面积型、体积型，求与面积有关的几何概型问题关鍵是计算问题的总面积以及事件的面积；几何概型问题还有以下几点容易造成失分，在备考时要高度关注：（1）不能正确判断事件是古典概型还是几何概型导致错误；（2）基本事件对应的区域测度把握不准导致错误；（3）利用几何概型的概率公式时, 忽视验证事件是否等可能性导致错误.9．一个几何体的三视图如图所示，该几何体表面上的点在正视图上的对应点为，点，，在俯视图上的对应点为，，，过直线作一平面与直线平行，则该平面截几何体所得截面多边形的周长为A．B．C．D．【答案】A【解析】由三视图还原几何体，可知该几何体是如图所示的四棱锥，设中点为，连接，由线面平行的判定定理可得为所求截面，利用三视图所给数据求出三角形各边长即可得结果.【详解】由三视图可知，该几何体是如图所示的四棱锥，其中平面，底面是直角梯形，，高，设中点为，连接，则是平行四边形，所以平面，平面，所以平面是所求截面，由勾股定理可得，的周长为，故选A.【点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力，属于难题.三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响，对简单组合体三视图问题，先看俯视图确定底面的形状，根据正视图和侧视图，确定组合体的形状.10．已知函数()2sin (0)4f x x πωω⎛⎫=-> ⎪⎝⎭的图象的相邻最高点间的距离为π，设()f x 的图象向左平移4π个单位后得到()g x 的图象，则函数()g x 在0,2π⎡⎤⎢⎥⎣⎦上的值域为A ．2,2⎡⎤⎣⎦B ．2,2⎡⎤-⎣⎦C ．[]2,2-D ．2,2⎡⎤-⎣⎦【答案】D【解析】由图象的相邻最高点间的距离为π，可求得函数周期，从而确定2ω=，利用三角函数的平移法则可得()g x 的解析式，求得52,444x πππ⎡⎤+∈⎢⎥⎣⎦，利用正弦函数的单调性可得结果. 【详解】Q 函数()2sin (0)4f x x πωω⎛⎫=-> ⎪⎝⎭的图象的相邻最高点间的距离为π，2T ππω∴==，得2ω=，()224f x sin x π⎛⎫=- ⎪⎝⎭向左平移4π可得，()2222444g x sin x sin x πππ⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，50,,2,2444x x ππππ⎡⎤⎡⎤∈∴+∈⎢⎥⎢⎥⎣⎦⎣⎦Q ，22,142sin x π⎡⎤⎛⎫∴+∈-⎢⎥ ⎪⎝⎭⎣⎦，()2,2g x ⎡⎤∈-⎣⎦，即()g x 的值域为2,2⎡⎤-⎣⎦，故选D.【点睛】本题主要考查三角函数的图象与性质、以及三角函数图象的平移法则，属于中档题. 能否正确处理先周期变换后相位变换这种情况下图象的平移问题，反映学生对所学知识理解的深度. 11．已知函数的图象的对称中心为，且的图象在点处的切线过点，则A ．1B ．2C ．3D ．4【答案】A 【解析】由函数的图象的对称中心为，可得，求得的值后，利用解方程即可得结果.【详解】 函数的图象的对称中心为，所以， ，即，得，，又的图象在点处的切线过点， ，即，解得，故选A.【点睛】本题主要考查导数的几何意义，以及函数的对称性的应用，属于难题. 函数的对称的性质：（1）若，则的图象关于对称；（2）若，则的图象关于对称.12．已知抛物线2:4C y x =，斜率为k 的直线l 与抛物线C 相交于A ，B 两点，与圆22:(5)9E x y -+=相切于点M ，且M 为线段AB 的中点，则弦长||AB =A ．2B ．4C ．37D ．6【答案】C【解析】首先利用点差法求出02ky =，结合圆心和切点的连线与切线垂直可得03x =，通过切点在圆上求出切点坐标，进而可求出直线方程，联立直线与抛物线将韦达定理与弦长公式相结合可得弦长. 【详解】设()11,A x y ，()22,B x y ，()00,M x y ， 则21122244y x y x ⎧=⎨=⎩，相减得()()()1212124y y y y x x +-=-，利用点差法可得02ky =，因为直线与圆相切，所以001 5y x k=--，所以03x =，将0x代入圆的方程可得0y =， 不失一般性可取M点坐标为(，则5k =， 故直线l的方程为)3y x =-，即55y x =-，联立24y x y x ⎧=⎪⎨⎪=⎩242410x x -+=，所以126x x +=，1214x x =，由弦长公式得AB == C. 【点睛】本题考查直线与抛物线、圆的位置关系，考查点差法，直线与抛物线的相交时弦长问题，属于中档题．二、填空题13．已知随机变量2(1,)X N σ:，若(01)0.3P X <<=，则(2)P X >=__________． 【答案】0.2【解析】随机变量()21,X N σ~，得到曲线关于1x =称，根据曲线的对称性得到200.501P X P X P X >=<=-<<（）（）（） ，根据概率的性质得到结果． 【详解】随机变量()21,X N σ~，∴曲线关于1x =对称，∴200.5010.2P X P X P X >=<=-<<=（）（）（），故答案为0.2. 【点睛】本题主要考查正态分布曲线的特点及曲线所表示的意义、函数图象对称性的应用等基础知识，属于基础题14．已知x ，y 满足约束条件220,220,20,x y x y x y -+≥⎧⎪--≤⎨⎪+-≤⎩则z x y =-的最大值为__________．【答案】2【解析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数求解即可. 【详解】画出220,220,20,x y x y x y -+≥⎧⎪--≤⎨⎪+-≤⎩表示的可行域，如图，由220,20,x y x y --=⎧⎪⎨⎪+-=⎩可得20x y =⎧⎪⎨⎪=⎩， 将z x y =-变形为y x z =-， 平移直线y x z =-，由图可知当直y x z =-经过点()2,0时， 直线在y 轴上的截距z -最小，z 最大， 最大值为202z =-=，故答案为2. 【点睛】本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值. 15．已知数列{}n a 的前n 项和为n S ，12a =，2n n S a λ=-，其中λ为常数，若13n n a b n =-，则数列{}n b 中的项的最小值为__________．【答案】1412-【解析】由12a =求得2,λ=再利用公式11,1,2n nn S n a S S n -=⎧=⎨-≥⎩求出()12132nnn n a b n ⎛⎫=⇒=- ⎪⎝⎭，根据11n n n n b b b b +-≤⎧⎨≤⎩求得1415n ≤≤从而可得结果. 【详解】12,2n n a S a λ==-Q ,1112S a a λ∴==-, 222,2,22n n S a λλ=-==-,①2n ≥时，1122n n S a --=-，②②-①化为()122n n a a n -=≥， 所以{}n a 是公比为2的等比数列，()11222,132nn nn n a b n -⎛⎫∴=⨯==-⨯ ⎪⎝⎭，由11n n n n b b b b +-≤⎧⎨≤⎩，可得()()()()111113122211131422n n n n n n n n +-⎧⎛⎫⎛⎫-⨯≤-⨯⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎨⎛⎫⎛⎫⎪-⨯≤-⨯ ⎪ ⎪⎪⎝⎭⎝⎭⎩， 解得()()()21312141513214n nn n n ⎧-≤-⎪⇒≤≤⎨-≤-⎪⎩， 即{}n b 中的项的最小值为14151412b b ==-，故答案为1412-. 【点睛】本题主要考查递推关系求通项公式，以及等比数列的定义，数列的最小项，属于难题. 已知数列前n 项和，求数列通项公式，常用公式11,1,2n nn S n a S S n -=⎧=⎨-≥⎩，将所给条件化为关于前n 项和的递推关系或是关于第n 项的递推关系，若满足等比数列或等差数列定义，用等比数列或等差数列通项公式求出数列的通项公式，否则适当变形构造等比或等数列求通项公式.16．已知六棱锥P ABCDEF -，底面ABCDEF 为正六边形，点P 在底面的射影为其中心.将该六棱锥沿六条侧棱剪开，使六个侧面和底面展开在同一平面上，若展开后点P 在该平面上对应的六个点全部落在一个半径为5的圆上，则当正六边形ABCDEF 的边长变化时，所得六棱锥体积的最大值为__________．【解析】设六边形的边长为()0x x >，，进而可将体积表示为关于自变量x 的函数，利用导数判断函数的单调性得其最大值即可. 【详解】如图所示，设六边形的边长为()0x x >，故3OG =， 又∵展开后点P 在该平面上对应的六个点全部落在一个半径为5的圆上，∴352PG x =-，故22335255322PO x x x ⎛⎫⎛⎫=--=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ∴六棱锥的体积2451131562553533222V x x x x =⨯⨯⨯-=- 令()()455530f x x xx =->，∴()()3432053543f x x x xx -='=，当43x ⎛∈ ⎝⎭时，()0f x '>，函数()f x 单调递增，当43x ⎫∈+∞⎪⎪⎝⎭时，()0f x '<，函数()f x 单调递减，故当43x =()f x 取得最大值，即体积最大， 815815. 【点睛】本题考查六棱锥的体积的最大值的求法，考查空间中线线、线面、面面间的位置关系、函数性质、导数等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、化归与转化思想，是中档题．三、解答题17．已知等差数列{}n a 的公差不为零，EF CE AC AB=，且211113a a a =⋅. （1）求使不等式0n a ≥成立的最大自然数n ；（2）求数列11{}n n a a +的前n 项和. 【答案】（1）13；（2）62550nn-.【解析】（1）由125a =，且211113a a a =⋅，列方程求出{}n a 的公差为d ，从而求出{}n a 的通项公式，然后列不等式求解即可；（2）由()()111227225n n a a n n +=-+-+ 1112227225n n ⎛⎫=-- ⎪-+-+⎝⎭，利用裂项相消法可求得数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和. 【详解】（1）设{}n a 的公差为d .由题意，可得()()21111012a d a a d +=+，于是()12250d a d +=.又125a =，0d ≠，所以2d =-. 故227n a n =-+.由2270n -+≥，可得13.5n ≤，所以满足题意的最大自然数n 为13.（2）因为()()111227225n n a a n n +=-+-+ 1112227225n n ⎛⎫=-- ⎪-+-+⎝⎭. 故前n 项和为12231111n n a a a a a a ++++L 1111111225232321227225n n ⎡⎤⎛⎫⎛⎫⎛⎫=--+-++- ⎪ ⎪ ⎪⎢⎥-+-+⎝⎭⎝⎭⎝⎭⎣⎦L111225225n ⎛⎫=-- ⎪-+⎝⎭1150504n =-+- 62550n n =-. 【点睛】本题主要考查等差数列的性质及裂项法求前n 项和，属于中档题. 裂项相消法是最难把握的求和方法之一，其原因是有时很难找到裂项的方向，突破这一难点的方法是根据式子的结构特点，常见的裂项技巧：(1)()1111n n k k n n k ⎛⎫=- ⎪++⎝⎭；（2）1k=； （3）()()1111212122121n n n n ⎛⎫=- ⎪-+-+⎝⎭；（4）()()11122n n n =++()()()11112n n n n ⎡⎤-⎢⎥+++⎣⎦；18．在ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ，若cos cos 2cos a C c AB b+=，点D 在线段AC 上，且2AD DC =，BC =3BD =. （1）求角B 的大小； （2）求ABC ∆的面积.【答案】（1）3B π=；（2【解析】（1）根据cos cos 2cos a C c AB b+=，利用正弦定理可得sin cos sin cos 2sin cos A C C A B B +=，由两角和的正弦公式结合诱导公式可得sin 2sin cos B B B =，从而得1cos 2B =，进而可得结果；（2）设AB x =，3(0,0)AC z x z =>>，在ABD ∆中，在CBD ∆中，在ABC ∆中，结合cos cos BDA BDC ∠=-∠，利用余弦定理列方程组求得x =面积公式可得结果. 【详解】 （1）根据cos cos 2cos a C c AB b+=可得cos cos 2cos a C c A b B +=，∴sin cos sin cos 2sin cos A C C A B B +=，∴()sin 2sin cos A C B B +=，∴()sin 2sin cos B B B π-=， 即sin 2sin cos B B B =，∴1cos 2B =. 又∵0B π<<，∴3B π=.（2）设AB x =，3(0,0)AC z x z =>>.在ABD ∆中，由余弦定理可得()2292cos 232z x BDA z+-∠=⨯⨯.在CBD ∆中，由余弦定理可得2912cos 23z BDC z+-∠=⨯⨯. 由于180BDA BDC ∠+∠=︒，故cos cos BDA BDC ∠=-∠， 即()2229291223223z x z cz+-+-=-⨯⨯⨯⨯， 整理可得22360z x +-=.①在ABC ∆中，由余弦定理可知2212239x x z +-=. 代入①式整理可得243330x x +-=.所以3523x =-. 据此可知ABC ∆的面积()1352323sin 2S B =-⨯ ()39535233322=-=-. 【点睛】本题主要考查正弦定理、余弦定理以及三角形的面积的应用，属于中档题. 本题主要考查余弦定理及特殊角的三角函数，属于简单题.对余弦定理一定要熟记两种形式：（1）2222cos a b c bc A =+-；（2）222cos 2b c a A bc+-=，同时还要熟练掌握运用两种形式的条件.另外，在解与三角形、三角函数有关的问题时，还需要记住30,45,60o o o等特殊角的三角函数值，以便在解题中直接应用.19．如图，在多面体ABCDEF 中，底面ABCD 是菱形，60DAB ∠=︒，2EA ED AB ===，EF AC P 且12EF AC =.（Ⅰ）求证：AD BE ⊥；（Ⅱ）若平面AED ⊥平面ABCD ，求平面BCF 与平面ABCD 所成的锐二面角的余弦值.【答案】（Ⅰ）见解析；（Ⅱ5. 【解析】（Ⅰ）取AD 的中点M ，连接EM ，BM ，易得EM AD ⊥，接着通过证明BM AD ⊥来得到AD ⊥平面EMB ，进而可得结论；（Ⅱ）通过面面垂直可得EM ⊥平面ABCD ，进而可建立如图所示的坐标系，求出平面BCF 的法向量，结合平面ABCD 的一个法向量为()0,0,1m =v，进而可求得最后结果.【详解】（Ⅰ）取AD 的中点M ，连接EM ，BM .∵EA ED =，∴EM AD ⊥. ∵底面ABCD 是菱形，60DAB ∠=︒，∴AB AD BD ==，∴BM AD ⊥，∵EM BM M ⋂=，∴AD ⊥平面EMB .∵BE ⊂平面EMB ，∴AD BE ⊥.（Ⅱ）∵EM AD ⊥，平面AED ⊥平面ABCD ，平面AED ⋂平面ABCD AD =，∴EM ⊥平面ABCD .∴可以M 为原点，MA ，MB ，ME 为x 轴，y 轴，z 轴建立空间直角坐标系，则()0,0,0M ，()1,0,0A ，()3,0C -，(3E ，()3,0B .∴(3ME =u u u v ，()2,0,0BC =-u u u v，()3,0AC =-u u u v ，∴13322EF AC u u u v u u u v ⎛⎫==- ⎪ ⎪⎝⎭， ∴3332MF ME EF ⎛=+=- ⎝u u u v u u u v u u u v ，即3332F ⎛- ⎝，∴33,32BF ⎛=- ⎝u u u v .设平面BCF 的一个法向量为(),,n x y z =v ，则3330,220,n BF x y z n BC x ⎧⋅=--+=⎪⎨⎪⋅=-=⎩u u u v v u u u v v 令1z =，则()0,2,1n =v .易知平面ABCD 的一个法向量为()0,0,1m =v.设平面BCF 与平面ABCD 所成的锐二面角为θ，∴5cos 51m n m n v vv vθ⋅===⋅⨯. ∴平面BCF 与平面ABCD 5【点睛】本题主要考查线线垂直的判定，核心内容为“线线垂直”“线面垂直”“面面垂直”之间可以相互转化，空间向量在求二面角中的应用，即二面角的大小与平面的法向量所成角之间相等或互补，主要通过题意或图形确定最后结果，属于中档题.20．为了解使用手机是否对学生的学习有影响，某校随机抽取100名学生，对学习成绩和使用手机情况进行了调查，统计数据如表所示（不完整）：（Ⅰ）补充完整所给表格，并根据表格数据计算是否有99.9%的把握认为学生的学习成绩与使用手机有关；（Ⅱ）现从上表不使用手机的学生中按学习成绩是否优秀分层抽样选出6人，再从这6人中随机抽取3人，记这3人中“学习成绩优秀”的人数为X，试求X的分布列与数学期望.参考公式：22()()()()()n ad bcKa b c d a c b d-=++++，其中n a b c d=+++.参考数据：【答案】（Ⅰ）见解析；（Ⅱ）见解析.【解析】（Ⅰ）根据题意即可将列联表完成，通过计算2K的值即可得最后结论；（Ⅱ）“学习成绩优秀”的有4人，“学习成绩一般”的有2人，X的所有可能取值为1，2，3，计算出其概率得到分布列，计算出期望.【详解】（Ⅰ）填表如下：由上表得()221001020403040605050K ⨯⨯-⨯=⨯⨯⨯ 16.66710.828≈>.故有99.9%的把握认为学生的学习成绩与是否使用手机有关. （Ⅱ）由题意得，所抽取的6位不使用手机的学生中， “学习成绩优秀”的有406460⨯=人，“学习成绩一般”的有206260⨯=人. X 的所有可能取值为1，2，3.()124236411205C C P X C ====，()2142361232205C C P X C ====，()304236413205C C P X C ====. 所以X 的分布列为：故数学期望为1311232555EX =⨯+⨯+⨯=. 【点睛】本题主要考查独立性检验的应用，离散型随机变量的分布列及其期望，考查了学生的计算能力，属于中档题.21．已知O 为坐标原点，椭圆2222:1(0)x y E a b a b+=>>的焦距为y x =截圆222:O x y a +=与椭圆E 所得的弦长之比为2，圆O 、椭圆E 与y 轴正半轴的交点分别为P ，A .（1）求椭圆E 的标准方程；（2）设点00(,)B x y （00y ≠且01y ≠±）为椭圆E 上一点，点B 关于x 轴的对称点为C ，直线AB ，AC 分别交x 轴于点M ，N ，证明：tan tan OPM ONP ∠=∠. 【答案】（1）2214x y +=；（2）详见解析. 【解析】（1）根据焦距为y x =截圆222:O x y a +=与椭圆E 所得的弦长之比为2，结合性质222a b c =+ ，列出关于a 、b 、c 的方程组，求出a 、b ，即可得结果；（2）由（1）可知，点A 的坐标为()0,1，点P 的坐标为()0,2，由直线AB的方程与直线AC 的方程令0y =，分别求得00,01x M y ⎛⎫ ⎪-⎝⎭，00,01x N y ⎛⎫⎪+⎝⎭，可证明24||OM ON OP ⋅==，即OM OP OPON=，从而可得结论.【详解】（1）根据题意可知c =223a b -=.因为直线y x =截椭圆E，2=，化简得224a b =. 所以21b =，24a =.故椭圆E 的标准方程为2214x y +=.（2）由（1）可知，点A 的坐标为()0,1，点P 的坐标为()0,2. 直线AB 的方程为0011y y x x -=+，令0y =，得00,01x M y ⎛⎫⎪-⎝⎭. 因为点B 关于x 轴的对称点为C ，所以()00,C x y -. 所以直线AC 的方程为011y y x x +=-+. 令0y =，得00,01x N y ⎛⎫⎪+⎝⎭.因为20002000111x x x OM ON y y y ⋅=⋅=-+-， 而点()00,B x y 在椭圆2214x y +=上，所以220014x y +=.即20241x y --，所以24||OM ON OP ⋅==，即OM OP OPON=，所以tan tan OPM ONP ∠=∠.【点睛】本题主要考查椭圆的几何性质、标准方程，直线与椭圆的位置关系，属于难题. 本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系，属于难题.用待定系数法求椭圆方程的一般步骤；①作判断：根据条件判断椭圆的焦点在x 轴上，还是在y 轴上，还是两个坐标轴都有可能；②设方程：根据上述判断设方程()222210x y a b a b +=>>或22221x y b a+= ()0a b >>；③找关系：根据已知条件，建立关于a 、b 、c 的方程组；④得方程：解方程组，将解代入所设方程，即为所求. 22．已知函数()ln f x x x =，()1g x x =-. （Ⅰ）求函数()()()f x G xg x =的单调区间； （Ⅱ）设441()()()4H x f x ag x =-的极小值为()a ϕ，当0a >时，求证：114141()()04a a e e a ϕ---≤≤. 【答案】（Ⅰ）()G x 的单调递增区间为(0,1)和(1,)+∞，无单调递减区间；（Ⅱ）见解析.【解析】（Ⅰ）对()G x 求导可得()()21ln 1x xG x x ---'=，设()1ln h x x x =--，对()h x 求导，判断()h x 的符号，进而可得()G x 的单调性；（Ⅱ）对()H x 进行求导，可得()H x 的极小值()4114a a a e ϕ-=-，对()a ϕ求导，易证()104a ϕϕ⎛⎫≤= ⎪⎝⎭，在将114104aa e --≥等价转化为()1ln 4104a a +-≥，令()()1ln 414r a a a =+-，对其求导求其最值即可.【详解】（Ⅰ）因为()ln 1x x G x x =-（0x >且1x ≠），所以()()21ln 1x x G x x ---'=. 设()1ln h x x x =--，则()11h x x'=-. 当1x >时，()110h x x=->'，()h x 是增函数，()()10h x h >=，所以()()21ln 01x xG x x --=>-'.故()G x 在()1,∞上为增函数； 当01x <<时，()110h x x=-<'，()h x 是减函数，()()10h x h >=，所以()()21ln 01x xG x x --=>-'，所以()G x 在()0,1上为增函数.故()G x 的单调递增区间为()0,1和()1,+∞，无单调递减区间. （Ⅱ）由已知可得()()44ln 1H x x x a x =--，则()()34ln 14H x xx a =+-'.令()0H x '=，得1ln 4x a =-，14a x e -=.当140,a x e -⎛⎫∈ ⎪⎝⎭时，()0H x '<，()H x 为减函数；当14,a x e -⎛⎫∈+∞ ⎪⎝⎭时，()0H x '>，()H x 为增函数，所以()H x 的极小值()()414114a a a H e a e ϕ--==-.由()4110a a e ϕ-'=-=，得14a =. 当10,4a ⎛⎫∈ ⎪⎝⎭时，()0a ϕ'>，()a ϕ为增函数； 当1,4a ⎛⎫∈+∞⎪⎝⎭时，()0a ϕ'<，()a ϕ为减函数. 所以()104a ϕϕ⎛⎫≤= ⎪⎝⎭.而()1141414a a a ee ϕ--⎛⎫-- ⎪⎝⎭11414141144a a a a e e e ---⎛⎫=--- ⎪⎝⎭ 11414aa e -=-.下证：0a >时，114104aa e --≥.()111144104ln 44aa a e a e a ---≥⇔≥⇔ ()111ln 41044a a a ≥-⇔+-≥. 令()()1ln 414r a a a =+-，则()22114144a r a a a a -='=-. 当10,4a ⎛⎫∈ ⎪⎝⎭时，()0r a '<，()r a 为减函数； 当1,4a ⎛⎫∈+∞⎪⎝⎭时，()0r a '>，()r a 为增函数. 所以()104r a r ⎛⎫≥= ⎪⎝⎭，即()1ln 4104a a +-≥. 所以114104aa e --≥，即()11414104a a a ee ϕ--⎛⎫--≥ ⎪⎝⎭.所以()1141414a a a e e ϕ--⎛⎫≥- ⎪⎝⎭. 综上所述，要证的不等式成立. 【点睛】本题主要考查了导数与单调性的关系，导数在证明不等式中的应用，解题的关键在于构造函数，属于难题.。

河南省天一大联考2024-2025学年高一地理下学期阶段性测试试题（三）考生留意：1.答题前，考生务必将自己的姓名、考生号填写在试卷和答题卡上，并将考生号条形码粘贴在答题卡上的指定位置。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共25小题，每小题2分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

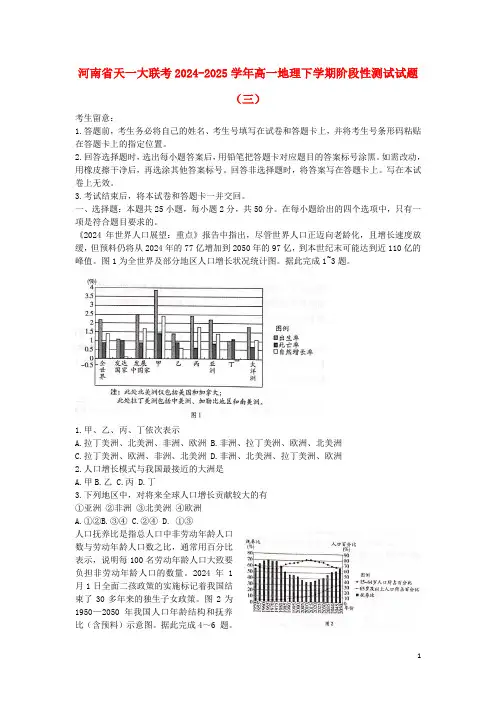
《2024年世界人口展望：重点》报告中指出，尽管世界人口正迈向老龄化，且增长速度放缓，但预料仍将从2024年的77亿增加到2050年的97亿，到本世纪末可能达到近110亿的峰值。

图1为全世界及部分地区人口增长状况统计图。

据此完成1~3题。

1.甲、乙、丙、丁依次表示A.拉丁美洲、北美洲、非洲、欧洲B.非洲、拉丁美洲、欧洲、北美洲C.拉丁美洲、欧洲、非洲、北美洲D.非洲、北美洲、拉丁美洲、欧洲2.人口增长模式与我国最接近的大洲是A.甲B.乙C.丙D.丁3.下列地区中，对将来全球人口增长贡献较大的有①亚洲②非洲③北美洲④欧洲A.①②B.③④C.②④D. ①③人口抚养比是指总人口中非劳动年龄人口数与劳动年龄人口数之比，通常用百分比表示，说明每100名劳动年龄人口大致要负担非劳动年龄人口的数量。

2024 年1月1日全面二孩政策的实施标记着我国结束了30多年来的独生子女政策。

图2为1950—2050年我国人口年龄结构和抚养比（含预料）示意图。

据此完成4～6 题。

4.1950—1965 年我国人口抚养比改变的主要缘由是A. 实行安排生育政策B.人口诞生率高图例C. 社会保障制度好D. 经济发展水平高5.从人口年龄结构的角度看，2005—2025年我国A.社会养老负担极重B. 经济发展活力低C.劳动力供应足够D.青少年升学压力小6.为应对 2024年以后人口抚养比改变产生的影响，我国可实行的措施是A. 严格执行少生优生政策B. 提高国际移民进入我国的门槛C. 完善农村基础设施建设D. 完善社会保障制度，改善医疗条件国家法定退休年龄的调整与该国人口增长状况有亲密关系。

绝密★启用前大联考2022—2023学年高一年级阶段性测试（三）数 学考生注意：1．答题前，考生务必将自己的姓名、考生号填写在试卷和答题卡上，并将考生号条形码粘贴在答题卡上的指定位置．2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效． 3．考试结束后，将本试卷和答题卡一并交回．一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．PA BC BA +-=（ ） A ．PBB ．CPC ．ACD ．PC2．已知向量a ，b 的夹角为π3，3a b ⋅=，2b =，则a =（ ） A ．2B ．3C ．6D ．123．已知向量a 与b 的方向相反，()2,3b =-，213a =，则a =（ ） A ．()6,4-B ．()4,6-C ．()4,6-D ．()6,4-4．已知ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，a =12b =，60B =︒，则A =（ ） A ．30°B ．45°C ．150°D ．30°或150°5．已知在ABC △中，5AB =，4BC =，4cos 5B =，则cos A =（ ）A ．35B ．34CD ．256．如图，在ABC △中，π3ABC ∠=，E 为AB 边的中点，F 为BC 边上的点，且34BF BC =，2AB =，4BC =，则AC EF ⋅=（ ）A ．6B ．9C ．10D ．197．如图，在矩形ABCD 中，E 为AD 边上靠近点A 的三等分点，F 为AB 边上靠近点B 的四等分点，且线段EF 交AC 于点P ．若AB a =u u u r r ，AD b =u u u r r ，则AP =u u u r（ ）A ．3344a b +r rB ．331313a b +r rC ．51142a b +r rD ．19416a b +r r8．已知锐角ABC △中，角A ，B ，C 的对边分别为a ，b ，c ．若()2c o s c o sc o s 3s i nA B C B +=，a =r6bc =，则b c +=（ ）A ．9B ．8C ．5D ．4二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．9．已知向量()2,1a =r ，()2,4b =-r，则（ ）A．a =rB ．14a a b ⎛⎫+ ⎪⎝⎭∥r r rC ．a b ⊥r rD ．a b a b +=+r r r r10．下列说法中正确的有（A ．若AB u u u r 与CD u u ur 是共线向量，则点A ，B ，C ，D 必在同一条直线上B ．若向量()1,3a =r ，()1,3a b -=--r r ，则a b ∥r rC ．若平面上不共线的四点O ，A ，B ，C 满足320OA OB OC -+=u u u r u u u r u u u r，则2AB BC=u u u r u u u rD ．若非零向量a r ，b r 满足a b a b ==-r r r r ，则a r 与a b +r r 的夹角是π311．已知向量a r ，b r 的夹角为π6，3a =r ，1b =r ，t ∈R ，则（ ）A ．b r 在a r方向上的投影向量的模为2B．a +r 在a r方向上的投影向量的模为2C ．ta b +r r 的最小值为14D ．ta b +r r 取得最小值时，()a tab ⊥+r r r12．已知ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，且()sin sin sin sin a A B c C b B -=-，则下列说法正确的是（ ） A ．π6C =B ．若ABC △c 的最小值为2B ．若1a =，5π12B =，则ABC △的面积为38+D ．若3b =，c =ABC △有且仅有一个三、填空题：本题共4小题，每小题5分，共20分．13．已知向量()1,3a =-，(),0b x =，()2,1c =，若()c a b ⊥+，则实数x 的值为______．14．已知14AB BC =，且BA mAC =，则实数m =______． 15．如图所示，向量OA 与OB 的夹角为5π6，向量OP 与OB 的夹角为π6，2OA OP ==，4OB =，若OP mOA nOB =+，（m ，n ∈R ），则m n +=______．16．已知ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，π4A =，22222b a c =+，则sin C =______． 四、解答题：共70分．解答应写出文字说明，证明过程或演算步骤． 17．（10分）已知向量()1,2a =r ，()1,b t =r（t ∈R ）．（Ⅰ）若()()a b a b +-∥r r r r，求t 的值；（Ⅱ）若1t =，a r 与a mb +r r的夹角为锐角，求实数m 的取值范围．18．（12分）已知1e u r ，2e u u r 为单位向量，且1e u r ，2e u u r 的夹角为120°，向量122a e e =+r u r u u r ，21b e e =-r u u r u r ．（Ⅰ）求a b ⋅r r ；（Ⅱ）求a r 与b r的夹角．19．（12分）已知在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，sin2sin B B =． （Ⅰ）求B ；（Ⅱ）若a c >，且a c +=，证明：2a c =． 20．（12分）已知ABC △的外心为点O ，且()CO CA CB λ=+u u u r u u u r u u u r（λ∈R ），P 为边AB 的中点．（Ⅰ）求证：CP AB ⊥； （Ⅱ）若514λ=，求ACB ∠的余弦值． 21．（12分）已知E 为ABC △内一点，F 为AC 边的中点．（Ⅰ）若30EA EB EC ++=u u u r u u u r u u u r ，求证：52BE BF =u u u r u u u r；（Ⅱ）若230EA EB EC ++=u u u r u u u r u u u r，EBC △，ABC △的面积分别为S '，S ，求证：6S S '=．22．（12分）如图，已知ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，222sin sin sin sin sin 3A CB A BC +-=-⋅．（Ⅰ）求B ；（Ⅱ）若2223a c c b ++=，152BA BC ⋅=-u u u r ，点D 在边AC 上，且BD u u u r 在BC u u u r 和BA u u u r 上的投影向量的模相等，求线段BD 的长．2022—2023学年高一年级阶段性测试（三）数学·答案一、单项选择题：本题共8小题，每小题5分，共40分． 1．答案 D命题意图 本题考查向量的线性运算．解析 PA BC BA PA AC PC +-=+=u u u r u u u r u u u r u u u r u u u r u u u r ．2．答案 B命题意图 本题考查向量的数量积运算．解析 由题意知π1cos 2332a b a b a a ⋅==⋅==r r r r rr ．3．答案 C命题意图 本题考查向量的坐标运算．解析 ∵a r 与b r 的方向相反，∴a b λ=r r （0λ<）．设(),a x y =r ，则()(),2,3x y λ=-，于是2,3.x y λλ=-⎧⎨=⎩由a =r 2252x y +=，即222491352λλλ+==，∴24λ=，∴2λ=-，∴()4,6a =-r ．4．答案 A命题意图 本题考查正弦定理．解析因为a =12b =，60B =︒，所以由正弦定理可得sin 12sin 122a BA b===，所以30A =︒或150°．因为b a >，所以B A >，所以30A =︒． 5．答案 A命题意图 本题考查余弦定理．解析 由余弦定理可得2222cos AC AB BC AB BC B =+-⋅⋅，解得3AC =，则在Rt ABC △中，3cos 5AC A AB ==． 6．答案 B命题意图 本题考查向量的数量积运算．解析 ()()()3142AC EF BC BA BF BE BC BA BC BA ⎛⎫⋅=-⋅-=-⋅- ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r223131512242424BC BA BC BA BC BA BA BC =-⋅-⋅+=-⋅+u u u r u u u r u u u r u u u r u u u r u u u r u uu r u u u r 5π5114cos 142494342BA BC =-⋅⋅=-⨯⨯⨯=u u u r u u u r ．7．答案 B命题意图 本题考查平面向量基本定理．解析 ∵E 为AD 边上靠近点A 的三等分点，F 为AB 边上靠近点B 的四等分点，∴13AE AD =u u u r u u u r ，34AF AB =u u u r u u u r ．设()433AP AC AB AD AF AE λλλ⎛⎫==+=+ ⎪⎝⎭u u u r u u u r u u u r u u u r u u ur u u u r ，∵E ，F ，P 三点共线，∴4313λλ+=，解得313λ=， 于是()()333131313AP AB AD AB AD a b λ=+=+=+u u u r u u u r u u u r u u u r u u u r r r． 8．答案 C命题意图 本题考查解三角形．解析 ∵()2cos cos cos A B C B +=，πA B C ++=，∴()2cos cos 2cos πA B A B B +--=，()2cos cos 2cos A B A B B -+=，∴2sin sin A B B =．∵ABC △为锐角三角形，∴sin 0B ≠，∴sin A =．而π0,2A ⎛⎫∈ ⎪⎝⎭，∴π3A =． 由余弦定理可得222π2cos 3a b c bc =+-，∴2276b c =+-，∴2213b c +=， 则5b c +====．二、多项选择题：本题共4小题，每小题5分，共20分．每小题全部选对的得5分，部分选对的得2分，有选错的得0分． 9．答案 AC命题意图 本题考查平面向量的模及向量垂直的定义．解析 因为()2,1a =r ，所以a =r 故A 正确；由题可知13,242a b ⎛⎫+= ⎪⎝⎭r r ，因为322102⨯-⨯≠，所以ar 与14a b +r r 不共线，故B 错误；因为()()2,12,40a b ⋅=⋅-=r r ，所以a b ⊥r r ，故C 正确；因为a r 与b r的方向不相同，所以a b a b +≠+r r r r，故D 错误．10．答案 BC命题意图 本题考查共线向量的定义及向量的运算．解析 AB u u u r 与CD u u ur 是共线向量，也可能是AB CD ∥，故A 错误；设(),b x y =r ，∵()1,3a =r ，()1,3a b -=--r r ，∴11,33,x y -=-⎧⎨-=-⎩解得2,6,x y =⎧⎨=⎩∴()2,6b =r ，又∵16320⨯-⨯=，∴a b ∥r r，故B 正确；由已知得()()220OA OB OC OB BA BC -+-=+=u u u r u u u r u u u r u u u r u u u r u u u r r ，∴2AB BC =u u u r u u u r，∴2AB BC=u u u ru u u r ，故C 正确；由()22a a b =-r r r 整理可得22b a b =⋅r r r ，设a r 与a b +r r的夹角是θ，则()22221322cos a a a a a ba ab θ+⋅+====⋅+r r r r r r r r r r ，∴a r 与a b +r r 的夹角是π6，故D 错误． 11．答案 ACD命题意图 本题考查平面向量的投影向量的定义、向量的模及向量垂直的定义．解析 因为b r 在a r方向上的投影向量的模为πcos 62b =r ，故A 正确；因为a +r 在a r方向上的投影向量的模为()22π331cos 9632a a a a a a+⨯⨯+⋅+⋅===r r r rr r，故B 错误；222222212921919264ta b t a ta b b tt t t t ⎛+=+⋅+=+⨯+=++=++ ⎝⎭r r r r r r，当t =ta b +r r 取得最小值14，此时()2990a ta b ta a b t ⎛⋅+=+⋅=+=⨯+= ⎝⎭r r r r r r ，所以()a tab ⊥+r r r ，故C ，D 正确． 12．答案 BC命题意图 本题考查解三角形．解析 ∵()sin sin sin sin a A B c C b B -=-，∴由正弦定理可得()22a abc b -=-，即222a b c ab +-=，由余弦定理可得2221cos 22a b c C ab +-==，∵0πC <<，∴π3C =，故A 错误；由题可知1sin 24ab C ==4ab =， 由余弦定理可得222222cos 24c a b ab C a b ab ab ab ab =+-=+-≥-==，∴2c ≥，当且仅当2a b ==时等号成立，故c 的最小值为2，故B 正确；由题可知π4A =，由正弦定理得sin sin a c A C =，∴sin sin 2a C c A ===， ∴ABC △的面积为115π3sin 122212448ac B +=⨯⨯=⨯=C 正确； 由余弦定理可得2222cos c a b ab C =+-，即2793a a =+-，3320a a -+=，解得1a =或2a =，故D 错误．三、填空题：本题共4小题，每小题5分，共20分． 13．答案 12-命题意图 本题考查向量的坐标运算．解析 由题可知()1,3a b x +=-r r ，由()c a b ⊥+r r r 知210x +=，∴12x =-．14．答案 15-命题意图 本题考查向量的运算．解析 ∵()1144BA AB BC BA AC =-=-=-+u u u r u u u r u u u r u u u r u u u r ，∴15BA AC mAC =-=u u u r u u u r u u u r ，∴15m =-．15．答案12+命题意图 本题考查向量的运算．解析 以O 为坐标原点，OB 所在直线为x 轴，垂直于OB 且向上的方向为y 轴建立平面直角坐标系，则()4,0B ．设()11,P x y ，()22,A x y，于是1π2cos6x ==1π2sin 16y ==，且25π2cos 6x ==25π2sin 16y ==．由OP mOA nOB =+u u u r u u u r u u u r得)()()4,0m n =+，∴4,1,n m =+=⎪⎩解得1,2m n =⎧⎪⎨=⎪⎩∴1m n +=+． 16．答案5命题意图 本题考查正弦定理与余弦定理的应用．解析 由22222b a c =+得2222c a b =-，而π4A =，由余弦定理可得2222cos a b c bc A =+-，即22222c b b c -=+，整理可得b =．所以222222952828c c a b c c =-=-=，于是a c =正弦定理可得sin sin a A c C ==πsin 5C ==．四、解答题：共70分．解答应写出文字说明，证明过程或演算步骤． 17．命题意图 本题考查平面向量共线及向量的夹角的定义．解析 （Ⅰ）由题可知()()()1,21,2,2a b t t +=+=+r r，()()()1,21,0,2a b t t -=-=-r r．∵()()a b a b +-∥r r r r ，∴()220t -=，∴2t =．（Ⅱ）若1t =，则()1,1b =r，()1,2a mb m m +=++r r ．∵a r 与a mb +r r的夹角为锐角，∴()0a a mb ⋅+>r r r ，且a r 与a mb +r r 不共线，∴()()1220,212,m m m m +++>⎧⎪⎨+≠+⎪⎩解得53m >-且0m ≠，∴m 的取值范围是()5,00,3⎛⎫-⋃+∞ ⎪⎝⎭．18．命题意图 本题考查向量的数量积及夹角的求解．解析 （Ⅰ）∵1e u r ，2e u u r 为单位向量，且1e u r ，2e u u r的夹角为120°，∴12111cos1202e e ⋅=⨯⨯︒=-u r u u r ．∴()()12212a b e e e e ⋅=+⋅-r r u r u u r u u r u r 1221221e e e e =⋅-+--u r u u r u u r u r 1312122=--++=-．（Ⅱ）设a r 与b r的夹角为θ．∵a ====rb ====r∴31cos 22a b a bθ⋅==-⨯=-⋅r rr r ．又∵[]0,180θ∈︒︒，∴120θ=︒，∴a r 与b r 的夹角为120°． 19．命题意图解析 （Ⅰ）因为sin2sin B B =，即2sin cos sin B B B =， 所以1cos 2B =．因为()0,πB ∈，所以π3B =． （Ⅱ）由余弦定理得222cos 2a c b B ac +-=，所以222122a c b ac+-=，即222ac a c b =+-．①因为a c +=，所以b =．② 将②代入①，得()2222123ac a c a ac c =+-++， 整理得()()220a c a c --=．因为a c >，所以2a c =． 20．命题意图 本题考查向量的运算． 解析 （Ⅰ）如图，连接OB ，OC ，OP ，CP ．∵ABC △的外心为点O ，P 为边AB 的中点，∴OP AB ⊥．∵2CA CB CP +=u u u r u u u r u u u r，∴()2CO CA CB CP λλ=+=u u u r u u u r u u u r u u u r ，∴C ，O ，P 三点共线，∴CP AB ⊥． （Ⅱ）由（Ⅰ）知CP AB ⊥．又P 为边AB 的中点，∴CA CB =，∴PCA PCB ∠=∠．∵OB OC =，∴PCB OBC ∠=∠，∴2POB PCB ACB ∠=∠=∠．∵cos OP OP POB OB OC ∠==，514λ=，∴()5577CO CP CO OP ==+u u u r u u u r u u u r u u u r ， ∴2577CO OP =u u u r u u u r ，即25CO OP =u u u r u u u r ，∴25OP OC =，即2cos 5ACB ∠=． 21．命题意图 本题考查向量的运算．解析 （Ⅰ）∵30EA EB EC ++=u u u r u u u r u u u r r ，∴3EA EC EB +=-u u u r u u u r u u u r ． 又F 为AC 边的中点，∴233EF EB BE =-=u u u r u u u r u u u r．∵BE EF BF +=u u u r u u u r u u u r，∴32BE BE BF +=u u u r u u u r u u u r ，∴52BE BF =u u u r u u u r ．（Ⅱ）如图，设BC 边的中点为P EF ，EP ．∵230EA EB EC ++=u u u r u u u r u u u r r，∴()2EA EC EB EC +=-+u u u r u u u r u u u r u u u r ，∴24EF EP =-u u u r u u u r ，即2EF EP =-u u u r u u u r，∴F ，E ，P 三点共线．设点E ，F 到BC 的距离分别为1d ，2d ，则12:1:3d d =． 设点A 到BC 的距离为3d ．∵F 是AC 的中点，∴23:1:2d d =， ∴13:1:6d d =，∴13::1:6S S d d '==，即6S S '=． 22．命题意图 本题考查解三角形．解析（Ⅰ）∵222sin sin sin sin sin 3A CB A BC +-=-，∴由正弦定理可得222sin 3a cb ac B +-=-． 由余弦定理可得222cos 2a c b B ac+-=，∴2cos sin 3ac B B =-，即tan B =()0,πB ∈，∴2π3B =． （Ⅱ）由（Ⅰ）知2π3ABC ∠=， ∴2222cos ac ABC ac a c b ∠==-=+-．又2223a c c b ++=，∴()22223ac a c a c c -=+-++，解得3a =．∵152BA BC ⋅=-u u u r u u u r ， ∴15cos 22ac ac ABC ∠=-=-，可得5c =． 由2223a c c b ++=可得292515b ++=，解得7b =．∵BD u u u r 在BC u u u r 和BA u u u r 上的投影向量的模相等，∴BD 为ABC ∠的平分线． 由角平分线的性质知AD c b AD a=-， 即573AD AD =-，解得358AD =． 在ABC △中，由正弦定理可得sin sin a b A ABC ==∠，∴sin 14A =． 在ABD △中，π3ABD ∠=， 由正弦定理可得sin sin BD AD A ABD =∠35=，解得158BD =．。

2023-2024学年河南省联考高一下册阶段性测试（三）数学试题一、单选题1．PA BC BA +-=（）A ．PBB ．CPC ．ACD ．PC【正确答案】D【分析】根据平面向量的线性运算法则，即可求解.【详解】根据向量的线性运算法则，可得PA BC BA PA AC PC +-=+=.故选：D.2．已知向量a ，b 的夹角为π3，3a b ⋅=，2b = ，则a = （）A ．2B ．3C ．6D ．12【正确答案】B【分析】直接利用向量的数量积运算即可求解．【详解】依题意，π1cos 2332a b a b a a ⋅=⋅⋅=⋅⋅==.故选：B.3．已知向量a 与b 的方向相反，()2,3b =-r ，a =，则a = （）A ．()6,4-B ．()4,6-C ．()4,6-D ．()6,4-【正确答案】C【分析】根据共线定理，可得两向量的数乘关系，设出向量坐标，建立方程，可得答案.【详解】∵a 与b的方向相反，∴a b λ= （0λ<）．设(),a x y = ，则()(),2,3x y λ=-，于是2,3.x y λλ=-⎧⎨=⎩由a = ，得2252x y +=，即222491352λλλ+==，∴24λ=，∴2λ=-，∴()4,6a =-．故选：C.4．已知ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，a =，12b =，60B =︒，则A =（）A ．30°B ．45°C ．150°D ．30°或150°【正确答案】A【分析】运用正弦定理，结合三角形大边对大角的性质进行求解即可.【详解】因为a =12b =，60B =︒，所以由正弦定理可得sin 12sin 122a B A b===，所以30A =︒或150°．因为b a >，所以B A >，所以30A =︒．故选：A5．已知在ABC 中，5AB =，4BC =，4cos 5B =，则cos A =（）A ．35B ．34C ．2D ．25【正确答案】A【分析】直接利用余弦定理可解得3AC =，由此可知ABC 为直角三角形，所以3cos 5AC A AB ==.【详解】由余弦定理可得2222cos AC AB BC AB BC B =+-⋅⋅，解得3AC =，所以222AB AC BC =+，所以ABC 为直角三角形，则在Rt ABC △中，3cos 5AC A AB ==．故选：A.6．如图，在ABC 中，π3ABC ∠=，E 为AB 边的中点，F 为BC 边上的点，且34BF BC = ，2AB =，4BC =，则AC EF ⋅=（）A ．6B ．9C ．10D ．19【正确答案】B【分析】运用向量运算法则将AC EF ⋅ 转化为51224AC EF BA BC ⋅-⋅+=，再代入向量数量积公式πcos 3BA BC BA BC ⋅⋅⋅= 即可求解.【详解】依题意，()()()3142AC EF BC BA BF BE BC BA BC BA ⎛⎫⋅=-⋅-=-⋅- ⎪⎝⎭223131512242424BC BA BC BA BC BA BA BC =-⋅-⋅+=-⋅+5π5114cos 142494342BA BC =-⋅⋅=-⨯⨯⨯= ．故选：B.7．如图，在矩形ABCD 中，E 为AD 边上靠近点A 的三等分点，F 为AB 边上靠近点B 的四等分点，且线段EF 交AC 于点P ．若AB a=，AD b = ，则AP = （）A ．3344a b+ B ．331313a b+C ．51142a b+ D ．19416a b+ 【正确答案】B【分析】AP AC λ= ，将AP 用,AE AF表示，再根据E ，F ，P 三点共线，求得λ，从而可的答案.【详解】∵E 为AD 边上靠近点A 的三等分点，F 为AB 边上靠近点B 的四等分点，∴13AE AD = ，34AF AB = ，设()433AP AC AB AD AF AE λλλ⎛⎫==+=+ ⎪⎝⎭ ，∵E ，F ，P 三点共线，∴4313λλ+=，解得313λ=，于是()()333131313AP AB AD AB AD a b λ=+=+=+ ．故选：B.8．已知锐角ABC 中，角A ，B ，C 的对边分别为a ，b ，c ．若()2cos cos cos A B C B +=，a =6bc =，则bc +=（）A ．9B ．8C ．5D ．4【正确答案】C【分析】利用诱导公式、两角和的余弦公式化简已知条件，求得A ，利用余弦定理求得b c +.【详解】∵()2cos cos cos A B C B +=，πA B C ++=，∴()2cos cos 2cos πA B A B B +--，()2cos cos 2cos A B A B B -+=，∴2sin sin A B B =．∵ABC 为锐角三角形，∴sin 0B ≠，∴sin A =π0,2A ⎛⎫∈ ⎪⎝⎭，∴π3A =．由余弦定理可得222π2cos 3a b c bc =+-，∴2276b c =+-，∴2213b c +=，则5b c +===．故选：C二、多选题9．已知向量()()2,1,2,4a b ==-，则（）A ．aB ．1//()4a ab + C ．a b⊥ D ．a b a b+=+ 【正确答案】AC【分析】根据平面向量的坐标表示与运算，结合向量的平行坐标表示和数量积的坐标运算公式，逐项判定，即可求解.【详解】由()2,1a =r，可得a = A 正确；由()()2,1,2,4a b ==- ，可得13(,2)42a b += ，因为322102⨯-⨯≠，所以a 与14a b + 不共线，所以B 错误；由2(2)140a b ⋅=⨯-+⨯=r r ，所以a b ⊥，故C 正确；由()()2,1,2,4a b ==- ，可得241(2)0⨯-⨯-≠，可得a 与b的方向不相同，所以a b a b +≠+ ，故D 错误．故选：AC.10．下列说法中正确的有（）A ．若AB与CD 是共线向量，则点A ，B ，C ，D 必在同一条直线上B ．若向量()1,3a = ，()1,3a b -=--，则a b ∥C ．若平面上不共线的四点O ，A ，B ，C 满足320OA OB OC -+=，则2AB BC=D ．若非零向量a ，b 满足a b a b ==- ，则a 与a b + 的夹角是π3【正确答案】BC【分析】对于A ，根据向量共线的定义，可得其正误；对于B ，利用向量共线定理，可得其正误；对于C ，根据向量减法，结合共线定理，可得其正误；对于D ，根据向量模的求解以及夹角公式，可得答案.【详解】AB与CD 是共线向量，也可能是AB CD ，故A 错误；设(),b x y = ，∵()1,3a = ，()1,3a b -=--，∴11,33,x y -=-⎧⎨-=-⎩解得2,6,x y =⎧⎨=⎩∴()2,6b = ，又∵16320⨯-⨯=，∴a b∥，故B 正确；由已知得()()220OA OB OC OB BA BC -+-=+= ，∴2AB BC =，∴2AB BC= ，故C 正确；由()22a a b =- 整理可得22b a b =⋅，设a 与a b + 的夹角是θ，则()2221322cos 2a b a a a b a a b θ+⋅+====⋅+ ，∴a 与a b + 的夹角是π6，故D 错误．故选：BC.11．已知向量a ，b 的夹角为π6，3a = ，1b = ，t R ∈，则（）A ．b 在a 方向上的投影向量的模为2B ．a在a方向上的投影向量的模为2C ．ta b + 的最小值为14D ．ta b + 取得最小值时，()a ta b⊥+【正确答案】AD【分析】AB 选项，利用投影的定义求解判断；CD 选项，利用数量积的运算律求解判断.【详解】因为b 在a方向上的投影向量的模为πcos 62b = ，故A 正确；因为a在a 方向上的投影向量的模为()22π331cos 9632a a a a a a +⨯⨯⋅⋅===，故B错误；2222222129219319264ta b t a ta b b t t t t ⎛+=+⋅+=+⨯+=+=++ ⎝⎭，当t =ta b + 取得最小值12，此时()2990262a ta b ta a b t ⎛⋅+=+⋅=+=⨯-+= ⎝⎭，所以()a tab ⊥+，故C 错误，D 正确．故选：AD12．已知ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且()sin sin sin sin a A B c C b B -=-，则下列说法正确的是（）A ．π6C =B ．若ABCc 的最小值为2C ．若1a =，5π12B =，则ABC的面积为38D ．若3b =，c =ABC 有且仅有一个【正确答案】BC【分析】由正、余弦定理及已知得π3C =，再根据选项综合应用正、余弦定理和三角形面积公式求解．【详解】∵()sin sin sin sin a A B c C b B -=-，∴由正弦定理可得22()a a b c b -=-，即222a b c ab +-=，对于A 选项，由余弦定理可得2221cos 22a b c C ab +-==，∵0πC <<，∴π3C =，故A 错误；对于B选项，由题可知1sin 24ab C ab =4ab =，由余弦定理可得222222cos 24c a b ab C a b ab ab ab ab =+-=+-≥-==，∴2c ≥，当且仅当2a b ==时等号成立，故c 的最小值为2，故B 正确；对于C 选项，由题可知π4A =，由正弦定理得sin sin a c A C =，∴sin sin 2a C c A ==∴ABC的面积为115πππsin 1221246ac B =⨯=+=故C 正确；对于D 选项，由余弦定理可得2222cos c a b ab C =+-，即2793a a =+-，2320a a -+=，解得1a =或2a =，故D 错误．故选：BC ．三、填空题13．已知向量()1,3a =- ，(),0b x =，()2,1c = ，若()c a b ⊥+ ，则实数x 的值为______．【正确答案】12-##0.5-【分析】利用平面向量的坐标运算，结合向量垂直的坐标表示求解作答.【详解】因为向量()1,3a =- ，(),0b x = ，则()1,3a b x +=-，又()2,1c = ，且()c a b ⊥+ ，因此2(1)30x -+=，解得12x =-，所以实数x 的值为12-.故12-14．已知14AB BC = ，且BA mAC = ，则实数m =______．【正确答案】15-##-0.2【分析】利用平面向量的线性运算求解.【详解】解：∵()1144BA AB BC BA AC =-=-=-+，∴15BA AC m AC =-= ，∴15m =-．故15-15．如图所示，向量OA 与OB 的夹角为5π6，向量OP 与OB 的夹角为π6，2OA OP == ，4OB = ，若OP mOA nOB =+ ，（m ，n R ∈），则m n +=______．【正确答案】312+【分析】建立直角坐标系，利用共线向量坐标表达公式进行求解即可.【详解】以O 为坐标原点，OB 所在直线为x 轴，垂直于OB 且向上的方向为y 轴建立平面直角坐标系，则()4,0B ．设()11,P x y ，()22,A x y ，于是1π2cos 36x ==，1π2sin 16y ==，且25π2cos36x ==-，25π2sin 16y ==．由OP mOA nOB =+得()()()3,13,14,0m n =-+，∴334,1,m n m ⎧=-+⎪⎨=⎪⎩解得1,3,2m n =⎧⎪⎨=⎪⎩∴312m n +=+．故312+16．已知ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，π4A =，22222b a c =+，则sin C =______．25【分析】综合运用正、余弦定理求解即可．【详解】由22222b a c =+得2222c a b =-，而π4A =，由余弦定理可得222222cos 2a b c bc A b c bc =+-=+，即22222c b b c -=+-，整理可得b =，所以222222952828c c a b c c =-=-=，于是a c =由正弦定理可得sinsin a A c C ==πsin sin 45C =，．四、解答题17．已知向量()1,2a =r，()1,b t = （R t ∈）．(1)若()()a b a b +-，求t 的值；(2)若1t =，a与a mb + 的夹角为锐角，求实数m 的取值范围．【正确答案】(1)2t =(2)()5,00,3⎛⎫-⋃+∞ ⎪⎝⎭【分析】（1）根据平面向量共线的坐标表示即可求t 值；（2）根据平面向量夹角的定义及其坐标表示即可求m 的取值范围．【详解】（1）由题可知(1,2)(1,)(2,2)a b t t +=+=+ ，(1,2)(1,)(0,2)a b t t -=-=-∵()()a b a b +- ，∴2(2)0t -=，∴2t =．（2）若1t =，则()1,1b = ，(1,2)a mb m m +=++ ，∵a与a mb + 的夹角为锐角，∴()0a a mb ⋅+> ，且a与a mb + 不共线，∴12(2)02(1)2m m m m+++>⎧⎨+≠+⎩，解得53m >-且0m ≠，∴m 的取值范围是()5,00,3⎛⎫-⋃+∞ ⎪⎝⎭．18．已知1e ，2e 为单位向量，且1e ，2e 的夹角为120°，向量122a e e =+ ，21b e e =-．(1)求a b ⋅ ；(2)求a 与b的夹角．【正确答案】(1)32-(2)23π【分析】（1）利用平面向量的数量积的运算律求解；（2）先求得a b ，，再利用夹角公式cos a b a bθ⋅=⋅求解.【详解】（1）解：∵1e ，2e 为单位向量，且1e ，2e的夹角为120°，∴12111cos1202e e ⋅=⨯⨯︒=- ．∴()()1221122113222112122a b e e e e e e e e ⋅=+⋅-=⋅-+-⋅=--++=-．（2）设a 与b的夹角为θ．∵a===b ==== ∴31cos 22a b a bθ⋅==-=-⋅ ．又∵[]0,θπ∈，∴23πθ=，∴a 与b 的夹角为23π．19．已知在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，sin 2sin B B =．(1)求B ；(2)若a c >，且a c +=，证明：2a c =．【正确答案】(1)π3B =(2)证明见解析【分析】（1）由正弦二倍角公式进行求解即可；（2）根据余弦定理，结合已知进行运算证明即可.【详解】（1）因为sin 2sin B B =，即2sin cos sin B B B =，所以1cos 2B =．因为()0,πB ∈，所以π3B =；（2）由余弦定理得222cos 2a c b B ac+-=，所以222122a c b ac +-=，即222ac a c b =+-．①因为a c +=，所以b =将②代入①，得()2222123ac a c a ac c =+-++，整理得()()220a c a c --=．因为a c >，所以2a c =．20．已知ABC 的外心为点O ，且()CO CA CB λ=+ （R λ∈），P 为边AB 的中点．(1)求证：CP AB ⊥；(2)若514λ=，求ACB ∠的余弦值．【正确答案】(1)证明见及解析(2)25【分析】（1）连接OB ，OC ，OP ，CP ，由ABC 的外心为点O ，P 为边AB 的中点，得到OP AB ⊥，再由()CO CA CB λ=+ ，得到C ，O ，P 三点共线即可；（2）由（1）知CP AB ⊥，P 为边AB 的中点，得到CA CB =，结合OB OC =，得到2POB PCB ACB ∠=∠=∠．再由cos OP OP POB OB OC∠==，514λ=求解.【详解】（1）如图，连接OB ，OC ，OP ，CP ．∵ABC 的外心为点O ，P 为边AB 的中点，∴OP AB ⊥．∵2CA CB CP += ，∴()2CO CA CB CP λλ=+= ，∴C ，O ，P 三点共线，∴CP AB ⊥．（2）由（1）知CP AB ⊥．又P 为边AB 的中点，∴CA CB =，∴PCA PCB ∠=∠．∵OB OC =，∴PCB OBC ∠=∠，∴2POB PCB ACB ∠=∠=∠．∵cos OP OP POB OB OC∠==，514λ=，∴()5577CO CP CO OP ==+ ，∴2577CO OP = ，即25CO OP = ，∴25OP OC =，即2cos 5ACB ∠=．21．已知E 为ABC 内一点，F 为AC 边的中点．(1)若30EA EB EC ++= ，求证：52BE BF = ；(2)若230EA EB EC ++= ，EBC ，ABC 的面积分别为S '，S ，求证：6S S ='．【正确答案】(1)证明见解析(2)证明见解析【分析】（1）利用平面向量的加减数乘运算的几何意义，结合三角形中几何性质，可得答案；（2）利用三角形线段的比例关系，结合三角形面积的等积变换，可得答案.【详解】（1）∵30EA EB EC ++= ，∴3EA EC EB +=- ．又F 为AC 边的中点，∴233EF EB BE =-= ．∵BE EF BF += ，∴32BE BE BF += ，∴52BE BF = ．（2）如图，设BC 边的中点为P ，连接EF ，EP ．∵230EA EB EC ++= ，∴()2EA EC EB EC +=-+ ，∴24EF EP =- ，即2EF EP =- ，∴F ，E ，P 三点共线．设点E ，F 到BC 的距离分别为1d ，2d ，则12:1:3d d =．设点A 到BC 的距离为3d ．∵F 是AC 的中点，∴23:1:2d d =，∴13:1:6d d =，∴13::1:6S S d d =='，即6S S ='．22．如图，已知ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，222sin sin sin sin sin sin 3A CB A BC +-=-⋅．(1)求B ；(2)若2223a c c b ++=，152BA BC ⋅=- ，点D 在边AC 上，且BD 在BC 和BA 上的投影向量的模相等，求线段BD 的长．【正确答案】(1)2π3B =(2)158【分析】（1）综合运用正、余弦定理即可求解；（2）由（1）及已知可求得5c =，7b =，又由BD 在BC 和BA 上的投影向量的模相等，知BD 为ABC ∠的平分线，由角平分线定理得358AD =，再在ABC 和ABD △中应用正弦定理求解即可．【详解】（1）∵222sin sin sin sin sin sin 3A B C A C B -+-=，∴由正弦定理可222sin a c b B =+-，由余弦定理可得222cos 2a c b B ac+-=，∴2cos s 3ac B ac inB =-即tan B =，∵()0,πB ∈，∴2π3B =．（2）由（1）知2π3ABC ∠=，∴2222cos ac ABC ac a c b ∠=-=+-又2223a c c b ++=，∴2222(3)ac a c a c c -=+-++，解得3a =．∵152BA BC ⋅=- ，∴15cos 22ac ac ABC ∠=-=-，可得5c =，由2223a c c b ++=可得292515b ++=212559b ++=，解得7b =．∵BD 在BC 和BA 上的投影向量的模相等，∴BD 为ABC ∠的平分线，由角平分线的性质知AD c b AD a =-，即573AD AD =-，解得358AD =，在ABC中，由正弦定理可得sin sin a b A ABC ==∠，∴sin A =在ABD △中，π3ABD ∠=，由正弦定理可得sin sin BD AD A ABD =∠358142=158BD =．。

阶段性测试答案一、单选题1.对于无法查明原因的现金短款，经过批准后应计入（A ）。

A.管理费用B.财务费用C.营业外支出D.其他应收款2.下列各项中，不通过“其他应收款”科目核算的是（C ）。

A.为职工垫付的房租B.应收保险公司赔款C.应向购货方收取的代垫运费D.存出保证金3.根据我国准则规定，存在现金折旧的情况下，应收账款入账价值应采用（D ）。

A.直接法B.间接法C.净价法D.总价法4.对银行已经入账，企业尚未入账的未达账项，企业编制银行存款余额调节表后，一般应当（D ）。

A.根据银行存款余额调节表进行账务处理B.根据银行对账单上的记录进行账务处理C.根据对账单和调节表自制凭证进行账务处理D.待结算凭证到达后再进行账务处理5.下列不属于未达账项的是（D ）。

A.开户单位已收、银行未收的账项B.开户单位已付，银行未付的账项C.银行已收、开户单位未收的账项D.银行已付，开户单位已付的账项6.某企业销售一批商品，增值税专用发票注明的价款为60万元，适用的增值税税率为17%，为购买方代垫的运杂费为2万元，款项尚未收回，则企业确认的应收账款为（ C ）。

A.60万元B.70.2万元C.72.2万元D.62万7.企业发生的下列各项内容中，不通过“其他货币资金”科目核算的是（B ）。

A.存出投资款B.备用金C.银行本票存款D.银行汇票存款8.某企业在2014年10月8日销售商品100件，增值税专用发票上注明的价款为50000元，增值税税额为8500元，企业为了及早收回货款而在合同中规定的现金折扣条件为2/10，1/20，N/30，假定计算现金折扣时不考虑增值税。

如果买方在2014年10月24日付清款项，该企业实际收款金额为（D ）元。

A.57330B.57500C.57915D.580009.以下各项中，不属于货币资金的是（D ）。

A.库存现金B.银行存款C.其他货币资金D.应收票据10.企业存放在银行的银行本票存款，应通过（A ）科目核算。

哈三中2022—2023学年度上学期高三阶段性测试数学试卷考试时间：120分钟试卷满分：150分注意事项：1．答题前，考生务必将自己的姓名、考生号、座位号填写在答题卡上．2．作答时，将答案写在答题卡上．写在本试卷上无效．3．考试结束后，将本试卷和答题卡一并交回．一、选择题（共60分）（一）单项选择题（共8小题，每小题5分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合{}{}1)1(log |,21|2<-=<<-=x x B x x A ，则=B A A ．{}21|<<-x x B ．{}|02x x <<C ．{}|13x x <<D ．{}|12x x <<2．已知向量=a (,2)m ，=b (2,1)，若()+⊥a b b ，则m =A ．8-B ．7-C ．72-D ．43．已知5s 6in 3)(πα+=，则)sin(256απ+=A ．725-B ．725C ．35D ．24254．南宋数学家在《详解九章算法》和《算法通变本末》中提出了一些新的垛积公式，所讨论的高阶等差数列与一般等差数列不同，高阶等差数列中前后两项之差并不相等，但是逐项差数之差或者高次差成等差数列．现有高阶等差数列，其前7项分别为1，2，4，7，11，16，22，则该数列的第20项为A ．172B ．183C ．191D ．2115．在正方体1111ABCD A B C D -中，E 为11B C 中点，过1,,A D E 的截面α与平面11AA B B 的交线为l ，则异面直线l 与1B C 所成角的余弦值为A．10B．5C．5D．56．若函数12log ()4,20()(01)1,2x x x f x a a a x -+-≤<⎧⎪=>≠⎨⎪-<-⎩且的值域是[3,)+∞，则实数a 的取值范围是A ．1(0,2B ．1[,1)2C ．(1,2]D ．[2,)+∞7．在ABC ∆中，角,,A B C 的对边分别为,,a b c ，若i sin1s n ,2A Cb a A b +==，则ABC ∆面积的最大值为A ．2B ．4C ．6D ．128．已知函数()f x 的定义域为R ，且(2)2()f x f x +=-，(23)f x -为偶函数，若(0)0f =，1()123nk f k ==∑，则n 的值为A ．117B ．118C ．122D ．123（二）多项选择题（共4小题，每小题5分．在每小题给出的四个选项中，有多项符合题目要求，全部选对得5分，部分选对得2分，有选错的得0分）9．已知n m ,是两条不同的直线，γβα，，是三个不同的平面，则下列说法不正确的是A ．若n m n m ⊥⊥⊥,,βα，则βα⊥B ．若γβγα⊥⊥，，则βα//C ．若,m αβα⊥⊥，则//m βD ．若γβα，，两两相交，则交线互相平行10．已知函数2c s )2(o 1f x x x ωω+=-的最小正周期为π，则下列说法正确的是A ．3x π=-为()f x 的极小值点B ．()f x 的图象关于(,0)2π-中心对称C ．()f x 在[,]ππ-上有且仅有5个零点D ．lg ()y f x =的定义域为,3{}x k Z x k k πππ<<+∈11．如图，在平行四边形ABCD 中，︒=∠==60,2,1A AD AB ,F E ,分别为AD AB ,的中点，沿EF 将AEF ∆折起到A EF '∆的位置（A '不在平面ABCD 上），在折起过程中，下列说法不正确的是A ．若M 是D A '的中点，则//BM 平面EF A 'B ．存在某位置，使CA BD '⊥C ．当二面角B EF A --'为直二面角时，三棱锥BDE A -'外接球的表面积为72πD ．直线C A '和平面ABCD 所成的角的最大值为6π12．已知函数()ln f x x ax =-，则下列说法正确的是A ．若()0f x ≤恒成立，则1a ≥B ．当0a <时，()y f x =的零点只有1个FME'A DCB AC ．若函数()y f x =有两个不同的零点12,x x ，则212x x e>D ．当1a =时，若不等式2ln ()xme m f x +≥恒成立，则正数m 的取值范围是1[,)e+∞二、填空题：本题共4小题，每小题5分，共20分．13．在等比数列{}n a 中，1232a a a ++=，4564a a a ++=，则101112a a a ++=．14．已知0,0a b >>，且2a b ab +=，则1912a b +--的最小值是．15．在ABC ∆中，13,34A C D AB A AE ==，BE 与DC 交于点F ，若AF AB AC λμ=+，则λμ+的值为．16．在三棱锥P ABC -中，二面角,P AB C P AC B P BC A------和的大小都为3π，5AB =，12BC =，13AC =，则三棱锥P ABC -的外接球与内切球的表面积的比值为．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．17．（本题满分10分）在ABC ∆中，设角,,A B C 的对边分别为,,a b c ，且2sin tan b A c C =．（1）求222a b c +；（2）求角C 的最大值．18．（本题满分12分）如图，在四棱锥ABCD P -中，底面ABCD 是梯形，//,90CD AB ABC ∠=︒，4=AB ，2==CD BC ，侧面⊥P AD 底面ABCD ，2==PD P A ，E 为P A 中点．（1）求证：//DE 平面PBC ；（2）求直线BD 和平面PBC 所成角的正弦值．DCBAEP19．（本题满分12分）已知等比数列{}n a 的公比1q >，且23414a a a ++=，31a +是2a ，4a 的等差中项，数列{}n b 满足：数列{}n n a b ⋅的前n 项和为2n n ⋅．（1）求数列{}n a 、{}n b 的通项公式；（2）若n n n c a b =+，11n n n n a d c c ++=，求数列{}n d 的前n 项和n S ．20．（本题满分12分）如图，经过村庄A 有两条夹角为60︒的公路AB ，AC ，根据规划，在两条公路之间的区域内建一工厂P ，分别在两条公路边上建两个仓库M ，N （异于村庄A ），要求1PM PN MN ===（单位：km ）．（1）当30AMN ∠=︒时，求线段AP 的长度；（2）设AMN θ∠=，当θ取何值时，工厂产生的噪音对居民的影响最小？（即工厂与村庄的距离最远）PNM CBA21．（本题满分12分）如图，在三棱柱111ABC A B C -中，1AB C ∆为等边三角形，四边形11AA B B 为菱形，AC BC ⊥，4AC =，3BC =．（1）求证：11AB A C ⊥；（2）线段1CC 上是否存在一点E ，使得平面1AB E 与平面ABC 的夹角的余弦值为14？若存在，求出点E 的位置；若不存在，请说明理由．22．（本题满分12分）已知函数()e 1xf x ax =--．（1）讨论函数()f x 的单调性；E 1C 1B 1A CBA（2）若函数()f x 有且只有一个零点，求实数a 的取值范围；（3）()0,x ∀∈+∞，关于x 的不等式12ln 2x e x tx x x -+≥+恒成立，求正实数t 的取值范围．哈三中2022—2023学年度上学期高三学年期中考试数学试卷答案一、选择题：题号123456789101112答案DCBCAABCBCDACDABDBC二、填空题：13.1614.15.7916.1394三、解答题：17.（1）222222222cos ,,2a b ab C c a b c c c+=+-==（2）222222144co 2s 2a b c a b ab a C a b ab b +-=≥==+max (0,),,33C C C πππ≤=∈18.（1）取PB 中点F ，连接CF EF ,，因为E 为P A 中点，所以EF AB EF ,//又AB CD AB CD 21,//=，所以CD EF CD EF =,//，所以CDEF 为平行四边形，所以DE //又PBC CF PBC DE 平面平面⊂⊄,所以PBCDE 平面//（2）以D 为原点，DA 为x 轴，DB 为y 轴建立空间直角坐标系，则0DB = ），平面PBC 的法向量(1,1,3)=--n ，所以BD 和平面PBC 所成角的正弦值为111119.（1）由23414a a a ++=，31a +是2a ，4a 的等差中项，可得()2343241421a a a a a a ++=⎧⎨+=+⎩，即324410a a a =⎧⎨+=⎩，即4410q q +=，解得2q =或12q =，又因为1q >，所以2q =，又由3121a a q==，所以1112n n n a a q --==，因为数列{}n n a b ⋅的前n 项和为2n n ⋅，当1n =时，111122a b =⨯=，当2n ≥时，112(1)2(1)2n n n n n a b n n n --=⋅--⋅=+⋅，当1n =时，112a b =满足上式，所以1(1)2n n n a b n -=+⋅，所以11(1)212n n n n b n --+⋅==+.（2）112,n n n n c a b n -=+=++11111n n n n n n a d c c c c +++==-，111111322n nn S c c n +=-=-++.20.（1）30,602,3,31AMN MAN MN AM ∠=︒∠=︒==22271,90,,33PM AMP AP AM PM AP =∠=︒=+==（2）2,,)23sinsin()33MN AM AMN AM πθππθ∆==--在中在PAM ∆中，222422sin )21(n()cos )3333(AP πππθθθ--⨯-+=+54sin(2)336πθ=+-当262θππ-=，3πθ=时，max AP =∴当3πθ=时，工厂生产的噪音对居民的影响最小21.（1）连接1A B ，1111,AA B B AB A B∴⊥ 菱形11,,BC BC AC B C AB B B=== 1ABC B BC ∴∆≅∆，190B CB ACB ∴∠=∠=︒11,,AC BC B C BC AC B C C ⊥⊥= ，111,AC AB C B C AB C ⊂⊂平面平面1BC AB C∴⊥平面111,AB AB C AB BC⊂∴⊥ 平面又111111,,,AB A B A B BC B A B A BC BC A BC⊥=⊂⊂ 平面平面DzxE1C 1B 1A CBA11AB A BC ∴⊥平面，又1111,A C A BC AB A C⊂∴⊥ 平面（2）取AC 中点D ，连接1B D11,,BC AB C BC ABC AB C ABC⊥⊂∴⊥ 平面平面平面平面又11111,,,AB C B D AC B D AB C AB C ABC AC∆⊥⊂= 在等边中平面平面平面1B D ABC ∴⊥平面，以D 为原点，建立如图所示的空间直角坐标系，则1(0,2,0),(0,0,(3,2,0),(0,2,0)A B B C -，设11,[0,1],(3,22,)CE CC BB E λλλλλ==∈--则，设平面1AB E 的法向量1(,,)n x y z =，11(0,2,(3,2(1),))AB EB λλλ==--，11110AB n EB n ⎧⋅=⎪⎨⋅=⎪⎩，则1,3)n λλ=-- ，显然，平面ABC 的法向量2(0,0,1)n =，121cos ,4n n <>=14=，解得1222(),55CE CC λ=-∴= 或舍22.（1）'()x f x e a =-，当0a ≤时，()f x 在R 上单调递增，当0a >时，()f x 在(,ln )a -∞上单调递减，在(ln ,)a +∞上单调递增（2）当0a ≤时，(0)0f =，()f x 在R 上单调递增，()f x 有一个零点0当0a >时，()f x 在(,ln )a -∞上单调递减，在(ln ,)a +∞上单调递增，,(),,()x f x x f x →-∞→+∞→+∞→+∞时时，(ln )ln 10,1f a a a a a ∴=--=∴=，综上，01a a ≤=或（3）1ln 1ln 2ln ln 13x x x e t x x x x e x---≥+--=---+，0x ∀>恒成立，令ln 10m x x =--≥，则ln 3mt m e ≥-+，0m ∀≥恒成立，令()3mg m m e =-+，'()1m g m e =-，()g m 在(0,)+∞上单调递减，()(0)2g m g ∴≤=，ln 2t ∴≥，2t e ≥。