七年级数学下册第五章同步练习及标准答案

人教版七年级下册数学第五章测试题及答案仅供学习交流123（第三题）ABCD 1234（第2题）12345678（第4题）ab c七年级数学下册第五章测试题姓名 ________ 成绩 _______一、单项选择题（每小题3分，共 30 分） 1、如图所示，∠1和∠2是对顶角的是（ ）ABC D121212122、如图AB ∥CD 可以得到（ ）A 、∠1＝∠2B 、∠2＝∠3C 、∠1＝∠4D 、∠3＝∠43、直线AB 、CD 、EF 相交于O ，则∠1＋∠2＋∠3（ ）。

A 、90° B 、120° C 、180° D 、140°4、如图所示，直线a 、b 被直线c 所截，现给出下列四种条件： ①∠2＝∠6 ②∠2＝∠8 ③∠1＋∠4＝180° ④∠3＝∠8，其中能判 断是a ∥b 的条件的序号是（ ）A 、①②B 、①③C 、①④D 、③④5、某人在广场上练习驾驶汽车，两次拐弯后，行驶方向与原来相 同，这两次拐弯的角度可能是（ ）仅供学习交流ABCD（第7题）A 、第一次左拐30°，第二次右拐30°B 、第一次右拐50°，第二次左拐130°C 、第一次右拐50°，第二次右拐130°D 、第一次向左拐50°，第二次向左拐130° 6、下列哪个图形是由左图平移得到的（ ）BD7、如图，在一个有4×4个小正方形组成的正方形网格中，阴影 部分面积与正方形ABCD 面积的比是（ ） A 、3：4 B 、5：8 C 、9：16 D 、1：2 8、下列现象属于平移的是（ ）① 打气筒活塞的轮复运动，② 电梯的上下运动，③ 钟摆的摆动，④ 转动的门，⑤ 汽车在一条笔直的马路上行走 A 、③ B 、②③ C 、①②④ D 、①②⑤ 9、下列说法正确的是（ ）A 、有且只有一条直线与已知直线平行B 、垂直于同一条直线的两条直线互相垂直C 、从直线外一点到这条直线的垂线段，叫做这点到这仅供学习交流A B CDE (第10题)ABCDE F G H 第13题条直线的距离。

第五章相交线与平行线5.1.1 相交线复习检测（5分钟）：1、如图所示，/1和/2是对顶角的图形有（）A.1个B.2 个C.3 个D.4 个2、如图，若/ 1=60° ,那么/ 2=3、如图是一把剪刀，其中 1 40,则24、如图三条直线AB,CD,EF相交于一点O, /AOD勺对顶角是，/AOC勺邻补角是，若/ A0C=50 ,贝U/ BOD= ./ COB= J AOE+ DOB + COF=5、如图，直线AB,CD相交于0,0评分/ AOC若/ AOD/DOB=50 ,?求/EOB勺度数.6、如图，直线a,b,c两两相交，/1=2/ 3, / 2=68° ,求/4的度数5.1.2 垂线复习检测（5分钟）：1、两条直线互相垂直，则所有的邻补角都相等.（）2、一条直线不可能与两条相交直线都垂直.（）3、两条直线相交所成的四个角中，如果有三个角相等，那么这两条直线互相垂直.（）4、两条直线相交有一组对顶角互补，那么这两条直线互相垂直.（）.5、如图1,OAL OB,OCL OC,O为垂足，若/AOC=3 5,则/BOD=.6、如图2,A0± BO,O为垂足，直线CDi点O,且/ BOD=2AOC则/ BOD=.7、如图3,直线AB CD相交于点0,若/E0D=40 , /B0C=130，那么射线0E与直线AB的位置关系是C8、已知：如图，直线AB,射线0位于点的位置关系.9、如图,AC± BC,C为垂足,CD± AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6 ,那么点C 到AB 的距离是，点A 到BC 的距离是，点B 到CD 的距离是 ,A 、B 两点间的距离是.10、如图，在线段AB AG AD AE AF 中AD 最短.小明说垂线段最短，因此线段AD 的 长是点A 到BF 的距离，对小明的说法，你认为对吗？11、用三角尺画一个是30的/AOB 在边OA±任取一点P,过P 作POL OB,垂足为Q, 量一量OP 的长，你发现点P 到OB 的距离与OP 长的关系吗？5.1.3同位角、内错角、同旁内角3、如图（6）,直线DE 截AB, AC,构成八个角： ①、指出图中所有的同位角、内错角、同旁内角复习检测（5分钟）：1、如图（4）,卜列说法不正确的是（ ）人./1与/2是同位角 B. / 2与/ 3是同位角C. / 1与/ 3是同位角D. / 1与/ 4不是同位角2、如图（5）,直线AB CDM 直线EF 所g, / A 和一 错角，/A 班是同旁内角.^ /\ \ /--- ---------- 4 届 -------------------- R图⑷ 图⑸—是同位角，/ A 和 ________ 是内A40（3） c'②、/人与/5, /A 与/6, /A 与/8,分别是哪一条直线截哪两条直线而成的什么 角？4、如图（7）,在直角 ABCt\ / C= 90 , DU AC 于 E,交 A.一 L①、指出当BG DE 被AB 所截时，/ 3的同位角、内错角和礴内他（门②、若/ 3+/ 4=180试说明/ 1 = /2=/3的理由.5.2.1平行线复习检测（5分钟）：1、在同一平面内，两条直线的位置关系有2、两条直线L 1与L 2相交点A,如果L 1//L ,那么12与L （）3、在同一平面内，一条直线和两条平行线中一条直线相交，那么这条直线与平行线中的另一边必.D ./3=/4 D. /BACW ACD4、两条直线相交，交点的个数是 ，两条直线平行，交点的个数是 _____________ 个.判断题5、6、7、85、不相交的两条直线叫做平行线.（）6、如果一条直线与两条平行线中的一条直线平行，那么它与另一条直线也互相平行.（）7、过一点有且只有一条直线平行于已知直线.（）8、读下列语句，并画出图形后判断.（1）直线a 、b 互相垂直，点P 是直线a 、b 外一点，过P 点的直线c 垂直于直线b. （2）判断直线a 、c 的位置关系，并借助于三角尺、直尺验证.9、试说明三条直线的交点情况，进而判定在同一平面内三条直线的位置情况5.2.2平行线的判定复习检测（10分钟）：1、如图1所示，下列条件中，能判断AB// CD 的是（）DAFCA./BADh BCDB. /1 = /2；C.AD C B如图5,直线a,b 被直线c 所截，现给出下列四个条件： ?①/ 1 = /5;②/ 1=/7;③/ 2+/ 3=180 ;@Z4=Z 7.其中能说明 a // b 的条件序号为（） A.①② B.①③ C.①④ D. ③④如果/ 9=，那么AD// BC;如果/ 9=，那么AB// CD.7、在同一平面内，若直线a,b,c 满足a±b,a ±c,则b 与c 的位置户系是8、如图所示，BE 是AB 的延长线，量得/ CBEh A=/ C. //.... AB E（1） 由/ CBEh A 可以判断//，根据是.⑵ 由/ CBEh C 可以判断//，根据是2、 如图2所示，如果/ D=/ EFC 那么（）A.AD // BCB.EF // BC 3、 F 列说法错误的是（）A.同位角不一定相等B. 内错角都相等C. 同旁内角可能相等D.同旁内角互补，两直线平行4、 5、如图5,如果/ 3=/7,那么,理由是 如果/ 5=/ 3,那么 ,理由是 如果/ 2+ /5=那么a // b,理由是6、如图4,若/ 2=/6，则，如果/3+/4+/ 5+/ 6=180 ,那么(4)C.AB // DCD.AD9、已知直线a、b被直线c所截，且/1+/ 2= 试判断直线a、b的位置关系，并说明理由.10、如图，已知AEM DG , 1 2 ,试问EF是否平行GH并说明理由.11、如图所示，已知/ 1=/ 2,AC平分/ DAB试说明DCI AB.12、如图所示，已知直线EF和AB,CM别相交于K,H,且EGL AB,/CHF=60 / E=30°试说明AB// CD.13、提高训练:如图所示，已知直线a,b,c,d,e,且/ 1=/ 2, / 3+/4=180° ,则a与c平行吗？劝什么？5.3.1平行线的性质复习检测（10分钟）:1、如图1所示,AB//CD则与/ 1相等的角（/1除外）共有（）A.5 个B.4 个C.3 个D.2 个 B AA B —(4) (5) (6)5、如图5,在甲、乙两地之间要修一条笔直的公路，从甲地测得公路的走向是南偏西(3)2、如图 2 所示,CD// AB,O 评分/ AOD,OFOE,/D=50，则/BOF 为(A.35B.30C.253、如图 3 所示,AB II CD,Z D=80CAD=, /ACD=?.4、如图 4,若 AD// BC,则/=/ D.20/ABC 廿=180 ;若 DC/ZAB,则/=/A,/ CAD:/ BAC=3:2则/56° ,甲、乙两地同时开工，若干天后公路准确接通，则乙地所修公路的走向是,因为.6、河南)如图6所示，已知AB// CD直线EF分别交AB,CD于E,F,EG?平分/ B-EF,若/ 1=72 ，贝U/2=.7、如图，AB/ZCQ / 1 = 102° ,求/ 2、/3、/4、/ 5的度数，并说明根据?8、如图，ERiz\ABC勺一个顶点A,且EF// BC 如果/ B= 40° , / 2= 75° ,那么/1、/3、/G / BAO /B+ 是多少度，并说明依据?9、如图，已知:DE/ZCB,/1 = /2,求证:CD平分/ ECB.10、如图所示，把一张长方形纸片ABCD& EF折叠，若/ EFG=50 ,求/ DEG勺度数.1111、如图所示，已知：AE平分/BAC CE平分/ACD且AB//CD求证：/1+/ 2=90° . 证明：・•. AB//CD (已知)・♦/BAC/ACD180 , ()又.. AE平分/ BAC C评分/ ACD (). 1 1•• 1 - BAC , 2 万ACD,( ___________________ ) __________1 1 0 0. .1 2 -( BAC ACD) —1800 90°.2 2即Z1+Z 2=90 .结论：若两条平行线被第三条直线所截，则一组同旁内角的平分线互相.推广：若两条平行线被第三条直线所截，则一组同位角的平分线互相^5.3.2命题、定理、证明复习检测(5分钟)：1、判断下列语句是不是命题(1)延长线段AB( ) (3)画线段AB的中点( (2)两条直线相交，只有一交点((4)若|x|=2 ,则x=2 ( )134、命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角;④同位角相等.其中假命题有（）A.1 个B.2个C.3个D.4个5、分别指出下列各命题的题设和结论（1）如果a// b, b // c,那么all c ⑵ 同旁内角互补，两直线平行 6、分别把下列命题写成“如果……，那么……”的形式 （1）两点确定一条直线； （2）等角的补角相等；（3）内错角相等.7、如图，已知直线a 、b 被直线c 所截，在括号内为下面各小题的推理填上适当的根据(1) '.'all b,「•/ 1=/ 3( ); (2) ・// 1=/ 3, ..・all b( ); (3) '.'all b,「•/ 1=/ 2( );(4) 「a// b,「./ 1+/ 4=180o ( (5) ・// 1=/ 2, ..・all b( ); (6) •// 1+/ 4=180o,「.a// b( ). 8、已知：如图 ABL BG BCLCD 且/ 1=/ 2, 证明：.「AB!BG BCLCD (已知)= =90（5）角平分线是一条射线（ 2、下列语句不是命题的是（ A.两点之间，线段最短 C.x 与y 的和等于0吗？ 3、下列命题中真命题是（ ）A.两个锐角之和为钝角）B.不平行的两条直线有一个交点 D.对顶角不相等.B.两个锐角之和为锐角D.锐角小于它的余角・ ・•/ 1 = /2 (已知)（等式性质）/ ACB=90 ()・ ••/ BCD^/ ACD 勺余角・ ・•/BCD^/B 的余角(已知) ・•・ / ACDN B ()5.4平移复习检测（5分钟）：1、下列哪个图形是由左图平移得到的（ ）B.沿射线EC 的方向移动C 冰C.沿射线BD 的方向移动BD 长;D.沿射线BD 的方向移动DC 长3、下列四组图形中，？有一组中的两个图形经过平移其中一个能得到 -另一个，这组图形9、已知: 求证: 证明: BE// CF (/ ACDM B・•. ACL BC (已知)2、如图所示，4FDE 经过怎样的平移可得到4A.沿射线EC 的方向移动DB 长; 如图，ACL BCC 垂足为CABC.()4、如图所示，△ DEF经过平移可以得到△ ABC那的对应角和ED的对应边分-别是（）A. / F,ACB. / BOD,BA;C. / F,BAD.5、在平移过程中，对应线段（）A.互相平行且相等；B.互相垂直且相等C.互相平行（或在同一条直线上）且相等6、在平移过程中，平移后的图形与原来的图形________ 都相同，？因-此对应线段和对应角7、如图所示，平移△ ABC可得到△ DEF,如果// C=60 ,那么/ E=?-度,/ EDF=/F= ______ 度，/DOB= .........8、将正方形ABCDg对角线AC方向平移，且平移后的图形的一个顶点恰好在AC的中点。

5.1.1 相交线姓名_____________一、选择题:1.如图所示,∠1和∠2是对顶角的图形有( )12121221A.1个B.2个C.3个D.4个2.如图1所示,三条直线AB,CD,EF 相交于一点O,则∠AOE+∠DOB+∠COF 等于( • )A.150°B.180°C.210°D.120°OFE D CB A O DCBA 60︒30︒34l 3l 2l 112(1) (2) (3) 3.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A.1个B.2个C.3个D.4个4.如图2所示,直线AB 和CD 相交于点O,若∠AOD 与∠BOC 的和为236°,则∠AOC•的度数为( )A.62°B.118°C.72°D.59°5.如图3所示,直线L 1,L 2,L 3相交于一点,则下列答案中,全对的一组是( ) A.∠1=90°,∠2=30°,∠3=∠4=60°; B.∠1=∠3=90°,∠2=∠4=30C.∠1=∠3=90°,∠2=∠4=60°;D.∠1=∠3=90°,∠2=60°,∠4=30° 二、填空题:1. 如图4所示,AB 与CD 相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.34D CBA 12OFED CB A OED CBA(4) (5) (6) 2.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.3.如图5所示,直线AB,CD,EF 相交于点O,则∠AOD 的对顶角是_____,∠AOC 的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.4.如图6所示,已知直线AB,CD 相交于O,OA 平分∠EOC,∠EOC=70°,则∠BOD =•______.5.对顶角的性质是______________________.6.如图7所示,直线AB,CD 相交于点O,若∠1-∠2=70,则∠BOD=_____,∠2=____.ODC BA 12OE D CBA OE DCBA(7) (8) (9)7.如图8所示,直线AB,CD 相交于点O,OE 平分∠AOC,若∠AOD-∠DOB=50°,•则∠EOB=______________. 8.如图9所示,直线AB,CD 相交于点O,已知∠AOC=70°,OE 把∠BOD 分成两部分,• 且∠BOE:∠EOD=2:3,则∠EOD=________. 三、解答题:1. 如图所示,AB,CD,EF 交于点O,∠1=20°,∠BOC=80°,求∠2的度数.OF EDCBA 122，如图所示,直线a,b,c 两两相交,∠1=2∠3,∠2=65°,求∠4的度数.cba3412答案:一、1.A 2.B 3.B 4.A 5.D 二、1.∠2和∠4 ∠3 2.155° 25° 155° 4.35° 5.对顶角相等 •6 .125° 55° 7.147.5° 8.42°三、1.∠2=60° 2.∠4=36°四、1.∠BOD=120°,∠AOE=30° 2.∠BOD=72° 3.∠4=32.5° 五、1.4条不同的直线相交于一点,图中共有12对对顶角(平角除外),n 条不同的直线相交于一点,图中共有(n 2-n)对对顶角(平角除外).2.6条直线最多可以把平面分成22个部分,n 条直线最多可以把平面分成(1)12n n +⎡⎤+⎢⎥⎣⎦个部分.六、∠AOC 与∠BOD 不一定是对顶角.如图1所示,当射线OC,OD 位于直线AB 的一侧 时,不是对顶角;如图2所示,当射线OC,OD 位于直线AB 的两侧时,是对顶角.(1)O D C BA21(2)O DCBA七、140°.5.1.3同位角、内错角、同旁内角同步练习姓名_____________一、填空题1.如图1，直线a 、b 被直线c 所截，∠1和∠2是 ，∠3和∠4是 ，∠3和∠2是 。

初中数学七年级下册第五章分式同步练习（2021-2022学年 考试时间：90分钟，总分100分） 班级：__________ 姓名：__________ 总分：__________一、单选题（10小题，每小题3分，共计30分） 1、下列计算中，正确的是（ ）A ．633422a a a ÷=B ．326a a a ⋅=C ．1133-⎛⎫=- ⎪⎝⎭D ．224a a a +=2、下列各式与1(2)--相等的是（ ） A ．12B ．-2C ．2D ．12-3、在研制新冠肺炎疫苗过程中，某细菌的直径大小为0.000000000072米，用科学记数法表示这一数字，正确的是（ ） A ．120.7210-⨯ B ．127.210-⨯ C ．117.210-⨯D ．107.210-⨯4、下列计算结果正确的是（ ） A ．55623a a a +=B ．()256a a a -⋅=-C ．2124-=D ．()021-=-5、空气的密度是1.293×10﹣3g /cm 3，用小数把它表示出来是（ ）g /cm 3． A ．0.0001293B ．0.001293C ．0.01293D ．0.12936、研究发现新冠肺炎病毒大小约为0.000000125米，数0.000000125用科学记数法表示为（ ） A ．125×10﹣9B ．12.5×10﹣8C ．1.25×10﹣7D ．1.25×10﹣67、若22224n n n n +++=，则n 的值为（ ） A ．0 B ．1C ．2D ．38、若41x +表示一个整数，则整数x 可取值共有（ ） A ．3个 B ．4个 C ．5个 D ．6个9、已知30x y -=（0x ≠），则分式22232xy y x xy+-的值为（ ）A ．2B ．－2C ．3D ．－310、已知实数,,x y z 满足x y xy z +==，则下列结论：①若0z ≠，则412723x xy y x xy y -+=-++；②若3x =，则6y z +=；③若0z ≠，则()()1111x y x y--=+；④若6z =，则2224x y +=，其中正确的个数是（ ） A ．1 B ．2 C ．3 D ．4二、填空题（5小题，每小题4分，共计20分） 1、202020218(0.125)⋅-=______；()0220213--⨯=___________．2、计算201(20212019)3-⎛⎫-+-= ⎪⎝⎭__________．3、当x _______时，分式293x x --的值为零．4、有一工程需在x 天内完成．如果甲单独工作，刚好能够按期完成：如果乙单独工作，就要超过规定日期3天．现在甲、乙合作2天后，余下的工程由乙单独完成，刚好在规定日期完成，则依题意列出的方程是________．5、若分式2xx -有意义，则x 的取值范围是 ___． 三、解答题（5小题，每小题10分，共计50分）1、先化简，再求值：224114422a a a a a a ⎛⎫-+-÷⎪-+-+⎝⎭，其中a ＝﹣1．2、（1）计算：()10213820162π-⎛⎫--+--- ⎪⎝⎭；（2）先化简，再求值．()()()222352x y x y x y y x ⎡⎤+-+--÷⎣⎦，其中2x =-，12y =． 3、计算：234()()23ba aabb ÷-⨯． 4、已知13x -=-，求代数式22()(22)11x x x x x-÷-+--的值．5、（1）计算：)22--；（2）化简：()()5311a a a a +--÷---------参考答案----------- 一、单选题 1、A 【分析】根据单项式除以单项式、同底数幂的乘法、负指数幂及合并同类项可进行排除选项． 【详解】解：A 、633422a a a ÷=，正确，故符合题意； B 、325a a a ⋅=，原计算错误，故不符合题意；C 、1133-⎛⎫= ⎪⎝⎭，原计算错误，故不符合题意；D 、2222a a a +=，原计算错误，故不符合题意； 故选A ． 【点睛】本题主要考查单项式除以单项式、同底数幂的乘法、负指数幂及合并同类项，熟练掌握单项式除以单项式、同底数幂的乘法、负指数幂及合并同类项是解题的关键． 2、D 【分析】根据负指数幂()1,0nna a a -=≠可直接进行求解． 【详解】解：由题意得：11(2)2--=-；故选D ． 【点睛】本题主要考查负指数幂，熟练掌握负指数幂的算法是解题的关键． 3、C 【分析】用科学记数法表示较小的数，一般形式为a ×10−n，其中1≤|a |＜10，n 为整数，据此判断即可． 【详解】110.0000000000727.210-=⨯故选C 【点睛】此题主要考查了用科学记数法表示较小的数，一般形式为a ×10−n，其中1≤|a |＜10，n 为由原数左边起第一个不为零的数字前面的0的个数所决定，确定a 与n 的值是解题的关键． 4、C 【分析】根据运算的法则逐一运算判断即可．【详解】解：A ：55523a a a +=，故此选项错误；B ：()257a a a-⋅=，故此选项错误；C ：2124-=，故此选项正确；D ：()021-=，故此选项错误；故答案为：C 【点睛】本题主要考查了同类型的合并，同底数幂的乘法，负指数幂，零指数幂，熟悉掌握运算的法则是解题的关键． 5、B 【分析】把1.293的小数点向左移3位即可． 【详解】解：30.001291.103293=⨯﹣ 故选B 【点睛】本题考查了还原科学记数法表示的小数，熟练掌握科学记数法的意义是解题的关键． 6、C 【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a ×10-n，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数n 由原数左边起第一个不为零的数字前面的0的个数所决定． 【详解】解：0.000000125=1.25×10-7， 故选：C ． 【点睛】本题考查用科学记数法表示较小的数，一般形式为a ×10-n，其中1≤|a |＜10，n 为由原数左边起第一个不为零的数字前面的0的个数所决定． 7、A 【分析】由题意可得：244n ⨯=，通过整理得：21n =，则可求得0n =． 【详解】解：22224n n n n +++=，244n ⨯=，21n =，0n =．故选：A ． 【点睛】本题主要考查了零指数幂法则，解答的关键是明确非0实数的0次方等于1． 8、D 【分析】 由x 是整数，41x +也表示一个整数，可知x +1为4的约数，即x +1=±1，±2，±4，从而得出结果． 【详解】 解：∵x 是整数，41x +也表示一个整数， ∴x +1为4的约数， 即x +1=±1，±2，±4，∴x =-2，0，-3，1，-5，3． 则整数x 可取值共有6个． 故选：D ． 【点睛】本题考查了此题首先要根据分式值是整数的条件，能够根据已知条件分析出x +1为4的约数，是解决本题的关键． 9、C 【分析】由题意可知x =3y ，然后根据因式分解法进行化简，再将x =3y 代入原式即可求出答案． 【详解】 解：∵x -3y =0， ∴x =3y ，原式= (23)(2)+-y x y x x y(63)3(32)+=-y y y y y y3=故选：C 【点睛】本题考查分式的运算，解题的关键是熟练运用因式分解法将分式化简，再把x 换成3y ． 10、D 【分析】①4272x xy y x xy y -+++转化为()()442727x y xy z z x y xy z z+--=+++，即可求解；②先求出y ，再求出z ，即可得到答案；③将()()11x y --变形求出值为1，再将11x y +变形求出值也为1，即可得到答案；④将2224x y +=进行变形为()2222x y x y xy +=+-，再将x y xy z +==整体代入，即可得到答案．【详解】解：①因为x y xy z +==，0z ≠所以，()()4441=27227273x y xy x xy y z z x xy y x y xy z z +--+-==-+++++，故此项正确；②因为，3x =，则x y xy +=． 所以，33y y +=解得：32y =；所以，313+422z x y =+==所以，31+4=622y z +=，故此项正确； ③因为0z ≠，x y xy z +==所以，()()()1111+=11x y y x xy x y xy z z --=--+=-+-+=；11=1y x x y z x y xy xy xy z+++===； 所以，()()1111x y x y--=+，故此项正确； ④因为6z =，x y xy z +==所以，()222222361224x y x y xy z z +=+-=-=-=，故此项正确； 故选D ． 【点睛】本题考查完全平方公式、分式的加法以及整体代入方法，解答本题的关键是明确题意，求出学会整体代入． 二、填空题1、-0.125 1 9【分析】根据积的乘方逆运算、零指数幂与负指数幂的性质即可求解．【详解】[]202020202021202020208(0.125)8(0.125)(0.125)8(0.125)(0.125)0.125⋅-=⋅-⨯-=⨯-⨯-=-；()02 20213--⨯=11 199⨯=故答案为：-0.125；19．【点睛】此题主要考查实数的运算，解题的关键是熟知幂的运算公式及零指数幂与负指数幂的性质．2、10【分析】利用负整数指数幂，零指数幂的法则，即可求解．【详解】解：2211(20212019)19110 313-⎛⎫-+-=+=+=⎪⎝⎭⎛⎫-⎪⎝⎭．故答案为：10．【点睛】本题主要考查了负整数指数幂，零指数幂的法则，熟练掌握负整数指数幂，零指数幂的法则是解题的关键．3、= -3【分析】根据分母为0是分式无意义，分式值为零的条件是分子等于零且分母不等于零列式计算即可． 【详解】 解：根据题意，∵分式293x x --的值为零，∴29030x x ⎧-=⎨-≠⎩，∴3x =-； 故答案为：3=-． 【点睛】本题考查的是分式为0的条件、分式有意义的条件，掌握分式值为零的条件是分子等于零且分母不等于零是解题的关键．4、1112(2)133x xx x ⎛⎫++-⋅= ⎪++⎝⎭ 【分析】有一工程需在x 天内完成，则甲的工作效率为1x，乙的工作效率为13x + ，则前两天完成的工作量为1123x x ⎛⎫+ ⎪+⎝⎭，乙单独做的工作量为()123x x -+，由此求解即可． 【详解】解：有一工程需在x 天内完成，则甲的工作效率为1x，乙的工作效率为13x + ， 由题意得：()11122133x xx x ⎛⎫++-= ⎪++⎝⎭ ， 故答案为：()11122133x x x x ⎛⎫++-= ⎪++⎝⎭．【点睛】本题主要考查了分式方程的实际应用，解题的关键在于能够准确找到等量关系列出方程． 5、2x ≠【分析】根据分母不等于零分式有意义，可得答案．【详解】 解：∵分式2x x -有意义， ∴20x -≠解得，2x ≠故答案为：2x ≠【点睛】本题考查的是分式有意义的条件，熟知分式有意义的条件是分母不等于零是解答此题的关键．三、解答题1、22a a +-，13-【分析】先计算括号内的异分母分式减法，再计算除法，最后将a =-１代入计算即可．【详解】 解：224114422a a a a a a ⎛⎫-+-÷ ⎪-+-+⎝⎭ 212221++⎛⎫=-⋅ ⎪--+⎝⎭a a a a a 1221a a a a ++=⋅-+22a a +=-， 当1a =-时，原式121123-+==---． 【点睛】此题考查分式的化简求值，正确掌握分式的混合运算是解题的关键．2、（1）4；（2）-+x y ，122【分析】（1）根据有理数的乘方、绝对值、零指数幂和负整数指数幂的计算方法可以解答本题；（2）根据完全平方公式、多项式乘多项式、多项式除以单项式可以化简题目中的式子，然后将x 、y 的值代入化简后的式子即可解答本题．【详解】（1）解：原式9812=-++4=；（2）解：原式()22222443352x xy y x xy xy y y x =++-+-+-÷ ()2222x xy x =-+÷x y =-+.当2x =-，12y =时，原式122=.【点睛】本题考查整式的混合运算、实数的运算、零指数幂和负整数指数幂，解答本题的关键是明确它们各自计算方法，求出所求式子的值．3、23a -根据分式的乘除法进行计算，注意进行约分．【详解】 解：原式223344b b a a a b=-⋅⋅ 23a =-．【点睛】本题考查了分式的乘除法，解决本题的关键是遇到除法，变为乘法计算，并注意约分.. 4、32【分析】根据题意首先对代数式进行化简，然后将13x -=-代入求解即可．【详解】 解：原式2222222211x x x x x x x x----+-=÷-- 2211x x x x =-÷-- 2112x x x x -=-⋅- 12x=-， 当1133x -=-=-时，原式13122()3=-=⨯-． 【点睛】本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．5、（1）1；（2）-1（1）根据绝对值的意义及零次幂的性质进行计算即可；（2）分别运用平方差公式及同底数幂的除法法则进行计算，再合并同类项即可．【详解】解：（1）)022--21=-1=；（2）()()5311a a a a +--÷ 221a a =--1=-．【点睛】本题考查了实数及整式的混合运算，熟练掌握相关运算法则及性质是解题的关键．。

一、选择题1．如图，两个直角三角形重叠在一起，将ABC 沿AB 方向平移2cm 得到DEF ，2cm CH =，4cm EF =，下列结论：①//BH EF ；②AD BE =；③BD CH =：④C BHD ∠=∠；⑤阴影部分的面积为26cm ．其中正确的是（ ）A ．①②③④B ．②③④⑤C ．①②③⑤D ．①②④⑤D解析：D【分析】 根据平移的性质可直接判断①②③，根据平行线的性质可判断④，阴影部分的面积=S 梯形BEFH ，于是可判断⑤，进而可得答案．【详解】解：因为将ABC 沿AB 方向平移2cm 得到DEF ，所以//BH EF ，AD BE =，DF ∥AC ，故①②正确；所以C BHD ∠=∠，故④正确；而BD 与CH 不一定相等，故③不正确；因为2cm CH =，4cm EF BC ==，所以BH=2cm ，又因为BE=2cm ，所以阴影部分的面积=S △ABC －S △DBH = S △DEF －S △DBH =S 梯形BEFH =()12422⨯+⨯=26cm ，故⑤正确；综上，正确的结论是①②④⑤．故选：D ．【点睛】本题考查了平移的性质，属于基础题目，正确理解题意、熟练掌握平移的性质是解题的关键．2．能说明命题“若a b >，则22a b >”是假命题的一个反例．．可以是（ ） A ．0a =，1b =-B ．2a =，1b =C ．2a =-，1b =-D ．0a =，2b = A 解析：A【分析】选取的a 的值满足a b >，但不满足22a b >即可．【详解】解：当a ＝0，b ＝﹣1时，满足a ＞b ，但不满足22a b >，故A 选项符合题意； 当a ＝2，b ＝1时，满足a ＞b ，也满足22a b >，故B 选项不符合题意；当a ＝﹣2，b ＝﹣1时，不满足a ＞b ，故C 选项不符合题意；当a ＝0，b ＝2时，不满足a ＞b ，故D 选项不符合题意；故选：A ．【点睛】本题考查了命题与定理：命题写成“如果…，那么…”的形式，这时，“如果”后面接的部分是题设，“那么”后面解的部分是结论．命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．3．对于命题“如果∠1+∠2＝90°，那么∠1≠∠2”，能说明它是假命题的反例是（ ） A ．∠1＝50°，∠2＝40°B ．∠1＝50°，∠2＝50°C ．∠1＝∠2＝45°D ．∠1＝40°，∠2＝40°C解析：C【分析】能说明是假命题的反例就是能满足已知条件，但不满足结论的例子．【详解】A 、满足条件∠1＋∠2＝90°，也满足结论∠1≠∠2，故A 选项错误；B 、不满足条件，故B 选项错误；C 、满足条件，不满足结论，故C 选项正确；D 、不满足条件，也不满足结论，故D 选项错误．故选：C ．【点睛】此题考查了命题与定理的知识，理解能说明它是假命题的反例的含义是解决本题的关键． 4．命题“垂直于同一条直线的两条直线互相平行”的条件是（ ）A ．垂直B ．两条直线互相平行C ．同一条直线D ．两条直线垂直于同一条直线D 解析：D【分析】命题有条件和结论两部分组成，条件是已知的部分，结论是由条件得出的推论．【详解】“垂直于同一条直线的两条直线互相平行”的条件是“两条直线垂直于同一条直线”，结论是“两条直线互相平行”．故选：D ．【点睛】本题考查了对命题的题设和结论的理解，解题的关键在于利用直线垂直的定义进行判断． 5．如图所示，下列条件能判断a ∥b 的有（ ）A．∠1+∠2＝180°B．∠2＝∠4 C．∠2+∠3＝180°D．∠1＝∠3B解析：B【分析】通过平行线的判定的相关知识点，并结合题中所示条件进行相应的分析，即可得出答案.【详解】A.∠1 ,∠2是互补角，相加为180°不能证明平行，故A错误.B.∠2=∠4，内错角相等，两直线平行，所以B正确.C. ∠2+∠3＝180°，不能证明a∥b，故C错误.D.虽然∠1=∠3，但是不能证明a∥b；故D错误.故答案选：B.【点睛】本题考查的知识点是平行线的判定，解题的关键是熟练的掌握平行线的判定.6．下列说法中不正确的个数为（）．①在同一平面内，两条直线的位置关系只有两种：相交和垂直．②有且只有一条直线垂直于已知直线．③如果两条直线都与第三条直线平行，那么这两条直线也互相平行．④从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离．⑤过一点，有且只有一条直线与已知直线平行．A．2个B．3个C．4个D．5个C解析：C【分析】根据在同一平面内，根据两条直线的位置关系、垂直的性质、平行线平行公理及推论、点到直线的距离等逐一进行判断即可．【详解】∵在同一平面内，两条直线的位置关系只有两种：相交和平行，故①不正确；∵过直线外一点有且只有一条直线垂直于已知直线．故②不正确；如果两条直线都与第三条直线平行，那么这两条直线也互相平行．故③正确；从直线外一点到这条直线的垂线段的长度，叫做这点到这条直线的距离．故④不正确；过直线外一点，有且只有一条直线与已知直线平行．故⑤不正确；∴不正确的有①②④⑤四个．故选：C．【点睛】本题考查了直线的知识；解题的关键是熟练掌握直线相交、直线垂直、直线平行以及垂线的性质，从而完成求解．7．下列命题是真命题的有（）个①对顶角相等，邻补角互补②两条直线被第三条直线所截，同位角的平分线平行③垂直于同一条直线的两条直线互相平行④过一点有且只有一条直线与已知直线平行A．0 B．1 C．2 D．3B解析：B【分析】根据平行线的性质定理、平行公理、对顶角和邻补角的概念判断即可．【详解】解：对顶角相等，邻补角互补，故①是真命题；两条平行线被第三条直线所截，同位角的平分线平行，故②是假命题；在同一平面内，垂直于同一条直线的两条直线互相平行，故③是假命题；过直线外一点有且只有一条直线与已知直线平行，故④是假命题；故正确的个数只有1个，故选：B．【点睛】本题考查的是平行的公理和应用，命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．8．如图所示，已知 AB∥CD，下列结论正确的是（）A．∠1=∠2 B．∠2=∠3 C．∠1=∠4 D．∠3=∠4C解析：C【分析】根据平行线的性质即可得到结论．【详解】∵AB∥CD，∴∠1=∠4，故选 C．【点睛】本题考查了平行线的性质，熟练掌握平行线的性质是解题的关键．9．如图，下列说法错误的是( )A ．若a ∥b ，b ∥c ，则a ∥cB ．若∠1＝∠2，则a ∥cC ．若∠3＝∠2，则b ∥cD ．若∠3＋∠5＝180°，则a ∥c C解析：C【解析】 试题分析：根据平行线的判定进行判断即可．解：A 、若a ∥b ，b ∥c ，则a ∥c ，利用了平行公理，正确；B 、若∠1=∠2，则a ∥c ，利用了内错角相等，两直线平行，正确；C 、∠3=∠2，不能判断b ∥c ，错误；D 、若∠3+∠5=180°，则a ∥c ，利用同旁内角互补，两直线平行，正确；故选C ．考点：平行线的判定．10．如图，已知AB CD ∕∕，AF 交CD 于点E ，且,40BE AF BED ⊥∠=︒，则A ∠的度数是（ ）A ．40︒B ．50︒C ．80︒D ．90︒B解析：B【分析】 直接利用垂线的定义结合平行线的性质得出答案．【详解】解：∵,40BE AF BED ⊥∠=︒，∴50FED ∠=︒，∵AB CD ∕∕，∴50A FED ∠=∠=︒．故选B ．【点睛】此题主要考查了平行线的性质以及垂线的定义，正确得出FED ∠的度数是解题关键．二、填空题11．下列说法中：（1）不相交的两条直线叫做平行线；（2）经过一点，有且只有一条直线与已知直线平行；（3）垂直于同一条直线的两直线平行；（4）直线//a b ，//b c ，则//a c ；（5）两条直线被第三条直线所截，同位角相等．其中正确的是________．（4）【分析】根据平行线的定义平行线的性质平行公理的推论解答【详解】（1）在同一平面内不相交的两条直线叫做平行线故该项错误；（2）过直线外一点有且只有一条直线与已知直线平行故该项错误；（3）在同一平解析：（4）【分析】根据平行线的定义，平行线的性质，平行公理的推论解答．【详解】（1）在同一平面内不相交的两条直线叫做平行线，故该项错误；（2）过直线外一点，有且只有一条直线与已知直线平行，故该项错误；（3）在同一平面内，垂直于同一条直线的两直线平行，故该项错误；（4）直线//a b ，//b c ，则//a c ，故该项正确；（5）两条平行线被第三条直线所截，同位角相等，故该项错误．故选：（4）．【点睛】此题考查判断语句，熟记平行线的定义，平行线的性质，平行公理的推论是解题的关键． 12．小明在楼上点A 处行到楼下点B 处的小丽的俯角是32 ，那么点B 处的小丽看点A 处的小明的仰角是_______________度．【分析】根据题意画出图形然后根据平行线的性质可以求得点B 处的小丽看点A 处的小明的仰角的度数本题得以解决【详解】解：由题意可得∠BAC ＝32°∵AC ∥BO ∴∠ABO ＝∠BAC ∴∠ABO ＝32°即点B 处解析：32【分析】根据题意画出图形，然后根据平行线的性质可以求得点B 处的小丽看点A 处的小明的仰角的度数，本题得以解决．【详解】解：由题意可得，∠BAC ＝32°，∴∠ABO ＝∠BAC ，∴∠ABO ＝32°，即点B 处的小丽看点A 处的小明的仰角等于32度，故答案为32．【点睛】本题利用平行线间角的关系求仰角俯角问题，解答本题的关键是明确题意，利用数形结合的思想解答．13．如图，已知ABC 中，4AB =、5AC =、6BC =，将ABC 沿直线BC 向右平移得到A B C '''，点A 、B 、C 的对应点分别是A '、B '、C '，连接AA '．如果四边形AA C B ''的周长为19，那么四边形AA C B ''的面积与ABC 的面积的比值是________．【分析】过点A 作BC 上的高根据平移的性质可得=且然后根据已知周长可得=2从而求出然后根据梯形的面积公式和三角形的面积公式即可求出结论【详解】解：过点A 作BC 上的高由平移的性质可得=且∴四边形为梯形∵ 解析：53【分析】过点A 作BC 上的高h ，根据平移的性质可得AA '=CC '，且//AA CC ''，5A C AC ''==，然后根据已知周长可得AA '=2，从而求出BC '，然后根据梯形的面积公式和三角形的面积公式即可求出结论．【详解】解：过点A 作BC 上的高h由平移的性质可得AA '=CC '，且//AA CC ''，5A C AC ''==∴四边形AA C B ''为梯形∵四边形AA C B ''的周长为19，∴AA '＋A C ''＋BC '＋AB=19∴AA '＋5＋6＋CC '＋4=19∴AA '=2∴CC '=2∴BC '=BC ＋CC '=8∴四边形AA C B ''的面积与ABC 的面积的比为()128521632h AA BC hBC ''++== 故答案为：53． 【点睛】 此题考查的是图形的平移问题，掌握平移的性质是解题关键．14．命题“等边三角形的每个内角都等于60°”的逆命题是_____命题．（填“真”或“假”）真【分析】逆命题就是原命题的假设和结论互换找到原命题的题设为等边三角形结论为每个内角都是60°互换即可判断命题是真是假；【详解】∵原命题为：等边三角形的每个内角都是60°∴逆命题为：三个内角都是60解析：真【分析】逆命题就是原命题的假设和结论互换，找到原命题的题设为等边三角形，结论为每个内角都是60°，互换即可判断命题是真是假；【详解】∵ 原命题为：等边三角形的每个内角都是60°，∴ 逆命题为：三个内角都是60°的三角形是等边三角形∴ 逆命题为真命题；故答案为：真．【点睛】本题考查了命题的真假，正确掌握原命题与逆命题之间的关系是解题的关键；15．如图，//EF AD ，//AD BC ，CE 平分BCF ∠，120DAC ∠=︒，20ACF ∠=︒，FEC ∠为______°．20【分析】根据平行线的性质可得进而可得∠ACB ＝60°根据角平分线的性质和角的和差可得∠BCE 根据平行线的性质可得∠FEC 【详解】∵∴∵∴∵又∵∴∵平分∴∠BCE ＝∠ECF ＝∠BCF ＝20°∵∴∴解析：20【分析】根据平行线的性质可得180DAC ACB ∠+∠=︒，进而可得∠ACB ＝60°，根据角平分线的性质和角的和差可得∠BCE ，根据平行线的性质可得∠FEC ．【详解】∵//AD BC ，∴180DAC ACB ∠+∠=︒．∵120DAC ∠=︒，∴180********ACB DAC ∠=︒-∠=︒-︒=︒．∵60BCF ACF ACB ∠+∠=∠=︒．又∵20ACF ∠=︒，∴602040BCF ACB ACF ∠=∠-∠=︒-︒=︒．∵CE 平分BCF ∠，∴∠BCE ＝∠ECF ＝12∠BCF ＝20° ∵//EF BC ，∴20FEC BCE ∠=∠=︒，∴20FEC ∠=︒．故答案为：20．【点睛】本题主要考查平行线的性质，涉及到角的和差，角平分线的性质，解题的关键是求得∠BCE ．16．如图，直线//m n ，点A B 、在直线n 上，点C F 、在直线m 上，连接,CA CB CD 、平分ACB ∠交AB 于点D ，平面内有点E ，连接,2180EC ECB BCF ︒∠+∠=，过点F 作//FG CE 交CD 于点,9,4G FGC ADC CAB ABC ︒∠-∠=∠=∠，则ACB =∠____________．【分析】根据条件找到等量关系计算即可；【详解】设∵∴∴∵∴∵ABD 在同一直线上∴∴在△ABC 中∴联立方程组：解得：度度度故答案是：【点睛】本题主要考查了平行线的综合应用结合三元一次方程组求解是解题的解析：2707【分析】根据条件2180︒∠+∠=ECB BCF ，9︒∠-∠=FGC ADC ，4∠=∠CAB ABC 找到等量关系计算即可；【详解】设2ABC x ∠=∠，1ACE ∠=∠，∵//m n ，∴BCF ABC ∠=∠，12ECB ECA ACB x ∠=∠+∠=∠+∠，∴()212180x ABC ∠+∠+∠=︒，∵//FG CE ，∴1FGC ECD x ∠=∠=∠+∠，∵A ，B ，D 在同一直线上，∴ADC ABC DCB ABC x ∠=∠+∠=∠+∠，∴()1119x ABC x x ABC x ABC ∠+∠-∠+∠=∠+∠-∠-∠=∠-∠=︒， 在△ABC 中，1802CAB x ABC ∠=︒-∠-∠，∴18024x ABC ABC ︒-∠-∠=∠，联立方程组：()2121801918024x ABC ABC x ABC ABC ⎧∠+∠+∠=︒⎪∠-∠=︒⎨⎪︒-∠-∠=∠⎩， 解得：1987ABC ∠=度，26117∠=度，2707x ∠=度． 故答案是：2707． 【点睛】本题主要考查了平行线的综合应用，结合三元一次方程组求解是解题的关键． 17．“等腰三角形的两条边相等”的逆命题是________________．（填真命题或假命题）真命题【分析】交换命题的题设和结论即可得到该命题的逆命题根据等腰三角形的定义判断即可【详解】等腰三角形的两条边相等的逆命题是：两条边相等的三角形是等腰三角形；它是真命题故答案为：真命题【点睛】本题考 解析：真命题【分析】交换命题的题设和结论即可得到该命题的逆命题，根据等腰三角形的定义判断即可．【详解】“等腰三角形的两条边相等”的逆命题是：两条边相等的三角形是等腰三角形；它是真命题，故答案为：真命题．【点睛】本题考查了命题的真假判断、逆命题的概念，掌握等腰三角形的定义是解题的关键． 18．如图，把直角梯形ABCD 沿AD 方向平移到梯形EFGH ，28HG cm =，5MG cm =，4MC cm =，则阴影部分的面积是___ 130cm2【分析】根据平移的性质可知梯形EFGH ≌梯形ABCD 那么GH=CDBC=FG 观察可知梯形EFMD 是两个梯形的公共部分那么阴影部分的面积就等于梯形MGHD 再根据梯形的面积计算公式计算即可【解析：130cm 2．【分析】根据平移的性质可知梯形EFGH ≌梯形ABCD ，那么GH=CD ，BC=FG ，观察可知梯形EFMD 是两个梯形的公共部分，那么阴影部分的面积就等于梯形MGHD ，再根据梯形的面积计算公式计算即可．【详解】解：∵直角梯形EFGH 是由直角梯形ABCD 平移得到的，∴梯形EFGH ≌梯形ABCD ，∴GH=CD ，BC=FG ，∵梯形EFMD 是两个梯形的公共部分，∴S 梯形ABCD -S 梯形EFMD =S 梯形EFGH -S 梯形EFMD ，∴S 阴影=S 梯形MGHD =12（DM+GH ）•GM=12（28-4+28）×5=130（cm 2）． 故答案是130cm 2．【点睛】本题考查了图形的平移，解题的关键是知道平移前后的两个图形全等．19．地铁某换乘站设有编号为A ，B ，C ，D ，E 的五个安全出口．若同时开放其中的两个安全出口， 疏散1000名乘客所需的时间如下： 安全出口编号A ，B B ，C C ，D D ，E A ，E 疏散乘客时间()s120 220 160 140 200 则疏散乘客最快的一个安全出口的编号是______．个安全出口疏散1000名乘客所需的时间分析对比能求出结果【详解】同时开放AE 两个安全出口疏散1000名乘客所需的时间为200s 同时开放DE 两个安全出口疏散1000名乘客解析：D【分析】利用同时开放其中的两个安全出口，疏散1000名乘客所需的时间分析对比，能求出结果．【详解】同时开放A 、E 两个安全出口，疏散1000名乘客所需的时间为200s ，同时开放D 、E 两个安全出口，疏散1000名乘客所需的时间为140s ，得到D 疏散乘客比A 快；同时开放A 、E 两个安全出口，疏散1000名乘客所需的时间为200s ，同时开放A 、B 两个安全出口，疏散1000名乘客所需的时间为120s ，得到A 疏散乘客比E 快；同时开放A 、B 两个安全出口，疏散1000名乘客所需的时间为120s ，同时开放B 、C 两个安全出口，疏散1000名乘客所需的时间为220s ，得到A 疏散乘客比C 快；同时开放B 、C 两个安全出口，疏散1000名乘客所需的时间为220s ，同时开放C 、D 两个安全出口，疏散1000名乘客所需的时间为160s ，得到D 疏散乘客比B 快．综上，疏散乘客最快的一个安全出口的编号是D ．故答案为：D ．【点睛】本题考查推理能力，进行简单的合情推理为解题关键．20．如图，直线////a b c ，直角三角板的直角顶点落在直线b 上，若135∠=︒，则2∠等于_______．【分析】如图利用平行线的性质得出∠3=35°然后进一步得出∠4的度数从而再次利用平行线性质得出答案即可【详解】如图所示∵∴∴∠4=90°−∠3=55°∵∴∠2=∠4=55°故答案为：55°【点睛】本解析：55︒【分析】如图，利用平行线的性质得出∠3=35°，然后进一步得出∠4的度数，从而再次利用平行线性质得出答案即可.【详解】如图所示，∵//a b ，135∠=︒，∴335∠=︒，∴∠4=90°−∠3=55°，∵////a b c ，∴∠2=∠4=55°.故答案为：55°.【点睛】本题主要考查了平行线的性质，熟练掌握相关概念是解题关键.三、解答题21．如图，AD 平分∠BAC ，点E ，F 分别在边BC ，AB 上，且∠BFE ＝∠DAC ，延长EF ，CA 交于点G ，求证：∠G ＝∠AFG ．解析：见解析【分析】先利用角平分线的定义得到∠BAD ＝∠DAC ，结合已知条件∠BFE ＝∠DAC ，可得∠BFE ＝∠BAD ，根据平行线的判定可证EG ∥AD ，再由平行线的性质得∠G ＝∠DAC ，∠AFG ＝∠BAD ，则利用等量代换即可证得结论．【详解】证明：∵AD 平分∠BAC ，∴∠BAD ＝∠DAC ，∵∠BFE ＝∠DAC ，∴∠BFE ＝∠BAD ，∴EG ∥AD ，∴∠G ＝∠DAC ，∠AFG ＝∠BAD ，∴∠G ＝∠AFG ．【点睛】本题考查了平行线的判定与性质，掌握平行线的判定的方法及利用性质证明角相等是解答此题的关键．22．填空（请补全下列证明过程及括号内的依据）已知：如图，12,B C ∠=∠∠=∠．求证：180B BFC ︒∠+∠=证明：∵12∠=∠（已知），且1CGD ∠=∠（__________________________），∴2CGD ∠=∠（_______________________________），∴//CE BF （____________________________），∴∠___________C =∠（_________________________），又B C ∠=∠（已知），∴∠_________________B =∠（等量代换），∴//AB CD （_________________），∴180B BFC ︒∠+∠=（_________________________）．解析：对顶角相等；等量代换；同位角相等，则两直线平行；BFD ；两直线平行，则同位角相等；BFD ；内错角相等，则两直线平行；两直线平行，则同旁内角互补【分析】结合题意，根据平行线的性质分析，即可得到答案．【详解】∵12∠=∠且1CGD ∠=∠（对顶角相等），∴2CGD ∠=∠（等量代换），∴//CE BF （同位角相等，则两直线平行），∴∠BFD C =∠（两直线平行，则同位角相等），又B C ∠=∠（已知），∴∠BFD B =∠（等量代换），∴//AB CD （内错角相等，则两直线平行），∴180B BFC ︒∠+∠=（两直线平行，则同旁内角互补）．故答案为：对顶角相等；等量代换；同位角相等，则两直线平行；BFD ；两直线平行，则同位角相等；BFD ；内错角相等，则两直线平行；两直线平行，则同旁内角互补．【点睛】本题考查了平行线的知识；解题的关键是熟练掌握平行线、内错角、同旁内角、同位角、对顶角的性质，从而完成求解．23．如图，点D 、E 分别为AB 、AC 上的点，点F 、G 为BC 上的点，连接DE ，连接DG 、EF 交于点H ．已知12180∠+∠=︒，3B ∠=∠，若66C ∠=︒，求DEC ∠的度数．请你将下面解答过程填写完整．解：∵12180∠+∠=︒∴//AB ________∴3ADE ∠=∠（________________________）∵3B ∠=∠∴_______B =∠∴//DE BC （____________________________）∴180C DEC ∠+∠=︒∵66C ∠=︒∴114DEC ∠=︒解析：见解析．【分析】先根据平行线的判定可得//AB EF ，再根据平行线的性质可得3ADE ∠=∠，从而可得ADE B ∠=∠，然后根据平行线的判定与性质可得．【详解】解：∵12180∠+∠=︒，∴//AB EF ，∴3ADE ∠=∠（两直线平行，内错角相等），∵3B ∠=∠，∴ADE B ∠=∠，∴//DE BC （同位角相等，两直线平行），∴180C DEC ∠+∠=︒，∵66C ∠=︒，∴114DEC ∠=︒．【点睛】本题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解题关键．24．如图，MN ，EF 分别表示两面镜面，一束光线AB 照射到镜面MN 上，反射光线为BC ，此时12∠=∠；光线BC 经过镜面EF 反射后的反射光线为CD ，此时34∠=∠，且//AB CD ．求证∶//MN EF ．解析：证明见解析【分析】利用//AB CD 推出ABC BCD ∠=∠，利用1234180ABC BCD ∠+∠+∠=∠+∠+∠=︒，得到23∠∠=，即可得到结论．【详解】解：证明：∵//AB CD ，∴ABC BCD ∠=∠，又∵1234180ABC BCD ∠+∠+∠=∠+∠+∠=︒，∴1234∠+∠=∠+∠，又∵12∠=∠，34∠=∠，∴23∠∠=，∴//MN EF ．【点睛】此题考查平行线的判定及性质，正确理解判定及性质定理并应用解决问题是解题的关键． 25．如图，//AD BC ，∠1=∠C ，∠B =60°，DE 平分∠ADC 交BC 于点E ，试说明//AB DE ．请完善解答过程，并在括号内填写相应的理论依据．解：∵//AD BC ，（已知）∴∠1=∠ =60°．（ ）∵∠1=∠C ，（已知）∴∠C =∠B =60°．（等量代换）∵//AD BC ，（已知）∴∠C +∠ =180°．（ ）∴∠ =180°-∠C =180°-60°=120°．（等式的性质）∵DE 平分∠ADC ，（已知）∴∠ADE =12∠ADC =12×120°=60°．（ ）∴∠1=∠ADE．（等量代换）∴//AB DE．（）解析：B；两直线平行，同位角相等；ADC；两直线平行，同旁内角互补；ADC；角平分线性质；内错角相等，两直线平行．【分析】利用平行线的性质和判定，角平分线的性质去进行填空．【详解】解∵//AD BC，（已知）∴∠1=∠B=60°．（两直线平行，同位角相等）∵∠1=∠C，（已知）∴∠C=∠B=60°．（等量代换）∵//AD BC，（已知）∴∠C+∠ADC=180°．（两直线平行，同旁内角互补）∴∠ADC=180°-∠C=180°-60°=120°．（等式的性质）∵DE平分∠ADC，（已知）∴∠ADE=12∠ADC=12×120°=60°．（角平分线性质）∴∠1=∠ADE．（等量代换）∴//AB DE．（内错角相等，两直线平行）【点睛】本题考查平行线的性质和判定，解题的关键是掌握平行线的性质和判定定理．26．如图，直线AB和CD相交于点O．（1）∠1的邻补角是____________，对顶角是___________；（2）若∠1＝40°，求出∠2，∠3，∠4的度数．解析：（1）∠2和∠4，∠3（2）∠2＝140°，∠3＝40°，∠4＝140°【分析】（1）根据对顶角和邻补角的定义解答即可；（3）根据邻补角的定义列式求出∠2，再根据对顶角相等解答．【详解】（1）∠1的邻补角是∠2和∠4，对顶角是∠3；（2）∵∠1＝40°，∴∠2=180°−∠1＝180°−40°＝140°，∴∠3＝∠1＝40°，∠4＝∠2＝140°．【点睛】本题考查了对顶角、邻补角，是基础题，熟记概念是解题的关键，要注意一个角的邻补角有两个．27．已知，//BC OA ，108B A ∠=∠=°，试解答下列问题：（1）如图①，则O ∠=__________，则OB 与AC 的位置关系为__________（2）如图②，若点E 、F 在线段BC 上，且始终保持FOC AOC ∠=∠，BOE FOE ∠=∠．则EOC ∠的度数等于__________；（3）在第（2）题的条件下，若平行移动AC 到图③所示①在AC 移动的过程中，OCB ∠与OFB ∠的数量关系是否发生改变，若不改变，求出它们之间的数量关系；若改变，请说明理由．②当OCA OEB ∠=∠时，求OCA ∠的度数．解析：（1）72°，平行；（2）36°；（3）①∠OCB=12∠OFB ；②∠OCA=54°． 【分析】（1）根据平行线的性质得出∠B+∠O=180°，求出∠O=72°，求出∠O+∠A=180°，根据平行线的判定得出即可； （2）根据角平分线定义求出1362EOC BOA ︒∠=∠=，即可得出答案； （3）①不变，求出∠OFB=2∠OCB ，即可得出答案； ②设∠BOE=∠EOF=α，∠FOC=∠COA=β，求出∠OCA=∠BOC=2α+β，α=β=18°，即可得出答案．【详解】解：（1）∵BC ∥OA ，∴∠B+∠O=180°，∵∠B=108°，∴∠O=72°，∵∠A=108°，∴∠O+∠A=180°，∴OB ∥AC ，故答案为：72°，平行；（2）∵∠FOC=∠AOC ， BOE FOE ∠=∠，∠BOA=72°， ∴11136222EOC EOF FOC BOF FOA BOA ︒∠=∠+∠=∠+∠=∠=， 故答案为：36°；（3）①不变，∵BC∥OA，∴∠OCB=∠AOC，又∵∠FOC=∠AOC，∴∠FOC=∠OCB，又∵BC∥OA，∴∠OFB=∠FOA=2∠FOC，∴∠OFB=2∠OCB，即∠OCB：∠OFB=1：2．即∠OCB=12∠OFB；②由（1）知：OB∥AC，∴∠OCA=∠BOC，由（2）可以设：∠BOE=∠EOF=α，∠FOC=∠COA=β，∴∠OCA=∠BOC=2α+β由（1）知：BC∥OA，∴∠OEB=∠EOA=α+β+β=α+2β∵∠OEB=∠OCA∴2α+β=α+2β∴α=β∵∠AOB=72°，∴α=β=18°∴∠OCA=2α+β=36°+18°=54°．【点睛】本题考查了平行线的性质，与角平分线有关的证明．能灵活运用平行线的性质和判定进行推理是解此题的关键．28．如图所示，在平面直角坐标系中，已知A（0，1）、B（2，0）、C（4，3）．（1）在平面直角坐标系中画出△ABC，作出△ABC向下平移3格后的△A1B1C1；（2）求△ABC的面积；（3）已知点Q为y轴上一点，若△ACQ的面积为8，求点Q的坐标．解析：（1）见解析；（2）4；（3）（0，5）或（0，-3）．【分析】（1）先在平面直角坐标系中描点，再连接，然后分别作出平移后的对应点，再顺次连接即可得；（2）利用割补法求解可得；（3）根据三角形面积公式求出AQ 的长，即可确定点Q 的坐标．【详解】解：（1）如图所示，（2）△ABC 的面积=111342421234222⨯-⨯⨯-⨯⨯-⨯⨯= （3）∵Q 为y 轴上一点，△ACQ 的面积为8， ∴1||482AQ ⨯⨯=， ∴AQ=4 ∴点Q 的纵坐标为：4+1=5或1-4=-3，故Q 点坐标为：（0，5）或（0，-3）．【点睛】本题主要考查的是作图-平移变换、点的坐标与图形的性质，明确△ABC 的面积=四边形的面积-3个直角三角形的面积是解题的关键．。

七年级数学（下）第五章《相交线与平行线——平行线的判定》练习题一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．下面几种说法中，正确的是A．同一平面内不相交的两条线段平行B．同一平面内不相交的两条射线平行C．同一平面内不相交的两条直线平行D．以上三种说法都不正确【答案】C2．如图所示，若∠1与∠2互补，∠2与∠4互补，则A．l3∥l4B．l2∥l5C．l1∥l5D．l1∥l2【答案】D【解析】因为∠1与∠2互补，∠2与∠4互补，可知∠1+∠2=180°，∠2+∠4=180°，所以∠1=∠4，根据内错角相等，两直线平行可得l1∥l2，故选D．3．一学员在广场上练习驾驶汽车，两次拐弯后，行驶方向与原来的方向相同，这两次拐弯的角度可能是A．第一次向右拐40°，第二次向左拐140°B．第一次向右拐40°，第二次向右拐140°C．第一次向左拐40°，第二次向左拐140°D．第一次向左拐40°，第二次向右拐40°【答案】D4．如图，是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是A．同位角相等，两直线平行B．内错角相等，两直线平行C．两直线平行，同位角相等D．两直线平行，内错角相等【答案】A【解析】三角板的∠CAB，沿着FE进行平移后角的大小没变，而平移前后的两个角是同位角，所以画图原理是“同位角相等，两直线平行”．5．如图，给出下面的推理：①∵∠B=∠BEF，∴AB∥EF；②∵∠B=∠CDE，∴AB∥CD；③∵∠B+∠BEC=180°，∴AB∥EF；④∵AB∥CD，CD∥EF，∴AB∥EF.其中正确的是A．①②③B．①②④C．①③④D．②③④【答案】B二、填空题：请将答案填在题中横线上．6．在同一平面内有四条直线a、b、c、d，已知：a∥d，b∥c，b∥d，则a和c的位置关系是__________．【答案】a∥c【解析】∵a∥d，b∥c，b∥d，∴a∥c．故答案为：a∥c．7．如图，直线a、b被直线c所截，若要a∥b，需增加条件__________（填一个即可）．【答案】答案不唯一，如∠1=∠3．【解析】∵∠1=∠3，∴a∥b（同位角相等，两直线平行），故答案为：∠1=∠3.8．如图所示，若∠1=70°，∠2=50°，∠3=60°，则________________∥________________.【答案】DE；AC三、解答题：解答应写出文字说明、证明过程或演算步骤．9．如图，已知∠1=∠3，AC平分∠DAB，你能推断出哪两条直线平行？请说明理由．【解析】可以推断出DC∥AB，理由如下：∵AC平分∠DAB，∴∠1=∠2(角平分线的定义)，又∵∠1=∠3，∴∠2=∠3(等量代换)，∴DC∥AB(内错角相等，两直线平行).10．如图，若∠1与∠B互为补角，∠B=∠E，那么直线AB与直线DE平行吗？直线BC与直线EF平行吗？为什么？【解析】BC∥EF，理由如下：∵∠1+∠B=180°，∴AB∥DE，∵∠1+∠B=180°，∠B=∠E.∴∠1+∠E=180°，又∠1=∠2，∴∠2+∠E=180°，∴BC∥EF.11．如图，已知∠A+∠ACD+∠D=360°，试说明:AB∥DE.12．如图，∠1=65°，∠2=65°，∠3=115°.试说明:DE∥BC，DF∥AB．根据图形，完成下面的推理:因为∠1=65°，∠2=65°，所以∠1=∠2.所以__________∥__________．（__________）因为AB与DE相交，所以∠1=∠4（__________），所以∠4=65°.又因为∠3=115°，所以∠3+∠4=180°.所以__________∥__________.（__________）。

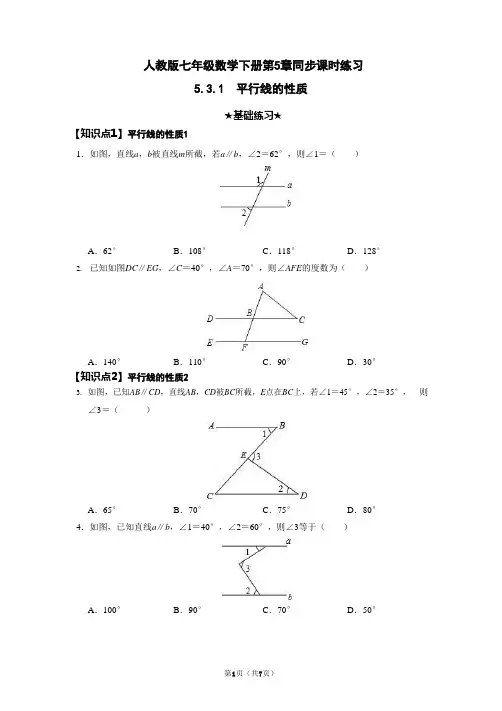
人教版七年级数学下册第5章同步课时练习5.3.1 平行线的性质★基础练习★【知识点1】平行线的性质11．如图，直线a，b被直线m所截，若a∥b，∠2＝62°，则∠1＝（）A．62°B．108°C．118°D．128°2.已知如图DC∥EG，∠C＝40°，∠A＝70°，则∠AFE的度数为（）A．140°B．110°C．90°D．30°【知识点2】平行线的性质23.如图，已知AB∥CD，直线AB，CD被BC所截，E点在BC上，若∠1＝45°，∠2＝35°，则∠3＝（）A．65°B．70°C．75°D．80°4．如图，已知直线a∥b，∠1＝40°，∠2＝60°，则∠3等于（）A．100°B．90°C．70°D．50°第1页（共7页）2【知识点3】平行线的性质35.如图，点E在AC的延长线上，AB∥CD，下列结论错误的是（）A．∠3＝∠4 B．∠A＝∠DCEC．∠1＝∠2 D．∠A+∠2+∠3＝180°6.如图，AB∥CD，∠1＝56°，FG平分∠EFD，则∠FGB的度数等于（）A．122°B．152°C．116°D．124°★提升练习★7.如图，将三角板与直尺贴在一起，使三角板的直角顶点C（∠ACB＝90°）在直尺的一边上，若∠2＝65°，则∠1的度数是（）A．15°B．25°C．35°D．65°8.如图所示，将含有30°角的三角板（∠A＝30°）的直角顶点放在相互平行的两条直线其中一条上，若∠1＝38°，则∠2的度数（）A．28°B．22°C．32°D．38°9.如图，∠BCD＝95°，AB∥DE，则∠α与∠β满足（）第3页（共7页）A ．∠α+∠β＝95°B ．∠β﹣∠α＝95°C ．∠α+∠β＝85°D ．∠β﹣∠α＝85°10. 如图，将一张长方形纸片沿EF 折叠后，使得点A 、B 分别落在点A 、B 的位置，如果∠2＝56°，那么∠1＝（）A ．56°B ．58°C ．62°D ．68°11. 如图，将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上，若∠2＝46°，则∠1的大小为（）A ．14°B ．16°C ．90°﹣αD ．α﹣44°12. 如图，直线l 1∥l 2，点A 在直线l 1上，以点A 为圆心，适当长为半径画弧，分别交直线l 1、l 2于B 、C 两点，连接AC 、BC ．若∠ABC ＝54°，则∠1的度数为（）A ．36°B ．54°C ．60°D ．72°13．如图，l 1∥l 2，l 4∥l 3，若∠1＝50°，则∠2＝．14. 如图，三角板直角顶点落在长方形纸片的一边上，∠1＝35°，则∠2＝ °．15.如图，将一张长方形的纸片沿折痕EF翻折，使点C、D分别落在点M、N的位置，且∠BFM= 1∠EFM，则∠AEN的度数为．216.如图所示，已知AD∥BC，BE平分∠ABC，∠A＝110°．求∠ADB的度数．17．如图，AB∥CD，∠CEF＝60°，∠ECD＝125°，求∠A的度数．18.如图，AB∥CD，AC交BD于点O，∠A＝40°，∠D＝45°．求∠1和∠2的度数．★拓展探究突破练习★19.如图，已知AM∥BN，∠A＝64°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．（1）①∠ABN的度数是；②∵AM∥BN，∴∠ACB＝∠；（2）求∠CBD的度数；（3）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由：若变化，请写出变化规律；（4）当点P运动到使∠ACB＝∠ABD时，∠ABC的度数是．第5页（共7页）参考答案1．C ．2．B ．3．D ．4．A ．5．A ．6．B ．7．B ．8．B ．9．D ．10．C ．11．B ． 12．D ．13．50°．14．55．15．36°．16. 解：如图所示：∵AD ∥BC ，∴∠A +∠ABC ＝180°，∠ADB ＝∠CBD ， 又∵∠A ＝110°，∴∠ABC ＝180°﹣110°＝70°， 又∵BE 平分∠ABC ， ∴∠CBD = 1²A 捸ᗂ2∴∠CBD = 1 × 11ᗂ° = 捸捸°，2 ∴∠ADB ＝55°．17. 解：如图，过点E 作EG ∥AB ， ∵AB ∥CD ， ∴EG ∥CD ， ∴∠GEC +∠C ＝180°∴∠GEC ＝180°﹣125°＝55° ∵EG ∥AB∴∠A ＝∠FEG ＝∠FEC +∠CEG ＝60°+55°＝115°． 答：∠A 的度数为115°．18. 解：∵AB ∥CD ，∴∠1＝∠A ， ∵∠A ＝40°， ∴∠1＝40°，又∵∠2＝∠D +∠1，∠D ＝45°， ∴∠2＝85°，由上可得，∠1的度数是40°，∠2的度数是85°． 19．解：（1）①∵AM ∥BN ，∠A ＝64°， ∴∠ABN ＝180°﹣∠A ＝116°， 故答案为：116°； ②∵AM ∥BN ， ∴∠ACB ＝∠CBN ，故答案为：CBN；（2）∵AM∥BN，∴∠ABN+∠A＝180°，∴∠ABN＝180°﹣64°＝116°，∴∠ABP+∠PBN＝116°，∵BC平分∠ABP，BD平分∠PBN，∴∠ABP＝2∠CBP，∠PBN＝2∠DBP，∴2∠CBP+2∠DBP＝116°，∴∠CBD＝∠CBP+∠DBP＝58°；（3）不变，∠APB：∠ADB＝2：1，∵AM∥BN，∴∠APB＝∠PBN，∠ADB＝∠DBN，∵BD平分∠PBN，∴∠PBN＝2∠DBN，∴∠APB：∠ADB＝2：1；（4）∵AM∥BN，∴∠ACB＝∠CBN，当∠ACB＝∠ABD时，则有∠CBN＝∠ABD，∴∠ABC+∠CBD＝∠CBD+∠DBN∴∠ABC＝∠DBN，由（1）∠ABN＝116°，∴∠CBD＝58°，∴∠ABC+∠DBN＝58°，∴∠ABC＝29°，故答案为：29°．第7页（共7页）。

2020年春季人教版七年级下册同步练习：5.4 平移一．选择题（共8小题）1．下列现象中是平移的是（）A．将一张纸沿它的中线折叠B．电梯的上下移动C．飞碟的快速转动D．翻开书中的每一页纸张2．下列现象中，不属于平移的是（）A．滑雪运动员在平坦的雪地上滑行B．钟摆的摆动C．大楼上上下下迎送来客的电梯D．火车在笔直的铁轨上飞驰而过3．同桌读了：“子非鱼焉知鱼之乐乎？”后，兴高采烈地利用电脑画出了几幅鱼的图案，请问：由图中所示的图案通过平移后得到的图案是（）A．B．C．D．4．如图，直线L1是由直线L2平移得到的，若∠1＝56°，则∠2的度数为（）A．∠2＝56°B．∠2＝124°C．∠2＝134°D．∠2＝114°5．如图，俄罗斯方块游戏中，图形A经过平移使其填补空位，则正确的平移方式是（）A．先向右平移5格，再向下平移3格B．先向右平移4格，再向下平移5格C．先向右平移4格，再向下平移4格D．先向右平移3格，再向下平移5格6．如图，△ABC沿着BC方向平移到△DEF，已知BC＝6、EC＝2，那么平移的距离为（）A．2 B．4 C．6 D．87．如图，表示直线a平移得到直线b的两种画法，下列关于三角板平移的方向和移动的距离说法正确的是（）A．方向相同，距离相同B．方向不同，距离不同C．方向相同，距离不同D．方向不同，距离相同8．将△ABC沿BC方向平移3个单位得△DEF．若△ABC的周长等于8，则四边形ABFD 的周长为（）A．14 B．12 C．10 D．8二．填空题（共4小题）9．把图形上的所有点都按照作的位置移动，叫作图形的平移．10．如图，某宾馆在重新装修后，准备在大厅的楼梯上铺上某种规格红色地毯，其侧面如图所示，则至少需要购买地毯米．11．如图，将周长为18cm的△ABC沿BC平移1cm得到△DEF．则AD＝cm．12．如图，面积为6cm2的直角三角形ABC沿BC方向平移至三角形DEF的位置，平移距离是BC的2倍，则图中四边形ABED的面积为cm2．三．解答题（共6小题）13．如图所示是9个全等三角形，其中有没有经过平移可以与另一个重合的？如果有，把它们找出来．14．先将方格纸中的图形向右平移3格，然后再向下平移2格．15．如图，在平面直角坐标系中，点A（0，﹣1），B（﹣3，﹣3），C（1，﹣3），将三角形ABC平移，使点A的对应点A'的坐标为（2，3）．（1）画出平移后的三角形A'B'C'；（2）点B'的坐标是．16．根据图中标示的数据，计算图形的周长（单位：mm）17．一座楼梯的示意图如图所示，现要在楼梯上铺一条地毯．（1）地毯至少需要多长？（2）如果楼梯的宽为b，那么地毯的面积为多少？18．如图，将三角形ABC沿AB方向平移AD距离得到三角形DEF，已知：AB＝16，BE＝6，EF＝8，CG＝1，求图中阴影部分的面积．参考答案一．选择题（共8小题）1．【解答】解：A、将一张纸沿它的中线折叠，不符合平移定义，故本选项错误；B、电梯的上下移动，符合平移的定义，故本选项正确；C、飞蝶的快速转动，不符合平移定义，故本选项错误；D、翻开书中的每一页纸张，不符合平移的定义，故本选项错误．故选：B．2．【解答】解：A、滑雪运动员在平坦的雪地上滑雪，属于平移得到，故本选项不合题意；B、钟摆的摆动，不属于平移得到，故本选项符合题意；C、大楼上上下下迎送来客的电梯，属于平移得到，故本选项不合题意；D、火车在笔直的铁轨上飞驰而过，属于平移得到，故本选项不合题意．故选：B．3．【解答】解：A、由图中所示的图案通过旋转而成，故本选项错误；B、由图中所示的图案通过翻折而成，故本选项错误C、由图中所示的图案通过旋转而成，故本选项错误；D、由图中所示的图案通过平移而成，故本选项正确．故选：D．4．【解答】解：∵直线L1是由直线L2平移得到的，∴L1∥L2，∴∠3＝∠1＝56°，∵∠3+∠2＝180°，∴∠2＝180°﹣56°＝124°．故选：B．5．【解答】解：图形A经过平移使其填补空位，则正确的平移方式是先向右平移4格，再向下平移4格．故选：C．6．【解答】解：由题意平移的距离为BE＝BC﹣EC＝6﹣2＝4，故选：B．7．【解答】解：由图和平移可得：三角板平移的方向不同，距离不同，故选：B．8．【解答】解：∵△ABC沿BC方向平移3个单位得△DEF，∴AD＝CF＝3cm，AC＝DF，∵△ABC的周长等于8，∴AB+BC+AC＝8，∴四边形ABFD的周长＝AB+BF+DF+AD＝AB+BC+CF+AC+AD＝8+3+3＝14（cm）．故选：A．二．填空题（共4小题）9．【解答】解：把图形上的所有点都按照同一方向作平行的位置移动，叫作图形的平移．故答案为：同一方向，平行．10．【解答】解：如图，利用平移线段，把楼梯的横竖向上向左平移，构成一个矩形，长宽分别为5.8米，2.6米，∴地毯的长度为2.6+5.8＝8.4米．故答案为：8.411．【解答】解：∵△ABC沿BC平移1cm得到△DEF．∴AD＝1cm．故答案为1．12．【解答】解：∵平移的距离是边BC长的两倍，∴BC＝CE＝EF，∴四边形ACED的面积是三个△ABC的面积；∴四边形ABED的面积＝6×（1+3）＝24cm2．故答案为：24．三．解答题（共6小题）13．【解答】解：如图所示：只有①和⑧经过平移可以与另一个重合．14．【解答】解：如图•，15．【解答】解：（1）如图，△A'B'C'为所作；（2）点B'的坐标为（﹣1，1）．故答案为（﹣1，1）．16．【解答】解：如图形的周长＝（29+14+10+11+2）×2＝132mm．17．【解答】解：（1）由题意得，地毯的长度为：a+h；（2）地毯的面积为：（a+h）b．18．【解答】解：∵将三角形ABC沿AB方向平移AD距离得到三角形DEF，AB＝16，BE ＝6，EF＝8，CG＝1，∴AB＝DE＝16，EF＝BC＝8，∴BD＝16﹣8＝8，BG＝8﹣1＝7，∴图中阴影部分的面积为：×8×7＝28．。

七年级数学（下）第五章《相交线与平行线——同位角、内错角、同旁内角》练习题一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．如图，以下说法正确的是A．∠1和∠2是内错角B．∠2和∠3是同位角C．∠1和∠3是内错角D．∠2和∠4是同旁内角【答案】C【解析】观察图形可得，∠1和∠2是同位角、∠2和∠3是对顶角、∠1和∠3是内错角、∠2和∠4是邻补角，所以正确的答案为C，故选C．2．如图，下列说法错误的是A．∠A与∠EDC是同位角B．∠A与∠ABF是内错角C．∠A与∠ADC是同旁内角D．∠A与∠C是同旁内角【答案】D3．如图所示，∠1与∠2不是同位角的是A．B．C．D．【答案】B【解析】A中，∠1与∠2有一边在同一条直线上，另一条边在被截线的同一方，是同位角，不符合题意；B中，∠1与∠2的两条边都不在同一条直线上，不是同位角，符合题意；C中，∠1与∠2有一条边在同一条直线上，另一条边在被截线的同一方，是同位角，不符合题意；D中，∠1与∠2有一边在同一条直线上，另一条边在被截线的同一方，是同位角，不符合题意.故选B．4．如图，属于内错角的是A．∠1和∠2 B．∠2和∠3C．∠1和∠4 D．∠3和∠4【答案】D5．∠1与∠2是直线a，b被直线c所截得的同位角，∠1与∠2的大小关系是A．∠1=∠2 B．∠1>∠2C．∠1<∠2 D．无法确定【答案】D【解析】因为不知道直线a、b之间的位置关系，所以∠1与∠2的大小关系无法确定．故选D．二、填空题：请将答案填在题中横线上．6．如图，如果∠2=100°，那么∠1的同位角等于__________，∠1的内错角等于__________，∠1的同旁内角等于__________.【答案】80°，80°，100°7．如图，∠ABC 与__________是同位角；∠ADB 与__________是内错角；∠ABC 与__________是同旁内角．【答案】∠EAD ，∠DBC 和∠EAD ，∠DAB 和∠BCD 【解析】根据同位角，内错角和同旁内角的概念进行判断， （1）ABC ∠与EAD ∠是同位角；（2）ADB ∠与DBC EAD ∠∠，是内错角； （3）ABC ∠与DAB BCD ∠∠，是同旁内角.故答案为：∠EAD ，∠DBC 和∠EAD ，∠DAB 和∠BCD ． 三、解答题：解答应写出文字说明、证明过程或演算步骤．8．如图，∠A 与哪个角是内错角，与哪个角是同旁内角？它们分别是哪两条直线被哪一条直线所截形成的？【解析】根据内错角的边构成“Z ”形，同旁内角的边构成“U ”形进行分析即可．A ∠与ACD ∠是内错角，它是直线AB ，DE 被直线AC 所截形成的； A ∠与ACB ∠是同旁内角，它是直线AB ，BC 被直线AC 所截形成的； A ∠与ACE ∠是同旁内角，它是直线AB ，CD 被直线AC 所截形成的；A∠是同旁内角，它是直线BC，AC被直线AB所截形成的．∠与B9．如图：（1）找出直线DC，AC被直线BE所截形成的同旁内角；（2）指出∠DEF与∠CFE是由哪两条直线被哪一条直线所截形成的什么角；（3）试找出图中与∠DAC是同位角的所有角．10．如图所示，如果内错角∠1与∠5相等，那么与∠1相等的角还有吗？与∠1互补的角有吗？如果有，请写出来，并说明你的理由.【解析】∠1=∠2，与∠1互补的角有∠3和∠4.理由：因为∠1=∠5，∠5=∠2，所以∠1=∠2.因为∠1=∠5，且∠5与∠3和∠4互补，所以与∠1互补的角有∠3和∠4.。

人教版七年级数学下册第五章相交线与平行线 5.1 相交线同步练习一、单选题（共10题；共30分）1.如图所示，∠1和∠2是对顶角的图形有( )A. 1个B. 2个C. 3个D. 4个2.如图，下列说法不正确的是（）A. ∠1和∠2是同旁内角B. ∠1和∠3是对顶角C. ∠3和∠4是同位角D. ∠1和∠4是内错角3.如图所示，∠1和∠2是对顶角的是（）A. B. C. D.4.下列说法中正确的个数为（）①两条直线相交成四个角，如果有两个角相等，那么这两条直线垂直；②两条直线相交成四个角，如果有一个角是直角，那么这两条直线垂直；③一条直线的垂线可以画无数条；④在同一平面内，经过一个已知点能画一条且只能画一条直线和已知直线垂直．A. 1B. 2C. 3D. 45.如图，∠1=15°，∠AOC=90°，点B，O，D在同一直线上，则∠2的度数为（）A. 75°B. 15°C. 105°D. 165°6.如图所示，下列说法错误的是（）A. ∠A和∠B是同旁内角B. ∠A和∠3是内错角C. ∠1和∠3是内错角D. ∠C和∠3是同位角7.如图，三条直线相交于点O．若CO⊥AB，∠1=56°，则∠2等于（）A. 30°B. 34°C. 45°D. 56°8.在下列语句中，正确的是（）．A. 在平面上，一条直线只有一条垂线;B. 过直线上一点的直线只有一条;C. 过直线上一点且垂直于这条直线的直线有且只有一条;D. 垂线段就是点到直线的距离9.如图，下列6种说法：①∠1与∠4是内错角；②∠1与∠2是同位角；③∠2与∠4是内错角；④∠4与∠5是同旁内角；⑤∠2与∠4是同位角；⑥∠2与∠5是内错角．其中正确的有( )A. 1个B. 2个C. 3个D. 4个10.如图所示，OA⊥OC，OB⊥OD，下面结论中，其中说法正确的是（）①∠AOB＝∠COD；②∠AOB＋∠COD＝90°；③∠BOC＋∠AOD＝180°；④∠AOC－∠COD＝∠BOC.A. ①②③B. ①②④C. ①③④D. ②③④二、填空题（共10题；共30分）11.如图，直线AB，CD相交于点O，EO⊥AB，垂足为点O，若∠AOD=132°，则∠EOC=________12.如图，已知直线AB与CD相交于点O，OA平分∠COE，若∠DOE=70°，则∠BOD=________．13.如图，∠1和∠2是________角，∠2和∠3 是________角。

第五章相交线与平行线1相交线学习要求1．能从两条直线相交所形成的四个角的关系入手，理解对顶角、互为邻补角的概念，掌握对顶角的性质．2．能依据对顶角的性质、邻补角的概念等知识，进行简单的计算．课堂学习检测一、填空题1．如果两个角有一条______边，并且它们的另一边互为____________，那么具有这种关系的两个角叫做互为邻补角．2．如果两个角有______顶点，并且其中一个角的两边分别是另一个角两边的___________ ________，那么具有这种位置关系的两个角叫做对顶角．3．对顶角的重要性质是_________________．4．如图，直线AB、CD相交于O点，∠AOE＝90°．(1)∠1和∠2叫做______角；∠1和∠4互为______角；∠2和∠3互为_______角；∠1和∠3互为______角；∠2和∠4互为______角．(2)若∠1＝20°，那么∠2＝______；∠3＝∠BOE－∠______＝______°－______°＝______°；∠4＝∠______－∠1＝______°－______°＝______°．5．如图，直线AB与CD相交于O点，且∠COE＝90°，则(1)与∠BOD互补的角有________________________；(2)与∠BOD互余的角有________________________；(3)与∠EOA互余的角有________________________；(4)若∠BOD＝42°17′，则∠AOD＝__________；∠EOD＝______；∠AOE＝______．二、选择题6．图中是对顶角的是( )．7．如图，∠1的邻补角是( )．(A)∠BOC (B)∠BOC 和∠AOF (C)∠AOF(D)∠BOE 和∠AOF8．如图，直线AB 与CD 相交于点O ，若AOD AOC ∠=∠31，则∠BOD 的度数为( )． (A)30° (B)45° (C)60°(D)135°9．如图所示，直线l 1，l 2，l 3相交于一点，则下列答案中，全对的一组是( )．(A)∠1＝90°，∠2＝30°，∠3＝∠4＝60° (B)∠1＝∠3＝90°，∠2＝∠4＝30° (C)∠1＝∠3＝90°，∠2＝∠4＝60° (D)∠1＝∠3＝90°，∠2＝60°，∠4＝30° 三、判断正误10．如果两个角相等，那么这两个角是对顶角．( )11．如果两个角有公共顶点且没有公共边，那么这两个角是对顶角．( )12．有一条公共边的两个角是邻补角．( ) 13．如果两个角是邻补角，那么它们一定互为补角． ( ) 14．对顶角的角平分线在同一直线上．( ) 15．有一条公共边和公共顶点，且互为补角的两个角是邻补角．( )综合、运用、诊断一、解答题16．如图所示，AB ，CD ，EF 交于点O ，∠1＝20°，∠BOC ＝80°，求∠2的度数．17．已知：如图，直线a ，b ，c 两两相交，∠1＝2∠3，∠2＝86°．求∠4的度数．18．已知：如图，直线AB，CD相交于点O，OE平分∠BOD，OF平分∠COB，∠AOD∶∠DOE＝4∶1．求∠AOF的度数．19．如图，有两堵围墙，有人想测量地面上两堵围墙内所形成的∠AOB的度数，但人又不能进入围墙，只能站在墙外，请问该如何测量?拓展、探究、思考20．如图，O是直线CD上一点，射线OA，OB在直线CD的两侧，且使∠AOC＝∠BOD，试确定∠AOC与∠BOD是否为对顶角，并说明你的理由．21．回答下列问题：(1)三条直线AB，CD，EF两两相交，图形中共有几对对顶角(平角除外)?几对邻补角?(2)四条直线AB，CD，EF，GH两两相交，图形中共有几对对顶角(平角除外)?几对邻补角?(3)m条直线a1，a2，a3，…，a m－1，a m相交于点O，则图中一共有几对对顶角(平角除外)?几对邻补角?2 垂线学习要求1．理解两条直线垂直的概念，掌握垂线的性质，能过一点作已知直线的垂线．2．理解点到直线的距离的概念，并会度量点到直线的距离．课堂学习检测一、填空题1．当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线______，其中一条直线叫做另一条直线的______线，它们的交点叫做______．2．垂线的性质性质1：平面内，过一点____________与已知直线垂直．性质2：连接直线外一点与直线上各点的_________中，_________最短．3．直线外一点到这条直线的__________________叫做点到直线的距离．4．如图，直线AB，CD互相垂直，记作______；直线AB，CD互相垂直，垂足为O点，记作____________；线段PO的长度是点_________到直线_________的距离；点M到直线AB的距离是_______________．二、按要求画图5．如图，过A点作CD⊥MN，过A点作PQ⊥EF于B．图a 图b 图c6．如图，过A点作BC边所在直线的垂线EF，垂足是D，并量出A点到BC边的距离．图a 图b 图c7．如图，已知∠AOB及点P，分别画出点P到射线OA、OB的垂线段PM及PN．图a 图b 图c8．如图，小明从A村到B村去取鱼虫，将鱼虫放到河里，请作出小明经过的最短路线．综合、运用、诊断一、判断下列语句是否正确(正确的画“√”，错误的画“×”)9．两条直线相交，若有一组邻补角相等，则这两条直线互相垂直．( ) 10．若两条直线相交所构成的四个角相等，则这两条直线互相垂直．( ) 11．一条直线的垂线只能画一条．( ) 12．平面内，过线段AB外一点有且只有一条直线与AB垂直．( ) 13．连接直线l外一点到直线l上各点的6个有线段中，垂线段最短．( ) 14．点到直线的距离，是过这点画这条直线的垂线，这点与垂足的距离．( ) 15．直线外一点到这条直线的垂线段，叫做点到直线的距离．( )16．在三角形ABC 中，若∠B ＝90°，则AC ＞AB ． ( )二、选择题17．如图，若AO ⊥CO ，BO ⊥DO ，且∠BOC ＝α，则∠AOD 等于( )．(A)180°－2α(B)180°－α (C)α2190+︒(D)2α－90°18．如图，点P 为直线m 外一点，点P 到直线m 上的三点A 、B 、C 的距离分别为P A ＝4cm ，PB ＝6cm ，PC ＝3cm ，则点P 到直线m 的距离为( )． (A)3cm(B)小于3cm(C)不大于3cm(D)以上结论都不对19．如图，BC ⊥AC ，CD ⊥AB ，AB ＝m ，CD ＝n ，则AC 的长的取值范围是( )．(A)AC ＜m (B)AC ＞n (C)n ≤AC ≤m(D)n ＜AC ＜m20．若直线a 与直线b 相交于点A ，则直线b 上到直线a 距离等于2cm 的点的个数是( )． (A)0(B)1(C)2(D)321．如图，AC ⊥BC 于点C ，CD ⊥AB 于点D ，DE ⊥BC于点E ，能表示点到直线(或线段)的距离的线段有( )． (A)3条 (B)4条 (C)7条(D)8条三、解答题22．已知：OA ⊥OC ，∠AOB ∶∠AOC ＝2∶3．求∠BOC 的度数．23．已知：如图，三条直线AB ，CD ，EF 相交于O ，且CD ⊥EF ，∠AOE ＝70°，若OG平分∠BOF ．求∠DOG ．拓展、探究、思考24．已知平面内有一条直线m 及直线外三点A ，B ，C ，分别过这三个点作直线m 的垂线，想一想有几个不同的垂足?画图说明．25．已知点M ，试在平面内作出四条直线l 1，l 2，l 3，l 4，使它们分别到点M 的距离是1.5cm ．·M26．从点O 引出四条射线OA ，OB ，OC ，OD ，且AO ⊥BO ，CO ⊥DO ，试探索∠AOC与∠BOD 的数量关系．27．一个锐角与一个钝角互为邻角，过顶点作公共边的垂线，若此垂线与锐角的另一边构成75直角，与钝角的另一边构成直73角，则此锐角与钝角的和等于直角的多少倍?3 同位角、内错角、同旁内角学习要求当两条直线被第三条直线所截时，能从所构成的八个角中识别出哪两个角是同位角、内错角及同旁内角．课堂学习检测一、填空题1．如图，若直线a ，b 被直线c 所截，在所构成的八个角中指出，下列各对角之间是属于哪种特殊位置关系的角?(1)∠1与∠2是_______；(2)∠5与∠7是______； (3)∠1与∠5是_______；(4)∠5与∠3是______； (5)∠5与∠4是_______；(6)∠8与∠4是______； (7)∠4与∠6是_______；(8)∠6与∠3是______； (9)∠3与∠7是______；(10)∠6与∠2是______．2．如图2所示，图中用数字标出的角中，同位角有______；内错角有______；同旁内角有______．3．如图3所示，(1)∠B 和∠ECD 可看成是直线AB 、CE 被直线______所截得的_______角； (2)∠A 和∠ACE 可看成是直线_______、______被直线_______所截得的______角． 4．如图4所示，(1)∠AED 和∠ABC 可看成是直线______、______被直线______所截得的_______角；图2 图3 图4(2)∠EDB和∠DBC可看成是直线______、______被直线_______所截得的______角；(3)∠EDC和∠C可看成是直线_______、______被直线______所截得的______角．综合、运用、诊断一、选择题5．已知图①～④，图①图②图③图④在上述四个图中，∠1与∠2是同位角的有( )．(A)①②③④(B)①②③(C)①③(D)①6．如图，下列结论正确的是( )．(A)∠5与∠2是对顶角(B)∠1与∠3是同位角(C)∠2与∠3是同旁内角(D)∠1与∠2是同旁内角7．如图，∠1和∠2是内错角，可看成是由直线( )．(A)AD，BC被AC所截构成(B)AB，CD被AC所截构成(C)AB，CD被AD所截构成(D)AB，CD被BC所截构成8．如图，直线AB，CD与直线EF，GH分别相交，图中的同旁内角共有( )．(A)4对(B)8对(C)12对(D)16对拓展、探究、思考一、解答题9．如图，三条直线两两相交，共有几对对顶角?几对邻补角?几对同位角?几对内错角?几对同旁内角?4 平行线及平行线的判定学习要求1．理解平行线的概念，知道在同一平面内两条直线的位置关系，掌握平行公理及其推论．2．掌握平行线的判定方法，能运用所学的“平行线的判定方法”，判定两条直线是否平行．用作图工具画平行线，从而学习如何进行简单的推理论证．课堂学习检测一、填空题1．在同一平面内，______的两条直线叫做平行线．若直线a与直线b平行，则记作______．2．在同一平面内，两条直线的位置关系只有______、______．3．平行公理是：_______________________________________________________________．4．平行公理的推论是如果两条直线都与______，那么这两条直线也______．即三条直线a，b，c，若a∥b，b∥c，则______．5．两条直线平行的条件(除平行线定义和平行公理推论外)：(1)两条直线被第三条直线所截，如果____________，那么这两条直线平行．这个判定方法1可简述为：____________，两直线平行．(2)两条直线被第三条直线所截，如果____________，那么____________．这个判定方法2可简述为：____________，____________．(3)两条直线被第三条直线所截，如果____________，那么____________．这个判定方法3可简述为：____________，____________．二、根据已知条件推理6．已知：如图，请分别依据所给出的条件，判定相应的哪两条直线平行?并写出推理的根据．(1)如果∠2＝∠3，那么____________．(____________，____________)(2)如果∠2＝∠5，那么____________．(____________，____________)(3)如果∠2＋∠1＝180°，那么____________．(____________，____________)(4)如果∠5＝∠3，那么____________．(____________，____________)(5)如果∠4＋∠6＝180°，那么____________．(____________，____________)(6)如果∠6＝∠3，那么____________．(____________，____________)7．已知：如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．(1)∵∠B＝∠3(已知)，∴______∥______．(____________，____________)(2)∵∠1＝∠D(已知)，∴______∥______．(____________，____________)(3)∵∠2＝∠A(已知)，∴______∥______．(____________，____________)(4)∵∠B＋∠BCE＝180°(已知)，∴______∥______．(____________，____________)综合、运用、诊断一、依据下列语句画出图形8．已知：点P是∠AOB内一点．过点P分别作直线CD∥OA，直线EF∥OB．9．已知：三角形ABC及BC边的中点D．过D点作DF∥CA交AB于M，再过D点作DE∥AB交AC于N点．二、解答题10．已知：如图，∠1＝∠2．求证：AB∥CD．(1)分析：如图，欲证AB∥CD，只要证∠1＝______．证法1：∵∠1＝∠2，(已知)又∠3＝∠2，( )∴∠1＝_______．( )∴AB∥CD．(___________，___________)(2)分析：如图，欲证AB∥CD，只要证∠3＝∠4．证法2：∵∠4＝∠1，∠3＝∠2，( )又∠1＝∠2，(已知)从而∠3＝_______．( )∴AB∥CD．(___________，___________)11．绘图员画图时经常使用丁字尺，丁字尺分尺头、尺身两部分，尺头的里边和尺身的上边应平直，并且一般互相垂直，也有把尺头和尺身用螺栓连接起来，可以转动尺头，使它和尺身成一定的角度．用丁字尺画平行线的方法如下面的三个图所示．画直线时要按住尺身，推移丁字尺时必须使尺头靠紧图画板的边框．请你说明：利用丁字尺画平行线的理论依据是什么?拓展、探究、思考12．已知：如图，CD ⊥DA ，DA ⊥AB ，∠1＝∠2．试确定射线DF 与AE 的位置关系，并说明你的理由．(1)问题的结论：DF ______AE ．(2)证明思路分析：欲证DF ______AE ，只要证∠3＝______． (3)证明过程：证明：∵CD ⊥DA ，DA ⊥AB ，( )∴∠CDA ＝∠DAB ＝______°．(垂直定义) 又∠1＝∠2，( )从而∠CDA －∠1＝______－______，(等式的性质) 即∠3＝＿＿＿．∴DF ＿＿＿AE ．(＿＿＿＿，＿＿＿＿)13．已知：如图，∠ABC ＝∠ADC ，BF 、DE 分别平分∠ABC 与∠ADC ．且∠1＝∠3． 求证：AB ∥DC ．证明：∵∠ABC ＝∠ADC ，.2121ADC ABC ∠=∠∴( ) 又∵BF 、DE 分别平分∠ABC 与∠ADC ，.212,211ADC ABC ∠=∠∠=∠∴ ( ) ∴∠______＝∠______．( ) ∵∠1＝∠3，( ) ∴∠2＝∠______．(等量代换) ∴______∥______．( )14．已知：如图，∠1＝∠2，∠3＋∠4＝180°．试确定直线a 与直线c 的位置关系，并说明你的理由．(1)问题的结论：a______c．(2)证明思路分析：欲证a______c，只要证______∥______且______∥______．(3)证明过程：证明：∵∠1＝∠2，( )∴a∥______．(________，________)①∵∠3＋∠4＝180°，( )∴c∥______．(________，________)②由①、②，因为a∥______，c∥______，∴a______c．(________，________)5 平行线的性质学习要求1．掌握平行线的性质，并能依据平行线的性质进行简单的推理．2．了解平行线的判定与平行线的性质的区别．3．理解两条平行线的距离的概念．课堂学习检测一、填空题1．平行线具有如下性质：(1)性质1：______被第三条直线所截，同位角______．这个性质可简述为两直线______，同位角______．(2)性质2：两条平行线__________________，_______相等．这个性质可简述为_____________，_____________．(3)性质3：__________________，同旁内角______．这个性质可简述为_____________，__________________．2．同时______两条平行线，并且夹在这两条平行线间的______________叫做这两条平行线的距离．二、根据已知条件推理3．如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．(1)如果AB∥EF，那么∠2＝______．理由是____________________________________．(2)如果AB∥DC，那么∠3＝______．理由是____________________________________．(3)如果AF∥BE，那么∠1＋∠2＝______．理由是______________________________．(4)如果AF∥BE，∠4＝120°，那么∠5＝______．理由是________________________．4．已知：如图，DE∥AB．请根据已知条件进行推理，分别得出结论，并在括号内注明理由．(1)∵DE∥AB，( )∴∠2＝______．(__________，__________)(2)∵DE∥AB，( )∴∠3＝______．(__________，__________)(3)∵DE∥AB( )，∴∠1＋______＝180°．(______，______)综合、运用、诊断一、解答题5．如图，∠1＝∠2，∠3＝110°，求∠4．解题思路分析：欲求∠4，需先证明______∥______．解：∵∠1＝∠2，( )∴______∥______．(__________，__________)∴∠4＝______＝______°．(__________，__________)6．已知：如图，∠1＋∠2＝180°．求证：∠3＝∠4．证明思路分析：欲证∠3＝∠4，只要证______∥______．证明：∵∠1＋∠2＝180°，( )∴______∥______．(__________，__________)∴∠3＝∠4．(______，______)7．已知：如图，AB∥CD，∠1＝∠B．求证：CD是∠BCE的平分线．证明思路分析：欲证CD是∠BCE的平分线，只要证______＝______．证明：∵AB∥CD，( )∴∠2＝______．(____________，____________)但∠1＝∠B，( )∴______＝______．(等量代换)即CD是________________________．8．已知：如图，AB∥CD，∠1＝∠2．求证：BE∥CF．证明思路分析：欲证BE∥CF，只要证______＝______．证明：∵AB∥CD，( )∴∠ABC＝______．(____________，____________)∵∠1＝∠2，( )∴∠ABC－∠1＝______－______，( )即______＝______．∴BE∥CF．(__________，__________)9．已知：如图，AB∥CD，∠B＝35°，∠1＝75°．求∠A的度数．解题思路分析：欲求∠A，只要求∠ACD的大小．解：∵CD∥AB，∠B＝35°，( )∴∠2＝∠______＝_______°．(____________，____________)而∠1＝75°，∴∠ACD＝∠1＋∠2＝______°．∵CD∥AB，( )∴∠A＋______＝180°．(____________，____________)∴∠A＝_______＝______．10．已知：如图，四边形ABCD 中，AB ∥CD ，AD ∥BC ，∠B ＝50°．求∠D 的度数．分析：可利用∠DCE 作为中间量过渡． 解法1：∵AB ∥CD ，∠B ＝50°，( )∴∠DCE ＝∠_______＝_______°． (____________，______) 又∵AD ∥BC ，( )∴∠D ＝∠______＝_______°．(____________，____________)想一想：如果以∠A 作为中间量，如何求解? 解法2：∵AD ∥BC ，∠B ＝50°，( )∴∠A ＋∠B ＝______．(____________，____________) 即∠A ＝______－______＝______°－______°＝______°． ∵DC ∥AB ，( )∴∠D ＋∠A ＝______．(_____________，_____________) 即∠D ＝______－______＝______°－______°＝______°．11．已知：如图，AB ∥CD ，AP 平分∠BAC ，CP 平分∠ACD ，求∠APC 的度数．解：过P 点作PM ∥AB 交AC 于点M ．∵AB ∥CD ，( )∴∠BAC ＋∠______＝180°．( ) ∵PM ∥AB ，∴∠1＝∠_______，( )且PM ∥_______．(平行于同一直线的两直线也互相平行) ∴∠3＝∠______．(两直线平行，内错角相等) ∵AP 平分∠BAC ，CP 平分∠ACD ，( )∠=∠∴211______，∠=∠214______．( ) 90212141=∠+∠=∠+∠∴ACD BAC ．( )∴∠APC ＝∠2＋∠3＝∠1＋∠4＝90°．( ) 总结：两直线平行时，同旁内角的角平分线______．拓展、探究、思考12．已知：如图，AB ∥CD ，EF ⊥AB 于M 点且EF 交CD 于N 点．求证：EF ⊥CD ．13．如图，DE∥BC，∠D∶∠DBC＝2∶1，∠1＝∠2，求∠E的度数．14．问题探究：(1)如果一个角的两条边与另一个角的两条边分别平行，那么这两个角的大小有何关系?举例说明．(2)如果一个角的两边与另一个角的两边分别垂直，那么这两个角的大小有何关系?举例说明．15．如图，AB∥DE，∠1＝25°，∠2＝110°，求∠BCD的度数．16．如图，AB，CD是两根钉在木板上的平行木条，将一根橡皮筋固定在A，C两点，点E是橡皮筋上的一点，拽动E点将橡皮筋拉紧后，请你探索∠A，∠AEC，∠C之间具有怎样的关系并说明理由．(提示：先画出示意图，再说明理由)．6 命题学习要求1．知道什么是命题，知道一个命题是由“题设”和“结论”两部分构成的．2．对于给定的命题，能找出它的题设和结论，并会把该命题写成“如果……，那么……”的形式．能判定该命题的真假．课堂学习检测一、填空题1．______一件事件的______叫做命题．2．许多命题都是由______和______两部分组成．其中题设是____________，结论是______ _____．3．命题通常写成“如果……，那么……．”的形式．这时，“如果”后接的部分是______，“那么”后接的部分是______．4．所谓真命题就是：如果题设成立，那么结论就______的命题．相反，所谓假命题就是：如果题设成立，不能保证结论______的命题．二、指出下列命题的题设和结论5．垂直于同一条直线的两条直线平行．题设是___________________________________________________________；结论是___________________________________________________________．6．同位角相等，两直线平行．题设是___________________________________________________________；结论是___________________________________________________________．7．两直线平行，同位角相等．题设是___________________________________________________________；结论是___________________________________________________________．8．对顶角相等．题设是___________________________________________________________；结论是___________________________________________________________．三、将下列命题改写成“如果……，那么……”的形式9．90°的角是直角．__________________________________________________________________．10．末位数字是零的整数能被5整除．__________________________________________________________________．11．等角的余角相等．__________________________________________________________________．12．同旁内角互补，两直线平行．__________________________________________________________________．综合、运用、诊断一、下列语句哪些是命题，哪些不是命题?13．两条直线相交，只有一个交点．( ) 14． 不是有理数．( )15．直线a与b能相交吗?( ) 16．连接AB．( )17．作AB⊥CD于E点．( ) 18．三条直线相交，有三个交点．( )二、判断下列各命题中，哪些命题是真命题?哪些是假命题?(对于真命题画“√”，对于假命题画“×”)19．0是自然数．( )20．如果两个角不相等，那么这两个角不是对顶角．( )21．相等的角是对顶角．( )22．如果AC＝BC，那么C点是AB的中点．( )23．若a∥b，b∥c，则a∥c．( )24．如果C是线段AB的中点，那么AB＝2BC．( )25．若x2＝4，则x＝2．( )26．若xy＝0，则x＝0．( )27．同一平面内既不重合也不平行的两条直线一定相交．( )28．邻补角的平分线互相垂直．( )29．同位角相等．( )30．大于直角的角是钝角．( )拓展、探究、思考31．已知：如图，在四边形ABCD中，给出下列论断：①AB∥DC；②AD∥BC；③AB＝AD；④∠A＝∠C；⑤AD＝BC．以上面论断中的两个作为题设，再从余下的论断中选一个作为结论，并用“如果……，那么……”的形式写出一个真命题．答：_____________________________________________________________________．32．求证：两条平行线被第三条直线所截，内错角的平分线互相平行．7 平移学习要求了解图形的平移变换，知道一个图形进行平移后所得的图形与原图形之间所具有的联系和性质，能用平移变换有关知识说明一些简单问题及进行图形设计．课堂学习检测一、填空题1．如图所示，线段ON是由线段______平移得到的；线段DE是由线段______平移得到的；线段FG是由线段______平移得到的．2．如图所示，线段AB在下面的三个平移中(AB→A1B1→A2B2→A3B3)，具有哪些性质．图a图b 图c(1)线段AB上所有的点都是沿______移动，并且移动的距离都________．因此，线段AB，A1B1，A2B2，A3B3的位置关系是____________________；线段AB，A1B1，A2B2，A3B3的数量关系是________________．(2)在平移变换中，连接各组对应点的线段之间的位置关系是______；数量关系是______．3．如图所示，将三角形ABC平移到△A′B′C′．图a 图b在这两个平移中：(1)三角形ABC的整体沿_______移动，得到三角形A′B′C′．三角形A′B′C′与三角形ABC的______和______完全相同．(2)连接各组对应点的线段即AA′，BB′，CC′之间的数量关系是__________________；位置关系是__________________．综合、运用、诊断一、按要求画出相应图形4．如图，AB∥DC，AD∥BC，DE⊥AB于E点．将三角形DAE平移，得到三角形CBF．5．如图，AB∥DC．将线段DB向右平移，得到线段CE．6．已知：平行四边形ABCD及A′点．将平行四边形ABCD平移，使A点移到A′点，得平行四边形A′B′C′D′．7．已知：五边形ABCDE及A′点．将五边形ABCDE平移，使A点移到A′点，得到五边形A′B′C′D′E′．拓展、探究、思考一、选择题8．如图，把边长为2的正方形的局部进行如图①～图④的变换，拼成图⑤，则图⑤的面积是( )．(A)18 (B)16 (C)12 (D)8二、解答题9．河的两岸成平行线，A，B是位于河两岸的两个车间(如图)．要在河上造一座桥，使桥垂直于河岸，并且使A，B间的路程最短．确定桥的位置的方法如下：作从A到河岸的垂线，分别交河岸PQ，MN于F，G．在AG上取AE＝FG，连接EB．EB交MN于D．在D处作到对岸的垂线DC，那么DC就是造桥的位置．试说出桥造在CD位置时路程最短的理由，也就是(AC＋CD＋DB)最短的理由．10．以直角三角形的三条边BC，AC，AB分别作正方形①、②、③，如何用①中各部分面积与②的面积，通过平移填满正方形③?你从中得到什么结论?第六章 实数6.1平方根学习要求1. 理解算术平方根和平方根的含义。

5.2 平行线及其判定一、单选题1.下列说法正确的有( )①同位角相等;②两点之间的所有连线中,线段最短;③过一点有且只有一条直线与已知直线平行;④两点之间的距离是两点间的线段;⑤已知同一平面内70AOB ∠=︒，30BOC ∠=︒,则100AOC ∠=︒;A. 1个B. 2个C. 3个D. 4个2.如图，已知,AB CD BC DA ==，下列结论:①BAC DCA ∠=∠;②ACB CAD ∠=∠;③//AB CD .其中正确的结论有( )A. 0个B.1个C. 2个D.3个3.如图，在下列四个条件中，可得CE AB ∥的条件是（ ）A.23∠∠=B.4180ACD ∠∠︒＋=C.14∠∠=D.2180BCE ∠∠︒＋=4.如图所示，一个零件ABCD 只需要满足AB 边与CD 边平行就合格，现只有一个量角器，测得拐角120ABC ∠︒=，60BCD ∠︒=，那么这个零件是否合格（ ）A.合格B.不合格C.不一定D.无法判断5.下列说法不正确的是( )A.100米跑道的跑道线所在的直线是平行线B.马路的斑马线所在的直线是平行线C.若//a b ，//b d ，则a d ⊥D.过直线外一点有且只有一条直线与已知直线平行6.如图，12∠∠=，则直线AB CD ∥的是（ ）A. B.C. D.7.一辆汽车在公路上行驶，两次拐弯后，仍在原来的方向上平行行驶，那么两个拐弯的角度是（ ）A.先向左转130°，再向左转50°B.先向左转50°，再向右转50°C.先向左转50°，再向右转40°D.先向左转50°，再向左转40°8.如图，点E 在BC 的延长线上，下列条件中不能判定AB CD ∥的是（ ）A.12∠∠＝B.34∠∠＝C.B DCE ∠∠＝D.180D DAB ∠∠︒＋＝二、填空题9.在同一平面内有三条直线，如果其中有且只有两条直线平行，那么这三条直线有且只有 个交点.10.如图所示，木工师傅用角尺画出工件边缘的两条垂线，则这两条垂线 .11.如图，要使CF BG ∥，你认为应该添加的一个条件是 .12.如图，70A ∠︒＝,O 是AB 上一点，直线OD 与AB 所夹角82BOD ∠︒＝，要使OD AC ∥，直线OD 绕点O 按逆时针方向旋转 度.13.已知，如图，ABC ADC ∠∠＝，BF DE ，分别平分ABC ∠与ADC ∠，且13∠∠＝.试说明:AB CD ∥.请根据条件进行推理，得出结论，并在括号内注明理由.解:BF DE ，分别平分ABC ∠与ADC ∠， 112ABC ∴∠∠＝，122ADC ∠∠＝( ) ABC ADC ∠∠＝,∴∠ ∠＝ .13∠∠＝，2∴∠＝ （等量代换）∴ ∥ ( )三、解答题14.已知，如图，AD 是一条直线，160∠︒=，2120∠︒＝.试说明//BE CF .参考答案1.答案：A①同位角不一定相等，错误；②两点之间的所有连线中，线段最短，正确；③过直线外一点有且只有一条直线与已知直线平行，错误；④两点之间的距离是两点间的线段的长度，错误；⑤已知同一平面内70,30AOB BOC ∠=︒∠=︒,则100AOC ∠=︒或40︒，错误。

七年级数学下册第五章相交线与平行线章节训练（2021-2022学年考试时间：90分钟，总分100分）班级：__________ 姓名：__________ 总分：__________一、单选题（10小题，每小题3分，共计30分）1、下列说法中，真命题的个数为（）①两条平行线被第三条直线所截，同位角相等；②在同一平面内，如果两条直线都与第三条直线垂直，那么这两条直线互相平行；③过一点有且只有一条直线与这条直线平行；④点到直线的距离是这一点到直线的垂线段；A．1个B．2个C．3个D．4个2、如图，△ABC沿直线BC向右平移得到△DEF，己知EC=2，BF=8，则CF的长为（）A．3 B．4 C．5 D．63、如图，∠1＝35°，∠AOC＝90°，点B，O，D在同一条直线上，则∠2的度数为（）A．125°B．115°C．105°D．95°4、如图，直线AB ，CD 相交于点O ，90AOE ∠=︒，90DOF ∠=︒，OB 平分DOG ∠，给出下列结论：①当50AOF ∠=︒时，50DOE ∠=︒；②OD 为EOG ∠的平分线；③若150AOD ∠=︒时，30EOF ∠=︒；④BOG EOF ∠=∠．其中正确的结论有（ ）A ．4个B ．3个C ．2个D ．1个5、下列语句中，正确的有（ ）①一条直线的垂线只有一条；②在同一平面内，过直线上一点有且仅有一条直线与已知直线垂直；③两直线相交，则交点叫垂足；④互相垂直的两条直线形成的四个角一定都是直角．A ．0个B ．1个C ．2个D ．3个6、如图，直线b 、c 被直线a 所截，则1∠与2∠是（ ）A ．对顶角B ．同位角C ．内错角D ．同旁内角7、 “小小竹排江中游，巍巍青山两岸走”，所描绘的图形变换主要是（ ）A ．平移变换B ．翻折变换C ．旋转变换D ．以上都不对8、直线AB 、BC 、CD 、EG 如图所示．若∠1=∠2，则下列结论错误的是（ ）A．AB∥CD B．∠EFB=∠3C．∠4=∠5D．∠3=∠5 9、以下命题是假命题的是（）A 2B．有两边相等的三角形是等腰三角形C．三角形三个内角的和等于180°D．过直线外一点有且只有一条直线与已知直线平行10、下列命题中是假命题的是（）A．实数与数轴上的点一一对应B．内错角相等，两直线平行C．平行于同一条直线的两条直线互相平行D．如果一个角的两边分别平行于另一个角的两边，那么这两个角相等二、填空题（5小题，每小题4分，共计20分）1、如图，AB∥CD，∠EGB＝50°，则∠CHG的大小为 _____．2、如图，AC平分∠DAB，∠1＝∠2，试说明AB CD∥．证明：∵AC平分∠DAB___( )___，∴∠1＝∠__________( )____，又∵∠1＝∠2____( )____，∴∠2＝∠__________( )____，∴AB∥__________( )____．3、如图，在直线AB上有一点O，OC⊥OD，OE是∠DOB的角平分线，当∠DOE＝20°时，∠AOC＝___°．4、将命题“直角三角形斜边上的中线等于斜边的一半”改写成“如果…那么…”的形式_________．5、如图，直线AB、CD相交于点O，∠AOD＋∠BOC＝240°，则∠BOC的度数为__________°．三、解答题（5小题，每小题10分，共计50分）1、如图，将长为5cm，宽为3cm的长方形ABCD先向右平移2cm，再向下平移1cm，得到长方形A B C D，则阴影部分的面积为多少2''''cm．2、在如图所示55⨯的网格中，每个正方形的边长都是1，横纵线段的交点叫做格点，线段AB的两个端点都在格点上，点P也在格点上；（1）在图①中过点P作AB的平行线；（2）在图②中过点P作PQ⊥AB，垂足为Q；连接AP和BP，则三角形ABP的面积是．3、已知点O为直线AB上一点，将直角三角板MON按如图所示放置，且直角顶点在O处，在MON∠内部作射线OC，且OC恰好平分BOM∠．（1）若24∠=︒，求AOM∠的度数；CON（2）若2∠的度数．∠=∠，求AOMBON CON4、如图，①过点Q作QD⊥AB，垂足为点D；②过点P作PE⊥AB，垂足为点E；③过点Q作QF⊥AC，垂足为点F；④连P，Q两点；⑤P，Q两点间的距离是线段______的长度；⑥点Q到直线AB的距离是线段______的长度；⑦点Q到直线AC的距离是线段______的长度；⑧点P到直线AB的距离是线段______的长度．5、读下列语句，用直尺和三角尺画出图形．（1）点P是直线AB外的一点，直线CD经过点P，且CD与AB平行；（2）直线AB与CD相交于点O，点P是AB、CD外的一点，直线EF经过点P，且EF∥AB，与直线CD相交于点E．---------参考答案-----------一、单选题1、B【分析】根据平行线的性质与判定，点到直线的距离的定义逐项分析判断即可【详解】①两条平行线被第三条直线所截，同位角相等，故①是真命题；②在同一平面内，如果两条直线都与第三条直线垂直，那么这两条直线互相平行，故②是真命题；③在同一平面内，过直线外一点有且只有一条直线与这条直线平行，故③不是真命题，④点到直线的距离是这一点到直线的垂线段的长度，故④不是真命题，故真命题是①②，故选B【点睛】本题考查了判断真假命题，平行线的性质与判定，点到直线的距离的定义，掌握相关性质定理是解题的关键．2、A【分析】证明BE=CF即可解决问题．【详解】解：由平移的性质可知，BC=EF，∴BE=CF，∵BF=8，EC=2，∴BE+CF=8-2=6，∴CF=BE=3，故选：A．【点睛】本题考查平移变换，解题的关键是熟练掌握平移的性质．平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行（或共线）且相等．3、A【分析】利用互余角的概念与邻补角的概念解答即可．【详解】解：∵∠1＝35°，∠AOC＝90°，∴∠BOC＝∠AOC−∠1＝55°．∵点B，O，D在同一条直线上，∴∠2＝180°−∠BOC＝125°．故选：A．【点睛】本题主要考查了角的和差运算，互余角的关系以及邻补角的关系．准确使用邻补角的关系是解题的关键．4、B【分析】由邻补角，角平分线的定义，余角的性质进行依次判断即可．【详解】解：∵∠AOE=90°，∠DOF=90°，∴∠BOE=90°=∠AOE=∠DOF，∴∠AOF+∠EOF=90°，∠EOF+∠EOD=90°，∠EOD+∠BOD=90°，∴∠EOF=∠BOD，∠AOF=∠DOE，∴当∠AOF=50°时，∠DOE=50°；故①正确；∵OB平分∠DOG，∴∠BOD=∠BOG，∴∠BOD=∠BOG=∠EOF=∠AOC，故④正确；∵150∠=︒，AOD∴∠BOD=180°-150°=30°，∴30∠=︒EOF故③正确；若OD为EOG∠的平分线，则∠DOE=∠DOG，∴∠BOG+∠BOD=90°-∠EOE，∴∠EOF=30°，而无法确定30∠=︒，EOF∴无法说明②的正确性；故选：B．【点睛】本题考查了邻补角，角平分线的定义，余角的性质，数形结合是解决本题的关键．5、C【分析】根据垂线的性质和定义进行分析即可．【详解】解：①一条直线的垂线只有一条，说法错误；②在同一平面内，过直线上一点有且仅有一条直线与已知直线垂直，说法正确；③两条直线相交，则交点叫垂足，说法错误；④互相垂直的两条直线形成的四个角一定是直角，说法正确．正确的共有2个；故选：C．【点睛】此题主要考查垂线的性质和定义以及真假命题的判断．6、B【分析】根据对顶角、同位角、内错角、同旁内角的特征去判断即可．【详解】∠1与∠2是同位角故选：B【点睛】本题考查了同位角的含义，理解同位角的含义并正确判断同位角是关键．7、A【分析】根据平移是图形沿某一直线方向移动一定的距离，可得答案．【详解】解：“小小竹排水中游，巍巍青山两岸走”所描绘的图形变换主要是平移变换，故选：A．【点睛】本题考查了平移变换，利用了平移的定义．8、D【分析】根据平行线的判定与性质、对顶角相等逐项判断即可．【详解】解：∵∠1=∠2，∴AB∥CD，故A正确，不符合题意；∴∠4=∠5，故C正确，不符合题意；∵∠EFB与∠3是对顶角，∴∠EFB=∠3，故B正确，无法判断∠3=∠5，故D错误，符合题意，故选：D．【点睛】本题考查平行线的判定与性质、对顶角相等，熟练掌握平行线的判定与性质是解答的关键．9、A【分析】分别利用算术平方根、等腰三角形的判定、三角形内角和公式、平行的相关内容，进行分析判断即可．【详解】解：A A是假命题，B、有两边相等的三角形是等腰三角形，B是真命题，C、三角形三个内角的和等于180°，C是真命题，D、过直线外一点有且只有一条直线与已知直线平行，D是真命题，故选：A．【点睛】本题主要是考查了真假命题，正确的命题为真命题，错误的命题为假命题，根据所学知识，对各个命题的正确与否进行分析，这是解决该题的关键．10、D【分析】根据题意利用实数的性质、平行线的判定等知识分别判断后即可得出正确选项．【详解】解：A、实数与数轴上的点一一对应，正确，是真命题，不符合题意；B、内错角相等，两直线平行，正确，是真命题，不符合题意；C、平行于同一直线的两条直线平行，正确，是真命题，不符合题意；D、如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补，故原命题错误，是假命题，符合题意．故选：D．【点睛】本题考查命题与定理的知识，解题的关键是了解实数的性质、平行线的判定等知识．二、填空题1、130°【解析】【分析】根据平行线的性质可得∠EHD＝∠EGB＝50°，再利用邻补角的性质可求解．【详解】解：∵AB∥CD，∠EGB＝50°，∴∠EHD＝∠EGB＝50°，∴∠CHG＝180°﹣∠EHD＝130°．故答案为：130°．【点睛】本题主要考查平行线的性质，邻补角，属于基础题．2、已知 3 角平分线的定义已知 3 等量代换CD内错角相等，两直线平行【解析】【分析】根据平行线证明对书写过程的要求和格式填写即可.【详解】证明：∵AC平分∠DAB(已知)，∴∠1＝∠ 3 (角平分线的定义)，又∵∠1＝∠2(已知)，∴∠2＝∠ 3 (等量代换)，∴AB∥CD (内错角相等，两直线平行)．故答案为：已知；3；角平分线的定义；已知；3；等量代换；CD；内错角相等，两直线平行【点睛】本题主要考查平行线证明的书写，正确的逻辑推理和书写格式是解题的关键.3、50【解析】【分析】先求出∠BOD，根据平角的性质即可求出∠AOC．【详解】∵OE是∠DOB的角平分线，当∠DOE＝20°∴∠BOD=2∠DOE＝40°∵OC⊥OD，∴∠AOC=180°-90°-∠BOD=50°故答案为：50．【点睛】此题主要考查角度求解，解题的关键是熟知角平分线的性质、直角的性质．4、如果一个三角形是直角三角形，那么它斜边上的中线等于斜边的一半【解析】【分析】由题意将命题的条件改成如果的内容，将命题的结论改为那么的内容进行分析即可．【详解】解：将命题“直角三角形斜边上的中线等于斜边的一半”改写成“如果…那么…”的形式为：如果一个三角形是直角三角形，那么它斜边上的中线等于斜边的一半．故答案为：如果一个三角形是直角三角形，那么它斜边上的中线等于斜边的一半．【点睛】本题主要考查命题与定理，理解“如果…那么…”的意义并找到命题的条件和结论是解题的关键．5、120【解析】【分析】由题意根据对顶角相等得出∠BOC=∠AOD进而结合∠AOD＋∠BOC＝240°即可求出∠BOC的度数．【详解】解：∵∠AOD＋∠BOC＝240°，∠BOC=∠AOD，∴∠BOC =120°．故答案为：120．【点睛】本题考查的是对顶角的性质，熟练掌握对顶角相等是解题的关键．三、解答题1、18【分析】利用平移的性质求出空白部分矩形的长，宽即可解决；【详解】由题意可得，空白部分是矩形，长为()523cm cm -=，宽为()312cm cm -=，∴阴影部分的面积253223218cm =⨯⨯-⨯⨯=；【点睛】本题主要考查了矩形的性质，平移的性质，准确计算是解题的关键．2、（1）见解析；（2）见解析，5．【分析】（1）根据平行线的画法即可得；（2）根据垂线的画法即可得，再利用1个长方形的面积减去3个直角三角形的面积即可得．【详解】解：（1）如图①，PC 即为所求．（2）如图②，PQ即为所求．三角形ABP的面积为111 343131425 222⨯-⨯⨯-⨯⨯-⨯⨯=，故答案为：5．【点睛】本题考查了平行线和垂线的画法等知识点，熟练掌握平行线和垂线的画法是解题关键．3、（1）48°；（2）45°．【分析】（1）先根据余角的定义求出∠MOC，再根据角平分线的定义求出∠BOM，然后根据∠AOM=180°-∠BOM 计算即可；（2）根据角的倍分关系以及角平分线的定义即可求解；【详解】解：（1）∵∠MON=90°，∠CON=24°，∴∠MOC=90°-∠CON=66°，∵OC平分∠MOB，∴∠BOM=2∠MOC=132°，∴∠AOM=180°-∠BOM=48°；（2）∵∠BON=2∠NOC，OC平分∠MOB，∴∠MOC=∠BOC=3∠NOC，∵∠MOC+∠NOC=∠MON=90°，∴3∠NOC+∠NOC=90°，∴4∠NOC=90°，∴∠BON=2∠NOC=45°，∴∠AOM=180°-∠MON-∠BON=180°-90°-45°=45°；【点睛】本题考查了角平分线的意义、互补、互余的意义，正确表示各个角，理清各个角之间的关系是得出正确结论的关键．4、①②③④作图见解析；⑤PQ；⑥QD；⑦QF；⑧PE【分析】由题意①②③④根据题目要求即可作出图示，⑤⑥⑦⑧根据两点之间距离及点到直线的距离的定义即可得出答案．【详解】①②③④作图如图所示；⑤根据两点之间距离即可得出P，Q两点间的距离是线段PQ的长度；⑥根据点到直线的距离可得出点Q到直线AB的距离是线段QD的长度；⑦根据点到直线的距离可得出点Q到直线AC的距离是线段QF的长度；⑧根据点到直线的距离可得出点P到直线AB的距离是线段PE的长度.【点睛】本题主要考查基本作图和两点之间距离及点到直线的距离，熟练掌握相关概念与作图方法是解题的关键．5、（1）见解析；（2）见解析【分析】（1）过直线AB外的点P作CD//AB即可；（2）先画两条相交直线AB与CD交于点O，再过直线AB、CD外的一点P作AB的平行线EF且交直线CD于点E．【详解】解： (1)如图所示：(1)如图所示：【点睛】本题主要考查了相交线与平行线的作图，培养学生的理解能力和动手操作能力以及数形结合思想成为解答本题的关键．。

七年级数学同步练习下册答案第五章相交线与平行线1．公共，反向延长线．2．公共，反向延长线．3．对顶角相等．4．略．5．(1)∠BOC，∠AOD；(2)∠AOE；(3)∠AOC，∠BOD；(4)137°43′，90°，47°43′．6．A．7．D．8．B．9．D．10．×，11．×，12．×，13．√，14．√，15．×．16．∠2＝60°．17．∠4＝43°．18．120°．提示：设∠DOE＝x°，由∠AOB＝∠AOD＋∠DOB＝6x＝180°，可得x＝30°，∠AOF＝4x＝120°．19．只要延长BO(或AO)至C，测出∠AOB的邻补角∠AOC(或∠BOC)的大小后，就可知道∠AOB的度数．20．∠AOC与∠BOD是对顶角，说理提示：只要说明A，O，B三点共线．证明：∵射线OA的端点在直线CD上，∴∠AOC与∠AOD互为邻补角，即∠AOC＋∠AOD＝180°，又∵∠BOD＝∠AOC，从而∠BOD＋∠AOD＝180°，∴∠AOB是平角，从而A，O，B三点共线．∴∠AOC与∠BOD是对顶角．21．(1)有6对对顶角，12对邻补角．(2)有12对对顶角，24对邻补角．(3)有m(m－1)对对顶角，2m(m－1)对邻补角．1．互相垂直，垂，垂足．2．有且只有一条直线，所有线段，垂线段．3．垂线段的长度．4．AB⊥CD；AB⊥CD，垂足是O(或简写成AB⊥CD于O)；P；CD；线段MO 的长度．5～8．略．9．√，10．√，11．×，12．√，13．√，14．√，15．×，16．√．17．B．18．B．19．D．20．C．21．D．22．30°或150°．23．55°．24．如图所示，不同的垂足为三个或两个或一个．这是因为：(1)当A，B，C三点中任何两点的连线都不与直线m垂直时，则分别过A，B，C三点作直线m的垂线时，有三个不同的垂足．(2)当A，B，C三点中有且只有两点的连线与直线m垂直时，则分别过A，B，C三点作直线m的垂线时，有两个不同的垂足．(3)当A，B，C三点共线，且该线与直线m垂直时，则只有一个垂足．25．以点M为圆心，以R＝1.5cm长为半径画圆M，在圆M上任取四点A，B，C，D，依次连接AM，BM，CM，DM，再分别过A，B，C，D点作半径AM，BM，CM，DM的垂线l1，l2，l3，l4，则这四条直线为所求．。