微观经济学(利润最大化与盈亏)

第八章利润最大化和竞争性供给教学笔记这一章确定了追求利润最大化的厂商的行为动机，揭示了这些厂商在竞争性市场的相互影响和作用。

这一章的每一节都很重要，它们构建了对竞争性市场供给一方的彻底完全的认识。

在学习这本教科书的第三部分之前，建立这样一个基础是非常必要的。

虽然这一章的材料都写得很清楚易懂，但是学生可能还是会对有些概念、思想感到很难理解，比如说那些有关厂商应该怎样选择最佳生产数量的思想、有关厂商怎样应用我们前面学习过的成本曲线的思想，等等。

这里有一个讲课的建议：花些时间研究与这一章的最后部分的习题中用到的表格相类似的表格。

研究一些与此类表格有关的例题对于学生理解不同类型的成本，以及相应的厂商的最佳产量是有帮助的。

8.1节确定了完全竞争市场的三个基本假设，8.2节对“厂商以利润最大化为经营目标”这一假设进行了讨论。

8.3节和8.5节对厂商的供给曲线进行了推导，8.1节和8.2节为8.3节、8.5节中供给曲线的推导打下了基础。

8.3节推导出一个一般性的结论：只要边际收入等于边际成本，厂商就应当生产。

这一节接下来确定了完全竞争（一个特殊的案例）的条件之一：价格等于边际收入，这个结论是8.1节中“接受价格”这个假设的直接的逻辑结果。

如果你的学生掌握微积分，那么通过对利润函数关于产量q求微分，可以导出边际成本与边际收入相等。

如果你的学生还没有掌握微积分，那么可以通过对数据表格的多加研究来理解当边际收入和边际成本相等时厂商能达到利润最大化目标这个结论。

这里有一点需要强调：完全竞争市场上，每个厂商只能通过产量的变化而不能通过价格的变化来取得最大利润。

为了正确理解完全竞争市场，我们在提出有关完全竞争市场的假设之前，也要对卖方垄断、寡头卖方垄断和垄断性竞争有一定的了解。

将讨论限定一个专门的范围，这个范围包括确定一个行业里有多少厂商、这个行业是否有进入壁垒、各个厂商的产品是否存在差异，以及行业里每个厂商对其他厂商对于其价格、数量方面的决策的反应做出的假设。

微观经济学知识点1、稀缺性：经济资源以及用经济资源生产的物品总是不能满足人类无穷无尽欲望的事实2、研究的问题：资源配置问题3、经济学基本问题：资源配置问题、资源利用问题、经济体制问题。

4、理性人假定：“理性人”假设（hypothesis of rational man ）是指作为经济决策的主体都是充满理智的， 既不会感情用事， 也不会盲从， 而是精于判断和计算， 其行为是理性的。

在经济活动中， 主体所追求的唯一目标是自身经济利益的最大化。

如消费者追求的是满足程度最大化， 生产者追求的是利润最大化。

“理性人”假设实际是对亚当·斯密“经济人”假设的延续。

1、①需求：是指在一定时期内，对应于某种商品各种可能的价格，消费者愿意并且能够购买的该商品的数量②需求量：是指消费者在某一价格下愿意购买的某种商品的数量③需求的变化：在商品自身价格不变的条件下，由于其他因素变动而引起的对商品需求数量的变化④需求量的变化：在影响需求的其他因素保持不变的情况下，由于商品自身价格变动所引起的对该商品需求量的变动2、供求规律：①在供给不变的情况下，需求增加导致均衡价格上升和均衡数量增加，需求减少导致均衡价格下降和均衡数量减少②在需求不变的情况下，供给增加导致均衡价格下降和均衡数量增加，供给减少导致均衡价格上升和均衡数量减少③当供给和需求同时增加或减少时，均衡数量同方向变化，均衡价格不确定④当供需反方向变动时，均衡价格与需求同方向变化，均衡数量不确定3、需求的价格弹性：表示在一定时期内，一种商品的需求量对该商品价格变化的反应程度或敏感程度需求价格弹性系数Ed = 需求量变化的百分比 / 价格变化的百分比QP P Q Ed ∆∆-= 4、点弹性的几何意义：需求曲线上任意一点的点弹性系数的值，等于这一点沿着需求曲线到横轴的距离比上其沿着需求曲线到纵轴的距离点弹性的类型： 1；1五种类型：①AC 段，Ed>1,富有弹性②CB 段，Ed<1,缺乏弹性③C 点Ed=1，单位弹性④A 点Ed→∞，完全有弹性⑤B 点Ed=0，完全无弹性5、需求的交叉价格弹性：①概念：表示在一定时期内，一种商品的需求量变动对其相关商品价格变动的反应程度或敏感程度。

Chapter 9第九章PROFIT MAXIMIZATION利润最大化Copyright ©2005 by South-Western, a division of Thomson Learning. All rights reserved.The Nature of Firms企业的性质• A firm is an association of individuals who have organized themselves for the purpose of turning inputs into outputs 企业是以把投入变为产出为目的的个人的联合•Different individuals will provide different types of inputs 不同的个人会提供不同类型的投入–the nature of the contractual relationship between the providers of inputs to a firm may be quite complicated企业投入的提供者之间合约关系的本质可能是非常复杂的Contractual Relationships合约关系•Some contracts between providers of inputs may beexplicit某些投入提供者之间的合约是显性的–may specify hours, work details, or compensation可能会具体说明小时、工作细节或者补偿•Other arrangements will be more implicit in nature其他安排本质上可能是隐性的–decision-making authority or sharing of tasks决策权威或者共同承担任务Modeling Firms’ Behavior企业行为模型•Most economists treat the firm as a single decision-making unit大多数经济学家把企业看做一个单一的决策制定单位–the decisions are made by a single dictatorialmanager who rationally pursues some goal决策是由理性地追求某些目标的单个独裁管理者做出的•usually profit-maximization（其目标）一般是利润最大化Profit Maximization利润最大化•A profit-maximizing firm chooses both its inputs and its outputs with the sole goal of achieving maximum economic profits利润最大化的企业，仅为了达到最大的经济利润的目的，选择投入和产出–seeks to maximize the difference between total revenue and total economic costs寻求总收益和总经济成本之间差别的最大化Profit Maximization利润最大化•If firms are strictly profit maximizers, they will make decisions in a “marginal” way如果企业是严格的利润最大化者，它们会以“边际”方式做出决定–examine the marginal profit obtainable fromproducing one more unit or hiring one additionallaborer检验通过额外雇佣一单位劳动力或多生产一单位产品，所能得到的边际利润Output Choice产出决策•Total revenue for a firm is given by企业的总收益为R(q) = p(q)⋅q•In the production of q, certain economic costs are incurred [C(q)]生产q，存在某些经济成本[C(q)]•Economic profits (π) are the difference between total revenue and total costs经济利润(π)是总收益和总成本之差π(q) = R(q) –C(q) = p(q)⋅q–C(q)Profit Maximization 利润最大化outputrevenues & costs RCq*Profits are maximized when the slope of the revenuefunction is equal to the slope of the cost function在收益函数的斜率等于成本函数斜率的点处，利润得以最大化The second-order conditionprevents us from mistaking q 0as a maximum二阶条件避免了把q 0错作为最大值q 0Marginal Revenue边际收益•If a firm faces a downward-sloping demand curve, marginal revenue will be a function of output如果企业面临一个向下倾斜的需求曲线，边际收益将是产出的函数•If price falls as a firm increases output, marginal revenue will be less than price 如果价格随着企业增加产出而降低，那么边际收益将小于价格Marginal Revenue边际收益•Suppose that the demand curve for a sub sandwich is假设对潜艇三明治的需求函数为q= 100 –10p•Solving for price, we get求解价格，我们得到p = -q/10 + 10•This means that total revenue is这意味着总收益为R= pq= -q2/10 + 10q•Marginal revenue will be given by边际收益为MR= dR/dq= -q/5 + 10Profit Maximization利润最大化•To determine the profit-maximizing output, we must know the firm’s costs为了决定利润最大化的产出水平，我们必须知道企业的成本•If subs can be produced at a constant average and marginal cost of $4, then如果三明治的平均成本和边际成本为$4 ，那么MR= MC-q/5 + 10 = 4q= 30Marginal Revenue and Elasticity边际收益和弹性e q,p< -1 （需求有弹性）MR> 0e q,p= -1（单位弹性）MR= 0e q,p> -1（需求无弹性）MR< 0Average Revenue Curve平均收益曲线•If we assume that the firm must sell all its output at one price, we can think of the demand curve facing the firm as its average revenue curve如果我们假定，企业必须在一个价格水平上卖出其所有的产出，我们可以把企业所面临的需求曲线看做其平均收益曲线–shows the revenue per unit yielded by alternative output choices 表示通过不同的产出选择，每单位产品获得的收入Marginal Revenue Curve边际收益曲线•The marginal revenue curve shows the extra revenue provided by the last unit sold边际收益曲线，表示了最后卖出的一单位产品所提供的额外收入•In the case of a downward-sloping demand curve, the marginal revenue curve will lie below the demand curve 在向下倾斜的需求曲线中，边际收益曲线将位于需求曲线的下方Marginal Revenue Curve边际收益曲线outputpriceD (average revenue)MRq 1p 1As output increases from 0 to q 1, total revenue increases so MR > 0随着产出从0增至q 1，总收益增加，所以MR > 0As output increases beyond q 1, total revenue decreases so MR < 0随着产出增至超过q 1，总收益减少，所以MR < 0Marginal Revenue Curve边际收益曲线•When the demand curve shifts, its associated marginal revenue curve shifts as well当需求曲线移动时，相应的边际收益曲线也会移动–a marginal revenue curve cannot be calculatedwithout referring to a specific demand curve没有相应的具体需求曲线，边际收益曲线不可能计算得出The Constant Elasticity Case弹性不变的情况•We showed (in Chapter 5) that a demand function of the form我们说明了（在第五章），下列形式的需求函数q = ap bhas a constant price elasticity of demand equal to b 需求价格弹性为常数b•Solving this equation for p, we get求解p，我们得到p = (1/a)1/b q1/b= kq1/b where k= (1/a)1/bThe Constant Elasticity Case弹性不变的情况•This means that这意味着R = pq = kq(1+b)/band 并且MR = dr/dq = [(1+b)/b]kq1/b= [(1+b)/b]p •This implies that MR is proportional to price 这意味着，MR是与价格成比例的Short-Run Supply by a Price-Taking Firm价格接受企业的短期供给outputpriceSMCSAC SAVCp* = MRq*Maximum profit occurs where p = SMC 最大利润在p = SMCShort-Run Supply by a Price-Taking Firm价格接受企业的短期供给outputpriceSMCSAC SAVCp* = MRq*Since p > SAC , profit > 0 因为p > SAC ,所以profit > 0Short-Run Supply by a Price-Taking Firm价格接受企业的短期供给outputpriceSMCSAC SAVCp* = MRq*If the price rises to p **, the firm will produce q **and π> 0如果价格上升为p **，企业生产q **并且π> 0q**p**Short-Run Supply by a Price-Taking Firm价格接受企业的短期供给outputpriceSMCSAC SAVCp* = MRq*If the price falls to p ***, the firm will produce q ***如果价格下降为p ***，企业会生产q ***q***p***Profit maximization requires that p =SMC and that SMC is upward-sloping利润最大化要求p =SMC 且SMC 为向上倾斜的π< 0Short-Run Supply by a Price-Taking Firm价格接受企业的短期供给•The positively-sloped portion of the short-run marginal cost curve is the short-run supply curve for a price-taking firm斜率为正的短期边际成本曲线部分，是价格接受企业的短期供给曲线–it shows how much the firm will produce at every possible market price它表示企业在每个可能的市场价格生产的数量–firms will only operate in the short run as long as total revenue covers variable cost只要总收入足以弥补可变成本，企业将在短期内运行•the firm will produce no output if p< SAVC 如果p< SAVC，企业不会生产价格接受企业的短期供给•Thus, the price-taking firm’s short-run supply curve is the positively-sloped portion of the firm’s short-run marginal cost curve above the point of minimum average variable cost所以价格接受企业的短期供给曲线是斜率为正的短期边际成本曲线上高于最低平均可变成本的部分–for prices below this level, the firm’s profit-maximizing decision is to shut down and produce no output对于低于这一水平的价格，企业的利润最大化决策是关闭不生产价格接受企业的短期供给outputpriceSMCSACSAVCThe firm’s short-run supply curve is the SMCcurve that is above SAVC企业的短期供给曲线是SMC 曲线在SAVC 曲线之上的部分Short-Run Supply短期供给•To find the firm’s shut-down price, we need to solve for SAVC 为找到企业关闭的价格水平，我们需要求解SAVCSVC= wq1/βk1-α/βSAVC= SVC/q= wq(1-β)/βk1-α/β•SAVC< SMC for all values of β< 1对于所有β< 1的值，SAVC < SMC–there is no price low enough that the firm will want to shut down 这里不存在足够低的价格，使得企业愿意关闭Profit Functions利润函数• A firm’s economic profit can be expressed as a function of inputs企业的经济利润可以表示为投入的函数π= pq-C(q) = pf(k,l) -vk-w l•Only the variables k and l are under the firm’s control只有变量k和l受企业的控制–the firm chooses levels of these inputs in order to maximize profits企业选择这些投入水平，以使得利润最大化•treats p, v, and w as fixed parameters in its decisions在决策中，把p,v和w看做固定参量Profit Functions 利润函数•A firm’s profit function shows its maximal profits as a function of the prices that the firm faces 企业的利润函数，表示由企业所面临的价格所决定的最大化利润函数]),([),(),,(,,l l l ll w vk k pf Max k Max w v p k k −−=π=ΠProperties of the Profit Function利润函数的性质•Homogeneity齐次性–the profit function is homogeneous of degreeone in all prices利润函数对所有价格是一次齐次的•with pure inflation, a firm will not change itsproduction plans and its level of profits will keep upwith that inflation对于纯粹通胀，企业不会改变其生产计划，利润水平将跟上通胀水平Properties of the Profit Function利润函数的性质•Nondecreasing in output price对产出价格是非递减的–a firm could always respond to a rise in theprice of its output by not changing its input oroutput plans对于其产出价格上升，企业总可以不改变其投入或者产出计划•profits must rise利润一定上升Properties of the Profit Function利润函数的性质•Nonincreasing in input prices对投入价格非递增–if the firm responded to an increase in an inputprice by not changing the level of that input, its costs would rise如果对于投入价格上升，企业不改变其投入的水平，其成本会上升•profits would fall利润会下降Producer Surplus in the Short Run短期内的生产者剩余•Because the profit function is nondecreasing in output prices, we know that if p2> p1因为利润函数对产出价格是非递减的，我们知道如果p2> p1，那么Π(p2,…) ≥Π(p1,…)•The welfare gain to the firm of this price increase can be measured by企业从这一价格增长得到的福利可以由下式衡量welfare gain = Π(p2,…) -Π(p1,…)Producer Surplus in the Short Run 短期内的生产者剩余outputpriceSMC p 1q 1If the market price is p 1, the firm will produce q 1如果市场价格是p 1，企业会生产q 1If the market price rises top2, the firm will produce q2如果市场价格是p 2，企业会生产q 2p 2q 2Producer Surplus in the Short Run 短期内的生产者剩余The firm’s profits rise by the shaded area 企业利润的增加量为阴影部分面积outputpriceSMC p 1q 1p 2q 2Producer Surplus in the Short Run 短期内的生产者剩余•Mathematically, we can use the envelope theorem results 数学上，我们可以使用包络定理的结果,...)(,...)( )/()( gain welfare 122121p p dp p dp p q p p p p Π−Π=∂Π∂==∫∫Producer Surplus in the Short Run短期内的生产者剩余•We can measure how much the firm values the right to produce at the prevailing price relative to a situation where it would produce no output我们可以衡量，相对于企业不生产的情况，企业对在当前价格生产的这一权利的估值Producer Surplus in the Short Run 短期内的生产者剩余outputpriceSMC p 1q 1Suppose that the firm’s shutdown price is p 0假设企业的关闭价格为p 0pProducer Surplus in the Short Run 短期内的生产者剩余•The extra profits available from facing a price of p 1are defined to be producer surplus 从面临的价格p 1中所得的额外利润定义为生产者剩余∫=Π−Π=1)(,...)(,...)( surplus producer 01p p dpp q p p。

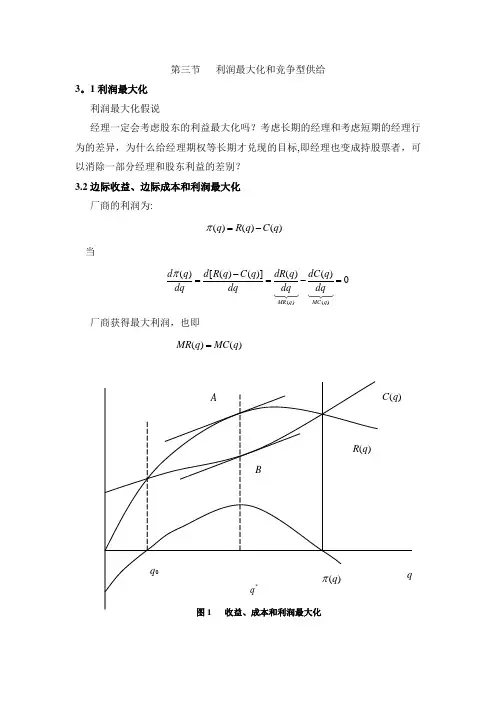
第三节 利润最大化和竞争型供给3。

1利润最大化 利润最大化假说经理一定会考虑股东的利益最大化吗？考虑长期的经理和考虑短期的经理行为的差异，为什么给经理期权等长期才兑现的目标,即经理也变成持股票者，可以消除一部分经理和股东利益的差别？ 3.2边际收益、边际成本和利润最大化 厂商的利润为:()()()q R q C q π=-当()()()[()()]()()0MR q MC q d q d R q C q dR q dC q dq dq dq dqπ-==-= 厂商获得最大利润，也即()()MR q MC q =3。

2。

1竞争性厂商的需求和边际收益第三节 利润最大化和竞争型供给（1）竞争型厂商的需求线是一条水平线，需求弹性是多大呢？ （2)边际收益呢?(),R q Pq MR P == 3。

2。

1竞争性厂商的需求和边际收益 在完全竞争下()0()d q P MC q dqπ=⇔= 实际上()()()()(())0()'()()()'()1()(1)()()(1)()()||MR q MR q MR q d q d P q q MC q P q q P q MC q dq dq P q q P q MC q P q MC q P q πε=⇔==⇔+=+=⇔-=3.3选择短期产量1()()P MC q q MC P -=⇒=图2.a 竞争性厂商的需求 图2.b 行业面临的需求微观经济学讲义 第三章 厂商理论 第三节 利润最大化和竞争型供给3.4竞争性厂商的短期供给曲线如图4中边际成本线，保本点以上的部分,即黑粗线所示部分。

1(),()c q MC P P MC q -=>Q图4 竞争性厂商的定价：亏损状态c q*2qQ图3 竞争性厂商的定价：盈利状态*1q3。

4.1厂商对投入品价格的反应3.4.1短期市场供给曲线逻辑:假定市场存在n 个厂商,市场总供给为1()()()ni i Q P q P D P ===∑,即每个厂商将价格是为给定，然后所有的厂商的供给构成市场的供给，市场供给和总需求共同决定这个P ，然后给定市场均衡的P ,每个厂商提供具体P 下的供给。

第19章利润最大化19.1本章要点●短期利润●长期利润●显示盈利的能力19.2重难点解读一、利润1．利润的表示方法利润可以被简单地定义为总收益与总成本之差（Profits are defined as revenues minus cost）。

假定一个厂商生产几种产品()1,...,n y y 和使用m 种投入品()1,...,m x x 。

令产品的价格为()1,...,n p p ，投入品的价格分别为()1,...,m w w ，则厂商的利润π可表示为：11i i i i i i p y w x π===-∑∑其中前一项为厂商的总收益，后一项为总成本。

2．不同的利润概念经济学上的利润指的是经济利润或称超额利润，等于总收益减总成本（含显性成本和隐性成本）。

经济学上指的正常利润是指厂商对自己所提供的企业家才能的报酬的支付，已经包含在隐性成本里了。

隐性成本是指厂商再生产过程中使用自身所拥有的那些生产要素所支付的实际费用。

会计利润是指厂商的总收益减去所有的显性成本以后的余额。

显性成本是指厂商为获得生产所需要的各种生产要素而发生的实际支出。

3．各利润概念之间的关系会计利润=总收益－会计成本经济利润=总收益－总成本=总收益－（显成本+隐成本）图19-1相关关系二、短期利润最大化1．短期利润最大化的必要条件在完全竞争市场下，假定要素2的投入水平2x 保持不变。

令厂商的生产函数为()12,f x x ，产出的价格为p ，两种投入品的价格为1w 和2w 。

厂商的利润最大化问题可表示为：()1121122max ,x pf x x w x w x --如果*1x 是要素1实现利润最大化的数量，由数理方法可得生产要素的边际产品价值（额外增加一个单位的要素投入而增加的产品的价值，强调价值的增加）应该等于它的价格：()1121,pMP x x w *=2．利用图形分析短期利润最大化令y 表示厂商的产出量，利润可表示为：1122py x x πωω=--整理得等利润线：2121w w y x x p p pπ=++等利润线表示产生固定利润水平的投入品和产出品的所有组合，如图19-2所示，斜率为1w p ，纵截距为22w x p pπ+。

中级微观经济学知识点微观经济学是研究经济系统中单一经济主体行为的经济学分支，包括个人、企业、政府及其他经济组织和市场。

它考察如何决策者通过资源有效地分配来满足需求，重点研究市场经济中的成本、收益和效率等问题。

以下是中级微观经济学知识点的概括。

一、产出及其成本1.1生产函数：它描述了生产过程中输入资源（比如原材料、劳动力等）与最终生产的输出结果的关系。

1.2成本曲线：它描述了生产一定量产品所需的平均成本（平均成本、边际成本等）和总成本的关系。

二、供求2.1供求模型：它描述了市场中供应和需求的关系，以及供求变化带来的价格变化。

2.2收益及其曲线：它描述了生产、消费和效率之间的关系，以及产品价格、消费者收益与制造方收益之间的关系。

三、对策3.1对策理论：它用数学建模的方法来研究双方在一定条件下如何博弈来获得最佳结果。

3.2双边市场：它研究在双边市场中，买方和卖方如何决策以达到最佳的交易结果。

四、公共经济学4.1公共货币：它描述了政府发行的货币和它们的相关性。

4.2税收政策：它研究了政府如何利用税收政策来调节国民收入和消费。

4.3政府干预：它描述了政府如何使用政策介入经济系统，以达到其目的。

五、经济效率5.1效率理论：它研究效用的分配，以及如何通过改变分配来提高总体效用。

5.2投入输出分析：它描述了经济生产系统中投入和输出之间的关系，以及能够改善经济效率的方法。

5.3收益最大化：它根据一定的利润最大化要求，研究最优资源配置方式。

总之，中级微观经济学知识点包括生产函数、成本曲线、供求模型、收益及其曲线、对策理论、双边市场、公共货币、税收政策、政府干预、效率理论、投入输出分析和收益最大化等。

深入研究中级微观经济学知识点，有助于我们更好地理解经济体系，从而推进经济发展。

第2章利润最大化一、判断题1．利润最大化行为弱公理是指厂商只有较弱的利润最大化动机。

（）【答案】F【解析】利润最大化行为弱公理是指竞争性厂商的供给量是产品价格的增函数，每种要素的需求函数是该要素价格的减函数。

弱公理也是利润最大化条件推导得出的，因此不能说厂商具有较弱的利润最大化动机。

2．不变要素就是在使用过程中与产量水平成固定比例的生产要素。

（）【答案】F【解析】不变要素是指其数量不受产量水平影响的要素，是企业固定数量的生产要素，即是企业的产量为零企业仍然要为此要素支付成本；可变要素是指其数量随产量水平变化而变化的要素。

3．某要素边际产量等于在其他要素投入量保持不变的条件下生产函数对该要素的偏导数。

（）【答案】T【解析】要素的边际产量是在其他要素投入量保持不变的条件下，增加一单位要素所引起的产量增加量。

4．若初始阶段要素x的边际产品价值随要素x投入的增加而上升，那么此时要素x边际产品价值等于要素价格也是厂商利润最大化条件。

（）【答案】F【解析】厂商要素投入在边际产量递增阶段，不能直接套用利润最大化的一阶条件。

当边际产量递增时，企业应该增加要素使用量。

5．若追求利润最大化的竞争性厂商面临产品价格提高，而且所有其他价格保持不变，那么厂商的产量不可能下降的。

（）【答案】T【解析】由利润最大化的弱公理0p y ∆∆≥，由于0p ∆≥，0y ∆≥是必然成立的。

6．若某竞争性行业中厂商生产函数均呈规模报酬不变的特点，那么他们的长期利润水平一定为零。

（）【答案】T【解析】对于在所有产量水平上都具有不变的规模报酬的一家竞争企业而言，唯一可能的长期利润水平是零。

假设它的均衡利润为正值。

如果要素的投入量增加一倍，产量将增加一倍。

利润也将翻番，但这与企业最初使利润最大化的选择相矛盾。

因此长期利润水平一定为0。

7．与消费理论对应，厂商利润最大化下也可能存在“吉芬要素”，这类要素价格下降反而引起对其需求的下降。

（）【答案】F【解析】根据利润最大化行为弱公理可知，竞争性厂商的供给量是产品价格的增函数，每种要素的需求函数是该要素价格的减函数。

微观经济学涉及的计算公式第二章需要了解的字母含义:需求数量Q d、供给数量Q s、需求的价格弹性系数E d、需求的收入弹性系数E m、需求的交叉弹性系数E xy、供给的弹性系数E s.需求函数Q d=a-bP;供给函数Q s=—a+bP；均衡价格：Q d=Q s弧弹性E=—（△Q/△P)*（P1+P2）/（Q1+Q2）;点弹性E= -(dQ/dP）*(P/Q）需求的价格弹性E：E>1表示当价格变化1%时需求量变化大于1%，为富有弹性;E<1为缺乏弹性;富有弹性时降价增收,缺乏弹性时提价增收。

需求的收入弹性E:E〈0时商品为低档品；E〈1商品为必需品；E>1商品为奢侈品。

需求的交叉弹性：E〈0两商品为互补品；E>0时两商品为替代品；E=0时两商品为不相关品。

影响供给弹性的因素：1.时间的长短；2。

产品生产成本状况；3.产品生产周期的长短。

第三章需要了解的字母含义：总效用TU、边际效用MU、边际替代率MRS12.边际效用MU x=dTU/dQ x；效用最大化的均衡条件：P1X1+P2X2=I.；MU1/P1=MU2/P2边际替代率MRS12 =MU1/MU2= P1/ P2恩格尔系数=食物支出/总收入（59％以上为贫困、50～59为温饱、40～49为小康、30～39为富裕、低于30%为最富裕）替代效应与收入效应第四章需要了解的字母含义：劳动L、资本K、总产量TP L、平均产量AP L、边际产量MP L、边际技术替代率MRTS LK、成本C、劳动价格w、资本价格r。

产量Q=AL a K b(A代表技术进步因素、a表示劳动贡献率、b表示资本贡献率）。

总产量AP L=TP L/L。

；边际产量MP L=dTP L/dL;边际技术替代率MRTS LK=△K/△L=MP L/MP K成本C=wL+rK;投入要素组合比例最优条件：w/r=MP L/MP K（产量最大、成本最小）根据产出变动和投入变动之间的关系，企业规模报酬变化可分为三种情况：Q=F(L,K)产量. 第一种：规模报酬递增：产量增加的比例大于各种生产要素增加的比例.F（aL,aK）>aF（L，K）；原因：1.生产专业化提高；2.可以使用专门的设备和更先进的技术；3.提高管理效率。

利润最大化观点认为：利润代表了企业新创造的财富，利润越多，则说明企业的财富增加得越多，越接近企业的目标。

每股盈余最大化观点实际上是利润最大化观点的一种转化形式，即把利润与投入的资本联系起来，并且只适用于股份制企业。

利润最大化的财务目标是西方微观经济学的理论基础，西方经济学家以边际收入等于边际成本来确定企业的产销量，使企业利润达到最大化，并以利润最大化来分析和评价企业的业绩。

利润最大化的财务目标的优点是：它强调了资本的有效利用，可以用这个指标来衡量企业是如何理性增长的，同时在实务中它容易被人理解操作性也很强。

它的缺点是：利润最大化容易导致企业片面的追求短期效益而忽视长远的发展；它忽视了企业每天都要面临的两大因素：不确定性和时间价值；还是最重要的一点是，利润最大花忽视了成本的投入与利润的比例关系。

1、企业的财务目标中，利润最大化和每股盈余最大化的共同缺点是（）。

A.没有考虑利润的取得时间B.没有考虑所获利润和投入资本额的关系C.没有考虑获取利润和所承担风险的关系D.导致股、经营者和债权人的冲突答案:AC解析：ABC都是利润最大化的缺点，AC是每股盈余最大化的缺点。

每股盈余最大化把企业的利润和股东投入的资本联系起来考察，克服了利润最大化一个缺点。

利润最大化的缺点是：（1）没有考虑利润实现时间和资金时间价值；（2）没有考虑风险题目；（3）没有反映创造的利润与投入资本之间的关系；（4）可能会导致公司短期财务决议计划倾向，影响公司长远发展。

优点：1、反映了当期经营活动中投入与产出对比的结果，在一定程度上体现了企业经济效益的高低。

2、利润的多少不仅体现了企业对国家的贡献，而且与企业的利息息息相关。

利润最大化对于企业的投资者、债权人和经营者和职工都是有利的。

3、利润这个指标在实际应用方面比较简便。

利润额直观、明确，容易计算，便于分解落实，大多数职工都能理解。

缺点：1、利润最大化中的利润额是一个绝对数，没有反映出所得利润额同投入资本额的关系。

第19章 利润最大化1．在短期内，如果不变生产要素的价格提高，利润会发生什么变化？答：在短期内，如果不变生产要素的价格提高，利润会降低。

厂商利润()()()00max max x x pf x z wx rz pf x z wx rz π≥≥⎡⎤=-+=--⎢⎥⎣⎦，，，其中r 和z 分别是固定要素的数量和价格。

特别地，短期内z 固定不变，所以r 和z 会以参数的形式出现在利润的表达式中。

所以，r 的提高会引起利润的下降。

2．如果某企业的生产技术能做到对于任何产量水平都是规模报酬递增的，在价格保持不变并且经营规模扩大一倍的情况下，它的利润会发生什么变化？答：它的利润会扩大到原来的两倍以上。

这是因为：对于一个处处规模报酬递增的企业，其生产函数满足()()f tx tf x >，其中1t >。

对任意的产量x ，其利润为()0max x pf x wx π≥=-，所以当企业生产规模扩大一倍后，其利润是 ()()00max 222max x x pf x wx pf x wx π≥≥⎡⎤=->-⎢⎥⎣⎦，因此其利润是原来的两倍以上。

3．如果一个企业在各种产出水平上都显示规模报酬递减，那么，把这个企业划分为两个相等规模的较小企业，它的总利润会发生什么变化？答：通过把一个企业分拆为规模更小的企业可以提高其总利润。

这是因为：对于一个处于规模报酬递减的企业，其生产函数满足()()f tx tf x <，其中1t >。

该企业的利润为：()()()0max x p w pf x wx pf x wx π**≥=-=-，，其中*x 是最优要素投入量。

若把该企业分成两个规模相等的小企业，则这两个小企业的总利润为：()1222x pf wx pf x wx ****⎡⎤⎛⎫->-⎢⎥ ⎪⎢⎥⎝⎭⎣⎦ 分拆后的总利润大于原来一个企业的利润，所以通过把一个企业分拆为规模更小的企业有利于提高其利润，而且分拆后的规模越小，则这些小企业的总利润就越高（比如在本题中，把企业分拆后的两个小企业再次按同样的方法分拆）。