中国石油大学2011自动控制原理期中考试试题(答 案)

自动控制原理习题及其解答第一章（略） 第二章例2-1 弹簧，阻尼器串并联系统如图2-1示，系统为无质量模型，试建立系统的运动方程。

解：(1) 设输入为y r ，输出为y 0。

弹簧与阻尼器并联平行移动。

(2) 列写原始方程式，由于无质量按受力平衡方程，各处任何时刻，均满足∑=0F ，则对于A 点有其中，F f 为阻尼摩擦力，F K 1，F K 2为弹性恢复力。

(3) 写中间变量关系式 (4) 消中间变量得 (5) 化标准形 其中:215K K T +=为时间常数，单位[秒]。

211K K K K +=为传递函数，无量纲。

例2-2 已知单摆系统的运动如图2-2示。

(1) 写出运动方程式 (2) 求取线性化方程解：（1）设输入外作用力为零，输出为摆角? ，摆球质量为m 。

（2）由牛顿定律写原始方程。

其中，l 为摆长，l ? 为运动弧长，h 为空气阻力。

（3）写中间变量关系式 式中，α为空气阻力系数dtd lθ为运动线速度。

（4）消中间变量得运动方程式0s i n 22=++θθθmg dt d al dtd ml （2-1) 此方程为二阶非线性齐次方程。

（5）线性化由前可知，在? ＝0的附近，非线性函数sin ? ≈? ，故代入式（2-1）可得线性化方程为例2-3 已知机械旋转系统如图2-3所示，试列出系统运动方程。

解：（1）设输入量作用力矩M f ，输出为旋转角速度? 。

（2）列写运动方程式 式中， f ?为阻尼力矩，其大小与转速成正比。

（3）整理成标准形为 此为一阶线性微分方程，若输出变量改为?，则由于代入方程得二阶线性微分方程式例2-4 设有一个倒立摆安装在马达传动车上。

如图2-4所示。

图2-2 单摆运动图2-3 机械旋转系统倒立摆是不稳定的，如果没有适当的控制力作用在它上面，它将随时可能向任何方向倾倒，这里只考虑二维问题，即认为倒立摆只在图2-65所示平面内运动。

控制力u 作用于小车上。

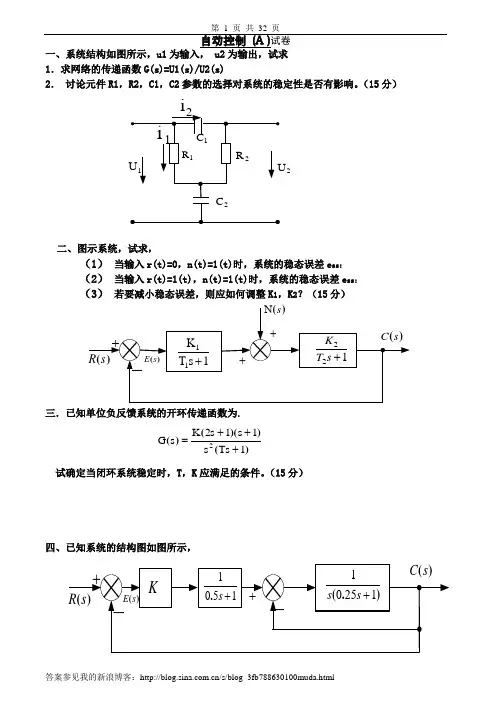
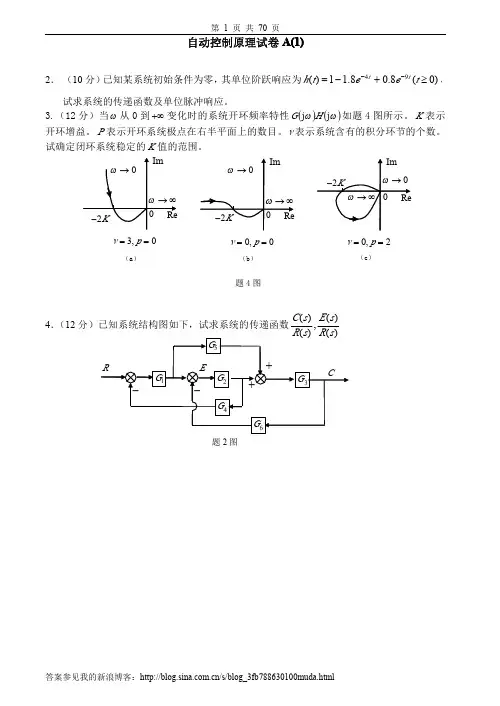
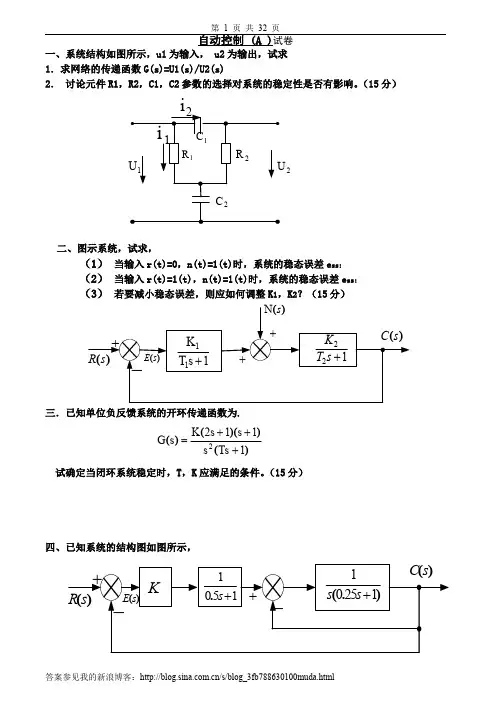
自动控制 (A )试卷一、系统结构如图所示，u1为输入， u2为输出，试求 1．求网络的传递函数G(s)=U1(s)/U2(s)2． 讨论元件R1，R2，C1，C2参数的选择对系统的稳定性是否有影响。

（15分）2二、图示系统，试求，（1） 当输入r(t)=0，n(t)=1(t)时，系统的稳态误差e ss;（2） 当输入r(t)=1(t)，n(t)=1(t)时，系统的稳态误差e ss; （3） 若要减小稳态误差，则应如何调整K 1，K 2？（15分）三．已知单位负反馈系统的开环传递函数为.)())(()(1Ts s 1s 12s K s G 2+++=试确定当闭环系统稳定时，T ，K 应满足的条件。

（15分）四、已知系统的结构图如图所示，（1） 画出当∞→0:K 变化时，系统的根轨迹图；（2） 用根轨迹法确定，使系统具有阻尼比50.=ζ时，K 的取值及闭环极点（共轭复根）。

（15分）五、已知最小相位系统的对数幅频特性渐近特性曲线，1.试求系统的开环传递函数G （s ）;2.求出系统的相角裕量γ;3．判断闭环系统的稳定性。

（15分）六、设单位反馈系统的开环传递函数如下，2s158s -+=)()(s H s G 1. 试画出系统的乃奎斯特曲线;2. 用乃氏判据判断系统的稳定性（15分） 七、已知单位反馈系统的开环传递函数为1)s(2s 4G +=)(s使设计一串联滞后校正装置，使系统的相角裕量040≥γ，幅值裕量10db K g≥，并保持原有的开环增益值。

（10分）自动控制理论B一． 试求图示系统的输出z 变换C(z).（20分）(b)(a)二.闭环离散系统如图所示，其中采样周期T =1s ，（20分）1． 试求系统的开环脉冲传递函数G(z); 2． 求系统的闭环脉冲传递函数)z (Φ； 3． 确定闭环系统稳定时K 的取值范围。

（注：()T 22e z z )s 1(Z ,1z Tz )s 1(Z ,1z z )s1(Z αα--=+-=-=）三. 设单位反馈线性离散系统如图所示，其中T ＝1秒，试求取在等速度 输入信号r (t )=1作用下，能使给定系统成为最少拍系统的数字控制器的脉冲传递函数D (z )。

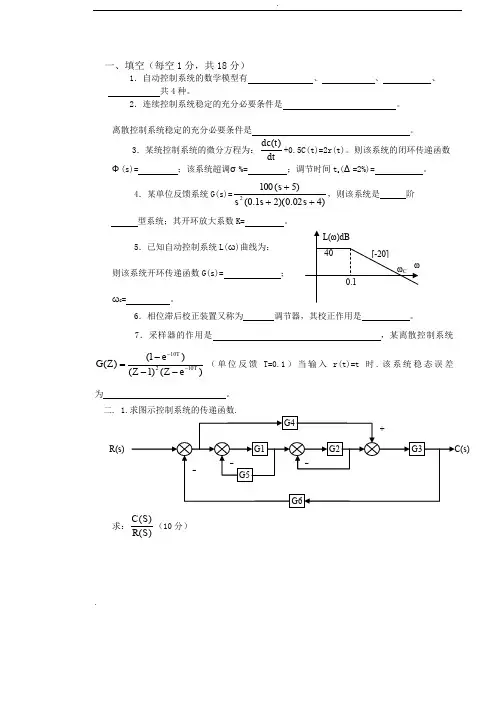
.一、填空（每空1分，共18分）1．自动控制系统的数学模型有 、 、 、共4种。

2．连续控制系统稳定的充分必要条件是 。

离散控制系统稳定的充分必要条件是 。

3．某统控制系统的微分方程为：dtt dc )(+0.5C(t)=2r(t)。

则该系统的闭环传递函数 Φ(s)= ；该系统超调σ%= ；调节时间t s (Δ=2%)= 。

4．某单位反馈系统G(s)=)402.0)(21.0()5(1002+++s s s s ，则该系统是 阶 型系统；其开环放大系数K= 。

5．已知自动控制系统L(ω)曲线为：则该系统开环传递函数G(s)= ；ωC = 。

6．相位滞后校正装置又称为 调节器，其校正作用是 。

7．采样器的作用是 ，某离散控制系统)()1()1()(10210T T e Z Z e Z G -----=（单位反馈T=0.1）当输入r(t)=t 时.该系统稳态误差为 。

二求：)()(S R S C （10分）R(s)2.求图示系统输出C（Z）的表达式。

（4分）四．反馈校正系统如图所示（12分）求：（1）K f=0时，系统的ξ，ωn和在单位斜坡输入下的稳态误差e ss.（2）若使系统ξ=0.707，k f应取何值？单位斜坡输入下e ss.=？..（1）（2）（3）五.已知某系统L（ω）曲线，（12分）（1）写出系统开环传递函数G（s）（2）求其相位裕度γ（3）欲使该系统成为三阶最佳系统.求其K=？，γmax=?六、已知控制系统开环频率特性曲线如图示。

P为开环右极点个数。

г为积分环节个数。

判别系统闭环后的稳定性。

.七、已知控制系统的传递函数为)1005.0)(105.0(10)(0++=s s s G 将其教正为二阶最佳系统，求校正装置的传递函数G 0（S ）。

（12分）一.填空题。

（10分）1.传递函数分母多项式的根，称为系统的2. 微分环节的传递函数为3.并联方框图的等效传递函数等于各并联传递函数之4.单位冲击函数信号的拉氏变换式5.系统开环传递函数中有一个积分环节则该系统为 型系统。

2010年中国⽯油⼤学⾃动控制期末考试试题2010—2011学年第1学期《⾃动控制原理》试卷（闭卷）专业班级测控08级班姓名学号开课系室⾃动化考试⽇期 2011年1⽉11⽇⼀、填空题（每空1分，共20分）1.⾃动控制基本控制⽅式包括_____________、_____________和复合控制。

2.对于⾃动控制系统性能的基本要求归结为三个⽅⾯，分别是：___________、___________、_____________。

3.线性定常系统的传递函数定义为，在_____________条件下，系统输出量的拉⽒变换与输⼊量的拉⽒变换之⽐。

传递函数只取决于系统的______________，⽽与系统输⼊量的形式⽆关。

4.对于稳定的⾼阶系统，闭环极点负实部的绝对值越⼤，其对应的响应分量衰减得越_____________（快/慢）。

在所有的闭环极点中，有些极点距离虚轴最近且周围没有闭环零点，这样的闭环极点称为_____________。

5.线性系统的稳态误差与系统的结构___________（有关/⽆关），与系统输⼊信号的⼤⼩和形式_____________ (有关/⽆关），线性系统的稳定性与输⼊信号⼤⼩和形式_______（有关/⽆关）。

6.在适当位置附加开环零极点可以改善系统性能。

当开环极点不变，附加⼀个负实数零点会使得根轨迹向S平⾯__________(左/右)半平⾯弯曲。

附加的零点越靠近虚轴，其对系统的影响就越__________ (⼤/⼩)。

7.串联超前校正是利⽤了校正环节的_____________特性，滞后校正是利⽤校正环节的_____________特性，两种校正⽅法都能增加了原系统的相⾓裕度。

8.如果离散控制系统的开环增益不变⽽增⼤采样周期则系统的稳定性变______（强/弱）；如果其采样周期不变⽽减⼩开环增益则系统的稳定性变_________(强/弱）。

9. ⾮线性系统与线性系统的本质区别在于不再适⽤_____________，⾮线性系统稳定分析更加复杂，可能存在_____个平衡状态，也可能出现⾃激振荡现象。

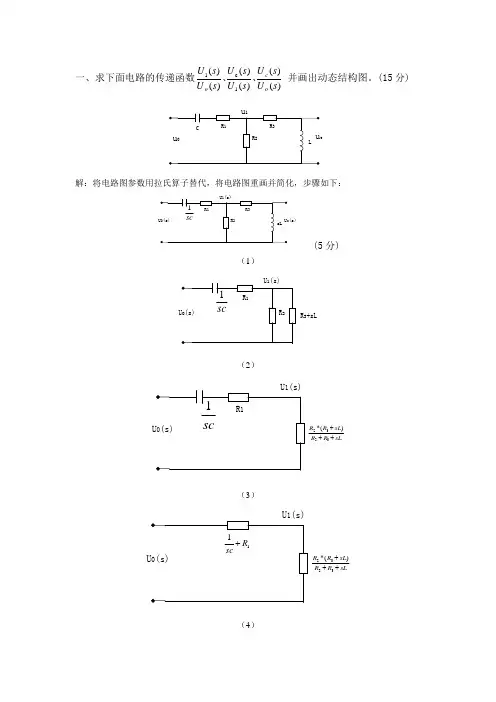
一、求下面电路的传递函数)()()()()()(1c 1s U s U s U s U s U s U o c o 、、并画出动态结构图。

(15分)解：将电路图参数用拉氏算子替代，将电路图重画并简化，步骤如下：(s)(5分)（1）R 3+sL（2）sLR R sL R R +++3232)(*（3）U 1(s)sLR R sL R R +++3232)(*（4）所以： 132323232011)(*)(*)()(R scsL R R sL R R sL R R sL R R s U s U ++++++++=(5分) 31)()(R sL sLs U s U c +=132323232301101)(*)(**)()(*)()()()(R scsL R R sL R R sL R R sL R R R sL sLs U s U s U s U s U s U c c +++++++++==系统的动态结构图为： (5分)本题考查要点： 电路图的数学模型和传递函数的关系，动态传递函数及结构图画法。

包含简单的电路简化过程。

二、对系统结构图进行简化并写出系统的开环传递函数、闭环传递函数、误差传递函数。

(15分)解:对结构图的简化过程如下：(10分)（1）（2）（3）（4）（5）所以系统的开环传递函数为：(5分)12151234323431)(*1)(H G G G G G H G G H G G G s G K ++++=121512343234312151234323431)(*111)(*1)(H G G G G G H G G H G G G H G G G G G H G G H G G G s G B +++++++++=12151234323431)(*111)()()(H G G G G G H G G H G G G s R s E s G E +++++==本题考查要点：结构图的简化方法（信号分支点和汇合点的移动、环节的合并）、几种传递函数的表示法。

第三章例3-1 系统的结构图如图3-1所示。

已知传递函数 )12.0/(10)(+=s s G 。

今欲采用加负反馈的办法，将过渡过程时间t s减小为原来的0.1倍，并保证总放大系数不变。

试确定参数K h 和K 0的数值。

解 首先求出系统的传递函数φ（s ），并整理为标准式，然后与指标、参数的条件对照。

一阶系统的过渡过程时间t s 与其时间常数成正比。

根据要求，总传递函数应为)110/2.0(10)(+=s s φ即HH K s K s G K s G K s R s C 1012.010)(1)()()(00++=+= )()11012.0(101100s s K K K HHφ=+++=比较系数得⎪⎩⎪⎨⎧=+=+1010110101100H HK K K 解之得9.0=H K 、100=K解毕。

例3-10 某系统在输入信号r (t )=(1+t )1(t )作用下，测得输出响应为：t e t t c 109.0)9.0()(--+= （t ≥0）已知初始条件为零，试求系统的传递函数)(s φ。

解 因为22111)(ss s s s R +=+=)10()1(10109.09.01)]([)(22++=+-+==s s s s s s t c L s C 故系统传递函数为11.01)()()(+==s s R s C s φ 解毕。

例3-3 设控制系统如图3-2所示。

试分析参数b 的取值对系统阶跃响应动态性能的影响。

解 由图得闭环传递函数为1)()(++=s bK T Ks φ系统是一阶的。

动态性能指标为)(3)(2.2)(69.0bK T t bK T t bK T t s r d +=+=+= 因此，b 的取值大将会使阶跃响应的延迟时间、上升时间和调节时间都加长。

解毕。

例 3-12 设二阶控制系统的单位阶跃响应曲线如图3-34所示。

试确定系统的传递函数。

解 首先明显看出，在单位阶跃作用下响应的稳态值为3，故此系统的增益不是1，而是3。

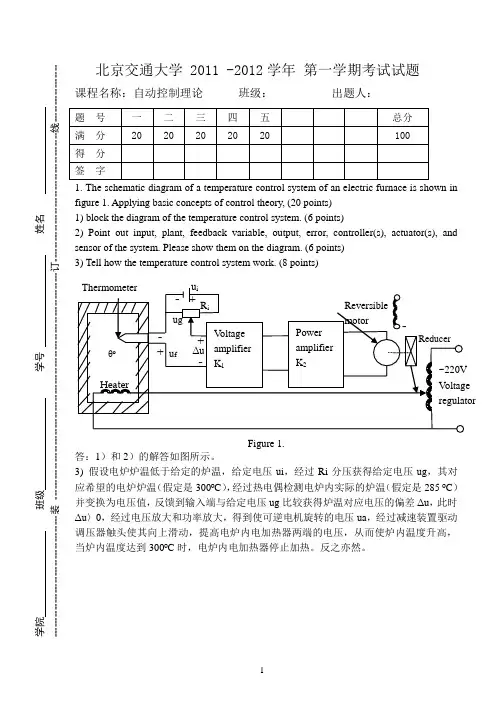
北京交通大学 2011 -2012学年 第一学期考试试题课程名称：自动控制理论 班级： 出题人：1. The schematic diagram of a temperature control system of an electric furnace is shown in figure 1. Applying basic concepts of control theory, (20 points) 1) block the diagram of the temperature control system. (6 points)2) Point out input, plant, feedback variable, output, error, controller(s), actuator(s), and sensor of the system. Please show them on the diagram. (6 points) 3) Tell how the temperature control system work. (8 points)Figure 1.答：1）和2）的解答如图所示。

3) 假设电炉炉温低于给定的炉温，给定电压ui ，经过Ri 分压获得给定电压ug ，其对应希望的电炉炉温（假定是300ºC ），经过热电偶检测电炉内实际的炉温（假定是285 ºC ）并变换为电压值，反馈到输入端与给定电压ug 比较获得炉温对应电压的偏差Δu ，此时Δu 〉0，经过电压放大和功率放大，得到使可逆电机旋转的电压ua ，经过减速装置驱动调压器触头使其向上滑动，提高电炉内电加热器两端的电压，从而使炉内温度升高，当炉内温度达到300ºC 时，电炉内电加热器停止加热。

反之亦然。

学院 班级 学号 姓名 ------------------------------------装 -------------------------------------------------------------------订--------------------------------------线------------------ 2 -2. Obtain the transfer function C (s)/R (s) of the op-amp circuit shown in figure 2, and determine the output steady-state value c ss (t ) and the steady-state error e ss (t ). Assume that 1,0.1,()5sin 5R M C F r t t μ=Ω== (20 points)Figure 2答：()()222211()10.010.11C s s R s s C R sC R s s φ===++++ (6 points)22110.1()0.010.1110.01j arctgj ωφωωωω==--++-424(5)33.73j arctg φ=-=︒()()()533.7,0ss c t t t ∴=-≥(10 points)()()()()()5sin 5533.7,0ss ss e t r t c t t t t ∴=-=--≥(4 points)3. Consider the system shown in figure 3,(20points)Figure 31) Write the open-loop transfer function of the system;(5 points) 2) Write the closed-loop transfer function of the transfer;（5 points ）3) If the Maximum overshoot (M p ) of the system is 16.3%,Peak time (t p ) is 1s,Determine the gain K and velocity-feedback constant τ（5 points ） 4) If)/(5.1)(s t t r ︒=, determine the steady-state error e ss .(5 points)答：（1） )110(10)1(101)1(10)(++=+++=ττs s K s s s s s Ks G（2） 2222210)110(10)(1)()(nn ns s Ks s Ks G s G s ωξωωτ++=+++=+=Φ（3）由 ⎪⎩⎪⎨⎧=-===--113.16212ξωπσςξπn p ooo o t e 联立解出⎪⎩⎪⎨⎧===263.063.35.0τωξn由（2） 18.1363.31022===n K ω，得出 318.1=K 。

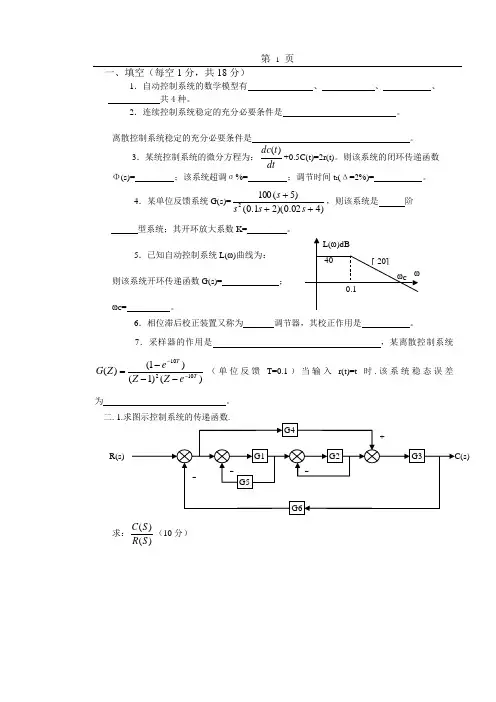
第 1 页一、填空（每空1分，共18分）1．自动控制系统的数学模型有 、 、 、共4种。

2．连续控制系统稳定的充分必要条件是 。

离散控制系统稳定的充分必要条件是 。

3．某统控制系统的微分方程为：dtt dc )(+0.5C(t)=2r(t)。

则该系统的闭环传递函数 Φ(s)= ；该系统超调σ%= ；调节时间t s (Δ=2%)= 。

4．某单位反馈系统G(s)=)402.0)(21.0()5(1002+++s s s s ，则该系统是 阶 型系统；其开环放大系数K= 。

5．已知自动控制系统L(ω)曲线为：则该系统开环传递函数G(s)= ；ωC = 。

6．相位滞后校正装置又称为 调节器，其校正作用是 。

7．采样器的作用是 ，某离散控制系统)()1()1()(10210TT e Z Z e Z G -----=（单位反馈T=0.1）当输入r(t)=t 时.该系统稳态误差为 。

二. 1.求：)()(S R S C （10分）R(s)第2页2.求图示系统输出C（Z）的表达式。

（4分）四．反馈校正系统如图所示（12分）求：（1）K f=0时，系统的ξ，ωn和在单位斜坡输入下的稳态误差e ss.（2）若使系统ξ=0.707，k f应取何值？单位斜坡输入下e ss.=？第 3 页（1） （2） （3）五.已知某系统L （ω）曲线，（12分）（1）写出系统开环传递函数G （s ） （2）求其相位裕度γ（3）欲使该系统成为三阶最佳系统.求其K=？，γmax =?六、已知控制系统开环频率特性曲线如图示。

P 为开环右极点个数。

г为积分环节个数。

判别系统闭环后的稳定性。

第 4 页七、已知控制系统的传递函数为)1005.0)(105.0(10)(0++=s s s G 将其教正为二阶最佳系统，求校正装置的传递函数G 0（S ）。

（12分）一.填空题。

（10分）1.传递函数分母多项式的根，称为系统的2. 微分环节的传递函数为3.并联方框图的等效传递函数等于各并联传递函数之4.单位冲击函数信号的拉氏变换式5.系统开环传递函数中有一个积分环节则该系统为 型系统。

《 自动控制原理 》典型考试试题（时间120分钟）院/系 专业 姓名 学号第二章：主要是化简系统结构图求系统的传递函数，可以用化简，也可以用梅逊公式来求一、（共15分）已知系统的结构图如图所示。

请写出系统在输入r(t)和扰动n(t)同时作用下的输出C(s)的表达式。

二 、（共15分）已知系统的结构图如图所示。

试求传递函数)()(s R s C ，)()(s N s C 。

三、（共15分）已知系统的结构图如图所示。

试确定系统的闭环传递函数C(s)/R(s)。

四、（共15分）系统结构图如图所示，求X(s)的表达式五、（共15分）已知系统的结构图如图所示。

试确定系统的闭环传递函数C(s)/R(s)和C(s)/D(s)。

六、（共15分）系统的结构图如图所示，试求该系统的闭环传递函数)()(s R s C 。

七、（15分）试用结构图等效化简求题图所示各系统的传递函数)()(s R s C 一、（共15分）某控制系统的方框图如图所示，欲保证阻尼比ξ=0.7和响应单位斜坡函数的稳态误差为ss e =0.25,试确定系统参数K 、τ。

二、（共10分）设图（a ）所示系统的单位阶跃响应如图（b ）所示。

试确定系统参数,1K 2K 和a 。

三、（共15分）已知系统结构图如下所示。

求系统在输入r(t)=t 和扰动信号d(t)=1(t)作用下的稳态误差和稳态输出)(∞C四、（共10分）已知单位负反馈系统的开环传递函数为：试确定引起闭环系统等幅振荡时的K 值和相应的振荡频率ω五、（15分）设单位反馈系统的开环传递函数为若系统以2rad/s 频率持续振荡，试确定相应的K 和α值六、（共15分）系统结构图如图所示。

（1）为确保系统稳定，如何取K 值？（2）为使系统特征根全部位于s 平面1-=s 的左侧，K 应取何值？（3）若22)(+=t t r 时，要求系统稳态误差25.0≤ss e ，K 应取何值？六、（15分）单位反馈系统的开环传递函数为)5)(3()(++=s s s K s G 为使系统特征根的实部不大于-1，试确定开环增益的取值范围。

第一章 习题答案1-1 根据题1-1图所示的电动机速度控制系统工作原理图(1) 将a,b 与c ，d 用线连接成负反馈状态；（2） 画出系统方框图。

解 (1)负反馈连接方式为:d a ↔，c b ↔；(2）系统方框图如图解1—1 所示。

1—2 题1—2图是仓库大门自动控制系统原理示意图。

试说明系统自动控制大门开闭的工作原理，并画出系统方框图。

题1-2图 仓库大门自动开闭控制系统解 当合上开门开关时，电桥会测量出开门位置与大门实际位置间对应的偏差电压，偏差电压经放大器放大后,驱动伺服电动机带动绞盘转动，将大门向上提起。

与此同时，和大门连在一起的电刷也向上移动，直到桥式测量电路达到平衡，电动机停止转动，大门达到开启位置。

反之,当合上关门开关时，电动机带动绞盘使大门关闭，从而可以实现大门远距离开闭自动控制。

系统方框图如图解1—2所示。

1—3 题1-3图为工业炉温自动控制系统的工作原理图。

分析系统的工作原理,指出被控对象、被控量和给定量，画出系统方框图。

题1-3图 炉温自动控制系统原理图解 加热炉采用电加热方式运行,加热器所产生的热量与调压器电压c u 的平方成正比，c u 增高，炉温就上升，c u 的高低由调压器滑动触点的位置所控制，该触点由可逆转的直流电动机驱动。

炉子的实际温度用热电偶测量，输出电压f u 。

f u 作为系统的反馈电压与给定电压r u 进行比较，得出偏差电压e u ，经电压放大器、功率放大器放大成a u 后，作为控制电动机的电枢电压。

在正常情况下，炉温等于某个期望值T °C,热电偶的输出电压f u 正好等于给定电压r u .此时,0=-=f r e u u u ，故01==a u u ，可逆电动机不转动，调压器的滑动触点停留在某个合适的位置上，使c u 保持一定的数值.这时，炉子散失的热量正好等于从加热器吸取的热量，形成稳定的热平衡状态，温度保持恒定。

当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失)，则出现以下的控制过程： 控制的结果是使炉膛温度回升,直至T °C 的实际值等于期望值为止。

. 专业资料可编辑 .一、填空（每空1分，共18分）1．自动控制系统的数学模型有 、 、 、共4种。

2．连续控制系统稳定的充分必要条件是 。

离散控制系统稳定的充分必要条件是 。

3．某统控制系统的微分方程为：dtt dc )(+0.5C(t)=2r(t)。

则该系统的闭环传递函数 Φ(s)= ；该系统超调σ%= ；调节时间t s (Δ=2%)= 。

4．某单位反馈系统G(s)=)402.0)(21.0()5(1002+++s s s s ，则该系统是 阶 型系统；其开环放大系数K= 。

5．已知自动控制系统L(ω)曲线为：则该系统开环传递函数G(s)= ；ωC = 。

6．相位滞后校正装置又称为 调节器，其校正作用是 。

7．采样器的作用是 ，某离散控制系统)()1()1()(10210TT e Z Z e Z G -----=（单位反馈T=0.1）当输入r(t)=t 时.该系统稳态误差. 专业资料可编辑 .为 。

二. 1.求图示控制系统的传递函数.求：)()(S R S C （10分）R(s). 专业资料可编辑 .2.求图示系统输出C （Z ）的表达式。

（4分）四．反馈校正系统如图所示（12分）求：（1）K f =0时，系统的ξ，ωn 和在单位斜坡输入下的稳态误差e ss . （2）若使系统ξ=0.707，k f应取何值？单位斜坡输入下e ss .=？T五.已知某系统L（ω）曲线，（12分）（1）写出系统开环传递函数G（s）（2）求其相位裕度γ（3）欲使该系统成为三阶最佳系统.求其K=？，γmax=?. 专业资料可编辑.. 专业资料可编辑 .（1）（2） （3）六、已知控制系统开环频率特性曲线如图示。

P 为开环右极点个数。

г为积分环节个数。

判别系. 专业资料可编辑 .七、已知控制系统的传递函数为)1005.0)(105.0(10)(0++=s s s G 将其教正为二阶最佳系统，求校正装置的传递函数G 0（S ）。

第 1 页一、填空（每空1分，共18分）1．自动控制系统的数学模型有 、 、 、共4种。

2．连续控制系统稳定的充分必要条件是 。

离散控制系统稳定的充分必要条件是 。

3．某统控制系统的微分方程为：dtt dc )(+0.5C(t)=2r(t)。

则该系统的闭环传递函数 Φ(s)= ；该系统超调σ%= ；调节时间t s (Δ=2%)= 。

4．某单位反馈系统G(s)=)402.0)(21.0()5(1002+++s s s s ，则该系统是 阶 型系统；其开环放大系数K= 。

5．已知自动控制系统L(ω)曲线为：则该系统开环传递函数G(s)= ；ωC = 。

6．相位滞后校正装置又称为 调节器，其校正作用是 。

7．采样器的作用是 ，某离散控制系统)()1()1()(10210TT e Z Z e Z G -----=（单位反馈T=0.1）当输入r(t)=t 时.该系统稳态误差为 。

二. 1.求：)()(S R S C （10分）R(s)第2页2.求图示系统输出C（Z）的表达式。

（4分）四．反馈校正系统如图所示（12分）求：（1）K f=0时，系统的ξ，ωn和在单位斜坡输入下的稳态误差e ss.（2）若使系统ξ=0.707，k f应取何值？单位斜坡输入下e ss.=？第 3 页（1） （2） （3）五.已知某系统L （ω）曲线，（12分）（1）写出系统开环传递函数G （s ） （2）求其相位裕度γ（3）欲使该系统成为三阶最佳系统.求其K=？，γmax =?六、已知控制系统开环频率特性曲线如图示。

P 为开环右极点个数。

г为积分环节个数。

判别系统闭环后的稳定性。

第 4 页七、已知控制系统的传递函数为)1005.0)(105.0(10)(0++=s s s G 将其教正为二阶最佳系统，求校正装置的传递函数G 0（S ）。

（12分）一.填空题。

（10分）1.传递函数分母多项式的根，称为系统的2. 微分环节的传递函数为3.并联方框图的等效传递函数等于各并联传递函数之4.单位冲击函数信号的拉氏变换式5.系统开环传递函数中有一个积分环节则该系统为 型系统。

中国石油大学远程教育《自动控制原理》自测题第一章自测题（30分钟）1．自动控制是在（没有人直接参与）的情况下，利用外加的设备或装置（即控制器），使机器、设备或生产过程即（被控对象）的某个工作状态或参数即（被控变量）自动地按照预定规律运行。

2．自动控制系统是指由（控制装置）与（被控对象）结合起来的，能够对被控对象的一些物理量进行自动控制的一个有机整体。

3．（被控对象）是要求实现自动控制的机器设备、生产过程，或其它对象。

4．（被控制量）是指被控制系统所要控制的物理量，一般指系统的输出量。

5．（控制量）是可以被改变，并影响被控制量的物理量，一般指系统的输入量。

6．破坏控制量与被控制量之间正常对应关系的因素称为（扰动）。

7．（控制装置）是指能够对被控对象起控制作用的设备总称，如控制器和调节阀。

8．（检测装置）是指测量系统某些物理量值的装置，如传感器。

9．一般控制系统包括（控制器）、（执行器）、（工艺对象）和传感器等四部分。

10．把取出的输出量送回输入端，并与输入信号相比较产生偏差信号的过程即为（反馈）。

11．反馈的类型包括（正反馈）和（负反馈），控制系统主要利用的反馈类型是（负反馈）。

12．反馈控制原理是将系统的输出信号引回输入端，与给定信号相减形成（控制偏差）信号。

然后根据偏差信号产生相应的控制作用，使控制偏差减少，最终消除消除控制偏差。

反馈信息使整个控制过程成为闭合控制系统，因此反馈控制也称为（闭环控制）。

13．自动控制系统的基本控制方式包括( 开环控制 )、(闭环控制或反馈控制）和复合控制。

14．对于自动控制系统的基本要求归结为三个方面，分别是：（稳定性）、（快速性）、（准确性）。

15．线性连续定常系统按照输入量的变化规律不同可以划分为（恒值控制系统）、（随动控制系统）和程序控制系统。

16．开环控制系统的特征是系统的输出量与输入量间不存在反馈的通道，输出量（不参与）控制。

17．控制系统按照信号的类型分为（连续控制系统）和（离散控制系统）。

《自动控制原理》试卷（一）A一、)(/)(s R s C二、 系统结构图如图所示，τ取何值时，系统才能稳定 ？ （10分）三、已知负反馈系统地开环传递函数为，42)2()(2+++=s s s K s W k(1) 试画出以K 为参数系统地根轨迹；(2) 证明根轨迹地复数部分为圆弧 . （15分）四、已知一单位闭环系统地开环传递函数为)15.0(100)(+=s s sW K ，现加入串联校正装置：101.011.0)(++=s s s W c ，试： （20分）（1） 判断此校正装置属于引前校正还是迟后校正？ （2） 绘制校正前、后系统及校正装置地对数幅频特性. （3） 计算校正后地相位裕量.五、非线性系统结构如图所示，设输入r=0, 绘制起始点在0)0(,1)0(00==>=c cc c 地c c -平面上地相轨迹. （15分）C )(s )(s o c六、采样控制系统如图所示，已知s T K 2.0,10==： （15分）1．求出系统地开环脉冲传递函数.2．当输入为)(1*)(1*)(1)(221t t t t t t r ++=时，求稳态误差ss e .七、用奈氏稳定判据判断如下图所示系统地稳定性.其中，（1）─（3）为线性系统，（4）─（6）为非线性系统. （15分）《自动控制原理》试卷（一）B一、 控制系统地结构如下图.(1) 当F （s ）=0时，求系统闭环传递函数)()()(s R s C s =Φ；(2) 系统中H2（s ）应满足什么关系，能使干扰F （s ）对输出C （s ）没有影响？（10分）二、． 设某控制系统方框图如图所示，要求闭环系统地特征值全部位于s ＝－1垂线之左，试确定参数K 地取值范围. （10分）三、.一单位负反馈系统地开环传函为)15.0()125.0()(++=s s s K s W ，欲使该系统对单位阶跃函数地响应为一振幅按指数规律衰减地简谐振荡时间函数，试用根轨迹法确定K 值范围（要求首先绘制根轨迹，求出并在图上标注主要地特征点参数）.（15分）四、如图（a ）和（b ）所示是两个单位反馈系统地开环对数幅频特性，它们都是最小相位地，且开环截止频率相等，均为c ω. （20分）1. 写出系统地开环传递函数.2. 比较两系统地稳定性，暂态性能（s t%,σ）和恒速输入下地稳态误差. 3. 将图（a ）所示地系统校正为图(b)所示地系统，应采用什么形式地串联校正装置？并写出此校正装置地传递函数)(s G c .五、．图所示为开环系统地幅相特性.图中P 为开环传递函数G(s)H(s)中具有正实部地极点数目.试详细分析闭环系统地稳定性. （16分）六．非线性系统结构如图所示，设输入r=0, 试描绘该系统地相平面图.（14分）七．设采样系统地方框图如图所示，其中)4()(1+=s s K s G , 采样周期T ＝0.25s ，求能使系统稳定地K1值范围. (15分))(/)(s R s CcC )(s系统地传递函数方块图如图所示.试确定K 和a 取何值时，系统将维持以角频率12-=s ω地持续振荡. （10分）三、已知负反馈系统地开环传递函数为，22+-s s 试画出以K 为参数系统地根轨迹；并求系统稳定时K 地取值范围. （15分）四、已知一单位闭环系统地开环传递函数为 )15.0(100)(+=s s s W K ，现加入串联校正装置：101.011.0)(++=s s s W c ，试： （20分）（4）判断此校正装置属于引前校正还是迟后校正？ （5）绘制校正前、后系统及校正装置地对数幅频特性. （6）计算校正后地相位裕量.五、非线性系统结构如图所示，设输入r=0, 试描绘该系统地相平面图. （15分）2． 求出系统地开环脉冲传递函数. 3． 判断闭环系统稳定性.3．当输入为)(1*)(1*)(1)(221t t t t t t r ++=时，求稳态误差ss e .)s《自动控制原理》试卷（二）B1. 控制系统地结构如下图.(3)当F （s ）=0时，求系统闭环传递函数)()()(s R s C s =Φ；(4)系统中H2（s ）应满足什么关系，能使干扰F （s ）对输出C （s ）没有影响？（10分）2． 设某控制系统方框图如图所示，要求闭环系统地特征值全部位于s ＝－1垂线之左，试确定参数K 地取值范围. （10分）3、设反馈控制系统中)5)(2()(2*++=ss s K s G ，1)(=s H要求：（1）概略绘制系统根轨迹图，判断系统地稳定性.（2）如果改变反馈通路传递函数使s s H 21)(+=，试判断)(s H 改变后系统地稳定性，研究)(s H 改变所产生地效应. （15分）4．已知一系统原有地特性为()()21.01100s s s W +=，校正装置地特性为()()()11.0101.0125.0+++=s s s s W c ，（1）画出原系统和校正装置地对数幅频特性.（2）当采用串联校正时，求校正后系统地开环传递函数，并计算其相位裕量γ(ωc)和增益裕量GM. （15分）5．图所示为开环系统地幅相特性.图中P 为开环传递函数G(s)H(s)中具有正实部地极点数目.试详细分析闭环系统地稳定性. （20分）6．已知非线性控制系统地结构图如图7-38所示.为使系统不产生自振，是利用描述函数法确定继电特性参数a,b 地数值.（15分）7．线性离散控制系统如下图所示，试确定使系统稳定地K 值范围. （15分）)1)(18.0(3++s s s b a r(t) +_c(t)《自动控制原理》 试卷（三）A 卷一、单项选择题：在下列各题中，有四个备选答案，请将其中唯一正确地答案填入题干地括号中.(本大题共9小题，总计40分) 1、(本小题3分)下列性能指标中，可以描述系统暂态性能地有――① 超调量②调节时间③稳态误差④调节频率⑤上升时间 A. ①②③④⑤ B. ①②④⑤ C. ①②③⑤ D. ①②③④答( )2、(本小题3分) 系统地传递函数可通过求取该系统地――而求得.A.阶跃响应函数B.脉冲响应函数C.斜坡响应函数D.抛物线响应函数答( )3、(本小题3分)如图所示是某系统地单位阶跃响应曲线，下面关于性能指标正确地是――A. s t r 6=B. s t s 4=C. s t p 14=D. %30%=δ答( )4、(本小题5分)已知控制系统开环传递函数为)43)(8(48)(22+++=s s s s s W ，则下述正确地是――A ．系统稳定 B.s 右半平面有2个根 C.2个纯虚根 D.全不正确答( ) 5、(本小题5分)13.102468101214t已知控制系统开环传递函数为)5)(2(10)(2++=s s s s W ，当输入46)(+=t t r 时，系统稳态误差为――A.0B. ∞C. 0.6D. 6答( )6、(本小题6分)系统根轨迹如图所示，当根轨迹与虚轴相交时，下述正确地是――A. 1=ξB. 162=KC. 42.2=ωD. 0=ω答()7、(本小题5分)下列线性系统判断中正确地是――A.（1）稳定B.（2）稳定C.（3）稳定D. 全不稳定答()8、(本小题5分)在采样控制系统中，为使采样信号不失真地恢复为原来地连续信号，则采样频率应至少大于――A. max21ω B. max ω C.max 2ω D. max 3ω 答()9、(本小题5分)设有一DDC 系统,T=1, Kc=1,试求单位阶跃响应在第几拍达到最大？σR)sA. 0.5拍B. 1拍C.2拍D. 3拍答()二、 计算题在下列各题中，(需要写出详细步骤、结果和画出必要地图形.) (本大题共3小题，总计60分)1．系统地传递函数方块图如图所示.试确定K 和a 取何值时，系统将维持以角频率12-=s ω地持续振荡.（20分）2．一单位负反馈系统地开环传函为)15.0()125.0()(++=s s s K s W ，欲使该系统对单位阶跃函数地响应为一振幅按指数规律衰减地简谐振荡时间函数，试用根轨迹法确定K 值范围（要求首先绘制根轨迹，求出并在图上标注主要地特征点参数）.（20分）如图（a ）和（b ）所示是两个单位反馈系统地开环对数幅频特性，它们都是最小相位地，且开环截止频率相等，均为c ω.（20分）要求：1. 写出系统地开环传递函数.2. 比较两系统地稳定性，暂态性能（s t %,σ）和恒速输入下地稳态误差.)s3. 将图（a）所示地系统校正为图(b)所示地系统，应采用什么形式地串联校正装置？并写出此校正装置地传递函数)(sGc.《自动控制原理》试卷（三）B卷一、单项选择题：在下列各题中，有四个备选答案，请将其中唯一正确地答案填入题干地括号中.(本大题共9小题，总计40分)1、(本小题3分)把系统输出量地拉氏变换与输入量地拉氏变换之比称为系统地传递函数.A.正确B.不正确C.部分正确D.无法判断答( )2、(本小题3分)线性系统地稳定性是系统本身固有地一种特性，与输入量及初始条件无关.A.正确B.不正确C.部分正确D.无法判断答( )3、(本小题3分)线性系统稳定地充分必要条件是：开环传递函数地所有极点均位于S复平面地左半平面.A. 正确B. 不正确C. 部分正确D. 无法判断答( )4、(本小题3分)输入量为单位斜坡函数时，要使系统地稳态误差为零，系统必须为Ⅰ型系统.A. 正确B.不正确C. 部分正确D. 无法判断答( )5、(本小题5分)下列那个线性系统闭环稳定.A.（1）稳定B.（2）稳定C.（3）稳定D. 都不稳定答( )6、(本小题5分)非线性系统闭环稳定判断中下列那个正确.A.（1）工作点不稳定B.（2）稳定C.（3）M 稳定N 不稳定D. 都不稳定答( ) 7、(本小题6分)已知系统地特征方程如下，判断系统稳定性地错误结论是哪个.0441086223456=++++++s s s s s sA. 系统临界稳定B. 没有S 右半平面根C. 有1对在虚轴上地根D. 有2 对在虚轴上地根答( ) 8、(本小题6分)非线性系统动态方程如下，试判断(-2,0)地奇点类型.A. 中心点B. 焦点C. 节点D. 鞍点答( ) 9、(本小题6分)某开环系统幅频特性波德图如下，试确定开环系统增益KA. 1B. 2C. 4D. 8答( )二、计算题：在下列各题中，需要写出详细步骤、结果和画出必要地图形. (本大题共3小题，总计60分) 1、 (本小题20分)设一反馈控制系统地开环传递函数如下，试绘制K1变化时系统特征方程地根轨迹，并求出系统稳定时K1地取值范围.025.02=+++x x x x12 4-1-2ωL(ω)dB)22)(3()()(21+++=s s s s K s H s G2、(本小题20分)设1型单位反馈系统原有部分地开环传递函数为：)1()(+=s s Ks G要求设计串联校正装置，使系统具有K=12及γ=40度地性能指标.3、(本小题20分)设采样系统地方框图如图所示，其中)4()(1+=s s K s G ,采样周期T ＝0.25s ，求能使系统稳定地K1值范围.《自动控制原理》试卷（四）A1. 控制系统地方框图如图所示，试用梅逊公式.10分0441086223456=++++++s s s s s s3. 设一反馈控制系统地开环传递函数如下，试绘制K1变化时系统特征方程地根轨迹.20分)22)(3()()(21+++=s s s s K s H s G4. 已知单位负反馈系统地开环传递函数：H1(s)C(s)+-- -)1)(120)(110()12(100)(++++=s ss s s s G试求系统地相角裕度和幅值裕度. 15分 5. 设1型单位反馈系统原有部分地开环传递函数为：)1()(+=s s Ks G要求设计串联校正装置，使系统具有K=12及γ=40度地性能指标. 15分 6. 试用等倾线法画出相轨迹.10分0=++∙∙∙x x x7．采样系统结构图如图所示，)15(10)(1+=s s s W ，采样周期T=1秒，试判断闭环系统地稳定性. 15分{}1)(1-=z z t Z{}e z ze Z aT at ---=《自动控制原理》试卷（四）B1．控制系统地方框图如图所示，试用梅逊公式求系统地传递函数.15分0160161023=+++s s s已知单位负反馈系统地开环传递函数为，)1()1()(-+=S S S K s WK，试：（1）绘制系统地根轨迹；（2）求系统稳定时K 地取值范围. [15分]3．已知单位负反馈系统地开环传递函数：)1)(120)(110()12(100)(++++=s ss s s s G试求系统地相角裕度和幅值裕度. 15分5．系统地结构图如图(a)所示，其中，W2(S)为最小相位环节，W2(S)由如图(b)所示地对数幅频特性确定出.试求系统稳定时K 地取值范围. 15分6．含有死区继电器特性地非线性系统地方框图如图所示，系统中线性部分地输入输出关系为：c r e y dt dcdtc d -==+22非线性系统部分地输入输出关系可用下式表示：⎪⎪⎬⎫⎪⎪⎨⎧-<-<<->==1,111,01,1)(e e e e f y试绘制其初始状态为3时地相轨迹.15分7．设采样系统地方框图如图所示，其中)4()(1+=s s K s G ,采样周期T ＝0.25s ，求能使系统稳定地K1值范围 15分(a)(b)《自动控制原理》试卷（五）A一、选择题：（共20分） 1、(本小题4分)系统地传递函数可通过求取该系统地――而求得.A.阶跃响应函数B.脉冲响应函数C.斜坡响应函数D.抛物线响应函数 答( ) 2、(本小题4分)如图所示是某系统地单位阶跃响应曲线，下面关于性能指标正确地是――A. s t r 6=B. s t s 4=C. s t p 14=D. %30%=δ答( )3、(本小题5分)已知控制系统开环传递函数为)5)(2(10)(2++=s s s s W ，当输入46)(+=t t r 时，系统稳态误差为――A.0B. ∞C. 0.6D. 6 4、(本小题4分)系统根轨迹如图所示，当根轨迹与虚轴相交时，下述正确地是――σ13.1024810tA. 1=ξB. 162=KC. 42.2=ωD. 0=ω答()5、(本小题4分)下列线性系统判断中正确地是――A.（1）稳定B.（2）稳定C.（3）稳定D. 全不稳定答()二、 控制系统地方框图如图所示，试用梅逊公式求系统地传递函数.10分.试确定K 和a 取何值时，系统将维持以角频率1-s 地持续振荡.（10分）四、已知已知单位反馈系统地开环传递函数为)1()(41)(2++=s s a s s Ga 地变化范围为[0，+∞），试绘制系统地闭环根轨迹. （15分）五、已知一最小相位系统开环地对数幅频特性如下图所示， （15分）试写出系统开环传递函数()s W k ，求系统相位裕量和增益裕量.)sH1(s) C(s)+- --六、非线性系统结构如图所示，设输入r=0, 绘制起始点在0)0(,1)0(00==>=c cc c 地c c -平面上地相轨迹. （15分）七、线性离散控制系统如下图所示，试确定使系统稳定地K 值范围. （15分）自动控制原理试卷A1卷一、本题共2小题. （20分）1．（10分）下图所示电路，求)()()(s U s U s W r C =.2．（10)()()(B s X s X s W r C =.函数.三、已知单位负反馈系统地开环传函为2)1)(s (s )(g++=s K s W k ， （15分）（一）画出系统根轨迹（关键点要标明）. （二）求使系统稳定地Kg 值范围.四、设系统开环传函为()()111)(-+=s Ts s W k τ，试分别大致画出τ<T ，τ=T, τ>T 三种情况下地奈氏图. （15分）五、已知一最小相位系统开环地对数幅频特性如下图所示， （20分）（1）试写出系统开环传递函数()s W k ，计算相位裕量γ(ωc)和增益裕量GM.（2）若系统原有地开环传递函数为()()21.01100s s s W +=，而校正后地对数幅频特性如下图所示，求串联校正装置地传递函数.六、画出两个常见地非线性元件地特性. （5分）七、求解差分方程 ()()()()t k f k f k f δ=++-+2132 （10分）其中，初始条件：()00=f ，()01=f ；输入条件：()⎩⎨⎧≠=∞=000t t t δ自动控制原理试卷B2卷一、填空. [12分]1．线性定常系统， ，把系统输出量地拉氏变换与输入量地拉氏变换之比称为系统地传递函数.2．线性系统地稳定性是系统本身固有地一种特性，与输入量及初始条件 . 3．线性系统稳定地充分必要条件是 .4．输入为单位斜坡函数时，要使系统稳态误差为零，系统必须为 型系统.5．采样系统在初始条件为零时，把 称为系统地脉冲传递函数.6．用开环频率特性分析研究系统暂态特性时，常常用 和 这两个特征量地.二、化简结构图（或用信号流图法）求闭环传递函数)()(s X s X r c . [12分]Xc(s)（1） （2）三、设单位负反馈地典型二阶系统地单位阶跃响应地超调量为δ%=25%，调节时间为ts(5%)=2秒，试求：（1）系统地开环传递函数；（2）输入为单位斜坡函数时地稳态误差. [14分]四、已知单位负反馈系统地开环传递函数为，)1()1()(-+=S S S K s W K ，试：（1）绘制系统地根轨迹；（2）求系统稳定时K 地取值范围. [12分] 五、包括两小题. [14分]1．绘制下列系统地相平面图. （1） 0=+x x（2） 01=-x 2．用奈氏稳定判据判断如下图所示系统地稳定性.其中，（1）─（3）为线性系统，（4）─（6）为非线性系统.六、采样系统结构图如图所示， 采样周期T=1秒，求闭环脉传递函数.[12分)2(10)(1+=s s s W七、已知原系统开环传递函数为)1(10)(+=S S S W ，现采用串联校正方法，使校正后为二阶工程最佳系统且开环放大系数不变，试： [12分] （1） 确定校正装置Wc(S)；（2） 绘制校正前、后及校正装置地对数幅频特性；八、已知系统地结构图如图（a ）所示，其中，15.0)12()(1++=S S K S W ，W2(S)为最小相位环节，其对数幅频特性如图(b)所示.试求使闭环系统稳定地K 值范围.[12分]自动控制原理试卷A3卷一、填空. [10分]1． ，把系统输出量地拉氏变换与输入量地拉氏变换之比称为系统地传递函数.2． 线性系统地稳定性是系统本身固有地一种特性，与输入量及初始条件 .线性系统稳定地充分必要条件是 .4． 输入为单位斜坡函数时，要使系统稳态误差为零，系统应为 型系统. 5． 线性离散系统在初始条件为零时，把 称为系统地脉冲传递函数.(a)dB (b)二、用化简结构图或信号流图方法求下列系统地闭环传递函数)()()(S X S X S W r C B =.[12分]三、已知典型二阶系统地单位阶跃响应曲线如图所示.试求：（1）开环传递函数.（2）单位斜坡函数输入时地稳态误差. [14分]四、已知负反馈系统地开环传递函数为sKW s s gK )1()(+=，试画出系统地根轨迹图.[12分]五、已知单位负反馈系统地开环传递函数为：)10()2(50)(2++=s s s s W K ，试： [12分]（1）绘制波德图； （2）计算相位裕量.六、本题包括两小题. [14分]（一）试用奈氏判据判断下图所示系统地稳定性.其中，（1）—（3）为线性系统， （4）—（6）为非线性系统.(1)(2)（二）绘制下列系统地相平面图.（1） 0=+x x（2） 1=x 七、系统地结构图如图(a)所示，其中，W2(S)为最小相位环节，W2(S)由如图(b)所示地对数幅频特性确定出.试求系统稳定时K 地取值范围. [14分]八、某离散系统结构图如图所示，)2(2)(+=s s s W ，采样周期T=1秒，试判断系统地稳定性.[12分]1)](1[-=z z t ZaT at e z ze Z ---=][自动控制原理试卷B3卷(a)一、推导下列网络地传递函数：)()(s Ur s U C [10分]二、用化简结构图或信号流图方法求闭环传递函数)(s X X c三、单位负反馈地典型二阶系统地单位阶跃响应地超调量为δ%=25%，调节时间为ts（5%）=2秒，求：（1）系统地开环传递函数；（2）输入为单位斜坡函数时地稳态误差. [15分]四、 已知负反馈系统地开环传递函数为)2)(1()(++=s s s s KWgk，试画出系统地根轨迹图. [14分]五、以下两题任选一题.（如全做，按第一题记分） [10分]（一） 已知单位负反馈系统地开环传递函数为)5()1(50)(2++=S S S S W K ，试绘制波德图.（二） 绘制下列系统地相平面图.（1） 0=+x x（2） 1=x六、用奈氏判据判断下列系统地稳定性.其中，（1）—（3）为线性系统，（4）—（5）为非线性系统. [15分]R 1 R 1 (1)(2)七、系统地结构图如图(a)所示，其中，W2(S)为最小相位环节，W2(S)由如图(b)所示地对数幅频特性确定出.试求系统稳定时K 地取值范围. [12分]八、采样系统结构图如图所示，)15.0(10)(1+=s s s W ，采样周期T=1秒，试判断系统地稳定性.[12分]aT at e z z e Z ---=][自动控制原理试卷A4卷(a)(b)一、选择题（每小题5分，共20分），请选择其中所有正确地答案，将相应地字母和题号写在答题纸上.（1） 输入量为单位斜坡函数时，要使系统为无差系统，系统类型必须为：a. 0型b. 1型c. 2型d. 2型以上（2） 线性系统稳定地充分必要条件是：a. 开环传递函数地所有极点均位于S 复平面地左半平面.b. 闭环传递函数地所有极点均位于S 复平面地左半平面.c. 闭环特征方程式地所有根均具有负实部.d. 以上答案都不正确.（3） 某非线性系统地非线性部分地描述函数负倒特性)(1A R -和线性部分频率特性W1(jω)如图一所示.两线交点处地ω=3.162；A=1.05和3.69.则 该闭环系统是：a. 稳定地b. 不稳定地c. 产生自持振荡，其角频率为3.162，振幅为1.05d. 产生自持振荡，其角频率为3.162，振幅为3.69e. 以上答案都不正确（4） 已知采样系统地输出Z 变换为)()(1)()()(z W z H z Xr z W z Xc +=，1它符合下述哪几个系统？二、[16分]系统结构如下图所示.（1）绘制P （0→∞）变化时，系统地根轨迹图；（2）确定使闭环系统地阶跃响应为单调变化过程时P 地最小值.三、[16分]已知一系统原有地特性为()()21.01100s s s W +=，校正装置地特性为()()()11.0101.0125.0+++=s s s s W c ，（1）画出原系统和校正装置地对数幅频特性.（2）当采用串联校正时，求校正后系统地开环传递函数，并计算其相位裕量γ(ωc)和增益裕量GM.四、[15分] 采样系统结构图如下图所示，)15(10)(1+=s s s W ，采样周期T=1秒，b.c.a.d.试判断闭环系统地稳定性.（注：aTe z z a s Z --=⎭⎬⎫⎩⎨⎧+1）五、[15分]下图所示系统，求传递函数)(X )(s r s X C 和)()(s N s X C .六、设单位负反馈地典型二阶系统地单位解跃响应地超调量为δ%=25%，调节时间为ts(5%)=2秒，求： [18分]（1）系统地开环传递函数；（2）输入为单位斜坡函数时地稳态误差.自动控制原理试卷B4卷二、选择题（每小题5分，共20分），请选择其中所有正确地答案，将相应地字母和题号写在答题纸上.（5） 单位负反馈系统地开环传递函数为16816)(2++=s s s W K ，则闭环系统地阻尼比ξ等于：a. 1b. 2c.22d.2 e. 以上答案都不正确单位负反馈系统地开环传递函数为1)(+=TS KS W K ，则闭环系统单位阶跃响应地调节时间ts （±5%误差带）为：a. 3T b. K T3 c. K T +13 ；而闭环单位阶跃响应地稳态误差为：d. K 1 e. K +11f. 0g. ∞h. 以上答案都不正确（7） 已知单位正反馈系统地开环传递函数为)1()(2S S K S W gK -=，给出其可能地根轨迹大致图形如图一、图二、图三所示，请选择：a. 图一正确b. 图二正确c. 图三正确d. 都不正确（8） 已知采样系统地输出Z 变换为)()(1)()()(z W z H z Xr z W z Xc +=，它符合下述哪几个系统？二、[16分]设单位负反馈系统地开环传递函数为：)22)(2()(2+++=S S S S KS W K试应用劳斯稳定判据确定K 为多大时将使系统阶跃响应出现振荡，并求出振荡角频率.b.c.a.d.三、已知一单位负反馈典型二阶系统地单位阶跃响应曲线如下图所示，求系统地闭环传递函数. （18分）四、[18分]已知系统结构图如图四(a)所示，（系统为最小相位系统）所示，系统校正后地开环对数幅频特性如图四(c)所示.试求原系统地传递函数W(s)，并计. Array五、[14分] 采样系统结构图如图五所示，T为采样周期且T=1秒.试：（1）求闭环脉冲传递函数.（2）判断系统地稳定性. （注：aTe z z a s Z --=⎭⎬⎫⎩⎨⎧+1）六、[14分]非线性系统地结构图如图六(a)所示，其中非线性特性地负倒描述函数-1/R(A)曲线如图六(b)所示.试画出线性部分地奈氏曲线，并用描 述函数法判断系统是否会发生自振.《自动控制原理》试卷A一、单选题（每题2分，共20分）1．控制系统中基本环节地划分，是根据（ ） A ．元件或设备地形式 B ．系统地物理结构 C ．环节地连接方式 D ．环节地数学模型2．绘制根轨迹时需计算入射角地情况为：开环传递函数有（ ） A ．实极点 B ．实零点 C ．共轭复极点D ．共轭复零点图六(a)图六(b)图五3．设一单位反馈控制系统地开环传递函数为G0(s)=)2s (s K4+，要求KV=20，则K=( )A ．10B ．20C ．30D ．404.输入为阶跃信号时，如果( )，则积分环节地输出信号地上升速度越快. A.输入信号地幅度越小，积分时间常数越小 B.输入信号地幅度越小，积分时间常数越大 C.输入信号地幅度越大，积分时间常数越小 D.输入信号地幅度越大，积分时间常数越大5.如果二阶振荡环节地对数幅频特性曲线存在峰值，则阻尼比ξ地值为( ) A.0≤ξ≤0.707 B.0<ξ<1 C.ξ>0.707 D.ξ>16．决定系统静态性能和动态性能地是系统传递函数地( ) A ．零点和极点 B ．零点和传递系数 C ．极点和传递系数D ．零点、极点和传递系数 7．设二阶振荡环节地传递函数G （s ）=16s 4s 162++，则其对数幅频特性渐近线地交接频率为（ ） A ．2rad/sB ．4rad/sC ．8rad/sD ．16rad/s8．已知系统前向通道和反馈通道地传递函数分别为G （s ）=sK 1)s (H ,)1s (s 10h +=-，当闭环临界稳定时，Kh 值应为（ ）A ．-1B ．-0.1C ．0.1D ．19．设单位负反馈系统地开环传函为G(s)=3)1s (22+，那么它地相位裕量γ地值为（ ）A.15ºB.60ºC.30ºD.45º10.某串联校正装置地传递函数为Gc(S)=K S ST 1T 1+β+(0<β<1)，则该装置是（ ） A.超前校正装置 B.滞后校正装置C.滞后——超前校正装置D.超前——滞后校正装置 二、填空（每题2分，共20分）1. 根据控制系统信号地形式，控制系统可分为______ __控制系统、________控制系统.2. 对于一个自动控制系统地性能要求可以概括为三个方面：____ ____、____ ____和 .3. 用时域法分析控制系统时，最常用地典型输入信号是________.4.若要求系统地快速性好，则闭环极点应距虚轴越__________越好.5. 如果根轨迹位于实轴上两个相邻地开环零点之间(其中一个零点可以位于无穷远处)，则在这两个零点之间必定存在________.6．伯德图分中频段、高频段和低频段，低频段能够反应系统地 ，中频段能够反映系统地暂态性能，高频段主要反映系统 .7.根轨迹图必对称于根平面地__________.8．分析稳态误差时，将系统分为0型系统、1型系统、2型系统…，这是按开环传递函数地__________环节数来分类地.9．采样控制系统中，如果希望从采样信号)(t f *中不失真地恢复原来地信号)(t f ，则采样频率s ω满足 .10. 线性定常系统地脉冲传递函数地定义 .三、简答题（每题5分，共20分）1. 绘制由基本环节组成地闭环控制系统地一般结构图.2.在0<ξ<1,ξ=0,ξ≥1三种情况下，标准二阶系统地单位阶跃响应特性分别是什么?3.. 如图是最小相位系统地开环对数幅频渐近特性，试写出其传递函数G(s).4、求下列方程地奇点，并判断奇点类型.0)1(2=+--x x x x四、系统方框图如图2所示，并求出传递函数()C s R s ().（8分）图2五. 已知一单位闭环系统地开环传递函数为 )15.0(100)(+=s s s W K ，现加入串联校正装置：101.011.0)(++=s s s W c ，试： （12分）（7） 判断此校正装置属于引前校正还是滞后校正？（说明原因） （8） 绘制校正前、后系统及校正装置地对数幅频特性. （3） 计算校正后系统地相位裕量.六、采样系统结构图如图所示，)15(10)(1+=s s s W ，采样周期T=1秒，试判断闭环系统地稳定性.[10分]{(1z Z {e Z 1）─（3）为线性系统，（4）─（5）为非线性系统. （10分）《自动控制原理》试卷B一、单选题（每题2分，共20分）1．根据给定值信号地特点分类，控制系统可分为( ). A.恒值控制系统、随动控制系统和程序控制系统B.反馈控制系统、前馈控制系统前馈—反馈复合控制系统C.最优控制系统和模糊控制系统D.连续控制系统和离散控制系统2．绘制根轨迹时需计算出射角地情况为：开环传递函数有（ ） A ．实极点 B ．实零点 C ．共轭复极点D ．共轭复零点3．．已知单位反馈控制系统在阶跃函数作用下，稳态误差ess 为常数，则此系统为（ ）A ．0型系统B ．I 型系统C ．Ⅱ型系统D ．Ⅲ型系统4开环系统频率特性G(jω)=3)j 1(3ω+，当ω=1rad/s 时，其频率特性相角θ(1)=( ). A.－45°B.－90°C.－135°D.－270°5． 过阻尼系统地动态性能指标是调整时间ts 和( ) A ．峰值时间tp B ．最大超调量σp C ．上升时间tr D ．衰减比σp ／σp′6．二阶振荡环节地相频特性)(ωθ，当∞→ω时，其相位移)(∞θ为( ) A ．-270°B ．-180°C ．-90°D ．0°7．设某系统开环传递函数为G(s)=)1s )(10s s (102+++，则其频率特性奈氏图起点坐标为 ( )A ．(-10，j0) B ．(-1，j0) C ．(1，j0) D ．(10，j0)8. 超前校正装置地频率特性为)1(j T 1jT 122>βω+ωβ+，其最大超前相位角Φm 为( ). A.sin-111+β-βB.sin-11T 1-T 22+C.sin-11T 1T 22+β-βD.sin-11T 1T 22+ωβ-ωβ9．确定根轨迹与虚轴地交点，可用( )A ．劳斯判据B ．幅角条件C ．幅值条件D ．0ds dk =10．设开环传递函数为G(s)H(s)＝)3)(2()1(+++s s s s k ，其根轨迹渐近线与实轴地交点为（ ）A ．0B ．－1C ．－2D ．－3二、填空（每题2分，共20分）1. 根据控制系统元件地性质，控制系统可分为________控制系统、________控制系统.2. 对于一个自动控制系统地性能要求地快速性可由暂态性能指标中 、 等决定.3. 用频域法分析控制系统时，最常用地典型输入信号是___ _____.4. 线性定常系统在正弦信号输入时，稳态输出与输入地相位移随频率而变化地函数关系称为__________.5. 如果根轨迹位于实轴上两个相邻地开环极点之间，则在这两个极点之间必定存在________.6．单位脉冲函数又称为δ函数，它地数学表达式是_______________.。

（完整版）自动控制原理简答题47、传递函数：传递函数是指在零初始条件下，系统输出量的拉式变换与系统输入量的拉式变换之比。

48、系统校正：为了使系统达到我们的要求，给系统加入特定的环节，使系统达到我们的要求，这个过程叫系统校正。

49、主导极点：如果系统闭环极点中有一个极点或一对复数极点据虚轴最近且附近没有其他闭环零点，则它在响应中起主导作用称为主导极点。

51、状态转移矩阵：()Att e φ=，描述系统从某一初始时刻向任一时刻的转移。

52、峰值时间：系统输出超过稳态值达到第一个峰值所需的时间为峰值时间。

53、动态结构图：把系统中所有环节或元件的传递函数填在系统原理方块图的方块中，并把相应的输入输出信号分别以拉氏变换来表示从而得到的传递函数方块图就称为动态结构图。

54、根轨迹的渐近线：当开环极点数 n 大于开环零点数 m 时，系统有n-m 条根轨迹终止于 S 平面的无穷远处，且它们交于实轴上的一点，这 n-m 条根轨迹变化趋向的直线叫做根轨迹的渐近线。

55、脉冲传递函数：零初始条件下，输出离散时间信号的z 变换()C z 与输入离散信号的变换()R z 之比，即()()()C z G z R z =。

56、Nyquist 判据（或奈氏判据）：当ω由-∞变化到+∞时， Nyquist 曲线（极坐标图）逆时针包围（-1，j0）点的圈数N ，等于系统G(s)H(s)位于s 右半平面的极点数P ，即N=P ，则闭环系统稳定；否则（N ≠P ）闭环系统不稳定，且闭环系统位于s 右半平面的极点数Z 为：Z=∣P-N ∣57、程序控制系统: 输入信号是一个已知的函数，系统的控制过程按预定的程序进行，要求被控量能迅速准确地复现输入，这样的自动控制系统称为程序控制系统。

58、稳态误差：对单位负反馈系统，当时间t 趋于无穷大时，系统对输入信号响应的实际值与期望值（即输入量）之差的极限值，称为稳态误差，它反映系统复现输入信号的（稳态）精度。

2011—2012学年第1学期《自动控制原理》期中考试试卷（适用专业：自动化、电气、测控）专业班级姓名学号开课系室自动化系考试日期一、 简答题 （15分）1. 反馈控制系统的基本组成有哪几部分？答：测量元件、给定元件、比较元件、放大元件、执行元件、校正元件2. 控制系统正常工作的最基本要求是什么？ 答：稳定性、快速性、准确性3. 什么是线性系统？线性系统的特征是什么？ 答：用线性微分方程描述的系统称为线性系统。

其特征是满足叠加原理，即叠加性与齐次性。

4. 控制系统的传递函数的定义和应用范围是什么？答：控制系统的传递函数的定义为：零初始条件下，系统输出量的拉氏变换与输入量的拉氏变换之比。

应用范围是：线性定常系统5. 控制器中加入比例+微分环节对控制系统的影响是什么？答：比例微分环节可增大系统的阻尼比，超调量增加，调节时间缩短，且不影响系统的稳态误差与自然振荡频率；允许选取较高的开环增益，因此在保证一定的动态性能条件下，可以减小稳态误差。

二、 (12分)如图1所示单容水箱，A 为水箱的横截面积，i Q 为输入流量，o Q 为输出流量，H 为水箱的实际液位， H Q o α=，α为流量系数。

当输入流量和输出流量相等时，液位维持在0H 处，000H Q Q o i α==。

（1） 以i Q 为输入，以H 为输出，建立该单容水箱的非线性微分方程模型。

（3分）（2） 对（1）中非线性微分方程在0H 处进行线性化，求线性化微分方程，并求单容水箱的传递函数。

（9分）图1解：（1）由物料平衡得下列方程 单容水箱的非线性微分方程模型为(1i dH Q dt A=- ① （3分） （2）考虑到代入①式得(00()1i i d H H Q Q dt A+∆=+∆- （2分）即(01i i d H Q Q dt A∆=+∆- ②在0H 处展开成Taylor 级数，只取到线性项H = （2分）代入②，并考虑000H Q Q o i α==，得 整理得1i d H H Q dt A ∆=∆ ③ （2分）③即为所求的线性微分方程 在③两边取拉氏变换得1()()i s H s Q s A ⎛⎫= ⎝（2分） 故其传递函数为1()()()i H s AG s Q s s α=== （1分）三、 （20分）结构图化简。