2010-2011年春季A卷答案

2011年上海市春季高考数学试卷一、填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每题填对得4分，否则一律得零分．1．（4分）函数f（x）=lg（x﹣2）的定义域是．2．（4分）若集合A={x|x≥1}，B={x|x2≤4}，则A∩B=．3．（4分）在△ABC中，tanA=，则sinA=．4．（4分）若行列式=0，则x=．5．（4分）若，，则x=（结果用反三角函数表示）6．（4分）（x+）6的二项展开式的常数项为．7．（4分）两条直线l1：x﹣y+2=0与l2：x﹣y+2=0的夹角的大小是．8．（4分）若S n为等比数列{a n}的前n项的和，8a2+a5=0，则=．9．（4分）若椭圆C的焦点和顶点分别是双曲线的顶点和焦点，则椭圆C的方程是．10．（4分）若点O和点F分别为椭圆+y2=1的中心和左焦点，点P为椭圆上的任意一点，则|OP|2+|PF|2的最小值为．11．（4分）根据如图所示的程序框图，输出结果i=．12．（4分）2011年上海春季高考有8所高校招生，如果某3位同学恰好被其中2所高校录取，那么录取方法的种数为．13．（4分）有一种多面体的饰品，其表面右6个正方形和8个正三角形组成（如图），则AB与CD所成的角的大小是．14．（4分）为求方程x5﹣1=0的虚根，可以把原方程变形为（x﹣1）（x2+ax+1）（x2+bx+1）=0，由此可得原方程的一个虚根为．二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．15．（5分）若向量，则下列结论正确的是（）A．B．C． D．16．（5分）f（x）=的图象关于（）A．原点对称B．直线y=x对称C．直线y=﹣x对称 D．y轴对称17．（5分）直线l：y=k（x+）与圆C：x2+y2=1的位置关系是（）A．相交或相切B．相交或相离C．相切D．相交18．（5分）若，，均为单位向量，则=（，）是++=（，）的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号规定区域内写出必要的步骤．19．（12分）已知向量=（sin2x﹣1，cosx），=（1，2cosx），设函数f（x）=•，求函数f（x）的最小正周期及x∈[0，]时的最大值．20．（14分）某甜品店制作蛋筒冰淇淋，其上半部分呈半球形，下半部分呈圆锥形（如图）．现把半径为10cm的圆形蛋皮分成5个扇形，用一个扇形蛋皮围成锥形侧面（蛋皮厚度忽略不计），求该蛋筒冰淇淋的表面积和体积（精确到0.01）．21．（14分）已知抛物线F：y2=4x（1）△ABC的三个顶点在抛物线F上，记△ABC的三边AB、BC、CA所在的直线的斜率分别为k AB，k BC，k CA，若A的坐标在原点，求k AB﹣k BC+k CA的值；（2）请你给出一个以P（2，1）为顶点、其余各顶点均为抛物线F上的动点的多边形，写出各多边形各边所在的直线斜率之间的关系式，并说明理由．22．（16分）定义域为R，且对任意实数x1，x2都满足不等式f（）≤的所有函数f（x）组成的集合记为M，例如，函数f（x）=kx+b∈M．（1）已知函数f（x）=，证明：f（x）∈M；（2）写出一个函数f（x），使得f（x0）∉M，并说明理由；（3）写出一个函数f（x）∈M，使得数列极限=1，=1．23．（18分）对于给定首项x0＞（a＞0），由递推公式x n+1=（x n+）（n ∈N）得到数列{x n}，对于任意的n∈N，都有x n＞，用数列{x n}可以计算的近似值．（1）取x0=5，a=100，计算x1，x2，x3的值（精确到0.01）；归纳出x n，x n+1，的大小关系；（2）当n≥1时，证明：x n﹣x n+1＜（x n﹣1﹣x n）；（3）当x0∈[5，10]时，用数列{x n}计算的近似值，要求|x n﹣x n+1|＜10﹣4，请你估计n，并说明理由．2011年上海市春季高考数学试卷参考答案与试题解析一、填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每题填对得4分，否则一律得零分．1．（4分）（2011•上海）函数f（x）=lg（x﹣2）的定义域是（2，+∞）．【分析】对数的真数大于0，可得答案．【解答】解：由x﹣2＞0，得x＞2，所以函数的定义域为（2，+∞）．故答案为：（2，+∞）．2．（4分）（2011•上海）若集合A={x|x≥1}，B={x|x2≤4}，则A∩B={x|1≤x ≤2} ．【分析】求解二次不等式化简集合B，然后直接利用交集运算求解．【解答】解：由A={x|x≥1}，B={x|x2≤4}={x|﹣2≤x≤2}，所以A∩B={x|x≥1}∩{x|﹣2≤x≤2}={x|1≤x≤2}．故答案为{x|1≤x≤2}．3．（4分）（2011•上海）在△ABC中，tanA=，则sinA=．【分析】由题意可得A为锐角，再由tanA==，sin2A+cos2A=1，解方程组求得sinA的值．【解答】解：在△ABC中，tanA=，则A为锐角，再由tanA==，sin2A+cos2A=1，求得sinA=，故答案为．4．（4分）（2011•上海）若行列式=0，则x=1．【分析】先根据行列式的计算公式进行化简，然后解指数方程即可求出x的值．【解答】解：∵=0，∴2×2x﹣4=0，即2x=2，∴x=1．故答案为：1．5．（4分）（2011•上海）若，，则x=（结果用反三角函数表示）【分析】利用反正弦函数的定义，由角的范围为，故可直接得到答案．【解答】解：由于，根据反正弦函数的定义可得x=故答案为6．（4分）（2011•上海）（x+）6的二项展开式的常数项为20．【分析】在二项展开式的通项公式中，令x的幂指数等于0，求出r的值，即可求得常数项．=•x6﹣r•x﹣r=•x6﹣2r．【解答】解：（x+）6的二项展开式的通项公式为T r+1令6﹣2r=0，求得r=3，故展开式的常数项为=20，故答案为20．7．（4分）（2011•上海）两条直线l1：x﹣y+2=0与l2：x﹣y+2=0的夹角的大小是．【分析】设两条直线的夹角为θ，求得tanθ=||的值，可得tan2θ的值，求得2θ 的值，可得θ的值．【解答】解：由于两条直线l1：x﹣y+2=0与l2：x﹣y+2=0的斜率分别为、1，设两条直线的夹角为θ，则tanθ=||=||==2﹣，∴tan2θ==，∴2θ=，θ=，故答案为．8．（4分）（2011•上海）若S n为等比数列{a n}的前n项的和，8a2+a5=0，则=﹣7．【分析】根据已知的等式变形，利用等比数列的性质求出q3的值，然后分别根据等比数列的通项公式及前n项和公式，即可求出结果．【解答】解：由8a2+a5=0，得到=q3=﹣8===﹣7故答案为：﹣7．9．（4分）（2011•上海）若椭圆C的焦点和顶点分别是双曲线的顶点和焦点，则椭圆C的方程是．【分析】先确定双曲线的顶点和焦点坐标，可得椭圆C的焦点和顶点坐标，从而可得椭圆C的方程【解答】解：双曲线的顶点和焦点坐标分别为（±，0）、（±3，0）∵椭圆C的焦点和顶点分别是双曲线的顶点和焦点，∴椭圆C的焦点和顶点坐标分别为（±，0）、（±3，0）∴a=3，c=∴∴椭圆C的方程是故答案为：10．（4分）（2011•上海）若点O和点F分别为椭圆+y2=1的中心和左焦点，点P为椭圆上的任意一点，则|OP|2+|PF|2的最小值为2．【分析】先求出左焦点坐标F，设P（x，y），根据P（x，y）在椭圆上可得到x、y的关系式，表示出|OP|2+|PF|2，再将x、y的关系式代入组成二次函数进而可确定答案．【解答】解：由题意，F（﹣1，0），设点P（x，y），则有+y2=1，解得y2=1﹣，因为|OP|2+|PF|2=x2+y2+（x+1）2+y2=x2+（x+1）2+2﹣x2=（x+1）2+2，此二次函数对应的抛物线的对称轴为x=﹣1，|OP|2+|PF|2的最小值为2．故答案为：2．11．（4分）（2011•上海）根据如图所示的程序框图，输出结果i=8．【分析】按要求一步步代入循环体，直到符合要求退出循环，即可得到结论．【解答】解：因为i=0，t=76；不满足t≤0，∴t=76﹣10=66，i=0+1=1；不满足t≤0，∴t=66﹣10=56，i=1+1=2；不满足t≤0，∴t=56﹣10=46，i=2+1=3；不满足t≤0，∴t=46﹣10=36，i=3+1=4；不满足t≤0，∴t=36﹣10=26，i=4+1=5；不满足t≤0，∴t=26﹣10=16，i=5+1=6；不满足t≤0，∴t=16﹣10=6，i=6+1=7；不满足t≤0，∴t=6﹣10=﹣4，i=7+1=8；满足t≤0，输出结果i=8．故答案为：8．12．（4分）（2011•上海）2011年上海春季高考有8所高校招生，如果某3位同学恰好被其中2所高校录取，那么录取方法的种数为168．【分析】解决这个问题得分三步完成，第一步把三个学生分成两组，第二步从8所学校中取两个学校，第三步，把学生分到两个学校中，再用乘法原理求解【解答】解：由题意知本题是一个分步计数问题，解决这个问题得分三步完成，第一步把三个学生分成两组，第二步从8所学校中取两个学校，第三步，把学生分到两个学校中，共有C31C22A82=168故答案为：168．13．（4分）（2011•上海）有一种多面体的饰品，其表面右6个正方形和8个正三角形组成（如图），则AB与CD所成的角的大小是．【分析】由图形补出正方体，可得所求的角即为ED与CD所成的角，在△CDE 中，由余弦定理可得答案．【解答】解：该饰品实际上就是正方体的8个顶角被切掉，切线经过正方体每条棱边的中点，如图：可得AB与CD所成的角即为ED与CD所成的角，设正方体的棱长为2，在△CDE中，可得CD=DE=，EC=，由余弦定理可得cos∠CDE==，故∠CDE=，故AB与CD所成的角为故答案为：14．（4分）（2011•上海）为求方程x5﹣1=0的虚根，可以把原方程变形为（x﹣1）（x2+ax+1）（x2+bx+1）=0，由此可得原方程的一个虚根为．【分析】化简方程的左边，比较系数，求出a，b，再求方程的虚根．【解答】解：由题可知（x﹣1）（x2+ax+1）（x2+bx+1）=（x﹣1）[x4+（a+b）x3+（2+ab）x2+（a+b）x+1]比较系数可得，∴∴原方程的一个虚根为，中的一个故答案为：．二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．15．（5分）（2011•上海）若向量，则下列结论正确的是（）A．B．C． D．【分析】由给出的两个向量的坐标，求出的坐标，然后直接进行数量积的坐标运算求解．【解答】解：由，则．所以．则．故选C．16．（5分）（2011•上海）f（x）=的图象关于（）A．原点对称B．直线y=x对称C．直线y=﹣x对称 D．y轴对称【分析】先判断函数的定义域，然后利用函数奇偶性的定义进行判断．【解答】解：因为函数的定义域为R，所以定义域关于原点对称．f（x）==，则f（﹣x）=2﹣x﹣2x=﹣（2x﹣2﹣x）=﹣f（x），即函数f（x）为奇函数．故函数f（x）的图象关于原点对称．故选A．17．（5分）（2011•上海）直线l：y=k（x+）与圆C：x2+y2=1的位置关系是（）A．相交或相切B．相交或相离C．相切D．相交【分析】根据点到直线的距离求出圆心到直线的距离d，再根据d与半径r的大小关系，得出结论．【解答】解：由于圆心（0，0），半径等于1，圆心到直线l：y=k（x+）的距离为d===＜＜r=1，故直线和圆相交，故选D．18．（5分）（2011•上海）若，，均为单位向量，则=（，）是++=（，）的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件【分析】均为单位向量，若，=（，）不成立；若=（，）可推得，由此可得．【解答】解：均为单位向量，，若，，则=（，）不成立；若均为单位向量，=（，）可推得所以“”是“”的必要不充分条件，故选B三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号规定区域内写出必要的步骤．19．（12分）（2011•上海）已知向量=（sin2x﹣1，cosx），=（1，2cosx），设函数f（x）=•，求函数f（x）的最小正周期及x∈[0，]时的最大值．【分析】利用两个向量的数量积公式求得函数f（x）的解析式为sin（2x+），根据x∈[0，]，利用正弦函数的定义域和值域求函数的最大值．【解答】解：∵向量=（sin2x﹣1，cosx），=（1，2cosx），函数f（x）=•=（sin2x﹣1）+2cos2x=sin2x+cos2x=sin（2x+），故函数的周期为=π．∵x∈[0，]，∴≤2x+≤，故当2x+=时，函数取得最大值为．20．（14分）（2011•上海）某甜品店制作蛋筒冰淇淋，其上半部分呈半球形，下半部分呈圆锥形（如图）．现把半径为10cm的圆形蛋皮分成5个扇形，用一个扇形蛋皮围成锥形侧面（蛋皮厚度忽略不计），求该蛋筒冰淇淋的表面积和体积（精确到0.01）．【分析】设出蛋筒冰淇淋的底面半径和高，由圆形蛋皮的周长等于5倍圆锥的底面周长求得圆锥底面半径，进一步求出圆锥的高，然后直接利用表面积公式和体积公式求解．【解答】解：设圆锥的底面半径为r，高为h．因为，所以r=2．则．则圆锥的表面积S=．体积V=．故该蛋筒冰淇淋的表面积约为87.96cm2，体积约为57.80cm3．21．（14分）（2011•上海）已知抛物线F：y2=4x（1）△ABC的三个顶点在抛物线F上，记△ABC的三边AB、BC、CA所在的直线的斜率分别为k AB，k BC，k CA，若A的坐标在原点，求k AB﹣k BC+k CA的值；（2）请你给出一个以P（2，1）为顶点、其余各顶点均为抛物线F上的动点的多边形，写出各多边形各边所在的直线斜率之间的关系式，并说明理由．【分析】（1）设B（x1，y1），C（x2，y2），把B、C点左边代入抛物线方程，利用斜率公式计算k AB﹣k BC+k CA的值即可；（2）先研究△PBC，四边形PBCD，五边形PBCDE，再研究n=2k，n=2k﹣1（k∈N，k≥2）边形的情形，最后研究n边形P1P2…Pn（k∈N，k≥3），按由特殊到一般的思路逐步得到结论；【解答】解：（1）设B（x1，y1），C（x2，y2），∵，，∴k AB﹣k BC+k CA=+=﹣+=0；（2）①研究△PBC，k PB﹣k BC+k CP=﹣+=﹣+==1；②研究四边形PBCD，k PB﹣k BC+k CD﹣k DP=﹣+﹣=0；③研究五边形PBCDE，k PB﹣k BC+k CD﹣k DE+k EP=﹣+﹣==1；④研究n=2k边形P1P2…P2k（k∈N，k≥2），其中P1=P，有﹣…+=0，证明：左边=+===0=右边；⑤研究n=2k﹣1边形P1P2…P2k﹣1（k∈N，k≥2），其中P1=P，有+﹣…+（﹣1）2k﹣2=1，证明：左边=+===1=右边；⑥研究n边形P1P2…Pn（k∈N，k≥3），其中P1=P，有+﹣…+（﹣1）n﹣1=，证明：左边=+（﹣1）n﹣1=[1+（﹣1）n﹣1]==右边．22．（16分）（2011•上海）定义域为R，且对任意实数x1，x2都满足不等式f（）≤的所有函数f（x）组成的集合记为M，例如，函数f（x）=kx+b ∈M．（1）已知函数f（x）=，证明：f（x）∈M；（2）写出一个函数f（x），使得f（x0）∉M，并说明理由；（3）写出一个函数f（x）∈M，使得数列极限=1，=1．【分析】（1）分类讨论，验证f（）≤成立，即可得到结论；（2）利用条件，构造函数f（x）=﹣x2，f（x）∉M，再取值验证即可；（3）利用条件，构造函数f（x）=满足f（x）∈M，验证条件即可．【解答】解：（1）证明：由题意，当x1≤x2≤0或0≤x1≤x2时，f（）≤成立设x1≤0≤x2，且＜0，∵﹣f（）==0∴f（）≤成立设x1≤0≤x2，且≥0，∵﹣f（）==0∴f（）≤成立∴综上所述，f（x）∈M；（2）如函数f（x）=﹣x2，f（x）∉M取x1=﹣1，x2=1，则=﹣1，f（）=0此时f（）≤不成立；（3）f（x）=满足f（x）∈M，且==1，==1．23．（18分）（2011•上海）对于给定首项x0＞（a＞0），由递推公式x n+1=（x n+）（n∈N）得到数列{x n}，对于任意的n∈N，都有x n＞，用数列{x n}可以计算的近似值．（1）取x0=5，a=100，计算x1，x2，x3的值（精确到0.01）；归纳出x n，x n+1，的大小关系；（2）当n≥1时，证明：x n﹣x n+1＜（x n﹣1﹣x n）；（3）当x0∈[5，10]时，用数列{x n}计算的近似值，要求|x n﹣x n+1|＜10﹣4，请你估计n，并说明理由．【分析】（1）利用数列递推式，代入计算，即可得到结论，同时可猜想结论；（2）作差，利用条件，证明其大于0，即可得到结论；（3）由题意，只要，由此可估计n的值．【解答】（1）解：∵x0=5，a=100，x n+1=（x n+）∴x1=（5+）≈4.74同理可得x2≈4.67，x3≈4.65猜想x n＞x n+1；（2）证明：x n﹣x n+1﹣（x n﹣1﹣x n）==∵；∴x n﹣x n+1==＞0∴x n＞x n+1∴；（3）解：由（2）知＜…＜由题意，只要，即2n＞104（x0﹣x1）∵∴n＞=15.1∴n=16．。

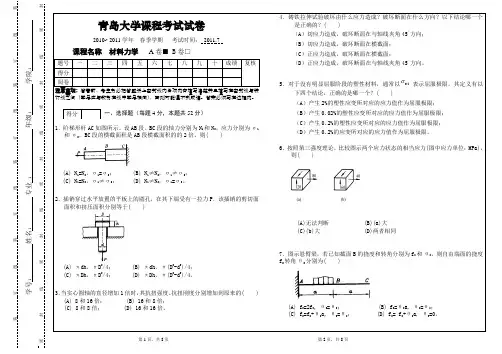
（共100分）一、单项选择题：（本题共10小题，每小题2分，共20分）三．（15分）置于空气中的凸透镜1L 和凹透镜2L 的焦距均为10cm ，2L 在1L 的右方35cm 处，在1L 左方20cm 处放一小物，试求其像的最后位置及性质，并作出光路图。

解：由题意知，201-=s cm ，101='f cm ，102-='f cm 由公式''111111s s f -=，对1L 成像，得10120111=--'s 得201='s cm 对2L ，1s '作为物对2L 成像''222111s s f -=，15)2035(2-=--=s cm10115112-=--'s 得62-='s cm 所以像最后位于2L 左侧6cm 处。

横向放大率：4.0)16()20()6(20221121-=-⨯--⨯='⋅'==s s s s βββ可见，成的是缩小、倒立的虚像。

利用牛顿公式计算：10111-=-=f s x cm 由牛顿公式，得：101010)(21211=--='-='x f x cm25)201035()](35[1122-=-+-='+-+-=f x f x cm 4251022222=--='-='x f x cm得横向放大率： 4.0104101021-=---==））（（βββ四．（12分）杨氏双缝实验装置中，双缝相距0.5mm 接受屏距双缝1m ，点光源距双缝30cm ，它发射λ=500nm 的单色光，试求：（1） 屏上干涉条纹的宽度；（2） 若点光源发出的光波为500±2.5nm 范围内的准单色光，求屏上能看到的干涉极大的最高级次；（3） 若光源具有一定的宽度，屏上干涉条纹消失时，它的临界宽度是多少？五. （16分）波长为600nm 的单色光正入射到一平面透射光栅上，有两个相邻的主最大分别出现在2.0sin 1=θ和3.0sin 2=θ处，第四级缺级。

华中科技大学文华学院2010－2011学年度第一学期《财务管理》期末考试试卷课程性质：必修使用围：本科考试时间：2011年01月13日考试方式：闭卷**专业班级学生：成绩一、单项选择题（每小题1分，共10分）1、目前我国企业财务管理的最优目标一般被认为是（）。

A．每股盈余最大化 B．利润最大化C. 股东财富最大化 D．产值最大化2、*企业的应收账款周转期为80天，应付账款的平均付款天数为40天，平均存货期限为70天，则该企业的现金周转期为（）。

A．190天 B．110天 C．50天 D．30天3、现有A、B两个方案，其期望值相同，甲方案的标准差是2.2，乙方案的标准差是2.5，则甲方案的风险（）乙方案的风险。

A．大于 B．小于 C．等于 D．无法确定4、不存在财务杠杆作用的筹资方式（）。

A．银行借款 B．发行债券 C．发行优先股 D．发行普通股5、下列有关联合杠杆系数的说法不正确的是（）。

A. 它反映产销量变动对普通股每股收益的影响B. DTL=DOL*DFLC. 复合杠杆系数越小，企业风险也越小D. 它是普通股每股利润变动率与息税前利润变动率之比6、所谓最优资本结构，是指( )。

A．企业价值最大的资本结构 B. 企业目标资本结构C. 加权平均资本成本最低的目标资本结构D. 企业价值最大，同时加权平均资本成本最低的资本结构7、投资决策评价方法中，对于互斥方案来说，最好的评价指标是（）。

A. 盈利能力指数法B. 部报酬率法C. 净现值法D. 会计报酬率法8、流动资产减去流动负债后的余额为( )。

A．流动资金 B. 毛营运资本 C. 净资产 D. 净营运资本9、丁企业向银行借入年利率8%的短期借款100万元，银行按借款合同保留了20%的补偿余额。

若该企业适用企业所得税税率为25%，不考虑其它借款费用，则该笔借款的资金成本为（）。

A．6.0% B. 7.5% C. 8.0% D. 10.0%10、丁企业拟投资8000万元，经测算，该项投资的经营期为4年，每年年末的现金净流量均为3000万元，则该投资项目的含报酬率为（）%。

专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪个朝代不属于中国古代文学的范畴？A. 先秦B. 唐朝C. 元朝D. 民国A. 杜甫B. 白居易C. 李白D. 王之涣3. 《红楼梦》的作者是谁？A. 曹雪芹B. 罗贯中C. 施耐庵D. 吴承恩4. 下列哪个成语出自《史记》？A. 画龙点睛B. 破釜沉舟C. 亡羊补牢D. 指鹿为马A. 《呐喊》B. 《彷徨》C. 《狂人日记》D. 《朝花夕拾》二、判断题（每题1分，共5分）1. 《诗经》是我国最早的一部诗歌总集。

（）2. 唐代诗人杜甫被誉为“诗鬼”。

（）3. 《水浒传》讲述了宋江等108位好汉的故事。

（）4. 《西游记》中的孙悟空会七十二变。

（）5. 《聊斋志异》是清代蒲松龄所著的短篇小说集。

（）三、填空题（每题1分，共5分）1. 中国古代文学分为先秦、________、唐宋、元明清四个阶段。

2. 《________》是屈原创作的抒情长诗，被誉为“屈赋”的代表作品。

3. 陶渊明是我国东晋时期著名的诗人，代表作有《归园田居》、《________》等。

4. 唐代诗人王之涣的《登鹳雀楼》中，描写了“________，黄河入海流”的壮丽景象。

5. 《________》是清代吴敬梓所著的长篇小说，被誉为“中国古典小说四大名著”之一。

四、简答题（每题2分，共10分）1. 简述《论语》的主要内容。

2. 介绍一首你喜欢的唐代诗歌，并简要分析其艺术特色。

3. 请列举三部元杂剧的代表作品。

4. 简述《水浒传》中宋江的人物形象。

5. 请阐述鲁迅《呐喊》中的主题思想。

五、应用题（每题2分，共10分）1. 分析《诗经》中的《关雎》表达了怎样的情感。

2. 请以《庐山谣》为例，分析唐代山水诗的艺术特点。

3. 比较分析《红楼梦》中贾宝玉与林黛玉的性格特点。

4. 请谈谈你对《狂人日记》中“吃人”一词的理解。

5. 分析《围城》中方鸿渐的人物形象及其象征意义。

六、分析题（每题5分，共10分）1. 请结合作品分析唐代诗人李白的诗歌风格及其成因。

一阅读80分（一）阅读下文，完成第1－6题。

（16分）①“天地玄黄，宇宙洪荒”，在人类产生之前，地球上的陆地都是莽莽荒原。

但人类一出现，即使是在最原始的时代，为了自身的生存和繁衍，总是在不断地消灭荒原。

因为只有这样，人类才能获得维持生命所必需的食物、燃料和栖身的场所。

多数人类学家认为，最早的人类产生在东非大裂谷，后来才迁移到世界各地。

促使早期人类迁移的因素不少，但最主要的还是生存的需要——随着人口的增长，总要有更大的生存空间。

②农业和城市是人类文明的两大进步，但随着大片农田和一座座城市的出现，荒原的面积不可避免地相应缩小。

无论是中国的先民“筚路蓝缕，以启山林”，还是欧洲的清教徒远航新大陆，他们的目的都是将荒原变成家园。

随着人口的增加，人类开发荒原的速度在不断加快。

特别是在工业化以后，在农田、牧地、居住区以外，工厂、矿山、油田、铁路、公路、港口等设施的规模也日益扩大，城市占据的面积也越来越大。

一般认为，到了21 世纪，地球上能够利用的土地已开发殆尽，地球上的陆地还有不少无人区，大片的原始荒原、特别是人类尚未进入的荒原已经屈指可数。

③在人类进入荒原的过程中，总是先选择自然条件相对适宜的地方，例如，已经发现的先民聚落遗址，一般都在生活和生产用水便利却离河流有一定距离的台地。

正因为如此，平原、河谷、海拔不高的台地、土壤疏松的土地、气候温暖且水量充沛的区域往往先得到开发，并且基本不再留下荒原，然后再扩展到丘陵、较低的山地，最后留下的荒原都是人类目前还无法利用、或利用成本太高的沙漠、戈壁、干旱区、峻峭的山区、传染病流行区、地质灾害区、热带丛林、高海拔或高纬度地区，以及多种不利因素兼而有之的地区。

也有些地方虽适宜开发，却因远离人类聚居区，或因交通闭塞，得以保持着原始状态。

④在人类基本定居，或有了一定的活动范围后，会尽可能避免进入荒原。

但是总有少数人由于种种原因，不得不穿越或深入荒原，如出使异域的外交官、负有军事任务的将士、长途贸易的商人、被流放或驱逐的犯人，还有人会由于偶然的原因误入荒原。

一、数字推理:1.【答案】D 解析：二级等差数列的变式：2，3，6，15，( 42 )二级等比数列：1 , 3 , 9 , (27)2.【答案】A 解析：每个数除以三的余数是0，2，2，0，2；每三个相邻余数之和均等于4。

3.【答案】A 解析：奇偶数项都是等差数列。

4.【答案】B 解析：3=14+2, 30=33+3, 29=52+4, 12=71+5, ( )=90+6=75.【答案】D 解析：4=2×3-2,9=4×3-3,23=9×3-4,64=23×3-5,( )=64×3-6=186二、数学计算:6.【答案】C 解析：(20×80+30×70)÷(20+30)=747.【答案】D 解析：由题目可知道，总人数一定除去22余1。

那么总人数一定是奇数，排除BC。

269=22×12+5,529=22×24+1,因此，排除A，只能选D。

另外，本题可通过列方程求解。

8.【答案】A 解析：由题目可知，该单位员工人数为42人。

那么得60分以下的人为42×(1－1／7－1／2－l／3)=19.【答案】C 解析：甲每小时跑3.5÷(1／5)=35/2圈，乙每小时跑16圈，丙每小时跑40/3圈，因此，要使他们同时在出发点相遇，一定使他们的圈数均为整数，应选C10.【答案】C 解析：设蜡烛的长度是Ｌ，粗蜡的燃烧速度是Ｌ／５，细蜡烛的速度是Ｌ／４；Ｔ时间后粗蜡烛的长度是Ｌ－Ｔ×Ｌ／５；细蜡烛的长度是：Ｌ－Ｔ×Ｌ／４；且有：Ｌ－Ｔ×Ｌ／５＝４×（Ｌ－Ｔ×Ｌ／４）；削去Ｌ，则Ｔ＝１５/４小时。

即选Ｃ11.【答案】C 解析：代入法，该家庭有3个女儿和4个男孩的时候，符合题目要求。

12.【答案】B 解析：由题目可知道，在相同时间里，李四所在的甲部门锯了7棵树，共锯了21次；张三锯了27段，属于乙部门，锯了9棵树，锯了18次；王五所在的丙部门锯了17棵树，锯了17次；因此，选择B。

2011年上海市春考语文试卷一阅读80分(一)阅读下文，完成剪1-6题。

(16分)①"天地玄黄，宇宙洪荒"，在人类产生之前，地球上的陆地都是莽莽荒原。

但人类一出现，即使是在最原始的时代，为了自身的生存和繁衍，总是在不断地消灭荒原。

因为只有这样，人类才能获得维持生命所必需的食物、燃料和栖身的场所。

多数人类学家认为，最早的人类产生在东非大裂谷，后来才迁移到世界各地。

促使早期人类迁移的因素不少，但最主要的还是生存的需卜随着人口的增长，总要有更大的生存空间。

②农业和城市是人类文明的两大进步，但随着大片农田和一座座城市的出现，荒原的面积不可避免地相应缩小。

无论是中国的先民"毕路蓝缕，以启山林"，还是欧洲的清教徒远航新大陆，他们的目的都是将荒原变成家园。

随着人口的增加，人类开发荒原的速度在不断加快。

特别是在工业化以后，在农田、牧地、居住区以外，工厂、矿山、油田、铁路、公路、港口等设施的规模也日益扩大，城市占据的面积也越来越大。

一般认为，到了21世纪，地球上能够利用的土地已开发殆尽，□□地球上的陆地还有不少无人区，□□大片的原始荒原、特别是人类尚未进入的荒原已经屈指可数。

③在人类进入荒原的过程中，总是先选择自然条件相对适宜的地方，例如，已经发现的先民聚落遗址，一般都在生活和生产用水便利却离河流有一定距离的台地。

正因为如此，平原、河谷、海拔不高的台地、土壤疏松的土地、气候温暖且水量充沛的区域往往先得到开发，并且基本不再留下荒原，然后再扩展到丘陵、较低的山地，最后留下的荒原都是人类目前还无法利用、或利用成本太高的沙漠、戈壁、干旱区、峻峭的山区、传染病流行区、地质灾害区、热带丛林、高海拔或高纬度地区，以及多种不利因素兼而有之的地区。

也有些地方虽适宜开发，却因远离人类聚居区，或因交通闭塞，得以保持着原始状态。

④在人类基本定居，或有了一定的活动范围后，会尽可能避免进入荒原。

但是总有少数人由于种种原因，不得不穿越或深入荒原，如出使异域的外交官、负有军事任务的将士、长途贸易的商人、被流放或驱逐的犯人，还有人会由于偶然的原因误入荒原。

学校______________班级______________专业______________考试号______________姓名______________山东省春季高考数学试题2011年真题第Ⅰ卷1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上． 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮．第Ⅰ卷（选择题，共60分）30个小题，每题2分，共60分．在每题列出的四个选项中，只有一项符合题目要求，请将该选项的字母代号填涂在答题卡上） ．已知全集{}U a b c =，，，集合{}M a b =，，集合{}N b c =，，则()MNUM 等于(A ) {}a b ，(B ) {}a c ，(C ) {}b c ，(D ) {}a b c ，，．下列四对函数中，表示同一函数关系的是(A ) y x =与y =(B ) 21x y -=与1y x =+(C ) 2lg y x =与2lg y x = ．下列函数中是偶函数的为(A ) cos y x =(B ) sin y x =(C ) ()21y x =-(D ) []223y x x =∈-，，．若sin 0θ>，cos 0θ<，则θ是(A ) 第一象限角(B ) 第二象限角(C ) 第三象限角(D ) 第四象限角．下列四个命题中真命题是(A ) 3x >是5x >的充分条件 (B ) 21x =是1x =的充分条件(C ) a b >是22ac bc >的必要条件(D ) 2πα=是sin 1α=的充要条件．不等式213x -<的解集是(A ) ()21-，(B ) ()2-∞，(C ) ()12-，(D ) ()2+∞，．已知命题 p ：x ∃∈R ，使10x -=；q ：x ∀∈R ，都有20x >．下列命题中真命题是(A ) p q ∧(B ) p q ∨(C ) p q ⌝∧(D ) p q ⌝∨8．如图所示，二次函数()y f x =与一次函数()y g x =的图象交于()()1242A B --，，，两点，则使()()f x g x <的x 的取值范围是 (A ) ()1-∞-， (B ) ()14-， (C ) ()4+∞， (D ) ()()14-∞-+∞，，9．若二次函数()222f x x mx m =+++的图象与x 轴有两个交点，则m 的取值范围是(A ) ()1-∞-，(B ) ()12-，(C ) ()2+∞，(D ) ()()12-∞-+∞，，10．如果三个正数a b c ，，成等比数列，那么lg lg lg a b c ，， (A ) 成等差数列但不成等比数列 (B ) 成等比数列但不成等差数列 (C ) 成等差数列且成等比数列(D ) 既不成等差数列也不成等比数列11．已知四边形ABCD ，→AB ＝2-→CD ，则该四边形是(A ) 梯形(B ) 矩形(C ) 菱形(D ) 正方形12．已知等差数列{}n a ，a 35=，a 713=，则该数列前10项的和为(A ) 90(B ) 100(C ) 110(D ) 12013．函数()f x x =在区间[]22-，上的单调性是(A ) 单调递增(B ) 单调递减(C ) 先递增后递减 (D ) 先递减后递增14．袋内有10个球，其中4个红球，3个黄球，3个蓝球，从中任取2个球，则恰有1个红球的概率为(A )13(B )25(C )715x )第8题图学校______________班级______________专业______________考试号______________姓名______________．经过点()11P -，且与直线30x y --=平行的直线方程为(A ) 20x y -+=(B ) 20x y --=(C ) 20x y ++=(D ) 20x y +-=．有下列四个不等式：① 2.5322> ② 0.20.10.80.8--> ③ log 23.5>log 23 ④ log 0.81.8>log 0.81.6 其中关系正确的是(A ) ①和③(B ) ②和④(C ) ②和③(D ) ①和④．使函数()2sin cos y x x π=-取得最大值的x 的取值集合是(A ) 24x x k k ππ⎧⎫=+∈⎨⎬⎩⎭， Z(C ) 22x x k k ππ⎧⎫=+∈⎨⎬⎩⎭， Z (D ) 2x x k k ππ⎧⎫=+∈⎨⎬⎩⎭， Z．若0.5log 0x <，则(A ) 1022x <<(B )1212x << (C ) 122x << (D ) 22x >．已知等比数列 11142，，，…，则32是该数列的 (A ) 第6项 (B ) 第7项 (C ) 第8项 (D ) 第9项．某职业学校共有学生3000名，其中男生1450名，女生1550名．有关部门为了调查学生身体素质情况，拟采用分层抽样的方法从该校抽取300名学生进行样本调查，则应在该校抽取的男、女生人数分别为 (A ) 140名，160名 (B ) 145名，155名 (C ) 150名，150名(D ) 155名，145名．已知点()23M -，到直线20x y c ++=c 的值为(A ) 4或6-(B ) 4-或6(C ) 4(D ) 6-．已知→a ＝()31-，，→b ＝()12-，，则 <→a ，→b > 等于(A) 6π(C ) 3π(D ) 34π．若5cos 13α=-，2παπ<<，则sin 3πα⎛⎫- ⎪⎝⎭等于(B )(C )(D )24．已知△ABC 中，90A ∠=︒， →AB ＝()1x ，，→BC ＝()42-，，则x 的值为(A ) 1或3-(B ) 1-或3(C ) 1-或3-(D ) 1或325．若中心在坐标原点，焦点在x 轴上的双曲线，虚轴长是实轴长的2倍，则其渐近线方程为(A ) 14y x =±(B ) 4y x =±(C ) 12y x =±(D ) 2y x =±26．经过点()23P ，且与圆22290x y x +--=相切的直线方程是(A ) 3110x y +-= (B ) 3110x y +-=或370x y -+= (C ) 370x y -+=(D ) 370x y --=或3110x y ++=27．某小组有6名同学，他们计划利用今年端午节的三天假期到敬老院服务，每天安排2人，每人只去一天，则不同的安排方法共有 (A ) 90种(B ) 270种(C ) 540种(D ) 720种28．某射手在相同条件下射击5次，命中环数分别为：7，9，9，8，7．则该样本的标准差为(A ) 0.64(B ) 0.80(C ) 0.89(D ) 129．已知抛物线24y x =，过其焦点且斜率为1的直线交抛物线于A B ，两点，则AB 等于 (A ) 6 (B ) 8 (C ) 10 (D ) 1230．如图所示，已知正方体1111ABCD A B C D -，则下列命题中错误．．的是 (A ) AD //平面1D BC(B ) 1D C 与平面ABCD 所成的角是45︒ (C ) 11A C 与BD 所成的角为45︒(D ) AC 与1BC 所成的角是60︒C DABC 1D 1A 1B 1第30题图学校______________班级______________专业______________考试号______________姓名______________第Ⅱ卷1．答卷前将密封线内的项目填写清楚．2．用钢笔或圆珠笔直接答在试卷上，解答题和应用题应写出推理、演算步骤． 3．本试题允许使用函数型计算器，凡使用计算器的题目，最后结果精确到0.01． 4个小题，每题3分，共12分．请将答案填在答题卡相应题号的横线上） ．已知函数()f x 为奇函数，()g x 为偶函数，它们的定义域均为R ．若()29f =，()34g -=-，则()()23f g -+=______．13-．在△ABC 中，若5AC =，120A ∠=︒BC 的长度为_____．7．若球的体积为，则该球的内接正方体的体积为_____．8．已知双曲线22221x y a b-= (00)a b >>，的右焦点2F 的坐标是()40，，过点2F 引圆222x y a +=的两条切线，切点分别为A B ，，120AOB ∠=︒(O 为坐标原点)，则该双曲线的标准方程为_____．221412x y -= 4个小题，共28分．请在答题卡相应的题号处写出解答过程）．(本小题7分) 光明职业学校营销专业的创业小组学生购进一批服装，每件的进价是60元．在销售过程中他们发现：当每件售价为75元时，日销售量为85件；当每件售价为90元时，日销售量为70件．假设日销售量p (件)与每件售价x (元)之间的函数关系为：p kx b =+(每件售价不低于进价，且货源充足) ． (1) 求出p 与x 之间的函数关系式；(2) 设每天的利润为y (元)，若不考虑其它费用，则每件售价为多少时每天的利润最大，最大利润是多少？(1) 由题意知75859070k b k b +=⎧⎨+=⎩，解得1160k b =-⎧⎨=⎩，p 与x 之间的函数关系式为160p x =-+，x ∈{}60160x x x ∈，≤ ≤ Z ． (2) 由题意知()()60160y x x =--+22209600x x =-+-()21102500x =--+，当110x =时，max 2500y =，而∈110{}60160x x x ∈，≤ ≤ Z ， 所以每件的售价为110元时，每天的利润最大，最大利润为2500元．36．(本小题6分) 已知()2sin sin cos 1222x x x f x ⎛⎫=+- ⎪⎝⎭．(1) 将()f x 化成正弦型函数，并写出函数的值域；(2) 若α是三角形的一个内角，且14f πα⎛⎫+= ⎪⎝⎭，求出α的值．解：(1) ()2sin sin cos 1222x x x f x ⎛⎫=+- ⎪⎝⎭22sin 2sin cos 1222x x x=+-22sin cos 12sin 222x x x ⎛⎫=-- ⎪⎝⎭sin cos x x =-4x π⎛⎫=- ⎪⎝⎭，()f x的值域是⎡⎣．(2) 因为()4f x x π⎛⎫=- ⎪⎝⎭，所以4f παα⎛⎫+= ⎪⎝⎭，学校______________班级______________专业______________考试号______________姓名______________又因为14f πα⎛⎫+= ⎪⎝⎭1α=，即sin α=因为0απ<<， 所以4πα=或34π． ．(本小题7分) 如图所示：△ABC 是边长为2的等边三角形，PA ⊥平面ABC ，3PA =， D 是BC 的中点． (1) 求证：BC ⊥平面PDA ； (2) 求二面角P BC A --的大小．证明：因为PA ⊥平面ABC ，BC ⊂平面ABC ，所以PA BC ⊥．因为△ABC 为等边三角形，D 为BC 中点， 所以AD BC ⊥． 又因为PAAD A =，所以BC ⊥平面PDA ．解：因为BC ⊥平面PDA ，PD ⊂平面PDA ，所以BC PD ⊥．又因为BC AD ⊥，所以PDA ∠为二面角P BC A --的平面角．因为D 是BC 的中点，2BC =，所以1CD =．又知AD BC ⊥，所以AD =．因为PA ⊥平面ABC ，AD ⊂平面ABC ，所以PA ⊥AD ．所以tan PA PDA AD ∠===， 因此60PDA ∠=︒．即二面角P BC A --的大小为60︒．38．(本小题8分) 已知椭圆中心在坐标原点，焦点在x，椭圆上的一点P 到左、右两焦点的距离之和为8． (1) 求出椭圆的标准方程；(2) 已知直线y x n =+与椭圆交于A ，B 两个不同的点，且弦AB 的中点M 恰好在圆221725x y +=上，求出n 的值．解：(1) 设椭圆的标准方程为22221x y a b+=，由题意得方程组22228a ca abc =⎧⎪⎪=⎨⎪⎪=+⎩，解方程组，得4a =，2b =， 则椭圆的标准方程为221164x y +=． (2) 设()11A x y ，，()22B x y ，，解方程组⎩⎪⎨⎪⎧221164x y += ①y x n =+ ②把②代入①并整理，得22584160x nx n ++-= ③因为直线与椭圆交于两个不同的点，所以()()228204160n n -->，解得n -<所以n 的取值范围是(-． PACBD 第37题图PACD第37题图学校______________班级______________专业______________考试号______________姓名______________由题意可知，1x 与2x 是方程③的两个根，所以1285n x x +=-， 从而 ()()1212y y x n x n +=+++122x x n =++825n n =-+25n =． 所以弦AB 的中点M 的坐标为455n n ⎛⎫- ⎪⎝⎭，．又因为点M 在圆221725x y +=上，所以224175525n n ⎛⎫⎛⎫-+=⎪ ⎪⎝⎭⎝⎭， 解得 1n =±．又因为(1±∈-，所以 1n =±．。

(A) 8和16倍；(B) 16和8倍；
(C) 8和8倍；(D) 16和16倍。
4．铸铁拉伸试验破坏由什么应力造成？破坏断面在什么方向？以下结论哪一个是正确的？( )
（A）切应力造成，破坏断面在与轴线夹角45º方向；
（B）切应力造成，破坏断面在横截面；
（C）正应力造成，破坏断面在横截面；
（D）正应力造成，破坏断面在与轴线夹角45º方向。
作图示梁的剪力图和弯矩图。
得分
三、（本题共12分）
阶梯形钢杆的两端在t1=5oC时被固定，杆件的A1=500mm2，A2=1000mm2。当温度升高到t2=25oC时，试求杆内各部分的应力。设钢的E=200GPa，=12.5×10-6/oC。
得分
四、（本题共12分）
铸铁梁受荷载情况如图示。已知截面对形心轴的惯性矩Iz = 403×10－7m4，铸铁抗拉强度
13．图示两端铰支压杆的截面为矩形。当其失稳时()
(A)临界压力Plj＝π2EIy／l2，挠曲线位于xy面内；
(B)临界压力Plj＝π2EIy／l2，挠曲线位于xz面内；
(C)临界压力Plj＝π2EIz／l2，挠曲线位于xy面内；
(D)临界压力Plj＝π2EIz／l2，挠曲线位于xz面内。
得分
二、作图题（本题共12分）
得分
一、选择题（每题4分，本题共52分）
1．阶梯形杆AC如图所示。设AB段、BC段的轴力分别为Nl和N2，应力分别为σ1和σ2，BC段的横截面积是AB段横截面积的的2倍。则( )
(A) N1=N2，σ1=σ2；(B) N1≠N2，σ1≠σ2；
(C) N1=N2，σ1≠σ2；(D) N1≠N2，σ1=σ2。
(A)提高—倍；(B)提高不到—倍；

浙江师范大学《毛泽东思想和中国特色社会主义理论体系概论》考试卷（A）（2010－2011学年第二学期）考试类别：公共必修课使用学生：全校考试时间：120分钟出卷时间：2011年5月说明：要求考生将全部答案写在答题纸上，否则作无效处理一、单项选择题（本大题共25小题，每小题1分，共25分。

）在每小题列出的四个备选项中只有一个是符合题目要求的，错选、多选或未选均无分。

1．市场经济作为资源配置的方式（）A．存在于资本主义制度，只为资本主义制度服务B．存在于不同的社会制度，可以为不同社会制度服务C．存在于社会主义制度，只为社会主义制度服务D．存在于剥削社会制度，可以为剥削社会制度服务2.社会主义制度建立后，我国之所以选择计划经济体制的主观原因在于（）A．我国生产力水平十分低下，国民经济实力薄弱，现代工业很少B．苏联在计划经济体制下社会主义建设取得巨大成就，对我国经济体制的选择产生直接影响C．在经济结构简单，科技水平不高，社会利益关系相对单纯的情况下，计划经济体制能够比较顺利地进行D．在理论上把计划经济看作是区别于资本主义的重要特征3．国有经济在国民经济中的主导作用主要表现在A．国有资产在社会主义总资产中占有量的优势B．国有经济能控制垄断性行业C．国有经济对国民经济的控制力D．国有经济在国民经济中占主体地位4．现阶段，以劳动者的劳动联合和劳动者的资本联合为主的股份合作制属于A．国有经济B．集体经济C．个体经济D．私营经济5.评价生产资料所有制形式是否优越，应以（）A．公有化程度的高低为标准B．公有制范围大小为标准C．“一大二公”为标准D．是否有利于生产力发展为标准6．决定我国现阶段分配格局的最终原因是（）A．我国以公有制为主体、多种所有经济共同发展的基本经济制度B．我国生产力的发展水平和特点C．社会主义的根本任务D．我国社会、经济发展的现实7.社会主义新农村建设的目的、也是衡量我们工作的基本尺度是（）A．生产发展B．生活宽裕C．乡风文明D．村容整洁8.建设资源节约型、环境友好型社会和实现可持续发展的重要途径是（）A．坚持速度与质量、结构与效益的统一B．促进区域协调发展C．发展循环经济D．处理好人口、资源、环境的关系9.社会主义民主政治的本质和核心要求是（）A.无产阶级政党的领导B.人民当家作主C.维护社会主义制度D.依法治国10.民族区域自治制度的核心是（）A.各民族一视同仁B.主权归中央，治权归地方C.发展民族经济，实现共同繁荣D.保障少数民族当家作主，管理本民族、本地方事务的权力11．中国特色社会主义文化建设的根本任务是（）A．进行思想道德建设和教育科学文化建设B．坚持百家齐放、百家争鸣的方针C．培育有理想、有道德、有文化、有纪律的公民D．继承和发扬优秀民族文化传统12.思想道德建设,解决的整个中华民族的（）A.国家统一和民族团结问题B.发展目标和发展方式问题C.精神支柱和精神动力问题D.民族基础和社会动力问题13．明确把“社会更加和谐”列为全面建设小康社会的一个重要目标是在党的（）A．十五大B．十六大C．十六届四中全会D．十六届六中全会14．构建社会主义和谐社会的根本出发点和落脚点是（）A．必须坚持科学发展B．必须坚持以人为本C．必须坚持改革开放D．必须坚持民主法治15.党的十七大指出,社会建设与人民幸福安康息息相关,我们国家应当加快推进社会建设的重点是（）A.经济B.教育C.民生D.社会保障16．学习“一国两制”后，下面四位同学表达自己的看法，你认为哪一个观点最符合“一国两制”的理论（）A．王山：“一国两制”只适用于中国，对其他国家不适用B．赵明：“一国两制”会改变中国大陆的社会主义性质C．许华：“一国两制”首先要坚持在世界上只有一个中国D．李立：“一国两制”就是要改变港澳台原由的资本主义制度17.2008年11月，大陆的陈云林和台湾的江丙坤分别代表两岸签署协议，促进了两岸三大通时代的到来。

A.借：保费收入 5 000B.借：退保金 5 000
贷：其他应付款 5 000 贷：其他应付款 5 000
C.借：其他应付款 5 000 D.借：其他应收款 5 000
贷：保费收入 5 000 贷：退保金 5 000
（答案：B；第88页正5行）
17．2010年10月20日，A保险公司在公开市场上买入股票，支付购买价款1000万元，支付相关交易费用5000元，该股票作为交易性金融资产核算。2010年12月31日，该投资的市价为1200万元。则该股票在2010年年末的计税基础为（ ）万元。A. 1000B. 1000.5C. 1200D. 1200.5
（答案：A.1000；第184页正7行）
18．寿险公司一般将下列哪一类金融资产划分为交易性金融资产？（ ）
A．应收利息B．投资连结保险账户的债券C．拟长期持有的债务D．贷款
（答案：B．投资连结保险账户的债券；第134页倒4行）
19. 下列金融资产中，属于贷款和应收款项的是：（ ）。
应收保费与应收利息 可转换债券 保户质押贷款 应收分保账款
贷：保单质押贷款——应计利息 250
D. 借：保单质押贷款—应计利息 250
贷：利息收入—保单质押贷款 250
（答案：D.；第93页20行）
③采用新的基于最佳估计原则下的准备金评估标准 ④合理进行影子会计调整
A.①②③ B.①②④ C.②③④ D.①②③④
（答案：A.①②③；第76页倒15行）
12．根据我国会计准则规定，保险公司至少应当于每年年度终了，以掌握的有关资料为依据，选择恰当的方法，对未决赔款准备金、寿险责任准备金、长期健康险责任准备金进行充足性测试。（ ）A. 对 B. 错
27.寿险公司在会计年度终了时，长期健康险责任准备金测试结果为重新计算确定的长期健康险责任准备金小于充足性测试日已确定的长期健康险责任准备金，则应做的处理为（ ）。

河南理工大学 2010-2011 学年第 2 学期《计算机网络》试卷（A 卷）1.在以太网标准10BASE-T 中，10时指 数据传输速率为10Mbps ，BASE 指传输模式为基带传输 。

2. 常用的有线传输介质有3种 同轴电缆 、 双绞线 、 光纤传输 。

3. 多路复用技术有 频分复用 ， 统计时分复用 ， 波分复用及码分复用。

4. 目前应用最为广泛的一类局域网是Ethernet 网，Ethernet 的核心技术是它随机采用型介质访问控制方法，即 CMSA/CD 。

5. 若HDLC 帧数据段中出现比特串“11111101011111011”，则比特填充后的输出为______ 1111101010111110011______。

6. 域名服务器分为_____本地域名服务器__、____根域名服务器________和授权域名服务器三类。

7. 对模拟数据进行数字信号编码的最常用方法是_ _PCM 编码______，T1载波和E1载波都采用了这种方法。

8. IP 地址的编址方法经历的三个历史阶段是 分类地址 、 划分子网 和构造超网三种。

9. 常用的IP 地址有A 、B 、C 三类，128.11.3.31是一个_____B_______类IP 地址，其网络标识（net-id ）为_____128.11_______，主机标识（host-id ）为___3.31_________。

10. 局域网的拓扑结构主要有 星型 、 环形 和 总线型 三种。

1． 通信信道的每一端可以是发送端，也可以是接受端，信息可由这一端传输到另一端，也可以从那一端传输到这一端，但在同一时刻，信息只能有一个传输的通信方式为（ B ） A 单工通信 B 半双工 C 全双工 D 模拟 2. 下面IP 属于D 类地址的是（ C ）A 10.10.5.168B 168.10.0.1C 224.0.0.2D 202.117.130.80 3. 以下哪个是MAC 地址（ B ）A OD-01-02-AAB 00-01-22-OA-AD-01C AO.O1.00D 139.216.000.012.002 4. ARP 请求服务采用的发送方式是 ( C )A 单播B 多播C 广播D 任播5. 广域网覆盖的地方范围从几十公里到几千公里，它的通信子网主要使用（ B ）. A 报文交换技术 B 分组交换技术 C 文件交换技术 D 电路交换技术6. 滑动窗口协议主要用于进行（ C ）A 差错控制B 安全控制C 流量控制D 拥塞控制7. 若数据链路的发送窗口尺寸WT=7，在发送过5号帧、并接到5号帧的确认帧后，发送方还可连续发送( D )A 2个帧B 4个帧C 6个帧D 7个帧 8. 要把学校里行政楼和实验楼的局域网互连,可以通过（ A ）实现。

华东交通大学2010—2011学年第二学期考试卷试卷编号： （ A ）卷编译原理（E ） 课程 课程类别：必修课考生注意事项：1、本试卷共 7 页，总分 100 分，考试时间 120 分钟。

2、考试结束后，考生不得将试卷、答题纸和草稿纸带出考场。

一、简答题 (每题 5 分，共 20 分)1． 简述编译程序与解释程序的主要差异？【答】编译程序产生中间代码，且效率高；解释程序不产生中间代码，且效率低。

2． 文法的二义性与语言的二义性是两个相同的概念吗？请说明理由。

【答】这两个概念是不相同的。

文法的二义性指的是文法所描述的语言中至少存在一个句子，而该句子对应两棵不同的语法树（或最左（右）推导）；而语言的二义性是指描述该语言的全部文法都是二义性的。

由于描述同一个语言的文法可以有多个，一个二义性文法也可能找到一个等价的无二义性文法，所以一个文法是二义性的，其描述的语言不一定就是二义性的。

3． 简述在句型分析中的自上而下与自下而上两类分析方法的主要差异？【答】自上而下的分析方法是从文法的开始符号出发，反复使用推导技术，试图把要分析的句型推导出来；自下而上的分析方法是从要分析的句型出发，反复使用归约技术，试图最终归约出文法的开始符号。

4．为什么说“素短语是包含有终结符的直接短语”的论断是错误的？并针对文法G[E]：(1) E→E+T | T (2) T→T*F | F (3) F→i 中的句型T+T+F，举一个反例加以进一步说明。

【答】在一个文法的句型中，其素短语是一个短语，它至少包含一个终结符，且除自身外不再包含其他素短语。

而不是说是一个直接短语。

例如：文法G[E]中的句型T+T+F，其一个素短语为：T+T，而T+T 是素短语，但不是直接短语。

二、形式文法与自动机题(共20 分)L={ a i b j a j b i| i＞0，j≥1 }【答】描述该语言的文法G[S]为：S→aAb |εA→bAa | ba2.对文法 G[E] : E→A│E+A │E–A A→B│A*B B→(E)│a写出句型B-(E)*a 的短语、直接短语和句柄。

2011年上海市春季高考数学试卷一、填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每题填对得4分，否则一律得零分．1．（4分）函数f（x）=lg（x﹣2）的定义域是．2．（4分）若集合A={x|x≥1}，B={x|x2≤4}，则A∩B=．3．（4分）在△ABC中，tanA=，则sinA=．4．（4分）若行列式=0，则x=．5．（4分）若，，则x=（结果用反三角函数表示）6．（4分）（x+）6的二项展开式的常数项为．7．（4分）两条直线l1：x﹣y+2=0与l2：x﹣y+2=0的夹角的大小是．8．（4分）若S n为等比数列{a n}的前n项的和，8a2+a5=0，则=．9．（4分）若椭圆C的焦点和顶点分别是双曲线的顶点和焦点，则椭圆C的方程是．10．（4分）若点O和点F分别为椭圆+y2=1的中心和左焦点，点P为椭圆上的任意一点，则|OP|2+|PF|2的最小值为．11．（4分）根据如图所示的程序框图，输出结果i=．12．（4分）2011年上海春季高考有8所高校招生，如果某3位同学恰好被其中2所高校录取，那么录取方法的种数为．13．（4分）有一种多面体的饰品，其表面右6个正方形和8个正三角形组成（如图），则AB与CD所成的角的大小是．14．（4分）为求方程x5﹣1=0的虚根，可以把原方程变形为（x﹣1）（x2+ax+1）（x2+bx+1）=0，由此可得原方程的一个虚根为．二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．15．（5分）若向量，则下列结论正确的是（）A．B．C． D．16．（5分）f（x）=的图象关于（）A．原点对称B．直线y=x对称C．直线y=﹣x对称 D．y轴对称17．（5分）直线l：y=k（x+）与圆C：x2+y2=1的位置关系是（）A．相交或相切B．相交或相离C．相切D．相交18．（5分）若，，均为单位向量，则=（，）是++=（，）的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号规定区域内写出必要的步骤．19．（12分）已知向量=（sin2x﹣1，cosx），=（1，2cosx），设函数f（x）=•，求函数f（x）的最小正周期及x∈[0，]时的最大值．20．（14分）某甜品店制作蛋筒冰淇淋，其上半部分呈半球形，下半部分呈圆锥形（如图）．现把半径为10cm的圆形蛋皮分成5个扇形，用一个扇形蛋皮围成锥形侧面（蛋皮厚度忽略不计），求该蛋筒冰淇淋的表面积和体积（精确到0.01）．21．（14分）已知抛物线F：y2=4x（1）△ABC的三个顶点在抛物线F上，记△ABC的三边AB、BC、CA所在的直线的斜率分别为k AB，k BC，k CA，若A的坐标在原点，求k AB﹣k BC+k CA的值；（2）请你给出一个以P（2，1）为顶点、其余各顶点均为抛物线F上的动点的多边形，写出各多边形各边所在的直线斜率之间的关系式，并说明理由．22．（16分）定义域为R，且对任意实数x1，x2都满足不等式f（）≤的所有函数f（x）组成的集合记为M，例如，函数f（x）=kx+b∈M．（1）已知函数f（x）=，证明：f（x）∈M；（2）写出一个函数f（x），使得f（x0）∉M，并说明理由；（3）写出一个函数f（x）∈M，使得数列极限=1，=1．23．（18分）对于给定首项x0＞（a＞0），由递推公式x n+1=（x n+）（n ∈N）得到数列{x n}，对于任意的n∈N，都有x n＞，用数列{x n}可以计算的近似值．（1）取x0=5，a=100，计算x1，x2，x3的值（精确到0.01）；归纳出x n，x n+1，的大小关系；（2）当n≥1时，证明：x n﹣x n+1＜（x n﹣1﹣x n）；（3）当x0∈[5，10]时，用数列{x n}计算的近似值，要求|x n﹣x n+1|＜10﹣4，请你估计n，并说明理由．2011年上海市春季高考数学试卷参考答案与试题解析一、填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每题填对得4分，否则一律得零分．1．（4分）（2011•上海）函数f（x）=lg（x﹣2）的定义域是（2，+∞）．【分析】对数的真数大于0，可得答案．【解答】解：由x﹣2＞0，得x＞2，所以函数的定义域为（2，+∞）．故答案为：（2，+∞）．2．（4分）（2011•上海）若集合A={x|x≥1}，B={x|x2≤4}，则A∩B={x|1≤x ≤2} ．【分析】求解二次不等式化简集合B，然后直接利用交集运算求解．【解答】解：由A={x|x≥1}，B={x|x2≤4}={x|﹣2≤x≤2}，所以A∩B={x|x≥1}∩{x|﹣2≤x≤2}={x|1≤x≤2}．故答案为{x|1≤x≤2}．3．（4分）（2011•上海）在△ABC中，tanA=，则sinA=．【分析】由题意可得A为锐角，再由tanA==，sin2A+cos2A=1，解方程组求得sinA的值．【解答】解：在△ABC中，tanA=，则A为锐角，再由tanA==，sin2A+cos2A=1，求得sinA=，故答案为．4．（4分）（2011•上海）若行列式=0，则x=1．【分析】先根据行列式的计算公式进行化简，然后解指数方程即可求出x的值．【解答】解：∵=0，∴2×2x﹣4=0，即2x=2，∴x=1．故答案为：1．5．（4分）（2011•上海）若，，则x=（结果用反三角函数表示）【分析】利用反正弦函数的定义，由角的范围为，故可直接得到答案．【解答】解：由于，根据反正弦函数的定义可得x=故答案为6．（4分）（2011•上海）（x+）6的二项展开式的常数项为20．【分析】在二项展开式的通项公式中，令x的幂指数等于0，求出r的值，即可求得常数项．=•x6﹣r•x﹣r=•x6﹣2r．【解答】解：（x+）6的二项展开式的通项公式为T r+1令6﹣2r=0，求得r=3，故展开式的常数项为=20，故答案为20．7．（4分）（2011•上海）两条直线l1：x﹣y+2=0与l2：x﹣y+2=0的夹角的大小是．【分析】设两条直线的夹角为θ，求得tanθ=||的值，可得tan2θ的值，求得2θ 的值，可得θ的值．【解答】解：由于两条直线l1：x﹣y+2=0与l2：x﹣y+2=0的斜率分别为、1，设两条直线的夹角为θ，则tanθ=||=||==2﹣，∴tan2θ==，∴2θ=，θ=，故答案为．8．（4分）（2011•上海）若S n为等比数列{a n}的前n项的和，8a2+a5=0，则=﹣7．【分析】根据已知的等式变形，利用等比数列的性质求出q3的值，然后分别根据等比数列的通项公式及前n项和公式，即可求出结果．【解答】解：由8a2+a5=0，得到=q3=﹣8===﹣7故答案为：﹣7．9．（4分）（2011•上海）若椭圆C的焦点和顶点分别是双曲线的顶点和焦点，则椭圆C的方程是．【分析】先确定双曲线的顶点和焦点坐标，可得椭圆C的焦点和顶点坐标，从而可得椭圆C的方程【解答】解：双曲线的顶点和焦点坐标分别为（±，0）、（±3，0）∵椭圆C的焦点和顶点分别是双曲线的顶点和焦点，∴椭圆C的焦点和顶点坐标分别为（±，0）、（±3，0）∴a=3，c=∴∴椭圆C的方程是故答案为：10．（4分）（2011•上海）若点O和点F分别为椭圆+y2=1的中心和左焦点，点P为椭圆上的任意一点，则|OP|2+|PF|2的最小值为2．【分析】先求出左焦点坐标F，设P（x，y），根据P（x，y）在椭圆上可得到x、y的关系式，表示出|OP|2+|PF|2，再将x、y的关系式代入组成二次函数进而可确定答案．【解答】解：由题意，F（﹣1，0），设点P（x，y），则有+y2=1，解得y2=1﹣，因为|OP|2+|PF|2=x2+y2+（x+1）2+y2=x2+（x+1）2+2﹣x2=（x+1）2+2，此二次函数对应的抛物线的对称轴为x=﹣1，|OP|2+|PF|2的最小值为2．故答案为：2．11．（4分）（2011•上海）根据如图所示的程序框图，输出结果i=8．【分析】按要求一步步代入循环体，直到符合要求退出循环，即可得到结论．【解答】解：因为i=0，t=76；不满足t≤0，∴t=76﹣10=66，i=0+1=1；不满足t≤0，∴t=66﹣10=56，i=1+1=2；不满足t≤0，∴t=56﹣10=46，i=2+1=3；不满足t≤0，∴t=46﹣10=36，i=3+1=4；不满足t≤0，∴t=36﹣10=26，i=4+1=5；不满足t≤0，∴t=26﹣10=16，i=5+1=6；不满足t≤0，∴t=16﹣10=6，i=6+1=7；不满足t≤0，∴t=6﹣10=﹣4，i=7+1=8；满足t≤0，输出结果i=8．故答案为：8．12．（4分）（2011•上海）2011年上海春季高考有8所高校招生，如果某3位同学恰好被其中2所高校录取，那么录取方法的种数为168．【分析】解决这个问题得分三步完成，第一步把三个学生分成两组，第二步从8所学校中取两个学校，第三步，把学生分到两个学校中，再用乘法原理求解【解答】解：由题意知本题是一个分步计数问题，解决这个问题得分三步完成，第一步把三个学生分成两组，第二步从8所学校中取两个学校，第三步，把学生分到两个学校中，共有C31C22A82=168故答案为：168．13．（4分）（2011•上海）有一种多面体的饰品，其表面右6个正方形和8个正三角形组成（如图），则AB与CD所成的角的大小是．【分析】由图形补出正方体，可得所求的角即为ED与CD所成的角，在△CDE 中，由余弦定理可得答案．【解答】解：该饰品实际上就是正方体的8个顶角被切掉，切线经过正方体每条棱边的中点，如图：可得AB与CD所成的角即为ED与CD所成的角，设正方体的棱长为2，在△CDE中，可得CD=DE=，EC=，由余弦定理可得cos∠CDE==，故∠CDE=，故AB与CD所成的角为故答案为：14．（4分）（2011•上海）为求方程x5﹣1=0的虚根，可以把原方程变形为（x﹣1）（x2+ax+1）（x2+bx+1）=0，由此可得原方程的一个虚根为．【分析】化简方程的左边，比较系数，求出a，b，再求方程的虚根．【解答】解：由题可知（x﹣1）（x2+ax+1）（x2+bx+1）=（x﹣1）[x4+（a+b）x3+（2+ab）x2+（a+b）x+1]比较系数可得，∴∴原方程的一个虚根为，中的一个故答案为：．二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．15．（5分）（2011•上海）若向量，则下列结论正确的是（）A．B．C． D．【分析】由给出的两个向量的坐标，求出的坐标，然后直接进行数量积的坐标运算求解．【解答】解：由，则．所以．则．故选C．16．（5分）（2011•上海）f（x）=的图象关于（）A．原点对称B．直线y=x对称C．直线y=﹣x对称 D．y轴对称【分析】先判断函数的定义域，然后利用函数奇偶性的定义进行判断．【解答】解：因为函数的定义域为R，所以定义域关于原点对称．f（x）==，则f（﹣x）=2﹣x﹣2x=﹣（2x﹣2﹣x）=﹣f（x），即函数f（x）为奇函数．故函数f（x）的图象关于原点对称．故选A．17．（5分）（2011•上海）直线l：y=k（x+）与圆C：x2+y2=1的位置关系是（）A．相交或相切B．相交或相离C．相切D．相交【分析】根据点到直线的距离求出圆心到直线的距离d，再根据d与半径r的大小关系，得出结论．【解答】解：由于圆心（0，0），半径等于1，圆心到直线l：y=k（x+）的距离为d===＜＜r=1，故直线和圆相交，故选D．18．（5分）（2011•上海）若，，均为单位向量，则=（，）是++=（，）的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件【分析】均为单位向量，若，=（，）不成立；若=（，）可推得，由此可得．【解答】解：均为单位向量，，若，，则=（，）不成立；若均为单位向量，=（，）可推得所以“”是“”的必要不充分条件，故选B三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号规定区域内写出必要的步骤．19．（12分）（2011•上海）已知向量=（sin2x﹣1，cosx），=（1，2cosx），设函数f（x）=•，求函数f（x）的最小正周期及x∈[0，]时的最大值．【分析】利用两个向量的数量积公式求得函数f（x）的解析式为sin（2x+），根据x∈[0，]，利用正弦函数的定义域和值域求函数的最大值．【解答】解：∵向量=（sin2x﹣1，cosx），=（1，2cosx），函数f（x）=•=（sin2x﹣1）+2cos2x=sin2x+cos2x=sin（2x+），故函数的周期为=π．∵x∈[0，]，∴≤2x+≤，故当2x+=时，函数取得最大值为．20．（14分）（2011•上海）某甜品店制作蛋筒冰淇淋，其上半部分呈半球形，下半部分呈圆锥形（如图）．现把半径为10cm的圆形蛋皮分成5个扇形，用一个扇形蛋皮围成锥形侧面（蛋皮厚度忽略不计），求该蛋筒冰淇淋的表面积和体积（精确到0.01）．【分析】设出蛋筒冰淇淋的底面半径和高，由圆形蛋皮的周长等于5倍圆锥的底面周长求得圆锥底面半径，进一步求出圆锥的高，然后直接利用表面积公式和体积公式求解．【解答】解：设圆锥的底面半径为r，高为h．因为，所以r=2．则．则圆锥的表面积S=．体积V=．故该蛋筒冰淇淋的表面积约为87.96cm2，体积约为57.80cm3．21．（14分）（2011•上海）已知抛物线F：y2=4x（1）△ABC的三个顶点在抛物线F上，记△ABC的三边AB、BC、CA所在的直线的斜率分别为k AB，k BC，k CA，若A的坐标在原点，求k AB﹣k BC+k CA的值；（2）请你给出一个以P（2，1）为顶点、其余各顶点均为抛物线F上的动点的多边形，写出各多边形各边所在的直线斜率之间的关系式，并说明理由．【分析】（1）设B（x1，y1），C（x2，y2），把B、C点左边代入抛物线方程，利用斜率公式计算k AB﹣k BC+k CA的值即可；（2）先研究△PBC，四边形PBCD，五边形PBCDE，再研究n=2k，n=2k﹣1（k∈N，k≥2）边形的情形，最后研究n边形P1P2…Pn（k∈N，k≥3），按由特殊到一般的思路逐步得到结论；【解答】解：（1）设B（x1，y1），C（x2，y2），∵，，∴k AB﹣k BC+k CA=+=﹣+=0；（2）①研究△PBC，k PB﹣k BC+k CP=﹣+=﹣+==1；②研究四边形PBCD，k PB﹣k BC+k CD﹣k DP=﹣+﹣=0；③研究五边形PBCDE，k PB﹣k BC+k CD﹣k DE+k EP=﹣+﹣==1；④研究n=2k边形P1P2…P2k（k∈N，k≥2），其中P1=P，有﹣…+=0，证明：左边=+===0=右边；⑤研究n=2k﹣1边形P1P2…P2k﹣1（k∈N，k≥2），其中P1=P，有+﹣…+（﹣1）2k﹣2=1，证明：左边=+===1=右边；⑥研究n边形P1P2…Pn（k∈N，k≥3），其中P1=P，有+﹣…+（﹣1）n﹣1=，证明：左边=+（﹣1）n﹣1=[1+（﹣1）n﹣1]==右边．22．（16分）（2011•上海）定义域为R，且对任意实数x1，x2都满足不等式f（）≤的所有函数f（x）组成的集合记为M，例如，函数f（x）=kx+b ∈M．（1）已知函数f（x）=，证明：f（x）∈M；（2）写出一个函数f（x），使得f（x0）∉M，并说明理由；（3）写出一个函数f（x）∈M，使得数列极限=1，=1．【分析】（1）分类讨论，验证f（）≤成立，即可得到结论；（2）利用条件，构造函数f（x）=﹣x2，f（x）∉M，再取值验证即可；（3）利用条件，构造函数f（x）=满足f（x）∈M，验证条件即可．【解答】解：（1）证明：由题意，当x1≤x2≤0或0≤x1≤x2时，f（）≤成立设x1≤0≤x2，且＜0，∵﹣f（）==0∴f（）≤成立设x1≤0≤x2，且≥0，∵﹣f（）==0∴f（）≤成立∴综上所述，f（x）∈M；（2）如函数f（x）=﹣x2，f（x）∉M取x1=﹣1，x2=1，则=﹣1，f（）=0此时f（）≤不成立；（3）f（x）=满足f（x）∈M，且==1，==1．23．（18分）（2011•上海）对于给定首项x0＞（a＞0），由递推公式x n+1=（x n+）（n∈N）得到数列{x n}，对于任意的n∈N，都有x n＞，用数列{x n}可以计算的近似值．（1）取x0=5，a=100，计算x1，x2，x3的值（精确到0.01）；归纳出x n，x n+1，的大小关系；（2）当n≥1时，证明：x n﹣x n+1＜（x n﹣1﹣x n）；（3）当x0∈[5，10]时，用数列{x n}计算的近似值，要求|x n﹣x n+1|＜10﹣4，请你估计n，并说明理由．【分析】（1）利用数列递推式，代入计算，即可得到结论，同时可猜想结论；（2）作差，利用条件，证明其大于0，即可得到结论；（3）由题意，只要，由此可估计n的值．【解答】（1）解：∵x0=5，a=100，x n+1=（x n+）∴x1=（5+）≈4.74同理可得x2≈4.67，x3≈4.65猜想x n＞x n+1；（2）证明：x n﹣x n+1﹣（x n﹣1﹣x n）==∵；∴x n﹣x n+1==＞0∴x n＞x n+1∴；（3）解：由（2）知＜…＜由题意，只要，即2n＞104（x0﹣x1）∵∴n＞=15.1∴n=16．。

教育学 试题第1页（共2页） 教育学 试题第2页（共2页）2010–2011学年度第2学期期末考试试卷（A 卷）学院 专业 本 科 级 教育学课程一．填空题：本大题共15空；每空1分，共15分。

答案请写在答题纸上。

1．教育的基本要素包括 、和 。

2．教育目的对教育活动具有 、 、 等功能。

3．理想师生关系的基本特征是、 和共享共创、教学相长。

4．主要的课堂教学策略有：策略、 策略和指导策略。

5．班级管理的内容包括 、 、班级教学管理和 四个方面。

6．新一轮基础教育课程改革实行国家、 和三级课程管理体系。

二．名词解释题：本大题共5小题；每小题3分，共15分。

答案请写在答题纸上。

1．教育 2．教学策略 3．教育制度 4．教育目的 5．班级管理 三．简答题：本大题共4小题；每小题5分，共20分。

答案请写在答题纸上。

1．如何正确理解教育的个体发展功能。

2．简要分析教育理论知识在教师专业成长中的地位和作用。

3．为什么说“教师即研究者”？4．班主任建设和管理班级组织的主要策略是什么？ 四．论述题：本大题共2小题；每小题15分，共30分。

答案请写在答题纸上。

1．试论述校本课程的利弊并分析教师在校本课程开发中的作用。

2．论述良好的师生关系构建的基本策略。

五．材料分析题：本大题共2小题；每小题10分，共20分。

答案请写在答题纸上。

1．新学期开学的时候，经常听到送孩子的家长对老师这样说：“我把孩子交给您了，请您严加管教，孩子不听话，要打要骂随您的便。

”请用所学教育学理论分析这一现象，看看它在哪些方面违背了现代教育思想。

2．我原来在小学是个很爱提问的人，可是每次提问都被否定了。

记得有一次，甲老师在教古诗《春晓》时，我觉得有疑问，就问：“老师说诗人春天好睡觉，连天亮都不晓得，那他夜里怎么能听见风雨声呢?”甲老师很不以为然地说：“这有什么奇怪的?早上起床到外面一看不就知道了吗?”我还想再问，老师挥手让我坐下，环视一下全班同学，多少带点嘲笑口吻说道：“大家说说看，是他对还是老师对?”同学们毫不犹豫地回答：“老师对!”当时我感到很尴尬，竟然对自己的判断产生了无端的怀疑。

海南大学2010-2011学年度第2学期试卷 科目：《线性代数与概率论》试题(A 卷)参考答一．选择题（每题3分，共24分）1、若三阶行列式M a a a a a a a a a =333231232221131211，则111213212223313233333333333a a a a a a a a a ---------=（ D ）。

(A) －9M (B) 9M (C) 27M (D) －27M2、设矩阵A 和C 分别是m n ⨯和s t ⨯，若要使ABC 有意义，则矩阵B 应是（ B ）。

(A) m t ⨯阵 (B) n s ⨯阵 (C) m s ⨯阵 (D) n t ⨯阵3、齐次线性方程120n x x x +++= 的基础解系中解向量的个数为（ C ）。

(A) 0 (B) 1 (C) 1n - (D) n4、在线性方程组Ax b =中，A 是86´阵，如果系数矩阵A 与增广矩阵(,)A b 的秩均为6，则Ax b =有( A ) .(A) 有唯一解 (B) 有无穷解 (C) 无解 (D) 无法确定是否有解5、一名射手连续向某目标射击三次，事件i A 表示第i 次射击时击中目标(1,2,3)i =，则三次射击至少有一次击中目标表示为：（ B ） （A ） 121323A A A A A A ++ （B ） 123A A A ++（C ） 123A A A ++ （D ）123A A A 6、已知离散型随机变量X 的概率分布为：X -1 0 1 2 4P101 51 101 51 52则下列概率计算结果中（ D ）正确.（A ）1}4{=<X P （B ）0}0{==X P （C ）1}1{=->X P （D ）103}21{=<<-X P 7、设离散型随机变量),,(~p n B X 若数学期望,2.1)(=X E 方差,08.1)(=X D 则参 数,n p 的值为（ A ）.（A ） 16,0.1n p == （B ） 4,0.4n p == （C ） 8,0.2n p == （D ） 2,0.8n p ==8、设随机变量X 的概率密度为()X f x ，则23Y X =-+的概率密度为 （ B ）（A ）13()22X y f --- （B ） 13()22X y f --（C ）13()22X y f +-- （D ） 13()22X y f +-二、填空题：（每题3分，共24分）1、已知171201,423132201A B 骣-÷ç骣÷-ç÷÷çç÷=?çç÷÷ç÷ç÷桫ç÷÷ç桫，则()T AB =_____0171413310骣÷ç÷ç÷ç÷ç÷ç÷ç÷÷ç-桫________. 2、设行列式1428211012341021D -=，则1113142A A A ++=________0______. 3、n 维向量组12(1,1,,1),(2,2,,2),,(,,,)m m m m a a a === 的秩为____1______.4、已知矩阵111121231A l 骣÷ç÷ç÷ç÷=ç÷ç÷ç÷÷ç+桫的秩为()2,R A =则l =____1______. 5、设随机变量X 和Y 相互独立，且()()1E X E Y ==，()2D X =，()3D Y =，则()D XY =____11______.()()()D XY E X Y E XY =-222[]()()()()E X E Y E X E Y =? 222()()()()E X E Y E X E Y =? 2222(()())(()())D X E X D Y E Y =+?-221()()=++-21311=11.6、设事件,,,A B C A B È发生的概率分别为0.4,0.3,0.6，则()P AB =____0.3_______.7、设随机变量123,,X X X 相互独立，其中1X 在[0,6]上服从均匀分布，2X 服从正态分布2(0,2)N ，3X 服从参数为3l =的泊松分布，记12323Y X X X =-+，则()D Y =______46_________.依题意21()()12b a D X -=，22()4D X s ==，3()3D X l ==，123123()(23)()4()9()46D Y D X X X D X D X D X =-+=++=.8、已知二维随机变量(,)X Y 的密度函数为4,01,01(,)0,xy x y f x y <<<<⎧=⎨⎩，其它.则{}P X Y ≤=___12_________. 111{}(,)42xx yP X Y f x y dxdy xdx ydy ≤≤===⎰⎰⎰⎰ 三、计算题（每题6分，共42分）1、计算行列式 3111131111311113D =. 解：3111131111311113D ==6666131111311113……………(3分) =61111131111311113=611110200002002=48. ……………(6分)2、解矩阵方程AX B X +=，其中01011111,2010153A B -⎛⎫⎛⎫ ⎪ ⎪=-= ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭.解：由AX B X +=得()I A X B -=。

安徽大学江淮学院2010 -20 11 学年第 2 学期《单片机原理》（A卷）考试试题参考答案及评分标准一、单项选择（在备选答案中选出一个正确答案，并将其号码填在题干后的括号内。

每题1分，共25分）1．程序计数器PC用来（ C ）A、存放指令B、存放正在执行指令的地址C、存放下一条指令的地址D、存放上一条指令的地址2．INTEL 8051 CPU是（ C ）位的单片机A、16B、4C、8D、准163．要用传送指令访问MCS-51片外ROM，它的指令操作码助记符应是（ C ）。

A、MOVB、MOVXC、MOVCD、以上都是4．在MCS-51单片机中，当晶振频率采用2MHZ时，一个机器周期等于（D ）微秒。

A. 3B. 4C.5D. 65．MCS-51单片机定时器工作方式2是指（ B ）的工作方式。

A、8位B、8位自动重装载C、13位D、16位6．单片机的堆栈指针SP始终是（ B ）。

A、指示堆栈底B、指示堆栈顶C、指示堆栈地址D、指示堆栈长度7．进位标志CY在（ C ）中。

A、累加器B、算逻运算部件ALUC、程序状态字寄存器PSWD、DPTR 8．单片机应用程序一般存放在（ B ）中。

A、内部RAMB、ROMC、寄存器D、外部RAM9．执行M O V I E，＃81H指令的意义是：（B）A、屏蔽中断源B、开放外部中断源0C、开放外部中断源1D、开放外部中断源0和110．执行如下三条指令后，30H单元的内容是（C ）M O V R 1，＃30HM O V 40H，＃0 E HM O V ﹫R 1，40HA、40HB、30H C 、0 E H D、F F H11．P0、P1口作输入用途之前必须（ A ）。

A、相应端口先置1B、相应端口先置0C、外接高电平D、外接上拉电阻12．一个EPROM的地址有A0----A11引脚，它的容量为（B ）。

A、2KBB、4KBC、11KBD、12KB13．对某单元的部分位取反，应采用下面哪种逻辑操作（ D ）。