DSP代码分析报告
- 格式:doc
- 大小:389.00 KB
- 文档页数:31

;************ GPIO.asm ***************.global _c_int0 ;定义全局变量 _c_int.global PHANTOM ;定义全局变量 PHANTOM.data ;data定义数据b0 .word 0fffEh ;turn-on GPIO0 ;b1 .word 0fffDh ;turn-on GPIO1b2 .word 0fffBh ;turn-on GPIO2b3 .word 0fff7h ;turn-on GPIO3b4 .word 0ffEFh ;turn-on GPIO0b5 .word 0ffDFh ;turn-on GPIO1b6 .word 0ffBFh ;turn-on GPIO2b7 .word 0ff7Fh ;turn-on GPIO3GPR0 .word 0.include f2407.h ;包含一个 f2407.h 文件KICK_DOG .macro ;看门狗控制寄存器LDP #00E0h ;DP-->7000h-707fh ;数据页指针将00E0赋给DP SPLK #05555h,WDKEY ;将05555h送给寄存器WDKEY SPLK #0aaaah,WDKEY ;同上LDP #0h ;DP-->0000h-007fh ;数据页指针将0赋给DP.end ;结束程序.text ;向下是个文本段_c_int0: ;开始执行程序LDP #0h ;数据页指针SETC I NTM ;关掉中断让程序正常运行SETC C NF ;B2程序存储器 0,数据 1,程序SPLK #0000h,IMR ;将0000送给寄存器中断屏蔽寄存器LACC IFR ;将中断标志寄存器IFR的值给了累加器SACL IFR ;将中断标志寄存器IFR的值LDP #00E0h ;数据页指针SPLK #0200h, SCSR1 ;将0200送给系统控制和状态寄存SPLK #006Fh,WDCR ;禁止看门狗复位KICK_DOG ;看门狗寄存器SPLK #0h,GPR0 ;将0送给等待寄存器GPR0OUT GPR0,WSGR ;将GPR0的值送给WSGRLDP #00E1h ;数据页指针SPLK #00000h,MCRA ;定义RA输入或输出SPLK #0FF00h,MCRB ;定义RB输入或输出SPLK #00000h,MCRC ;定义RC输入或输出SPLK #0FFFFh,PADATDIR ;端口A输出高电平SPLK #0FFFFh,PBDATDIRSPLK #0FFFFh,PCDATDIRSPLK #0FFFFh,PEDATDIRSPLK #0FFFFh,PFDATDIRMAIN: ;主程序LDP #0 ;数据页指针LOOP: ;循环LDP #00E1h ;数据页指针setc x f ;给xf高电平,使发光二极管发光SPLK #0FFFFh,PADATDIR ;端口A输出高电平SPLK #0FFFFh,PBDATDIRSPLK #0FFFFh,PCDATDIRSPLK #0FFFFh,PEDATDIRSPLK #0FFFFh,PFDATDIRCALL D ELAY ;调用延迟程序clrc x f ;清零SPLK #0FF00h,PADATDIR ;端口A数据和方向控制寄存器输出低电平SPLK #0FF00h,PBDATDIRSPLK #0FF00h,PCDATDIRSPLK #0FF00h,PEDATDIRSPLK #0FF00h,PFDATDIRB MAIN ;无条件跳转到主程序DELAY: ;延迟D_LOOP: ;RPT #0FFh ;重复0FF+1次NOP ;无动作RET ;跳转到 CALL DELAYPHANTOM: ; 假中断KICK_DOG ;看门狗寄存器B RET ;无条件跳转到 CALL DELAY。

dsp 研究报告DSP(数字信号处理)研究报告一、引言数字信号处理(DSP)是一种将连续信号转换为离散信号并利用数值计算机技术对其进行处理的领域。
随着计算机和通信技术的迅速发展,DSP在各个领域的应用也变得越来越广泛。
本报告将介绍DSP的基本原理、应用领域以及未来的发展趋势。
二、基本原理DSP的基本原理是对离散信号进行数字化处理。
主要包括信号采样、量化、编码和数值计算等环节。
通过这些处理步骤,可以实现对信号的滤波、变换、压缩和识别等操作。
其中,采样是将连续信号转换为离散信号的过程,量化是测量离散信号幅度的过程,编码是将量化结果转化为二进制数的过程,数值计算是在计算机上对二进制数进行运算和处理的过程。
三、应用领域1. 通信领域:DSP广泛应用于通信系统中的调制解调、编码解码、信道均衡、差错控制等方面。
通过DSP技术,可以实现高效率和高质量的信号传输,提高通信系统的性能。
2. 音频领域:DSP在音频处理方面的应用也非常广泛。
例如,音频信号的降噪、混响、均衡等处理,以及音频压缩、编码、解码等技术都离不开DSP的支持。
3. 映像领域:DSP在映像处理中可以实现图像增强、去噪、边缘检测、图像压缩、图像识别等功能。
这些技术在医学影像、监控系统、数字摄像等方面有重要应用。
4. 传感器信号处理:传感器信号是一些外界环境的模拟信号,通过DSP技术可以对其进行预处理、滤波、增强和识别等操作,获得有用的信息。
5. 音视频编解码:DSP技术在音视频编解码方面有着重要作用。
通过DSP算法,可以将高位率的音视频信号压缩为低位率的信号,实现高效的传输和存储。
四、未来发展趋势随着计算机和通信技术的不断发展,DSP技术也在不断完善和演进。
未来的发展趋势主要包括以下几个方面:1. 高性能和低功耗:随着芯片制造工艺的进步,DSP芯片将实现更高的性能和更低的功耗。
这将推动DSP技术在各个领域的应用向更广泛、更深入的方向发展。
2. 多核并行计算:为了满足大规模信号处理的需求,DSP芯片将趋向于多核并行计算的方向。

dsp研究报告DSP(Digital Signal Processing,数字信号处理)是一种用于对数字信号进行处理和分析的技术。
随着计算机技术的发展和普及,DSP在各个领域中得到了广泛的应用。
本研究报告旨在介绍DSP的基本原理和应用领域,并分析其在音频处理和图像处理中的具体实例。
DSP的基本原理是将连续时间的模拟信号转换为离散时间的数字信号,并对其进行计算和处理。
这种转换过程包括信号采样、量化和编码等步骤。
DSP可以通过数字滤波、频谱分析、时域处理等技术实现对信号的处理和改变。
在音频处理方面,DSP被广泛应用于音乐制作、声音增强和音频压缩等领域。
例如,通过数字滤波可以去除噪音、平衡音频频谱;通过时域处理可以实现回声消除、混响效果等;通过音频压缩可以降低音频的文件大小。
DSP技术在音频处理中发挥重要作用,提高了音频的质量和可靠性。
在图像处理方面,DSP被广泛应用于图像增强、边缘检测和图像压缩等领域。
例如,通过平滑滤波和锐化滤波可以改善图像的质量和清晰度;通过边缘检测可以提取出图像中的物体边缘和轮廓;通过图像压缩可以减小图像文件的大小。
DSP技术在图像处理中能够提供丰富的功能,增强了视觉效果和图像的传输效率。
综上所述,DSP是一种重要的数字信号处理技术,广泛应用于音频处理和图像处理等领域。
通过数字滤波、频谱分析、时域处理等技术,DSP可以实现对信号的处理和改变。
在音频处理方面,DSP可以提高音频的质量和可靠性;在图像处理方面,DSP可以增强图像的质量和清晰度。
随着技术的不断进步,DSP在更多领域中的应用也将得到进一步的扩展和发展。

dsp 研究报告
DSP(Digital Signal Processing,数字信号处理)是指利用数
字技术对信号进行处理和分析的过程。
随着计算机技术的发展,DSP技术逐渐成为信号处理领域的重要工具。
本研究报告旨
在介绍DSP的基本原理、应用领域以及未来发展趋势。
首先,DSP的基本原理是将模拟信号通过采样、量化和编码
转换成数字信号,然后通过数字滤波、变换、调制等处理方法对信号进行处理。
与模拟信号相比,数字信号具有较强的抗干扰能力和稳定性,能够更好地满足实际应用的需求。
其次,DSP在许多领域都有广泛的应用。
在通信领域,DSP
可以用于音频、视频传输和压缩,提高传输速度和质量。
在图像处理领域,DSP可以用于图像增强、模式识别和人脸识别
等方面。
在音频处理方面,DSP可以用于音频效果处理、音
频合成等方面。
此外,DSP还广泛应用于雷达、声纳、医学
图像处理等领域。
然而,随着科技的不断发展,DSP技术也在不断更新和演进。
未来,DSP的应用将更加广泛,包括物联网、人工智能、虚
拟现实等方面。
同时,DSP系统的实时性、低功耗和高效率
等方面也将得到进一步提升。
总之,DSP技术作为数字信号处理的重要工具,已经在多个
领域得到应用。
通过对信号的处理,可以提高信号的质量、速度和准确性。
未来,DSP的发展将更加注重应用的广泛性和
效率的提升,为我们的生活带来更多的便捷和可能性。
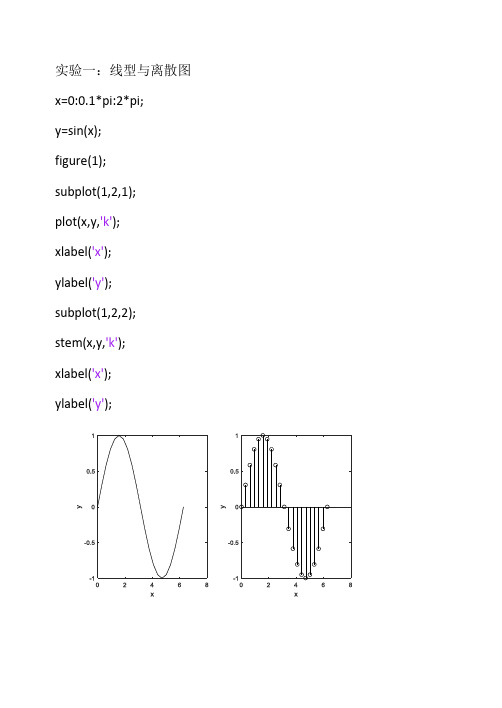
实验一:线型与离散图x=0:0.1*pi:2*pi;y=sin(x);figure(1);subplot(1,2,1);plot(x,y,'k');xlabel('x');ylabel('y');subplot(1,2,2);stem(x,y,'k');xlabel('x');ylabel('y');实验二:函数:function[X,wk]=DFT(x,M)N=length(x);n=0:N-1;for k=0:M-1wk(k+1)=2*pi/M*k;X(k+1)=sum(x.*exp(-j*wk(k+1)*n)); endclc;clear all;A=444.128;a=50*sqrt(2)*pi;w0=50*sqrt(2)*pi;fs=input('输入采样频率fs=');T=1/fs;N=50;n=0:N-1;xa=A*exp(-a*n*T).*sin(w0*n*T); subplot(1,2,1);stem(n,xa,'.');grid;M=100;[Xa,wk]=DFT(xa,M);f=wk*fs/(2*pi);subplot(1,2,2);plot(f,abs(Xa));grid;1000hz500hz200hzDFT程序:Clcclear allxbn=[1,0,0,0];hbn=[1,2.5,2.5,1]N=4;n=0:N-1;Xb=fft(xbn,N);Xh=fft(hbn,N);ybn=conv(xbn,hbn); subplot(3,2,1); stem(n,xbn,'.');title('xbn wave'); subplot(3,2,2); stem(n,abs(Xb),'.'); title('Xb wave');subplot(3,2,3);stem(n,hbn,'.');title('hbn wave'); subplot(3,2,4);stem(n,abs(Xh),'.'); title('Xh wave');n1=0:6;Xy=fft(ybn,8);subplot(3,2,5);stem(n1,ybn,'.');title('ybn wave')n2=0:7;subplot(3,2,6);stem(n2,abs(Xy),'.'); title('Xy wave结果:hbn =1.00002.5000 2.5000 1.0000实验三:第一个方程:clc;clear all;a1=[1 ,0.75,0.125];b1=[1,-1];n=0:20;x1=[1 zeros(1,20)];subplot(2,3,1);y1filter=filter(b1,a1,x1); stem(n,y1filter);title('y lfilter');xlabel('x');ylabel('y');x1=[1 zeros(1,10)];[h]=impz(b1 ,a1,10); subplot(2,3,2);y1conv=conv(h,x1);n=0:19;stem(n,y1conv,'filled') subplot(2,3,3);impz(b1 ,a1,21);n=0:20;x2=ones(1,21);subplot(2,3,4);y1filter=filter(b1,a1,x2); stem(n,y1filter);title('y1filter_step'); xlabel('x');ylabel('y');x2=ones(1,21);[h]=impz(b1,a1,20);y1=conv(h,x2);y1conv=y1(1:21);n1=0:20;subplot(2,3,5);stem(n1,y1conv,'filled'); title('y1conv');xlabel('n');ylabel('y1[n]');subplot(2,3,6);b1=1;impz(b1,a1);第二个方程:clc;clear all;a1=[1];b1=[0.25,0.25,0.25,0.25]; n=0:20;x1=[1 zeros( 1,20)];y1filter=filter(b1,a1,x1); subplot(2,3,1);stem(n,y1filter);title('y 1filter');xlabel('x');ylabel('y');x1=[1 zeros(1,10)];[h]=impz(b1,a1,10);y1conv=conv(h,x1);n=0:19;subplot(2,3,2);stem(n,y1conv,'filled') subplot(2,3,3);impz(b1,a1,21);n=0:20;x2=ones(1,21);y1filter=filter(b1,a1,x2); subplot(2,3,4);stem(n,y1filter);title('y1filter_step'); xlabel('x');ylabel('y');x2=ones(1,21);[h]=impz(b1,a1,20);y1=conv(h,x2);y1conv=y1(1:21);n1=0:20;subplot(2,3,5);stem(n1,y1conv,'filled');title('y1conv');xlabel('n');ylabel('y1[n]');subplot(2,3,6);n=0:20;a1=1;b1=[0,0.25,0.5,0.75,ones(1,17)] ;impz(b1,a1,21);第一个方程结果第二个方程结果:实验四:程序:clc;clear all;num=[0.0528 0.0797 0.1295 0.1295 0.797 0.0528];den=[1 -1.8107 2.4947 -1.8801 0.9537 -0.2336];[z,p,k]=tf2zp(num,den);m=abs(p);disp('零点');disp(z);disp('极点');disp(p);disp('增益系数');disp(k);sos=zp2sos(z,p,k);figure(1)subplot(2,3,5);zplane(num,den)k=256;w=0:pi/k:pi;h=freqz(num,den,w);subplot(2,3,1);plot(w/pi,real(h));grid title('实部')xlabel('\omega/\pi');ylabel('幅度')subplot(2,3,2);plot(w/pi,imag(h));gridtitle('虚部')xlabel('\omega/\pi');ylabel('Am plitude')subplot(2,3,3);plot(w/pi,abs(h));gridtitle('幅度谱')xlabel('\omega/\pi');ylabel('幅值')subplot(2,3,4);plot(w/pi,angle(h));gridtitle('相位谱')xlabel('\omega/\pi');ylabel('弧度')figure(2)freqz(num,den,128);结果:零点-1.5870 + 1.4470i -1.5870 - 1.4470i 0.8657 + 1.5779i 0.8657 - 1.5779i -0.0669 + 0.0000i 极点0.2788 + 0.8973i 0.2788 - 0.8973i 0.3811 + 0.6274i 0.3811 - 0.6274i 0.4910 + 0.0000i 增益系数0.0528实验五:clc;clear all;wp=input('通带内频率wp=');ap=input('容许幅度误差ap=');ws=input('频率ws=');as=input('阻带衰减as=');fs=1;[N,Wn]=buttord(wp,ws,ap,as,'s'); [Z,P,K]=buttap(N);[Bap,Aap]=zp2tf(Z,P,K);[b,a]=lp2lp(Bap,Aap,Wn);[bz,az]=bilinear(b,a,fs);[H,W]=freqz(bz,az,64);subplot(2,1,1);stem(W/pi,abs(H));grid;xlabel('频率');ylabel('幅度');subplot(2,1,2);stem(W/pi,20*log10(abs(H))); grid;xlabel('频率');ylabel('幅度(dB)');bzaz结果:通带内频率wp=0.1*pi容许幅度误差ap=0.5频率ws=0.5*pi阻带衰减as=20bz =0.0238 0.0714 0.0714 0.0238 az =1.0000 -1.6217 1.0505 -0.2384实验六:Blackman方式:clc;clear all;b=fir1(21,0.5,blackman(22)); figure(1);y=freqz(b,1);subplot(2,2,1);plot(abs(y));grid;title('幅度响应');subplot(2,2,2); plot(angle(y)); grid;title('相位响应'); subplot(2,2,3); cj=impz(b,1,20); stem(cj);title('冲激响应'); grid;Hamming方式:clc;clear all;b=fir1(21,0.5,hamming(22)); figure(1);y=freqz(b,1);subplot(2,2,1);plot(abs(y));grid;title('幅度响应');subplot(2,2,2); plot(angle(y)); grid;title('相位响应'); subplot(2,2,3); cj=impz(b,1,20); stem(cj);title('冲激响应'); grid;Hanning方式:clc;clear all;b=fir1(21,0.5,hanning(22)); figure(1);y=freqz(b,1);subplot(2,2,1);plot(abs(y));grid;title('幅度响应');subplot(2,2,2); plot(angle(y)); grid;title('相位响应'); subplot(2,2,3); cj=impz(b,1,20); stem(cj);title('冲激响应'); grid;实验七:0个过渡点:clc;clear all;N=64;wc=0.8*pi;k=0:N-1;phase=(-pi*k*(N-1)/N+pi/2);HK=[zeros(1,26),ones(1,13),zero s(1,25)];HK1=HK.*exp(j*phase);hn=ifft(HK1,N);figure(1);freqz(hn,1,512);[H,W]=freqz(hn,1,512);figure(2);subplot(3,1,1);stem(k,hn);title('h(n)')subplot(3,1,2);plot(W/pi,abs(H));title('|H(eiw)|')subplot(3,1,3);plot(W/pi,20*log10(abs(H))); title('20lg|H(eiw)|');clc;clear all;N=64;wc=0.8*pi;k=0:N-1;phase=(-pi*k*(N-1)/N+pi/2);HK=[zeros(1,25),0.5,ones(1,13), 0.5,zeros(1,24)];HK1=HK.*exp(j*phase);hn=ifft(HK1,N); figure(1);freqz(hn,1,512);[H,W]=freqz(hn,1,512);figure(2);subplot(2,1,1);plot(W/pi,abs(H));title('|H(eiw)|')subplot(2,1,2);plot(W/pi,20*log10(abs(H))); title('20lg|H(eiw)|');clc;clear all;N=64;wc=0.8*pi;k=0:N-1;phase=(-pi*k*(N-1)/N+pi/2);HK=[zeros(1,24),1/3,2/3,ones(1, 13),2/3,1/3,zeros(1,23)];HK1=HK.*exp(j*phase);hn=ifft(HK1,N); figure(1);freqz(hn,1,512);[H,W]=freqz(hn,1,512);figure(2);subplot(2,1,1);plot(W/pi,abs(H));title('|H(eiw)|')subplot(2,1,2);plot(W/pi,20*log10(abs(H))); title('20lg|H(eiw)|');实验八:clc;clear all;x=[4,-2,0,-4,-6 ...-4,-2, -4,-6,-6 ...-4,-4,-6, -6,-2 ...6,12,8,0,-16, -38 ...-60,-84,-90,-66 ...-32,-4,-2,-4,8,12 ...12, 10,6,6,6,4,0,0 ...0,0,0, -2,-4,0,0,0 ...-2,-2,0, 0,-2,-2 ...-2,-2,0];subplot(3,1,1);plot([0:length(x)-1],x,'k'); title('输入')N=21;wn=hamming(N+1);wp=0.2*pi; h=fir1(N,wp/pi,wn);y=conv(x,h);subplot(3,1,2);plot([0:length(y)-1],y,'r'); title('经FIR滤波')A=0.2318;a=A*[1,2,1];b1=[1,0.4164,-0.6006];b2=[1,0.3093,-0.1888];b3=[1,0.2692,-0.0349];y1=filter(a,b1,x);y2=filter(a,b2,y1);y3=filter(a,b3,y2);subplot(3,1,3);plot([0:length(y3)-1],y3,'m'); title('经IIR滤波')。

DSP实验报告一引言本实验旨在通过实际操作,探索数字信号处理(DSP)的基本概念和技术。
DSP是一种通过数字计算来处理连续时间信号的技术,被广泛应用于音频处理、图像处理、通信系统等领域。
本实验将重点介绍数字信号的采样、量化和离散化过程,并通过实际编程实现。
实验过程1. 信号的采样1.1 信号的定义在DSP领域,信号是指随着时间变化的某种物理量,可以是声音、图像等。
我们首先需要定义一个连续的信号,用于采样和处理。
在本次实验中,我们选择了一个简单的正弦信号作为示例:x(t) = A \\sin(2\\pi f t)其中,A表示幅值,f表示频率,t表示时间。
1.2 采样过程为了将连续信号转换为离散信号,我们需要对信号进行采样。
采样是指在一定时间间隔内对连续信号进行测量。
我们可以通过模拟采样器来模拟采样过程。
在本实验中,我们选择了采样频率为100Hz,即每秒采样100次。
使用Python编程实现采样过程:import numpy as np# 信号参数设置A =1f =10# 采样频率设置fs =100# 采样点数设置N =100# 生成时间序列t = np.arange(N) / fs# 生成采样信号x = A * np.sin(2* np.pi * f * t)上述代码中,我们通过调整A和f的值来模拟不同的信号。
生成的信号将存储在x变量中,可以用于后续处理。
2. 信号的量化2.1 量化过程量化是指将连续信号的幅值转换为离散的数值。
在实际应用中,我们通常使用有限位数来表示信号的幅值。
常用的量化方式有线性量化和非线性量化。
在本实验中,我们选择了线性量化方式。
具体的量化过程可以通过下列Python代码实现:import math# 量化位数设置bits =8# 量化步长计算step_size =2* A / (2** bits -1)# 信号的量化x_quantized = np.round(x / step_size) * step_size上述代码中,我们通过调整bits的值来控制量化位数。
DSP技术----实验报告姓名: 赵广元学号: 1428403058学院: 电子信息学院班级: 电子信息工程实验一DSP程序的调试与分析一实验目的1.熟悉ccs集成开发环境,掌握工程的建立,编译和链接方法2.熟悉DSP程序调试的基本方法3.利用DSP实现DFT算法对离散信号进行频谱分析二实验内容1.输入信号的模拟2.输出信号的图形显示和分析3.对DSP程序进行剖析三实验原理1.输入信号的构造方法离散时间信号可以用若干个幅值不同的正弦信号叠加而成,单个正弦信号的离散时间表示方式为)2sin()(xfsfnn⨯⨯=π,其中,f表示信号源频率,fs表示采样频率。
2.离散傅里叶变换公式∑-=⋅=1)()(NNknNWnxkX;其中,10,2kn-≤≤=-NkeW knNjNπ离散傅里叶变换的目的是把信号由时域变换到频域,在频域分析信号特征,是数字信号处理领域常用的方法。
四实验设备1.PC一台2.TMS320VC5416 DSK一套五实验过程1.首先打开C5416 DSK CCS,界面如下图所示:选择Project→new命令新建一个工程并命名,选择file→new→source file建立源代码文件,输入程序代码后保存:2.新建源程序文件mydft,输入代码并保存3.新建cmd文件my5416,输入代码并保存4.保存源文件到当前工程所在的文件夹,然后在当前工程窗口选择当前工程,调用右键菜单,选择add files to project命令,打开一个文件选择对话框,选择刚保存的源文件加入到工程中之后编译文件发现错误后新建dst.h文件并保存再次编译发现还有一个而错误,此时在工程名上右击选择options设置includes libraries(-1)为rts.lib在complier选项卡中设置为advancedfile →load program加入断点后运行5.用图形分析工具分析输入输出信号选择view→graph→time/frequency分析in signal:以及out signal:6.用view→watch window7.输入已知信号file→file I/O选择sin信号运行后即可看到in signal 窗口输入信号波形变为sin函数8.新建GEL文件,输入代码并保存File →load GEL下载之后即可在菜单栏GEL选项下看到DFT controlGEL →DFT control→data input,可以分别得到输入为方波或锯齿波对应的输出波形:9.用剖析区间的方法来确定processing 函数所耗费的时间在程序相应位置加入断点,打开菜单栏上的profile →clock setup →auto 分析结果时使用profile →view clock (需要勾选enable )10.保存工作区File →workspace →save workspace as →命名需要查询保存的工作区只需要file →workspace →load workspace六 实验经验总结实验主要目的是熟悉使用ccs 集成环境,掌握工程的建立,编译,链接等方法并学会调试DSP程序,对输入输出信号的图形显示和分析以及剖析DSP程序。
DSP报告基于CCS和ICETEK5509实验箱----FFT算法的C语言实现与验证学院:计算机学院班级:通信0801姓名:·····学号:3080601022同组成员:···指导老师:···一、课程设计目的1、熟悉FFT的基本原理及A/D转换的基本原理2、针对理论课、实验课中无时间和不方便提及内容和需强调重点进行补充与完善;3、以原理算法的实现与验证体会DSP技术的系统性,并加深基本原理的体会。
二、课程设计要求1.设计一个以ICETEK5509为硬件主体,FFT为核心算法的频谱分析系统方案;2.用C语言编写系统软件的核心部分,熟悉CCS调试环境的使用方法,在CCS IDE中仿真实现方案功能;3.在实验箱上由硬件实现频谱分析。
三、课程设计内容1、FFT算法C语言实现与验证1)参考教材P371的14.3节完成CCS环境中的FFT工程的建立;2)设计检测信号,验证FFT算法的正确性及FFT的部分性质;3)运用FFT完成IFFT计算;2、单路,多路模数转换(AD)1)回顾CCS的基本操作流程,尤其是开发环境的使用;2)参考实验指导和示例工程掌握5509芯片A/D的C语言基本控制流程;3)仔细阅读工程的源程序,做好注释,为后期开发做好系统采集前端设计的准备;3、系统集成,实现硬件频谱分析1)整合前两个工程,实现连续信号的频谱分析工程的构建;2)参考A/D转换示例和DSP系统功能自检示例完成硬件连接,并测试开发系统运行效果;3)基于现有系统,对于实时频谱分析给出进一步开发设计和系统改良方案。
四、课程设计原理1.(软仿真)先利用sin函数验证FFT的正确性2.(硬仿真)将信号模拟信号经过AD采样后,转为离散的数字信号,将这些信号存储进缓冲区,然后读出缓冲区数据,经过变址运算后做蝶形运算,得到的数据进行IFFT运算,将运算后的图与开始的输入信号做对比。
DSP汇编指令总结DSP汇编指令总结⼀、寻址⽅式:1、⽴即寻址:短⽴即寻址(单指令字)长⽴即数寻址(双指令字)第⼀指令字第⼆指令字16位常数=16384=4000h2、直接寻址ARU 辅助寄存器更新代码,决定当前辅助寄存器是否和如何进⾏增或减。
N规定是否改变ARP值,(N=0,不变)4.3.1、算术逻辑指令(28条)4.3.1.1、加法指令(4条);4.3.1.2、减法指令(5条);4.3.1.3、乘法指令(2条);4.3.1.4、乘加与乘减指令(6条);4.3.1.5、其它算数指令(3条);4.3.1.6、移位和循环移位指令(4条);4.3.1.7、逻辑运算指令(4条);4.3.2、寄存器操作指令(35条)4.3.2.1、累加器操作指令(6条)4.3.2.2、临时寄存器指令(5条)4.3.2.3、乘积寄存器指令(6条)4.3.2.4、辅助寄存器指令(5条)4.3.2.5、状态寄存器指令(9条)4.3.2.6、堆栈操作指令(4条)4.3.3、存储器与I/O操作指令(8条)4.3.3.1、数据移动指令(4条)4.3.3.2、程序存储器读写指令(2条)4.3.3.3、I/O操作指令(2条)4.3.4、程序控制指令(15条)4.3.4.1、程序分⽀或调⽤指令(7条)4.3.4.2、中断指令(3条)4.3.4.3、返回指令(2条)4.3.4.4、其它控制指令(3条)4.3.1、算术逻辑指令(28条)4.3.1.1、加法指令(4条);▲ADD▲ADDC(带进位加法指令)▲ADDS(抑制符号扩展加法指令)▲ADDT(移位次数由TREG指定的加法指令)4.3.1.2、减法指令(5条);★SUB(带移位的减法指令)★SUBB(带借位的减法指令)★SUBC(条件减法指令)★SUBS(减法指令)★SUBT(带移位的减法指令,TREG决定移位次数)4.3.1.3、乘法指令(2条);★MPY(带符号乘法指令)★MPYU(⽆符号乘法指令)4.3.1.4、乘加与乘减指令(6条);★MAC(累加前次积并乘)(字数2,周期3)★MAC(累加前次积并乘)★MPYA(累加-乘指令)★MPYS(减-乘指令)★SQRA(累加平⽅值指令)★SQRS(累减并平⽅指令)4.3.1.5、其它算数指令(3条);★ABS(累加器取绝对值指令)★NEG(累加器取补码指令)★NORM(累加器规格化指令)返回4.3.1.6、移位和循环移位指令(4条);▲ SFL(累加器内容左移指令)▲ SFR(累加器内容右移指令)▲ROL(累加器内容循环左移指令)▲ROR(累加器内容循环右移指令)返回4.3.1.7、逻辑运算指令(4条);▲ AND(逻辑与指令)▲ OR(逻辑或指令)▲ XOR(逻辑异或指令)▲ CMPL(累加器取反指令)返回4.3.2、寄存器操作指令(35条)4.3.2.1、累加器操作指令(6条)▲ LACC(装载累加器指令)▲ LACT(装载累加器)*按TREG低4位指定的次数移位▲ LACL(装载累加器低16位指令)▲ ZALR(装载累加器指令)▲ SACL(移位并存储累加器低半部)▲ SACH(移位并存储累加器⾼半部)返回4.3.2.2、临时寄存器指令(5条)▲ LT(装载TREG指令)▲ LTA(装载TREG并累加上次乘积指令)▲ LTS (装载TREG并减去上次乘积指令)▲ LTD(装载TREG并累加上次乘积及数据移动指令)▲LTP(装载TREG和累加器指令)返回4.3.2.3、乘积寄存器指令(6条)▲ PAC (乘积寄存器内容载⼊累加器)▲ APAC (PREG与累加器相加)▲ SPAC(累加器和乘积寄存器相减)▲ LPH(装载PREG⾼16位指令)▲ SPL(存储PREG低16位指令)▲ SPH(存储PREG⾼16位指令)返回4.3.2.4、辅助寄存器指令(5条)★LAR(装载当前辅助寄存器AR)★SAR(存储辅助寄存器指令)★MAR(修改当前辅助寄存器)★SBRK(从当前辅助寄存器减去短⽴即数)返回4.3.2.5、状态寄存器指令(9条)★LST(装载状态寄存器)★SST(存储状态寄存器)★SETC(控制位置“1”指令)★SETC(控制位置“1”指令)★LDP(装载数据指针DP指令)★BIT(位测试指令)★BITT(测试由TREG指定bit code指令)★CMPR(⽐较当前辅助寄存器AR和AR0)返回4.3.2.6、堆栈操作指令(4条)★PUSH(累加器低16位进栈指令)★POP(栈顶内容弹出⾄累加器低16位指令)★POP(栈顶内容弹出⾄累加器低16位指令)★POPD(弹栈⾄数据存储器指令)返回4.3.3、存储器与I/O操作指令(8条)4.3.3.1、数据移动指令(4条)▲DMOV(数据存储器内部数据移动指令)▲SPLK(存储长⽴即数⾄数据存储器指令)▲BLDD(数据存储器内部的数据块移动)▲ BLPD(从程序存储器到数据存储器的数据块传送)4.3.3.2、程序存储器读写指令(2条)★TBLR(读程序存储器数据到数据存储器)★TBLW(写程序存储器)4.3.3.3、I/O操作指令(2条)★IN(数据输⼊指令)★OUT(数据输出指令)4.3.4、程序控制指令(15条)4.3.4.1、程序分⽀或调⽤指令(7条)★B(⽆条件转移指令)★BANZ(辅助寄存器内容不等于零转移)★CALL(⽆条件⼦程序调⽤指令)★BACC(按累加器内容转移指令)★CALA(由累加器指定地址的⼦程序调⽤指令)★CC(条件调⽤指令)4.3.4.2、中断指令(3条)★INTR(软中断指令)★TRAP(软件陷阱中断)★NMI(⾮屏蔽中断)4.3.4.3、返回指令(2条)★RET(⽆条件从⼦程序或中断返回)★RETC(条件返回指令)4.3.4.4、其它控制指令(3条)★RPT(重复执⾏下条指令)★NOP(空操作)★IDEL(暂停)返回。
代码优化总结在优化一段代码之前,首先要找出这段程序中最消耗时间的那一段程序,对最耗时程序段的优化会带来很大的优化效果收益。
一般而言,这个最耗时的程序一般位于一个循环体内,而且这个循环体的循环次数非常之多。
下面是具体的一些优化措施:1.在循环体内最好不要有条件判断句,尤其是在内层循环。
因为内层循环太多的条件判断句会打断程序执行的流水线2.while和for循环的选取。
如果知道循环次数的话,选用for语句3.在循环体内,尽量不要使用系统函数调用,因为系统调用会消耗太多的时间。
4.如果函数条用的代码量很小,而且使用的次数又非常的多得话,将这一段函数改成内联函数,这样可以减少函数调用的开销。
5.如果有几层循环的话,将循环次数多得放在内层循环里。
6.用移位运算来代替乘法运算。
7.在循环体内最好不要用数学函数。
尤其是power、除法操作、模数操作是非常耗时的运算。
应该用其他的方法来实现这些操作。
以上的这些只是在程序优化时的一些参考,其实程序的优化总体来说分成算法上的优化和程序结构上的优化,如果想要实现很高的优化效率的话,应该从算法上入手。
但是程序结构上的优化也是必不可少的,它能够使我们充分发掘CPU的性能。
DSP上C代码的优化一:代码优化A:数据类型优化1)整数Use unsigned int instead of int if it is known that the value will never be negative.Integer arithmetic is much faster than floating-point arithmetic some processors can handle unsigned integer arithmetic considerably faster than signed so, the best declaration for an int variable in a tight loop would be: unsigned int variable_name.2)除法和取余运算In standard processors, depending on numerator (x) and denominator (y), a 32 bit division takes 20-140 cycles to execute.It will be better to use unsigned division by ensuring that one of the operands is unsigned, as this is faster than signed division.3) 全局变量Global variables are never allocated to registers.Hence, the compiler cannot cache the value of a global variable in a register, resulting in extra loads and stores when global are used. So, avoid using global variables inside critical loops.If a function uses global variables heavily, it is beneficial to copy those global variables into local variables so that they can be assigned toregisters. This is possible only if those global variables are not used by any of the functions which are called. Then it will take less amount of time to execute.4)函数的指针参数如果函数的参数有指针参数,并且这个指针的值在函数被调用期间被使用很多次,而且每次使用并不会改变指针参数所指向的变量的值,那么在函数内部将这个指针参数的值赋值给一个局部变量。
中南大学DSP原理及应用课程结业论文报告题目:DSP代码分析报告院系:信息科学与工程学院专业班级:自动化07XX学生姓名:绿筠散人学号:指导老师:2010年5月目录第一部分FFT的TMS320C54x实现一.基本原理概述 (3)二.(汇编)主要程序分析 (4)三.算法分析 (10)四.数据存储空间及关键寻址方式分析 (11)第二部分应用DSP2407开发板实现LED的定时器控制一.基本原理概述 (12)二.(C语言)主要程序分析 (13)三.算法分析 (15)四.头文件和变量声明分析 (17)五.结果分析 (29)第三部分总结 (30)第四部分参考资料 (31)第一部分FFT的TMS320C54x实现一.基本原理概述FFT,即为快速傅氏变换。
用定点DSP芯片实现FFT程序时,防止中间结果溢出的方法是对中间数值归一化。
根据N点DFT公式,应用Parseval定理可得对于有限长离散数字信号{x[n]},0≤x≤N-1,它的频谱离散数学值{X(K)}可由离散傅氏变换(DFT)求得。
DFT 定义为:也可以方便的把它改写成如下形式:Wnk 的周期性是DFT 的关键之一。
为了强调起见,常用表达式WN取代W 以便明确地给出Wnk 的周期为N。
由DFT 的定义可以看出,在x[n]为复数序列的情况下,完全可以直接运算N点DFT 需要(N ——1)2次复数乘法和N(N-1)次复数加法。
因此,对于一些相当大的N 值(如1024 点)来说,直接计算它的DFT 所需要的计算量是很大的。
一个优化的实数FFT 算法是一个组合以后的算法。
原始的2N 个点的实输入序列组合成一个N 点的复序列,然后对复序列进行N 点的FFT 运算,最后再由N 点复数输出拆散成2N 点的复数序列,这2N 点的复数序列与原始的2N 点的实数输入序列的DFT 输出一致。
FFT 的基本思想在于:将原来的N 点序列分成两个较短的序列,这些序列的DFT 可很简单地组合起来得到原序列的DFT。
例如,若N 为偶数,将原有的N 点序列分成两个(N/2)点序列,那么计算N 点DFT 将只需要约[(N/2)2*2]=N2/2次复数乘法。
即比直接计算少作一半乘法。
因子(N/2)2 表示直接计算(N/2)点DFT 所需要的乘法次数,而乘数2 代表必须完成两个DFT。
上述处理方法可以反复使用,即(N/2)点的DFT 计算也可以化成两个(N/4)点DFT(假定N/2 为偶数),从而又少作一半乘法。
使用这种方法,在组合输入和拆散输出的操作中,FFT 的运算量减半。
这样,利用实数FFT 算法来计算实输入序列的DFT 的速度几乎是一般复FFT 算法的两倍。
假定序列{x[n]}的点数N 是2 的幂,按上述处理方法,定义两个分别为x[n]的偶数项和基数项的(N/2)点序列x1[n]和x2[n],即:二.(汇编)主要程序分析程序由四个子程序组成:rfft-task: 主调用函数,调用其他子程序,实现统一的接口。
bit-rev: 实现输入数据的比特反转。
fft:实现N点复数FFT,FFT变换以同地址的方式完成。
在运算过程中,为了避免运算结果溢出,对每个蝶形的运算结果右移一位。
因为第一级和第二级蝶形运算不需要乘法,所以fft的实现可以分为三个功能块:第一级蝶形运算,第二级蝶形运算,第三级至logN级蝶形运算。
unpack: fft运算结果可以看做将原2N点实数的奇地址数据作N点复数的实部R,偶地址数据作N点复数的虚部I.利用FFT的对称性,可以由N点复数的FFT结果求R和I的FFT 结果。
再利用2N点实数的FFT变换和上述结果的关系得到最后的结果。
;rfft-taskK-DATA-IDX-1 .set 2 ;第一级运算时各组蝶形地址增量K-DATA-IDX-1 .set 4 ;第二级运算时各组蝶形地址增量K-DATA-IDX-1 .set 8 ;第三级运算时各组蝶形地址增量K-DATA-IDX-1 .set 4 ;第三级运算时每组蝶形的蝶形数.def rfft-task.asg AR1 ,FFT-TWID-P.sect “rfft-prg”Rff-task:STMRPTMVPDSTM #sin,FFT_TWID_PRPT #K_FFT_SIZE_1 ;将正弦表从程序区搬移到数据区MVPD #sine-table,*FFT_TWID_P+STM #cosn-table,*FFT_TWID_PRPT #K_FFT_SIZE_1 ;将余弦表从程序区搬移到数据区CALL bit-revCALL fftCALL unbackRET.def bit_rev.asg AR2,REORDERED_DA TA.asg AR3,ORIGINAL_INPUT.asg AR7,DATA_PROC_BUF.sect “rft_prg”Bit_rev:SSBX FRCT ;MVDK *(d-input-addr),ORIGINAL-INPUT ;AR3指向数据块首地址STM #fft-data,DATA-PROC-BUF ;AR7指向数据处理缓冲区首地址MVMM DATA-PROC-BUF,RERDERED-DATA;;AR2指向比特反转数据首地址STM #K-FFT-SIZE-1,BRCRPTBD bit-rev-end-1STM #K-FFT-SIZE-1,AR0 ;AR0=缓冲区大小的1/2MVDD *ORIGINAL-INPUT+,*REORDERED-DA TA+MVDD *ORIGINAL-INPUT+.*REORDERED-DA TA+MAR *ORGIGINAL-INPUT+0BBit-rev-end: ;返回实数FFT主模块RETFft.asg AR1,GROUP-COUNTER.asg AR2,PX.asg AR3,QX.asg AR4,WR.asg AR5,WI.asg AR6,BUTTERFLY-COUNTER.asg AR7,DATA-PROC-BUF ;for stage 1&2.asg AR7,STAGE-COUNTER ;for the remaining stages .SECT “rfft-prg’Fft:Stage 1STM #0,BK ;BK=0 SO THAT *ARN+0%=ARN+0 LD #-1,ASM ;每级输入除以二,避免溢出MVMM DATA-PROC-BUF,PX ;px送到prLD *PX,16,A ;A:=PRSTM #fft-data+K-DATA-IDX-1,QX ;QX送到qrSTM #K-FFT-SIZE/2-1,BRCRPTBD stagelend-1STM #K-DATA—IDX-1+1,AR0SUB *QX,16,A,B :B:=PR-QRADD *QX,16,A ;A:=PR+QRSTH A,ASM,*PX+ ;P R’:=(PR+QR)/2 ST B,QX+ ;QR’:=(PR-QR)/2||LD *PX,A ;A:=PISUB *QX,16,A,B ;B:=PI-QIADD *QX,16,A ;A:=PI+QISTH A,ASM,*PX+0 ;PI’:=(PI+QI)/2ST B,*QX+0% ;QI’:=(PI-QI)/2||LD *PX,A ;A:=NEXT PRStagelend:;stage 2MVMM DATA-PROC-BUF,PX ;PX送到PRSTM #fft-data+K-DATA-IDX-2,X ;QX送到QRSTM #K-FFT-SIZE/4-1,BRC ;LD *PX,16,A ;A:=PRRPBD stage2end-1STM #K-DATA-IDX-2+1,AR0;第一个蝶形SUB *QX,16,A,B ;B:=PR-QRADD *QX,16,A ;A:=PR+QRSTH A,ASM,*PX+ ;PR’:=(P R+QR)/2ST B,*QX+ ;QR’=(pr-qr)/2||LD *PX,A ;A:=PISUB *QX,16,A,B ;B:=PI-QIADD *QX,16,A ;A:=PI+QISTH A,ASM,*PX+ ;PI’:=(PI+QI)/2STH B,ASM,*QX+ ;QI’:=(PI-QI)/2;第二个蝶形MAR *QX+ADD *PX,*QX,A ;A:=PR+QISUB *PX,*QX,B ;B:=PR-QISTH A,ASM,*PX+ ;PR:=(pr+qi)/2SUB *PX,QX,A ;A:=PI-QRST B,*QX ;QR’:=(PI-QR)||LD *QX+,B ;B :==QRST A,*PX ;PI;=(PI-QR)/2||ADD *PX+0%,A ;A;=PI+QRST A,*QX+0% ;QI’=(PI+QR)/2||LD *PX,A ;A:=PRStage2end:;stage 3到stage logN-1STM #K-TWID-TBL-SIZE,BK ;BK=twiddle table size alwaysST #K-TWID-IDX-3,*(d-twid-dix) ;init index of twiddle tableSTM #K-TWID-IDX-3,AR0 ;AR0=index of twiddle tabbleSTM #COSINE,WR ;init WR pointerSTM #sine,WI ;init WI pointerSTM #K_LOGN-2-1,STAGE_COUNTER ;init stage counterST #K_FFT_SIZE/8-1,*9D_GRPS_CNT0 ;INIT GROUP COUNTERSTM ##K_fly_count_3_1,butterfly_counter;init index for input dataStage:STM #fft_data,px ;px->prLD *(d_data_idx),aADD *(px),aSTLM A,QX ;QX->QRMVDK *(_grps_cnt),group_counter ;ar1包含group counter groupRPTBD butterflyend-1LD *WR,TMPY *QX,AMACR WI,QX,AADD PX,16,A,BST B,PXSUB PX,BST B,QXMPY QX,AMASR QX,WR,AADD PX,16,A,BST B,QXSUB PX,BLD WR,TST B,PXMPY QX,AButterflyend: ;为下一组更新指针PSHM AR0MVDK *(d_data_idx),AR0Mar px+0 ;增加PX指针MAR QX+0 ;增加QX指针POPM ar0MAR QX-LD *(D_DA TA_IDX),ASUB 1,A,BSTLM B,BUTTERFLY_COUNTERSTL A,1, *(D_DA TA_IDX)LD *(d_grps_cnt),ASTL A,ASM, *(d_grps_cnt)LD *(d_twid_idx),ASTL A,ASM, *(d_twid_idx)MVDK *(d_twid_idx),AR0BANZ stage,*STAGE_COUNTER-Fft_end:RET ;返回实数FFT主模块;unpack.sect “rfft_prg”Unpack: :计算中间值RP,RM,IP,IM .asg AR2,XP_K.asg AR3,XP_NMINUSK.asg AR6,XM_K.asg AR7,XM, NMINUSKSTM #fft_data+2,XP_KSTM FFT_DATA+2*K_FFT_SIZE-2,XP_NMINUSKSTM FFT_DATA+2*K_FFT_SIZE+3,XM_NMINUSKSTM FFT_DATA+4*K_FFT_SIZE-1,XM_KSTM #-2+K_FFT_SIZE/2,BRCBPTBD phase3end-1STM #3,AR0ADD *XP_k,*XP_Nminusk,ASUB *XP_k,*XP_Nminusk,BSTH A,ASM,*XP_k+ ; 存储IP[K]到AR[K]STH A,ASM,*XP_ Nminusk +STH B,ASM,*XP_k-NEG BSTH AB,ASM,*XM_ Nminusk –ADD *XP_k,*XP_Nminusk,ASUB *XP_k,*XP_Nminusk,BSTH A,ASM,*XP_k+ ;存储IP[K]到AI[K]STH A,ASM,*XP-Numinusk-0 ;store IP[N-k]=IP[k] atAI[N-K] STH B,ASM,*XM-K- ;store IM[k] at AR[2R[2N-k] NEG B ;B:=I[N-k]-I[k]=2*IM[N-k]STH B,ASM,*XM-Nminusk+0 ;store IM[N-k] at AR[A-k]Phase3end:ST #0,*XM-K- ;RM[N/2]=0ST #0,*XM-K ;IM[N/2]=0;计算AR[0],AI[0],AR[N],AN[N].asg AR2,AX-K.asg AR4,IP-0.asg AR5,AX-NSTM #fft-data,AX-K ;AR2->AR[0] (TEMPRP[0])STM #fft-data+1,IP-0 ;AR4->AI[0] (tempIP[0])STM #fft-data+2*K-FFT-SIZE+1,AX-N ;AR->AI[N]ADD *AX,*IP-0,A ;A:=RP[0]+IP[0]SUB *AX-K,*IP-0,B ;B:=RP[0]-IP[0]STH A,ASM,*AX-K+ ;AR[0]=(RP[0]+IP[0])/2ST #0,*AX-K ;AI[0]=0MVDD *AX-K+,*AX-N- ;AI[N]=0STH B,ASM,*AX-N ;AR[N]=(RP[0]-IP[0])/2;计算最终输出值AR[K],AI[K].asg AR3,AX-2Nminusk.asg AR4,COS.asg AR5,SINSTM #fft-data+4*K-FFT-SIZE-1,AX-2Nminusk ;AR3->AI[2N-1(temp PM[1])]STM #cosine+K-TWID-TBL-SIZE/K-FFT-SIZE,COS ;AR4存到cos(k*pi/N)STM #sine+K-TWID-TBL-SIZE/K-FFT-SIZE,SIN ;ARF->sin(k*pi/N)STM #K-FFTSIZE-2,BRCRPTBD phase4end-1STM #K-TWID-TBL-SIZE/K-FFT-SIZE,AR0;index of twiddle tablesLD *AX-K+,16,A ;A:=RP[k] || AR2->IP[k]MACR *COS,*AX-K,A ;A:=A+cos(k*pi/N)*IP[k]MASR *SIN,*AX-2Nminusk-,A ;A:=A-sin(k*pi/N*N*RM[k]LD *AX-2Nminusk+,16,B ;B:=IM[K] ||AR3->RM[K]MASR *SIN+0%,*AX-K,B ;B :=B-sin(k*pi/N*IP[k]N)MASR *COS+0%,*AX-2Nminusk,B ; B:=B-sin(k*pi/*IP[k]N)STH A,ASM,*AX-K+ ;AR[K]=A/2STH B,ASM,*AX-K+ ;AI[K]=B/2NEG B ;B:=-B三.算法分析该程序是一个16-1024点基2实数FFT的TMS320C54x汇编程序。