模式识别上机作业[1]培训课件
- 格式:doc
- 大小:364.00 KB
- 文档页数:13





模式识别※第一章绪论§课前索引§1.1 模式识别和模式的概念§1.2 模式的描述方法§1.3 模式识别系统§1.4 有关模式识别的若干问题§1.5 本书内容及宗旨§本章小节§本章习题※第二章贝叶斯决策理论与统计判别方法§课前索引§2.1 引言§2.2 几种常用的决策规则§2.3 正态分布时的统计决策§本章小节§本章习题※第三章非参数判别分类方法§课前索引§3.1引言§3.2线性分类器§3.3 非线性判别函数§3.4 近邻法§3.5 支持向量机§本章小结§本章习题※第四章描述量选择及特征的组合优化§课前索引§4.1 基本概念§4.2 类别可分离性判据§4.3 按距离度量的特征提取方法§4.4 按概率距离判据的特征提取方法§4.5 基于熵函数的可分性判据§4.6 基于Karhunen-Loeve变换的特征提取§4.7 特征提取方法小结§4.8 特征选择§本章小节§本章习题※第五章非监督学习法§课前索引§5.1 引言§5.2 单峰子类的分离方法§5.3 聚类方法§5.4 非监督学习方法中的一些问题§本章小节§本章习题※第六章人工神经元网络§课前索引§6.1 引言§6.2 Hopfield模型§6.3 Boltzmann机§6.4 前馈网络§6.5 人工神经网络中的非监督学习方法§6.6 小结§本章习题第一章绪论本章要点、难点本章是这门课的绪言,重点是要弄清“模式识别”的名词含义,从而弄清这门课能获得哪方面的知识,学了以后会解决哪些问题。


![模式识别上机作业[1]](https://uimg.taocdn.com/4fbb1a9e69dc5022aaea006a.webp)
模式识别上机作业队别:研究生二队姓名:孙祥威学号:112082作业一:1{(0,0),(0,1)}ω=,2{(1,0),(1,1)}ω=。
用感知器固定增量法求判别函数,设1(1,1,1)w=,1kρ=。
写程序上机运行,写出判别函数,打出图表。
解答:1、程序代码如下:clc,clearw=[0 0 1;0 1 1;-1 0 -1;-1 -1 -1];W=[1 1 1];rowk=1;flag=1;flagS=zeros(1,size(w,1));k=0;while flagfor i=1:size(w,1)if isempty(find(flagS==0))flag=0;break;endk=k+1;pb=w(i,:)*W';if pb<=0flagS(i)=0;W=W+rowk*w(i,:);elseflagS(i)=1;endendendW,kwp1=[0 0;0 1;];wp2=[1 0;1 1];plot(wp1(:,1),wp1(:,2),'o')hold onplot(wp2(:,1),wp2(:,2),'*')hold ony=-0.2:1/100:1.2;plot(1/3*ones(1,size(y)),y,'r-') axis([-0.25 1.25 -0.25 1.25])2、判别函数。
计算得到增广权矢量为*(3,0,1)T w =-,故判别函数表达式为:1310x -+=3、分类示意图:图 1 感知器算法分类结果图作业二:在下列条件下,求待定样本(2,0)T x =的类别,画出分界线,编程上机。
1解答:经计算,两类的协方差矩阵不相等。
设12()()P P ωω=,计算时相关项直接略去。
1、计算时,参考书中P96页式(4-1-31)等。
程序代码如下:clc,clear,close all D1=[1,1,2;1,0,-1;]; D2=[-1,-1,-2;1,0,-1;]; u1=mean(D1,2); u2=mean(D2,2);c1=zeros(size(D1,1),size(D1,1)); for i=1:size(D1,2)c1=c1+D1(:,i)*D1(:,i)'; endc1=c1/size(D1,2)-u1*u1';c2=zeros(size(D2,1),size(D2,1)); for i=1:size(D2,2)c2=c2+D2(:,i)*D2(:,i)'; endc2=c2/size(D2,2)-u2*u2'; I=eye(size(c1,1),size(c1,1)); ic1=c1\I; ic2=c2\I; W1=-0.5*ic1; W2=-0.5*ic2; w1=ic1*u1;; w2=ic2*u2;;w10=-0.5*log(det(c1))-0.5*u1'*ic1*u1; w20=-0.5*log(det(c2))-0.5*u2'*ic2*u2; syms x1 x2; x=[x1;x2];fprintf('决策界面方程为:')D=x'*(W1-W2)*x+(w1-w2)'*x+(w10-w20); pretty(D)fprintf('(2,0)代入决策面方程的值为:') value=subs(D,{x1,x2},[2 0]) figure ezplot(D) hold onplot(D1(1,:),D1(2,:),'bo')plot(D2(1,:),D2(2,:),'ks') plot(2,0,'rp')运行结果显示,决策面方程为:11248180x x x -=。
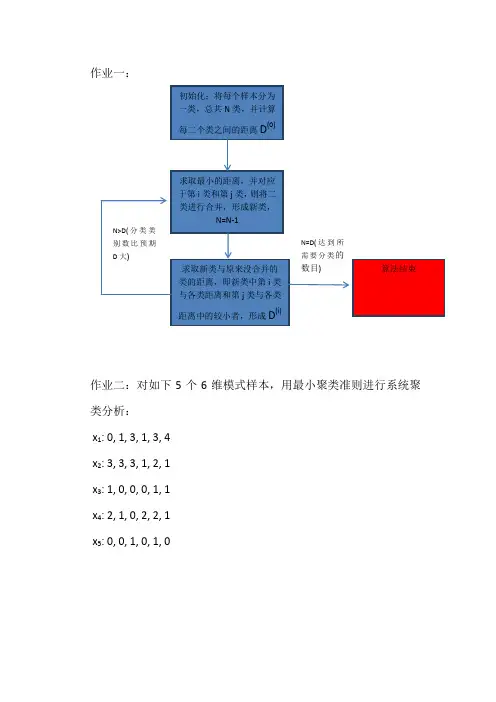
作业一:作业二:对如下5个6维模式样本,用最小聚类准则进行系统聚类分析: x 1: 0, 1, 3, 1, 3, 4 x 2: 3, 3, 3, 1, 2, 1 x 3: 1, 0, 0, 0, 1, 1 x 4: 2, 1, 0, 2, 2, 1 x 5: 0, 0, 1, 0, 1, 01、 计算D (0)=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛0 12 3 5 2612 0 7 15 243 7 0 24 55 15 24 0 2326 24 5 23 0,因为x3与x5的距离最近,则将x3与x5分为一类。
同时可以求出x1,x2,x4与x3,5的距离,如x1到x3,5的距离为x1到x3的距离与x1与x5的距离中取最小的一个距离。
2、 则D (1)=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛0 7 15 2470 24 515 24 0 2324 5 23 0,同样现在该矩阵中x4与x3,5的距离最近,则可以将x3,4,5分为一类,这样分类结束,总共可以将x1,x2,x3,x4,x5分为三类,其中:x1为第一类;x2为第二类;x3和x4和x5为第三类。
• 作业三:(K-均值算法)• 选k=2,z 1(1)=x 1,z 2(1)=x 10,用K-均值算法进行聚类分析由图可以看出这二十个点的坐标:x1(0,0),x2(1,0),x3(0,1),x4(1,1),x5(2,1),x6(1,2),x7(2,2),x8( 3,2),x9(6,6),x10(7,6),x11(8,6),x12(6,7),x13(7,7),x14(8,7),x 15(9,7),x16(7,8),x17(8,8),x18(9,8),x19(8,9),x20(9,9)。
1、选2个初始聚类中心,z1(1)=x1,z2(1)=x10.2、求取其它十八个点分别到x1与x10的距离:x2到x1的距离为1;x2到x10的距离为6x3到x1的距离为1;x3到x10的距离为x4到x1的距离为;x4到x10的距离为x5到x1的距离为;x5到x10的距离为5x6到x1的距离为;x6到x10的距离为x7到x1的距离为2;x7到x10的距离为x8到x1的距离为;x8到x10的距离为4x9到x1的距离为6;x9到x10的距离为1x11到x1的距离为10;x11到x10的距离为1x12到x1的距离为;x12到x10的距离为x13到x1的距离为7;x13到x10的距离为1x14到x1的距离为;x14到x10的距离为x15到x1的距离为;x15到x10的距离为x16到x1的距离为;x16到x10的距离为2x17到x1的距离为8;x17到x10的距离为x18到x1的距离为;x18到x10的距离为2x19到x1的距离为;x19到x10的距离为x20到x1的距离为9;x20到x10的距离为所以其中x2到x8距离x1近些,则可以将x2到x8与x1分为一类,而x9与x11到x20与x10分为另一类;3、通过将第一类中的所有x1到x8的坐标求取平均来计算该类别的中心坐标,求取新的类别的中心坐标z1(2)= (5/4,9/8),同理可以求出另一类的中心坐标z2(2)= (92/12,22/3)4、然后重新计算各点距离这二点中心坐标的距离,最后可以得出x1到x8仍然为第一类,x9到x20仍然为第二类。


模式识别上机作业队别:研究生二队姓名:孙祥威学号:112082作业一:1{(0,0),(0,1)}ω=,2{(1,0),(1,1)}ω=。
用感知器固定增量法求判别函数,设1(1,1,1)w=,1kρ=。
写程序上机运行,写出判别函数,打出图表。
解答:1、程序代码如下:clc,clearw=[0 0 1;0 1 1;-1 0 -1;-1 -1 -1];W=[1 1 1];rowk=1;flag=1;flagS=zeros(1,size(w,1));k=0;while flagfor i=1:size(w,1)if isempty(find(flagS==0))flag=0;break;endk=k+1;pb=w(i,:)*W';if pb<=0flagS(i)=0;W=W+rowk*w(i,:);elseflagS(i)=1;endendendW,kwp1=[0 0;0 1;];wp2=[1 0;1 1];plot(wp1(:,1),wp1(:,2),'o')hold onplot(wp2(:,1),wp2(:,2),'*') hold ony=-0.2:1/100:1.2;plot(1/3*ones(1,size(y)),y,'r-') axis([-0.25 1.25 -0.25 1.25])2、判别函数。
计算得到增广权矢量为*(3,0,1)T w =-,故判别函数表达式为:1310x -+=3、分类示意图:图 1 感知器算法分类结果图作业二:在下列条件下,求待定样本(2,0)T x =的类别,画出分界线,编程上机。
1、二类协方差相等;2、二类协方差不等。
训练样本号k 1 2 3 1 2 3 特征1x1 1 2-1 -1 -2解答:经计算,两类的协方差矩阵不相等。
设12()()P P ωω=,计算时相关项直接略去。
1、计算时,参考书中P96页式(4-1-31)等。
程序代码如下:clc,clear,close all D1=[1,1,2;1,0,-1;]; D2=[-1,-1,-2;1,0,-1;]; u1=mean(D1,2); u2=mean(D2,2);c1=zeros(size(D1,1),size(D1,1)); for i=1:size(D1,2)c1=c1+D1(:,i)*D1(:,i)'; endc1=c1/size(D1,2)-u1*u1';c2=zeros(size(D2,1),size(D2,1)); for i=1:size(D2,2)c2=c2+D2(:,i)*D2(:,i)'; endc2=c2/size(D2,2)-u2*u2'; I=eye(size(c1,1),size(c1,1)); ic1=c1\I; ic2=c2\I; W1=-0.5*ic1; W2=-0.5*ic2; w1=ic1*u1;; w2=ic2*u2;;w10=-0.5*log(det(c1))-0.5*u1'*ic1*u1; w20=-0.5*log(det(c2))-0.5*u2'*ic2*u2; syms x1 x2; x=[x1;x2];fprintf('决策界面方程为:')D=x'*(W1-W2)*x+(w1-w2)'*x+(w10-w20); pretty(D)fprintf('(2,0)代入决策面方程的值为:') value=subs(D,{x1,x2},[2 0]) figure ezplot(D)hold onplot(D1(1,:),D1(2,:),'bo') plot(D2(1,:),D2(2,:),'ks') plot(2,0,'rp')运行结果显示,决策面方程为:11248180x x x -=。
2、计算结果。
从程序运行结果可以看出,(2,0)T x =带入决策界面方程值为96,可见属于第一类1ω。
见下图:图2 两类协方差不等分类结果图图中,黑色方块为第二类2ω,蓝色圆圈为第一类1ω,红色五角星即为要判断类别的(2,0)T x =。
绿色交叉的两条直线即为决策面曲线。
左上和右下为第一类,右上和左下为第二类。
作业三:有训练集资料矩阵如下表所示,现已知,9N =、1233N N N ===、2n =、3M =,试问,(2,2)T X =-应属于哪一类? 训练样本号k 1 2 3 1 2 3 1 2 3 特征1x0 2 1-1 -2 -20 0 1三类的分界线。
解答:经计算,三类的协方差矩阵不相等。
设123()()()P P P ωωω==,计算时相关项直接略去。
1、计算时,参考书中P96页式(4-1-31)等。
程序代码如下:clc,clear,close all D1=[0 2 1;0 1 0;]; D2=[-1 -2 -2;1 0 -1;]; D3=[0 0 1;-2 -1 -2]; X=[-2 2]; u1=mean(D1,2); u2=mean(D2,2); u3=mean(D3,2);c1=zeros(size(D1,1),size(D1,1)); for i=1:size(D1,2)c1=c1+D1(:,i)*D1(:,i)'; endc1=c1/size(D1,2)-u1*u1';c2=zeros(size(D2,1),size(D2,1)); for i=1:size(D2,2)c2=c2+D2(:,i)*D2(:,i)'; endc2=c2/size(D2,2)-u2*u2';c3=zeros(size(D3,1),size(D3,1)); for i=1:size(D3,2)c3=c3+D3(:,i)*D3(:,i)'; endc3=c3/size(D3,2)-u3*u3'; I=eye(size(c1,1),size(c1,1)); ic1=c1\I; ic2=c2\I; ic3=c3\I; W1=-0.5*ic1; W2=-0.5*ic2; W3=-0.5*ic3; w1=ic1*u1; w2=ic2*u2;w3=ic3*u3;w10=-0.5*log(det(c1))-0.5*u1'*ic1*u1;w20=-0.5*log(det(c2))-0.5*u2'*ic2*u2;w30=-0.5*log(det(c3))-0.5*u3'*ic3*u3;syms x1x2real;x=[x1;x2];D12=x'*(W1-W2)*x+(w1-w2)'*x+(w10-w20);D13=x'*(W1-W3)*x+(w1-w3)'*x+(w10-w30);D23=x'*(W2-W3)*x+(w2-w3)'*x+(w20-w30);fprintf('一、二类决策界面方程为:')pretty(D12)fprintf('一、三类决策界面方程为:')pretty(D13)fprintf('二、三类决策界面方程为:')pretty(D23)DD1=x'*W1*x+w1'*x+w10;DD2=x'*W2*x+w2'*x+w20;DD3=x'*W3*x+w3'*x+w30;value=[];fprintf(['(' num2str(X(1)) ',' num2str(X(2)) ')代入1-2决策面方程的值为:'])v1=subs(DD1,{x1,x2},X)fprintf(['(' num2str(X(1)) ',' num2str(X(2)) ')代入1-3决策面方程的值为:'])v2=subs(DD2,{x1,x2},X)fprintf(['(' num2str(X(1)) ',' num2str(X(2)) ')代入2-3决策面方程的值为:'])v3=subs(DD3,{x1,x2},X)V=[v1 v2 v3];fprintf(['可见('num2str(X(1)) ','num2str(X(2)) ')属于第'num2str(find(V==max(V))) '类。
\n'])figurehold onh=ezplot(D12);set(h,'Color','r')h=ezplot(D13);set(h,'Color','b')h=ezplot(D23);set(h,'Color','y')plot(D1(1,:),D1(2,:),'ko')plot(D2(1,:),D2(2,:),'ks')plot(D3(1,:),D3(2,:),'kp')plot(X(1),X(2),'r*')title('分界线及样本点分布')1-2类决策面方程为:221211229633618240140737488355328x x x x x x -+--+=1-3类决策面方程为:2121226612660x x x x x ++-+=2-3类决策面方程为:222121122512627241802251799813685248x x x x x x ---+-=2、计算结果。
从程序运行结果可以看出,(2,0)T x =带入三个判决函数(略去()i P ω相关项)计算的值分别为-95.3521、-17.3521、-29.3521,可见属于第二类2ω。
分类界面参见下图:图3 三类协方差不等分类结果图作业四:样本1 2 3 4 5 6 7 8 1x 0 2 1 5 6 5 6 7 2x2133445解答:1、程序代码如下:clc,clear,close allExampleData=[0,0,2,2,4,4,5,6,6,7,-4,-2,-3,-3,-5,1,0,0,-1,-1,-3; 6,5,5,3,4,3,1,2,1,0,3,2,2,0,2,1,-1,-2,-1,-3,-5;]; Data=[0,2,1,5,6,5,6,7;0,2,1,3,3,4,4,5;];N=size(Data,2);Data=[1:N;Data];G1=Data;G2=[];N1=size(G1,2);N2=size(G2,2);X1=mean(G1,2);X1=X1(2:end);X2=[0;0];E=N1*N2/N*(X1-X2)'*(X1-X2);RE=[];ZY=[];LE=E;while LE<=ELE=E;n1=size(G1,2);e1=[];for i=1:n1g1=G1;g2=G2;g2=[g2 g1(:,i)];g1(:,i)=[];nn1=size(g1,2);nn2=size(g2,2);x1=mean(g1,2);x1=x1(2:end);x2=mean(g2,2);x2=x2(2:end);ee1=nn1*nn2/N*(x1-x2)'*(x1-x2);e1=[e1;ee1];endE=max(e1);RE=[RE;E];I=find(e1==E);nzy=G1(1,I);ZY=[ZY;nzy];if LE<=EG2=[G2 G1(:,I)];G1(:,I)=[];endendRE=[(1:length(RE))' ZY RE]figureplot(G1(2,:),G1(3,:),'o')hold onplot(G2(2,:),G2(3,:),'*')2、对分法聚类结果。